1 Introduction

With the development of portable and mobile systems, the question of how to supply long-term power for these systems becomes an important issue. The microgas turbine engine is one of promising solutions to provide long-term and high-density power sources. In a microsystem such as the microgas turbine engine, air bearings play an increasingly important role because air bearings are a better and more feasible alternative to the conventional ball bearings and oil-lubricated fluid bearings (Piekos 2000; Savoulides et al. 2001). Due to the consequences of scaling downsizing as well as the current limitations in microfabrication technologies, the performance of air bearings used in microsystems has still to be investigated.

Piekos (2000) investigated the performance of a short journal air bearing in a microturbine system. Savoulides et al. (2001) proposed a low order model to analyze the performance of a hybrid gas bearing. With the selected stiffness and damping coefficients, the motion stability of a journal bearing was analyzed. However, the analysis of a whole micro air bearing system including both journal and thrust bearings is rare.

In this paper, the motion stability of the thrust bearing is analyzed using a simplified model developed by Constantinscu and Galetuse (1987, 1990). It is found that the motion stability and load capacity have contradictive requirements on the groove patterns of the thrust air bearing. The requirements on both the load capacity and stability should, therefore, be considered in order to obtain a practically balanced thrust bearing.

The dynamic performance of a journal air bearing with a low aspect ratio (L/D < 0.1) is studied. Due to the small value of L/D, the compressibility of the air bearing is not readily observed; its load capacity increases linearly with its bearing number that is an indicator of rotational speed. The investigation also reveals that the shock tolerance in the radial direction of the journal air bearing increases with its bearing number Λ, that is, the bearing system demonstrates an increasing shock tolerance capacity when its rotational speed is increased. The shock tolerance also increases with the bearing aspect ratio of L/D, and its initial equilibrium eccentricity ratio ε 0.

2 Governing equation

The governing equation for air bearings (Hamrock 1994) is expressed as below.

$$ \frac{\partial } {{\partial x}}{\left( {ph^{3} \frac{{\partial p}} {{\partial x}}} \right)} + \frac{\partial } {{\partial z}}{\left( {ph^{3} \frac{{\partial p}} {{\partial z}}} \right)} = 6R\mu \omega \frac{{\partial {\left( {ph} \right)}}} {{\partial x}} + 12\mu \frac{{\partial {\left( {ph} \right)}}} {{\partial t}}, $$
(1)
$$ h = C{\left( {1 + \varepsilon \cos \,\theta } \right)} + g{\left( {x,z} \right)}\quad {\text{for a journal bearing,}} $$
(2a)
$$ h = C + g{\left( {x,z} \right)}\quad {\text{for a thrust bearing,}} $$
(2b)

and

$$ g{\left( {x,z} \right)} = \left\{ \begin{aligned}{} & h_{{\text{g}}} {\text{, in groove region,}} \\ & 0,{\text{ on ridge region}}{\text{.}} \\ \end{aligned} \right. $$
(3)

The boundary conditions are:

$$ p = p_{{\text{a}}} {\text{, at }}z = 0,{\text{ }}z = l\;{\text{\& }}r = r_{i} ,{\text{ }}r = r_{e} {\text{, }} $$
(4a)
$$ p{\left( \theta \right)} = p{\left( {\theta + 2\pi } \right)}{\text{, }} $$
(4b)

where p is the pressure, h the height of fluid film, R the radius, μ the viscosity, ω the angular speed, C the bearing clearance, ε the eccentricity ratio with ε = e/C, h g the groove depth, p a the ambient pressure, and l is the journal bearing length. r i and r e stand for the inner- and outer-radii of the thrust air bearing, respectively.

In the static state, the second term on the right-hand side of Eq. 1 becomes zero; the system condition can, therefore, be expressed as P = P(ω). In the dynamic state, let ω (n+1)= ω (n)+Δω (n+1), and P (n+1) = P (n)+ΔP (n+1), then Eq. 1 is linearized by the incremental variational method. Discretizing the linearized equation with Galerkin methods gives the following finite element equation:

$$ {\left[ {A_{{i,j}} } \right]}{\left\{ {\Delta P_{i} } \right\}}^{{(n + 1)}} = {\left\{ {D_{j} } \right\}}^{{(n)}} . $$
(5)

Equation 5 can be solved by increasing the angular velocity step-by-step until the specified speed is reached, so that the pressure distribution and other dynamic characteristics can be obtained (Zhang et al. 2005).

3 Load capacity

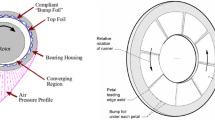
Figure 1 shows the schematic of a micro air bearing system to be investigated. The limitation in the dimension of a microdevice results in a very low aspect ratio of its bearing length versus diameter (L/D) comparing with conventional journal bearings. Therefore, the journal bearings in these microdevices are usually plain journal bearings only. The load capacity of journal bearings with different aspect ratios is explored. Figure 2 shows the non-dimensional load capacity versus bearing number Λ of journal bearings at different aspect ratios of L/D = 0.075 (dashed line) and 0.0438 (solid line), where the bearing number Λ?is defined as Λ=6μωR 2/(p a C 2) and p a = 1.0135 × 105 Pa. It is observed that, in the cases of these two short bearings, the non-dimensional load capacity almost linearly increases with its bearing numbers, and the load capacity also increases with the aspect ratio of L/D. Up to Λ = 40, the effect of air compressibility is not obvious, as shown in Fig. 2.

Fig. 1
figure 1

Schematic drawing of the micro air bearing. a Section view; b parameters and groove distribution of the dynamic thrust bearing

Full size image
Fig. 2
figure 2

Load capacity versus bearing numbers of plain journal bearings

Full size image

The dynamic characteristics of thrust air bearings are also studied. It is found that the load capacity of a thrust air bearing increases linearly with its bearing number Λ. Besides the bearing number Λ??the effects of other parameters on the load capacity of the thrust bearing are shown in Fig. 3a–d. Figure 3a shows that the load capacity of a thrust air bearing increases with its groove number of N g. From N g = 6 to15, the load capacity increases quickly as a function of the groove numbers. For larger groove numbers, this increase slows down and gradually becomes flat. The effect of the groove angle α on the load capacity is illustrated in Fig. 3b. As can be seen from the figure, the peaks in the load capacity curve moves upwards as the groove numbers increase from N g = 8 to 30. The effect of the groove depth ratio G d on the load capacity is shown in Fig. 3c. The groove depth ratio G d is defined as G d = h g/A c, with h g and A c being the groove depth and axial clearance, respectively. Figure 3d illustrates the effect of the groove width ratio a g, which is defined as a g = W g/(W g + W r), as illustrated in Fig. 1.

Fig. 3
figure 3

Dynamic load capacity of the thrust bearing against various parameters. a Load capacity versus groove numbers; b load capacity versus groove angles; c load capacity versus groove depth ratio; d load capacity versus groove width ratio

Full size image

4 Motion stability

The motion stability of a thrust air bearing is a critical problem for applications of air bearings in microdevices. In this section, the motion stability is analyzed with a simplified formula developed by Constantinscus and Galetuse (1987, 1990). A dimensionless parameter called the compressibility number Λc = 3μωr 2 e /(p a A 2 c ) is used to determine the stability of a thrust bearing. When the value of Λc is smaller than a critical value Λ*, the thrust air bearing is considered to be working in a stable state, otherwise it is unstable. Figure 4a–d show the results of the stability analysis. Figure 4a shows the critical compressibility Λ* versus the groove depth ratio G d (G d = h g/A c) at different groove angles. The smallest Λ* occurs at different values of G d for different values of the groove angle α. For α ? (° the minimum Λ* is 10.94 at G d = 4.5; and the minimum Λ* appears at smaller value of G d with the increase of α. Figure 4b demonstrates the load capacity versus the groove depth ratio G d at different groove angles Comparing Fig. 4a, b, it is noticed that the minimum Λ* occurs close to the point where the maximum load capacity is achieved. For example, the maximum value of W/Λc is at G d = 5.0 for α = 9°, which is very close to the minimum point of Λ*, as shown in Fig. 4a. Figure 4c shows the result of the critical compressibility Λ* versus groove width ratio a g. It is found that Λ* simply decreases with the increase in a g. Figure 4d illustrates the effect of the grooved area ratio R m (R m  = r m /r e ), which stands for the ratio of the grooved area versus the total area of a thrust air bearing. Figure 4d shows saddle points for different values of R m at different values of α. Similar to the situation in Fig. 4a, b, the maximum load capacity occurs close to the point where the minimum value of Λ* is found, which means that the stability and load capacity have contradictive requirements on the parameters that determine the groove pattern.

Fig. 4
figure 4

Motion stability of thrust bearings against various parameters

Full size image

Based on the above investigation, the optimum parameters for a thrust air bearing with spirally grooved patterns can be recommended as: N g = 15, α = 14°, G d = 3.5, a g = 0.5, R m  = 0.7, and λ = 0.5, where λ = r i /r e . With the selected optimum parameters, when a device with an axial clearance of A c = 10 μm is rotating at 1,000,000 rpm, the thrust bearing has the following dynamic performance: load capacity W = 0.63 N, stiffness K = 2.12 × 105 N/m, damping coefficient D = 0.95 N s/m, and power consumption P = 6.19 W. The stability analysis shows that the actual compressibility number Λc = 9.61, which means Λc < Λ* = 16.57. The thrust air bearing is, therefore, considered to be stable.

5 Shock tolerance

The shock tolerance of a journal air bearing is an important performance indicator for a microsystem. A shock can be induced by dropping, aerodynamic buffeting, or external vibration. The impulsive load caused by a shock will results in two different types of failures. The first failure type is that the shock force surpasses the load capacity of the air bearing and causes the rotor to hit the wall. The second type is that the shock load reduces the motion stability, causes the whirling of the air bearing, and eventually causes the rotor to contact the wall. Due to the very short duration of most shocks, the second type of shock failure seldom occurs. The first type of shock tolerance is, therefore, investigated in this section.

Assuming that a shock with an acceleration of a s is acting in the direction of the bearing normal load, which is in the radial direction of the rotor (Fig. 5), the work produced by the resultant force during this shock can be defined as below.

Fig. 5
figure 5

Schematic drawing to illustrate the radial shock and eccentricity

Full size image
$$ \begin{aligned}{} & E = {\int\limits_{e_{0} }^{e_{1} } {{\left( {ma_{{\text{s}}} + w_{0} - w_{{\text{b}}} } \right)}{\text{d}}e = C} }{\int\limits_{\varepsilon _{0} }^{\varepsilon _{1} } {{\left( {ma_{{\text{s}}} + w_{0} - w_{{\text{b}}} } \right)}{\text{d}}\varepsilon } } \\ & = C{\left[ {{\left( {\varepsilon _{1} - \varepsilon _{0} } \right)}{\left( {ma_{{\text{s}}} + w_{0} } \right)} - {\int\limits_{\varepsilon _{0} }^{\varepsilon _{1} } {{\left( {w_{{\text{b}}} } \right)}{\text{d}}\varepsilon } }} \right]}, \\ \end{aligned} $$
(6)

where m is the mass of the rotor, ω 0 the applied static load, ω b the bearing response force during shock, C the bearing clearance, ε the eccentricity ratio with ε = e/C, and e is the eccentricity of rotor. Before the bearing touches the wall, the net work E is zero. Hence,

$$ A_{{\text{s}}} = \frac{1} {{mg{\left( {\varepsilon _{1} - \varepsilon _{0} } \right)}}}{\int\limits_{\varepsilon _{0} }^{\varepsilon _{1} } {{\left( {w_{{\text{b}}} } \right)}{\text{d}}\varepsilon } } - \frac{{w_{0} }} {{mg}}. $$
(7)

Let

$$ w_{{\text{b}}} = w_{{{\text{b}}_{0} }} + {\left( {\frac{{{\text{d}}w}} {{{\text{d}}\varepsilon }}} \right)}_{{\varepsilon _{0} }} {\text{d}}\varepsilon, $$

because of \( w_{{{\text{b}}_{{\text{0}}} }} = w_{0} \) then Eq. 7 can be expressed as below.

$$ A_{{\text{s}}} = \frac{1} {{2M_{g} }}{\left( {\varepsilon _{1} - \varepsilon _{0} } \right)}{\left( {\frac{{{\text{d}}W}} {{{\text{d}}\varepsilon }}} \right)}_{{\varepsilon _{0} }} , $$
(8)

where A s = a s /g, M g  = mg/W 0 , W = w/W 0, and W 0 = 2RLp a = DLp a.

A dimensionless parameter A s M g is defined as the normalized bearing shock tolerance. Figure 6 shows the shock tolerance A s M g versus the initial eccentricity ratio ε 0 for a journal bearing of L/D = 0.075 at bearing number Λ = 5. The end eccentricity ε 1 is defined as ε 1 = 0.995, which means that the journal bearing almost touches the bearing wall. In Fig. 6, curve 1 shows the shock tolerance calculated using Eq. 8, which uses the stiffness at the initial point ε 0; while curve 2 shows the result obtained by integrating Eq. 7, which employs variable stiffness; and curve 3 is the result using the average value of stiffness at the starting and ending points. It is observed that the model using the starting point stiffness for curve 1 underestimated the shock tolerance; the average stiffness model for curve 3, however, overestimated the shock tolerance, comparing with the variable stiffness model used for curve 2. Although it is much easier to calculate the shock tolerance with the fixed-point model, the variable stiffness model needs, therefore, to be used for accurate prediction of the shock tolerance for a journal air bearing.

Fig. 6
figure 6

Shock tolerance of journal bearings at different conditions

Full size image

The effect of bearing number Λ on the shock tolerance is investigated in this section using variable stiffness. The results are shown in Fig. 7a, b for the aspect ratios of L/D = 0.075 and 0.0483, respectively. It is observed that a higher shock tolerance is obtained at a higher aspect ratio L/D, because a journal bearing, which has higher aspect ratio L/D, has higher values of load capacity and stiffness. Therefore, it has a higher shock resistant capacity. Figure 7a, b also show that the higher shock tolerance can be obtained with higher value of the bearing number if the rotation starts from the same initial eccentricity ratio ε 0. This means that the shock tolerance will increase with the rotational speed, provided all geometric parameters are kept unchanged. By using the results illustrated in Fig. 7a, b, the shock tolerance of a bearing system can be easily calculated. For example, the prototype of a bearing system shown in Fig. 7b has following parameters: D = 8.28 mm, L = 0.4 mm, L/D = 0.0483, and m = 5.26 × 10−2 g. When the radial clearance of C is 10 μm and the bearing system rotates at 1,000,000 rpm, the bearing number Λ is around 20. Its shock tolerance is, therefore, estimated as 100 g at the initial eccentricity ratio of ε 0 = 0.5. A reduced radial clearance C will increase its shock tolerance. For instance, even at the rotation speed of 250,000 rpm, the air bearing would be capable of resisting 100 g of shock with the initial eccentricity ratio of ε 0 = 0.5, provided its radial clearance C is reduced to 5 μm.

Fig. 7
figure 7

Shock tolerance of journal air bearings with different bearing numbers. a For a journal bearing with L/D = 0.075; b for a journal bearing with L/D = 0.0483

Full size image

A prototype of turbine device has been realized using the recommended bearing configurations with a journal length of L = 0.4 mm and an aspect ratio of L/D = 0.0483. Due to the limitation of manufacturing capability, the radial clearance C is ∼20 μm. The primary tests of this prototype demonstrate that a stable operation of 15,000 rpm has been achieved.

6 Conclusions

This paper investigated the dynamic performance of micro air bearings in microsystems, including journal and thrust air bearings. It is found that the load capacity of the journal air bearing with low aspect ratio (L/D < 0.1) is linearly proportional to its bearing number, and increasing the ratio L/D will increase its load capacity. The compressibility of the journal bearing is not obviously observed due to the small aspect ratio of L/D. It is also found that the shock tolerance increases with its bearing number, the aspect ratio L/D and the initial equilibrium eccentricity ratio ε 0. For dynamic thrust air bearings, the load capacity, and stability have contradictive requirements on the parameters that determine the pattern of the spiral grooves of the thrust bearings. The investigation also illustrates that a high load capacity design of a thrust bearing will possibly result in an unstable working condition. Therefore, both load capacity and stability should be considered and balanced in the air bearing design.