1 Introduction

Most phenomena in nature are inherently nonlinear, and many of these nonlinear phenomena can be represented by nonlinear equations. Nonlinear equations can be encountered frequently in science, mathematics, engineering and many other fields, and effectively finding the solutions of nonlinear equations becomes a considerable hot spot in academia and industry [1,2,3,4,5,6]. Figure 1 is a 3D surface diagram of solution for the second-order dynamic nonlinear equation (g(x) = 0.1x2−0.1 x −1.2), and Fig. 2 is a 3D surface diagram of solution for the third-order dynamic nonlinear equation (g(x(t),t) = 0.01(x−cos2t)(x−cos2t-5)(x+cos2t+5)). As shown in Figs. 1, 2, the solutions of the two equations are real time and dynamic. In the past decades, the Newton iteration method in the numerical analysis has been commonly used to find the solutions of NE [7,8,9,10,11]. However, the Newton iteration method also has many shortcomings. For example, the Newton iteration method is a local convergence, and the Heisen matrix must be invertible [12]. In order to improve the Newton iterative for solving DNE, many improved Newton-like iterations have been proposed [13,14,15,16,17,18].

Fig. 1
figure 1

Dynamic solution of the second-order dynamic nonlinear equation

Full size image
Fig. 2
figure 2

Dynamic solution of the third-order dynamic nonlinear equation

Full size image

Recurrent neural network (RNN) as a kind of deep learning method and its intrinsic advantages of GPU parallel computing [22, 23] is widely used in many fields [3, 19,20,21]. As two kinds of classic typical RNNs, the gradient-based neural network (GNN) and zeroing neural network (ZNN) developed quickly in recent years. GNN is designed as a neural network evolving along the negative gradient-descent direction to make the error norm decrease to zero with time [24]. Based on the existing RNN and GNN, the ZNN was proposed by Zhang et al. [25]. Because of its better robustness and convergence performance [26], ZNN has attracted more and more attention in dealing with time-varying problems. The robustness and convergence of ZNN model are affected by different AFs [27]. Considering these facts, various novel AFs are proposed to improve its convergence speed [28,29,30,31,32,33].

In the previously reported ZNN models, many studies focused on how to find the solution of the time-varying matrix equations, and they did not consider the robustness of the model. In actual applications, many models are disturbed by noise, and their efficiency and accuracy are seriously deteriorated by noise and disturbance. To overcome interference, many scholars have also studied the robustness of the ZNN model. For example, a NTZNN model is proposed in [34,35,36], which works appropriately under various interferences. However, its convergence time is not controllable, and its robustness still needs to be improved. A robust nonlinear zeroing neural network (RNZNN) is presented in Ref. [28], which enables the ZNN model to converge in fixed time. Therefore, the ability for real-time computation and robustness of the ZNN model is further enhanced.

In this paper, a BFCZNN with a new AF for finding the real-time solution of DNE is proposed. The proposed BFCZNN model further improves the convergence speed and robustness of the recently reported RNZNN model [28], and its feasibility and superiority are verified by simulated and experimental verification. The main work of this paper is summarized in the following.

A new AF is applied to the proposed BFCZNN model for solving DNE.

The proposed BFCZNN model has faster convergence speed and better robustness than the original ZNN model, and its convergence and robustness are verified by theoretical analysis and numerical verification.

Two robot path tracking examples by noise are applied for its further applications.

2 Problem formulation

2.1 The model of DNE

DNE problems can be summarized in mathematics as follows:

$$ f(x(t),t) = 0\begin{array}{*{20}c} {} & { \in R} \\ \end{array} $$
(1)

where t is the time, x(t) is the unknown dynamic parameter and f(•) is the nonlinear AF. Our purpose is to find the theoretical solution x*(t) of DNE (1) with the proposed BFCZNN model in fixed time. In order to achieve this purpose, we suppose DNE (1) at least has one solution. In addition, the construction of original ZNN for solving DNE (1) is introduced in the following part.

2.2 Zeroing neural network (ZNN)

First, according to the expression of (1), a dynamic error function e(t) is adopted as:

$$ f(x(t),t) = e(t). $$
(2)

Here, if e(t) converges to zero, the state parameter x(t) will satisfy f(x(t), t) = 0. Solving the DNE (1) is equivalent to make the error function e(t) converge to zero.

Second, according to the method in [25], the expression of DNE (1) problem solved by ZNN model is as follows:

$$ \frac{{d{\text{e}}(t)}}{dt} = - \gamma \psi \left( {{\text{e}}(t)} \right) $$
(3)

where γ > 0 is a adjustable parameter and ψ(•) is an activation function (AF).

Let us perform time differentiation on both sides of equation (2)

$$ \frac{de(t)}{{dt}} = \frac{\partial f}{{\partial x}} \times \frac{\partial x}{{\partial t}} + \frac{\partial f}{{\partial t}} $$
(4)

At last, substituting equation (3) into (4), the ZNN model is realized as:

$$ \frac{\partial f}{{\partial x}}\mathop x\limits^{ \bullet } (t) = - \gamma \psi (f(x(t),t)) - \frac{\partial f}{{\partial x}}. $$
(5)

It has been proved that the ZNN model (5) is stable with any monotonically increasing odd AF [3, 21], and choosing different AFs will lead to different convergence performances and robustness of the ZNN model. The commonly used AFs and the recently reported new AF in the robust nonlinear zeroing neural network (RNZNN) [28] are listed in Table 1.

Table 1 Different AFs
Full size table

In the table, 1 > p > 0, ξ 1 > 0, ξ 2 > 0, η> 0, ω > 0 and sgnn (·) is defined as:

$$ \text{sgn} ^{n} \left( x \right) = \left\{ \begin{gathered} \hfill \left| x \right|^{n} \begin{array}{*{20}c} , & {x > 0} \\ \end{array} \\ \hfill 0\begin{array}{*{20}c} , & {x = 0} \\ \end{array} \\ \hfill - \left| x \right|^{n} \begin{array}{*{20}c} , & {x < 0} \\ \end{array} \\ \end{gathered} \right\} $$
(6)

The convergence performance of ZNN model(5) can be significantly influenced by adopting different AFs ψ(•), e.g., if the ZNN model (5) choosing LAF and PSAF will converge exponentially [3]; if the ZNN model (5) choosing SBPAF will converge in finite time [21]; and if the NAF in [28] is adopted, the RNZNN model will converge in fixed time [28]. Although the RNZNN with NAF in ref. [28] can converge in fixed time, its convergence speed and robustness can be further improved.

3 Analysis of BFCZNN model

Generally, we want a neural network to converge as fast as possible. Moreover, any neural network will be affected by external noise, so the convergence performance and robustness are two important indicators of a neural network.

Based on the existing AFs in the previous works, a new AF is obtained as follows:

$$ \phi (x) = w_{1} \exp \left( {\left| x \right|^{p} } \right)\left| x \right|^{1 - p} {\text{sgn}} (x)/p + \left( {w_{2} \left| x \right|^{q} + w_{3} \left| x \right|^{\frac{1}{q}} } \right){\text{sgn}} (x) $$
(7)

where 1>p>0, 1>q>0, p ≠ q, w1 > 0, w2 > 0, w3 > 0.

Then, the proposed BFCZNN model for solving DNE (1) is proposed as follows:

$$ \frac{\partial f}{{\partial x}}\mathop x\limits^{ \bullet } (t) = - \gamma \phi (f(x(t),t)) - \frac{\partial f}{{\partial x}}. $$
(8)

In the following section, the noise suppression and convergence of BFCZNN (9) will be analyzed, and formula (9) is the BFCZNN model attacked by noise.

$$ \frac{\partial f}{{\partial x}}\mathop x\limits^{ \bullet } (t) = - \gamma \varphi (f(x(t),t)) - \frac{\partial f}{{\partial x}} + n(t) $$
(9)

where n(t) stands for external noise.

3.1 BFCZNN analysis with convergence

In the previous section, we mentioned that the BFCZNN model has the property of convergence in fixed time. In this part, the convergence time of BFCZNN for solving DNE (1) will be analyzed. Before analyzing BFCZNN models, the following theorem of the ZNN for solving the DNE is proposed.

Theorem 1

Assuming the DNE (1) is solvable and starting from any random initial state, the neural state solutions x(t) of the BFCZNN model (8) converge to the theoretical roots x*(t) of DNE (1) in fixed time ts:

$$ t_{s} \le \frac{1}{{\gamma w_{1} }} $$

where design parameters γ and w1 are defined as before.

Proof

According to eq. (3), the error function e(t) of BFCZNN model (8) can be expressed as:

$$ \frac{{d{\text{e}}\left( t \right)}}{dt} = - \gamma \varphi \left( {{\text{e}}(t)} \right). $$

Letting the Lyapunov function \(u(t) = e^{2} (t)\), the time differentiation of u(t) is

$$ \frac{{d{\text{u}}(t)}}{dt} = 2\mathop e\limits^{ \bullet } (t)e(t) = - 2\gamma \varphi (e(t))e(t). $$

When we use AF (7) with the above formulation, we have

$$ \begin{aligned} \dot{u}(t) & = - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p \\ & = - 2\gamma (w_{1} \exp (u^{{p/2}} )u^{{1 - p/2}} /p \\ \end{aligned} $$

We can compute the fixed time of BFCZNN model (11) by solving inequality \(\mathop u\limits^{ \bullet } (t) \le - 2\gamma (w_{1} \exp (u^{p/2} )u^{1 - p/2} /p\)

$$ t_{{\text{s}}} \le \frac{{1 - \exp ( - u^{p/2} (0))}}{{\gamma w_{1} }} \le \frac{1}{{\gamma w_{1} }}. $$

When \({\text{exp}}( - u^{p/2} (0)) = \exp ( - \left| {e(0)} \right|^{{^{p/2} }} ) \in (0,1]\), the convergence time of BFCZNN model (8) is

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

We can draw the following conclusions that the ZNN model in (8) is fixed-time stable.

4 Robustness analysis of BFCZNN

This section will verify the effectiveness and robustness of the proposed BFCZNN model (9) attacked by various noises.

4.1 Case 1: Dynamic non-bounded noise (DNBN)

Theorem 1

Consider the proposed BFCZNN model (9) with DNBN time-varying disturbances, e.g., n(t) = kt , and it should be satisfying |n(t)| ≤ δ|e(t)|. Let \(x(0) \in R\) be an initial matrix and γw1 ≥δ (δ ∈ (0, +∞)). The BFCZNN model (9) starts from any random initial state; the neural state solutions x(t) of the BFCZNN model (9) converge to the theoretical roots x*(t) of DNE (1) in fixed time ts.

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

The parameters γ and w1 are the same as previously defined.

Proof

According to (3), assume \({\text{e}}(t) \in R\), n(t) = k*t is a NVN. Therefore, the error function e(t) of BFCZNN model (11) can be expressed as:

$$ \frac{{d{\text{e}}(t)}}{dt} = - \gamma \varphi \left( {{\text{e}}(t)} \right) + n(t). $$

Here, we choose the Lyapunov function candidate u(t)=|e(t)|2 to prove the fixed-time convergence of the BFCZNN model (9) with DNBN. The time differentiation of u(t) is

$$ \frac{{d{\text{u}}(t)}}{{dt}} = 2\mathop e\limits^{ \bullet } (t)e(t) = - 2(\gamma \phi (e(t)) + n(t)e(t) $$

Because the new AF (7) is used, |n(t)| ≤ δ|e(t)| and γw1 ≥δ, we can obtain the following result:

$$ \begin{aligned} \dot{u}(t) & = - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2e(t)n(t) - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2(\delta \left| {e(t)} \right|)^{2} - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p \\ & = - 2\gamma (w_{1} \exp (u^{{p/2}} )u^{{1 - p/2}} /p \\ \end{aligned} $$

We can compute the fixed time of BFCZNN model (9) by solving inequality \(\mathop u\limits^{ \bullet } (t) \le - 2\gamma (w_{1} \exp (u^{p/2} )u^{1 - p/2} /p\).

$$ t_{{\text{s}}} \le \frac{{1 - \exp ( - u^{p/2} (0))}}{{\gamma w_{1} }} \le \frac{1}{{\gamma w_{1} }}. $$

When \({\text{exp}}( - u^{p/2} (0)) = \exp ( - \left| {e(0)} \right|^{{^{p/2} }} ) \in (0,1]\), the convergence time of BFCZNN model (9) is

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

We can draw the following conclusions that the BFCZNN model in (9) is fixed-time convergence with DNBN.

4.2 Case 2: Dynamic bounded non-vanishing noise (DBNVN)

Theorem 2

Assuming DNE (1) is solvable, and the external noise n(t) = k or n(t) = k*sin(t) is a DBNVN, it satisfies |n(t)| ≤ δ|e(t)| and δ ≤ min(γω 2 , γω 3 ). Let \({\text{x}}(0) \in R\) be an initial matrix and γw 1 ≥δ (δ ∈ (0, +∞)). The BFCZNN model (9) starts from any random initial state; the neural state solutions x(t) of the BFCZNN model (9) converge to the theoretical roots x*(t) of DNE (1) in fixed time t s :

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

Proof

As the same as Theorem 1, according to (3), assume \({\text{e}}(t) \in R\), and n(t) is a VN. Therefore, the error function e(t) of BFCZNN model (9) can be expressed as:

$$ \frac{{d{\text{e}}(t)}}{dt} = - \gamma \varphi \left( {{\text{e}}(t)} \right) + n(t). $$

Here, we choose the Lyapunov function candidate u(t)=|e(t)|2 to prove the fixed-time convergence of the BFCZNN model (9) with DBNVN. The time differentiation of u(t) is

$$ \frac{{d{\text{u}}(t)}}{dt} = 2\mathop e\limits^{ \bullet } (t)e(t) = - 2(\gamma \varphi (e(t)) + n(t)e(t). $$

Because the new AF (7) is used, |n(t)| ≤ δ|e(t)| and γw1 ≥δ, we can obtain the following result:

$$ \begin{aligned} \dot{u}(t) = & - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2e(t)n(t) - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2(\delta \left| {e(t)} \right|)^{2} - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p \\ & = - 2\gamma (w_{1} \exp (u^{{p/2}} )u^{{1 - p/2}} /p \\ \end{aligned} $$

Similar to the proof of case 1, let us solve the above differential inequality; it is also easily derived that the convergence time of BFCZNN model (9) under a DBNVN is

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

Therefore, BFCZNN model (9) also exhibits a predefined time convergence property even under a DBNVN. The proof is thus complete.

4.3 Case 3: Dynamic random-form noise

We have previously discussed the robustness of the model with a single type of noise. But in practice, many noises can be linear combinations of multiple noises. Therefore, it is necessary to analyze the robustness of dynamic random-form noise.

Theorem 3

When DNE (1) is solvable, BFCZNN model (9) is attacked by random-form disturbances n(t), and n(t) satisfies |n(t)| ≤ δ|e(t)| and δ ≤ min(γω2 , γω3). Let \({\text{x}}(0) \in R\) be an initial matrix and γw1 ≥δ (δ ∈ (0, +∞)). The BFCZNN model (9) starts from any random initial state; the neural state solutions x(t) of the BFCZNN model (9) converge to the theoretical roots x*(t) of DNE (1) in fixed time ts.

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

Proof

According to (3), assume \({\text{e}}(t) \in R\), and n(t) is a random-form noise. Therefore, the error function e(t) of BFCZNN model (9) can be expressed as:

$$ \frac{{d{\text{e}}(t)}}{dt} = - \gamma \phi \left( {{\text{e}}(t)} \right) + n(t). $$

Here, we choose the Lyapunov function candidate u(t)=|e(t)|2 to prove the fixed-time convergence of the BFCZNN model (9) with dynamic random-form noise. The time differentiation of u(t) is

$$ \frac{{d{\text{u}}(t)}}{dt} = 2\mathop e\limits^{ \bullet } (t)e(t) = - 2(\gamma \phi (e(t)) + n(t)e(t). $$

Because the new AF (7) is used, |n(t)| ≤ δ|e(t)| and γw1 ≥δ, we can obtain the following result:

$$\begin{aligned} \dot{u}(t) = & - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2e(t)n(t) - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p + 2(\delta \left| {e(t)} \right|)^{2} - (w_{2} \left| {e(t)} \right|^{q} + w_{3} \left| {e(t)} \right|^{{\frac{1}{q}}} )\text{sgn} (x)e(t) \\ & \le - 2\gamma (w_{1} \exp (\left| {e(t)} \right|^{p} )\left| {e(t)} \right|^{{2 - p}} /p \\ & = - 2\gamma (w_{1} \exp (u^{{p/2}} )u^{{1 - p/2}} /p \\ \end{aligned}$$

Based on the previous proof, it is easily derived that the convergence time of BFCZNN model (9) under a dynamic random-form noise is

$$ t_{s} \le \frac{1}{{\gamma w_{1} }}. $$

We can draw the following conclusions that the BFCZNN model (9) is also fixed-time stable in this case.

5 Comparative numerical simulation verification

The convergence and stability of the BFCZNN model are theoretically analyzed in the previous sections. In order to further prove the superiority of the new AF, in this part, comparative simulation verification of the different AFs of ZNN models is presented. One robotic application is presented.

Example 1

Third-order dynamic nonlinear equation (TODNE)

In order not to lose generality, the design parameters w1 = w2 =2, γ =1, p = 0.5, q=5, and the following third-order DNE (TODNE) is considered:

$$ g(x(t),t) = 0.01(x - \cos 3t)(x - \cos 3t - 5)(x + \cos 3t + 5). $$
(10)

According to formula (10), we can get the theoretical solution of the TODNE (i.e., x*(t) = cos(3t), x*(t) = cos(3t)+5, x*(t)= −cos(3t)−5). We will solve TODNE (10) with the proposed BFCZNN model (9) and the ZNN model activated by different AFs in two cases: One is to find the solution of TODNE (10) in noiseless environment and the other one is to find the solution of TODNE (10) in noise polluted environment.

Figures 3, 4 are the computer numerical simulation results for solving TODNE (10) with the proposed BFCZNN model (9) and the ZNN model activated by different AFs in noiseless environment (the red dotted lines represent the theoretical solution at each moment, and the solid lines represent the solutions of neural network models). Fig. 3 is the neural state solutions x(t) generated by the BFCZNN (8) for solving TODNE (10) in the noiseless environment, and Fig. 4 is the simulated residual errors of the different models. Different from Fig. 3, Figs. 5, 6 are the computer numerical simulation in random noises results for TODNE. The random noise shown in Fig. 5 is a combination of constant noise and periodic noise. The random noise shown in Fig. 7 is a combination of non-vanishing noise and periodic noise. The random noise shown in Fig. 8 is a combination of all noises mentioned in Table 2.

Fig. 3
figure 3

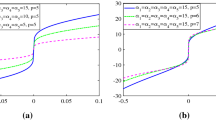
Neural state solutions x(t) of the different ZNN models for solving TODNE (10) without noise. Error trace of the different ZNN models without noise. a State trace of the RNZNN (8) without noise, b state trace of BFCZNN (10) without noise, c state trace of the ZNN model by LAF without noise, d state trace of the ZNN model by SBPF without noise

Full size image
Fig. 4
figure 4

Transient residual errore(t)of a the different ZNN models for solving TODNE (10) without noise. a Error trace of the different ZNN models without noise

Full size image
Fig. 5
figure 5

Neural state solutions x(t) of the different ZNN models for solving TODNE (10) with CN and PN a Error trace of the different ZNN models with CN and PN. a State trace of the RNZNN (8) with CN and PN, b state trace of BFCZNN (11) with CN and PN, c state trace of the ZNN model by LAF with CN and PN and d state trace of the ZNN model by SBPF with CN and PN

Full size image
Fig. 6
figure 6

Transient residual errore(t)of a the different ZNN models for solving TODNE (10) with NVN and PN. a Error trace of the different ZNN model with NVN and PN

Full size image
Fig. 7
figure 7

Neural state solutions x(t) of the different ZNN models for solving TODNE (10) with NVN and PN. a State trace of the RNZNN (8) with NVN and PN, b state trace of the BFCZNN (10) with NVN and PN, c state trace of the ZNN model by LAF with NVN and PN, d state trace of the ZNN model by SBPF with NVN and PN

Full size image
Fig. 8
figure 8

Neural state solutions x(t) of the different ZNN models for solving TODNE (10) with CN, NVN and PN. a State trace of the RNZNN (8) with CN, NVN and PN, b state trace of the BFCZNN (10) with CN, NVN and PN, c state trace of the ZNN model by LAF with CN, NVN and PN, d state trace of the ZNN model by SBPF with CN, NVN and PN

Full size image
Table 2 Different noises
Full size table

Following Figs. 3, 4, the ZNN model can effectively find the solution of TODNE with all the AFs in Table 1 in ideal environment, but their convergence time is different. It takes 5 seconds for the LAF to converge, and SBPF also needs about 3 seconds, while the BFCZNN (8) spends only about 0.2s. The BFCZNN (8) model is the most effective model in ideal environment.

Based on Figs. 5, 9, it can be seen that the ZNN model with LAF and SBPF for solving TODNE is very vulnerable to random noise. When being attacked by constant and periodic noises, the ZNN model with LAF and SBPF fails to solve TODNE (28). The residual error of the RNZNN in Ref. [28] decreases to 0, and its neural state solutions still converge to the theoretical solutions of the TODNE. However, the convergence rate of RNZNN in Ref. [28] is not as fast as that of the BFCZNN model, which demonstrates that the BFCZNN (9) has better robustness than the other three AFs under random noise attacks.

Fig. 9
figure 9

Transient residual errore(t)of a the different ZNN models for solving TODNE (10) with CN and PN. a Error trace of the different ZNN models with CN and PN

Full size image

To be more realistic, we have combined different kinds of noises to carry out simulation experiment. Figures 6 and 7 present the simulation results of the other three AFs and BFCZNN (9) attacked by the combination of four types of noises in Table 1, which include PN n(t)=0.5cost, CN n(t)=0.5, NVN n(t)=0.15t and VN n(t)=exp(-t). Following Figures 5 and 10, it can be observed that the external noises seriously affected the convergence performance of the ZNN model with LAF and SBPF. The deviation between them and the theoretical solutions is large, so they cannot complete the task well. However, the BFCZNN (9) and RNZNN in ref. [28] always converge quickly to the theoretical solutions of the TODNE under various noise disturbances, but the convergence speed of the proposed BFCZNN model is still faster than the RNZNN model in Ref. [28], which further demonstrate the better robustness of the BFCZNN (9) than the existing NAF in Ref. [28].

Fig. 10
figure 10

Transient residual errore(t)of a the different ZNN models for solving TODNE (10) with CN, NVN and PN, b error trace of the different ZNN models with CN, NVN and PN

Full size image

Example 2

Application to robot manipulator

In this part, a robot manipulator simulation control is designed to verify the feasibility of the BFCZNN model further. The geometric model of the robot manipulator control (RMC) was introduced in Ref. [30]. According to Ref. [30], we can obtain the position level kinematics equation of the RMC as follows:

$$ R(t) = \xi (\Theta (t)). $$
(11)

According to Eq. (11), the RMC’s velocity level kinematics equation can be expressed as:

$$ \mathop R\limits^{ \bullet } (t) = J(\Theta )\mathop \Theta \limits^{ \bullet } (t) $$
(12)

where R(t) represents the position vector of the end-effector, ξ(•) is a mapping function, matrix Θ (Θ=[φ,θT]T)∈Rn+2 consists of the angle vector of the platform φ (φ=[φ1,φr]T) and the joint space vector θ (θ=[θ1,θ2,……,θn]T, and the Jacobian matrix J(Θ)= ∂ξ(Θ)/∂Θ.

Generally, \(\mathop R\limits^{ \bullet } (t)\) is known and \(\mathop \Theta \limits^{ \bullet } (t)\) is unknown in (12), which means the positioning control of RMC is actually realized by solving Eq. (12). Equation (12) can be seen as a time-varying linear matrix equation, and the proposed BFCZNN can be applied to solve this matrix equation.

For better comparison, the BFCZNN model (9) and the ZNN activated by LAF are both applied to the positioning control of RMC. The positioning control models are shown as follows:

$$ J(\Theta (t))\mathop \Theta \limits^{ \bullet } = \mathop R\limits^{ \bullet } (t) - \gamma \phi (R(t) - \zeta (\Theta (t))) + N(t) $$
(13)
$$ J(\Theta (t))\mathop \Theta \limits^{ \bullet } = \mathop R\limits^{ \bullet } (t) - \gamma \psi (R(t) - \zeta (\Theta (t))) + N(t). $$
(14)

Equations 13, 14 are the positioning control models of the RMC using the BFCZNN and ZNN activated by LAF. Noises n(t)=0.15 stand for CN.

By ZNN for solving the kinematics equation, the manipulator is controlled to make a circular trajectory motion at a specified position, and the initial state of the RMC is set as Θ(0) = [π/6, π/3, π/6, π/3, π/6, π/3]T, and the task duration is 20 s. The experiment results are displayed in Figs. 11 and 12.

Fig. 11
figure 11

The trace tracking results of the manipulator generated by the proposed model (13) with new AF. a Tracking motion trace. b Desired path and actual trajectory. c Position errors

Full size image
Fig. 12
figure 12

The trace tracking results of the manipulator generated by the proposed model (13) with LAF. a Tracking motion trace. b Desired path and actual trajectory. c Position errors

Full size image

Figures 11 and 12 are the trajectory tracking results of RMC generated by the proposed BFCZNN (9) and the ZNN model with constant noise n(t)=0.15. Following Figs. 11 and 12, it can be seen that the RMC by BFCZNN can accurately locate and complete the circular trajectory tracking task, and its tracking position errors are less than 2.5×10−4 m with constant vanishing noise. At the same time, the RMC controlled by ZNN model cannot complete the circular trajectory tracking task. The successful circle-tracking task further verifies the robustness and effectiveness of the proposed BFCZNN.

Example 3

Experimental results

In order to verify the physical realizability of the BFCZNN (9) for solving the position level kinematics problem of RMC (13), a physical experiment is conducted with IRB120 robot manipulator in this section. The end-effector tasks are to track the circle path of example 2. Figure 13 shows the motion trajectory of the IRB120 robot manipulator on the simulation platform. As can be seen from Fig. 13, the red trajectory is basically the same as the circle in Fig. 11 of example 2. These physical experiments further verify the effectiveness, accuracy and physical applicability of the proposed BFCZNN for resolving the position level kinematics equation of redundant robot manipulators.

Fig. 13
figure 13

BFCZNN (9) solves the position level kinematics equation of the RMC (13)

Full size image

6 Conclusion

A new ZNN model for solving DNE is presented and investigated in this paper. The convergence and robustness of the BFCZNN model are analyzed theoretically and verified by simulation, and the simulation results are consistent with the theoretical analysis results. Compared with the original ZNN model, the new BFCZNN model is proved to have better robustness and faster convergence, which will satisfy the scientific and engineering applications demanding accurate and fast online real-time computation. The future research directions can be focused on how to further enhance the robustness of the model, and its real application to control the industrial robot manipulator.