1 Introduction

Amplitude phase shift keying (APSK) is a high-order modulation scheme with its high spectral efficiency and power [1] and also known to be very reliable in nonlinear wireless channels. In this respect, it has been adopted and employed in many commercial standards related to digital video broadcasting, such as second-generation digital video broadcasting DVB.S2 [2]. It achieves a high-rate transmission and shows better error performance, near to the Shannon limit, when compared with customary modulation schemes like QAM or PSK, especially when combined with distinguished channel codes like low-density parity-check (LDPC) codes or turbo codes [3, 4]. For the same coding scheme, it was shown in [5] that double-ring APSK modulation scheme has outperformed 16-QAM and 16-PSK due to its inherent robustness against the nonlinearities of the high-power amplifiers (HPAs). However, the demodulation process of APSK modulation scheme requires an exhaustive computation, where the complexity gradually increases with the size of the constellation.

In traditional receivers, after the demodulation process the received complex-valued signals are passed through a demapper, or decoder, which can be either an independent or an iterative decoder. The decoders can be divided mainly into two broad categories, namely hard-decision decoders and soft-decision decoders, where the former gets use of Hamming distances and the latter gets use of Euclidian distances between the received signal samples and the associated code words. In hard-decision decoding, hard bit information (0 or 1) is passed through the decoder, while in soft-decision decoding a probabilistic decoding algorithm is used in which soft bit information is passed through the decoder that carries the probability value associated with that particular bit. Although hard-decision decoding is computationally simpler, soft-decision decoding has better performance in terms of low bit-error rate (BER). A detailed performance analysis of soft- and hard-decision decoding can be found in [6].

In [7], the concept of APSK using product constellation labeling was introduced and two simplified demappers were proposed. It was concluded that the performance degradation introduced by the simplified demappers was negligible compared with the conventional max-log-MAP demappers over either AWGN or Rayleigh channels, i.e., for a code rate of 1/2 and gray labeling it is about 0.05 dB for independent demapping and about 0.1 dB for iterative demapping. A new bits-to-symbol mapping for 4 + 12 + 16-APSK in the nonlinear AWGN channel was proposed in [8] by analyzing the relation among the signal constellation, using both Hamming and Euclidean distances between the signal points on the constellation and BER performance depending on the nonlinearity of high-power amplifier (HPA). The proposed scheme was stated to have a simpler mapping structure, and the BER performance is better than that of the bit mapping in the DVB.S2 standard. In [9], a simplification method with a binary search scheme for linear regions was proposed for demodulation of general APSK signals, which can be applied to all types of APSK constellations where the complexity was stated to grow logarithmically with the constellation size, as opposed to existing schemes where the complexity grows linearly. An efficient soft demapping method was proposed in [10] for high-order modulation schemes combined with iterative decoding. The method employs a decision threshold instead of using Euclidean distance estimation, where computing operations are reduced. It was stated that larger complexity reduction with higher modulation order can be obtained, and simulation results using block turbo codes showed that approximating BER performance to that of the exhaustive estimation demapping algorithm can be achieved.

In [11], an alternative approximation to [10] in the computation of the LLR was presented where it consists of avoiding square root operations and the comparisons such as those required in max-log method, and about 0.5-dB degradation with respect to the max-log approach was noted for the proposed scheme. A simplified soft-decision demapping algorithm was presented in [12] to reduce the computational complexity compared to conventional algorithms with negligible performance degradation and a reduction of hardware resources required by about 81%. Similarly, another soft-decision demapping algorithm with low computational complexity for coded 4 + 12-APSK was proposed in [13]. It was noted that the proposed algorithm requires only a few summation, subtraction and multiplication operations to calculate the LLR value of each bit, and shows the same error performance as a conventional max-log algorithm.

A few soft demapping algorithms using maximum-a-posteriori (MAP) approach have been proposed in the literature to convey soft or hard bit information to decoders. Even though MAP-based decoding is known to be the optimal solution for symbol detection, one can exploit the parallel nature of artificial neural networks (ANN) as an alternative solution to that problem. In this respect, the problem of correct symbol detection can be considered as a constrained optimization problem that seeks for the nearest code word for each received symbol among the given code words. It was shown by Huang and Babri [14] that a single-hidden layer feedforward neural network (SLFN) can be trained with a finite training set to learn N distinct observations with zero error. A simplified version of SLFNs, which randomly chooses the input weights and analytically adjusts the output weights of SLFNs, is called extreme learning machine (ELM) [15] and is widely used in a variety of regression and classification problems [16, 17].

An ANN-based solution to the problem of detection and correction of linear block codes in AWGN channel was proposed in [18]. A multilayer perceptron (MLP) trained by the back-propagation (BP) algorithm was used to compare the performance of BPSK signaling with soft- and hard-decision decoders, and it was stated to have better performance for low signal-to-noise ratios. The behavior of a neural receiver combined with conventional equalizers was investigated in [19] to improve the detection of QAM modulated signals by compensating for nonlinear distortions of amplifiers. In [20], a radial basis function (RBF) neural network was proposed to learn the characteristic of M-QAM signal constellations in OFDM systems under the effect of noise and phase error, where hybrid learning process was used to train the RBF network. It was stated that neural networks combined with conventional equalizers improve the performance especially in compensating for nonlinear distortions of the amplifier. It was shown that neural equalizers were less disturbed by a small shift of operation point and, in general, QAM modulation with larger amount of levels can get more advantageous on neural equalizers. A learning-based framework to solve both equalization and symbol detection for QAM was studied in [21], where the received signal was transformed to a 2-tuple real-valued vector and then fed into a real-valued ELM. The proposed algorithm was compared with other learning-based equalizers using complex-valued ELM, complex-valued radial basis function (CRBF), complex-valued minimal resource allocation network (CMRAN), k-nearest neighbor (k-NN), back-propagation (BP) neural network and stochastic gradient boosting (SG-boosting). Obtained results in the study showed that ELM-based proposed scheme quite outperforms other ANN algorithms in terms of both symbol error rate (SER) and also training and testing times. In this sense, this framework emphasizes the strength of ELM-based classification in both equalization and symbol detection.

In this study, we propose a novel soft demapping algorithm for APSK signaling based on extreme learning machine, for both coded and uncoded scenarios. To the best of our knowledge, ELM-based demappers have not been used for the state-of-the-art APSK modulation scheme before. It will be shown that symbol detection using ELM can be efficiently employed as a good alternative to other proposed soft demappers. For the sake of clarity, we restrict our work to the cases of 16-APSK and 32-APSK constellations, where our model can be applied for higher-order (64-, 128- or 256-APSK) constellations as well.

2 Preliminaries

2.1 Amplitude phase shift keying (APSK)

The M-ary APSK constellation, either be a regular or an irregular type, is composed of \(R\) arbitrarily concentric rings where each ring having uniformly spaced by symbols with an arbitrary phase. The size of the constellation and the points are designed in a way to optimize the performance of the overall modulation scheme in terms of low peak-to-average power ratio (PAPR), low BER and high transmission rate [2]. In this respect, DVB-S2 gets use of irregular constellations where each concentric ring has different number of constellation points [9]. A detailed analysis considering the optimization of constellation performance can be found in [22].

The APSK signal points form a complex number set which is given by

$${\mathbf{S}}_{{\text{APSK}}} = \left\{ {\begin{array}{*{20}l} {r_{1} \exp \left[ {j\left( {\left( {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {n_{1} }}} \right. \kern-0pt} {n_{1} }}} \right)i + \theta_{1} } \right)} \right]} \hfill & {i = 0, \ldots ,n_{1} - 1} \hfill \\ {r_{2} \exp \left[ {j\left( {\left( {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {n_{2} }}} \right. \kern-0pt} {n_{2} }}} \right)i + \theta_{2} } \right)} \right]} \hfill & {i = 0, \ldots ,n_{2} - 1} \hfill \\ \vdots \hfill & \vdots \hfill \\ {r_{3} \exp \left[ {j\left( {\left( {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {n_{R} }}} \right. \kern-0pt} {n_{R} }}} \right)i + \theta_{R} } \right)} \right]} \hfill & {i = 0, \ldots ,n_{R} - 1} \hfill \\ \end{array} } \right.$$
(1)

where \(n_{\ell }\) denotes the number of points, \(r_{\ell }\) denotes the radius, and \(\theta_{\ell }\) denotes the relative phase shift of the \(\ell\)th ring, and \(1 \le \ell \le R\). This type of modulation schemes is termed as \(n_{1} + n_{2} + \cdots + n_{{n_{R} }}\)-APSK constellations. The optimum constellation radius ratio γ for 4 + 12-APSK is defined as \(\gamma = {{R_{2} } \mathord{\left/ {\vphantom {{R_{2} } {R_{1} }}} \right. \kern-0pt} {R_{1} }}\) and for 4 + 12 + 16-APSK as \(\gamma_{1} = {{R_{2} } \mathord{\left/ {\vphantom {{R_{2} } {R_{1} }}} \right. \kern-0pt} {R_{1} }}\) and \(\gamma _{2} = {{R_{3} } \mathord{\left/ {\vphantom {{R_{3} } {R_{1} }}} \right. \kern-0pt} {R_{1} }}\), where Fig. 1a, b depicts the 4 + 12-APSK and 4 + 12 + 16-APSK constellations, respectively.

Fig. 1
figure 1

a 4 + 12-APSK, b 4 + 12 + 16-APSK constellations

Full size image

2.2 Log-likelihood ratio (LLR)

A major part of conventional receivers employ the maximum-a posteriori (MAP) rule for optimum detection [23]. In many cases, having a priori information about message probabilities is difficult and actually not available, so symbolling at the transmitter is commonly assumed to be equal likely. In this sense, a MAP detector becomes a maximum-likelihood (ML) detector [23]. MAP detectors, i.e., ML detectors, exploit the bit-wise likelihood ratios to make a decision on the received bit to be either a zero or one. The logarithmic MAP (log-MAP) and the max-logarithmic MAP (max-log-MAP) [24] are the simplified approximations of the MAP decision rule, usually employed in most of the receivers to decrease the hard burden of calculations.

The log-likelihood ratios (LLRs) are known to be very operative metrics that offer low dynamic range and simplification for decoding of many powerful codes, such as LDPC or turbo codes. The LLR for a given received symbol r is defined as the logarithmic ratio of the conditional probabilities \(P_{r} \left( {b_{j} | r} \right)\) of a particular bit (\(b_{j}\)) to be zero or one

$${\text{LLR}}\left( {b_{j} } \right) = \ln \left( {\frac{{P_{r} \left( {b_{j} = 0 | r} \right)}}{{P_{r} \left( {b_{j} = 1 | r} \right)}}} \right)$$
(2)

and for an independent demapping (no a priori information, i.e., assuming equiprobable symbols) of M-ary modulation over an AWGN channel, it can be written as

$${\text{LLR}}\left( {b_{j} } \right) = \ln \left( {\frac{{\mathop \sum \nolimits_{{x \in {\mathcal{X}}_{j}^{\left( 0 \right)} }} f_{i} }}{{\mathop \sum \nolimits_{{x \in {\mathcal{X}}_{i}^{\left( 1 \right)} }} f_{i} }}} \right)$$
(3)

where \({\mathcal{X}}_{j}^{\left( b \right)}\) is the constellation subset with the \(j\)th bit being \(b \left\{ {0,1} \right\}\) and \(f_{i}\) is the conditional probability density function of the received symbol given by

$$f_{i} = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}e^{{\frac{{ - \left| {r - s_{i} } \right|^{2} }}{{2\sigma^{2} }}}} \quad i = 0,1, \ldots M - 1$$
(4)

where \(\sigma^{2}\), \(r\) and \(s_{i}\) denote the variance, received symbol and \(i\)th symbol of the constellation, respectively. Obviously, the computational cost dramatically increases with the constellation size, since a large amount of exponential, square root and logarithm operations are need to be performed by the decoder. However, the amount of operations can be significantly reduced by using the max-log approximation [24] which is based on the Jacobian logarithm [25] identity expressed by

$$\ln \left( {e^{{x_{1} }} + e^{{x_{2} }} + \cdots + e^{{x_{n} }} } \right) \approx \hbox{max} \left( {x_{1} ,x_{2} , \ldots x_{n} } \right)$$
(5)

Using the given approximation in Eq. (3), Eq. (5) can be simplified to

$${\text{LLR}}\left( {b_{j} } \right) \approx \hbox{max} \left( {D_{{x \in {\mathcal{X}}_{j}^{\left( 0 \right)} }} } \right)\, - \,\hbox{max} \left( {D_{{x \in {\mathcal{X}}_{j}^{\left( 1 \right)} }} } \right)$$
(6)

where

$$D_{{x \in {\mathcal{X}}_{j}^{\left( b \right)} }} = - \,\frac{{\left| {r - s_{i} } \right|^{2} }}{{2\sigma^{2} }} b \left\{ {0,1} \right\}, i = 0,1, \ldots M - 1$$
(7)

It can be concluded that Eq. (6) actually implies that the max-log LLR approximation leads to the minimum Euclidian distance between the received symbol and the constellation points, in bit-wise manner.

2.3 Extreme learning machine (ELM)

It is known that a single-hidden layer feedforward neural network (SLFN) with N hidden neurons can be trained to learn N distinct observations with arbitrarily small error [15]. Unlike the traditional applications of feedforward networks, input weights and first hidden layer biases are not needed to be tuned, where they can be chosen arbitrarily and the output weights of SLFNs can be analytically determined [15]. In fact, this approach makes extreme learning fast and simple and also provides a good generalization performance for SLFNs, which is known as extreme learning machine (ELM) algorithm.

ELM has several significant superiorities over other classical popular gradient-based learning algorithms such as back-propagation. It offers the following benefits: (1) It is extremely fast, i.e., it can train SLFNs much faster; (2) it provides the smallest norm of weights while tending to reach the smallest training error; (3) it can be trained to work for nondifferentiable activation functions; (4) it uses only single-hidden layer, and it is much simpler than most learning algorithms for feedforward neural networks [26].

The output of standard SLFNs can be calculated using the equation given by Huang et al. [15].

$$y=\sum \nolimits_{j=1}^k\beta_j g\left(\sum\nolimits_{i=1}^nw_{ij}\cdot x_i +b_j\right)$$
(8)

where \(x_{i }\) is the input, and \(n\) and \(k\) are the number of neurons in the input and hidden layer, respectively. \(w_{ij }\) represents the input, and \(\beta_{i}\) represents the output weights, \(b_{j}\) is the biases of the neurons in the hidden layer, and \(g\left( . \right)\) is the activation function. Equation (5) can be written compactly in the following form as

$${\mathbf{H}}\beta = y$$
(9)

where

$${\mathbf{H}} = \left[ {\begin{array}{*{20}c} {g\left( {w_{11} \cdot x_{1} + b_{1} } \right)} & \ldots & {g\left( {w_{k1} \cdot x_{1} + b_{k} } \right)} \\ \cdots & \vdots & \ldots \\ {g\left( {w_{n1} \cdot x_{n} + b_{1} } \right)} & \ldots & {g\left( {w_{kn} \cdot x_{n} + b_{k} } \right)} \\ \end{array} } \right]_{nxk} \quad {\text{and}}\quad \beta = \left[ {\begin{array}{*{20}c} {\beta_{1} } \\ \vdots \\ {\beta_{n} } \\ \end{array} } \right]_{kx1}$$
(10)

\({\mathbf{H}}\) is called the hidden layer output matrix of the neural network. To obtain the SLFNs with zero error mean, i.e., \(\sum\nolimits_{j = 1}^{N} {y_{j} - t_{j} = 0,}\) where \(t\) indicates the desired output and \(N\) indicates the number of events, the input weights and biases are randomly assigned and output weights can be determined by using the smallest minimum norm least squares solution proposed by Huang et al. [15]:

$$\hat{\beta }=\mathbf{H}^\dag y$$
(11)

where \(\bf H^\dag\) is the Moore–Penrose generalized inverse of matrix \({\mathbf{H}}\).

Obviously, ELM is a very powerful tool and can be applied to a general class of classification and regression frameworks. In his excellent studies given in [27, 28], Huang et al. showed that ELM has high generalization and approximation capabilities. As stated before, the complexity of demapping of APSK signals is quite a tedious work, especially in high-order constellations. Although there are several proposed studies in the literate for simplification of the MAP rule at the expense of moderate performance degradation, nearly most of the proposed algorithms are application-specific, either for the given particular constellation size or proper only for independent decoding. On the other side, the literature surveys given in the previous section show that the ANN-based frameworks are almost dedicated to channel equalization, except the proposed study given by Muhammad et al. [21]. This study successfully considers both QAM equalization and symbol detection in OFDM systems using ELM, and it is important to show that ELM outperforms other ANN algorithms and can be effectively used in symbol detection, as well as equalization.

In this manner, the strength of ELM in classification can be effectively exploited for symbol detection of the state-of-the-art modulation scheme APSK. Unlike [21], our study involves only symbol detection over an AWGN channel and compares the performance of ELM-based demapping against the optimal MAP-based demapping.

3 System model and proposed algorithm

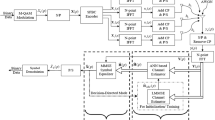
The general layout of a digital communication system used in our model is illustrated in Fig. 2. First, a random binary signal is generated and fed into a constellation mapper and then sent to the M-APSK modulator to be transmitted. The transmitted symbols \(s_{k}\) passing through the channel get affected with random noise. In our simulations, different signal-to-noise ratios (SNR) are tested to measure the performance of our proposed model. At the receiver side, the received noisy symbols \(r_{k}\) are demodulated and fed into an ELM-based constellation demapper for symbol detection.

Fig. 2
figure 2

A model of a digital communication system utilizing ELM-based demapper

Full size image

Before starting the simulation, the proposed ELM-based demapper, which is given in Fig. 2, has been trained and tested with a sufficient amount of data sets at different noise levels. During the training and testing stages, two types of data sets have been used to check the performance of the proposed demapper. The first type data set consists of symbols affected by different noise levels, which will be hereafter called as mixed-type SNR data set, whereas the second type of data set consists of symbols affected only by one level of noise, which will be called as fixed-type SNR data set. In fact, the purpose of this distinction between the two data sets is to implement a demapper employing two types of scenarios. In the first case, the tuning parameters gained from mixed-type SNR data set will be used equally for all received symbols, without looking at their SNRs (i.e., noise level). In the second case, since we have a priori knowledge about SNR of each upcoming symbol, we can use the relevant tuning parameters gained from each fixed-type SNR accordingly. In other words, we will have a lookup table composed of different parameters for different SNRs, and ELM-based demapper will check for the SNR level of the received symbols (i.e., frames) at particular time intervals and use relevant parameters from the table. It should be noted that these checking instants for the SNR of the received signal depend on the time-varying nature of the channel and can be adequately adjusted.

An illustration for the training and testing process is depicted in Fig. 3, where 4 + 12-APSK constellation has been considered here as an example, and this analogy actually applies for all constellation sizes. The red-colored squares represent the complex symbol points, and the blue-colored dots represent the noisy complex symbol points, as shown in the left side of Fig. 3. The constructed noisy symbols are then used in the ELM network for training and testing process. The steps of our training and testing process can be summarized as follows:

Fig. 3
figure 3

Training and testing process given for 4 + 12-APSK constellation with SNR = 5 dB

Full size image
  1. 1.

    First, a sufficient number of complex random noisy signals have been generated for each complex symbol, at each different SNR level (i.e., between 0 and 20 dB at multiples of 1 dB).

  2. 2.

    The real and imaginary parts of each complex symbol and its corresponding noisy patterns have been collected in a data set.

  3. 3.

    For the first case scenario, the whole data set obtained in step 2 has been shuffled to obtain mixed-type SNR data set. The ELM network shown in Fig. 3 has been trained and tested with this type data set applying 10-fold cross-validation, and the obtained weights and biases have been saved to be used as mixed-type SNR parameters.

  4. 4.

    For the second case scenario, the whole data set in obtained step 2 has been grouped with respect to SNR levels, maintaining 21 different sub-data sets associated with 21 different SNRs. For each obtained sub-data set, i.e., fixed-type SNR data set, the ELM network given in Fig. 3, has been trained and tested in the same way as in step 3. Finally, the relevant weights and biases obtained for each SNR have been saved into a lookup table, respective to its SNR value.

During the training and testing stages, different activation functions (sigmoid, sinusoidal, hard limiter, triangular basis and radial basis) and different number of hidden neurons have been used to choose the case which optimizes our network. The training and test accuracies versus number of hidden neurons (NHN) for different activation functions obtained from mixed-type data set are given in Fig. 4a–d and for both 4 + 12- and 4 + 12 + 16-APSK constellations. The test results show that sigmoid, sinusoidal and radial basis activation functions have the best accuracies among them in both constellations, and each of them has nearly the same performance. In our simulations, we have utilized sigmoid activation function with 50 neurons and radial basis activation function with 75 neurons for 4 + 12- and 4 + 12 + 16-APSK constellations to get maximum test accuracy, respectively.

Fig. 4
figure 4

Training and test accuracies of mixed-type data set, a, b 4 + 12-APSK and c, d 4 + 12 + 16-APSK constellation

Full size image

For the second type of data set, the same activation functions were used with different number of neurons for each SNR and similarly sigmoid and sinusoidal activation functions gave the best accuracies among them. Therefore, for the sake of figure readability, only the performances of these two activation functions versus SNR for different NHNs are individually illustrated in Fig. 5a–f for both 4 + 12- and 4 + 12 + 16-APSK constellations. In both constellations, both sigmoid and sinusoidal activation functions gave nearly identical test accuracies, as can be seen from the given figures. The training and test results for both constellations showed that for data sets with SNRs between 0 and 5 dB a number of 30 neurons, for data sets with SNRs between 6 and 12 dB a number of 25 neurons and for data sets with SNRs between 12 and 20 dB a number of 20 neurons were sufficient to obtain reasonable test accuracies. Our decision rule here was based on using minimum neurons and also obtaining a wider range of SNRs in which the same training parameters could be applied without losing a major degradation in the performance. In this regard, we could minimize the number of parameters to be used in the lookup table.

Fig. 5
figure 5

Test accuracies of fixed-type data set, a–c 4 + 12-APSK and d–f 4 + 12 + 16-APSK constellation

Full size image

The parameters obtained from the training stage are summarized in Table 1. After completing the selection of parameters from training stage, Monte-Carlo based simulations were carried out in the application stage.

Table 1 Selected parameters from training stage
Full size table

A detailed test accuracy analysis is provided in Table 2, where we have conducted a numerous tests to check for the performance of the selected network parameters indicated in Table 1 versus different type of data sets. It can be clearly seen from Table 2 that the best test accuracy for mixed-type data set was achieved using mixed-type parameters. Similarly, the best test accuracies for fixed-type data sets were achieved using related fixed-type parameters. Therefore, the test results obtained in Table 2 indicate the validity of the chosen network parameters.

Table 2 Test accuracies of different type data sets under selected parameters
Full size table

4 Simulation results

After completing the training and test stages, obtained net parameters (i.e., input/output weights and number of hidden neurons) have been used to simulate our proposed model. The parameters used in the simulations are given in Table 3. The simulation stage consists of both uncoded and coded data scenarios, where we have tried to validate and compare the performance of the proposed ELM-based demapper algorithm against the max-log LLR algorithm (Eq. 6).

Table 3 Simulation parameters
Full size table

4.1 Uncoded modulation

For uncoded data case, the two type networks that have been obtained in training stages with mixed- and fixed-type SNR have been used in the simulation stage, which we will shortly call as ELM-mixed and ELM-fixed, respectively. The bit-error rate (BER) and symbol error rate (SER) results of ELM-mixed, ELM-fixed and log-max LLR algorithms for both constellations are given in Fig. 6a–d.

Fig. 6
figure 6

The BER and SER results of uncoded simulation versus SNR, a, b 4 + 12-APSK and c, d 4 + 12 + 16-APSK constellation

Full size image

The results show that the BER and SER of the proposed ELM-based demappers have a competitive performance against the optimal LLR algorithm, where ELM-mixed slightly outperforms ELM-fixed. It is also important to note that for especially low amount of SNRs (i.e., the worst cases), both of the proposed algorithms have nearly the same performance with the max-log LLR algorithm, whereas for higher SNRs, ELM-mixed has approximately less than 0.5-dB degradation and ELM-fixed has approximately less than 1-dB degradation than max-log LLR algorithm, respectively. In fact, this gap could be further reduced by increasing the number of hidden neurons which have been tried to be kept low enough to decrease the complexity of the design. Although the implementation of ELM-mixed requires approximately a double number of hidden neurons when compared with ELM-fixed, it uses less parameter than ELM-fixed so it can be preferred when dealing with constraint memory. On the other hand, ELM-fixed can be alternatively used to decrease the number of computations.

4.2 Coded modulation

In the second case scenario which uses coded data simulation, we have considered the low-density parity-check (LDPC) [3] codes which is known to have an excellent performance among other error correcting mechanisms. LDPC codes can be efficiently decoded through iterative decoding process, using either hard-decision or soft-decision decoding. In this regard, our study will also highlight the capability of LDPC codes in error correction. Although soft-decision decoding enhances the performance of LDPC codes, the proposed ELM-based demapper employs a hard-decision strategy; therefore, we have used the bit flipping (BF) algorithm for hard-decision decoding of LDPC codes.

The BF algorithm is a simple hard-decision message-passing algorithm based on the idea of belief propagation used to decode LDPC codes. Tanner graph is a bipartite graph which is used to represent LDPC codes in graphical form [29], and it has check nodes and variable nodes to pass the message along the edges. First, the variable node (message node) sends its bit information to the check node and then the check node returns an updated message to the variable node according to the parity-check equation. This process is repeated until maximum number of pre-defined decoder iterations has been passed or the decoder halts automatically when the parity-check equations get satisfied.

The BER of ELM-mixed, ELM-fixed and log-max LLR algorithms using hard-decision decoding for both 4 + 12- and 4 + 12 + 16-APSK constellations is shown in Fig. 7a, b. The results show that a similar performance like in uncoded scenario has been achieved, where ELM-mixed slightly outperforms ELM-fixed, as expected. A maximum amount of 20 iterations has been used in the coded simulation where the results of the 1st and the 10th iterations are only depicted in Fig. 7a–b, since there was not a significant improvement in the BER results after the 10th iteration. It can be easily seen from the figure that for low amount of SNRs both of the proposed algorithms have nearly the same performance with the max-log LLR algorithm, and for high amount of SNRs, a max of 0.5- and 1-dB degradations has been obtained with ELM-mixed and ELM-fixed, respectively. Moreover, in the case of 4 + 12 + 16-APSK, ELM-mixed even outperforms the max-log LLR algorithm after about 10 dB SNR in the 1st iteration and after about 6 dB SNR in the 10th iteration, as shown in Fig. 7b.

Fig. 7
figure 7

The BER results of coded simulation versus SNR, a 4 + 12-APSK and b 4 + 12 + 16-APSK constellation

Full size image

Simulation results show that the performance of the proposed soft demapping algorithm using ELM works quite well for both coded and uncoded APSK. At low SNRs nearly the same performance with the max-log LLR algorithm has been achieved, and at high SNRs only a maximum of 0.5- and 1-dB performance degradation is introduced for ELM-mixed and ELM-fixed-type scenarios, respectively. It is evident that the obtained successful performances indicate the high generalization and approximation capabilities of ELM [27, 28]. These results also well suit to the literature findings obtained in [21]. Although obtaining inverse matrix seems as a complex issue for real-time applications, it should be noted that the training stage is carried out only for one time to obtain optimum weights and biases before starting the application. And after they have been obtained, the only issue is to weigh the inputs and sum them to acquire the output, which is a straightforward algebraic process. Based on this fact, the proposed approach can be easily applied in real-time applications.

5 Conclusions

The symbol detection in high-order modulation schemes like APSK is a crucial issue. In this study, symbol demapping process was considered as a classification framework and an extreme learning machine (ELM)-based demapper was proposed to perform an efficient detection as an alternative to other soft demappers. The proposed algorithm has been tested for both uncoded and coded modulation scenarios using both fixed-type and mixed-type network parameters obtained from the training stage of fixed-type and mixed-type SNR data sets. The simulation results showed that ELM-based demapper can be adequately used in hard-decision decoders to perform symbol detection task with a good BER and SER performance. Especially in low SNRs, the proposed algorithm has nearly the same performance with the optimal max-log LLR algorithm. And in the case of high SNRs the performance of the proposed algorithm is comparatively successful. Furthermore, this study also demonstrates the power of LDPC codes in error correction when comparing the simulation results obtained from uncoded and coded modulation.