1 Introduction

Due to the energy crisis, power industries consider load forecasting as one of the most important ways of managing the electric energy consumption. Financial aspects of load forecasting in deregulated power systems are important for all participants in electricity energy markets such as GENCOs, DISCOs and consumers [1, 2]. For instance, accurate load forecasting reduces the operation costs by enhancing economic load dispatch, unit commitment and ancillary services [3, 4]. There are four types of load forecasting including very short-term, short-term, mid-term and long-term load forecasting. Utilities use mid-term load forecasting more than the other types of load forecasting in dealing with fuel energy markets. In short, accurate load forecasting leads to an economic and reliable power system planning and operation [5, 6].

Load pattern depends on many factors such as seasonal effects, holidays, local temperature, humidity percentage and wind speed, which make load forecasting a very complicated procedure [7]; however, all these factors are not of the same significance. In fact, some of these irrelevant or redundant features should be discarded while maintaining the others [8]. Therefore, the first important step in load forecasting is feature selection, which is extracting the best input data from the variables. Another key step in forecasting is extracting a function that describes the relationship between the input data and the future load behavior precisely [7]. The other problem is forecasting the loads for the countries with two different calendars [9]. In short, the mentioned problems make the load forecasting even more complex.

Generally, there are two basic approaches in the literature for dealing with forecasting problems. The first approach consists of statistical techniques such as time series [10], smooth transition periodic autoregressive [11] and nonlinear regression [12]. The second approach consists of Artificial Intelligence algorithms such as artificial neural network-based method [13,14,15,16,17,18,19], fuzzy logic systems [2, 6] and gradient boosting machines and Gaussian process [20], and support vector machine (SVM) [21]. Due to its ability to deal with four kinds of problems including classification, clustering, regression and function estimation, SVM has been one of the most popular methods recently. In addition, owing to its structure, SVM can deal with a large number of variables as the input vector. Moreover, the SVM has overcome trapping in local minima, which is the problem of the traditional algorithm, and the solution is always unique and globally optimal. SVM shows good results in dealing with under-fitting and over-fitting problems which are common problems in using other artificial neural networks [22]. The ability of SVM as a regression technique has been called support vector regression (SVR). This method has been one of the most interesting regression methods in recent years dealing with forecasting problems. Moreover, this method was applied by the winner of the European network on intelligent technologies competition [23]. The other SVM-based method for the next day load forecasting is least squares support vector machine (LS-SVM) [24].

Despite SVM ability and efficacy in forecasting problems, the SVM suffers from two drawbacks, which are determining the parameters of SVM, and selecting the proper input data. Abbas and Arif [25] used GA for determining parameters of SVM. The main drawback with this paper is the huge amount of irrelevant input data. In proposed method by Hong [26], the chaotic artificial bee colony has been used to find out parameters of SVM, and a recurrent neural network has been implemented to improve the performance of mapping nonlinear load pattern. Another hybrid approach which implements SVR in order to forecast short-term load has been introduced by Duan et al. [27]. The main advantage of this reference is reducing the number of training samples by using the fuzzy clustering approach. In this reference, a fuzzy C-means (FCM) has been used to find the optimal training samples from clustered historical load data. Then, the particle swarm optimization (PSO) has been used for training these data and optimizing parameters of SVR. Yang et al. [28] improved SVM accuracy by using rough set (RS) data preprocessing method which reforms input data. In [29], Wu employed Wavelet function as the SVR kernel function. In addition, PSO algorithm with Gaussian and adaptive mutation has been implemented to optimize the parameters of proposed Wavelet SVR model.

All aforementioned SVR-based methods have been used an evolutionary algorithm to optimize the parameters of SVR model. Among these algorithms, the GA seems more efficient than the other algorithms [30]. However, only a few references have used a powerful method to deal with nonlinearity of input data in preparing and clustering step.

Recently, kernel-based methods which can detect dependencies kind have been used in the literature. These methods can by that dominate the load properties by formulating the feature space in terms of kernels. Formulation of feature space by kernels is the advantage of kernel machines as opposed to the rest load forecasting methods mentioned earlier; it allows the modeler to control the forecasting process by selecting the kernel form and promotes model flexibility by ordering a high variety of kernels [31, 32]. Furthermore, kernel fuzzy C-mean (KFCM) clustering method based on fuzzy SVM provides good performance in classification problems with outliers or noises [33]. Moreover, two-step correlation analysis (CA–CA) method boosts the forecast accuracy by pre-forecasting when the input data are limited [34]. In order to reduce the complexity between the historical data and other related variables, KFCM is used in the present paper for data preprocessing and finding the most effective candidate as the SVR model inputs. Considering the limitation of input data in MTLF, the CA–CA method is used as another approach to data preprocessing.

The rest of the paper is organized as follows. In Sect. 2, the basic theory of KFCM, CA–CA, time-series reconstruction, SVR and WSVR methods are discussed. Section 3 explains the proposed method. Experimental results are discussed in Sects. 4, and 5 contains the conclusion.

2 Methodology

In this paper, two methods are used for data preprocessing. The first method, which has not been used before, is the kernel clustering approach, which conducts clustering in the high-dimensional feature space. The second method, which is used for data preprocessing, is two-step correlation analysis. In the next step, the time-series reconstruction technique is applied to select input data. Finally, prepared data are used as training samples of the wavelet support vector regression (WSVR) model.

2.1 Kernel fuzzy C-mean (KFCM) clustering

Clustering approaches allow us to classify a large amount of data into two (or more) classes based on the similarity between each pair of data. However, in most cases, it is very difficult to find a hard boundary between classes. In using fuzzy clustering approach, each data point is assigned to all clusters with a fuzzy membership degree between 0 and 1. This type of clustering approaches which do clustering into a high-dimensional feature space via a specified kernel function is known as kernel clustering approaches. The most powerful fuzzy clustering method is the FCM algorithm [31]. Recently, FCM has been generalized using Mercer’s kernel theory like any other clustering algorithm. Recent studies on classification problems in noisy datasets show the superiority of kernel fuzzy clustering approach over conventional fuzzy clustering [31, 33]. The KFCM algorithm is proposed as follows [33]:

  1. 1.

    Choose cluster number C and stop criterion \(\varepsilon \in \left( {0,1} \right)\);

  2. 2.

    Select kernel function \(K\left( {x_{i} ,x_{j} } \right)\) and its parameters that satisfy Mercer’s condition;

  3. 3.

    Initialize random centroids Vj, j = 1,2,…,C;

  4. 4.

    Compute membership degree of ith vector in the jth cluster uij, i = 1,..,N and j = 1,..,C

    $$u_{ij} = \frac{{\left( {1/d^{2} \left( {x_{i} ,v_{j} } \right)} \right)^{1/m - 1} }}{{\sum\nolimits_{p = 1}^{C} {\left( {1/d^{2} \left( {x_{i} ,v_{p} } \right)} \right)^{1/m - 1} } }}$$
    (1)

    where

    $$d^{\text{2}} \left( {x_{i} ,v_{p} } \right) = K\left( {x_{i} ,x_{i} } \right) - \text{2}K\left( {x_{i} ,v_{p} } \right) + K\left( {v_{p} ,v_{p} } \right) = \text{2} - \text{2}K\left( {x_{i} ,v_{p} } \right)$$
    (2)
  5. 5.

    Compute the new kernel matrices \(K\left( {x_{i} ,\hat{v}_{p}^{{\text{new}}} } \right)\) and \(K\left( {\hat{v}_{p}^{{\text{new}}} \text{,}\hat{v}_{p}^{{\text{new}}} } \right)\)

    $$K\left( {x_{i} ,v_{p}^{{\text{new}}} } \right) = \varphi \left( {x_{i} } \right) \bullet \varphi \left( {v_{p}^{{\text{new}}} } \right) = \frac{{\sum\nolimits_{k = 1}^{l} {\left( {u_{kp} } \right)^{m} K\left( {x_{k} ,x_{i} } \right)} }}{{\sum\nolimits_{k = 1}^{l} {\left( {u_{kp} } \right)^{m} } }}$$
    (3)
    $$K\left( {v_{p}^{{\text{new}}} ,v_{p}^{{\text{new}}} } \right) = \varphi \left( {v_{p}^{{\text{new}}} } \right) \bullet \varphi \left( {v_{p}^{{\text{new}}} } \right) = \frac{{\sum\nolimits_{k = 1}^{l} {\sum\nolimits_{n = 1}^{l} {\left( {u_{kp} } \right)^{m} \left( {u_{np} } \right)^{m} K\left( {x_{k} ,x_{n} } \right)} } }}{{\left( {\sum\nolimits_{k = 1}^{l} {\left( {u_{kp} } \right)^{m} } } \right)^{2} }}$$
    (4)

    where

    $$\varphi \left( {v_{p}^{{\text{new}}} } \right) = \frac{{\sum\nolimits_{k = 1}^{l} {\left( {u_{kp} } \right)^{m} \varphi \left( {x_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{l} {\left( {u_{kp} } \right)^{m} } }}$$
    (5)
  6. 6.

    Update membership degree \(u_{ij}\) to \(u_{ij}^{{\text{new}}}\) according to Eq. (1).

  7. 7.

    If \(\mathop {\text{max}}\nolimits_{i,j} \left| {u_{ij}^{{}} - u_{ij}^{{\text{new}}} } \right| < \varepsilon\) stop algorithm, otherwise go to step (5).

2.2 Two-step correlation analysis (CA–CA)

In the first step of CA–CA method, the correlation between the input candidate and the output is computed. When the correlation index is higher, the candidate is more effective. If the computed correlation index is lower than a predetermined value Core1, then this candidate is deleted; otherwise, it is kept for the next step, in which the cross-correlation index between each pair of data, kept in step 1, is computed. If the computed index is less than predetermined value Core2, the selected data are saved; otherwise, the data with the lowest correlation with regard to output are deleted, while the others are saved [17, 34].

2.3 Time-series reconstruction

The phase space reconstruction technique provided by Takens, Aeyels and Sauer is a powerful application to analyze a univariate time series [35]. Suppose that each sub-partition of fuzzy clustering approach and candidate data driven from two-step correlation analysis can be assumed as a multidimensional stochastic time series including N data point. Regarding Takens embedding theory for any feature vector denoted by \(\{ x_{i} \} ,\;i = 1,2, \ldots ,N\). The nth delay vector can be reconstructed as \(X_{n} = \left\{ {x_{n} ,x_{n - \tau } , \ldots ,x_{n - (d - \tau )} } \right\}\) where d demonstrates the embedding dimension and τ is the time constant [36]. In this paper, AMI method [36] is used to choose optimum τ. In addition, Cao’s method [37] is applied to determine an acceptable embedding dimension d. Thus, the reconstructed phase space matrix of corresponding time series can be denote as Eq. (6)

$$X = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{1 + \tau } } & \cdots & {x_{1 + (d - 1)\tau } } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{{\hat{l}}} } & {x_{{\hat{l} + \tau }} } & \cdots & {x_{{\hat{l} + (d - 1)\tau }} } \\ \end{array} } \right]_{N \times d}$$
(6)

where \(N = N_{\text{subset}} - \, \left( {d - 1} \right) \times \tau\) and \(N_{\text{subset}} .\) is the data points total number in the nth subset. The next state of Eq. (6) is the corresponding target vector as Eq. (7)

$$Y = \left[ {\begin{array}{*{20}c} {x_{{\text{1} + d\tau }} } & {x_{{\text{2} + d\tau }} } & { \cdots } & {x_{{\hat{l} + d\tau }} } \\ \end{array} } \right]_{{\hat{l} \times \text{1}}}^{T}$$
(7)

2.4 SVR

Through mapping the input data to high-dimensional feature space, SVM uses linear regression which is less complicated compared to using nonlinear regression in low-dimensional feature space [38]. For a dataset \(\left\{ {\left( {x_{i} ,y_{i} } \right)} \right\},\; \, i = 1, \ldots ,N\) where denotes the ith input vector; our objective is to find a linear estimation function in this feature space as follows [21]:

(8)

where \(\left\langle , \right\rangle\) denotes the inner product, φ(x) is the mapped vectors, w denotes the weight vector and b is the balance. Since φ is fixed, these parameters are computed from the data by minimizing the following risk function. Since φ is fixed, these parameters are computed from the data by minimizing the following risk function [21]:

$$R = \frac{1}{2}\left\| w \right\|^{2} \,+\, {\text{CR}}_{{\text{emp}}} = \frac{1}{2}\left\| w \right\|^{2} \,+\, C\sum\limits_{i = 1}^{N} {L\left( {\hat{f}(x_{i} ) - y_{i} } \right)}$$
(9)

and

$$L\left( {\hat{f}(x_{i} ) - y_{i} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\left| {\hat{f}(x_{i} ) - y_{i} } \right| \le \varepsilon } \hfill \\ {\left| {\hat{f}(x_{i} ) - y_{i} } \right| - \varepsilon ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(10)

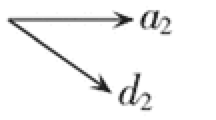
where L is Vapnik’s ε-insensitive loss function which is shown in Fig. 1, \(\frac{1}{2}\left\| w \right\|^{2}\) is the regularization term and C is the penalty factor which is the trade-off between regularization term and the loss function.

Fig. 1
figure 1

Vapnik ε-insensitive loss function

Full size image

As illustrated in Fig. 1, by introducing \(\xi_{i}^{{}}\) and \(\xi_{i}^{*}\) two positive slack variables that represent the error between actual values and margin support vectors, Eq. (9) can be written as [21]:

$$\varPhi \left( {w,\xi ,\xi^{*} } \right) = \frac{1}{2}\left\| w \right\|^{2} \,+ \,C\sum\limits_{i = 1}^{N} {\xi_{i} + \xi_{i}^{*} }$$
(11)
$$\text{St:}\;\left\{ {\begin{array}{*{20}l} {y_{i} - \left( {\left\langle {\varphi (x),w} \right\rangle + b} \right) \, \le \, \varepsilon + \xi_{i}^{*} } \hfill \\ {\left( {\left\langle {\varphi (x),w} \right\rangle + b} \right) - y_{i} \, \le \, \varepsilon + \xi_{i} } \hfill \\ {\xi_{i} , \, \xi_{i}^{*} \, \ge \, 0} \hfill \\ \end{array} } \right.$$
(12)

Using Lagrangian multipliers and applying the Karush–Kuhn–Tucker conditions, the following dual optimization problem is defined [21]:

$$\begin{aligned} &\text{Min}\; \, \frac{\text{1}}{\text{2}}\sum\limits_{{i = \text{1}}}^{l} {\sum\limits_{{j = \text{1}}}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i}^{{}} } \right)\left( {\alpha_{j}^{*} - \alpha_{j}^{{}} } \right)\left( {\varphi (x_{i}^{{}} } \right) \bullet \varphi \left( {x_{j}^{{}} )} \right)} } \hfill \\ &\quad + \, \varepsilon \sum\limits_{i = 1}^{l} {\left( {\alpha_{i}^{*} + \alpha_{i}^{{}} } \right)} - \, \sum\limits_{i = 1}^{l} {y_{i}^{{}} \left( {\alpha_{i}^{*} - \alpha_{i}^{{}} } \right)} \hfill \\ \end{aligned}$$
(13)

Subject to constraints:

$$\begin{aligned}& \sum\limits_{i = 1}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i}^{{}} } \right)} = \text{0}, \hfill \\ &\quad \text{0} \le \, \alpha_{i}^{{}} , \, \alpha_{i}^{*} \le C\text{,}\quad i = \text{1},{ \ldots },N \hfill \\ \end{aligned}$$
(14)

Solving the optimization problem in Eq. (13) leads to the values \(\alpha_{i}^{{}} \text{,}\;\alpha_{i}^{*}\), which are the parameters of SVM regression function [21]:

$$f\left( x \right) = \sum\limits_{{i = 1}}^{l} {\left( {\alpha _{i}^{*} - \alpha _{i} } \right)} \left\langle {\varphi \left( {x_{i} } \right),\varphi \left( {x_{j} } \right)} \right\rangle + b$$
(15)

Using a different function known as kernel instead of the dot product of the point φ (xi) and φ (xj) makes the SVR algorithm nonlinear. If a kernel function \(K\left( {x_{i} ,x_{j} } \right)\) satisfies the Mercer’s conditions, then it will be called an admissible SV kernel. Choosing a good kernel function is challenging and depends on the problem stiffness and input vectors. In this paper, the wavelet kernel function introduced by Li et al. [39] is used as a kernel function in Eq. (15).

2.5 WSVR

As mentioned in Sect. 2.4, an inner dot-product kernel is the formation of an SV’s kernel, which must satisfy Mercer’s condition. However, it is difficult to decompose a translation invariant kernel \((\text{i}.\text{e}.\;K(x_{i} ,x_{j} ) = K(x_{i} - x_{j} ))\) into the product of two functions and proof them as admissive SV kernels. According to [21], a translation invariant kernel is an admissible SV kernel if and only if the Fourier transform in Eq. (16) is nonnegative.

$$F\left[ K \right]\left( \omega \right){ = }\left( { 2\pi } \right)^{{{\raise0.7ex\hbox{${ - {\text{N}}}$} \!\mathord{\left/ {\vphantom {{ - {\text{N}}} \text{2}}}\right.\kern-0pt} \!\lower0.7ex\hbox{$\text{2}$}}}} \, \int_{{R^{N} }} {\text{e}^{{ - j\left( {\omega x} \right)}} K\left( x \right)\text{d}x} \,$$
(16)

More conditions for kernel functions are presented in [21]. According to wavelet theory, a function can be approximated by a family function produced by mother wavelet (h(x)), which must satisfy the following condition [30, 39]:

$$W_{h} = \int_{\text{0}}^{\infty } {\frac{{\left| {H(\omega )} \right|^{2} }}{\left| \omega \right|}\text{d}\omega < \infty }$$
(17)

where \(H\left( \omega \right)\) is the Fourier transform of h(x). Any function that was proved in the condition (17) can be a dilation and translation function as:

$$h_{{a,c}} (x) = \left| a \right|^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} h\left( {\frac{{x - c}}{a}} \right).$$
(18)

According to Tensor theory, an N-dimensional wavelet function can be written as [40]:

$$h\left( X \right){ = }\prod\limits_{{i = \text{1}}}^{N} {h\left( {x_{i} } \right)}$$
(19)

where every \(h_{i} \left( x \right),\quad i = \text{1},{ \ldots },N\) must separately satisfy the condition in Eq. (16). For any admissible mother wavelet function, the wavelet kernel that satisfies the translation invariant theorem can be presented as:

$$K(x,x^{\prime}) = \prod\limits_{{i=1}}^{N} {h\left( {\frac{{x_{i}- x_{i}^{\prime } }}{a}} \right)}.$$
(20)

The Morlet’s wavelet function is used as the mother wavelet in this paper as showed in Eq. (21) [30],

$$h(x)=\text{cos}({1.75x})\exp(-x^{2}/2).$$
(21)

Considering Eq. (21), it has been proofed that the Morlet’s wavelet kernel function in Eq. (20) can be defined as (22) which is an acceptable SV kernel function [30]

$$K(x,x^{\prime } ) = \prod\limits_{i}^{N} {\left( {\cos \left( {1.75 \times \frac{{\left( {x_{i} - x_{i}^{\prime } } \right)}}{a}} \right)\exp \left( { - \frac{{\left\| {x_{i} - x_{i}^{\prime } } \right\|^{2} }}{{2a^{2} }}} \right)} \right)} .$$
(22)

In order to measure the forecast error, mean absolute percentage error (MAPE) is used as an index for performance evaluation. This index is given by the following equation.

$$\text{MAPE} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{{\left| {\widehat{{L_{F} }}\left( i \right) - L_{{\text{Actual}}} \left( i \right)} \right|}}{{L_{{\text{Actual}}} \left( i \right)}}}$$
(23)

where i is the number of days, \(\widehat{{L_{F} }}\left( i \right)\) is the forecasted load of the ith day and \(L_{{\text{Actual}}} \left( i \right)\) is the ith day actual load.

3 The proposed method

In the first step of the proposed method, four attributes are considered as feature vectors of each day including daily peak load, daily temperature, calendar attributes and holiday index. In the first step, the best input data are selected in the clustering stage by the KFCM and the CA–CA methods. Then, for each subset driven from the second step, the reconstructed matrices of corresponding time series in phase space are represented in Eqs. (6) and (7). Having considered the time-series modeling, the training dataset for a particular day is formatted as (24):

$$\left[ {\left\{ {x_{i} , \, x_{{i + \text{1}}} , \ldots , \, x_{{i + \, \left( {d - \text{1}} \right) \, \tau }} } \right\},\;\text{temperature},\;\text{type}\;\text{of}\;\text{day},\;\text{holiday}\;\text{index}} \right].$$
(24)

According to Eq. (24), each training sample consists of at most d + 9 feature vectors, which include the following data: time delay vector corresponding to the ith normalized peak load in the length of d, normalized average daily temperature; seven binary digits denoting the day of week and one binary digit, 0 or 1, which represent the holiday index. Consequently, the training data are arranged in a matrix of size \(N_{{\text{subset}}} \times \, \left( {d + \text{9}} \right)\). According to Eq. (7), the training target vector Y is the normalized daily peak load that shifted τ days ahead by considering the last vector of the reconstructed load matrix. Solving the SVR optimization problem by GA in training stage and finding the optimal αi′s and α * i ′s, the regression (predictor) function will be formed as:

$$f\left( x \right) = \sum\limits_{{i = \text{1}}}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i}^{{}} } \right)} k\left( {x_{i} ,x_{j} } \right) + b$$
(25)

where k is the wavelet kernel defined in Eq. (22). D number of historical data are used as the input data of Eq. (25) for forecasting the next day peak load. The flowchart corresponding to the proposed methods is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of proposed MTLF

Full size image

4 Experimental results

The first dataset is tested for obtaining the minimum possible error within EUNITE 2001 competition, and the second one is Iran’s power system during 2002–2005. The main objective of this section is to analyze the data and find a relationship between consumption loads and other available information.

4.1 Data analysis

In 2001, EUNITE held a competition for load forecasting of January 1999. The input data were consumption load data (Jan. 1997–Dec. 1998), average daily temperature (Jan. 1995–Dec. 1998), calendar information and holiday indices (Jan. 1997–Dec. 1998) [41]. These data are discussed widely by Bo-Juen et al. [23].

Iran’s power system data are as follows. The hourly power consumption data from 2002 to 2005 [42], the calendar information and the holiday indices [43]. In this paper, one of system specification, i.e., Iran meteorological data are not considered due to Iran geographical breadth and the presence of all three cold, tropical and temperate climates; as the south region of Iran has tropical climate, while the northwest region is rather cold. Therefore, the long-term meteorological forecasting is a highly complicated task.

As Fig. 3 shows, the power consumption increases significantly within a 3-year period, indicating that the country is in development state. Amjady and Keynia [34] recommendation is using a 2-year historical data for short-term prediction of Iran’s power system, considering its rapidly changing consumption pattern. Based on Fig. 4, it can be noticed that although average power consumption rises significantly, it follows a similar pattern for working days during the period March 21, 2002–March 20, 2005. However, this pattern is different for weekends inasmuch as the maximum power consumption decreases during Thursdays, Fridays and holidays.

Fig. 3
figure 3

Monthly averages of the load—Iran’s power system (March 21, 2002–March 20, 2005)

Full size image
Fig. 4
figure 4

Hourly load averages for each day of the week—Iran’s power system (March 21, 2002–March 20, 2005)

Full size image

In Iran, most of the religious holidays are based on the lunar calendar. However, the official calendar in Iran is the solar calendar. Given the fact that a lunar year is 11 days shorter than a solar year, holidays are dissimilar each year in Iran. In fact, the calendar information and holiday indices are the most important factors in predicting the electrical power of Iran’s power system [34]. Therefore, it is required to adjust the solar calendar for most holidays except Fridays, which is Iran’s weekend. Such complications make modeling Iran power consumption a difficult task.

4.2 Numerical results

The proposed MTLF methods are programmed in MATLAB and are tested on two datasets. The test results are discussed in this section.

4.2.1 EUNITE competition data

In this section, the kernel-based fuzzy clustering approach, introduced in Sect. 2.1, is employed to divide the EUNITE dataset into two subsets. The obtained results for each day fuzzy membership degree are shown in Fig. 5. Owing to the negative correlation between electrical power data and average daily temperature, according to Fig. 6, the load dataset is divided into two subsets: data of cold months of the year (October–March) and data for spring and summer (April–September).

Fig. 5
figure 5

Fuzzy membership degree for a subset 1, b subset 2—EUNITE data (1997–1998)

Full size image
Fig. 6
figure 6

Kernel-based fuzzy C-mean clustering results—EUNITE data (1997–1998)

Full size image

By using the AMI method, the time delay value is separately computed for the maximum daily power load time series and average daily temperature time series. Subsequently, the embedding dimension values are computed using Cao’s method. The computed results are presented in Table 1. The results of the proposed methods are explained blow:

Table 1 Embedding dimension and the time delay constant for various time series
Full size table
  1. 1.

    Forecasting using KFCM clustering and WSVR (KFCM–WSVR)

In this section, clustering and retrieving the desired time series is performed by using the time-series modeling with and without considering the average daily temperature data as a feature vector. Due to the lack of access to temperature values of January 1999, the average daily temperature data of two past Januaries extracted from historical data were used.

Using the proposed method, which is described in Sect. 3, the MAPE value is 1.34 and 1.31% for the dataset with and without temperature, respectively. As illustrated in Fig. 7, once the temperature inputs are ignored, the obtained results are relatively more accurate. The modeling in Ref. [23], which was the winner of EUNITE competition with the error value of 1.95%, also proves that even using real temperature values does not improve the prediction results.

Fig. 7
figure 7

Forecasts and actual load—EUNITE data (January 1999)

Full size image
  1. 2.

    Forecasting by using the two-step correlation analysis and WSVR (CA–CA-WSVR)

In this method, the power data of January 1998 were selected as the target vector. Next, two analytical correlative steps were applied in order to find the data of maximum linear correlation with target vector.

A comparison between the optimum results obtained from two proposed methods and January 1999 actual load is illustrated in Fig. 7. As shown in Table 2, the results obtained using CA–CA-WSVR indicate lower MAPE as compared to the results of KFCM–WSVR; however, the maximum error value obtained from this method reveals a rise as compared to previous method. This difference in error values can be attributed to several reasons. First, appropriate input vectors are not chosen properly due to the nonlinear nature of the load. Secondly, applying the past year data as a sample of target vector which generates error in the next steps of modeling process. Thirdly, choosing the insufficient embedding dimension, which might increase error value owing to the computations uncertainty through Cao’s method. The simulation results are compared with some published methods based on SVM in Table 2. Bo-Juen et al. [23] reduced the MAPE to 1.95% by using their proposed SVM method and won the EUNITE competition in 2001. Abbas and Arif [25] applied genetic algorithm in optimizing and obtaining the parameters of SVM and improved the obtained results. Amjady and Keynia [34] applied two correlative analytical steps in order to select target features of the Evolutionary Algorithm and Levenberg–Marquardt Algorithm-based predictions. The proposed algorithm known as CA–CA–EA–LM has an error value of 1.60%. El-Attar et al. [44] reached an error value of 1.52% by using a local SVM model (LSVM). They presented a weighted model for their previous method (LWSVM), and improved error value to 1.34% [35], which is almost equal to this research MAPE for KFCM–WSVR with temperature data. Having used least square SVM (LS-SVM) and chaos theory, Haishan and Xiaoling [45] reached to MAPE value of 1.1% which is in the range of the error values generated using KFCM–WSVR and CA–CA-WSVR in this paper.

Table 2 Comparison of the proposed models and other models—EUNITE network data
Full size table

4.2.2 Iran’s power system

The historical data of electrical power network within March 21, 2002 to March 20, 2005 are used to predict maximum daily power consumption of March 21, 2004 to April 20, 2004.

In the KFCM–WSVR method, the optimum embedding dimension is extracted for the developed time series. The results of implementing of Cao’s method are shown in Fig. 8. We calculate the E1(d) and the E2(d) using 369 data driven from KFCM method where we let the time delay \(\tau\) equal to 1. Due to the random nature of load data, the future load values are independent of the past load values, and thus E2(d) will be equal to 1 for any given d in this case; where d is embedding dimension. As shown in Fig. 8, E1(d) stops changing when d is greater than d0. Therefore, d0 + 1 is the minimum embedding dimension we look for. Using the embedding dimension values which are descried in Fig. 8, Eqs. 6 and 7, the training matrix is calculated as below.

$${\text{Training}}\;{\text{Matrix}} = \left[ {L_{728} \begin{array}{*{20}l} {L_{1} } \hfill & {L_{2} } \hfill & \cdots \hfill & {L_{6} } \hfill & {L_{7} } \hfill & {T_{8} } \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {L_{2} } \hfill & {L_{3} } \hfill & \cdots \hfill & {L_{7} } \hfill & {L_{8} } \hfill & {T_{9} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {L_{722} } \hfill & {L_{723} } \hfill & \cdots \hfill & {L_{727} } \hfill & {L_{728} } \hfill & {T_{729} } \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {L_{723} } \hfill & {L_{724} } \hfill & \cdots \hfill & {L_{728} } \hfill & {L_{729} } \hfill & {T_{730} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]_{369 \times 16}$$
(26)
$${\text{Target}}\;{\text{Matrix }} = \left[ {\begin{array}{*{20}l} {L_{8} } \hfill & {L_{9} } \hfill & \ldots \hfill & {L_{729} } \hfill & {L_{730} } \hfill \\ \end{array} } \right]_{1 \times 369}^{T}$$
(27)
Fig. 8
figure 8

Values E1 and E2 for the data from Iran’s power system

Full size image

Results of Table 1 are used to retrieve dynamic state of the studied system. Due to embedding dimension uncertainty, the values 5 < d < 8 are tested. As show in Table 3, the MAPE value is equal to 2.00% for d = 6.

Table 3 Comparison of obtained result for different value of embedding dimension—Iran’s power system
Full size table

In CA–CA-WSVR method, the similarity of the target day specifications and the selected sample vector is the factor that must be considered. For a numerical example, in order to forecast the load of March 21, 2004, the similar day in 2003 is considered as a target vector. In the first step of CA–CA method, the last two years daily load data are used as candidate inputs. The correlation between the target day and these data is calculated which are shown in Fig. 9. Then, the data with correlation index equal to or less than Core1, which is selected 0.7, will be deleted, while other data are kept for step 2. In step 2, the cross-correlation index between each pair of data, kept in step 1, is computed. Then, the data with correlation index equal to or less than Core2, which is selected 0.7, will be deleted while keeping other data. After the two-step correlation, the data shown in Table 4 are selected as input vectors.

Fig. 9
figure 9

Results of the first step of the correlation analysis for March 21, 2004—Iran’s power system

Full size image
Table 4 Results of the correlation analysis for the Iran’s power system (March 21, 2002)
Full size table

In training phase for each SV, the same day/month in the last year must be deleted from the training set and considered as the unseen validation. Therefore, the number of validation data is equal to number of test data. In the training stage, the optimal SVM parameters are found using GA. The population size, crossover ratio, mutation percentage and mutation ratio in GA are 50, 0.8, 0.3 and 0.04, respectively. After 200 iterations, the penalty factor, error margin and scaling parameter of wavelet kernel calculated by GA are 1.4739, 0.01636 and 0.4051, respectively.

The results obtained from KFCM–WSVR and CA–CA-WSVR are presented in Fig. 10. Table 5 shows that our CA–CA-WSVR model has better forecast accuracy and stability than the proposed KFCM–WSVR data model, due to less value of average MAPE. According to Table 2 and Table 5, it is clear that the MAPE value of our proposed method showed 45% improvement comparing to all average MAPE values of Table 2. This enhanced accuracy is mainly related to the forecast block and especially its preprocessing mechanism. Ref. [45] which used chaos theory and time-series reconstruction as its preprocessing method with SVM has shown results with less accuracy comparing to the proposed model in this paper. Therefore, selecting efficient preprocessing is an important for forecasting. Moreover, Ref. [34] which used the same preprocessing method as our paper, but with Levenberg–Marquardt, has also shown results with larger MAPE value. This indicates that choosing an efficient preprocessing method is not enough.

Fig. 10
figure 10

Actual load (solid line), forecast with KFCM–WSVR (dash dot line with pentacle sign), forecast with CA–CA-WSVR (dash line with square sign)—Iran’s power system (March 21, 2004–April 20, 2004)

Full size image
Table 5 Obtained results with proposed forecast models—Iran’s power system
Full size table

Both proposed methods, KFCM and CA–CA, provide acceptable results except for only some days such as March 21. The error in this day is mainly due to selecting inappropriate candidate as input vectors for the model. In fact, considering the optimal embedding dimension, the load data of March 13–20 are used as input vectors in KFCM model in order to forecast the load of March 21. However, there is not enough similarity between input vectors, which are the last days of a year, and the target vector, which is the first day of a year. This is mostly because the commercial load consumption is high in the last days of the year. The errors of forecasting for the next days are higher in KFCM method due to the fact that it uses the last day’s data for forecasting the next day, and thus there always exists an accumulated error for forecasting the next days. For example, the error of predicted data for March 21 is used for March 22. Nevertheless, the CA–CA model does not use embedding windows, and thus the error in it is much lower.

5 Conclusion

A new method is suggested in this work for MTLF, which is an important part of today power systems studies. Two hybrid SVR-based methods are proposed for reducing the complexity between the load data and other related variables and improve MTLF accuracy. A kernel-based fuzzy clustering technique and a two-step correlation analysis are separately used to extract the optimal subset from historical data. Simulation results on EUNITE competition data show that the suggested methods are more efficient in comparison with other related methods. Moreover, the suggested methods are evaluated on Iran’s power system data. The advantage of the proposed methods is using Mercer’s kernel theory, which allows us to deal with nonlinear data. The performance of the proposed KFCM–WSVR method shows its less sensitivity to weather data. Furthermore, the simulations confirm that the CA–CA-WSVR model shows better results in comparison with KFCM–WSVR mode.