The MST problem in network with uncertain edge weights and uncertain topology

Abstract

In real path selection decisions, besides the cost of the path which is the major decision factor, the chance of the path connection is also significant. A path which has low weight but low chance of existence is not a good choice for decision-making. In order to make network optimization more in line with the actual situation, this paper studies one model of it on a network whose existence and weight of edges are both indeterminate. The aim of this paper is to obtain a spanning tree which satisfies the connectivity constraint and minimizes the total weight as well. The study uses conditional uncertain variable to describe the relationship between these two aspects of uncertain variables. On this basis, three different models of the UMST problem are suggested, and the equivalence relation between the MST model of uncertain networks with uncertain edge existence and weight and the MST of related deterministic networks is found. Examples of experiments with specific numerical values are provided to verify the variation in the network when two variables are considered simultaneously.

1 Introduction

We live in a network society. In a sense, modern society is a complex network system composed of computer information network, telephone communication network, energy and material distribution network and so on. Network system is a special form of system, its nodes are the components of the system, and the edges represent the interaction and dependence between the components of the system. The system is the indispensable material foundation of our society which is closely related to our production and living. Therefore, the research on network system is particularly important. A lot of optimization problems are involved in network system, and one of typical examples is the solution of minimal spanning tree which can be applied to facility location, circuit and network design and so on.

In classical graph theory (Harary 1962; Bondy and Murty 1976; Gross et al. 2018; West 2001), the existence of edges and vertices is determined; thus, a classical graph with definite edge weights becomes a classical network, which is the object of the deterministic network optimization research. Many scholars have researched the MST problem in determining network in depth and developed effective algorithms for solving it, such as Gen and Cheng (1999), Öncan (2007), Zhout and Gen (1998), Narula and Ho (1980), Julstrom (2004). And the stochastic MST problem appeared to handle more practical issues (Ishii et al. 1981; Torkestani and Meybodi 2012; Swamy and Shmoys 2006; Dhamdhere et al. 2005). However, when historical data were missing, it would be unrealistic to use deterministic or probability models to deal with MST problems. For purpose of solving the uncertainty phenomenon, particularly those with only expert data and subjective estimates, in 2007, Liu established the theory of uncertainty (Liu 2007) and revised and improved the definition when 2010 (Liu 2010). Through the efforts of many researchers over the years, the theory has now developed into one branch of mathematics, which has made great progress both in theory (Liu 2008; Li and Liu 2009; Yao 2013, 2015) and in application (Liu and Liu 2009; Gao et al. 2010; Zhu 2010; Liu 2013; Peng 2013; Zhou et al. 2022).

After the uncertainty theory was proposed, the networks with uncertain edge weights were defined as uncertain networks in 2010 (Liu 2010). Under this definition, Peng and Li (Peng and Li 2011) discussed the minimum spanning tree problem in uncertain networks. They also designed three optimization models for UMST problems from the perspectives of minimum expected value, minimum inverse distribution at a certain confidence level and minimum distribution. The uncertain quadratic MST problem was introduced in 2014 by Zhou et al. (2014). Gao and Jia (2017) studied an uncertain MST problem in which the degree of each vertex of the tree is limited for the first time.

Although there have been so many researches on UMST, they only think about the edge of network which has an uncertain weight; then, how would the UMST problem be like if the existence of the edge is not certain either? The connectivity is a fundamental conception of graph theory, which can be easily verified in classical graphs where edges and vertices are determined. But in practical matters, the emergence of uncertainty factors will cause different scenarios and new discussions. Gao and Gao (2013) have discussed significance of the connectedness index of uncertain graph where whether two nodes are linked is uncertain, and introduced the maximum connectedness index spanning tree. After learning the results of previous studies, we propose a new uncertain network environment, assuming that the existence and weight of edges in the network are uncertain, to research the spanning tree that can not only satisfy the connectivity limit but also achieve the minimum total weight.

The rest of the paper is formed as follows. In Sect. 2, we present a few fundamental concepts and theorems about uncertainty theory. The UMST problem in uncertain network considering connectedness limit is studied in Sect. 3. And we analyze three different UMST models to solve the problem in Sect. 4. Then, in Sect. 5, numerical experiments are given to explain and support the conclusions. In Sect. 6, we summarized this paper briefly.

2 Preliminary

In this section, we introduce some fundamental concepts and properties of the uncertainty theory, which will be used throughout this paper.

Definition 1

(Liu 2007, 2009) Let $\Gamma$ be a nonempty set, and $\mathcal {L}$ is a $\sigma$-algebra over $\Gamma$, a set function $\mathcal {M}:\mathcal {L}\rightarrow [0,1]$ is called an uncertain measure if it satisfies the following axioms:

Axiom 1

(Normality axiom) $\mathcal {M}\{\Gamma \}=1$ for the universal set $\Gamma$;

Axiom 2

(Duality axiom) $\mathcal {M}\{\Lambda \}+\mathcal {M}\{\Lambda ^c\}=1$ for any event $\Lambda$;

Axiom 3

(Subadditivity axiom) For every countable sequence of events $\Lambda _1, \Lambda _2, \ldots ,$ we have $\mathcal {M}\{\bigcup _{i=1}^{\infty }{\Lambda _i} \} \le \sum _{i=1}^{\infty }{\mathcal {M}\{ \Lambda _i \}}$;

Axiom 4

(Product axiom) Let $(\Gamma _k, \mathcal {L}_k, \mathcal {M}_k)$ be uncertainty spaces for $k = 1, 2, 3,\ldots$. The uncertain measure $\mathcal {M}$ satisfies the following formula:

$$\begin{aligned} \mathcal {M}\left\{ \prod _{k=1}^{\infty }{\Lambda _k}\right\} =\bigwedge _{k=1}^{\infty }{\mathcal {M}_k\{ \Lambda _k \}} \end{aligned}$$

(1)

where $\Lambda _k$ are arbitrarily chosen events from $\mathcal {L}_k$ for $k=1, 2, 3, \ldots ,$ respectively.

The triplet $(\Gamma , \mathcal {L}, \mathcal {M})$ is called an uncertainty space.

Definition 2

(Liu 2007) An uncertain variable is a measurable function $\xi$ from an uncertainty space $(\Gamma , \mathcal {L}, \mathcal {M})$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set $\{ \xi \in B \} =\{ \gamma \in \Gamma \mid \xi ( \gamma ) \in B \}$ is an event.

Definition 3

(Liu 2007) The uncertainty distribution $\Phi$ of an uncertain variable $\xi$ is defined by $\Phi ( x ) =\mathcal {M}\{ \xi \le x \}$ for any real number x.

For example, an uncertain variable $\xi$ is called an Boolean uncertain variable if $\xi$ only has two possible value 0 and 1 , and $\mathcal {M}\{\xi = 1\} = \alpha$, $\mathcal {M}\{\xi = 0\} = 1-\alpha$. Then, the distribution of $\xi$ is shown in Fig. 1a.

$$\begin{aligned} \Phi (x) =\left\{ \begin{array}{ccl} 0,&{} &{}{x< 0}\\ 1-\alpha ,&{} &{}{0 \le x < 1}\\ 1,&{} &{}{x \ge 1} \end{array} . \right. \end{aligned}$$

(2)

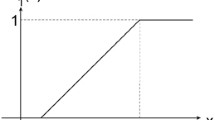
An uncertain variable $\xi$ is called linear if it has a linear uncertainty distribution (Fig. 1b)

$$\begin{aligned} \Phi (x) =\left\{ \begin{array}{ccl} 0,&{} &{}{x< a}\\ (x-a)/(b-a),&{} &{}{a \le x < b}\\ 1,&{} &{}{x \ge b} \end{array} . \right. \end{aligned}$$

(3)

Fig. 1

Uncertainty distributions

Definition 4

(Liu 2010) An uncertainty distribution $\Phi (x)$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0 \le \Phi (x) \le 1$, and $\lim _{x\rightarrow -\infty } \Phi ( x ) =0, \lim _{x\rightarrow +\infty } \Phi ( x ) =1$.

Definition 5

(Liu 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi (x)$. Then, the inverse function $\Phi ^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\xi$.

It can be easily found that the linear uncertainty distribution is regular with the inverse uncertainty distribution

$$\begin{aligned} \Phi ^{-1}(\alpha ) = (1-\alpha )a + \alpha b. \end{aligned}$$

(4)

Liu et al. (2016) extended the classical operational law to that for general monotonic (not necessarily strictly monotonic) functions, following from which the concept of generalized inverse uncertainty distribution was also suggested.

Definition 6

(Liu et al. 2016) Let $\xi$ be an uncertain variable. A function $G : [0, 1] \mapsto \mathfrak {R}$ is called the generalized inverse uncertainty distribution of $\xi$ if $\mathcal {M}\{ \xi \le G( \alpha ) \} = \bar{\alpha }$ where $\bar{\alpha } = \sup \{\beta \mid G(\beta ) = G(\alpha )\}$.

The generalized inverse uncertainty distribution is defined for noncontinuous and not strictly increasing uncertainty distribution on the domain [0, 1], which is a natural extension of the concept of inverse uncertainty distributions with regard to regular uncertainty distributions since we have $\bar{\alpha } = \alpha$ for all $\alpha \in [0, 1]$ if $\xi$ is a regular uncertain variable.

Theorem 1

(Liu et al. 2016) Let $\Psi (x)$ be an uncertainty distribution of the uncertain variable $\xi$, and denote by $D_{\Psi }$ the domain of values of $\Psi (x)$. Then, the generalized inverse uncertainty distribution of $\xi$ can be derived as

$$\begin{aligned} \tilde{\Psi }^{-1}(\alpha ) =\left\{ \begin{array}{rclcl} \sup \{x \mid \Psi (x) = 0\},&{} &{}\alpha = 0&{}\\ \forall x_0 \in \{x \mid \Psi (x) = \alpha \},&{} &{}0< \alpha< 1,&{} \alpha \in D_{\Psi }\\ \inf \{x \mid \Psi (x) \ge \alpha \},&{} &{}0< \alpha < 1, &{}\alpha \notin D_{\Psi } \\ \inf \{x \mid \Psi (x) = 1\},&{} &{}\alpha = 1.&{} \end{array} \right\} .\nonumber \\ \end{aligned}$$

(5)

Definition 7

(Liu 2009) The uncertain variables $\xi _1, \xi _2, \ldots , \xi _n$ are said to be independent if $\mathcal {M}\{ \bigcap _{i=1}^n{\{ \xi _i\in B_i \}} \} = \underset{1\le i\le n}{\min }\mathcal {M}\{ \xi _i \in B_i \}$ for any Borel sets $B_1, B_2, \ldots , B_n$ of real numbers.

Definition 8

(Liu 2007) Let $(\Gamma , \mathcal {L}, \mathcal {M})$ be an uncertainty space and A and $A_1$ be two uncertain events with $\mathcal {M}\{A\}>0$. Then, the conditional uncertain measure of $A_1$ given A is

$$\begin{aligned} \mathcal {M}\{A_1 \vert A\} =\left\{ \begin{array}{ccl} \frac{\mathcal {M}\{A_1 \cap A\}}{\mathcal {M}\{A\}},&{} &{}if\,\, \frac{\mathcal {M}\{A_1 \cap A\}}{\mathcal {M}\{A\}}<0.5\\ 1-\frac{\mathcal {M}\{A^C_1 \cap A\}}{\mathcal {M}\{A\}},&{} &{}if\,\, \frac{\mathcal {M}\{A^C_1 \cap A\}}{\mathcal {M}\{A\}}<0.5\\ 0.5,&{} &{}otherwise \end{array} . \right. \end{aligned}$$

(6)

In this case, the triple $(\Gamma , \mathcal {L}, \mathcal {M}\{\cdot \vert A\})$ is also an uncertainty space, which is usually called the conditional uncertainty space of $(\Gamma , \mathcal {L}, \mathcal {M})$ given A.

Definition 9

(Liu 2007) Let $\xi$ be an uncertain variable. Then, the expected value of $\xi$ is defined by

$$\begin{aligned} E\left[ \xi \right] =\int _0^{+\infty }{\mathcal {M}\{ \xi \ge x \}}\text {d}x-\int _{-\infty }^0{\mathcal {M}\{ \xi \le x \}}\text {d}x \end{aligned}$$

(7)

provided that at least one of the two integrals is finite.

Theorem 2

(Liu 2007) Let $\xi$ be an uncertain variable with uncertainty distribution $\Phi (x)$. Then,

$$\begin{aligned} E\left[ \xi \right] =\int _0^{+\infty }{( 1-\Phi ( x ))}\text {d}x-\int _{-\infty }^0{\Phi ( x )}\text {d}x. \end{aligned}$$

(8)

Theorem 3

(Liu 2010) Let $\xi$ and $\eta$ be independent uncertain variables with finite expected values. Then, for any real numbers a and b, we have

$$\begin{aligned} E\left[ a\xi + b\eta \right] = aE\left[ \xi \right] +bE\left[ \eta \right] . \end{aligned}$$

(9)

3 The UMST problem considering the connectedness limitation

3.1 Deterministic MST problem

Let $G = (V,E,W)$ denote a connected graph consisting of the vertex set $V = \{v_1, v_2, \cdots , v_n\}$, the edge set $E = \{e_1, e_2, \ldots , e_m\}$, and the edge weight vector $W = (w_1, w_2, \ldots , w_m)^T$. A spanning tree $T = (V, S)$ of G is a connected acyclic subgraph containing all vertices, where S is the set of edges contained in T. Then, discovering a spanning tree whose total value of edge weight is not more than the total edge weight of any other spanning trees is the purpose of MST problem in deterministic networks.

Definition 10

Under the assumption that $G = (V, E, W)$ is a connected graph, a spanning tree $T_0$ is referred to as a minimum spanning tree if

$$\begin{aligned} \sum \limits _{e_i \in T_0} w_i \le \sum \limits _{e_j \in T} w_j \end{aligned}$$

(10)

holds for any spanning tree T.

The mathematical model of the DMST problem is as follows

$$\begin{aligned} \left\{ \begin{array}{l} \min \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{w_{ij}x_{ij}}}\\ subject\,\, to:\\ \,\, \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{x_{ij}}}=n-1\\ \,\, \sum \limits _{i\in S}{\sum \limits _{j\in S}{x_{ij}}}\le \left| S \right| -1, \forall S\subset V\,\,and\,\,\left| S \right| \ge 2\\ \end{array} \right. \end{aligned}$$

(11)

where $w_{ij}$ means the weight of the edge between $v_i$ and $v_j$, and $x_{ij} = \{0,1\}$ is a Boolean variable which values as 1 when the tree contains the edge $e_{ij}$ $i,\,\ j = 1, 2, \ldots , n$.

3.2 Uncertain MST problem considering connectedness

The UMST problem that only considers weights of edges being uncertain variables has been discussed for years (Peng and Li 2011; Zhou et al. 2014; Gao and Jia 2017). Now let’s take the uncertain topology structure into consideration, thinking the UMST problem with both uncertain topology structure and uncertain weights. Let $G = (V, \mathcal {E}, \mathcal {W})$ denote the uncertain network, where $V = \{v_1, v_2, \cdots , v_n\}$ is the collection of nodes, $\mathcal {E} = \{\xi _{11}, \xi _{12}, \ldots , \xi _{nn}\}$ is the set of uncertain edges, $\mathcal {W} = \{w_{11}, w_{12}, \cdots , w_{nn}\}$ is the set of uncertain weights of edges. We assume that $\xi _{ij}, \,\ i, j = 1, 2, \ldots , n$ are independent uncertain Boolean variables, which mean the edge between $v_i$ and $v_j$ exists with a degree of confidence, and $w_{ij}, \,\ i, j = 1, 2, \cdots , n$ are independent and positive uncertain variables which obey regular uncertainty distributions.

Then, the UMST model can be described as follows

$$\begin{aligned} \left\{ \begin{array}{l} \min \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{w_{ij}\xi _{ij}}}\\ subject\,\, to:\\ \,\, \mathcal {M}\left\{ \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{\xi _{ij}}}=n-1\right\} \ge \alpha _1\\ \,\, \mathcal {M}\left\{ \sum \limits _{i\in S}{\sum \limits _{j\in S}{\xi _{ij}}}\le \left| S \right| -1, \forall S\subset V\,\,and\,\,\left| S \right| \ge 2\right\} \ge \alpha _2\\ \end{array} \right. \end{aligned}$$

(12)

where $\alpha _1, \alpha _2$ are given confidence level.

Although $w_{ij}$ are independent with each other and so as $\xi _{ij}$, there may have relationships between $w_{ij}$ and $\xi _{ij}$. If $\xi _{ij} = 0$, the connection between $v_i$ and $v_j$ is disappeared; then, it’s meaningless to talk about the weight of the edge $\xi _{ij}$. Experts give the assumption of the uncertainty distribution of $w_{ij}$ must under the circumstances that the edge exits. Then, the distribution of $w_{ij}$ can satisfy the equation

$$\begin{aligned} \Phi _{ij}(x) = \mathcal {M}\{w_{ij} \le x\} = \mathcal {M}\{(w_{ij} \le x) \cap (\xi _{ij} = 1) \}. \end{aligned}$$

(13)

Use conditional variable $\eta _{ij} = \{w_{ij}\mid \xi _{ij}=1\}$ to describe the weight $w_{ij}$ given the edge $\xi _{ij}$ exits, the UMST model can be changed as

$$\begin{aligned} \left\{ \begin{array}{l} \min \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{\eta _{ij}x_{ij}}}\\ subject\,\, to:\\ \,\, \mathcal {M}\left\{ \sum \limits _{i=1}^{n-1}{\sum \limits _{j=i+1}^n{\xi _{ij}}}=n-1\right\} \ge \alpha _1\\ \,\, \mathcal {M}\left\{ \sum \limits _{i\in S}{\sum \limits _{j\in S}{\xi _{ij}}}\le \left| S \right| -1, \forall S\subset V\,\,and\,\,\left| S \right| \ge 2\right\} \ge \alpha _2\\ \end{array} \right. \end{aligned}$$

(14)

where $\alpha _1, \alpha _2$ are given confidence level and $x_{ij}=\{0, 1\}, i,j = 1, 2, \ldots , n$ are Boolean decision variables.

Through this way, we transform the decision function with two kinds of uncertain variables into a function with one kind uncertain variable $\eta = \{w\mid \xi =1\}$.

From Definition 8, it’s easily founded that the distribution of $\eta _{ij}$ is

$$\begin{aligned} \Psi _{ij}(x)=\left\{ \begin{array}{ccl} \frac{\Phi _{ij}(x)}{\alpha _{ij}},&{} &{}if\,\, \Phi _{ij}(x)<\frac{1}{2}\alpha _{ij}\\ 1-\frac{1-\Phi _{ij}(x)}{\alpha _{ij}},&{} &{}if\,\, 1-\Phi _{ij}(x)<\frac{1}{2}\alpha _{ij}\\ 0.5,&{} &{}otherwise \end{array} \right. \end{aligned}$$

(15)

where $\Phi _{ij}(x)$ is the uncertainty distribution of $w_{ij}$ as defined in (13), $\mathcal {M}\{\xi _{ij}=1\}=\alpha _{ij}$, $\mathcal {M}\{\xi _{ij}=0\}=1-\alpha _{ij}$.

4 Three types of UMST model

For the UMST model considering connectedness, in the uncertain network $G = (V, \mathcal {E}, \mathcal {W})$, we can denote a spanning tree T’s total weight of as $W(T, \alpha _T)$, i.e.,

$$\begin{aligned} W(T, \alpha _T) = \sum \limits _{\mathcal {M}\{\xi _i\in T\}\ge \alpha _T}\eta _{i} \end{aligned}$$

(16)

where $\eta _{i} = \{w_i\mid \xi _i = 1\}$, $\alpha _T$ is a known confidence level, meaning the connectedness of T must larger than requirement. As $\eta _{i}$ is an uncertain variable whose uncertainty distribution is not regular (15), $W(T, \alpha _T)$ is not a regular uncertain variable either.

In this section, we are talking about three transformations to the UMST model on the purpose of converting the uncertain model into determinate model, which are the expected UMST, the $\alpha$-UMST and the most UMST.

4.1 Expected UMST

Definition 11

Suppose $G = (V, \mathcal {E}, \mathcal {W})$ be an uncertain network with n nodes, independent Boolean uncertain variables $\xi _{ij}, \,\ i,j = 1, 2, \ldots , n$ be the edges, and independent uncertain variables $w_{ij}, \,\ i,j= 1, 2, \ldots , n$ be the weights of the edges. A spanning tree $T_0$ is called an uncertain expected UMST with connectedness above $\alpha _T$ if

$$\begin{aligned} E\left[ W(T_0, \alpha _T)\right] \le E\left[ W(T, \alpha _T)\right] \end{aligned}$$

(17)

holds for every other uncertain spanning tree T, where $E\left[ W(T, \alpha _T)\right]$ stands for the expected value weight of T under given confidence level $\alpha _T$ and $E\left[ W(T_0, \alpha _T)\right]$ stands for the expected value weight of $T_0$ under given confidence level $\alpha _T$.

Theorem 4

Given an uncertain network $G = (V, \mathcal {E}, \mathcal {W})$, a spanning tree $T_0$ is an uncertain expected minimum spanning tree with connectedness above $\alpha _T$ if and only if

$$\begin{aligned} \sum \limits _{\mathcal {M}\{\xi _i\in T_0\}\ge \alpha _T} E\left[ \eta _{i}\right] \le \sum \limits _{\mathcal {M}\{\xi _j\in T\}\ge \alpha _T} E\left[ \eta _{j}\right] \end{aligned}$$

(18)

holds for any other uncertain spanning tree T, where $E\left[ \eta _{i}\right]$ are the expected values of uncertain weights $\eta _{i} = \{w_i\mid \xi _i = 1\}, \,\ i = 1, 2, \cdots , m$ respectively.

Proof

Given that $\eta _{i}$ are independent uncertain variables, according to Theorem 3 and Eq. (16), we have

$$\begin{aligned} E\left[ W(T_0, \alpha _T)\right]= & {} E \left[ \sum \limits _{\mathcal {M}\{\xi _i\in T_0\}\ge \alpha _T}\eta _{i}\right] \nonumber \\= & {} \sum \limits _{\mathcal {M}\{\xi _i\in T_0\}\ge \alpha _T} E\left[ \eta _{i}\right] . \end{aligned}$$

(19)

Similarly,

$$\begin{aligned} E\left[ W(T, \alpha _T)\right]= & {} E \left[ \sum \limits _{\mathcal {M}\{\xi _j\in T\}\ge \alpha _T}\eta _{j}\right] \nonumber \\= & {} \sum \limits _{\mathcal {M}\{\xi _j\in T\}\ge \alpha _T} E\left[ \eta _{j}\right] . \end{aligned}$$

(20)

Therefore, we get that $E\left[ W(T_0, \alpha _T)\right] \le E\left[ W(T, \alpha _T)\right]$ holds if and only if $\sum \limits _{\mathcal {M}\{\xi _i\in T_0\}\ge \alpha _T} E\left[ \eta _{i}\right] \le \sum \limits _{\mathcal {M}\{\xi _j\in T\}\ge \alpha _T} E\left[ \eta _{j}\right]$ is true, the theorem holds. $\square$

4.2 $\alpha$-UMST

Definition 12

Let $G = (V, \mathcal {E}, \mathcal {W})$ be an uncertain network with n nodes, independent Boolean uncertain variables $\xi _{ij}, \,\ i,j = 1, 2, \ldots , n$ be the edges, and independent uncertain variables $w_{ij}, \,\ i,j= 1, 2, \ldots , n$ be the weights of the edges. A spanning tree $T_0$ is called an uncertain $\alpha$-UMST with connectedness above $\alpha _T$ if

$$\begin{aligned}{} & {} \min \{w\mid \mathcal {M}\{W(T_0, \alpha _T)\le w \}\ge \alpha \} \nonumber \\{} & {} \quad \le \min \{w\mid \mathcal {M}\{W(T, \alpha _T)\le w \}\ge \alpha \} \end{aligned}$$

(21)

holds for every uncertain spanning tree T, where $\alpha _T$ and $\alpha$ are both given confidence levels.

Since $\Psi _{T}(x)$ is an increasing function, then we can get

$$\begin{aligned}{} & {} \min \{w\mid \mathcal {M}\{W(T, \alpha _T)\le w \}\ge \alpha \} \nonumber \\{} & {} \quad = \min \{w \mid \Psi _{T}(w) \ge \alpha \} = \{w\mid \Psi _{T}(w) = \alpha \}; \end{aligned}$$

(22)

in other words, Definition 12 is equal to find an uncertain spanning tree $T_0$ which satisfies

$$\begin{aligned} \Psi _{T_0}^{-1}(\alpha ) \le \Psi _{T}^{-1}(\alpha ) \end{aligned}$$

(23)

for every spanning tree T of G, where $\alpha$ is a given confidence level.

Theorem 5

Let $\xi _1, \xi _2, \ldots , \xi _n$ be be independent uncertain variables with uncertainty distributions $\Phi _1, \Phi _2, \ldots , \Phi _n$ and the domain of values of distributions $D_{\Phi _1}, D_{\Phi _2}, \ldots , D_{\Phi _n}$, respectively. If f is a continuous and strictly increasing function, then

$$\begin{aligned} \xi = f(\xi _1, \xi _2, \ldots , \xi _n) \end{aligned}$$

(24)

has an inverse uncertainty distribution

$$\begin{aligned} \Psi ^{-1}(\alpha ) = f(\Phi ^{-1}_1(\alpha ), \Phi ^{-1}_2(\alpha ), \ldots , \Phi ^{-1}_n(\alpha )) \end{aligned}$$

(25)

when $\alpha \in (0, 1)$ and $\alpha \in D_\Psi$, where $D_\Psi = \bigcap \limits _{i=1}^{n}{D_{\Phi _i}}$.

Proof

For simplicity, we only prove the case $n = 2$. At first, when $\alpha \in D_\Psi$, it is clear that $\Psi ^{-1}(\alpha ) = f(\Phi _1^{-1}(\alpha ), \Phi _2^{-1}(\alpha ))$ is a continuous function with respect to $\alpha$. Next, we need to prove that $\mathcal {M}\{\xi \le \Psi ^{-1}(\alpha )\} = \alpha$.

As

$$\begin{aligned} \{\xi \le \Psi ^{-1}(\alpha )\} \equiv \{f(\xi _1, \xi _2) \le f(\Phi _1^{-1}(\alpha ), \Phi _2^{-1}(\alpha ))\}, \end{aligned}$$

(26)

and $f(\cdot )$ is a strictly increasing function, we have

$$\begin{aligned} \{\xi \le \Psi ^{-1}(\alpha )\} \supset \{\xi _1\le \Phi _1^{-1}(\alpha )\}\cap \{ \xi _2 \le \Phi _2^{-1}(\alpha )\}, \end{aligned}$$

(27)

$$\begin{aligned} \{\xi \le \Psi ^{-1}(\alpha )\} \subset \{\xi _1\le \Phi _1^{-1}(\alpha )\}\cup \{ \xi _2 \le \Phi _2^{-1}(\alpha )\}. \end{aligned}$$

(28)

Depending on the properties of independent uncertainties, it’s easy to get

$$\begin{aligned}{} & {} \mathcal {M}\{\xi _1\le \Phi _1^{-1}(\alpha )\} \wedge \mathcal {M}\{\xi _2 \le \Phi _2^{-1}(\alpha )\} \nonumber \\{} & {} \quad \le \mathcal {M}\{\xi \le \Psi ^{-1}(\alpha )\}, \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \mathcal {M}\{\xi _1\le \Phi _1^{-1}(\alpha )\} \vee \mathcal {M}\{\xi _2 \le \Phi _2^{-1}(\alpha )\} \nonumber \\{} & {} \quad \ge \mathcal {M}\{\xi \le \Psi ^{-1}(\alpha )\}. \end{aligned}$$

(30)

Following Theorem 1, when $\alpha \in D_{\Phi _1}$, $\mathcal {M}\{\xi _1 \le \Phi _1^{-1}(\alpha )\} = \mathcal {M}\{\xi _1 \le \forall x_0 \in \{x\mid \Phi _1(x) = \alpha \}\} = \alpha$, and for the same reason $\mathcal {M}\{\xi _2 \le \Phi _2^{-1}(\alpha )\} = \alpha$ when $\alpha \in D_{\Phi _2}$. Hence when $\alpha \in D_\Psi = D_{\Phi _1} \cap D_{\Phi _2}$, (29) and (30) can be changed to

$$\begin{aligned} \alpha \le \mathcal {M}\{\xi \le \Psi ^{-1}(\alpha )\} \le \alpha , \end{aligned}$$

(31)

meaning that $\mathcal {M}\{\xi \le \Psi ^{-1}(\alpha )\} = \alpha$. The theorem is proved. $\square$

Theorem 6

Let $G = (V, \mathcal {E} , \mathcal {W})$ be an uncertain network with n nodes, independent Boolean uncertain variables $\xi _{ij}, \,\ i,j = 1, 2, \ldots , n$ be the edges, and independent uncertain variables $w_{ij}, \,\ i,j= 1, 2, \ldots , n$ be the weights of the edges. A spanning tree $T_0$ is called an uncertain $\alpha$-UMST with connectedness above $\alpha _T$ if and only if

$$\begin{aligned} \sum \limits _{\mathcal {M}\{\xi _i \in T_0\} \ge \alpha _T}\Psi _i^{-1}(\alpha )\le \sum \limits _{\mathcal {M}\{\xi _j \in T\} \ge \alpha _T}\Psi _j^{-1}(\alpha ) \end{aligned}$$

(32)

holds for every other spanning tree T, where $\Psi _i^{-1}(\alpha )$ is the generalized inverse uncertainty distribution of $\eta _{i} = \{w_i \mid \xi _i = 1\}, \,\ i = 1, 2, \cdots , m$, $\alpha _T \in (0,1)$ and $\alpha \in D_T$, $D_T$ is the intersection of all the domain of uncertainty distributions of $\eta _{i}, \,\ i = 1, 2, \ldots , m$.

Proof

From Theorem 5, for each spanning tree of G, the generalized inverse uncertainty distribution of it’s total weight $W(T,\alpha _T) = \sum _{\mathcal {M}\{\xi _{j} \in T\}\le \alpha _T}\eta _{j}$ is

$$\begin{aligned} \Psi _{T}^{-1}(\alpha ) = \sum _{\mathcal {M}\{\xi _{j} \in T\}\le \alpha _T}\Psi _j^{-1}(\alpha ) \end{aligned}$$

(33)

where $\Psi _j^{-1}(\alpha )$ is the generalized inverse uncertain distribution of $\eta _{j} = \{w_{j}\mid \xi _{j} = 1\}$, $\alpha \in D_{\Psi _T}$ and $\alpha _T \in (0,1)$.

Hence, when $\alpha \in D_T$, $D_T \subset D_{\Psi _{T_0}}$ and $D_T \subset D_{\Psi _T}$, $\Psi _{T_0}^{-1}(\alpha ) \le \Psi _T^{-1}(\alpha )$ holds if and only if $\sum \limits _{\mathcal {M}\{\xi _i \in T_0\} \ge \alpha _T}\Psi _i^{-1}(\alpha )\le \sum \limits _{\mathcal {M}\{\xi _j \in T\} \ge \alpha _T}\Psi _j^{-1}(\alpha )$ is true, the theorem holds. $\square$

4.3 Most UMST

Definition 13

Let $G = (V, \mathcal {E}, \mathcal {W})$ be an uncertain network with n nodes, independent Boolean uncertain variables $\xi _{ij}, \,\ i,j = 1, 2, \ldots , n$ be the edges, and independent uncertain variables $w_{ij}, \,\ i,j= 1, 2, \cdots , n$ be the weights of the edges. Give an upper limit $x^*$ on the weight value, a spanning tree $T_0$ is referred to as the most UMST with connectedness above $\alpha _T$ if

$$\begin{aligned} \Psi _{T_0}(x^*) \ge \Psi _{T}(x^*) \end{aligned}$$

(34)

holds for any spanning tree T.

This definition states that for a given appropriate weight upper limit $x^*$, among all possible spanning trees whose total weight is less than or equal to the predetermined maximum weight $x^*$, the most UMST $T_0$ has the greatest chance.

Theorem 7

Assume there has a connected uncertain network $G = (V, \mathcal {E}, \mathcal {W})$ and a weight upper limit $x^*$, the most UMST $T_0$ of G is equal to the $\alpha$-UMST of G, where $\alpha \in D_T$ and $\alpha = \Psi _{T_0}(x^*)$.

Proof

When $\alpha \in D_T$, the distribution of spanning tree T is an increasing function for x, and $\Psi _T^{-1}$ is an increasing function for $\alpha$.

As to $T_0$, which is the $\alpha$-UMST, it must hold $\Psi _{T_0}^{-1}(\alpha ) = x_1 \le x_2 = \Psi _T^{-1}(\alpha )$ for any other T, that is

$$\begin{aligned} \Psi _{T_0}(x_1) = \Psi _{T}(x_2) \end{aligned}$$

(35)

when $x_1 \le x_2$, then when $x_1 = x_2 = x^*$, there must be

$$\begin{aligned} \Psi _{T_0}(x^*) \ge \Psi _{T}(x^*) \end{aligned}$$

(36)

which is the definition of the most UMST. The proof is proved. $\square$

4.4 Summary of three models

Since we take uncertain net topology $\xi _{ij}$ and uncertain edge weight $w_{ij}$ into account at the same time, the UMST model holds a new kind of variable $\eta _{ij} = \{w_{ij}\mid \xi _{ij}=1\}$ whose uncertainty distribution is irregular and a limitation $\alpha _T$ about connectedness. Therefore, it makes sense that discussing on these three typical transformations for the UMST problem model. And the specific differences of models after taking uncertain edge existence into consideration will be demonstrated in the next section.

5 Numerical examples

Here we will present several numerical experiments on the UMST models to show the difference between the model under the classical uncertain network and the model under the uncertain network considering connectedness. We set up an uncertain undirected network G with six vertices and possible connections between each vertex (Fig. 2). The network has uncertain edges $\xi _{ij} (i, j = 1, 2, \ldots , 6)$ and uncertain weights $w_{ij} (i, j = 1, 2, \cdots , 6)$.

Fig. 2

Uncertain complete network of six nodes

Assuming that all edges $\xi _{ij}$ are independent with each other, and so as to weights $w_{ij}$, $i, j = 1, 2, \ldots , 6$. The distributions of variables are shown in Table 1.

Table 1 Parameter values in Fig. 2

We choose the genetic algorithm to solve UMST problem, and the parameters of GA are as follows: mutation rate is 0.1, crossover rate is 0.8, population size is 100, iteration times is 200.

Example 1

Expected-UMST

In the classical uncertain network, it is easy to calculate the expected value of uncertain variable $w \sim \mathcal {L}(a,b)$ by the equation $E\left[ w \right] = \frac{a+b}{2}$. Then, the expected minimum spanning tree $T_0$ of uncertain weight of Fig. 3 has edge set $\{(1,2), (1,3), (1,4), (3,5), (1,6)\}$, and the weight of $T_0$ is

$$\begin{aligned} E\left[ W(T_0, \mathcal {W})\right]= & {} E\left[ w_{12}\right] + E\left[ w_{13}\right] + E\left[ w_{14}\right] \nonumber \\{} & {} + E\left[ w_{35}\right] + E\left[ w_{16}\right] = 27.5. \end{aligned}$$

(37)

Fig. 3

Expected MST with uncertain weights

Given that the existences of edges are also uncertain, the result of EUMST can be great different:

First of all, the expected value is changed, as the uncertainty distribution of uncertain conditional variable $\eta$ is not $\mathcal {L}(a,b)$. From (15) and (8), the distribution and expected value of $\eta _{ij} = \{w_{ij}\mid \xi _{ij}=1\}$ are

$$\begin{aligned} \Psi _{ij} ( x ) =\left\{ \begin{array}{ccl} 0,&{} &{}x<a\\ \frac{x-a}{\alpha _{ij}( b-a )},&{} &{}a\le x<a+\frac{\alpha _{ij}}{2}( b-a )\\ 0.5,&{} &{}a+\frac{\alpha _{ij}}{2}(b-a) \le x\le b-\frac{\alpha _{ij}}{2}( b-a)\\ 1-\frac{b-x}{\alpha _{ij}(b-a)},&{} &{}b-\frac{\alpha _{ij}}{2}(b-a)<x<b\\ 1,&{} &{}x\ge b \end{array} \right. \nonumber \\ \end{aligned}$$

(38)

and

$$\begin{aligned} E\left[ \eta _{ij}\right] =b-\frac{( 2+\alpha _{ij})(b-a)}{4} \end{aligned}$$

(39)

where $\mathcal {M}\{\xi _{ij}=1\}=\alpha _{ij}$, $\{w_{ij}\cap (\xi _{ij}=1)\} \sim \mathcal {L}(a,b)$, $i,j = 1, 2, \cdots , 6$.

Secondly, the result is affected by the prescribed connectedness level $\alpha _T$. It can be seen in Fig. 4 that with different $\alpha _T$ the results of expected UMST are different.

Fig. 4

Expected MST with uncertain weights and uncertain topological structure

The connectedness of $T^0_1$ is 0.90, and the weight is 38.27. As to $T^0_2$, the connectedness is 0.84 and the weight is 31.195. When we set the connectedness of tree must greater than 0.7, the weight of UMST is 24.855, and $E\left[ W(T^0_4,0.6)\right] = 24.165$. Although the image of $T^0_5$($\alpha _T=0.5$) is same as $T_0$ (Fig. 3), $E\left[ W(T^0_5,0.5)\right] = 23.245$ is different from $E\left[ W(T_0, \textbf{W})\right] = 27.5$.

Example 2

$\alpha -\textbf{UMST}$

According to the requirement of Theorem 6, the first step is to know the value range of $\alpha$ in case of unsolvable situation.

Fig. 5

Image of distribution of $\eta _{ij} = \{w_{ij}\mid \xi _{ij}=1\}$

From (38), the domain of values $D_{\Psi _{ij}} = \left[ 0,1\right]$, $i,j=1,2,\ldots ,6$; hence, $D_T = \bigcap \limits _{i,j=1}^{6}{D_{\Psi _{ij}}} = \left[ 0,1\right]$. By Theorem 1, we can calculate the generalized inverse uncertainty distribution. The image and detail value are shown in Fig. 5 and Table 2.

Table 2 Parameter values in Examples 1, 2

There are two determinants about $\alpha$-UMST: $\alpha _T$ related to the tree’s edges’ existence and $\alpha$ which is in connection with the tree’s weight value. Example 1 has already embodied the influence of $\alpha _T$; moreover, when the limitation of $\alpha _T$ is fixed, there would be a different tree for the change of the $\alpha$ value that reflects uncertain distribution minimum spanning tree is an ideal model. Figure 6 shows three kinds of results about different combination of $\alpha _T$ and $\alpha$.

Fig. 6

$\alpha$-UMST in different determinants

Example 3

Most UMST

Here we use 99-method to estimate the distribution of spanning tree’s weight, as it is difficult to declare the distribution of $f(\xi _{1},\xi _{2},\ldots ,\xi {n})$ where $\xi _{i}, \,\i =1,2,\ldots ,n$ holds different distribution.

$\mathbf {99-Method.}$ Liu (2010) proposed that for an uncertain variable $\xi$ with uncertainty distribution $\Phi$, its empirical distribution could be obtained by a 99-table, in which 0.01, 0.02, 0.03, $\cdots$, 0.99 are taken at moderate intervals from the interval (0,1), and $x_1, \,\ x_2, \,\ \cdots , \,\ x_{99}$ are the inverse uncertainty distribution values $\Phi ^{-1}(0.01), \,\ \Phi ^{-1}(0.02), \,\ \Phi ^{-1}(0.03), \ldots , \Phi ^{-1}(0.99)$ that corresponds to the first row of numbers.

0.01	0.02	0.03	$\cdots$	0.99
$x_1$	$x_2$	$x_3$	$\cdots$	$x_{99}$

If more accurate estimation is required, we can generalize the 99-method to any fixed scale. By the 99-table, we may express an empirical uncertainty distribution $\Psi (x)$ to approximate the uncertainty distribution $\Phi (x)$ of the uncertain variable $\xi$ as

$$\begin{aligned}{} & {} \Psi (x) =\nonumber \\{} & {} \left\{ \begin{array}{ccl} 0,&{} &{} x < x_1 \\ \alpha _{i}+(\alpha _{i+1}-\alpha _{i})\frac{x-x_{i}}{x_{i+1}-x_i},&{} &{} x_i\le x\le x_{i+1} \,\ i = 1,2,\cdots ,99\\ 1,&{} &{} x>x_{99} \end{array}. \right. \end{aligned}$$

(40)

As for a strictly increasing function $f(\cdot )$ of $\xi _{i}$ with uncertainty distribution $\Phi _{i}$, $i = 1,2,\ldots ,n$, the 99-table for it is shown as follows that could be used for estimating the distribution of $W(T,\alpha _T) = \sum \limits _{\mathcal {M}\{\xi _i \in T\} \ge \alpha _T}\eta _{i}$.

0.01	$\cdots$	0.99
$f(\Phi _1^{-1}(0.01),\ldots ,\Phi _n^{-1}(0.01))$	$\cdots$	$f(\Phi _1^{-1}(0.99),\ldots ,\Phi _n^{-1}(0.99))$

As a further discussion of Example 2, we choose $\alpha _T = 0.7$ to draw the uncertainty distribution curve of W(T, 0.7) by 99-method and the curves are shown in Fig. 7.

Fig. 7

Distributions of W(T, 0.7) for different spanning tree T

The four curves represent different spanning trees of G in Fig. 2 when the limitation of connectedness is 0.7: T0 is the UMST whose distribution is the minimum one among any other spanning trees; T1 has the edge set $\{(1,3),(1,4),(1,5),(1,6),(2,5)\}$; T2’s edge set is $\{(1,3),(1,4),(1,5),(1,6),(2,4)\}$; $\{(1,4),(1,5),(1,6),(2,5),(3,6)\}$ is the edge set of T3.

Above all, through the increasing trend of every curve, it is visually observed that Theorem 7 holds and the equal result of the most UMST and the $\alpha$-UMST when $\alpha =\Psi _{T_0}(x^*) \in D_T$. Then, the distribution curve of T0 overlaps with the curve of T1 and T2, which means the UMST of minimal distribution of G is not a fixed tree. This observation corresponds to the result of Example 2 in Fig. 6b, c.

6 Conclusions

In this paper, we have studied the expected UMST model, the $\alpha$-UMST model, and the most UMST model in uncertain networks with uncertain edge existence and uncertain edge weights, using conditional uncertain variables to connect two nondeterminacy aspects of a network. With the new consideration about uncertain topological structure, we prove the transformations of these three models to deterministic models and then solve the MST problem through the genetic algorithm. The conclusions are illustrated by numerical experiments, and the differences between the new uncertain considerations and the classical uncertain networks are discussed.