1 Introduction

Time series forecasting is important in a multitude of domains such as finance, weather, traffic monitoring, budget analysis, military planning, advanced manufacturing, supply chain, and disease pandemic (Lee et al. 2022; Alghamdi et al. 2022; Kelany et al. 2020; Ma et al. 2022; Volkova et al. 2017; Sezer et al. 2020). Forecasting is crucial for individuals and organizations in proactive decision making and policy planning. Nowadays, there is a wide array of machine learning and deep learning models for forecasting with time series data, which vary from one domain to another (Henrique et al. 2019; Zhong and Enke 2019; Aguilar-Rivera et al. 2015; Yu et al. 2017, 2018; Jiang and Zhang 2018; Karevan and Suykens 2020; Hewage et al. 2021; Johnstone and Sulungu 2021).

Generally, time series data samples have repeating long-term or short-term patterns, or both. In such cases, one can attempt to learn these repeating patterns by using convolutional and/or new recurrent neural networks or other attention-based learning mechanisms (Lai et al. 2018). In financial domains, on the other hand, data samples normally have a few recurring patterns along with a high level of randomness (Tang and Shi 2021). As a result, it is challenging to design and train a deep neural network (DNN) to produce accurate predictions. Existing state-of-the-art DNNs do not perform well on these data samples, e.g. in daily trading data with volatile information (Lai et al. 2018).

Fig. 1
figure 1

A “shifting” issue of MSE and CORR in financial time series data forecasting. At point A, the actual price decreases, while the forecasted price increases

Full size image

To evaluate a forecasting algorithm, three widely used performance metrics are mean square error (MSE), mean absolute error (MAE), and correlation (CORR) (Lai et al. 2018). However, in financial analysis, a low value of MSE or a high value of CORR may not be useful, especially if the interest is in the tendency of the market, e.g. a higher or lower price on the next day. Figure 1 depicts a limitation of MSE and CORR in analysing financial data. Specifically, we use Huber regression (Sun et al. 2020) to forecast a daily time series. We achieve an exceptionally low MSE and high CORR, and the forecasting estimates become a “shifting” version of the ground truth. This shifting issue presents a crucial obstacle, which essentially makes the algorithm unusable. Therefore, in this paper, we propose new performance metrics to evaluate a time series forecasting algorithm, i.e. mean weighted square error (MWSE) and mean weighted square ratio (MWSR), as explained in the next section.

Fig. 2
figure 2

The process of extracting features from multivariate time series data

Full size image

Our proposed approach leverages machine learning to establish a pipeline consisting of data pre-processing tasks, including feature extraction, feature elimination, and feature selection. During feature extraction, an algorithm computes the correlations among multiple time series data and extracts three types of time-domain features: long-term, medium-term, and short-term features. These features capture irregularities and fluctuations throughout the historical data. As shown in Fig. 2, the correlation coefficients act as cross-domain features, while time-domain features are extracted independently for each time series data. In addition, we use XGBoost (Chen et al. 2015) for feature elimination. It is an ensemble method based on decision trees in a gradient boosting framework. We rank the features based on their scores and eliminate those having a score lower than a specified threshold. Then, we perform feature selection using a binary particle swarm optimization (PSO) algorithm (Assareh et al. 2010).

In summary, the contributions of this paper are:

  1. 1.

    We propose two new metrics, namely MWSE and MWSR, for performance evaluation pertaining to financial time series forecasting;

  2. 2.

    We propose a method that can operate with univariate and multivariate time series data forecasting. In multivariate time series data, the correlation coefficients are computed to facilitate forecasting.

  3. 3.

    We leverage machine learning (e.g. linear regression) as the basis of our proposed method. The underlying algorithms can be applied to a wide array of domains, especially where computational resources are limited (e.g. without GPUs).

  4. 4.

    We evaluate our proposed method with benchmark problems, which outperforms state-of-the-art algorithms with respect to MWSE and MWSR, especially in short-term time series forecasting.

The rest of the article is organized as follows. In Sect. 2, we present existing studies related to financial time series forecasting. In Sect. 3, our proposed method is explained in detail. In Sect. 4, we present performance evaluation and comparison of our proposed method against several state-of-the-art methods. Concluding remarks are given in Sect. 5.

2 Related work

Many statistical methods are available in the literature for time series forecasting. Auto-regressive integrated moving average (ARIMA) is widely used in many applications (Singh and Mohapatra 2019; Büyükşahin and Ertekin 2019; Liu et al. 2016; Amini et al. 2016; Barak and Sadegh 2016; Xu et al. 2022). ARIMA is a generalization of auto-regressive moving average (ARMA), which is a combination of auto-regressive (AR) and moving average (MA) techniques. ARMA models operate under the assumption that the time series is stationary. In contrast, ARIMA models handle nonstationary time series by incorporating a parameter to represent the number of non-seasonal differences with respect to stationarity. To build an ARIMA model, the Box–Jenkins method (Box et al. 2015) can be used. It consists of an iterative three-stage procedure, i.e. model identification, parameter estimation, and model checking. Owing to the high computational cost of ARIMA models, they are seldom used in dealing with higher dimensional multivariate time series data. Our developed method, which is based on machine learning, offers an alternative to handle multivariate time series data in a computationally efficient manner.

Vector auto-regression (VAR) achieves a high performance among statistical models in multivariate time series forecasting. VAR generalizes univariate auto-regressive models by enabling processing and analysis of multivariate time series. Owing to its simplicity and effectiveness, it has been widely used in various areas (Bashir and Wei 2018; Vankadara et al. 2022; Wang et al. 2022; Ouma et al. 2022; Safikhani and Shojaie 2022; Deshmukh and Paramasivam 2016; Taveeapiradeecharoen et al. 2019; Munkhdalai et al. 2020; Ngueyep and Serban 2015; Maleki et al. 2020), especially for handing a variety of time series data such as financial data and gene expression series. Several variants of VAR have also been developed, e.g. Gaussian VAR and Elliptical VAR. Gaussian VAR model assumes that the latent innovations are independent and identically distributed (Qiu et al. 2015). Gaussian VAR is restrictive to processing of light-tailed time series. In Qiu et al. (2015), Gaussian VAR was generalized to Elliptical VAR, in order to accommodate heavy-tailed time series. Nevertheless, similar to ARIMA, VAR is also computationally inefficient.

Considering time series forecasting as a regression problem allows us to devise efficient methods such as support vector regression (SVR), ridge regression, and Lasso regression (Lu et al. 2009; Henrique et al. 2018; Ristanoski et al. 2013; Liu et al. 2021). Many regression models with different loss functions and regularization terms have been employed for time series forecasting (Alhnaity and Abbod 2020; Liu and Li 2020; Gupta et al. 2019). These linear methods are efficient for multivariate time series forecasting, owing to the availability of high-quality off-the-shelf solvers in the machine learning community. However, such models fail to capture complex nonlinear relationships in multivariate time series data. In contrary, our proposed method leverages time-domain features to capture the nonlinear relationships in multivariate time series forecasting.

It is a challenging task to develop highly accurate forecasting models for financial data, because they are highly nonlinear, irregular, and volatile in nature. While many traditional statistical models have been used for exchange rate forecasting, such as ARIMA, VAR, linear regression, generalized auto-regressive conditional heteroscedasticity (GARCH) and co-integration models (Chortareas et al. 2011; Tseng et al. 2001; McCrae et al. 2002; Moosa and Vaz 2016; West and Cho 1995; Carriero et al. 2009; Joseph 2001), they perform poorly and become unusable when handling complex financial time series data. A multiscale decomposition ensemble learning method (Sun et al. 2019) was developed for exchange rate forecasting using a combination of variational mode decomposition (VMD) and a support vector neural network (SVNN). Firstly, the exchange rate time series was decomposed into several components with VMD. Then, the SVNN was used to predict the obtained component series and produce the ensemble results. The VMD/SVNN model outperformed single and ensemble-based forecasting models.

Prophet is a popular method for time series forecasting (Taylor and Letham 2018). It is robust against outliers, missing values, and trend shifts in analysing time series, leading to reliable and high-quality forecasts. It is currently used in real-world environments such as by Facebook to generate reliable forecasts in planning and goal setting. Prophet provides functions to adjust predictions based on human-interpretable parameters. Depending on the problem domain, an expert in the field can effectively adjust the relevant parameters to produce an accurate prediction. Prophet uses an additive regression model that normally works well with default parameters, while users can make adjustments to the relevant components to optimize the quality of forecasting.

Long-term dependencies in time series data can be handled by using recurrent neural networks (RNNs), which is equipped with an optional attention mechanism. However, RNNs fail to capture temporal patterns across multiple time steps. A novel attention mechanism was proposed in (Shih et al. 2019). It uses a set of filters and works in the frequency domain to capture temporal patterns. The mechanism enables the attention component to learn interdependencies among multiple variables, leading to discovery of patterns across multiple time steps.

Long short-term memory (LSTM) is a type of RNNs that has a “larger” memory bank to handle time series efficiently. An improved version of LSTM, namely long short-term memory network-enhanced forget-gate network (LSTM-EFG), was introduced in (Devi et al. 2020). Specifically, LSTM-EFG uses cuckoo search optimization (CSO) (Gandomi et al. 2013) to overcome the limitations of traditional forecasting models. It has shown its usefulness as an operational tool for wind power plant management.

A long- and short-term time-series network (LSTNet) (Lai et al. 2018) was proposed to learn the inherent involvement of long-term and short-term patterns in multivariate time series. LSTNet outperforms state-of-the-art methods on different data sets in terms of MSE and CORR. However, LSTNet does not perform well on financial data, where residuals are uncommon. Different types of time-domain features and an objective function of PSO are used in our proposed method to tackle the problems.

3 Proposed methods

Our method leverages PSO, XGBoost and ridge regression, as explained in the following subsections.

3.1 Background

3.1.1 PSO

PSO is a population-based meta-heuristic algorithm. The motivation of PSO originates from the social activity of a flock of fishes, where each individual (i.e. a particle) acts as a candidate solution. Particles move around in the search space to find the optimal position. Their movements are motivated by a cognitive desire to perform an efficient exploration. Because PSO does not use gradient information, its objective function has to be differentiable. Although PSO is originally used for tackling search problems in a continuous search-space problems, it is possible to utilize a binary version of PSO (Kennedy and Eberhart 1997) for optimization in the discrete space. In particular, we use binary PSO for feature selection in this study. Specifically, a particle is treated as a vector of n variables \(p_i = [x_{i1}, x_{i2},\ldots , x_{\text {in}}]\) where \(i > 0\) and \(x_{ij} \in \{0,1\}\). If \(x_{ij} = 0\), the corresponding feature is “off” and vice versa. By using an objective function, F, we can select a set of features that optimizes F by movements of all particles \(p_i\). Figure 3 depicts the use of binary PSO in feature selection.

Fig. 3
figure 3

The relationship between binary PSO and feature selection

Full size image

3.1.2 XGBoost

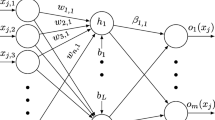
XGBoost, developed in (Chen and Guestrin 2016), uses gradient boosting to ensemble a set of weak decision-tree-based regressors. Decision trees are generated by computing the gradient descent information of an objective function. XGBoost generates a decision score for each feature, which is then used to rank features and remove irrelevant features with respect to a threshold. Figure 4 shows a general structure of XGBoost.

Fig. 4
figure 4

Architecture of XGBoost

Full size image

3.1.3 Ridge regression

Linear regression treats the relationship between inputs and outputs as a linear function. Due to its simplicity, the method is sensitive to a small change in inputs, and is especially unstable against outliers. In such scenarios, the model weights of the model can be arbitrarily large. To tackle this problem, we modify the loss function to incorporate a regularized term that applies penalties with respect to large weights. Using this mechanism in ridge regression, we can restrict the absolute values of weights corresponding to less important inputs. The following functions represent the loss function of ridge regression:

$$\begin{aligned} F(\theta ) = \sum _{i = 1}^{l}\left( y_{i} - \sum _{j=1}^{k}\theta _j x_{ij}\right) ^{2} + \alpha \sum _{j = 1}^{k}\theta _{j}^{2}, \end{aligned}$$

where \(\theta \) is the weights (parameters) while \(\alpha \ge 0\) controls the amplitude of regularization.

3.1.4 Evaluation metrics

We use the following metrics to evaluate the forecasting performance: empirical correlations (CORR), coefficient of determination (\(R^2\)), mean square error (MSE), mean absolute error (MAE) and our proposed metrics mean weighted square error (MWSE) and mean weighted square ratio (MWSR).

Specifically,

$$\begin{aligned} \text{ CORR } = \frac{1}{n}\sum _{i=1}^{n}\frac{\sum _{j}(y_{ij} - M({\varvec{y}_{i}}))({\hat{y}}_{ij} - M({\varvec{y_{i}}} ))}{\sqrt{\sum _{t}(y_{ij} - M({\varvec{y_{i}}} ))^{2}(\hat{y}_{ij} - M({\varvec{y_{i}}} ))^{2}}}, \end{aligned}$$
(1)

where y and \(\hat{y}\) \(\in \textbf{R}^{n\times J}\) are the true and predicted values, respectively. \(M(\cdot )\) denotes the mean function. By using the same notation, we have the following definitions:

$$\begin{aligned}{} & {} R^{2} = 1 - \frac{\sum _{i}(y_{i} - \hat{y}_{i})^{2}}{\sum _{i}(y_{i} - M(\varvec{y}))^{2}}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \quad {\text {MSE}} = \sum _{i = 1}^{n}\frac{(y_{i} - \hat{y}_{i})^{2}}{n}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \quad {\text {MAE}} = \sum _{i=1}^{n}\frac{\mid y_{i} - \hat{y}_{i}\mid }{n}. \end{aligned}$$
(4)

In finance, users normally are interested in the tendency of an item, i.e. increase or decrease in the stock price the next day. Therefore, we define MWSE to amplify terms that provide an incorrect tendency and vice versa.

$$\begin{aligned} {\text {MWSE}} = \sum _{i = 2}^{n}\frac{\varvec{\Phi }{\left( (y_{i} - y_{i-1})({{\hat{{y}}}}_{i} - {{\hat{y}}}_{i-1})\right) }(y_{i} - {{\hat{y}}}_{i})^{2}}{n-1}, \end{aligned}$$
(5)

and

$$\begin{aligned} \varvec{\Phi }(x) ={\left\{ \begin{array}{ll} \alpha , &{} \hbox { if}\ x<0.\\ 1 - \alpha , &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

where \(\alpha \in [0.5, 1]\).

In addition, we formulate another metrics, i.e. MWSR, to reflect the dominance of incorrect prediction terms within MSE, specifically where a low MWSR score is desirable.

$$\begin{aligned} {\text {MWSR}} = \frac{{\text {MWSE}}}{{\text {MSE}}}. \end{aligned}$$
(6)

3.2 Proposed scheme

Fig. 5
figure 5

Flowchart of our proposed scheme

Full size image

Our proposed model consists of four stages, as shown in Fig. 5. In feature extraction, we use three windows to capture different parts of the available time series data. These windows represent long-term, medium-term, and short-term characteristics of time-series data. Specifically, the short-term window provides knowledge on the most recent trends or fluctuations in the time series. The medium-term window extends a little further back in time and captures medium-term characteristics (e.g. in weeks). The long-term window aims to focus on long-term characteristics in the time series (e.g. months). In each window, we employ the TSFresh library (Christ et al. 2018) to extract time-domain features. To limit the number of features generated by TSFresh, we select the top 20 relevant features, as follows.

  1. 1.

    Absolute energy

    $$\begin{aligned} \sum _{i=1}^{n} x_i^2. \end{aligned}$$
    (7)
  2. 2.

    Mean absolute change

    $$\begin{aligned} \frac{1}{n} \sum _{i=1}^{n-1} \mid x_{i+1} - x_{i}\mid . \end{aligned}$$
    (8)
  3. 3.

    Mean

    $$\begin{aligned} {\bar{x}} = \frac{1}{n} \sum _{i=1}^{n} x_i. \end{aligned}$$
    (9)
  4. 4.

    Standard deviation

    $$\begin{aligned} \delta = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (x_{i} - {\bar{x}})^2}. \end{aligned}$$
    (10)
  5. 5.

    Variation coefficient

    $$\begin{aligned} \dfrac{\sqrt{\frac{1}{n} \sum _{i=1}^{n} (x_{i} - {\bar{x}})^2}}{{\bar{x}}}. \end{aligned}$$
    (11)
  6. 6.

    Skewness

    $$\begin{aligned} s = \frac{\sum _{i=1}^{n} (x_{i} - {\bar{x}})^3}{\delta ^3}. \end{aligned}$$
    (12)
  7. 7.

    Kurtosis

    $$\begin{aligned} \frac{\sum _{i=1}^{n} (x_{i} - {\bar{x}})^4}{(n-1)s^4}. \end{aligned}$$
    (13)
  8. 8.

    Maximum

    $$\begin{aligned} {\textbf {Max}}_{i=1}^{n} \{x_i\}. \end{aligned}$$
    (14)
  9. 9.

    Minimum

    $$\begin{aligned} {\textbf {Min}}_{i=1}^{n} \{x_i\}. \end{aligned}$$
    (15)
  10. 10.

    Benford correlation

    $$\begin{aligned} \log _{10}\left( 1+\frac{1}{d}\right) , \end{aligned}$$
    (16)

    where d is a leading digit number from 1 to 9.

  11. 11.

    Root mean square

    $$\begin{aligned} \sqrt{\frac{1}{n} \sum _{i=1}^{n} x_i^2}. \end{aligned}$$
    (17)
  12. 12.

    Absolute sum of changes

    $$\begin{aligned} \sum _{i=1}^{n-1} \mid x_{i+1}- x_i \mid . \end{aligned}$$
    (18)
  13. 13.

    C3 (lag = 1 and lag = 2)

    $$\begin{aligned} \frac{1}{n-2\,\text{ lag }} \sum _{i=1}^{n-2\,\text{ lag }} x_{i + 2 \cdot \text{ lag }} \cdot x_{i + \text{ lag }} \cdot x_{i}. \end{aligned}$$
    (19)
  14. 14.

    Quantile (\(q = 0.1\) and \(q = 0.9\)).

  15. 15.

    Autocorrelation (\(l = 1, \,l = 2, \, l = 3\)).

    $$\begin{aligned} \frac{1}{(n-l)\sigma ^{2}} \sum _{t=1}^{n-l}(x_{t}-{\bar{x}} )(x_{t+l}-{\bar{x}}) \end{aligned}$$
    (20)

The last five raw data samples are used as features in our model, resulting in a total of 65 features. In the case of multivariate data forecasting, we calculate the Pearson correlation coefficient for every pair of time series signals. Figure 6 shows our feature extraction procedure with multiple windows.

Fig. 6
figure 6

Multiple windows for time domain features

Full size image

Subsequently, we eliminate the less important or irrelevant features using XGBoost with a loss function on MWSE. The features with an importance factor lower than 1e-6 are removed. Then, binary PSO is employed to select the best features with respect to an objective function based on MWSE. Finally, we use ridge regression for forecasting. Algorithm 1 presents our proposed method in detail. In the case of multivariate time series, the algorithm is repeatedly applied to each signal.

figure a

4 Performance evaluation

4.1 Simulation study

To evaluate our proposed method, a well-known challenging problem is used, i.e. the crypto-currency signal (EOS) forecasting problem (EOSIO 2022). We collect trading data of EOS from 1 January, 2019 to 1 August, 2021. The data set has 5 different time series, i.e. opening price, maximum price, minimum price, closing price, and volume. We take the logarithm of the data samples and scale them within the range of [0, 1]. Our aim is to predict the EOS data sample in the next 1, 2, and 3 days. We conduct two case studies: univariate and multivariate time series forecasting. In the univariate case, we predict the daily closing price of EOS. In the multivariate case, we predict 5 time series signals concurrently. We use the most recent 120 (4 months) data samples for performance evaluation. The remaining data samples are divided for training and validation with a ratio of 4:1.

The following algorithms are used for performance comparison:

  1. 1.

    We use ARIMA and VAR for univariate and multivariate cases, respectively. In each case, the algorithm is trained only once. To avoid re-training of the model on a daily basis, we derive a Kalman filter retrieved from the trained model and establish the new model. By observing partial autocorrelation, autocorrelation, and augmented Dickey–Fuller statistics, we adopt the following parameters for ARIMA and VAR: {lag = 2, difference = 0, moving average window = 10}.

  2. 2.

    We use Prophet from Facebook to predict EOS data in both univariate and multivariate cases. Both settings of daily training (one-step prediction) or one-time training (multi-step prediction) are evaluated to select the best model. The default parameters of Prophet are utilized.

  3. 3.

    In LSTNet, we employ a grid search to obtain the optimal parameters: {window = 72, skip = 6, batch size = 16, epochs = 100, learning rate = 0.01, and highway window = 12}.

  4. 4.

    In our proposed algorithm, we use a heuristic search to yield the following parameters: {long-term window = 90, medium-term window = 45, short-term window = 7, PSO acceleration factor = 2.05, weight = 0.7, distance = L2, number of iterations = 3000, and number of particles = number of features}.

4.2 Results and discussion

Tables 1 and 2 present the performance of one-day ahead prediction from four algorithms in univariate and multivariate settings, respectively. Our model outperforms other algorithms, and achieves the lowest MWSE and MWSR scores. In other words, our model is capable of predicting the price trend well, especially in short-term and univariate setting. ARIMA provides stable results in terms of MSE, MAE and CORR, while LSTNet depicts good MWSR values in the multivariate case. Prophet performs the worst in this study.

Table 1 Results of four algorithms in univariate prediction (horizon = 1)
Full size table
Table 2 Results of four algorithms in multivariate prediction (horizon = 1)
Full size table

Similarly, Tables 3 and 4 summarize the performance of four algorithms with a horizon of 2 with respect to univariate and multivariate time series forecasting, respectively. Tables 5 and 6 show the performance of four algorithms with a horizon of 3 in univariate and multivariate settings, respectively. Since Prophet uses the multi-day ahead prediction strategy, its results are the same with different horizons. As such, Prophet is useful for long-term prediction. ARIMA and LSTNet produce good results with horizons of 2 and 3, indicating their usefulness in medium-term forecasting.

Table 3 Results of four algorithms in univariate prediction (horizon = 2)
Full size table
Table 4 Results of four algorithms in multivariate prediction (horizon = 2)
Full size table
Table 5 Results of four algorithms in univariate prediction (horizon = 3)
Full size table
Table 6 Results of four algorithms in multivariate prediction (horizon = 3)
Full size table
Table 7 Results of four algorithms in multivariate prediction with horizon (H) of 1, 2, 3, and 4, using ETH symbol from 1 January, 2019 to 1 January, 2023
Full size table

Furthermore, we conducted an extended experiment to evaluate the effectiveness and robustness of our proposed method. Based on trading data of the Ethereum platform (ETH) from January 1, 2019, to January 1, 2023, we apply multivariate prediction with horizons of 1, 2, 3, and 4 for four algorithms. The results of MSE, MAE, CORR, MWSE, and MWSR for each horizon are recorded, as summarized in Table 7. Clearly, our proposed method outperforms all other compared algorithms in terms of expanding the time series data set and changing the symbol (namely ETH).

5 Conclusion

In this paper, we have proposed two new metrics, namely MWSE and MWSE, for reliable performance evaluation of financial time series forecasting, particularly for financial data. Instead of relying on raw values, MWSE and MWSR are designed to measure the trend characteristics of financial time series data, which is a critical aspect in finance when the focus is on identifying trends such as increases or decreases in prices over a period of time. We have conducted a performance comparison study with different state-of-the-art algorithms on a challenging problem pertaining to crypto-currency time series data, i.e. EOS. The results have indicated that our proposed method is efficient for short-term forecasting. ARIMA and LSTNet are good for medium-term forecasting, while Prophet is useful for long-term forecasting. For further work, we will develop a software tool for short-term forecasting daily trading price forecasting for fintech applications.