1 Introduction

Linear programming is a mathematical concept for determining the optimal value (maximum or minimum value) of a linear function. It is used for obtaining the most optimal solution for a problem with given linear constraints. The technique of linear programming problem was introduced by a Russian mathematician L.V.Kantorovich. In 1947, Dentzig proposed simplex algorithm for solving LP problems. In classical set theory, the membership elements of a set are associated in binary terms according to a bivalent condition. Fuzzy set theory has been described as the situations in which each datum is imprecise or vague information and it is determined by indeterminate boundaries. The membership function of a fuzzy set is a generalization of indicator function for classical sets. In 1965, Lotfi Zadeh introduced the concept of fuzzy logic. Zadeh (1965), Tanaka et al. (1974) proposed a method for solving fuzzy mathematical programming problems using the concept of decision making in fuzzy environment. Zimmermann (1978) proposed a method for solving fuzzy linear programming (FLP) problem using multi-objective linear programming techniques.

Many researchers proposed different way for solving FLP problems. Maleki et al. (2000); Maleki (2002); Liu (2001); Jimenez et al. (2007); Nasseri (2008) have proposed a new defuzzification technique to solve fuzzy linear programming problems. Peraei et al. (2001) introduced a method for solving FLP problems by using the concept of Millen’s transform. Ebrahimnejad et al. (2010) introduced a new primal–dual algorithm for solving FLP problems. R. Saneifard and R. Saneifard (2011) developed a technique for defuzzification of fuzzy numbers using Mellin’s transform. Alaulden and Sanar (2014) proposed fuzzy models for solving FLP problems in which the parameters are fuzzy numbers using the defuzzification approach for Mellin’s transform.

In 1983, Krassimir Atanassov introduced the concept of intuitionistic fuzzy set theory which is characterization of fuzzy set and the indicator functions of fuzzy sets are special cases of the membership and nonmembership functions which belong to the interval [0, 1]. Angelov (1997) proposed optimization technique in intuitionistic fuzzy numbers. Dubey and Mehra (2011) proposed a method to solve intuitionistic linear programming problems based on the technique of indices value and ambiguity. Paravathi and Malathi (2012a) introduced the concept of optimization problems in intuitionistic fuzzy environment. Chakraborty et al. (2014) proposed method to solve intuitionistic fuzzy optimization using possibility, necessity and credibility measures.

Biswas and Kumar de (2016) proposed a new ranking function for intuitionistic fuzzy numbers using the concept based on probability density function and applied for solving linear bilevel fuzzy stochastic programming problems where the parameters are normal intuitionistic fuzzy numbers. Aggarwal et al. (2017) proposed an extension of Tanaka and Asai approach for solving Atanassov’s I-fuzzy LP problem, where the parameters are represented by I-fuzzy numbers. Kabiraj et al. (2019) developed a method to solve intuitionistic fuzzy linear programming problems using the technique based on a Zimmerman’s approach for solving FLP problems. Kabiraj et al. Kabiraj et al. (2019) Proposed a method to solve intuitionistic fuzzy linear programming problems using \((\alpha ,\beta )\) cut, when the coefficient matrix of the constraints and the cost coefficients is represented by triangular intuitionistic fuzzy numbers. Robinson et al. (2019) introduced a new approach to solve intuitionistic fuzzy optimization problems and the canonical representation of trapezoidal intuitionistic fuzzy number conveys the value, ambiguity and fuzziness of the original numbers.

A generalization of the classic set, fuzzy set, intuitionistic fuzzy set is based on neutrosophic sets. In 1998, Smarandache developed neutrosophic sets which parameters are imprecise, incomplete and inconsistent information in the real world. Wang et al. (2005) proposed interval neutrosophic sets. Wang et al. (2010) have presented the single value neutrosophic set which is generalization of classic set, fuzzy set, interval-valued fuzzy set, intuitionistic fuzzy set and paraconsistent set.

Hussian et al. (2017) proposed neutrosophic LP problems which independent parameters are handled with imprecise parameters. Abdel-Basset et al. (2018) proposed a new ranking function for solving the fully neutrosophic linear programming problems where parameters are represented as trapezoidal neutrosophic numbers. Singh et al. (2019) suggested Abdel Basset et al. method to solve a fully NLP problems, and we pointed out the mathematical incorrect assumptions of Abdel Basset et al. method. Many researchers have used the neutrosophic approach for solving optimization problems. Bera and Mahapatra (2019) introduced the concept of single-valued neutrosophic number in a generalized way such as generalized single-valued trapezoidal neutrosophic number(\(G_{SVTN}\)-number), generalized single-valued triangular neutrosophic number (\(G_{SVTrN}\)-number) and developed simplex algorithm for solving NLP problems. Bera and Mahapatra (2020a) developed Big-M simplex method for solving neutrosophic linear programming problem and it is applied with real-life problems. Bera and Mahapatra (2020b) developed defuzzification approach to convey objective and R.H.S. coefficients of the neutrosophic LPP into crisp LPP based on centroid method.

Das and Dash (2020) introduced a new ranking method to solve neutrosophic linear programming problems with mixed constraints where parameters were in the form of triangular neutrosophic numbers with blended requirements. Darehmiraki (2020) proposed new parametric ranking function to solve neutrosophic linear programming problem. Nafei et al. (2020) have presented an interval neutrosophic LP problems where its parameters are represented by triangular interval neutrosophic numbers and applied a new ranking technique for transformed interval neutrosophic linear programming problems into crisp linear programming problems. Basumatary and Broumi (2020) proposed interval-valued triangular neutrosophic Lp problems which parameters based on interval-valued triangular numbers. Walid Abdelfattah (2020) proposed a method to solve NLP problems based on parametric approach. Sagayakavitha and Sudha (2020) proposed a new approach for solving neutrosophic linear programming problem with symmetric triangular neutrosophic numbers. Khatter (2020) proposed approach to solve neutrosophic linear programming problems with possibilistic mean.

Unfortunately, all neutrosophic linear programming problem methods and studies of the related SVTrN numbers in the existing literature do not provide the de-neutrosophication concept of Mellin’s transform for solving neutrosophic linear programming problem approach till now. In fact, the neutrosophic linear programming problem based on the Mellin’s transform using the concept of probability density function of a SVTrN numbers has not been studied in existing literature so far. Since the ranking technique is very easy to determine SVTrN numbers, we establish a neutrosophic linear programming problem algorithm for SVTrN numbers objective and constraints functions to realize neutrosophic linear programming problem under indeterminate and uncertain environments. The ranking technique has been proposed for solving the neutrosophic linear programming problem with minimal computational efforts. The Mellin’s transform is used to represent the mathematical characteristic of SVTrN number. The main goal of this paper,

  1. 1.

    To define a new effective method for computing de-neutrosophication of SVTrN number, it has been introduced for finding the crisp values of the SVTrN numbers using the proportional probability density function which is associated with truth, indeterminacy and falsity membership functions of SVTrN numbers.

  2. 2.

    To propose neutrosophic linear programming problem, including the SVTrN number objective functions and SVTrN number constrained functions.

  3. 3.

    To present a solution algorithm for neutrosophic linear programming problem.

The main contribution of this paper is that the de-neutrosophication technique and the neutrosophic linear programming problem algorithm are proposed for the first time to realize neutrosophic linear programming problem in incomplete, uncertainty and indeterminacy environments.

In this paper, we presented a new ranking technique for solving neutrosophic linear programming problem. The proposed method result is efficient than existing Khatter (2020) method. In Sect. 2, some basic definitions are presented. Section  3 proposes a new ranking function of SVTrN number. Section 4 proposes algorithm for solving NLP problems. Section 5 discusses numerical problems. Comparative analysis is presented in Sect. 6. Section 7 concludes the paper.

2 Preliminaries

In this section, we give some preliminaries as follows:

Definition 1

(Hussian et al. 2017) Let X be a nonempty set. A neutrosophic set A in X is defined as \(A = \left\{ x,T_A(x),I_A(x),F_A(x)\right\} ,T_A(x),I_A(x),F_A(x)\in \left[ 0,1\right] \), where \(T_A(x),I_A(x),F_A(x)\) are truth membership degree, an indeterminacy-membership degree and a falsity membership degree with \(0 \le T_A(x)+I_A(x)+F_A(x)\le 3\).

Definition 2

(Hussian et al. 2017) Let \(a_1,a_2,a_3\in R\) such that \(a_1\le a_2 \le a_3\) . A SVTrN number \({\tilde{a}}= <(a_1,a_2,a_3 );\omega _{\tilde{a}},\mu _{\tilde{a}},y_{\tilde{a}}>\) is a special set on the real number set R, whose truth membership, indeterminacy membership and falsity membership functions are defined by \(T_{\tilde{a}}(x),I_{\tilde{a}}(x)\) and \(F_{\tilde{a}}(x)\), respectively.

$$\begin{aligned} T_{\tilde{a}}(x)= & {} \left\{ \begin{array}{ll} \frac{x-a_1}{a_2-a_1}\omega _{\tilde{a}}, &{}\text { for } a_1 \le x\le a_2 \\ \omega _{\tilde{a}}, &{} \text{ for } x=a_2\\ \frac{a_3-x}{a_3-a_2}\omega _{\tilde{a}}, &{} \text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(1)
$$\begin{aligned} I_{\tilde{a}}(x)= & {} \left\{ \begin{array}{ll} \frac{a_2-x+(x-a_1){\mu _{\tilde{a}}}}{a_2-a_1}, &{}\text { for } a_1 \le x\le a_2 \\ \mu _{\tilde{a}}, &{} \text{ for } x=a_2 \\ \frac{x-a_2+(a_3-x){\mu _{\tilde{a}}}}{a_3-a_2}, &{} \text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(2)
$$\begin{aligned} F_{\tilde{a}}(x)= & {} \left\{ \begin{array}{ll} \frac{a_2-x+(x-a_1){y_{\tilde{a}}}}{a_2-a_1}, &{}\text { for } a_1 \le x\le a_2 \\ y_{\tilde{a}}, &{} \text{ for } x=a_2 \\ \frac{x-a_2+(a_3-x){y_{\tilde{a}}}}{a_3-a_2}, &{} \text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(3)

Definition 3

(Hussian et al. 2017) Let \({\tilde{a}}\) = \(\left\langle \left( a_1,a_2,a_3 \right) ; {\omega _{\tilde{a}}},{\mu _{\tilde{a}}},{y_{\tilde{a}}} \right\rangle \) and \({\tilde{b}}\) = \(\left\langle \left( b_1,b_2,b_3 \right) ; {\omega _{\tilde{b}}},{\mu _{\tilde{b}}},{y_{\tilde{b}}} \right\rangle \) be two SVTrN numbers and \(r \ne 0\) be any real number. Then

  1. 1.

    \({\tilde{a}+\tilde{b}}\) = \( \left\langle \left( a_1+b_1,a_2+b_2,a_3+b_3 \right) ; \min \left\{ {\omega _{\tilde{a}}},{\omega _{\tilde{b}}}\right\} , \max \left\{ {\mu _{\tilde{a}}},{\mu _{\tilde{b}}}\right\} ,\max \left\{ {y_{\tilde{a}}},{y_{\tilde{b}}}\right\} \right\rangle \)

  2. 2.

    \(r{\tilde{a}}\) \(=\left\{ \begin{array}{ll} \left\langle \left( ra_1,ra_2,ra_3 \right) ; {\omega _{\tilde{a}}},{\mu _{\tilde{a}}},{y_{\tilde{a}}} \right\rangle , &{} \text{ for } r>0 \\ \left\langle \left( ra_3,ra_2,ra_1 \right) ; {\omega _{\tilde{a}}},{\mu _{\tilde{a}}},{y_{\tilde{a}}} \right\rangle , &{} \text{ for } r<0 \end{array} \right. \)

3 Proposed ranking technique for single-valued triangular neutrosophic numbers

In this section, we introduce the concept of Mellin’s transform to find the expected value of the function of a random variable using proportional probability density function associated with the truth and indeterminacy and falsity membership functions of the SVTrN numbers.

3.1 Probability density function from membership functions

Let \({\tilde{a}}\)= \(\left\langle \left( a_1,a_2,a_3 \right) ; {\omega _{\tilde{a}}},{\mu _{\tilde{a}}},{y_{\tilde{a}}} \right\rangle \) be SVTrN number. Now we define the ranking method by which we can associate a probability density function (p.d.f.) to the membership function, nonmembership function and indeterminacy membership function of \({\tilde{a}}\).

Proportional probability distribution Let us define three probability density functions \(f_1(x), f_2(x)\) and \(f_3(x)\) corresponding to the truth membership function \(T_{\tilde{a}}(x)\), an indeterminacy membership function \(I_{\tilde{a}}(x)\) and falsity membership function \(F_{\tilde{a}}(x)\), respectively.

(i) Probability density function from truth membershipfunction: Define a p.d.f \(f_1(x)=k_1T_{\tilde{a}}(x)\) associated with \({\tilde{a}}\), where \(k_1\) is a constant obtained by using property of p.d.f.

Let

$$\begin{aligned} f_1(x)=k_1T_{\tilde{a}}(x) \end{aligned}$$
(4)

then

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }f_1(x)dx=1 \end{aligned}$$
(5)
$$\begin{aligned}&\Rightarrow k_1\int \limits _{-\infty }^{\infty }T_{\tilde{a}}(x)dx=1 \end{aligned}$$
(6)
$$\begin{aligned}&\Rightarrow k_1\left[ \int \limits _{a_1}^{a_2}\frac{(x-a_1)}{(a_2-a_1)}{\omega _{\tilde{a}}}dx +\int \limits _{a_2}^{a_3}\frac{(a_3-x)}{(a_3-a_2)}{\omega _{\tilde{a}}}dx\right] =1 \end{aligned}$$
(7)
$$\begin{aligned}&\Rightarrow k_1{\omega _{\tilde{a}}}\left[ \int \limits _{a_1}^{a_2}\frac{(x-a_1)}{(a_2-a_1)}dx +\int \limits _{a_2}^{a_3}\frac{(a_3-x)}{(a_3-a_2)}dx\right] =1\nonumber \\&\Rightarrow k_1{\omega _{\tilde{a}}}\left[ \frac{a_2+a_1}{2}-a_1+a_3-\frac{(a_3+a_2)}{2}\right] =1\nonumber \\&\Rightarrow k_1=\frac{2}{{(a_3-a_1)}{\omega _{\tilde{a}}}} \end{aligned}$$
(8)

Thus,

$$\begin{aligned} f_1(x)=\left\{ \begin{array}{ll} \frac{2(x-a_1)}{(a_2-a_1)(a_3-a_1)}, &{}\text { for } a_1 \le x\le a_2 \\ \frac{2}{(a_3-a_1)}, &{} \text{ for } x=a_2\\ \frac{2(a_3-x)}{(a_3-a_2)(a_3-a_1)}, &{}\text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(9)

(ii) Probability density function from indeterminacy membership function: Define a p.d.f \(f_2(x)=k_2I_{\tilde{a}}(x)\) associated with \({\tilde{a}}\), where \(k_2\) is a constant obtained by using property of p.d.f.

Let

$$\begin{aligned} f_2(x)=k_2I_{\tilde{a}}(x) \end{aligned}$$
(10)

then

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }f_2(x)dx=1 \end{aligned}$$
(11)
$$\begin{aligned}&\Rightarrow k_2\int \limits _{-\infty }^{\infty }I_{\tilde{a}}(x)dx=1 \end{aligned}$$
(12)
$$\begin{aligned}&\Rightarrow k_2 \left[ \int \limits _{a_1}^{a_2}\frac{(a_2-x+\mu _{\tilde{a}}(x-a_1))}{(a_2-a_1)}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+\mu _{\tilde{a}}(a_3-x)}{(a_3-a_2)}dx\right] =1 \end{aligned}$$
(13)
$$\begin{aligned}&\Rightarrow k_2 \left[ \int \limits _{a_1}^{a_2}\frac{(a_2-x+\mu _{\tilde{a}}x-\mu _{\tilde{a}}a_1)}{(a_2-a_1)}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+\mu _{\tilde{a}}a_3-\mu _{\tilde{a}}x}{(a_3-a_2)}dx\right] =1\nonumber \\&\Rightarrow \frac{k_2}{2}[{(a_3-a_1)+\mu _{\tilde{a}}(a_3-a_1)}]=1\nonumber \\&\Rightarrow k_2=\frac{2}{{(a_3-a_1)}(1+{\mu _{\tilde{a}}})} \end{aligned}$$
(14)

Thus,

$$\begin{aligned} f_2(x)=\left\{ \begin{array}{ll} \frac{a_2-x+{\mu _{\tilde{a}}}(x-a_1)}{a_2-a_1}\frac{2}{{(a_3-a_1)}(1+{\mu _{\tilde{a}}})}, &{}\text { for } a_1 \le x\le a_2 \\ \mu _{\tilde{a}}\frac{2}{{(a_3-a_1)}(1+{\mu _{\tilde{a}}})}, &{} \text{ for } x=a_2 \\ \frac{x-a_2+{\mu _{\tilde{a}}}(a_3-x)}{a_3-a_2}\frac{2}{{(a_3-a_1)}(1+{\mu _{\tilde{a}}})}, &{} \text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(15)

(iii) Probability density function from falsity membership function: Define a p.d.f \(f_3(x)=k_3F_{\tilde{a}}(x)\) associated with \({\tilde{a}}\), where \(k_3\) is a constant obtained by using property of p.d.f. Let

$$\begin{aligned} f_3(x)=k_3F_{\tilde{a}}(x) \end{aligned}$$
(16)

then

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }f_3(x)dx=1 \end{aligned}$$
(17)
$$\begin{aligned}&\Rightarrow k_3\int \limits _{-\infty }^{\infty }F_{\tilde{a}}(x)dx=1 \end{aligned}$$
(18)
$$\begin{aligned}&\Rightarrow k_3 \left[ \int \limits _{a_1}^{a_2}\frac{(a_2-x+y_{\tilde{a}}(x-a_1))}{(a_2-a_1)}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+y_{\tilde{a}}(a_3-x)}{(a_3-a_2)}dx\right] =1 \end{aligned}$$
(19)
$$\begin{aligned}&\Rightarrow k_3 \left[ \int \limits _{a_1}^{a_2}\frac{(a_2-x+y_{\tilde{a}}x-\mu _{\tilde{a}}a_1)}{(a_2-a_1)}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+y_{\tilde{a}}a_3-\mu _{\tilde{a}}x}{(a_3-a_2)}dx\right] =1\nonumber \\&\Rightarrow \frac{k_3}{2}[{(a_3-a_1)+y_{\tilde{a}}(a_3-a_1)}]=1\nonumber \\&\Rightarrow k_3=\frac{2}{{(a_3-a_1)}(1+{y_{\tilde{a}}})} \end{aligned}$$
(20)

Thus,

$$\begin{aligned} f_3(x)=\left\{ \begin{array}{ll} \frac{a_2-x+{y_{\tilde{a}}}(x-a_1)}{a_2-a_1}\frac{2}{{(a_3-a_1)}(1+{y_{\tilde{a}}})}, &{}\text { for } a_1 \le x\le a_2 \\ y_{\tilde{a}}\frac{2}{{(a_3-a_1)}(1+{y_{\tilde{a}}})}, &{} \text{ for } x=a_2 \\ \frac{x-a_2+{y_{\tilde{a}}}(a_3-x)}{a_3-a_2}\frac{2}{{(a_3-a_1)}(1+{y_{\tilde{a}}})}, &{} \text { for } a_2 \le x\le a_3 \\ 0, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(21)

Let f(x) be the probability density function corresponding to the single-valued triangular neutrosophic number \({\tilde{a}}\) defined as

$$\begin{aligned} f(x)=\lambda f_1(x)+(1-\lambda )f_2(x)+(1-\lambda )f_3(x), (0\le \lambda \le 1) \end{aligned}$$
(22)

where the coefficient \(\lambda \in [0,1] \) is a weight by which it represents the decision maker’s preference information.

3.2 Mellin’s transform

From our survey, we can say that different application area has been taken as Mellin’s transform. R. Saneifard and R. Saneifard (2011) developed a technique for defuzzification of fuzzy numbers using Mellin’s transform.

Authors information

Types of membership function

Main contribution

Peraei et al. (2001)

Trapezoidal membership function

Linear programming problem

R.Saneifard and A. Asghary (2011)

Trapezoidal membership function

Selecting army equip System

Barik and Biswal (2012)

Linear triangular and trapezoidal membership function

Probabilistic fuzzy quadratic programming problem

Alaulden and Sanar (2014)

Linear membership function and convex non linear membership function

Project network

Biswas and De (2016)

Linear triangular membership and nonmembership functions

Fuzzy stochastic linear bi level programming problem

Amer (2019)

General fuzzy case

Bi level nonlinear fractional programming problem

Yanbing et al. (2019)

Interval type 2 trapezoidal fuzzy number

Bench marking problem

As we know it any probability density function with finite support is associated an expected value. We used Mellin’s transform to obtain this expected value of neutrosophic numbers.

Definition 4

The Mellin’s transform \(M_X(s)\) of a p.d.f f(x), where \( x (0<x<\infty )\) is positive, is defined as

$$\begin{aligned} M_X(s)=\int \limits _{0}^{\infty }x^{s-1}f(x)dx \end{aligned}$$
(23)

whenever the integral exists. Here X denoted the random variable corresponding to the single-valued triangular neutrosophic numbers \({\tilde{a}}\).

The Mellin’s transform has a unique one-to-one correspondence, \(f(x)\leftrightarrow M_X(s)\), which is an essential tool for studying the distributions of products of random variables and it is closely related to the Laplace, Fourier transform and gamma functions.

The first moment of a probability distribution function about the origin represents the mean of the distribution. Then we obtain the Mellin’s transform in terms of expected value (mean), (i.e.,) \(M_X=E[X]\)

The expected value of any function g(x) of the random variable X, whose probability density function is f(x), is given by

$$\begin{aligned} E[g(x)]=\int \limits _{-\infty }^{+\infty }g(x)f(x)dx \end{aligned}$$
(24)

It follows that

$$\begin{aligned} M_X(s)=E[X^{(s-1)}]=\int \limits _{-\infty }^{+\infty }x^{(s-1)}f(x)dx. \end{aligned}$$
(25)

Here \(s=2,\)

$$\begin{aligned} E[X]=\int \limits _{-\infty }^{+\infty }xf(x)dx. \end{aligned}$$
(26)

If \(\tilde{a}=(a_1,a_2,a_3);\omega _{\tilde{a}},\mu _{\tilde{a}},y_{\tilde{a}}\) is a single-valued triangular neutrosophic numbers, then the Mellin’s transform is obtained by

$$\begin{aligned}&M_X(s)=\int \limits _{0}^{\infty }x^{s-1}f(x)dx \end{aligned}$$
(27)
$$\begin{aligned}&M_X(s)=\int \limits _{0}^{\infty }x^{s-1}(\lambda f_1(x)\nonumber \\&\quad +(1-\lambda )f_2(x)+(1-\lambda )f_3(x))dx\nonumber \\&=2\lambda \left[ \int \limits _{a_1}^{a_2}\frac{(x-a_1)x^{s-1}}{(a_2-a_1)(a_3-a_1)}dx +\int \limits _{a_2}^{a_3}\frac{(a_3-x)x^{s-1}}{(a_3-a_2)(a_3-a_1)}dx\right] \nonumber \\&+(1-\lambda )\left[ \int \limits _{a_1}^{a_2}\frac{a_2-x +{\mu _{\tilde{a}}}(x-a_1)}{a_2-a_1}\frac{2x^{s-1}}{{(a_3-a_1)}(1+{\mu _{\tilde{a}}})}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+{\mu _{\tilde{a}}}(a_3-x)}{a_3-a_2}\frac{2x^{s-1}}{{(a_3-a_1)} (1+{\mu _{\tilde{a}}})}dx\right] \nonumber \\&\quad +(1-\lambda )\left[ \int \limits _{a_1}^{a_2}\frac{a_2-x +{y_{\tilde{a}}}(x-a_1)}{a_2-a_1}\frac{2x^{s-1}}{{(a_3-a_1)}(1+{y_{\tilde{a}}})}dx\right. \nonumber \\&\quad \left. +\int \limits _{a_2}^{a_3}\frac{x-a_2+{y_{\tilde{a}}}(a_3-x)}{a_3-a_2}\frac{2x^{s-1}}{{(a_3-a_1)}(1+{y_{\tilde{a}}})}dx\right] \nonumber \\&=2\lambda \left[ \frac{1}{(a_2-a_1)(a_3-a_1)}[\int \limits _{a_1}^{a_2}((x-a_1)x^{s-1})dx]\right. \nonumber \\&\quad \left. +\frac{1}{(a_3-a_2)(a_3-a_1)}[\int \limits _{a_2}^{a_3}(a_3-x)x^{s-1}dx]\right] \nonumber \\&+(1-\lambda )\left[ \frac{1}{(a_2-a_1)(a_3-a_1)(1+{\mu _{\tilde{a}}})}\right. \nonumber \\&\quad [\int \limits _{a_1}^{a_2}(2x^{s-1})(a_2-x+{\mu _{\tilde{a}}}(x-a_1))]dx \nonumber \\&\frac{1}{(a_3-a_2)(a_3-a_1)(1+{\mu _{\tilde{a}}})}\nonumber \\&\quad \left. [\int \limits _{a_2}^{a_3}(x-a_2+{\mu _{\tilde{a}}}(a_3-x))(2x^{s-1})]dx\right] \nonumber \\&+(1-\lambda )\left[ \frac{1}{(a_2-a_1)(a_3-a_1)(1+{y_{\tilde{a}}})}\right. \nonumber \\&[\int \limits _{a_1}^{a_2}(2x^{s-1})(a_2-x+{y_{\tilde{a}}}(x-a_1))]dx \nonumber \\&\quad +\frac{1}{(a_3-a_2)(a_3-a_1)(1+{y_{\tilde{a}}})}\nonumber \\&\left. [\int \limits _{a_2}^{a_3}(x-a_2+{y_{\tilde{a}}}(a_3-x))(2x^{s-1})]dx\right] \end{aligned}$$
(28)

Now it is possible to the Mellin’s transform in terms of expected values. For \(s=2\), Mellin’s transform converted to the definition of expectation of random variable. We find the expected or de-neutrosophication value of single-valued triangular neutrosophic numbers \(s=2\) has been considered.

$$\begin{aligned}&=\frac{2\lambda }{6(a_3-a_1)}[(a_3^2-a_1^2)+a_2(a_3-a_1)]\\&\quad +\frac{2(1-\lambda )}{6(a_3-a_1)(1+\mu _{\tilde{a}})}[2(a_3^2-a_1^2)-a_2(a_3-a_1)\\&\quad +\mu _{\tilde{a}}(a_3^2-a_1^2)+a_2\mu _{\tilde{a}}(a_3-a_1)]\\&\quad +\frac{2(1-\lambda )}{6(a_3-a_1)(1+y_{\tilde{a}})}[2(a_3^2-a_1^2)-a_2(a_3-a_1)\\&\quad +y_{\tilde{a}}(a_3^2-a_1^2)+a_2\mu _{\tilde{a}}(a_3-a_1)]\\&= \lambda \left\{ \frac{(a_1+a_2+a_3)}{3}\right\} \\&\quad +(1-\lambda )\left\{ \frac{{\mu _{\tilde{a}}(a_1+a_2+a_3)+2(a_3+a_1)-a_2}}{3(1+{\mu _{\tilde{a}}})}\right\} \\&\quad + (1-\lambda )\left\{ \frac{{y_{\tilde{a}}(a_1+a_2+a_3)+2(a_3+a_1)-a_2}}{3(1+{y_{\tilde{a}}})}\right\} \end{aligned}$$

Then the crisp equivalent value of the single-valued triangular neutrosophic numbers is found as

$$\begin{aligned} V({\tilde{a}},\lambda )= & {} \lambda \left\{ \frac{(a_1+a_2+a_3)}{3}\right\} \\&+(1-\lambda )\left\{ \frac{{\mu _{\tilde{a}}(a_1+a_2+a_3)+2(a_3+a_1)-a_2}}{3(1+{\mu _{\tilde{a}}})}\right\} \\&+(1-\lambda )\left\{ \frac{{y_{\tilde{a}}(a_1+a_2+a_3)+2(a_3+a_1)-a_2}}{3(1+{y_{\tilde{a}}})}\right\} \end{aligned}$$

where \(\lambda \in [0,1]\) represents the index of optimism for decision makers with preference information. A largest value of \(\lambda \) indicates the higher degree. For \(\lambda \in \left[ 0,\frac{1}{2}\right) \) indicates pessimistic behavior, \(\lambda \in \left( \frac{1}{2},1\right] \) which is represented as optimistic behavior and \(\lambda =0.5\) which is implied with moderate decision maker.

Proposition 1

Let \({\tilde{a}}\)= \(\left\langle \left( a_1,a_2,a_3 \right) ; {\omega _{\tilde{a}}},{\mu _{\tilde{a}}},{y_{\tilde{a}}} \right\rangle \) and \({\tilde{b}}\)= \(\left\langle \left( b_1,b_2,b_3 \right) ; {\omega _{\tilde{b}}},{\mu _{\tilde{b}}},{y_{\tilde{b}}} \right\rangle \) be two single-valued triangular neutrosophic numbers. Then relation between the ranking function is defined as \((0\le \lambda \le 1)\)

  1. 1.

    \({\tilde{a}}< {\tilde{b}}\) then \(V({\tilde{a}},\lambda )\le V({\tilde{b}},\lambda )\)

  2. 2.

    \({\tilde{a}}> {\tilde{b}}\) then \(V({\tilde{a}},\lambda )\ge V({\tilde{b}},\lambda )\)

  3. 3.

    \({\tilde{a}}= {\tilde{b}}\) then \(V({\tilde{a}},\lambda )= V({\tilde{b}},\lambda )\)

4 Solution of the neutrosophic linear programming problems using Mellin’s transform

In this section, we can use the Mellin’s transform for solving neutrosophic linear programming problems with single-valued triangular neutrosophic numbers. Let us consider a general form of neutrosophic linear programming problem.

$$\begin{aligned}&\text {Maximize(Minimize)} \, Z=\sum \limits _{j=1}^{n} {\tilde{c}}_{j} x_j\\&\text {Subject to} \sum \limits _{i=1}^{m}{\tilde{a}}_{ij}x_j \le (\ge ,=){\tilde{b}}_i\\&x_j \ge 0, i=1,2,...,m, j=1,2,...,n \end{aligned}$$

where \({\tilde{c}}_j,{\tilde{a}}_{ij},{\tilde{b}}_i\) are single-valued triangular neutrosophic number.

4.1 Algorithm

In this section to find an optimal solution for neutrosophic linear programming problem using Mellin’s transform has been proposed. The method is as follows:

Step 1: Check whether the given neutrosophic linear programming problem is maximization or minimization. If the NLP problem is of minimization type, convert the given neutrosophic linear programming problem into maximization problem by using the relation \( \mathrm min Z= - \mathrm max (-Z)\).

Step 2: Convert all the inequalities of the constraints into equation by introducing slack/surplus variables.

Step 3: Apply means of Mellin’s ranking technique with SVTrN numbers which is acceptance of maximum truth membership, minimum indeterminacy and falsity membership functions. Then the problem is written as

$$\begin{aligned}&\text {Maximize(Minimize)}Z=\sum \limits _{j=1}^{n} V({\tilde{c}}_{j},\lambda ) x_j\\&\text {Subject to} \sum \limits _{i=1}^{m}V({\tilde{a}}_{ij},\lambda )x_j \le (\ge ,=)V({\tilde{b}}_i,\lambda ) \\&x_j \ge 0 \\ \end{aligned}$$

where \({\tilde{c}}_j,{\tilde{a}}_{ij},{\tilde{b}}_i\) are SVTrN numbers and \(x_j\in R\),\(i=1,2,...,m,j=1,2,...,n\)

Step 4: By using Mellin’s ranking technique, each SVTrN numbers are converted into real line.

Step 5: Create an initial simplex table for the given neutrosophic linear programming problem and obtain an initial basic feasible solution to the problem in the form \(x_B=B^{-1}b\).

Step 6: To test the optimality of the net evaluation \(Z_j-C_j, \forall j\)

  1. 1.

    If all \(Z_j-C_j\ge 0\). stop, the current basic feasible solution is optimal.

  2. 2.

    If atleast one of \(Z_j-C_j<0\), then proceed next step.

Step 7: Rules for finding pivot element

  1. 1.

    If there exists one or more value of \(Z_j-C_j<0\), then take most negative value entry in the basis \(a_k\). \(Z_k-C_k= \mathrm min(Z_j-C_j),\forall j\) such that \(Z_j-C_j<0,j=k\).

  2. 2.

    If all \(a_{ik}\ge 0\), then there exists unbounded solution of the given NLP problem.

  3. 3.

    If \(a_ik>0\), then compute the ratio min\({\frac{b_i}{a_{ik}},a_{ik}>0},i=1,2,...,m\). The element \(a_{ik}\) is called the pivot element; the \(i^{th}\) row and \(k^{th}\) column are called the pivot row and pivot column.

Step 8: Calculate the new entries of the simplex table

  1. 1.

    Let the minimum occurs corresponding to the basis \(x_{bk}\) , then common element \(a_{kr}\), which occurs at intersection of \(k^{th}\) row and \(r^{th}\) column is known as the leading element.

  2. 2.

    \(a_{kj}=\frac{a_kj}{a_kr}\) and \(a_{ij}=a_{ij}-\frac{a_{kj}}{a_{kr}}a_{ir}\) where \(i=1,2,...,m,i\ne k,j=1,2,...,n\).

Step 9: Go to step 4 and proceed the procedures in step 5 and 6, until we get obtain optimal solution.

5 Numerical examples

To illustrate the proposed algorithm for solving neutrosophic optimization problems by using defuzzification approach. Consider the following examples adopted by Khatter (2020) and the achieved solutions are compared with predefined approach Khatter (2020).

Example 1

Beaver Creek Pottery Company employs skilled crafts operations to manufacture clay bowls and mugs. The resource used for manufacturing the pottery is clay and skilled labor. Given the resources, it is desired to know how many items to manufacture each day in order to maximize profit. The following resource requirements for production and profit per product presented:

Product

Labor(Hr./Unit)

Clay(Lb./Unit)

Profit($/unit)

Bowl

\({\tilde{1}}\)

\({\tilde{4}}\)

\({\tilde{40}}\)

Mug

\({\tilde{2}}\)

\({\tilde{3}}\)

\({\tilde{50}}\)

There are around 40 h of labor and around 120 pounds of clay available each day for production. Then the problem can be formulated as neutrosophic linear programming problem where all the coefficients of objective function, constraints variables and right-hand side of constraints variables are SVTrN numbers.

$$\begin{aligned}&\text {Maximize} Z =\tilde{40} x_1 +\tilde{50} x_2 \\&\text {Subject to} \, { \tilde{1}}x_1 +{\tilde{2}}x_2 \le {\tilde{40}}\\&{\tilde{4}}x_1+{\tilde{3}}x_2 \le {\tilde{120}}\\&x_1,x_2\ge 0 \end{aligned}$$

where

$$\begin{aligned} \tilde{40}= & {} \left\langle (30,40,50);0.7,0.4,0.3\right\rangle ,\\ \tilde{50}= & {} \left\langle (40,50,60);0.6,0.5,0.2\right\rangle \\ {\tilde{1}}= & {} \left\langle (0.5,1,3);0.6,0.4,0.1\right\rangle ,\\ {\tilde{2}}= & {} \left\langle (0,2,6);0.6,0.4,0.1\right\rangle \\ {\tilde{4}}= & {} \left\langle (1,4,12);0.4,0.3,0.2\right\rangle ,\\ {\tilde{3}}= & {} \left\langle (1,3,10);0.7,0.4,0.3\right\rangle \\ \tilde{40}= & {} \left\langle (20,40,60);0.4,0.3,0.5\right\rangle ,\\ \tilde{120}= & {} \left\langle (100,120,140);0.7,0.4,0.3\right\rangle \end{aligned}$$

By applying the proposed ranking technique of single-valued triangular neutrosophic numbers are converted by crisp value as

$$\begin{aligned}&V(\tilde{40},\lambda )=80-40\lambda , V(\tilde{50},\lambda )=100-50\lambda \\&V({\tilde{1}},\lambda )=3.812-2.312\lambda ,V({\tilde{2}},\lambda )=6.4156-3.7489\lambda \\&V({\tilde{4}},\lambda )=14-8.3376\lambda , V({\tilde{3}},\lambda )=11.8057-7.139\lambda \\&V(\tilde{40},\lambda )=80-40\lambda , V(\tilde{120},\lambda )=240-120\lambda \end{aligned}$$

Then the crisp linear programming problem is

$$\begin{aligned}&\text {Maximize} Z =(80-40\lambda ) x_1 + (100-50\lambda ) x_2 \\&\text {Subject to} \, (3.812-2.312\lambda ) x_1+(6.4156-3.7489\lambda )x_2 \\&\le (80-40\lambda ) \\&(14-8.3376\lambda ) x_1+(11.8057-7.139\lambda ) x_2 \\&\le (240-120\lambda ) x_1,x_2\ge 0 \;\;{ \text{ a }nd }\;\; \lambda \in [0,1]\\ \end{aligned}$$

Then the weighted value for different decision maker’s \(\lambda \) is given in Table 1, and using proposed algorithm, we obtain optimal solution for different feasibility degree of \(\lambda \) given in Table 2.

Table 1 Weighted value for different parameter \(\lambda \)
Full size table
Table 2 Optimal solution for different feasibility degree \(\lambda \)
Full size table

In this problem, our proposed approach gives better optimal results by comparing the existing result of Khatter (2020).

In Khatter (2020), there are objective function values 1571.45 for \(\lambda =0\) and 278.76 for \(\lambda =1\), whereas using our proposed approach, the objective function values come to 1520.36 for \(\lambda =0\) and 945.18 for \(\lambda =1\).

We observed proposed approach decision maker’s results, if \(\lambda (0\le \lambda \le 1 )\) increases when the objective function values are decreased. Moreover, different values of objective function for proposed method are efficient with Khatter (2020) results.

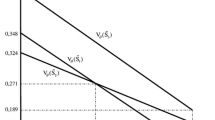
Hence, we consider different feasibility degrees for \(\lambda (\lambda \in [0,1])\) in that situation of truth, an indeterminacy and falsity with imprecision and incomplete parameters. A comparison result between Khatter (2020) and new technique with optimal value is shown in Fig. 1.

Fig. 1
figure 1

Optimal solution for different feasibility degree \(\lambda \)

Full size image

Example 2

Consider the NLP problems with objective coefficients are single-valued triangular neutrosophic numbers and which problem is adopted by Khatter (2020)

$$\begin{aligned}&\text {Maximize}\, Z =\tilde{25} x_1 +\tilde{48} x_2 \\&\text {Subject to} 15x_1 +30x_2 \le 45000\\&24x_1+6x_2 \le 24000\\&21x_1+14x_2 \le 28000\\&x_1,x_2\ge 0 \end{aligned}$$

where \(\tilde{25} =\left\langle (19,25,33);0.8,0.1,0.4\right\rangle \), \(\tilde{48} =\left\langle (44,48,54);0.75,0.25,0\right\rangle \) By applying the proposed ranking technique of single-valued triangular neutrosophic numbers are converted by crisp value as

$$\begin{aligned}&V(\tilde{25},\lambda )=52.416-26.746 \lambda , V(\tilde{48},\lambda )\\&=98.53-49.86\lambda \\&\text {Maximize}\, Z =(52.416-26.746\lambda )x_1\\&\quad +(98.53-49.86\lambda ) x_2 \\&\text {Subject to} 15x_1 +30x_2 \le 45000\\&24x_1+6x_2 \le 24000\\&21x_1+14x_2 \le 28000\\&x_1,x_2\ge 0,\lambda \in [0,1] \end{aligned}$$

Then the weighted value for different decision maker’s \(\lambda \) is given in Table 3, and using proposed algorithm, we obtain optimal solution for different feasibility degree of \(\lambda \) given in Table 4.

Table 3 Weighted value for different parameter \(\lambda \)
Full size table
Table 4 Optimal solution for different feasibility degree \(\lambda \)
Full size table
Table 5 Comparison results for proposed method
Full size table

In this problem, our proposed approach gives better optimal result by comparing the existing result of Khatter (2020).

In Khatter (2020), there are objective function values 141345 for \(\lambda =0\) and 42092.5 for \(\lambda =1\), whereas using our proposed approach, the objective function values come to 149372.5 for \(\lambda =0\) and 73672.5 for \(\lambda =1\).

We observed proposed approach decision maker’s results, if \(\lambda (0\le \lambda \le 1 )\) increases when the objective function values are decreased. Moreover, different values of objective function for proposed method are efficient with Khatter (2020) results.

Hence, we consider different feasibility degree for \(\lambda (\lambda \in [0,1])\) in that situation of truth, an indeterminacy and falsity with imprecision and incomplete parameters. A comparison result between Khatter (2020) and new technique with optimal value is shown in Fig. 2.

Fig. 2
figure 2

Optimal solution for different feasibility degree \(\lambda \)

Full size image

6 Comparative analysis of the proposed method with the existing method Khatter (2020)

In application Sect. 5, we compare the proposed method with other existing method (Khatter 2020) in the literature and comparison results are given in Table 5.

As can be seen from Table 5, the optimal values are found by different parameter \(\lambda \) presented. Therefore, the optimal values are compared Khatter (2020) probability mean method. The advantages of the proposed ranking method are:

  1. 1.

    The proposed ranking technique based on Mellin’s transform can be applied for neutrosophic linear programming problem algorithm, which reflects minimal computational efforts.

  2. 2.

    Our proposed method is better than the existing method (Khatter 2020) because our objective value outcome is maximized.

  3. 3.

    Our proposed method is maximization type of problems; then, the objective value is also maximized the existing methods.

In this paper, proposed method sufficiently considers that various decision maker’s for \(\lambda \) which method is compared with Khatter (2020) method as shown in Figs. 1 and 2. We observed, in Figs. 1 and 2, decision maker’s values if \(\lambda \) increases when the objective values are decreased.

7 Conclusion

This paper presented a new ranking technique for neutrosophic numbers. Then proposed method can be used to find the crisp value of single-valued triangular neutrosophic numbers. Based on this proposed technique to solve neutrosophic linear programming problem, the proposed method is most efficient for our existing method.