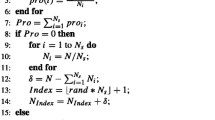Differential evolution with Gaussian mutation and dynamic parameter adjustment

Abstract

Differential evolution (DE) is a remarkable evolutionary algorithm for global optimization over continuous search space, whose performance is significantly influenced by its mutation operator and control parameters (scaling factor and crossover rate). In order to enhance the performance of DE, we adopt a novel Gaussian mutation operator and a modified common mutation operator to collaboratively produce new mutant vectors, and employ a periodic function and a Gaussian function to generate the required values of scaling factor and crossover rate, respectively. In the proposed variant of DE (denoted by GPDE), the two adopted mutation operators are adaptively applied to generate the corresponding mutant vector of each individual based on their own cumulative scores, the periodic scaling factor can provide a better balance between exploration ability and exploitation ability, and the Gaussian function-based crossover rate will possess fluctuant value, which possibly enhance the population diversity. To verify the performance of proposed GPDE, a suite of thirty benchmark functions and four real-world problems are applied to conduct the simulation experiment. The simulation results demonstrate that the proposed GPDE performs significantly better than five state-of-the-art DE variants and other two meta-heuristics algorithms.

1 Introduction

Differential evolution (DE), proposed by Storn and Price (Storn and Price 1997), is a simple yet efficient evolutionary algorithm (EA) for the global numerical optimization. Due to its simple structure and ease of use, DE has been successfully applied to solve many real-world problems, including decision-making (Zhang et al. 2010), dynamic scheduling (Tang et al. 2014), parameter optimization (Gong and Cai 2014), spam detection (Idris et al. 2014), system fault diagnosis (Zhao et al. 2014), motion estimation (Cuevas et al. 2013) and so on. More details on the recent research about DE can be found in the literature reviews (Neri and Tirronen 2010; Das and Suganthan 2011a) and the references therein.

Three evolutionary operators (mutation, crossover and selection) and three control parameters (population size, scaling factor and crossover rate) are included in the original DE algorithm, which have significant influence on its performance. Thus, many researchers have been engaged in improving DE by designing new evolutionary operators, combining multiple operators and adopting adaptive or self-adaptive strategies for those control parameters. Although various variants of DE have been proposed, there still exists a big room for improvement, owing to the thorny work of balancing the global exploration ability and local exploitation ability (Lin and Gen 2009; Črepinšek et al. 2013).

Using Gaussian function can randomly produce new solutions around a given position, which may provide an excellent exploitation ability. Meanwhile, periodic or fluctuant parameter adjustment strategy possibly can achieve a good balance between the exploitation operation around the already-found good solutions and the exploration operation for seeking out non-visited regions in the search space. Inspired by the above observations, we design a novel Gaussian mutation operator (which, respectively, takes the position of the best individual among three randomly selected individuals and the distance between the other two as the mean and standard deviation of Gaussian distribution) and a modified common mutation operator (denoted by DE/rand-worst/1) to collaboratively produce the new potential position for every individual, and the collaborative rule between them relies on their own cumulative scores during the evolutionary process. In addition, the scaling factor adopts a cosine function to realize the objective of adjusting its value periodically, and the crossover rate employs a Gaussian function to dynamically adjust the population diversity during the evolutionary process. At last, a novel DE variant is proposed via combining the above-mentioned Gaussian mutation operator, DE/rand-worst/1 and parameter adjustment strategies, which is called GPDE for short. A suite of 30 benchmark functions with different dimensions and four real-world optimization problems are applied to evaluate the performance of GPDE, and its performance is compared to five excellent DE variants and two up-to-date meta-heuristics algorithms. The comparative results show that GPDE obviously outperforms the seven compared algorithms. Moreover, the parameter analysis expresses that the adopted control parameters within GPDE are robust.

The remainder of this paper is organized as follows. Section 2 briefly introduces the basic operators of original DE algorithm. Section 3 reviews some currently related works on DE. Section 4 provides a detailed description of the proposed GPDE algorithm and its overall procedure. Section 5 presents the comparison between GPDE and seven compared algorithms. Section 6 draws the conclusions.

2 Differential evolution

DE is a population-based stochastic search algorithm which simulates the natural evolutionary process via mutation, crossover and selection to move its population toward the global optimum. The DE algorithm mainly contains the following four operations.

2.1 Initialization operation

Similar to other EAs, DE searches for a global optimum in the D-dimensional real parameter space with a population of vectors $\varvec{x}_{i}=[x_{i,1},x_{i,2},\ldots ,x_{i,D}], i=1,2,\ldots ,\text {NP}$, where $\text {NP}$ is the population size. An initial population should cover the entire search space by uniformly randomizing individuals between the prescribed lower bounds $\varvec{L}=\big [L_{1},L_{2},\ldots ,L_{D}\big ]$ and upper bounds $\varvec{U}=\big [U_{1},U_{2},\ldots ,U_{D}\big ]$. The jth component of the ith individual can be initialized as follows,

$$\begin{aligned} \begin{array}{c} x_{i,j}=L_{j}+ \text {rand}[0,1]\cdot \big (U_{j}-L_{j}\big ), \end{array} \end{aligned}$$

(1)

where $\text {rand}[0,1]$ represents a uniformly distributed random number within the interval [0, 1] and is used throughout the paper.

2.2 Mutation operation

After the initialization operation, DE employs a mutation operation to produce a mutant vector $\varvec{v}_{i}{=}\big [v_{i,1},v_{i,2},\ldots ,v_{i,D}\big ]$ for each target vector $\varvec{x}_{i}$. The followings are five most frequently used mutation operators implemented in various DE algorithms.

• (1) DE/rand/1

  $$\begin{aligned} \varvec{v}_{i}=\varvec{x}_{r_{1}}+F\cdot (\varvec{x}_{r_{2}}-\varvec{x}_{r_{3}}). \end{aligned}$$

  (2)

• (2) DE/best/1

  $$\begin{aligned} \varvec{v}_{i}=\varvec{x}_{\mathrm{best}}+F\cdot (\varvec{x}_{r_{1}}-\varvec{x}_{r_{2}}). \end{aligned}$$

  (3)

• (3) DE/current-to-best/1

  $$\begin{aligned} \varvec{v}_{i}=\varvec{x}_{i}+F\cdot (\varvec{x}_{\mathrm{best}}-\varvec{x}_{r_{1}})+F\cdot (\varvec{x}_{r_{2}}-\varvec{x}_{r_{3}}). \end{aligned}$$

  (4)

• (4) DE/best/2

  $$\begin{aligned} \varvec{v}_{i}=\varvec{x}_{\mathrm{best}}+F\cdot (\varvec{x}_{r_{1}}-\varvec{x}_{r_{2}})+F\cdot (\varvec{x}_{r_{3}}-\varvec{x}_{r_{4}}). \end{aligned}$$

  (5)

• (5) DE/rand/2

  $$\begin{aligned} \varvec{v}_{i}=\varvec{x}_{r_{1}}+F\cdot (\varvec{x}_{r_{2}}-\varvec{x}_{r_{3}})+F\cdot (\varvec{x}_{r_{4}}-\varvec{x}_{r_{5}}). \end{aligned}$$

  (6)

  The indices $r_{1}, r_{2}, r_{3}, r_{4}$ and $r_{5}$ in the above equations are mutually exclusive integers randomly generated from set $\{1,2,\ldots ,\text {NP}\}$ and are also different from the index i. The parameter F is called the scaling factor, which is a positive real number for scaling the difference vectors. The vector $\varvec{x}_{\mathrm{best}}=(x_{\mathrm{best},1},x_{\mathrm{best},2},\ldots ,x_{\mathrm{best},D})$ is the best individual in the current population.

2.3 Crossover operation

After the mutation operation, DE performs a binomial crossover operator on target vector $\varvec{x}_{i}$ and its corresponding mutant vector $\varvec{v}_{i}$ to produce a trial vector $\varvec{u}_{i}=\big [u_{i,1},u_{i,2},\ldots ,u_{i,D}\big ]$. This process can be expressed as

$$\begin{aligned} u_{i,j} = \left\{ \begin{array}{ll} v_{i,j}, &{}\quad \text {if}~ \big (\text {rand}[0,1]\le \text {CR}~\text {or}~j=j_{\mathrm{rand}}\big )\\ x_{i,j}, &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(7)

The crossover rate $\text {CR}$ is a user-specified constant within the interval (0, 1) in original DE, which controls the fraction of trial vector components inherited from the mutant vector. The index $j_{\mathrm{rand}}$ is an integer randomly chosen from set $\{1, 2, \ldots , D\}$, which is used to ensure that the trial vector has at least one component different from the target vector.

2.4 Selection operation

After the crossover operation, a selection operation is executed between the trial vector and the target vector according to their fitness values $f(\cdot )$, and the better one will survive to the next generation. Without loss of generality, we only consider minimization problems. Specifically, the selection operator can be expressed as follows:

$$\begin{aligned} \varvec{x}_{i} = \left\{ \begin{array}{ll} \varvec{u}_{i}, &{} \quad \text {if}~ f(\varvec{u}_{i})\le f(\varvec{x}_{i})\\ \varvec{x}_{i}, &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(8)

From the expression of selection operator (8), it is easy to see that the population of DE either gets better or remains the same in fitness status, but never deteriorates.

3 Related work

In the past decades, many meta-heuristic algorithms have been proposed, such genetic algorithm (Goldberg 1989), differential evolution (Storn and Price 1997), particle swarm optimization (Kennedy et al. 2001), ant colony optimization (Dorigo and Blum 2005), joint operations algorithm (Sun et al. 2016) and so on. These meta-heuristic algorithms have been successfully applied in various fields, such as production planning (Lan et al. 2012), procurement planning (Sun et al. 2010), location problems (Wang and Watada 2012), workforce planning (Yang et al. 2017). Among these meta-heuristic algorithms, DE has shown outstanding performance in solving many test functions and real-world problems, but its performance highly depends on the selected evolutionary operators and the values of control parameters. To overcome these drawbacks, many variants have been proposed to improve the performance of DE. In this section, we only provide a brief overview of the enhanced approaches which is related to our work.

There are lots of researchers who tried to enhance DE via designing new mutation operators or combining multiple operators. Qin et al. (2009) proposed a self-adaptive DE (SADE) which focuses on the mutation operator selection and crossover rate of DE. Zhang and Sanderson (2009) presented a self-adaptive DE with optional external archive (JADE) which employs a new mutation operator called “DE/current-to-pbest.” Han et al. (2013) introduced a group-based DE variant (GDE) which divides the population into two groups and each group employs a different mutation operator. Wang et al. (2013) proposed a modified Gaussian bare-bones DE variant (MGBDE) which combines two mutation operators, and one of the mutation operators is designed based on Gaussian distribution. Das et al. (2009) presented two kinds of topological neighborhood models and embedded them into the mutation operators of DE. Gong et al. (2011a) introduced a simple strategy adaptation mechanism (SaM) which can be used for coordinating different mutation operators. Many other DE variants also adopted new designed mutation operator or multi-mutation operator strategies with different searching features, such as NDi-DE (Cai and Wang 2013), MS-DE (Wang et al. 2014), CoDE (Wang et al. 2011), HLXDE (Cai and Wang 2015), MDE_pBX (Islam et al. 2012), AdapSS-JADE (Gong et al. 2011b), IDDE (Sun et al. 2017).

Some other researchers applied parameter adjustment to improve the performance of DE. For instance, Draa et al. (2015) introduced sinusoidal differential evolution (SinDE), which adopts two sinusoidal formulas to adjust the values of scaling factor and crossover rate. Brest et al. (2006) proposed a self-adaptive scheme for the DE’s control parameters. Liu and Lampinen (2005) applied fuzzy logic controllers to adapt the value of crossover rate. Zhu et al. (2013) adopted an adaptive population tuning scheme to enhance DE. Ghosh et al. (2011) introduced a control parameter adaptation strategy, which is based on the fitness values of individuals in DE population. Yu et al. (2014) proposed a two-level adaptive parameter control strategy, which is based on the optimization states and the fitness values of individuals. Sarker et al. (2014) introduced a new mechanism to dynamically select the best performing combinations of control parameters, which is based on the success rate of each parameter combination. Karafotias et al. (2015) provided a comprehensive overview about the parameter control in evolutionary algorithms.

Actually, many aforementioned references simultaneously utilize new evolutionary operators and adaptive control parameters to enhance the performance of DE, including SADE (Qin et al. 2009), JADE (Zhang and Sanderson 2009), MGBDE (Wang et al. 2013) and CoDE (Wang et al. 2011). In addition, Mallipeddi et al. (2011) employed a pool of distinct mutation operators along with a pool of values for each control parameter which coexists and competes to produce offsprings during the evolutionary process. Yang et al. (2015) proposed a mechanism named auto-enhanced population diversity to automatically enhance the performance of DE, which is based on the population diversity at the dimensional level. Biswas et al. (2015) presented an improved information-sharing mechanism among the individuals to enhance the niche behavior of DE. Tang et al. (2015) introduced a novel variant of DE with an individual-dependent mechanism which includes an individual-dependent parameter setting and mutation operator. However, these DE variants still cannot resolve the problems of premature convergence or stagnation when handling complex optimization problems.

4 Description of GPDE

In this section, we firstly provide a detailed description of the new Gaussian mutation operator, the modified common mutation operator and the cooperative rule between them, and then summarize the overall procedure of GPDE.

4.1 Gaussian mutation operator

Gaussian distribution is very important and often used in statistics and natural sciences to represent real-valued random variable, which can be denoted by $N(\mu , \sigma ^{2})$, where $\mu$ and $\sigma$ are its mean and standard deviation, respectively. It is well known that there is 3-$\sigma$ rule which exists in Gaussian distribution. Specifically, about 68% of the values drawn from the Gaussian distribution $N(\mu , \sigma ^{2})$ are within the interval $[\mu -\sigma ,\mu +\sigma ]$; about 95% of the values lie within the interval $[\mu -2\sigma ,\mu +2\sigma ]$; and about 99.7% are within the interval $[\mu -3\sigma ,\mu +3\sigma ]$.

The 3-$\sigma$ rule of Gaussian distribution provides a wonderful chance to control the hunting zone which depends on the requirement of considered problem. Actually, Gaussian distribution has been widely used to adjust the values of control parameters, such as SADE (Qin et al. 2009), MGBDE (Wang et al. 2013), DEGL (Das et al. 2009) and MDE_pBE (Islam et al. 2012), but rarely applied to generate new mutation operator. In order to take full advantage of Gaussian distribution, we propose the following novel mutation operator which combines crossover operator to directly produce the new trial vector (denoted by $\varvec{u}_{i}^{g}=(u_{i,1}^{g},u_{i,2}^{g},\ldots ,u_{i,D}^{g})$) for the ith individual, $i=1,2,\ldots ,\text {NP}$,

$$\begin{aligned}&u_{i,j}^{g} = \left\{ \begin{array}{ll} N\left( x_{r_{1},j},\big (x_{r_{2},j}\quad -x_{r_{3},j}\big )^{2}\right) , &{}\quad \text {if}~~ \big (j=j_{\mathrm{rand}}\\ ~\quad \text {or}~\text {rand}[0,1]\le \text {CR}_{t}^{i}\big ),\\ x_{i,j}, &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(9)

where the indices $r_{1}, r_{2}, r_{3}$ are mutually exclusive integers randomly generated from the set $\{1,2,\ldots ,\text {NP}\}$ and are also different from the base index i. Note that the $r_{1}$th individual is the best one among the three randomly selected individuals, and the novel Gaussian mutation operator $N\left( x_{r_{1},j},\big (x_{r_{2},j}-x_{r_{3},j}\big )^{2}\right)$ in formula (9), respectively, takes the position $x_{r_{1},j}$ of the best one and the distance $|x_{r_{2},j}-x_{r_{3},j}|$ between the other two as the mean and standard deviation; meanwhile, it will only be executed when meeting the triggering condition $\big (j=j_{\mathrm{rand}}~\text {or}~\text {rand}[0,1]\le \text {CR}_{t}^{i}\big )$, which means that the proposed Gaussian mutation operator only transfers a certain proportional dimensions of each corresponding individual to new positions around the best selected one. Furthermore, if the new position of one dimension is within one standard deviation $|x_{r_{2},j}-x_{r_{3},j}|$ away from the mean $x_{r_{1},j}$, we can call that it executes the exploitation operation in this dimension; otherwise, it carries out the exploration operation. Therefore, according to the 3–$\sigma$ rule, the designed Gaussian mutation operator can simultaneously conduct exploitation and exploration works, especially the former one. In addition, dynamic parameter $\text {CR}_{t}^{i}$ expresses the crossover rate of the ith individual in the tth generation, which can be computed by

$$\begin{aligned} \text {CR}_{t}^{i}=N(0.5,V), ~~i=1,2,\ldots ,\text {NP},~t=1,2,\ldots ,T,\nonumber \\ \end{aligned}$$

(10)

where V indicates the variance of Gaussian distribution N(0.5, V), and it is applied to control the fluctuation of crossover rate, and T is the maximum allowable generation. It should be pointed out that V is a user-specified constant and it has to simultaneously ensure that the value of dynamic crossover rate $\text {CR}_{t}^{i}$ has a certain extent of fluctuation and almost falls into the range [0, 1], and thus its reasonable interval is [0.01, 0.1]. Actually, the individuals employing different crossover rates in the same generation can potentially enhance the population diversity.

4.2 DE/rand-worst/1

In mutation operator, the base individual can be taken as the center point of the searching area, the difference vector is applied to set the searching direction, and the scale factor is employed to control the step size. In a general way, a better base individual has a higher probability to produce better offsprings, a more proper direction induces a more efficient searching behavior of the population, and a periodic scaling factor has potential advantage in balancing exploration ability and exploitation ability. Based on the aforementioned considerations, we incorporate the fitness information of selected individuals and a periodic scaling factor to modify the most popular mutation operator (DE/rand/1). The obtained modified mutation operator DE/rand/1 (denoted by DE/rand-worst/1) which combines crossover operator is applied to directly produce the new trial vector (denoted by $\varvec{u}_{i}^{m}=(u_{i,1}^{m},u_{i,2}^{m},\ldots ,u_{i,D}^{m}), i=1,2,\ldots ,\text {NP}$) of each individual, the corresponding formula can be described as follows,

$$\begin{aligned} u_{i,j}^{m} = \left\{ \begin{array}{ll} x_{r_{1}^{\prime },j}+F_{t}\cdot (x_{r_{2}^{\prime },j}-x_{r_{3}^{\prime },j}), &{}\quad \text {if}~~ \big (j=j_{\mathrm{rand}}~\text {or}\\ ~\quad \quad \; \text {rand}[0,1]\le \text {CR}_{t}^{i}\big ),\\ x_{i,j}, &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(11)

where the indices $r_{1}^{\prime }, r_{2}^{\prime }$ and $r_{3}^{\prime }$ are mutually exclusive integers randomly chosen from the set $\{1,2,\ldots ,\text {NP}\}$, which are also different from the index i. Moreover, the $r_{3}^{\prime }$th individual is the worst one among the three randomly selected individuals, which can ensure that the base individual is not the worst one and the searching direction is relatively better. In addition, note that the mutation operator DE/rand-worst/1 in formula (11) has the same triggering condition with Gaussian mutation operator in formula (9). About the periodic scaling factor, we apply a cosine function to realize the periodic adjustment strategy, which can be expressed via the following formula,

$$\begin{aligned} F_{t}=\big |\text {cos}(t \cdot \text {FR} \cdot \pi )\big |, \end{aligned}$$

(12)

where $F_{t}$ is the value of scaling factor in the tth generation, and $\text {FR}$ represents the frequency of cosine function, which is a user-specified constant and applied to adjust the turnover rate between the exploration and exploitation operations. Usually, a smaller frequency $\text {FR}$ corresponds to a smaller turnover rate.

Table 1 Summary of the IEEE CEC 2014 benchmark functions

Table 2 Comparative results on functions $f_{1}-f_{15}$ with $D=30$

Table 3 Comparative results on functions $f_{16}-f_{30}$ with $D=30$

Table 4 Comparative results on functions $f_{1}-f_{15}$ with $D=50$

Table 5 Comparative results on functions $f_{16}-f_{30}$ with $D=50$

Table 6 Comparative results on functions $f_{1}-f_{15}$ with $D=100$

Table 7 Comparative results on functions $f_{16}-f_{30}$ with $D=100$

Table 8 Comparative results on real-world problems $\textit{rf}_{1}-\textit{rf}_{4}$

Table 9 Statistical results on all test functions and real-world problems

4.3 Cooperative rule

Up to now, two mutation operators (Gaussian and DE/rand-worst/1) have been introduced, which combine a same crossover operator to produce the new trial vector $\varvec{u}_{i}$ for each individual, and then the cooperative rule between them becomes a burning problem. A natural and reasonable rule is that adaptively executing one of the two mutation operators in terms of their own performance. To evaluate the performance of adopted mutation operators during the evolutionary process, we introduce a new concept called “cumulative score” into the mutation operation. For the two adopted mutation operators, their cumulative scores during the evolutionary process can be obtained via the following three steps. Firstly, the values of their initial cumulative scores are set (denoted by $\text {CS}_{0}^{g}$ and $\text {CS}_{0}^{m}$) to 0.5. Secondly, suppose that the values of their historical cumulative scores are $\text {CS}_{t-1}^{g}$ and $\text {CS}_{t-1}^{m}$, and then their single-period scores in the current generation (denoted by $S_{t}^{g}$ and $S_{t}^{m}$) can be obtained via the following two formulas, respectively.

$$\begin{aligned} S_{t}^{g}= & {} \left\{ \begin{array}{ll} \frac{C_{t}^{g}}{N_{t}^{g}}, &{} \quad \text {if}~~ N_{t}^{g}>0,\\ \frac{\text {CS}_{t-1}^{g}}{t}, &{} \quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(13)

$$\begin{aligned} S_{t}^{m}= & {} \left\{ \begin{array}{ll} \frac{C_{t}^{m}}{N_{t}^{m}}, &{} \quad \text {if}~~ N_{t}^{m}>0,\\ \frac{\text {CS}_{t-1}^{m}}{t}, &{} \quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(14)

where the indices $N_{t}^{g}$ and $N_{t}^{m}$ represent the numbers of new trial vectors produced by Gaussian mutation operator and DE/rand-worst/1 in the tth generation, respectively. Actually, the value of $N_{t}^{g}$ always is equals to $\text {NP}-N_{t}^{m}$, owing to the fact that the population only executes $\text {NP}$ times of mutation operators in one generation. And the indices $C_{t}^{g}$ and $C_{t}^{m}$, respectively, represent the success times of the two operators’ execution, where the concept of success means that the new produced trial vector is better than the original target vector. Note that formulas (13) and (14) express that the current single-period score of each adopted mutation operator is equal to its current success rate when executing at least once in the current generation, otherwise takes its average value of historical cumulative score. Thirdly, after obtaining the current single-period scores of the two adopted mutation operators, their current cumulative scores can be updated by the following two formulas,

$$\begin{aligned} \text {CS}_{t}^{g}= & {} \text {CS}_{t-1}^{g}+S_{t}^{g}, \end{aligned}$$

(15)

$$\begin{aligned} \text {CS}_{t}^{m}= & {} \text {CS}_{t-1}^{m}+S_{t}^{m}. \end{aligned}$$

(16)

Now, the value of a parameter involved in cooperative rule can be derived in terms of the two mutation operators’ cumulative scores, which can be calculated by,

$$\begin{aligned} \text {CS}_{t}=\frac{\text {CS}_{t}^{g}}{\text {CS}_{t}^{g}+\text {CS}_{t}^{m}}, \end{aligned}$$

(17)

where parameter $\text {CS}_{t}$ is applied to control the selection probability of Gaussian mutation operator in the next generation. Furthermore, the detailed cooperative rule can be described as follows,

$$\begin{aligned} \varvec{u}_{i}=\left\{ \begin{array}{ll} \varvec{u}_{i}^{g}, &{} \quad \text {if}~~ \text {rand}[0,1]<\text {CS}_{t},\\ \varvec{u}_{i}^{m}, &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(18)

The cooperative rule (18) shows that the chance of executing the adopted two mutation operators relies on their own cumulative scores, and the one with higher cumulative score has more chance to produce the trial vectors. After the new trial vector produced, GPDE will compare the fitness values of each individual $\varvec{x}_{i}$ and its new trial vector $\varvec{u}_{i}$ and then produce the offspring via the selection operator (8).

4.4 The overall procedure of GPDE

We have provided a detailed description of Gaussian mutation operator, DE/rand-worst/1, and the cooperative rule between them. Now, we summarize the overall procedure of GPDE into Algorithm 1.

5 Comparison and result analysis

In this section, we firstly provide the test functions, real-world problems and compared DE algorithms, secondly present the comparative results between GPDE and the other seven algorithms, and analyze the effects of control parameters on the performance of GPDE at last.

5.1 Test functions and real-world problems

In order to evaluate the performance of GPDE, we apply a set of 30 well-known test functions from IEEE CEC 2014 (Liang et al. 2013) and four real-world problems to conduct the comparative experiment. Specifically, based on the characteristics of the 30 test functions, they can be divided into four classes, which are summarized in Table 1. Moreover, the adopted test functions are carried out in the comparative experiment when their dimensions are equal to 30, 50 and 100, respectively. In addition, the four real-world problems (denoted by $\textit{rf}_{1}, \textit{rf}_{2}, \textit{rf}_{3}$ and $\textit{rf}_{4}$, respectively) are widely used to evaluate the performance of various algorithms, which are applications to parameter estimation for frequency-modulated sound waves (Das and Suganthan 2011b), spread spectrum radar poly-phase code design (Das and Suganthan 2011b), systems of linear equations (García-Martínez et al. 2008), and parameter optimization for polynomial fitting problem (Herrera and Lozano 2000), respectively.

5.2 Compared algorithms and parameter configurations

In our comparative experiment, GPDE is compared with five excellent DE variants, including SADE (Qin et al. 2009), JADE (Zhang and Sanderson 2009), GDE (Han et al. 2013), MGBDE (Wang et al. 2013) and SinDE (Draa et al. 2015). To be specific, SADE and JADE are two state-of-the-art DE variants, and GDE and MGBDE are recently proposed variants both of which adopt two different mutation operators; in particular, MGBDE employs a similar Gaussian mutation operator with GPDE, and SinDE is an up-to-date DE variant, which applies two sinusoidal functions to adjust the values of mutation scaling factor and crossover rate. These selected DE variants not only have outstanding performance, but also have some similar aspects to our proposed GPDE, that is why we take them as the comparison object. In addition, two good performing state-of-the-art meta-heuristic algorithms, i.e., cooperative coevolving particle swarm optimization with random grouping [denoted by CCPSO2 (Li and Yao 2012] and collective resource-based artificial bee colony with decentralized tasking (denoted by C-ABC (Bose et al. 2014) for short), are used to enrich the comparative experiment.

Fig. 1

Convergence graphs (mean curves) for eight algorithms on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=30$ over 50 independent runs

Fig. 2

Convergence graphs (mean curves) for eight algorithms on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=30$ over 50 independent runs

Fig. 3

Convergence graphs (mean curves) for eight algorithms on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=50$ over 50 independent runs

Fig. 4

Convergence graphs (mean curves) for eight algorithms on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=50$ over 50 independent runs

Fig. 5

Convergence graphs (mean curves) for eight algorithms on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=100$ over 50 independent runs

Fig. 6

Convergence graphs (mean curves) for eight algorithms on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=100$ over 50 independent runs

Table 10 Parameter configurations of different GPDEs

For all the aforementioned compared algorithms, except the population sizes $\text {NP}$, which, respectively, are equal to D and 5D for test functions and real-world problems, the other involved control parameters keep the same with their corresponding literature. In GPDE, there are only three user-specified control parameters, including population size $\text {NP}$, periodic adjustment parameter $\text {FR}$ and the variance V of crossover rate. Note that the values of $\text {FR}$ and V are, respectively, set to 0.05 and 0.1, and the value of $\text {NP}$ always takes the same as its competitors, and all these three values will keep no change for all the adopted test functions and real-world problems. In addition, all the compared algorithms are tested 50 independent runs for every function and the mean results are used in the comparison, and the maximum allowable generations are set to 10000 for all the test functions and real-world problems.

5.3 Comparative results

To evaluate the performances of the participant algorithms and provide a comprehensive comparison, we, respectively, report the mean (denoted by “Mean”) fitness error value $\big (f\big (\varvec{x}_{\mathrm{best}}\big )-f\big (\varvec{x}^{*}\big )\big )$, the corresponding standard deviation (Std.) and the statistical conclusion of comparative results based on 50 independent runs, where $\varvec{x}_{\mathrm{best}}$ is the best obtained solution and $\varvec{x}^{*}$ is the known optimal solution. In addition, the statistical conclusions of the comparative results are based on the paired Wilcoxon rank sum test which is conducted at 0.05 significance level to assess the significance of the performance difference between GPDE and each competitor. We mark the three kinds of statistical significance cases with “$+$,” “$=$” and “−” to indicate that GPDE is significantly better than, similar to, or worse than the corresponding competitor, respectively. The comparative results of test functions with different dimensions are summarized in Tables 2, 3, 4, 5, 6, 7 and 8, and the best results are indicated with boldface font to highlight the best algorithm for each test function. Moreover, the numbers of the three cases $(+/=/-)$ obtained by the compared results are summarized in Table 9.

Table 9 shows that GPDE obtains the best overall performance among the eight compared algorithms. In details, for the 94 functions, GPDE performs better than SADE, JADE, GDE, MGBDE, SinDE, C-ABC and CCPSO2 on 60, 59, 70, 67, 52, 65 and 72 functions, and only loses in 20, 17, 10, 21, 15, 5 and 13 functions, respectively. Moreover, GPDE outperforms its competitors on every adopted dimensions of test functions and has no worst “Mean” in 94 functions, which means that GPDE is robust, and thus it is a reliable algorithm for handling various problems with different dimensions.

In addition, to observe the convergence characteristics of the compared algorithms, we select 36 functions with different dimensions and plot their convergence graphs based on the mean values over 50 runs in Figs. 1, 2, 3, 4, 5 and 6. Obviously, GPDE has a wonderful convergence rate. As a conclusion, the experimental results and convergence graphs have demonstrated that GPDE performs significantly better than the other seven compared algorithms.

5.4 Robustness analysis of control parameters

Generally speaking, the involved control parameters may have important effects on the algorithmic performance, but it is good news for the users if the control parameters is robust. To verify the robustness of control parameters in GPDE, we compare various GPDEs with different parameter configurations, which are listed in Table 10. Note that we only evaluate the robustness of periodic adjustment parameter $\text {FR}$ and the variance V of crossover rate, because population size $\text {NP}$ usually has no obvious effect on the performance of DE.

Since most of the results obtained by different GPDEs are very close to each other, we only select 36 test functions with different dimensions whose results have relatively clear differences to reveal the robustness of control parameters $\text {FR}$ and V via convergence graphs. The convergence graphs of 36 selected functions obtained by GPDEs with different parameter configurations are plotted in Figs. 7, 8, 9, 10, 11 and 12.

Fig. 7

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=30$ over 50 independent runs

Fig. 8

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=30$ over 50 independent runs

Three discoveries can be found out from Figs. 7, 8, 9, 10, 11 and 12. Above all, the results of GPDEs with different parameter configurations have no obvious fluctuation, which implies that the control parameters of GPDE are robust. Secondly, the variance V of crossover rate has a slightly bigger influence on the performance of GPDE than periodic adjustment parameter $\text {FR}$, because V has more direct effect on the population diversity than $\text {FR}$. At last, under a prescribed limit, a bigger value of V leads to a better result, because a bigger value of V is often corresponding to a better population diversity.

6 Conclusions

Fig. 9

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=50$ over 50 independent runs

Fig. 10

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=50$ over 50 independent runs

Fig. 11

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{1}, f_{2}, f_{3}, f_{4}, f_{12}$ and $f_{13}$ with $D=100$ over 50 independent runs

Fig. 12

Convergence graphs (mean curves) for the GPDE with different parameter configurations on functions $f_{18}, f_{19}, f_{20}, f_{21}, f_{29}$ and $f_{30}$ with $D=100$ over 50 independent runs

Differential evolution is an excellent evolutionary algorithm for global numerical optimization, but it is not completely free from the problems of premature convergence and stagnation. In order to alleviate these problems and enhance DE, we propose a new variant called GPDE. In GPDE, a novel Gaussian mutation operator who, respectively, takes the position of the best individual among three randomly selected individuals and the distance between the other two as the mean and standard deviation, and a modified common mutation operator is applied to cooperatively generate the mutant vectors. Moreover, scaling factor adopts a cosine function to adjust its value periodically, which has potential advantage in balancing the exploration and exploitation abilities, and crossover rate employs a Gaussian function to produce its value dynamically, which can adjust the population diversity. The test suite of IEEE CEC-2014 which contains 30 test function and four real-world problems, and seven remarkable meta-heuristic algorithms are used to evaluate the performance of GPDE, and the obtained results show that GPDE performs much better than the other seven compared DE algorithms. In addition, the parameter analysis indicates that the control parameters involved in GPDE are robust.