1 Introduction

The fuzzy set theory introduced by Zadeh (1965) has achieved a great success in various fields. Later, Zadeh (1975) introduced the type-2 fuzzy sets (T2 FSs), which was an extension of the fuzzy set, and the membership values are type-1 fuzzy sets on interval \([0,1]\). Mendel (2001) further generalized the interval fuzzy set and defined the notion of IT2 FSs, which has been found useful to deal with vagueness and uncertainty in decision problems, such as perceptual computing (Mendel and Wu 2010; Mendel et al. 2010), control system (Wu and Tan 2006; Wagner and Hagras 2010; Wu 2012), time-series forecasting (Khosravi et al. 2012; Chakravarty and Dash 2012; Miller et al. 2012), information aggregation (Zhou et al. 2010, 2011; Huang et al. 2014) and decision-making (Chen and Lee 2010; Wang et al. 2012; Chen and Wang 2013).

MADM is a widespread method, which is applied to find the most desirable alternatives according to the information about attributes and weights provided by decision makers (Damghani et al. 2013; Xu 2010). TOPSIS, introduced by Yoon and Hwang (1981), uses the similarity to ideal solution to solve MADM problems, where the performance ratings and weights are given as crisp values. Later, Triantaphyllou and Lin (1996) introduced fuzzy TOPSIS method based on fuzzy arithmetic operations. Chen (2000) extended TOPSIS method to fuzzy group decision-making situations. Wang and Elhag (2006) proposed a fuzzy TOPSIS method based on alpha level sets. Wang and Lee (2007) generalized TOPSIS method in fuzzy MADM environment. Chen and Tsao (2008) and Ashtiani et al. (2009) extended the TOPSIS method to interval-valued fuzzy numbers environment. Boran et al. (2009) proposed an intuitionistic fuzzy TOPSIS method for supplier selection problem. Li (2010) proposed TOPSIS-based NLP methodology with interval-valued intuitionistic fuzzy sets. Tan (2011) introduced a multi-criteria interval-valued intuitionistic fuzzy group decision-making method using Choquet integral-based TOPSIS method. Robinson and AmirtharajE (2011) developed TOPSIS method under triangular intuitionistic fuzzy sets. Behzadian et al. (2012) summarized the research on TOPSIS applications and methodologies. In addition to the developments of fuzzy TOPSIS in traditional type-1 fuzzy formats, a notable progress was the appearance of interval type-2 fuzzy TOPSIS method proposed by Chen and Lee (2010). They first computed the ranking values of the IT2 FSs elements in weighted decision matrix, then counted the crisp relative distance through traditional TOPSIS computing process. However, both the defuzzification from the very beginning and the crisp distance computation are approximate, which do not realize the IT2 FSs formats crossing the whole computing process, and lead to decision information loss.

In this paper, we provide an analytical solution to IT2 FSs-based TOPSIS model with KM algorithm. KM algorithm (Karnik and Mendel 2001) is a kind of the standard way to compute the centroid and perform type reduction for type-2 fuzzy sets and systems (Hagras 2007; Mendel 2007a, 2013). It transforms the fractional nonlinear programming problems into identifying the switch points of \(\alpha \) levels, which is monotonically and superexponentially convergent to the optimal solution (Mendel and Liu 2007). Some applications of KM algorithm in decision-making have also been proposed. Wu and Mendel (2007) used the KM algorithm to compute the linguistic weighted average (LWA) of type-2 fuzzy sets. Liu and Mendel (2008) proposed a new \(\alpha \)-cut algorithm for solving the fuzzy weighted averaging (FWA) problem with the KM algorithm. Liu et al. (2012) proposed the analytical solution to FWA with KM algorithm. Liu and Wang (2013) introduced the analytical solution to generalized FWA with KM algorithm as well.

Based on KM algorithm (Karnik and Mendel 2001; Liu et al. 2012), we propose an analytical solution to the TOPSIS model with IT2 FSs variables. First, similar to the case of type-1 fuzzy TOPSIS method (Kao and Liu 2001; Li et al. 2009), we transform the IT2 FSs TOPSIS model into several interval fractional NLP problems with \(\alpha \) levels for finding the fuzzy relative closeness among the alternatives. Then, we use the KM algorithm to identify the switch points of the interval fractional NLP problems with \(\alpha \) levels. The switch points are the optimal values of the interval parameters, which can be used to directly express the optimal solutions to the interval fractional NLP problems in an analytical way. Finally, we propose a computational procedure to obtain the analytical solution to IT2 FSs-based TOPSIS method. Compared with the current interval type-2 fuzzy TOPSIS method proposed by Chen and Lee (2010), it realizes the actual sense of IT2 FSs-based TOPSIS method computation, as the defuzzification of the fuzzy relative closeness is dealt with at the end of the computing process, not from the very beginning. It is accurate, as the fractional NLP problem considers all the conditions when computing the IT2 FSs-based fuzzy relative closeness, and all the switch points are identified through expressions.

The paper is organized as follows. Section 2 introduces the concept of IT2 FSs, KM algorithm and fuzzy TOPSIS method. Section 3 proposes the fractional NLP models of IT2 FSs-based TOPSIS model with KM algorithm. Section 4 introduces the analytical solution to IT2 FSs-based TOPSIS model, and discusses some properties of it. Section 5 illustrates a MADM problem under IT2 FSs environment, and compares the results with that of the original method. Section 6 summarizes the main results and draws conclusions.

2 Preliminaries

In this section, we introduce the concepts of IT2 FSs, KM algorithm and the process of computing fuzzy TOPSIS method.

2.1 IT2 FSs and KM algorithm

2.1.1 IT2 FSs

The type-2 fuzzy sets are characterized by a fuzzy membership function, where the membership value is a fuzzy set in \([0,1]\), not a crisp number.

Definition 1

Zadeh (1975) The type-2 fuzzy sets are represented by a type-2 membership function \(\mu _{\tilde{\tilde{A}}}\), which can be shown as:

$$\begin{aligned} \tilde{\tilde{A}}&=\int _{x\in X}\int _{u\in J_{x}} \mu _{\tilde{\tilde{A}}}(x,\mu )/(x,u)\\&=\int _{x\in X} \left[ \int _{u\in J_{x}} \mu _{\tilde{\tilde{A}}}(x,\mu )/(x,u)\right] \bigg /x, \end{aligned}$$

where \(x\) is the primary variable, \(J_{x}\in [0,1]\) is the primary membership of \(x\), \(u\) is the secondary variable, and \(\int _{u\in J_{x}} \mu _{\tilde{\tilde{A}}}(x,\mu )/(x,u)\) is the secondary membership function at \(x\).

Mendel (2001) generalized the interval fuzzy set and defined the notion of IT2 FSs, which are defined as follows.

Definition 2

Mendel (2001) The IT2 FSs \(\tilde{\tilde{A}}\) is an objective, which has the parametric form as:

$$\begin{aligned} \tilde{\tilde{A}}=\int _{x\in X}\int _{u\in J_{x}} 1/(x,u)=\int _{x\in X} \left[ \int _{u\in J_{x}} 1/(x,u)\right] \Bigg /x, \end{aligned}$$

where \(x\) is the primary variable, \(J_{x}\in [0,1]\) is the primary membership of \(x\), \(u\) is the secondary variable, and \(\int _{u\in J_{x}} 1/(x,u)\) is the secondary membership function at \(x\).

Definition 3

Mendel (2007b) For the IT2 FSs \(\tilde{\tilde{A}}\), the footprint of uncertainty of \(\tilde{\tilde{A}}(\mathrm{FOU}(\tilde{\tilde{A}}))\) is defined as:

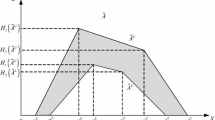
$$\begin{aligned} \mathrm{FOU}(\tilde{\tilde{A}})=\bigcup \limits _{x \in X} J_x=\{(x,y): y\in J_x=[\tilde{A}^U(x),\tilde{A}^L(x)]\}, \end{aligned}$$
(1)

where FOU is shown as the shaded region in Fig. 1. It is bounded by an upper membership function (UMF) \(\tilde{A}^U(x)\) and a lower membership function (LMF) \(\tilde{A}^L(x)\).

Fig. 1
figure 1

The sample of interval type-2 fuzzy sets

Full size image

Definition 4

Lee and Chen (2008) Suppose \(\tilde{\tilde{A}}_i\) be an trapezoidal IT2 FSs shown in Fig. 1, where \(\tilde{\tilde{A}}_i\!=\!\!\big ((x^U_{i1},x^U_{i2},x^U_{i3},x^U_{i4};\) \(H_1(\tilde{A}^U_i),H_2(\tilde{A}^U_i)), (x^L_{i1},x^L_{i2},x^L_{i3},x^L_{i4};H_1(\tilde{A}^L_i),H_2(\tilde{A}^L_i)))\), the ranking value \(\mathrm{Rank}(\tilde{\tilde{A}}_i)\) can be defined as Eq. (2).

$$\begin{aligned} \mathrm{Rank}(\tilde{\tilde{A}}_i)=\,&M_1(\tilde{A}^U_i)+M_1(\tilde{A}^L_i)+M_2(\tilde{A}^U_i)+M_2(\tilde{A}^L_i)\nonumber \\&+M_3(\tilde{A}^U_i) +M_3(\tilde{A}^L_i)- \frac{1}{4}\left( S_1(\tilde{A}^U_i)\right. \nonumber \\&\left. +S_1(\tilde{A}^L_i)+S_2(\tilde{A}^U_i)+S_2(\tilde{A}^L_i)\right. \nonumber \\&\left. + S_3(\tilde{A}^U_i)+S_3(\tilde{A}^L_i)+S_4(\tilde{A}^U_i)+S_4(\tilde{A}^L_i)\right) \nonumber \\&+H_1(\tilde{A}^U_i)+H_1(\tilde{A}^L_i)+ H_2(\tilde{A}^U_i)+H_2(\tilde{A}^L_i), \end{aligned}$$
(2)

In Eq. (2), \(M_p(\tilde{A}^L_i)\) denotes the average of elements \(x^j_{ip}\) and \(x^j_{i(p+1)}\), \( M_p(\tilde{A}^j_i)=\frac{x^j_{ip}+x^j_{i(p+1)}}{2}\), \(p=\) 1, 2, 3. \(S_q(\tilde{A}^j_i)\) denotes the standard deviation of elements \(x^j_{iq}\) and \(x^j_{i(q+1)}\), \(S_q(\tilde{A}^j_i)=\sqrt{\frac{1}{2} \sum \nolimits _{k=q}^{q+1}\left( x^j_{ik}-M_q(\tilde{A}^j_i)\right) ^2}\), \(q=1,2,3. \) \(S_4(\tilde{A}^j_i)=\) \(\sqrt{\frac{1}{4} \sum \nolimits _{k=1}^4 \left( (x^j_{ik})^2-\frac{1}{4}\sum \nolimits _{k=1}^4 x^j_{ik}\right) ^2}\) denotes the standard deviation of elements \(x^j_{ik}\) \((k=1,2,3,4)\), \(j\in \{U,L\}\). \(H_p(\tilde{A}^j_i)\) denotes the membership value of element \(x^j_{p+1}\) in trapezoidal membership function \(\tilde{A}^j_i\), \(p=1,2\), \(j\in \{U,L\}\), \(i=1,2,\ldots ,n\).

It is obvious that IT2 FSs is the simplest form of type-2 fuzzy sets. In this paper, we just discuss the TOPSIS method under IT2 FSs environment.

2.1.2 KM algorithm

KM algorithm (Karnik and Mendel 2001) is a type reduction method in IT2 FSs, which was originally used to compute the centroid of IT2 FSs. The principle of which can be described as follows.

Definition 5

Mendel and Liu (2007) For an interval type-2 fuzzy set \(\tilde{A}\), the centroid \(c_{\widetilde{A}}=[c_l, c_r]\) can be defined as the maximum and minimum solutions to the following interval fractional programming, respectively.

$$\begin{aligned} y(\theta _1,\theta _2,\ldots ,\theta _n) \triangleq \frac{\sum \limits _{i=1}^nx_i \theta _i}{\sum \limits _{i=1}^n\theta _i}, \end{aligned}$$
(3)

where \(x_i\)s are increasing in the domain \(X\), and \(\theta _i\) can be changed between the lower membership function (LMF) \(\underline{\mu }_{\widetilde{A}}(x_i)\) and upper membership function (UMF) \(\overline{\mu }_{\widetilde{A}}(x_i)\).

The derivative of function \(y(\theta _1,\theta _2,\ldots ,\theta _n)\) with variable \(\theta _k(k=1,2,\ldots ,n)\) is denoted as:

$$\begin{aligned} \frac{\partial y(\theta _1,\theta _2,\ldots ,\theta _n)}{\partial \theta _k}&=\frac{\partial }{\partial \theta _k} \left( \frac{\sum \nolimits _{i=1}^nx_i \theta _i}{\sum \limits _{i=1}^n\theta _i}\right) \nonumber \\&=\frac{x_k-y(\theta _1,\theta _2,\ldots ,\theta _n)}{\sum \limits _{i=1}^n\theta _i}. \end{aligned}$$
(4)

In Eq. (4), because of \(\sum \nolimits _{i=1}^n\theta _i > 0\), it is concluded that \(x_k\) is the switch point, which determines the monotonicity of function \(y(\theta _1,\theta _2,\ldots ,\theta _n)\). That is if

$$\begin{aligned} {\left\{ \begin{array}{ll} x_k \ge y(\theta _1,\theta _2,\ldots ,\theta _n), y(\theta _1,\theta _2,\ldots ,\theta _n) \\ \qquad \hbox {monotonically increases with} ~x_k;\\ x_k < y(\theta _1,\theta _2,\ldots ,\theta _n), y(\theta _1,\theta _2,\ldots ,\theta _n) \\ \qquad \hbox {monotonically decreases with} ~x_k. \end{array}\right. } \end{aligned}$$
(5)

According to Eq. (5), suppose the maximum (minimum) of \(\theta _k\) is \(\overline{\mu }_{\widetilde{A}}(x_i) (\underline{\mu }_{\widetilde{A}}(x_i))\), it is implied that \(y(\theta _1,\theta _2,\ldots ,\theta _n)\) reaches the minimum, i.e., \(y^L\), if (1) for those values of \(k\), it follows \(x_k < y(\theta _1,\theta _2,\ldots ,\theta _n)\), such that \(\theta _k=\overline{\mu }_{\widetilde{A}}(x_i)\); (2) for those values of \(k\), it follows \(x_k > y(\theta _1,\theta _2,\ldots ,\theta _n)\), such that \(\theta _k=\underline{\mu }_{\widetilde{A}}(x_i)\). Similarly, it can easily be deduced that \(y(\theta _1,\theta _2,\ldots ,\theta _n)\) reaches the maximum, i.e., \(y^U\), if (1) for those values of \(k\), it follows \(x_k > y(\theta _1,\theta _2,\ldots ,\theta _n)\), such that \(\theta _k=\overline{\mu }_{\widetilde{A}}(x_i)\); (2) for those values of \(k\), it follows \(x_k < y(\theta _1,\theta _2,\ldots ,\theta _n)\), such that \(\theta _k=\underline{\mu }_{\widetilde{A}}(x_i)\). Combined with these conclusions together, it is easy to verify that \(y^L\) or \(y^U\) switch only once between \(\overline{\mu }_{\widetilde{A}}(x_i)\) and \(\underline{\mu }_{\widetilde{A}}(x_i)\).

Coupled with these facts altogether, the centroid of IT2 FSs \(\widetilde{A}\), \(c_{\widetilde{A}}=[c_l, c_r]\), can be computed as:

$$\begin{aligned} c_l=\frac{\sum _{i=1}^{k_l}{x}_i\overline{\mu }_{\widetilde{A}}(x_i)+\sum _{i=k_l+1}^N{x}_i\underline{\mu }_{\widetilde{A}} (x_i)}{\sum _{i=1}^{k_l}\overline{\mu }_{\widetilde{A}}(x_i)+\sum _{i=k_l+1}^N\underline{\mu }_{\widetilde{A}}(x_i)} \end{aligned}$$
(6)
$$\begin{aligned} c_r=\frac{\sum _{i=1}^{k_r}{x}_i\underline{\mu }_{\widetilde{A}}(x_i)+\sum _{i=k_r+1}^N{x}_i\overline{\mu }_{\widetilde{A}} (x_i)}{\sum _{i=1}^{k_r}\underline{\mu }_{\widetilde{A}}(x_i)+\sum _{i=k_r+1}^N\overline{\mu }_{\widetilde{A}}(x_i)} \end{aligned}$$
(7)

where \(k_l\) and \(k_r\) are called “switch points” with \({x}_{k_l}\le c_l\le {x}_{k_l+1}\) and \({x}_{k_r}\le c_r\le {x}_{k_r+1}\). The determination of \(k_l\) and \(k_r\) can be performed using the KM algorithm (Mendel and Liu 2007). The computation process is omitted because we only use the principle of them.

2.2 The process of computing fuzzy TOPSIS method

2.2.1 The process of computing type-1 TOPSIS method

Suppose a fuzzy MADM problem has \(n\) alternatives \(A_{1-n}\), and \(m\) decision criteria \(C_{1-m}\), \(\tilde{x}_{ji}\) \((j=1,2,\ldots ,m;\) \(i=1,2,\ldots ,n)\) is the type-1 fuzzy rating of alternative \(A_j\) for criteria \(C_i\), \(\tilde{w}_i\) is the type-1 fuzzy weight for criteria \(C_i\).

The process of computing type-1 fuzzy TOPSIS method can be summarized as follows (Wang and Elhag 2006).

  • Step 1. Construct the decision matrix \(\tilde{X}\), and normalize average decision matrix as \(\tilde{\bar{X}}=(\tilde{x}_{ji})_{m \times n}\).

  • Step 2. Construct the weighting matrix \(\tilde{W_p}\), and normalize average weighting matrix as \(\tilde{\bar{W}}=(\tilde{w}_i)_{1 \times n}\).

  • Step 3. Define the positive ideal solution and the negative ideal solution.

  • Step 4. Compute the fuzzy relative closeness for alternatives as below.

$$\begin{aligned}&\mathrm{RC}_j =\frac{\sqrt{\sum _{i=1}^n (w_i x_{ji})^2}}{\sqrt{\sum _{i=1}^n (w_i x_{ji})^2}+\sqrt{\sum _{i=1}^n (w_i(x_{ji}-1))^2}}\\&\quad \mathrm{s.t.}\,\,w^L_i \le w_i \le w^U_i, i=1,2,\ldots ,n.\nonumber \\&\qquad \quad x^L_{ji} \le x_{ji} \le x^U_{ji}, j=1,2,\ldots ,m.\nonumber \end{aligned}$$
(8)

As \(\mathrm{RC}_j\) is a triangular fuzzy number, the lower and upper limits can be obtained by the following fractional NLP models:

$$\begin{aligned}&\mathrm{RC}^L_j=\min \frac{\sqrt{\sum _{i=1}^n (w_ix^L_{ji})^2}}{\sqrt{\sum _{i=1}^n (w_ix^L_{ji})^2}+\sqrt{\sum _{i=1}^n (w_i(x^L_{ji}-1))^2}} \nonumber \\&\quad \mathrm{s.t.}\,\,w^L_i \le w_i \le w^U_i, i=1,2,\ldots ,n. \end{aligned}$$
(9)
$$\begin{aligned}&\mathrm{RC}^U_j=\max \frac{\sqrt{\sum _{i=1}^n (w_ix^U_{ji})^2}}{\sqrt{\sum _{i=1}^n (w_ix^U_{ji})^2}+\sqrt{\sum _{i=1}^n (w_i(x^U_{ji}-1))^2}}\nonumber \\&\quad \mathrm{s.t.}\,\,w^L_i \le w_i \le w^U_i, i=1,2,\ldots ,n. \end{aligned}$$
(10)

where \(x_{ji}=[x^U_{ji},x^L_{ji}]\) and \(w_i=[w^U_i,w^L_i]\) are the intervals of \(\tilde{x}_{ji}\) and \(\tilde{w}_i\), and \(\mathrm{RC}_j=\left[ \mathrm{RC}^U_j,\mathrm{RC}^L_j\right] \).

  • Step 5. Defuzzify and rank alternatives in terms of their relative closenesses. The bigger the \(\mathrm{RC}^*_j\) is, the better alternative \(A_j\).

2.2.2 The process of computing IT2 FSs TOPSIS method

Suppose a fuzzy MADM problem has \(n\) alternatives \(A_{1-n}\), and \(m\) decision criteria \(C_{1-m}\), \(\tilde{\tilde{x}}_{ji}\) is the interval type-2 fuzzy average evaluation for alternative \(A_j\) with criteria \(C_i\), \(\tilde{\tilde{w}}_i\) is the interval type-2 fuzzy average weighting with criteria \(C_i\).

According to Chen and Lee (2010), the process of computing IT2 FSs TOPSIS method is denoted as follows.

  • Step 1–3. Construct the fuzzy-weighted decision matrix \(\bar{Y}_w=(\tilde{\tilde{v}})_{m \times n}=\tilde{\tilde{w}}_i \otimes \tilde{\tilde{x}}_{ji}(j=1,2,\ldots ,m;\) \(i=1,2,\ldots ,n)\).

  • Step 4. Compute the ranking values of the elements in fuzzy-weighted decision matrix \(\bar{Y}_w\) using Eq. (2), and construct the crisp ranking-weighted decision matrix \(\bar{Y}^*_w=\mathrm{Rank}(\tilde{\tilde{v}}_{ji})\).

  • Step 5. Define the positive ideal solution and the negative ideal solution from matrix \(\bar{Y}^*_w\).

  • Step 6. Calculate the distances of the alternative from the ideal solution and the negative ideal solution.

  • Step 7. Calculate the crisp relative closeness to the ideal solution.

  • Step 8. Rank alternatives in terms of their crisp relative closenesses. The bigger the \(\mathrm{RC}^*_j\) is, the better alternative \(A_j\).

3 The fractional NLP models of IT2 FSs-based TOPSIS method

Here, we extend the type-1 fuzzy TOPSIS method to IT2 FSs environment. Through solving the fractional NLP models of IT2 FSs fuzzy relative closeness with KM algorithm, the analytical solutions to IT2 FSs-based TOPSIS can be obtained.

3.1 The fractional NLP models for IT2 FSs-based TOPSIS method

Suppose \(\tilde{\tilde{x}}_i\) and \(\tilde{\tilde{w}}_i\) are the normalized IT2 FSs, \(\tilde{\tilde{x}}_i \in [\tilde{x}^U_i(\alpha _j), \tilde{x}^L_i(\alpha _j)]\), \(\tilde{\tilde{w}}_i \in [\tilde{w}^U_i(\alpha _j), \tilde{w}^L_i(\alpha _j)]\), \(\tilde{x}^L_i(\alpha _j) \in [a_{ir}\) \((\alpha _j), b_{il}(\alpha _j)]\), \(\tilde{x}^U_i(\alpha _j) \in [a_{il}(\alpha _j), b_{ir}(\alpha _j)]\), \(\tilde{w}^L_i(\alpha _j) \in [c_{ir}\) \((\alpha _j), d_{il}(\alpha _j)]\) and \(\tilde{w}^U_i(\alpha _j) \in [c_{il}(\alpha _j), d_{ir}(\alpha _j)]\), the UMF and LMF of which has the same maximum and minimum membership value, respectively, are shown in Fig. 2.

Fig. 2
figure 2

The interval type-2 fuzzy sets of \(\tilde{\tilde{x}}_i\) and \(\tilde{\tilde{w}}_i\)

Full size image

Provided that the membership value of \(\tilde{x}^L_i(\alpha )\) \((\tilde{w}^L_i(\alpha ))\) and \(\tilde{x}^U_i(\alpha )(\tilde{w}^U_i(\alpha ))\) is denoted as \(h^L_{\tilde{x}_i(\alpha )} (h^L_{\tilde{w}_i(\alpha )})\) and \(h^U_{\tilde{x}_i(\alpha )}\) \((h^U_{\tilde{w}_i(\alpha )})\), respectively. The corresponding maximum and minimum membership value of which is denoted as \(h_{\max }\) and \(h_{\min }\), respectively. That is

$$\begin{aligned}&h_{\max }=\max \limits _{\forall i \in [1,n]} h^U_{\tilde{x}_i(\alpha )}=\max \limits _{\forall i \in [1,n]} h^U_{\tilde{w}_i(\alpha )}, \\&h_{\min }=\min \limits _{\forall i \in [1,n]} h^L_{\tilde{x}_i(\alpha )}=\min \limits _{\forall i \in [1,n]} h^L_{\tilde{w}_i(\alpha )}. \end{aligned}$$

According to Problem (8), the fuzzy relative closeness of IT2 FSs-based TOPSIS method for each alternative by solving NLP models is denoted as Problem (11), which is also shown in Fig. 3.

$$\begin{aligned}&\widetilde{\widetilde{\mathrm{RC}}}_j \triangleq \frac{\sqrt{\sum _{i=1}^n (w_i x_{ji})^2}}{\sqrt{\sum _{i=1}^n (w_i x_{ji})^2}+\sqrt{\sum _{i=1}^n (w_i(x_{ji}-1))^2}}\\&\quad \mathrm{s.t.}\,\,\tilde{w}^L_i(\alpha ) \le w_i \le \tilde{w}^R_i(\alpha ), i=1,2,\ldots ,n,\nonumber \\&\quad \tilde{x}^L_{ji}(\alpha ) \le x_{ji} \le \tilde{x}^R_{ji}(\alpha ), j=1,2,\ldots ,m,\nonumber \end{aligned}$$
(11)

where \(\tilde{x}^L_{ji}(\alpha ) (\tilde{w}^L_i(\alpha ))\) is the left region of IT2 FSs \(\tilde{\tilde{x}}_{ji}(\tilde{\tilde{w}}_i)\), \(\tilde{x}^R_{ji}(\alpha )(\tilde{w}^R_i(\alpha ))\) is the right region of IT2 FSs \(\tilde{\tilde{x}}_{ji}(\tilde{\tilde{w}}_i)\), \(x_{ji}(\alpha )=[\tilde{x}^L_{ji}(\alpha ), \tilde{x}^R_{ji}(\alpha )]\) and \(w_i(\alpha )=[\tilde{w}^L_i(\alpha ),\) \( \tilde{w}^R_i(\alpha )]\) are the \(\alpha \)-level sets of \(\tilde{\tilde{x}}_{ji}\) and \(\tilde{\tilde{w}}_i\).

Fig. 3
figure 3

The interval type-2 fuzzy sets of \(\widetilde{\widetilde{\mathrm{RC}}}\)

Full size image

Similar to the principle of Problems (9) and (10), the left and right region can be obtained by solving fractional NLP models as Problems (12) and (13), respectively.

$$\begin{aligned}&\widetilde{\mathrm{RC}}^L_j(\alpha ) \triangleq \min \frac{\sqrt{\sum \limits _{i=1}^n (w_i\tilde{x}^L_{ji}(\alpha ))^2}}{\sqrt{\sum \limits _{i=1}^n (w_i \tilde{x}^L_{ji}(\alpha ))^2}\!+\!\sqrt{\sum \limits _{i=1}^n (w_i(\tilde{x}^L_{ji}(\alpha )\!-\!1))^2}}\nonumber \\&\quad \mathrm{s.t.}\,\, \tilde{w}^L_i(\alpha ) \!\le \! w_i \!\le \! \tilde{w}^R_i(\alpha ), i=1,2,\ldots ,n.\nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned}&\widetilde{\mathrm{RC}}^R_j(\alpha ) \!\triangleq \! \max \frac{\sqrt{\sum \limits _{i=1}^n (w_i\tilde{x}^R_{ji}(\alpha ))^2}}{\sqrt{\sum \limits _{i=1}^n (w_i\tilde{x}^R_{ji}(\alpha ))^2}\!+\!\sqrt{\sum \limits _{i=1}^n (w_i(\tilde{x}^R_{ji}(\alpha )\!-\!1))^2}}\nonumber \\&\quad s.t.\,\, \tilde{w}^L_i(\alpha ) \!\le \! w_i \!\le \! \tilde{w}^R_i(\alpha ), i=1,2,\ldots ,n.\nonumber \\ \end{aligned}$$
(13)

where \(\tilde{x}^L_{ji}(\alpha )=[a_{jil}(\alpha ), a_{jir}(\alpha )]\), \(\tilde{x}^R_{ji}(\alpha )=[b_{jil}(\alpha ),\) \(b_{jir}(\alpha )]\), \(\tilde{w}^L_i(\alpha )=[c_{il}(\alpha ), c_{ir}(\alpha )]\) and \(\tilde{w}^R_i(\alpha )=[d_{il}(\alpha ),\) \(d_{ir}(\alpha )]\).

It is obvious that \(\widetilde{\widetilde{\mathrm{RC}}}_j (\alpha )=[\widetilde{\mathrm{RC}}^L_j(\alpha ), \widetilde{\mathrm{RC}}^R_j(\alpha )]\) can be generated by solving NLP Problems (12) and (13).

According to Eq. (8), the final interval type-2 fuzzy relative closeness \(\widetilde{\widetilde{\mathrm{RC}}}_j (\alpha )\) can be expressed as:

$$\begin{aligned} \widetilde{\widetilde{\mathrm{RC}}}_j&=\bigcup \limits _\alpha [\widetilde{\mathrm{RC}}^L_j(\alpha ),\widetilde{\mathrm{RC}}^R_j(\alpha )], \quad 0 < \alpha \le 1, \end{aligned}$$
(14)

Next, we introduce a new NLP problem, through which the optimal solution to Problems (12) and (13) can be computed indirectly.

Theorem 1

For \(\tilde{\tilde{x}}\) and \(\tilde{\tilde{w}}\) is the IT2 FSs-based aggregated element and weight, respectively. Let

$$\begin{aligned}&\tilde{\tilde{f}}_j \triangleq \frac{\sum \limits _{i=1}^n \left( \tilde{\tilde{w}}_i (\tilde{\tilde{x}}_{ji}-1)\right) ^2}{\sum \limits _{i=1}^n (\tilde{\tilde{w}}_i \tilde{\tilde{x}}_{ji})^2},\nonumber \\&\quad \mathrm{s.t.}\,\tilde{w}^L_i(\alpha ) \le \tilde{\tilde{w}}_i \le \tilde{w}^R_i(\alpha ), i=1,2,\ldots ,n,\nonumber \\&\qquad \quad \tilde{x}^L_{ji}(\alpha ) \le \tilde{\tilde{x}}_{ji} \le \tilde{x}^R_{ji}(\alpha ), j=1,2,\ldots ,m. \end{aligned}$$
(15)

if \(\tilde{\tilde{x}}_{ji}=\tilde{x}^L_{ji}\) and \(\tilde{x}^L_{ji}\) reaches its minimum (maximum) point, then the left region \(\tilde{f}^L(\alpha )\) and \(\widetilde{\mathrm{RC}}^L(\alpha )\) obtain its maximum (minimum) and minimum (maximum) values correspondingly; otherwise, if \(\tilde{\tilde{x}}_{ji}=\tilde{x}^R_{ji}\) and \(\tilde{x}^R_{ji}\) reaches at minimum (maximum) point, then the right region \(\tilde{f}^R(\alpha )\) and \(\widetilde{\mathrm{RC}}^R(\alpha )\) get the maximum (minimum) and minimum (maximum) in correspondence.

Proof

See Appendix A. \(\square \)

From the conclusions of Theorem 1, it is evident to see that the optimal solution to Problem (11) can be realized if Problem (15) holds.

Accordingly, the optimal solutions to Problems (12) and (13) can be computed by solving Problems (16) and (17) indirectly.

$$\begin{aligned}&\tilde{f}^{*L}_j(\alpha ) \triangleq \min \frac{\sum \limits _{i=1}^n \left( w_i (\tilde{x}^L_{ji}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^n (w_i \tilde{x}^L_{ji}(\alpha ))^2},\nonumber \\&\quad \mathrm{s.t.}\,\,\tilde{w}^L_i(\alpha ) \le w_i \le \tilde{w}^R_i(\alpha ),\quad i=1,2,\ldots ,n. \end{aligned}$$
(16)
$$\begin{aligned}&\tilde{f}^{*R}_j(\alpha ) \triangleq \max \frac{\sum \limits _{i=1}^n \left( w_i (\tilde{x}^R_{ji}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^n (w_i \tilde{x}^R_{ji}(\alpha ))^2}, \nonumber \\&\quad \mathrm{s.t.}\,\,\tilde{w}^L_i(\alpha ) \le w_i \le \tilde{w}^R_i(\alpha ),\quad i=1,2,\ldots ,n. \end{aligned}$$
(17)

Then, the fuzzy relative closeness of IT2 FSs-based TOPSIS method can be obtained through solving Eqs. (18), (19).

$$\begin{aligned} \widetilde{\mathrm{RC}}^{*L}(\alpha ) \triangleq \frac{1}{1+\sqrt{\tilde{f}^{*L}(\alpha )}}, \end{aligned}$$
(18)
$$\begin{aligned} \widetilde{\mathrm{RC}}^{*R}(\alpha ) \triangleq \frac{1}{1+\sqrt{\tilde{f}^{*R}(\alpha )}}. \end{aligned}$$
(19)

3.2 The fractional NLP models of IT2 FSs-based TOPSIS method with KM algorithm

Here, we prove Problem (15) satisfies the principle of KM algorithm.

Let us rewrite the objective function of Problem (15) into the relation between \(\tilde{\tilde{f}}(\tilde{\tilde{w}}_j)\) and \(\tilde{\tilde{w}}_j\), and get

$$\begin{aligned} \tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)=\frac{\sum \limits _{j=1}^m \left( \tilde{\tilde{w}}_j (x_j-1)\right) ^2}{\sum \limits _{j=1}^m (\tilde{\tilde{w}}_j x_j)^2}. \end{aligned}$$

Then, the derivative of \(\tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)\) to \(\tilde{\tilde{w}}_k(k=1,2,\) \(\ldots ,n)\) can be expressed as:

$$\begin{aligned}&\frac{\partial \tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)}{\partial \tilde{\tilde{w}}_k} \nonumber \\&\quad =\frac{2\tilde{\tilde{w}}_k (x_k-1)^2-2 \tilde{\tilde{w}}_k x^2_k f(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)}{\sum \limits _{j=1}^m (\tilde{\tilde{w}}_j x_j)^2}. \end{aligned}$$
(20)

From Eq. (20), it is obvious that

$$\begin{aligned}&\frac{\partial \tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)}{\partial \tilde{\tilde{w}}_i}\nonumber \\&{\left\{ \begin{array}{ll} \ge 0, \quad \text{ if } \quad \frac{(x_k-1)^2}{x^2_k} \ge \tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n),\\ < 0, \quad \text{ if } \quad \frac{(x_k-1)^2}{x^2_k} < \tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)). \end{array}\right. } \end{aligned}$$
(21)

It is concluded that the extreme points of \(\tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\) \(\tilde{\tilde{w}}_n)\) can be obtained through changing the direction of weighting \(\tilde{\tilde{w}}_k\). If we compute \(\tilde{f}^{*R} (\tilde{f}^{*L})\), \(\tilde{\tilde{w}}_k\) switches only once between \(\tilde{w}^R_k(\alpha )\) and \(\tilde{w}^L_k(\alpha )\). Hence, the computation of the maximum (minimum) of \(\tilde{\tilde{f}}(\tilde{\tilde{w}}_1,\tilde{\tilde{w}}_2,\ldots ,\tilde{\tilde{w}}_n)\) can be converted into solving the maximum (minimum) of \(\tilde{\tilde{w}}_i=\tilde{w}^R_k(\alpha )\) (\(\tilde{\tilde{w}}_i=\tilde{w}^L_k(\alpha )\)).

According to the principle of KM algorithm, if \(\tilde{x}^L_i(\alpha )\) and \(\tilde{x}^R_i(\alpha )\) are increasingly orders, the solutions to \(\tilde{\tilde{f}}(\tilde{\tilde{x}})\) are reduced to finding the switch points of \(k_L\) and \(k_R\).

Putting all of these facts together, problems (16) and (17) can be transformed into Eqs. (22) and (23).

(22)
(23)

In Eqs. (22), (23), \(\tilde{a}_i(\alpha )\) and \(\tilde{b}_i(\alpha )\) are increasing orders; \(\tilde{f}^{*L}\) and \(\tilde{f}^{*R}\) denotes the left region and right region of the function \(\tilde{\tilde{f}}\); \(k_L \triangleq k_L(\alpha )\) and \(k_R \triangleq k_R(\alpha )\), both of which are the switch points, such that

$$\begin{aligned}&\tilde{a}_{k_L}(\alpha ) \le \tilde{f}^{*L} \le \tilde{a}_{k_L+1}(\alpha ),\end{aligned}$$
(24)
$$\begin{aligned}&\tilde{b}_{k_R}(\alpha ) \le \tilde{f}^{*R} \le \tilde{b}_{k_R+1}(\alpha ). \end{aligned}$$
(25)

As \(\tilde{\tilde{f}}\) is a monotonically increasing function, Eqs. (22), (23) can be changed into Eqs. (26)–(29).

$$\begin{aligned}&f^*_\mathrm{Ll}(\alpha ,k) \triangleq \min _{\begin{array}{c} \forall \tilde{a}_i \in [a_{il},a_{ir}]\\ \forall \tilde{c}_i \in [c_{il},c_{ir}], \forall \tilde{d}_i \in [d_{il},d_{ir}] \end{array}}\nonumber \\&\quad \quad \times \frac{\sum \limits _{i=1}^{k_\mathrm{Ll}} \left( \tilde{d}_i(\alpha ) (\tilde{a}_i(\alpha )-1)\right) ^2+\sum \limits _{i=k_\mathrm{Ll}+1}^n \left( \tilde{c}_i(\alpha ) (\tilde{a}_i(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^{k_\mathrm{Ll}} \left( \tilde{d}_i(\alpha ) \tilde{a}_i(\alpha )\right) ^2 +\sum \limits _{i=k_\mathrm{Ll}+1}^n \left( \tilde{c}_i(\alpha ) \tilde{a}_i(\alpha )\right) ^2}\nonumber \\&\quad \triangleq \min _{\begin{array}{c} \forall \tilde{c}_i \in [c_{il},c_{ir}]\\ \forall \tilde{d}_i \in [d_{il},d_{ir}] \end{array}} \nonumber \\&\quad \times \frac{\sum \limits _{i=1}^{k_\mathrm{Ll}} \left( \tilde{d}_i(\alpha ) (a_{il}(\alpha )\!-\!1)\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Ll}\!+\!1}^n \left( \tilde{c}_i(\alpha ) (a_{il}(\alpha )\!-\!1)\right) ^2}{\sum \limits _{i\!=\!1}^{k_\mathrm{Ll}} \left( \tilde{d}_i(\alpha ) a_{il}(\alpha )\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Ll}\!+\!1}^n \left( \tilde{c}_i(\alpha ) a_{il}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
(26)
$$\begin{aligned}&\quad f^*_\mathrm{Lr}(\alpha ,k) \triangleq \max _{\begin{array}{c} \forall \tilde{c}_i \in [c_{il},c_{ir}]\\ \forall \tilde{d}_i \in [d_{il},d_{ir}] \end{array}}\nonumber \\&\quad \times \frac{\sum \limits _{i=1}^{k_\mathrm{Lr}} \left( \tilde{d}_i(\alpha ) (a_{ir}(\alpha )\!-\!1)\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Lr}\!+\!1}^n \left( \tilde{c}_i(\alpha ) (a_{ir}(\alpha )\!-\!1)\right) ^2}{\sum \limits _{i\!=\!1}^{k_\mathrm{Lr}} \left( \tilde{d}_i(\alpha ) a_{ir}(\alpha )\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Lr}\!+\!1}^n \left( \tilde{c}_i(\alpha ) a_{ir}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
(27)
$$\begin{aligned}&f^*_\mathrm{Rl}(\alpha ,k) \triangleq \min _{\begin{array}{c} \forall \tilde{c}_i \in [c_{il},c_{ir}]\\ \forall \tilde{d}_i \in [d_{il},d_{ir}] \end{array}}\nonumber \\&\quad \times \frac{\sum \limits _{i=1}^{k_\mathrm{Rl}} \left( \tilde{c}_i(\alpha ) (b_{il}(\alpha )\!-1)\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Rl}\!+\!1}^n \left( \tilde{d}_i(\alpha ) (b_{il}(\alpha )-\!1)\right) ^2}{\sum \limits _{i=1}^{k_\mathrm{Rl}} \left( \tilde{c}_i(\alpha ) b_{il}(\alpha )\right) ^2\!+\!\!\sum \limits _{i=k_\mathrm{Rl}\!+\!1}^n \left( \tilde{d}_i(\alpha ) b_{il}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
(28)
$$\begin{aligned}&f^*_\mathrm{Rr}(\alpha ,k) \triangleq \max _{\begin{array}{c} \forall \tilde{c}_i \in [c_{il},c_{ir}]\\ \forall \tilde{d}_i \in [d_{il},d_{ir}] \end{array}}\nonumber \\&\quad \times \frac{\sum \limits _{i=1}^{k_\mathrm{Rr}}\! \big (\! \tilde{c}_i(\alpha ) (b_{ir}(\alpha )-1)\!\big )^2+\sum \limits _{i=k_\mathrm{Rr}+1}^n\! \left( \tilde{d}_i(\alpha ) (b_{ir}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^{k_\mathrm{Rr}} \!\big (\tilde{c}_i(\alpha ) b_{ir}(\alpha )\!\big )^2+\sum \limits _{i=k_\mathrm{Rr}+1}^n\! \left( \tilde{d}_i(\alpha ) b_{ir}(\alpha )\!\right) ^2}\!,\nonumber \\ \end{aligned}$$
(29)

In Eqs. (26)–(29), \(a_{il}(\alpha )\), \(a_{ir}(\alpha )\), \(b_{il}(\alpha )\) and \(b_{ir}(\alpha )\) are increasing orders.

Suppose the left region \(\tilde{f}^L(\alpha )\) and the right region \(\tilde{f}^R(\alpha )\) can be denoted as:

$$\begin{aligned} \tilde{f}^L(\alpha )&= [f_\mathrm{Ll}(\alpha ),f_\mathrm{Lr}(\alpha )], \\ \tilde{f}^R(\alpha )&= [f_\mathrm{Rl}(\alpha ),f_\mathrm{Rr}(\alpha )] . \end{aligned}$$

In the following, we propose the expressions to compute the fuzzy relative closeness for Eqs. (26)–(29).

Theorem 2

The following properties are true.

  1. (1)

    In Eq. (26), \(f_\mathrm{Ll}\) can be specified as Eq. (30), where \(a_{il}(\alpha )\) is an increasing order, \(k_\mathrm{Ll}\) is the switch point satisfying \(a_{{k_\mathrm{Ll},l}}(\alpha ) \le f^*_\mathrm{Ll}(\alpha ,k) \le a_{{k_\mathrm{Ll}+1},l}(\alpha )\).

  2. (2)

    In Eq. (27), \(f_\mathrm{Lr}\) can be specified as Eq. (31), where \(a_{ir}(\alpha )\) is an increasing order, \(k_\mathrm{Lr}\) is the switch point satisfying \(a_{{k_\mathrm{Lr},r}}(\alpha ) \le f^*_\mathrm{Lr}(\alpha ,k) \le a_{{k_\mathrm{Lr}+1},r}(\alpha )\).

    $$\begin{aligned}&f^*_\mathrm{Ll}(\alpha ,k)\nonumber \\&\quad =\frac{\sum \limits _{i=1}^{k_\mathrm{Ll}} \left( d_{ir}(\alpha ) (a_{il}(\alpha )-1)\right) ^2+\sum \limits _{i=k_\mathrm{Ll}+1}^n c_{il}(\alpha )\left( a_{il}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^{k_Ll} \left( d_{ir}(\alpha ) a_{il}(\alpha )\right) ^2+\sum \limits _{i=k_\mathrm{Ll}+1}^n \left( c_{il}(\alpha ) a_{il}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
    (30)
    $$\begin{aligned}&f^*_\mathrm{Lr}(\alpha ,k)\nonumber \\&\quad =\frac{\sum \limits _{i=1}^{k_\mathrm{Lr}} \left( d_{il}(\alpha ) (a_{ir}(\alpha )-1)\right) ^2+\sum \limits _{i=k_\mathrm{Lr}+1}^n c_{ir}(\alpha )\left( a_{ir}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^{k_Lr} \left( d_{il}(\alpha ) a_{ir}(\alpha )\right) ^2+\sum \limits _{i=k_\mathrm{Lr}+1}^n \left( c_{ir}(\alpha ) a_{ir}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
    (31)
    $$\begin{aligned}&f^*_\mathrm{Rl}(\alpha ,k)\nonumber \\&\quad =\frac{\sum \limits _{i=1}^{k_\mathrm{Rl}} \left( c_{ir}(\alpha ) (b_{il}(\alpha )-1)\right) ^2+\sum \limits _{i=k_\mathrm{Rl}+1}^n d_{il}(\alpha ) \left( b_{il}(\alpha )-1)\right) ^2}{\sum \limits _{i=1}^{k_\mathrm{Rl}} \left( c_{ir}(\alpha ) c_{ir}(\alpha )\right) ^2+\sum \limits _{i=k_\mathrm{Rl}+1}^n \left( d_{il}(\alpha ) b_{il}(\alpha )\right) ^2},\nonumber \\\end{aligned}$$
    (32)
    $$\begin{aligned}&f^*_\mathrm{Rr}(\alpha ,k)\nonumber \\&\quad =\!\frac{\sum \limits _{i=1}^{k_\mathrm{Rr}} \left( c_{il}(\alpha ) (b_{ir}(\alpha )\!-\!1)\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Rr}\!+\!1}^n d_{ir}(\alpha ) \left( b_{ir}(\alpha )\!-\!1)\right) ^2}{\sum \limits _{i=1}^{k_\mathrm{Rr}} \left( c_{il}(\alpha ) b_{ir}(\alpha )\right) ^2\!+\!\sum \limits _{i=k_\mathrm{Rr}\!+\!1}^n \left( d_{ir}(\alpha ) b_{ir}(\alpha )\right) ^2},\nonumber \\ \end{aligned}$$
    (33)
  3. (3)

    In Eq. (28), \(f_\mathrm{Rl}\) can be specified as Eq. (32), where \(b_{il}(\alpha )\) is an increasing order, \(k_\mathrm{Rl}\) is the switch point satisfying \(b_{{k_\mathrm{Rl},l}}(\alpha ) \le f^*_\mathrm{Rl}(\alpha ,k) \le b_{{k_\mathrm{Rl}+1},l}(\alpha )\).

  4. (4)

    In Eq. (29), \(f_\mathrm{Rr}\) can be specified as Eq. (33), where \(b_{ir}(\alpha )\) is an increasing order, \(k_\mathrm{Rr}\) is the switch point satisfying \(b_{{k_\mathrm{Rr},r}}(\alpha ) \le f^*_\mathrm{Rr}(\alpha ,k) \le b_{{k_\mathrm{Rr}+1},r}(\alpha )\).

Proof

See Appendix B. \(\square \)

Remark 1

In Theorem 2, there may exist intersection among the aggregated elements in Eqs. (30)–(33). If they do, the aggregated elements \(a_{il}(\alpha )\), \(a_{ir}(\alpha )\), \(b_{il}(\alpha )\) or \(b_{ir}(\alpha )\) must be ordered increasingly in each subsection with different \(\alpha \) levels, and write the corresponding function \(f^*\), respectively.

From the conclusions of Theorem 2, it can easily be seen that \(k=k_\mathrm{Ll}\), \(k=k_\mathrm{Lr}\), \(k=k_\mathrm{Rl}\) and \(k=k_\mathrm{Rr}\) in Eqs. (30)–(33) becomes the optimal solutions to Eqs. (34)–(37), respectively.

$$\begin{aligned} f_\mathrm{Ll}(\alpha )=\min \limits _{k=0,1,\ldots ,n-1} f_\mathrm{Ll}(\alpha ,k), \end{aligned}$$
(34)
$$\begin{aligned} f_\mathrm{Lr}(\alpha )=\max \limits _{k=0,1,\ldots ,n-1} f_\mathrm{Lr}(\alpha ,k), \end{aligned}$$
(35)
$$\begin{aligned} f_\mathrm{Rl}(\alpha )=\min \limits _{k=0,1,\ldots ,n-1} f_\mathrm{Rl}(\alpha ,k), \end{aligned}$$
(36)
$$\begin{aligned} f_\mathrm{Rr}(\alpha )=\max \limits _{k=0,1,\ldots ,n-1} f_\mathrm{Rr}(\alpha ,k). \end{aligned}$$
(37)

Coupled with the conclusions of Theorem 1, the switch point \(k=k_\mathrm{Ll}\), \(k=k_\mathrm{Lr}\), \(k=k_\mathrm{Rl}\) and \(k=k_\mathrm{Rr}\) in Eqs. (34)–(37) is also the optimal solution to Eqs. (38)–(41), respectively. It follows that

$$\begin{aligned} \mathrm{RC}_\mathrm{Ll}(\alpha )&=\frac{1}{1+\sqrt{f_\mathrm{Ll}(\alpha )}}\nonumber \\&=\min \limits _{k=0,1,\ldots ,n-1} \mathrm{RC}_\mathrm{Ll}(\alpha ,k), \end{aligned}$$
(38)
$$\begin{aligned} \mathrm{RC}_\mathrm{Lr}(\alpha )&=\frac{1}{1+\sqrt{f_\mathrm{Lr}(\alpha )}}\nonumber \\&=\max \limits _{k=0,1,\ldots ,n-1} \mathrm{RC}_\mathrm{Lr}(\alpha ,k), \end{aligned}$$
(39)
$$\begin{aligned} \mathrm{RC}_\mathrm{Rl}(\alpha )&=\frac{1}{1+\sqrt{f_\mathrm{Rl}(\alpha )}}\nonumber \\&=\min \limits _{k=0,1,\ldots ,n-1} \mathrm{RC}_\mathrm{Rl}(\alpha ,k), \end{aligned}$$
(40)
$$\begin{aligned} \mathrm{RC}_\mathrm{Rr}(\alpha )&=\frac{1}{1+\sqrt{f_\mathrm{Rr}(\alpha )}}\nonumber \\&=\max \limits _{k=0,1,\ldots ,n-1} \mathrm{RC}_\mathrm{Rr}(\alpha ,k). \end{aligned}$$
(41)

4 The analytical solution to IT2 FSs-based TOPSIS model

4.1 The identification of the switch points

Next, we introduce another functions called difference functions to compute the switch points in Eqs. (34)–(37).

Theorem 3

The optimal solution to Eqs. (34)–(37) with \(k=k_\mathrm{Ll}\), \(k=k_\mathrm{Lr}\), \(k=k_\mathrm{Rl}\) and \(k=k_\mathrm{Rr}\) can be determined as Eqs. (42)–(45), respectively.

  1. (1)

    In Eq. (42),

    $$\begin{aligned} d_\mathrm{Ll}(\alpha ,k)&= \sum \limits _{i=1}^{k_\mathrm{Ll}} (a_{k_\mathrm{Ll}+1,l}(\alpha )-a_{il}(\alpha ))(2a_{k_\mathrm{Ll}+1,l}(\alpha )a_{il}(\alpha )\nonumber \\&\quad -\, a_{k_\mathrm{Ll}+1,l}(\alpha )-a_{il}(\alpha )) (d_{ir}(\alpha ))^2 \nonumber \\&\quad +\,\sum \limits _{i=k_\mathrm{Ll}+2}^n(a_{k_\mathrm{Ll}+1,l}(\alpha )-a_{il}(\alpha ))(2a_{k_\mathrm{Ll}+1,l}(\alpha )a_{il}(\alpha )\nonumber \\&\quad -\,a_{k_\mathrm{Ll}+1,l}(\alpha )-a_{il}(\alpha )) (c_{il}(\alpha ))^2, \end{aligned}$$
    (42)

    \(d_\mathrm{Ll}(\alpha ,k)\) is a decreasing function with respect to \(k(k=0,1,\ldots ,n-1)\), and there exists \(k=k_\mathrm{Ll}(k_\mathrm{Ll}=1,2,\ldots ,n-1)\), such that \(d_\mathrm{Ll}(\alpha ,k_\mathrm{Ll}-1) \ge 0\) and \(d_\mathrm{Ll}(\alpha ,k_\mathrm{Ll}) < 0\). So, \(k_\mathrm{Ll}\) is the optimal solution to Eq. (34), i.e., \(k_\mathrm{Ll}=k^*\). Moreover, when \(k=0,1,\ldots ,k_\mathrm{Ll}\), \(f(\alpha ,k)\) is an increasing function concerning \(k\); when \(k=k_\mathrm{Ll},k_\mathrm{Ll}+1,\ldots ,n\), \(f(\alpha ,k)\) is a decreasing function with respect to \(k\). So, \(k_\mathrm{Ll}\) is the global maximum solution to Eq. (34) with \(f_\mathrm{Ll}(\alpha )=f(\alpha ,k_\mathrm{Ll})\).

  2. (2)

    In Eq. (43),

    $$\begin{aligned} d_\mathrm{Lr}(\alpha ,k)&\! =\! \sum \limits _{i=1}^{k_\mathrm{Lr}} (a_{k_\mathrm{Lr}+1,r}(\alpha )-a_{ir}(\alpha ))(2a_{k_\mathrm{Lr}\!+\!1,r}(\alpha )a_{ir}(\alpha )\nonumber \\&\quad -\,a_{k_\mathrm{Lr}+1,r}(\alpha )-a_{ir}(\alpha )) (d_{il}(\alpha ))^2 \nonumber \\&\quad +\!\sum \limits _{i=k_\mathrm{Lr}\!+\!2}^n(a_{k_\mathrm{Lr}\!+\!1,r}(\alpha )\!-\!a_{ir}(\alpha ))\nonumber \\&\qquad \times (2a_{k_\mathrm{Lr}\!+\!1,r}(\alpha )a_{ir}(\alpha )\nonumber \\&\quad -\, a_{k_\mathrm{Lr}+1,r}(\alpha )-a_{ir}(\alpha ))(c_{ir}(\alpha ))^2, \end{aligned}$$
    (43)

    \(d_\mathrm{Lr}(\alpha ,k)\) is a decreasing function with respect to \(k(k=0,1,\ldots ,n-1)\), and there exists \(k=k_\mathrm{Lr}(k_\mathrm{Lr}=1,2,\ldots ,n-1)\), such that \(d_\mathrm{Lr}(\alpha ,k_\mathrm{Lr}-1) \ge 0\) and \(d_\mathrm{Lr}(\alpha ,k_\mathrm{Lr}) < 0\). So, \(k_\mathrm{Lr}\) is the optimal solution to Eq. (35), i.e., \(k_\mathrm{Lr}=k^*\). Moreover, when \(k=0,1,\ldots ,k_\mathrm{Lr}\), \(f(\alpha ,k)\) is an increasing function concerning \(k\); when \(k=k_\mathrm{Lr},k_\mathrm{Lr}+1,\ldots ,n\), \(f(\alpha ,k)\) is a decreasing function with respect to \(k\). So, \(k_\mathrm{Lr}\) is the global maximum solution to Eq. (35) with \(f_\mathrm{Lr}(\alpha )=f(\alpha ,k_\mathrm{Lr})\).

  3. (3)

    In Eq. (44),

    $$\begin{aligned} d_\mathrm{Rl}(\alpha ,k)&= -\sum \limits _{i=1}^{k_\mathrm{Rl}} (b_{k_\mathrm{Rl}+1,l}(\alpha )-b_{il}(\alpha ))\nonumber \\&\qquad (2b_{k_\mathrm{Rl}+1,l}(\alpha )b_{il}(\alpha )\nonumber \\&\quad -\, b_{k_\mathrm{Rl}+1,l}(\alpha )-b_{il}(\alpha )) (c_{ir}(\alpha ))^2 \nonumber \\&\quad -\sum \limits _{i={k_\mathrm{Rl}}+2}^n(b_{k_\mathrm{Rl}+1,l}(\alpha )-b_{il}(\alpha ))\nonumber \\&\quad \times (2b_{k_\mathrm{Rl}+1,l}(\alpha )b_{il}(\alpha )\nonumber \\&\quad -\, b_{k_\mathrm{Rl}+1,l}(\alpha )-b_{il}(\alpha ))(d_{il}(\alpha ))^2, \end{aligned}$$
    (44)

    \(d_\mathrm{Rl}(\alpha ,k)\) is an increasing function with respect to \(k(k=0,1,\ldots ,n-1)\), and there exists \(k=k_\mathrm{Rl}(k_\mathrm{Rl}=1,2,\ldots ,n-1)\), such that \(d_\mathrm{Rl}(\alpha ,k_\mathrm{Rl}-1 \le 0)\) and \(d_\mathrm{Rl}(\alpha ,k_\mathrm{Rl} > 0)\). Hence, \(k_\mathrm{Rl}\) is the optimal solution to Eq. (36), i.e., \(k_\mathrm{Rl}=k^*\). Moreover, when \(k=0,1,\ldots ,k_\mathrm{Rl}\), \(f(\alpha ,k)\) is a decreasing function of \(k\); when \(k=k_\mathrm{Rl},k_\mathrm{Rl}+1,\ldots ,n\), \(f(\alpha ,k)\) is an increasing function of \(k\). So, \(k_\mathrm{Rl}\) is the global minimum solution to Eq. (36) with \(f_\mathrm{Rl}(\alpha )=f(\alpha ,k_\mathrm{Rl})\).

  4. (4)

    In Eq. (45),

    $$\begin{aligned} d_\mathrm{Rr}(\alpha ,k)&= -\sum \limits _{i=1}^{k_\mathrm{Rr}} (b_{k_\mathrm{Rr}+1,r}(\alpha )-b_{ir}(\alpha ))\nonumber \\&\quad \times \,(2b_{k_\mathrm{Rr}+1,r}(\alpha )b_{ir}(\alpha )\nonumber \\&\quad -\,b_{k_\mathrm{Rr}+1,r}(\alpha )-b_{ir}(\alpha )) (c_{il}(\alpha ))^2 \nonumber \\&\quad -\sum \limits _{i=k_\mathrm{Rr}+2}^n(b_{k_\mathrm{Rr}+1,r}(\alpha )-b_{ir}(\alpha ))\nonumber \\&\quad \times \,(2b_{k_\mathrm{Rr}+1,r}(\alpha )b_{ir}(\alpha )\nonumber \\&\quad -\,b_{k_\mathrm{Rr}+1,r}(\alpha )-b_{ir}(\alpha ))(d_{ir}(\alpha ))^2, \end{aligned}$$
    (45)

    \(d_\mathrm{Rr}(\alpha ,k)\) is an increasing function with respect to \(k(k=0,1,\ldots ,n-1)\), and there exists a value of \(k=k_\mathrm{Rr}(k_\mathrm{Rr}=1,2,\ldots ,n-1)\), such that \(d_\mathrm{Rr}(\alpha ,k_\mathrm{Rr}-1 \le 0)\) and \(d_\mathrm{Rr}(\alpha ,k_\mathrm{Rr} > 0)\). Hence, \(k^*\) is the optimal solution to Eq. (37), i.e., \(k_\mathrm{Rr}=k^*\). Moreover, when \(k=0,1,\ldots ,k_\mathrm{Rr}\), \(f(\alpha ,k)\) is a decreasing function of \(k\); when \(k=k_\mathrm{Rr},k_\mathrm{Rr}+1,\ldots ,n\), \(f(\alpha ,k)\) is an increasing function of \(k\). So, \(k_\mathrm{Rr}\) is the global minimum solution to problem (37) with \(f_\mathrm{Rr}(\alpha )=f(\alpha ,k_\mathrm{Rr})\).

Proof

See Appendix C. \(\square \)

Remark 2

In Theorem 3, the optimal solutions to Eqs. (42)–(45) may not be unique, that is to say, there may exist multiple results of \(k^*\) with respect to a difference function. In that case, these optimal solutions must be located together as continuous sequence, and have the same fuzzy relative closeness, which constitute the global analytical solutions to Eqs. (30)–(33).

From the conclusions of Theorem 3, it can easily be seen that the switch points in Eqs. (30)–(33) can be obtained by computing the difference functions of Eqs. (42)–(45), which are also the optimal switch points in Eqs. (38)–(41).

Combined with the conclusions of Theorem 2 and Theorem 3, the procedure of computing fuzzy relative closeness for IT2 FSs-based TOPSIS method can be concluded in Tables 1, 2.

Table 1 The process of computing the UMF \(\widetilde{\mathrm{RC}}^U\) for IT2 FSs-based fuzzy relative closeness
Full size table
Table 2 The process of computing the LMF \(\widetilde{\mathrm{RC}}^L\) for IT2 FSs-based fuzzy relative closeness
Full size table

Remark 3

As IT2 FSs is bounded by UMF \(\tilde{A}^U(x)\) and LMF \(\tilde{A}^L(x)\), both of which are type-1 fuzzy sets, it is obvious that the analytical solution to IT2 FSs-based TOPSIS method shown in Tables 1, 2 is also applicable to type-1 fuzzy TOPSIS method.

4.2 The procedure of the analytical solution to IT2 FSs-based TOPSIS model

Based on the proposed process for computing fuzzy relative closeness in Tables 1, 2, the procedure of the analytical solution to IT2 FSs-based TOPSIS method can be summarized as follows.

  • Step 1. Construct the decision matrix \(\tilde{\tilde{X}}\), and normalize average decision matrix as \(\tilde{\tilde{\bar{X}}}=(\tilde{\tilde{x}}_{ji})_{m \times n}\).

  • Step 2. Construct the weighting matrix \(\tilde{\tilde{W}}\), and normalize average weighting matrix as \(\tilde{\tilde{\bar{W}}}=\) \((\tilde{\tilde{w}}_i)_{1 \times n}\).

  • Step 3. Define the positive ideal solution \(A^*=\{1,1,\ldots ,\) \(1\}\) and the negative ideal solution \(A^-=\{0,0,\ldots \) \(,0\}\).

  • Step 4. Write the normalized average evaluations and weights with \(\alpha (\alpha \in [0,1])\) level as: \(a_{il}(\alpha )\), \(a_{ir}(\alpha )\), \(b_{il}(\alpha )\), \(b_{ir}(\alpha )\), \(c_{il}(\alpha )\), \(c_{ir}(\alpha )\), \(d_{il}(\alpha )\) and \(d_{ir}(\alpha )\).

  • Step 5. Compute the UMF \(\widetilde{\mathrm{RC}}^U_j(\alpha )\) of IT2 FSs-based fuzzy relative closeness according to Table 1.

  • Step 6. Compute the LMF \(\widetilde{\mathrm{RC}}^L_j(\alpha )\) of IT2 FSs-based fuzzy relative closeness according to Table 2.

  • Step 7. Draw the closed form of IT2 FSs-based fuzzy relative closeness \(\widetilde{\widetilde{\mathrm{RC}}}^*_j\) according to the final expressions in Steps 5–6.

  • Step 8. Computing the ranking values Rank(\(\widetilde{\widetilde{\mathrm{RC}}}^*_j\)) according to Eq. (2), the bigger the Rank(\(\widetilde{\widetilde{\mathrm{RC}}}^*_j\)) is, the better alternative \(A_j\).

5 Example

The example was investigated by Chen and Lee (2010), there are three alternatives \(A_{1-3}\) evaluated against four criteria \(C_{1-4}\) by three decision makers \(D_{1-3}\). The linguistic evaluation variables are duplicated in Table 3. Tables 4, 5 show the average weights and assessments provided by the three decision makers. The aggregated fuzzy numbers are obtained by averaging the fuzzy opinions of the three decision makers, that is \(\tilde{\tilde{w}}_j=\frac{1}{3}\sum \nolimits _{k=1}^3 \tilde{\tilde{w}}_j^k (j=1,2,\ldots ,4)\) and \(\tilde{\tilde{x}}_{ij}=\frac{1}{3}\sum \nolimits _{k=1}^3 \tilde{\tilde{x}}_{ij}^k\) \((i=1,2,3; j=1,2,\ldots ,4)\), where \(\tilde{\tilde{w}}_j^k\) and \(\tilde{\tilde{x}}_{ij}^k\) are the relative weights and the ratings given by the \(k\)th decision maker, respectively.

Table 3 Linguistic variables for the evaluation of the criteria
Full size table
Table 4 The relative weights of the five criteria provided by decision makers
Full size table
Table 5 The evaluation of the three candidates by all decision makers
Full size table

5.1 Computing process

Here, we take alternative \(A_1\) as an example, and show the process of computing the IT2 FSs-based fuzzy relative closeness in an analytical way.

  • Step 1 Construct the decision matrix \(\tilde{X}\), and normalize the fuzzy average decision matrix, which is shown in Table 5.

  • Step 2 Construct the weighting matrix \(\tilde{W}\), and normalize the fuzzy average weighting matrix as \(\tilde{\bar{W}}=(\tilde{w}_i)_{1 \times n}\) shown in Table 4.

  • Step 3 Define the positive ideal solution \(A^*=\{1,1,\ldots ,1\}\) and the negative ideal solution \(A^-=\{0,0,\ldots ,0\}\).

  • Step 4 Write the average fuzzy evaluations for alternative \(A_1\) and the average weights with \(\alpha \) level, respectively.

    $$\begin{aligned}&\tilde{x}^U_{11}(\alpha )=(0.57+0.2\alpha ,0.93-0.16\alpha ),\\&\tilde{x}^U_{21}(\alpha )=(0.77+0.16\alpha ,1-0.07\alpha ),\\&\tilde{x}^U_{31}(\alpha )=(0.77+0.16\alpha ,1-0.07\alpha ),\\&\tilde{x}^U_{41}(\alpha )=(0.77+0.16\alpha ,1-0.07\alpha ),\\&\tilde{w}^U_1(\alpha )=(0.83+0.14\alpha ,1-0.03\alpha ),\\&\tilde{w}^U_2(\alpha )=(0.83+0.14\alpha ,1-0.03\alpha ),\\&\tilde{w}^U_3(\alpha )=(0.43+0.2\alpha ,0.83-0.2\alpha ),\\&\tilde{w}^U_4(\alpha )=(0.77+0.16\alpha ,1-0.07\alpha ). \end{aligned}$$

  • Step 5 Compute the fuzzy relative closeness \(\mathrm{RC}_\mathrm{Ll}\) for alternative \(A_1\).

  1. (1)

    Sort the aggregated elements \(a_{il}(\alpha )\) \((i=1,2,3,4)\) in increasing order. According to the expressions of the aggregated elements \(a_{il}(\alpha )\) \((i=1,2,3,4)\), the graph can be drawn as Fig. 4. For any \(\alpha \in [0,1]\), it follows that \(a_{1l}\) \((\alpha ) \le a_{2l}(\alpha )=a_{31}(\alpha )=a_{41}(\alpha )\). Hence, the order of \(a_{il}(i=1,2,3,4)\) need not be changed.

  2. (2)

    Construct the left difference functions \(d_\mathrm{Ll}(\alpha ,k)\) \((k=0,1,2,3)\) for alternative \(A_1\). According to Eq. (42), the difference functions \(d_\mathrm{Ll}(\alpha ,k)(k=0,1,2,3)\) for alternative \(A_1\) are denoted as Eq. (46)–(48), which are also shown in Fig. 5.

Fig. 4
figure 4

The plots of \(a_{il} (\alpha )\) for alternative \(A_1\)

Full size image
Fig. 5
figure 5

The plots of \(d_\mathrm{Ll}(\alpha ,k)\) for alternative \(A_1\)

Full size image
$$\begin{aligned} d_\mathrm{Ll}(\alpha ,0)&= \sum \limits _{i=2}^4 (a_{1l}-a_{il})(2a_{1l}a_{il}-a_{1l}-a_{il})c^2_{il} \nonumber \\&= (a_{1l}-a_{2l})(2a_{1l}a_{2l}-a_{1l}-a_{2l})c^2_{2l}\nonumber \\&+\,(a_{1l}-a_{3l})(2a_{1l}a_{3l}-a_{1l}-a_{3l})c^2_{3l}\nonumber \\&+\,(a_{1l}-a_{4l})(2a_{1l}a_{4l}-a_{1l}-a_{4l})c^2_{4l}\nonumber \\&= 0.13558+0.00022\alpha ^5+0.00102\alpha ^4\nonumber \\&-\,0.00498\alpha ^3-0.03225\alpha ^2-0.00521\alpha \end{aligned}$$
(46)
$$\begin{aligned} d_\mathrm{Ll}(\alpha ,1)&= \sum \limits _{i=1}^1 (a_{2l}-a_{il})(2a_{2l} a_{il}-a_{2l}-a_{il}) d^2_{ir}\nonumber \\&+\sum \limits _{i=3}^5 (a_{2l}-a_{il})(2a_{2l} a_{il}-a_{2l}-a_{il}) c^2_{il}\nonumber \\&= (a_{2l}-a_{1l})(2a_{2l}a_{1l}-a_{2l}-a_{1l})d^2_{1r}\nonumber \\&+\,(a_{2l}-a_{3l})(2a_{2l}a_{3l}-a_{2l}-a_{3l})c^2_{3l}\nonumber \\&+\,(a_{2l}-a_{4l}) (2a_{2l}a_{4l}-a_{2l}-a_{4l})c^2_{4l}\nonumber \\&= -0.08878+0.00006\alpha ^4-0.00262\alpha ^3\nonumber \\&+\,0.0063\alpha ^2+0.04482\alpha \end{aligned}$$
(47)
$$\begin{aligned} d_\mathrm{Ll}(\alpha ,2)=d_\mathrm{Ll}(\alpha ,3)=d_\mathrm{Ll}(\alpha ,1) \end{aligned}$$
(48)
  1. (3)

    Find the switch point of difference function \(d_\mathrm{Ll}(\alpha ,k^*)\) for alternative \(A_1\). From Fig. 5, it can easily be seen that for any \(\alpha \in [0,1],\) it follows \(d_\mathrm{Ll}(\alpha ,0)\ge 0\) and \(d_\mathrm{Ll}(\alpha ,1)<0\). According to the conclusions of Theorem 3(1), it is obvious that if \(\alpha \in [0,1]\), such that the switch point \(k^*=k_\mathrm{Ll}=1\).

  2. (4)

    Write the expression of function \(f_\mathrm{Ll}(\alpha )\) for alternative \(A_1\). According to Eq. (30), when \(k_\mathrm{Ll}=1\), the closed-form expression of function \(f_\mathrm{Ll}(\alpha )\) can be denoted as Eq. (49).

$$\begin{aligned}&f_\mathrm{Ll}(\alpha ) =\frac{\sum \limits _{i=1}^1 (d_{ir}(a_{il}-1))^2+\sum \limits _{i=2}^5 (c_{il}(a_{il}-1))^2}{\sum \limits _{i=1}^1 (d_{ir}a_{il})^2+\sum \limits _{i=2}^5 (c_{il}a_{il})^2}\nonumber \\&\quad \!=\!\frac{0.26249\!+\!0.00222\alpha ^4\!+\!0.00783\alpha ^3\!+\!0.04464\alpha ^2-0.25662\alpha }{1.19451\!+\!0.00222\alpha ^4\!+\!0.03546\alpha ^3\!+\!0.27503\alpha ^2\!+\!0.95576\alpha }.\nonumber \\ \end{aligned}$$
(49)
  1. (5)

    Write the analytical solution to \(\widetilde{\mathrm{RC}}_\mathrm{Ll}(\alpha )\) for alternative \(A_1\). Substitute Eq. (49) in Eq. (38), for \(\forall \alpha \in [0,1]\), the closed-form function of fuzzy relative closeness \(\widetilde{\mathrm{RC}}_\mathrm{Ll}(\alpha )\) can be expressed as Eq. (50).

    $$\begin{aligned}&\mathrm{RC}_\mathrm{Ll}(\alpha )\nonumber \\&\quad \!=\!\frac{1}{1\!+\!\sqrt{\frac{0.26249+0.00222\alpha ^4+0.00783\alpha ^3+0.04464\alpha ^2-0.25662\alpha }{1.19451+0.00222\alpha ^4+0.03546\alpha ^3+0.27503\alpha ^2+0.95576\alpha }}},\nonumber \\&\qquad \alpha \in [0,1]. \end{aligned}$$
    (50)
  2. (6)

    Write the analytical solution to fuzzy relative closeness \(\widetilde{\mathrm{RC}}_\mathrm{Rr}(\alpha )\) for alternative \(A_1\). Similarly, the maximal fuzzy relative closeness \(\mathrm{RC}_\mathrm{Rr}\) for alternative \(A_1\) can be shown as Eq. (51).

    $$\begin{aligned}&\mathrm{RC}_\mathrm{Rr}(\alpha )\nonumber \\&\quad \!=\!\frac{1}{1\!+\!\sqrt{\frac{0.00338+0.00073\alpha ^4+0.00378\alpha ^3+0.03611\alpha ^2+0.01657\alpha }{3.28473+0.00073\alpha ^4-0.0089\alpha ^3+0.09888\alpha ^2-0.91246\alpha }}},\nonumber \\&\qquad \alpha \in [0,1]. \end{aligned}$$
    (51)
  3. (7)

    Draw the closed form of UMF \(\widetilde{\mathrm{RC}}^U_1\) for alternative \(A_1\). Combined with Eqs. (50) and (51) together, the closed form of UMF \(\widetilde{\mathrm{RC}}^U\) for alternative \(A_1\) can be written as Eq. (52).

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{RC}_\mathrm{Ll}(\alpha )=\frac{1}{1{+}\sqrt{\frac{0.26249+0.00222\alpha ^4+0.00783\alpha ^3+0.04464\alpha ^2-0.25662\alpha }{1.19451+0.00222\alpha ^4+0.03546\alpha ^3+0.27503\alpha ^2+0.95576\alpha }}},\\ \qquad \qquad \qquad \qquad \alpha \in [0,1];\\ \mathrm{RC}_\mathrm{Rr}(\alpha )=\frac{1}{1+\sqrt{\frac{0.00338+0.00073\alpha ^4+0.00378\alpha ^3+0.03611\alpha ^2+0.01657\alpha }{3.28473+0.00073\alpha ^4-0.0089\alpha ^3+0.09888\alpha ^2-0.91246\alpha }}},\\ \qquad \qquad \qquad \qquad \alpha \in [0,1]. \end{array}\right. }\nonumber \\ \end{aligned}$$
(52)

  • Step 6 Compute the LMF \(\widetilde{\mathrm{RC}}^L_1\) of relative closeness for alternative \(A_1\). According to the computing process in Table 2, the closed-form function of fuzzy relative closeness \(\widetilde{\mathrm{RC}}^L_1\) can be obtained as Eq. (53).

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{RC}_\mathrm{Lr}(\alpha )=\frac{1}{1+\sqrt{\frac{0.14539+0.00021\alpha ^4+0.00225\alpha ^3+0.01748\alpha ^2-.11196\alpha }{1.74131+0.00021\alpha ^4+0.00695\alpha ^3+0.10378\alpha ^2+0.70266\alpha }}}, \\ \qquad \qquad \qquad \qquad \alpha \in [0,1];\\ \mathrm{RC}_\mathrm{Rl}(\alpha )=\frac{1}{1+\sqrt{\frac{0.02042+0.00008\alpha ^4+0.00077\alpha ^3+0.01437\alpha ^2+0.031\alpha }{2.87556+0.00008\alpha ^4-0.00159\alpha ^3+0.03131\alpha ^2-0.48538\alpha }}},\\ \qquad \qquad \qquad \qquad \alpha \in [0,1]. \end{array}\right. }\nonumber \\ \end{aligned}$$
(53)

  • Step 7 With the same method, compute the whole closed-form function of fuzzy relative closeness for alternatives \(A_2\) and \(A_3\). The pictures of IT2 FSs-based fuzzy relative closeness for the three alternatives are shown in Fig. 6.

  • Step 8 Using Eq. (2), the final ranking values of the IT2 FSs-based fuzzy relative closeness for the three alternatives are computed as: Rank\((A_1)=8.83836\), Rank\((A_2)=8.95285\), Rank\((A_3)=8.75709\). That is the best alternative is \(A_2\), and the ranking of the alternatives is

    $$\begin{aligned} A_2 \succ A_1 \succ A_3. \end{aligned}$$
Fig. 6
figure 6

The fuzzy relative closeness for the three candidates

Full size image

5.2 Discussion

Compared with Chen and Lee (2010), it is coincidental that the ranking results are the same. But the proposed method is completely different from that of Chen and Lee (2010), the differences of which are summarized as follows.

  1. (1)

    It realizes the actual sense of IT2 FSs-based TOPSIS method computation. As the IT2 FSs formats are kept through the whole computing process when solving the fuzzy relative distance functions for the three alternatives, and the defuzzification is dealt with at the end of the computing process, instead of the defuzzification from the very beginning of Chen and Lee (2010).

  2. (2)

    It is accurate. As the fractional NLP models consider all conditions when computing the IT2 FSs-based fuzzy relative closeness for the three alternatives. And the switch points of which are recognized through solving difference functions. By computing the algebraic formula of the object function within \(\alpha \in [0,1]\), the analytical solution to IT2 FSs-based TOPSIS model can also be obtained, which avoids information loss in computing process. However, in Chen and Lee (2010), after the defuzzification of the elements in weighted decision matrix, the crisp relative closeness is computed through traditional TOPSIS method, which cause decision information loss.

  3. (3)

    Moreover, a global accurate picture of the IT2 FSs-based fuzzy relative closeness for the three alternatives can also be, respectively, obtained, which provides a possibility to further analyze the properties of the results.

6 Conclusion

In this paper, we have proposed an analytical solution to IT2 FSs-based TOPSIS model for solving the fuzzy MADM problems. First, we have created the fractional NLP problems to find the fuzzy relative closeness. Second, based on the principle of KM algorithm, we have transformed the fractional NLP problem into identifying the switch points of \(\alpha \) levels. Finally, by computing the algebraic formula of object function within \(\alpha \in [0,1]\), we obtained the analytical solution to IT2 FSs-based TOPSIS model. Moreover, we have also discussed some properties of the proposed method. The main difference from Chen and Lee (2010) is that it keeps IT2 FSs format for the evaluations and weights in the whole computing process, and realizes the actual sense of IT2 FSs-based TOPSIS solution. It is accurate, as the computation is a continuous process and all the switch points are found through solving expressions. Moreover, a global picture of the fuzzy relative closeness can also be obtained for further analysis.