A modified differential evolution-based combined routing and sleep scheduling scheme for lifetime maximization of wireless sensor networks

Abstract

In recent years, wireless sensor networks (WSNs) have transitioned from being objects of academic research interest to a technology that is frequently employed in real-life applications and rapidly being commercialized. Nowadays the topic of lifetime maximization of WSNs has attracted a lot of research interest owing to the rapid growth and usage of such networks. Research in this field has two main directions into it. The first school of researchers works on energy efficient routing that balances traffic load across the network according to energy-related metrics, while the second school of researchers takes up the idea of sleep scheduling that reduces energy cost due to idle listening by providing periodic sleep cycles for sensor nodes. As energy efficiency is a very critical consideration in the design of low-cost sensor networks that typically have fairly low node battery lifetime, this raises the need for providing periodic sleep cycles for the radios in the sensor nodes. Until now, these two fields have remained more or less disjoint leading to designs where to optimize one component, the other one must be pre-assumed. This in turn leads to many practical difficulties. To circumvent such difficulties in the performance of sensor networks, instead of separately solving the problem of energy efficient routing and sleep scheduling for lifetime maximization, we propose a single optimization framework, where both the components get optimized simultaneously to provide a better network lifetime for practical WSN. The framework amounts to solving a constrained non-convex optimization problem by using the evolutionary computing approach, based on one of the most powerful real-parameter optimizers of current interest, called Differential Evolution (DE). We propose a DE variant called modified semi-adaptive DE (MSeDE) to solve this optimization problem. The results have been compared with two state-of-the-art and widely used variants of DE, namely JADE and SaDE, along with one improved variant of the Particle Swarm Optimization (PSO) algorithm, called comprehensive learning PSO (CLPSO). Moreover, we have compared the performance of MSeDE with a well-known constrained optimizer, called $\varepsilon$-constrained DE with an archive and gradient-based mutation that ranked first in the competition on real-parameter constrained optimization, held under the 2010 IEEE Congress on Evolutionary Computation (CEC). Again to demonstrate the effectiveness of the optimization framework under consideration, we have included results obtained with a separate routing and sleep scheduling method in our comparative study. Our simulation results indicate that in all test cases, MSeDE can outperform the competitor algorithms by a good margin.

1 Introduction

An ad-hoc wireless sensor network (WSN) consists of a number of sensors spread across a geographical area. Each sensor has wireless communication capability and some level of intelligence for signal processing and networking of the data. The development of WSNs was originally motivated by military applications such as battlefield surveillance. However, they are currently being employed in many industrial and civilian application areas including industrial process monitoring and control, machine health monitoring, environment and habitat monitoring, healthcare applications, home automation, and traffic control (Callaway 2003; Zhao and Guibas 2004; Bulusu and Jha 2005; Chong and Kumar 2003). A few excellent surveys on the present state-of-the-art research on sensor networks can be traced in Al-Karaki and Kamal (2004), Akyildiz et al. (2002), Pottie and Kaiser (2000), Bojkovic and Bakmaz (2008) and Yick et al. (2008).

A typical WSN consists of various numbers of nodes ranging from tens to thousands that performs signal transmission through the channels to share the information they sense and obtain from the field through the above-mentioned components. A WSN consisting of randomly deployed sensor nodes is presented in Fig. 1. After the initial sensors are deployed in the field, they can usually organize a suitable network infrastructure with several multi-hop connections between the nodes. There are many types of sensor deployment schemes reported in literature (Chang et al. 2009; Nojeong and Varshney 2005). These infield sensors collect information directly from the field using their various working modes. This information is then processed thoroughly to get an overview of the network field under concern. The main idea in this WSN is that although the battery powers that are driving the sensors in the actual field are limited, the overall network should be efficiently designed, such that aggregate power of the entire network remains under control for the required mission.

Fig. 1

Wireless sensor network

One major problem for WSN is the limit of energy for the battery-driven nodes, which basically imposes the limit on the network lifetime to be achieved. Consequently, the most important task for a WSN is to increase the battery time and hence the overall network lifetime (Raghunathan and Ganeriwal 2006; Li and Alregib 2009; Dagher et al. 2007). The definition for the network lifetime for a wireless sensor network is the time till the first sensor runs out of its battery energy. Recent research works in lifetime maximization of WSNs have been basically divided into two threads. The first one is to design an energetically efficient routing scheme (Rogers et al. 2005) so that the whole network lifetime gets maximized. Among various existing routing protocols, which already have been proposed, the protocols which are cluster-based and chain-based obtain well-accepted solutions to minimize the power consumption in the network and thereby prolong the network lifetime. There are also some routing protocols named LEACH (Heinzelman et al. 2000), PEAGSIS (Lindsey and Raghavendra 2002), LBERRA (Yu and Wei 2007) where all these energy-efficient routing protocols aims to balance traffic loads, and hence energy consumption among sensor nodes across the network. Till date, the ongoing researches formulated this problem into various linear programming (LP) problems depending on conditions like power consumption models, ranging from simple models that only consider payload transmission power (Madan and Lall 2006; Kim et al. 2007) or both transmission and reception power (Chang and Tassiulas 2004) to more realistic ones that include power consumption on control message passing (Dong 2005) and idle listening (Hua and Yum 2008). They have also considered different medium access control (MAC) constraints such as half-duplex constraint, link capacity constraint (Madan and Lall 2006; Kim et al. 2007), and interference constraint (Madan et al. 2006).

Secondly, we know that idle listening can be a major concern for the WSN for wasting energy because in most of the cases we assume that network traffic load is light. In order to reduce the energy consumption of the sensors, the sensor nodes are allowed to periodic sleep cycles. Again a lot of researches are going on in the field of sleep scheduling which focuses to reach a trade-off between and latency/reliability but also the distribution and the balance of energy consumption across the network very much relies upon the design of duty cycles and active/sleep patterns. This is due to the fact that if an upstream node keeps resending packets to its downstream node then it wastes a lot of transmission power, if during this time of transmission of the upstream node the downstream node sleeps too much. This problem has been solved somewhat by synchronizing wake-up slots [S-MAC (Ye et al. 2004) and T-MAC] which simply lengthens the data packet preamble [B-MAC (Polastre and Culler 2004)], or sends multiple short preambles till heard by the receiver [TICER (Lin et al. 2004)]. Some way or the other, all prior existing sleep scheduling schemes (Chachra and Marefat 2006; Subramanian and Fekri 2006; Bulut and Korpeoglu 2007) assumes a pre-determined routing table. In other words, upstream–downstream (i.e., transmitter–receiver) node pairs as well as the amount of traffic going through the pairs are fixed in advance.

Most prior work considers the energy efficient routing and sleep-scheduling (Hou et al. 2008; Hua and Yum 2008) as a completely different domain. They have optimized a particular component while having completely pre-assumed the other. In a recent work in Liu et al. (2010), they have said that they considered the routing and sleep scheduling both, and our problem formulation is based on the work.

Our aim in this research is to optimize jointly the routing and the sleep scheduling to maximize the overall network lifetime. Here the routing, sleep scheduling and traffic load allocation has been incorporated into a one optimization framework. This formulation considered more realistic power consumption model which includes energy costs due to payload transmission and reception, preamble transmission, as well as idle listening. As turns out, this optimization framework is a constrained non-convex problem. The Differential Evolution (DE) (Storn and Price 1995, 1997) algorithm emerged as a very competitive form of evolutionary computing more than a decade ago which appeared as a technical report by Rainer Storn and Kenneth V. Price in 1995 (Storn and Price 1995, 1997). DE algorithm is a simple yet very powerful algorithm and its variants have been used for solving various constrained optimization problems. In this paper we propose a new variant of DE, namely modified semi-adaptive DE (MSeDE), where we have modified the mutation strategy by a deterministic procedure of varying the scale factor ($F)$ and the crossover probability constant (Cr) and used an improved version of a recent type of crossover strategy ($p$-best crossover). Due to constraints we have used the $\varepsilon$-constraint technique to convert an unconstrained optimization algorithm MSeDE into a constrained one. The performance of MSeDE has been compared with some famous variants of DE like JADE (Zhang and Sanderson 2009) and SaDE (Qin et al. 2009), and one powerful variant of PSO, namely CLPSO (Liang et al. 2006). To have an even-handed comparison we have also incorporated the $\varepsilon$-constraint technique in these three algorithms as the constraint handling technique. Moreover we also have compared the performance of MSeDE with a dedicated constrained optimizer, namely $\varepsilon$DEag Takahama and Sakai (2010) and also presented the results obtained for a subset of benchmark problems that was devised for the 2006 IEEE CEC Special Session/Competition on Evolutionary Constrained Real Parameter single objective optimization. Again to prove that the optimization framework under consideration is useful we have included S-RS method as a competitor which is one of the best optimizer for separate routing and sleep scheduling design method. The main objective in the S-RS method is to iteratively update the routing decisions and sleep scheduling separately through mathematical programming, with one component fixed while tuning the other one. The results clearly indicate that MSeDE can obtain high quality solutions better than its competitors under various simulation strategies.

The rest of the paper is organized as follows: Sect. 2 describes the system modeling and the optimization framework. Section 3 describes classical DE algorithm and the application of DE and its variants to constrained optimization problems. In Sect. 4 our proposed algorithm MSeDE is described in sufficient detail. In Sect. 5 a short description of the $\varepsilon$-constraint handling technique is presented. A series of experiments are conducted and the results are analyzed in Sect. 6 to illustrate the performance of the proposed algorithm. Finally, conclusions of our research and guidelines for future work are given in Sect. 7.

2 System model and optimization framework

Prior to the formulation of the optimization equation to model the whole system for combined routing and sleep scheduling, we will make some assumptions. At first we consider that all the nodes in the WSN are static and they are randomly located at a region. Again like most of the prior works the traffic load in the network has been considered as light and as a consequence the transmissions are collision free. The routing matrix is defined by $R = \{r_{ij}\}$, the average rate at which packets are flowed over the link from node $i$ to $j$, where $r_{ij}$ is fixed to be zero if nodes $i$ and $j$ are not within the RF range of each other (Liu et al. 2010). The neighbor set $N_{i}$ of node $i$ is given by,

$$\begin{aligned} j\left\{ {\begin{array}{l} \in N_i \quad \mathrm{node}\;j\;\mathrm{is\;in\;the\;RF\;range\;of\;node\;}i \\ \notin N_i \quad \mathrm{otherwise} \\ \end{array}} \right. \end{aligned}$$

(1)

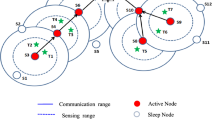
A sensor node can practically be in two modes. It can be either in active mode or in sleep mode governed by its sleep schedule as depicted in Fig. 2. In active mode a node is transmitting energy and packets to the other nodes situated within its RF range, and in sleep mode a node is turned off and its power consumption is zero. For a particular node, the sleep time is $T_\mathrm{S}^i$ during which it does not take part in energy dealing and after this duration it wakes up. The most important thing is to note that for a particular node in the field, the sleep time is same and it is not time dependent but it varies with every node due to different traffic and battery condition. A particular node wakes up and enters into active mode time to time to see whether it has packets to send to any node or it has some packets to receive. An active period can also be divided into three slots, such as idle listening slot, data transmission slot and data reception slot. More specifically, it is said to be an idle listening slot if the node neither transmits nor receives data packets within this active period. In this case, the active period consists of two parts, i.e., RF initialization and channel detection. The definition of a data transmission slot in the active mode is that in this slot the node transmits packets while data reception slot is that in this slot a node receives a packet.

Fig. 2

Asynchronous sleep scheduling mechanism

Now we are going to describe how a node transmits and receives a signal in this proposed system and the process of energy consumption for each node. The entire timing diagram of a transmitting and receiving sensor is shown in Fig. 3.

Fig. 3

Timing diagram in different active periods (Liu et al. 2010)

After waking up the first operation performed by a node is the initialization of its RF circuits. Let us assume for initialization the time required is $T_\mathrm{ini}$ and the energy utilized is $E_\mathrm{ini}$. If the node has some packets to transmit then first it listens for $T_\mathrm{l}^{i}$ time to examine whether any other neighboring nodes are transmitting or not. Let $T_\mathrm{idl}^i =T_\mathrm{ini} +T_\mathrm{l}$ be the total time for which the node wakes up and goes to sleep again. The length of $T_\mathrm{idl}^i$ will be discussed later. The node sends a request to send (RTS) preamble if it finds that the channel is idle for $T_\mathrm{idl}^i$ time. If the target receiver is in active mode and receives this RTS preamble it replies via a clear to send (CTS) packet. Then the transmitting node sends the data packet which is acknowledged by the receiver by an ACK packet. But if the receiver is in sleep mode, then the transmitter resends the RTS preamble after going to the power saving mode for time $T_\mathrm{save}$ and the transmitter repeats this process until it finds that the receiver is awake and has received the RTS preamble. In our case we assume that the receiver takes $p_\mathrm{rec}$ amount of power to receive any packet whereas the transmitter takes $p_\mathrm{trans}$ amount of power for transmitting any packets including the preambles. We also assume that $T_\mathrm{dp}$ is the duration of a data packet by assuming that all the packet lengths are the same. Without loss of generality, we assume that the RTS, CTS and ACK preambles are of duration $T_\mathrm{p}$. To ensure that all transmitter-receiver pairs are “sufficiently” connected and communication of other links in the same RF range is correctly detected, $T_\mathrm{idl}^i$ should be long enough to cover at least two consecutive RTS preambles (including the $T_\mathrm{save}$ between them) of all sensor nodes within its RF range. Otherwise if $T_\mathrm{idl}^i$ is too short a node may not be able to capture an RTS preamble transmitted in its RF range. Hence, it requires

$$\begin{aligned} T_\mathrm{idl}^i \ge \mathop {\max }\limits _{j\in N_i } ( {2\,T_\mathrm{ini} +3\,T_\mathrm{p} +T_\mathrm{save}^j }). \end{aligned}$$

(2)

It is evident from Eq. (2) that $T_\mathrm{idl}^i$ is determined by the longest $T_\mathrm{save}$ in node $i$’s neighbor. This implies that if different nodes have different values of $T_\mathrm{save}$, then the nodes having lower value of $T_\mathrm{save}$ can always increase their $T_\mathrm{save}$ without affecting the value of the idle listening time $T_\mathrm{idl}^i$ of node $i$. Hence, it is the most energy efficient way to let all sensor nodes have the same$T_\mathrm{save}$, for otherwise we can always let the ones with smaller $T_\mathrm{save}$’s increase their $T_\mathrm{save}$’s to save energy. Onwards we will assume that $T_\mathrm{save}$ is the same across all nodes. Moreover, we assume that $T_\mathrm{idl}^i$ is equal to the shortest allowable duration, i.e.,

$$\begin{aligned} T_\mathrm{idl} =( {2\,T_\mathrm{ini} +3\,T_\mathrm{p} +T_\mathrm{save} }), \end{aligned}$$

(3)

unless otherwise stated. Likewise, the channel detection power is $p_\mathrm{rec}$.

Now our task is to compute the energy consumed by a node during the active period which could be either the idle listening mode, or a data transmitting mode or a data receiving mode. In the data transmitting mode, the average energy consumption for node $i$ to transmit one packet to node $j$ is given by,

$$\begin{aligned} \begin{array}{l} \overline{E} _\mathrm{trans}^{ij} =( {E_\mathrm{ini} +p_\mathrm{rec} \,T_\mathrm{idl} })-E_\mathrm{ini} +p_\mathrm{trans} T_\mathrm{dp} +p_\mathrm{rec} T_\mathrm{p} \\ \quad + \left( {E_\mathrm{ini} +( {p_\mathrm{trans} +p_\mathrm{rec} })\,T_\mathrm{p} }\right) \times \left( {\frac{T_\mathrm{s}^j /2-( {2\,T_\mathrm{p} +T_\mathrm{save} +T_\mathrm{ini} +2\,T_\mathrm{p} })}{T_\mathrm{ini} +2\,T_\mathrm{p} +T_\mathrm{save} }+2}\right) \\ \end{array}\nonumber \\ \end{aligned}$$

(4)

In Eq. (4) the term ($E_\mathrm{ini}+p_\mathrm{rec} T_\mathrm{idl})$ accounts for the energy required for RF circuit initialization and channel detection. The energy cost due to sending the RTS preamble until a CTS packet is recognized corresponds to the combined terms:

$$\begin{aligned}&E_\mathrm{ini} +\left( {E_\mathrm{ini} +\left( {p_\mathrm{trans} +p_\mathrm{rec} }\right) \,T_\mathrm{p} }\right) \nonumber \\&\quad \times \left( {\frac{T_\mathrm{s}^j /2-\left( {2\,T_\mathrm{p} +T_\mathrm{save} +T_\mathrm{ini} +2\,T_\mathrm{p} }\right) }{T_\mathrm{ini} +2\,T_\mathrm{p} +T_\mathrm{save} }+2}\right) \end{aligned}$$

(5)

The term $p_\mathrm{trans} \cdot T_\mathrm{dp}$ is due to the energy consumption for sending the data packet and the term $p_\mathrm{rec} \cdot T_\mathrm{p}$ is due to the reception of the ACK packet. In Eq. (5), in particular $T_\mathrm{s}^{j}$/2 is the average residual sleep time of node $j$ seen by node $i$ when node $i$initiates a transmission to node $j \cdot E_\mathrm{ini} + (p_\mathrm{trans}+p_\mathrm{rec}) .\, T_\mathrm{p}$ is the amount of energy consumed due to one RTS transmission and the possible CTS detection. Note that there is no RF initialization in the first RTS packet transmission, as the sensor node is already on. Similarly, there is no $T_\mathrm{save}$ following the last RTS/CTS exchange, as can be seen in Fig. 3. Hence, the term $\left( {\frac{T_\mathrm{s}^j /2-\left( {2\,T_\mathrm{p} +T_\mathrm{save} +T_\mathrm{ini} +2\,T_\mathrm{p} }\right) }{T_\mathrm{ini} +2\,T_\mathrm{p} +T_\mathrm{save} }+2}\right)$ is basically the average number of RTS preambles the transmitter has to transmit until one is captured by node $j$, and the term at $-E_\mathrm{ini}$ at the beginning of Eq. (5) reflects the fact that no RF initialization is required for the first RTS transmission. Next, the energy consumed by a node to receive a data packet can be calculated as follows:

$$\begin{aligned} \overline{E} _\mathrm{rec} =\left( {E_\mathrm{ini} +p_\mathrm{rec} \,\frac{T_\mathrm{idl} }{2}}\right) +p_\mathrm{rec} \,T_\mathrm{p} +2\,p_\mathrm{trans} T_\mathrm{p} \end{aligned}$$

(6)

The first term on the right hand side, i.e., ($E_\mathrm{ini} + p_\mathrm{rec} \cdot T_\mathrm{idl}/2)$ is the energy consumed for initializing the RF circuit and the average energy cost to detect the RF channel before desired RTS is received. The second term $p_\mathrm{rec} \cdot T_\mathrm{p}$ is the energy cost for receiving the data packet, while the third term, i.e., $2p_\mathrm{trans} \cdot T_\mathrm{p}$ is the energy cost to transmit the CTS and ACK packets. Moreover the energy consumed due to idle listening is given by,

$$\begin{aligned} E_\mathrm{idl} =E_\mathrm{ini} +p_\mathrm{rec} \left( {T_\mathrm{idl} -T_\mathrm{ini} }\right) \end{aligned}$$

(7)

Now we are going to calculate the average power consumed by node $i$. Let us assume that we consider a very large time $T$ within which node $i$ has transmitted $N^{ij}_\mathrm{trans}$ packets to node $j$, received $N^{i}_\mathrm{rec}$ packets, and experienced $N^{ i}_\mathrm{idle}$ active/sleep cycles without data transmission/reception, i.e., $N^{ i}_\mathrm{idle}$ idle listening slots. The average power consumption under these assumptions is,

$$\begin{aligned} \overline{p} _i =\frac{\sum \nolimits _{j\in N_i } {\overline{E} _\mathrm{trans}^{ij} N_\mathrm{trans}^\mathrm{ij} +\overline{E} _\mathrm{rec} N_\mathrm{rec}^i +E_\mathrm{idl} N_\mathrm{idle}^i } }{T}, \end{aligned}$$

(8)

To be specific the average rate at which node $i$ transmits packets to node $j$ is given by

$$\begin{aligned} r_{ij} =\frac{N_\mathrm{trans}^{ij} }{T}, \end{aligned}$$

(9)

and the average rate at which node $i$ receives packets from other nodes can be expressed as,

$$\begin{aligned} \sum \limits _{j\in N_i } {r_{ji} } =\frac{N_\mathrm{rec}^i }{T}. \end{aligned}$$

(10)

Substituting (9) and (10) in Eq. (8) we get,

$$\begin{aligned} \overline{p} _i =\sum \limits _{j\in N_i } {\overline{E} _\mathrm{trans}^{ij} \,r_{ij} } +\overline{E} _\mathrm{rec} \sum \limits _{j\in N_i } {r_{ji} } +\frac{E_\mathrm{idl} }{T_\mathrm{idl} +T_\mathrm{s}^i } \end{aligned}$$

(11)

where we have assumed light traffic load so that a node is in idle modes most of the time, i.e.,

$$\begin{aligned} T\approx \left( {T_\mathrm{idl} +T_\mathrm{s}^i }\right) N_\mathrm{idle}^i. \end{aligned}$$

(12)

It follows from Eq. (11) that the lifetime of a node $i$ denoted by $T^{i}_\mathrm{lt}$ is confined by its battery capacity through the following equation

$$\begin{aligned} T_\mathrm{lt}^i \le \left( {{B_i }/{\overline{p} _i }}\right) \end{aligned}$$

(13)

By utilizing the above formulae and derivations, an optimization framework can be modeled. We try to find the optimal routing matrix ${{\varvec{R}}}=\{r_{ij}\}$ and sleep time ${{\varvec{T}}}_\mathrm{s} =\{T^{ i}_\mathrm{s}\}$ so that the network lifetime which is defined by the time till the first sensor node gets exhausted of its battery power is maximized. We have,

$$\begin{aligned} \begin{array}{ll} &{}\mathop {\max }\limits _{R,T_\mathrm{s} } \,\mathop {\min \,T_\mathrm{lt}^i }\limits _i \\ \mathrm{such\,that}\,\;&{}\overline{p} _i T_\mathrm{lt}^i \le B_i \quad \forall i \\ &{}\sum \limits _{j\in N_i } {r_{ji} } -\sum \limits _{j\in N_i } {r_{ij} } =D_i -S_i \quad \forall i \\ &{}r_{ij} \ge 0,\,\mathrm{\forall } i,j\;\,T_\mathrm{s}^i >0,\forall i \\ \end{array} \end{aligned}$$

(14)

Basically the constraint in 3rd line of Eq. (14) is a flow conservation constraint, where $S_{i}$ is the average packet generation rate of node $i$ as a source and $D_{i}$ is the average rate at which packets are absorbed by node $i$ as a destination. If node $i$ is not a source or destination then $S_{i}$ and $D_{i}$ are equated to 0. We can formulate the above max-min problem as a maximization problem where minimizing $(1/t)$ is equivalent to maximizing $t$.

$$\begin{aligned} \begin{array}{ll} &{}\mathop {\min }\limits _{R,T_s,t} \frac{1}{t}\\ \mathrm{such\,that}&{}\frac{\overline{p} _i t}{B_i }\le 1 \\ &{}\frac{\sum \nolimits _{j\in N_i } {r_{ji} } -\sum \nolimits _{j\in N_i } {r_{ij} } }{D_i -S_i }=1 \\ &{}r_{ij} \ge 0\;\forall i,j,T_s^i >0,\forall i\quad t>0 \\ \end{array} \end{aligned}$$

(15)

Till now the optimization framework has been designed. It is clear that the objective function contains an inequality constraint (line 2 of Eq. 15) and an equality constraint (line 3 of Eq. 15) which entails the use of a constraint handling technique with the constraints being normalized to 1. The constraints in the last line of Eq. (15) are basically bound constraints which can be tackled easily. In the next section we will describe the classical DE family of algorithms in detail and also briefly review the applications of DE in the constrained optimization domain.

3 Differential evolution and its application to constrained optimization

3.1 Classical DE family of algorithms

DE has emerged as one of the most powerful stochastic real-parameter optimizers of current interest. The computational steps employed by a DE algorithm are similar in spirit to any standard evolutionary algorithm (EA). However, unlike the traditional EAs, DE-variants perturb the current-generation population members with the scaled differences of randomly selected and distinct population members. This is called differential mutation. Therefore, no separate probability distribution has to be used for generating the offspring. DE is a simple real parameter optimization algorithm which works through a simple cycle of stages. We explain each stage separately in the following Sects. 3.1.1–3.1.4.

3.1.1 Initialization of the parameter vectors

DE searches for a global optimum point in a $D$-dimensional real parameter space $\mathfrak {R}^D$. It begins with a randomly initiated population of Np $D$-dimensional real-valued parameter vectors. Each vector, also known as genome/chromosome, forms a candidate solution to the multi-dimensional optimization problem. We shall denote subsequent generations in DE by $G=0,1\ldots ,G_{\max }$. Since the parameter vectors are likely to be changed over different generations, we may adopt the following notation for representing the $i$th-vector of the population at the current generation:

$$\begin{aligned} \vec {X}_{i,G} =[x_{1,i,G},x_{2,i,G},x_{3,i,G} ,\ldots ,x_{D,i,G} ]. \end{aligned}$$

(16)

For each parameter of the problem, there may be a certain range within which the value of the parameter should be restricted, often because parameters are related to physical components or measures that have natural bounds (for example if one parameter is a length or mass, it cannot be negative). The initial population (at $G=0$) should cover this range as much as possible by uniformly randomizing individuals within the search space constrained by the prescribed minimum and maximum bounds: ${\vec {X}}_{\min } =\{x_{1,\min } ,x_{2,\min } ,\ldots ,x_{D,\min } \}$ and $\vec {X}_{\max } =\{x_{1,\max } ,x_{2,\max } ,\ldots ,x_{D,\max }\}$.

Hence we may initialize the $j$-th component of the $i$-th vector as:

$$\begin{aligned} x_{j,i,0} =x_{j,\min } +\mathrm{rand}_{i,j} [0,1]\cdot (x_{j,\max } -x_{j,\min } ), \end{aligned}$$

(17)

where $\mathrm{rand}_{i,j} [0,1]$ is a uniformly distributed random number lying between 0 and 1 (actually $0\le \mathrm{rand}_{i,j} [0,1]\le 1)$ and is instantiated independently for each component of the $i$-th vector.

3.1.2 Mutation with difference vectors

After initialization, DE creates a donor vector $\vec {V}_{i,G}$ corresponding to each population member or target vector $\vec {X}_{i,G}$ in the current generation through mutation. It is the method of creating this donor vector, which differentiates between the various DE schemes. Five most well known mutation strategies implemented in the public-domain DE codes available online at http://www.icsi.berkeley.edu/~storn/code.html are listed below:

$$\begin{aligned}&``\hbox {DE}/\hbox {rand}/1'':\;\;\vec {V}_{i,G} =\vec {X}_{r_1^i ,G} +F\cdot (\vec {X}_{r_2^i ,G} -\vec {X}_{r_3^i ,G} ).\nonumber \\ \end{aligned}$$

(18a)

$$\begin{aligned}&``\hbox {DE}/\hbox {best}/\hbox {1}'':\;\vec {V}_{i,G} =\vec {X}_{best,G} +F\cdot (\vec {X}_{r_1^i ,G} -\vec {X}_{r_2^i ,G} ).\nonumber \\ \end{aligned}$$

(18b)

$$\begin{aligned}&``\hbox {DE}/\hbox {current}\hbox {-to}\hbox {-best}/\hbox {1}'':\;\vec {V}_{i,G} =\vec {X}_{i,G}\nonumber \\&\,\quad +F\cdot (\vec {X}_{best,G} -\vec {X}_{i,G} )+F\cdot (\vec {X}_{r_1^i ,G} -\vec {X}_{r_2^i ,G} ).\end{aligned}$$

(18c)

$$\begin{aligned}&``\hbox {DE}/\hbox {best}/\hbox {2}'':\;\vec {V}_{i,G} =\vec {X}_{best,G} +F\cdot (\vec {X}_{r_1^i ,G} -\vec {X}_{r_2^i ,G} )\nonumber \\&\quad +F\cdot (\vec {X}_{r_3^i ,G} -\vec {X}_{r_4^i ,G} ).\end{aligned}$$

(18d)

$$\begin{aligned}&``\hbox {DE}/\hbox {rand}/\hbox {2}'':\;\vec {V}_{i,G} =\vec {X}_{r_1^i ,G} +F\cdot (\vec {X}_{r_2^i ,G} -\vec {X}_{r_3^i ,G} )\nonumber \\&\quad +F\cdot (\vec {X}_{r_4^i ,G} -\vec {X}_{r_5^i ,G} ). \end{aligned}$$

(18e)

The indices $r_1^i$, $r_2^i$, $r_3^i$, $r_4^i$ and $r_5^i$ are mutually exclusive integers randomly chosen from the range [1, Np], and all are different from the running index $i$. These indices are randomly generated once for each donor vector. The scaling factor $F$ is a positive control parameter for scaling the difference vectors. $\vec {X}_{best,G}$ is the best individual vector with the best fitness (i.e., lowest objective function value for minimization problem) in the population at generation $G$. The general convention used for naming the various mutation strategies is DE$/x/y/z$, where DE stands for differential evolution, x represents a string denoting the vector to be perturbed and y is the number of difference vectors considered for perturbation of x. z stands for the type of crossover being used (exp: exponential; bin: binomial). The following section discusses the crossover step in DE.

3.1.3 Crossover

To enhance the potential diversity of the population, a crossover operation comes into play after generating the donor vector through mutation. The donor vector exchanges its components with the target vector $\vec {X}_{i,G}$ under this operation to form the trial vector $\vec {U}_{i,G} =[u_{1,i,G} ,u_{2,i,G} ,\ldots ,$ $u_{D,i,G} ]$. In the most popular binomial crossover scheme of DE, the crossover is performed on each of the $D$ variables, whenever a randomly generated number between 0 and 1 is less than or equal to a constant Cr $\in$ [0, 1], called the crossover rate. In this case, the number of parameters inherited from the donor has a (nearly) binomial distribution and may be outlined as:

$$\begin{aligned} u_{j,i,G} =\Bigg \{{\begin{array}{l} {v_{j,i,G} } \\ {u_{j,i,G} }\\ \end{array} }{\begin{array}{l} \quad {\mathrm{if\,rand}_{i,j} [0,1]\le { Cr}\,\mathrm{or} j=j_\mathrm{rand}}\\ \quad \mathrm{otherwise} \\ \end{array}} \end{aligned}$$

(19)

where, as before, rand$_{i,j}$[0,1] is a uniformly distributed random number, which is instantiated anew for each $j$-th component of the $i$-th parameter vector. $j_\mathrm{rand} \quad \in [1,2,{\ldots }D]$ is a randomly chosen index, which ensures that $\vec {U} _{i,G}$ gets at least one component from $\vec {V}_{i,G}$. It is generated once for each vector per generation. We note that for this additional demand, Cr is only approximating the true probability $P_\mathrm{Cr}$ of the event that a component of the trial vector will be inherited from the donor.

3.1.4 Selection

To keep the population size constant over subsequent generations, the next step of the algorithm calls for selection to determine whether the target or the trial vector survives to the next generation, i.e., at $G=G+1$. The selection operation is described as:

$$\begin{aligned} \vec {X} _{{i,G + 1}} = \left\{ {\begin{array}{ll} {\vec {U} _{{i,G}} } &{} \quad {if\,f\left( {\vec {U} _{{i,G}} } \right) \le f\left( {\vec {X} _{{i,G}} } \right) } \\ {\vec {X} _{{i,G}} } &{} \quad \mathrm{otherwise} \\ \end{array} } \right\} \end{aligned}$$

(20)

where $f(\vec {X})$is the objective function to be minimized. Therefore, if the new trial vector yields an equal or lower value of the objective function, it replaces the corresponding target vector in the next generation; otherwise the target is retained in the population. Hence, the population either gets better (with respect to the minimization of the objective function) or remains the same in fitness status, but never deteriorates. Note that in Eq. (20) the target vector is replaced by the trial vector even if both yields the same value of the objective function—a feature that enables DE-vectors to move over flat fitness landscapes with generations. Also note that throughout the article, we shall use the terms objective function value and fitness interchangeably. But, always for minimization problems, a lower objective function value will correspond to higher fitness.

3.1.5 Summary of DE iteration

A classical DE algorithm consists of the four basic steps—initialization of a population of search variable vectors, mutation, crossover or recombination, and finally selection. After having initialized the trial solutions, an iteration proceeds in which the DE operators, like mutation, crossover and selection, are executed in order to bring about the improvement of the population over successive generations. The terminating condition can be defined in a few ways like: (1) by a fixed number of iterations $G_\mathrm{max}$, with a suitably large value of $G_\mathrm{max}$ depending upon the complexity of the objective function, (2) when best fitness of the population does not change appreciably over successive iterations, and alternatively (3) attaining a pre-specified objective function value.

3.2 DE for constrained optimization

Most of the real world optimization problems involve finding a solution that not only is optimal, but also satisfies one or more constraints. A general formulation for constrained optimization may be given as:

Find $\vec {X}=\left[ {x_1 ,x_2 ,\ldots ,x_D } \right] ^T$, $\vec {X}\in \mathfrak {R}^D$

$$\begin{aligned}&\quad \quad \hbox {To minimize}\;f( {\vec {X}})\end{aligned}$$

(21a)

$$\begin{aligned}&\hbox {Subjected to:}\nonumber \\&\quad \quad \hbox {Inequality constraints:}\;g_i ( {\vec {X}})\le 0,\;i=1,2,\ldots ,K\nonumber \\ \end{aligned}$$

(21b)

$$\begin{aligned}&\quad \quad \hbox {Equality constraints:}\;h_j ( {\vec {X}})=0,\;\;j=1,2,\ldots ,N\nonumber \\ \end{aligned}$$

(21c)

$$\begin{aligned}&\quad \hbox {And Boundary constraints:}\;x_{j,\min } \le x_j \le x_{j,\max } \end{aligned}$$

(21d)

Storn (1999) first applied DE for solving inequality constrained problems. He proposed a multi-member DE, namely CADE: constraint adaptation with DE that generates $M (M > 1)$ offspring for each individual with three randomly selected distinct individuals in the current generation, and then only one of the $M + 1$ individuals will proceed to the next generation. This concept was also used to solve constrained optimization problems by Mezura-Montes et al. (2005). A hybridization of dynamic stochastic ranking and the multimember DE framework was proposed by Zhang et al. (2008) which obtained promising results on the 22 benchmarks taken from the CEC 2006 competition on constrained optimization (Liang et al. 2006).

Mezura-Montes et al. (2004) and Zielinski and Laur (2006) incorporated Deb’s feasibility rules (Deb 2000) into DE for handling constrained optimization. Lampinen used DE to tackle constrained problems (Lampinen 2002) by using Pareto dominance in the constraints space. Kukkonen and Lampinen (2006) presented a generalized DE-based approach to solve constrained multi-objective optimization problems. Certain hybrid approaches have also been undertaken by researchers like DE with gradient-based mutation by Takahama and Sakai (2006) and PSO-DE (PESO+) by Munoz-Zavala et al. (2006). Mezura-Montes et al. (2006) proposed a DE approach that attempts to increase the probability of each parent to generate a better offspring. This is done by allowing each solution to generate more than one offspring but using a different mutation operator, which combines information of the best solution in the population and also information of the current parent to find new search directions. Tasgetiren and Suganthan presented a multi-populated DE algorithm (Tasgetiren and Suganthan 2006) to solve real-parameter constrained optimization problems. They employed the notion of a near feasibility threshold in the proposed algorithm to penalize infeasible solutions.

On the other hand, researchers had tried to control the parameters of DE in such a way that it is able to tackle constrained optimization problems. An adaptive control of scale factor and crossover probability constant was proposed by Brest et al. (2006). Huang et al. (2006) used an adaptive mechanism to select among a set of DE variants to be used for the generation of new vectors based on a success measure. Moreover, they also adapted some DE parameters to control the variation operators. Very recently (Mezura-Montes and Palomeque-Ortiz 2009) presented the adaptive parameter control in the diversity differential evolution (DDE) (Mezura-Montes et al. 2005) algorithm for constrained optimization. Three parameters, namely the scale factor $F$, the crossover rate Cr, and the number of offspring generated by each target vector NO, are self-adapted by encoding them within each individual, and a fourth parameter called selection ratio Sr is controlled by a deterministic approach.

A cooperative co-evolutionary-based DE approach was proposed by Huang et al. (2007). They designed a special penalty function for constraint handling. Then a co-evolution model is presented and DE is employed to perform evolutionary search in spaces of both solutions and penalty factors. So the solutions and penalty factors evolve interactively and self-adaptively and so both good solutions and satisfactory penalty factors can be obtained simultaneously. A local exploration-based DE for constrained global optimization has been proposed by Ali and Kajee-Bagdadi (2009). They used a restricted version of the pattern search (PS) method (Lewis and Torczon 1999) as their local technique. Some other constraint handling techniques like superiority of feasible points (SFP) and the parameter free penalty (PFP) are also used.

4 The MSeDE algorithm

The performance of DE algorithm is dependent on algorithmic control parameters like population size Np, crossover rate Cr and scale factor $F$. No free lunch (NFL) theorems (Wolpert and Macready 1997) for optimization state that for any algorithm elevated performance over one class of problems is offset by performance over another class. The use of hybridization of search methods, parameter adaptation can come handy while dealing with an extended problem set. To analyze the impact of these parameters, DE has been subjected to many theoretical studies (Caponio et al. 2009; Zaharie 2009; Neri et al. 2011; Weber et al. 2010, 2011; Gamperle et al. 2002; Mezura-Montes et al. 2006; Gamperle et al. 2002) and empirical investigations (Zhang and Sanderson 2009; Qin et al. 2009; Brest et al. 2006; Ali and Kajee-Bagdadi 2009) to suggest an optimal setting for enhancing the performance of DE. Most of these studies sourced from the inherent drawback in DE framework leading to stagnation of search moves (Feoktistov 2006) due to constant control parameters while some focused on limited memory management for real world applications (Neri et al. 2011). Here, our benchmark problem is highly multimodal. We have to maximize the average network lifetime. Here we have considered the node which provides minimum network lifetime and have maximized it. To convert it into a minimization problem we have taken the inverse of the cost function as described earlier also. In this research work, we propose a parameter adaptation synergized with modified mutation strategy and crossover for improving the performance of DE on constrained domain as has been proved experimentally later on.

In this section, we outline MSeDE and discuss the steps of the algorithm in detail. The algorithm employs a new mutation scheme called DE/current-to-constr_best/1 to produce mutant vector which undergoes a modified version of $p$-best crossover scheme called $p$-BCX, and adapts the control parameters $F$ and Cr in each generation in a deterministic manner. The idea of super-fit/best solution has been replaced by the concept of feasible best solution with the objective of making solutions reach feasible region earlier in the optimization process, and incorporating their components in the newly generated offspring vectors, through crossover and mutation, aids the process.

4.1 DE/current-to-constrbest/1

The oldest of the DE mutation schemes is DE/rand/1/bin, developed by Storn and Price (1995, 1997), and is said to be the most successful and widely used scheme in the literature. However, Wolpert and Macready (1997) and Caponio et al. (2009) indicate that DE/best/2 and DE/best/1 may have some advantages over DE/rand/1. The authors of Mezura-Montes et al. (2006) are of the opinion that the incorporation of best solution (with lowest objective function value for minimization problems) information is beneficial and use DE/current-to-best/1 in their algorithm. Compared to DE/rand/$k$, greedy strategies like DE/current-to-best/$k$and DE/best/$k$ benefit from their fast convergence by guiding the evolutionary search with the best solution so far discovered, thereby converging faster to that point. But, as a result of such exploitative tendency, in many cases, the population may lose its diversity and global exploration abilities within a relatively small number of generations, thereafter getting trapped to some locally optimal point in the search space. In addition, DE employs a greedy selection strategy (the better between the target and the trial vectors is selected) and uses a fixed scale factor $F$ (typically in [0.4, 1]). Thus, if the difference vector $\vec {X}_{r_1 ,G} -\vec {X}_{r_2 ,G}$, used for perturbation is small (this is usually the case when the vectors come very close to each other and the population converges to a small domain), the vectors may not be able to explore any better region of the search space, thereby finding it difficult to escape large plateaus or suboptimal peaks/valleys. Thus while delving with constrained optimization problems, the concept of best solution does not always hold due to the boundary of feasible region. The present best solution (in terms of fitness value) may not be the best feasible solution if it lies in the infeasible region of the decision space owing to the constraint violation. Such cases call for a modification of the meaning of best solution. We must rather be concerned with the feasible best solution or the one with the least constraint violation of the current population.

Taking these facts into consideration and to overcome the limitations of fast but less reliable convergence performance of DE/current-to-best/1 scheme, in this article, we use a less greedy and more explorative variant of the DE/current-to-best/1 mutation strategy by utilizing the feasible best vector or the one with least constraint violation of a dynamic group of $q$ % of the randomly selected population members for each target vector. This scheme, called DE/current-to-constr_best/1, can be expressed as:

$$\begin{aligned} \vec {V}_{i,G} =\vec {X}_{i,G}&+ F_{i,G}.\left( \vec {X}_{\mathrm{constr}\_\mathrm{best},G}- \vec {X}_{i,G} \right) \nonumber \\&+ F_{i,C}.\left( \vec {X}_{r_1^i ,G} -\vec {X}_{r_2^i ,G} \right) \!, \end{aligned}$$

(22)

where $\vec {X}_{r_1^i ,G}$ and $\vec {X}_{r_2^i ,G}$ are two distinct vectors picked up randomly from the current population and, from the current population $q$ % vectors are randomly chosen and among them the one with least constraint violation is set as $\vec {X}_{\mathrm{constr}\_\mathrm{best},G}$. In the event of all the $q$ % vectors being feasible (i.e., constraint violation being 0) obtain the one with best functional value. Under this scheme, the target solutions are not always attracted towards the same best position (which may be infeasible) found so far by the entire population. Instead the attraction is distributed among a certain proportion of population members which have less or zero constraint violation and this feature is helpful in guiding the solutions towards feasible region of solution space while avoiding premature convergence at local optima (Zaharie 2009). The parameter $q$ is known as the group size which controls the greediness of the mutation scheme DE/current-to-constr_best/1. The effect of the variation of $q$ on the performance of the algorithm is discussed in Sect. 6. Also note that we have used two scale factors $F_{i,G}$ and $F_{i,C}$ in the differential mutation. The rationale behind their usage will be discussed after the detailing of the crossover used.

4.2 The p-BCX crossover

The crossover operation used in MSeDE is a modification of the $p$-best crossover (Islam et al. 2012) where for each donor vector, a vector is randomly selected from the p % top-ranking vectors (according to their objective function values) in the current population and then binomial crossover is performed between the donor vector and the randomly selected $p$-best vector to generate the trial vector at the same index. Due to the inclusion of system constraints, the top p % top-ranking vectors have been selected based on their overall constraint violation and not their functional value. This crossover scheme shall be referred to as $p$-BCX as it uses $p$-best population members based on their constraint violation and makes use of two Cr variables. The logic behind $p$-BCX crossover performed for each $D$-dimensional parent vector $\vec {X}_{i,G}$ can be outlined as follows:

Randomly select a vector from the $p$ best vectors of the population based on constraint violation: $\vec {X}_{pbest,G}$.

Generate $j_\mathrm{rand}$ = ceil(rand(1$, D))$

For $j$= 1 to $D$

$$\begin{aligned} {\begin{array}{l} R=\mathrm{rand}(0,1); \\ \mathrm{if} (j=j_\mathrm{rand} \hbox { or }R\le { Cr}_1 )\\ \qquad \qquad u_{j,i,G} =v_{j,i,G} ; \\ \mathrm{else \, if}({ Cr}_1 <\,R\le { Cr}_2 ) \\ \qquad \qquad u_{j,i,G} =x_{j,i,G} ; \\ \mathrm{else}\\ \qquad \qquad u_{j,i,G} =x_{j,p\mathrm{best},G} ;\\ \end{array}} \end{aligned}$$

(23)

End For

The underlying idea behind this crossover scheme is that the useful genetic information contained in the top-ranking individuals (according to their constraint function values) is to be injected into the trial vector or offspring in order to improve their movement towards feasible decision space and also enhance the convergence speed which is essential in this particular problem. But at the same time, the information contained in the parent member is never ignored altogether. This deviation from the $p$-best crossover brings about improvement in performance as shall be demonstrated in the next section experimentally. This crossover scheme being greedy in nature, we have to choose the optimal value of the parameter $p$. Effect of the variation of $p$ on the performance of MSeDE is clearly illustrated in Sect. 6.

4.3 Parameter adaptation schemes in MSeDE

The parameter adaptation schemes used in MSeDE are dependent on two factors. The scale factor $F$ has been adapted with focus on trade-off between exploration and exploitation for a stable searching behaviour of DE. In the case of crossover rate Cr, the adaptation allows for the controlled recombination of components.

4.3.1 Scale factor adaptation (F)

In this mutation scheme, two factors solely determine the changing position of the population members. Attraction of the $i$-th member towards the top-ranking vectors as obtained from the differential vector $\left( \vec {X}_{\mathrm{constr}\_\mathrm{best},G} -\vec {X}_{i,G} \right)$ and the random component $\left( \vec {X}_{r_1^i ,G} -\vec {X}_{r_2^i ,G} \right)$ needs to be balanced. In this article we aim at elevating $F$ whenever a particle is situated far away from the favorable region where the suspected optima lies, i.e., the fitness value of the particle differs much from the best solution value. On the other hand we should reduce $F$ whenever the objective function value of the particle nears the best solution. These particles are subjected to lesser perturbation so that they can finely search the surroundings of some suspected optima. This bi-objective decision criterion is obtained by the usage of two scale factors that help to maintain attraction towards the feasible basins in functional landscape without sacrificing the fine searching ability of the algorithm. The choice of probability distributions for instantiating $F_G$ and $F_C$ (G and $C$ stands for Gaussian and Cauchy), as is evident from Eq. (24), is dependent on the intrinsic property of the distributions. Less randomness is suitable for fine local search and the short tail property of Gaussian distribution (bell-shaped curve) satisfies our objective and is thus used for sampling the value of $F_G$ which helps in performing random search ($\vec {X} _{r_1^i ,G}$ and $\vec {X}_{r_2^i ,G}$ being chosen randomly). On the other hand, Cauchy distribution has a far wider tail than the traditional Gaussian distribution and can be judiciously used when the feasible region (or the best fit solution) is far away from the current search point. The values of $F_C$ sampled from the tail region give adequate perturbation so that premature convergence can be avoided by producing large fly-by movements. But the amount of perturbation needs to be controlled in the end stages of the run. The scheme may be outlined as:

$$\begin{aligned} \begin{array}{l} F_G \sim \left| {N(\mu ,\sigma ^2)} \right| \!; \\ F_C =\left| {Q(r;x_0 ,\gamma )} \right| \!; \\ \end{array} \end{aligned}$$

(24)

where $N(\mu ,\sigma ^2)$ denotes normally distributed number with mean $\mu$ and variance $\sigma ^2$, and $Q(r;x_0 ,\gamma )$ denotes the quantile function of Cauchy distribution with location parameter $x_0$ and scale parameter $\gamma$. The value of $\mu$ and $x_0$ are set to 0, and $r$ is sampled randomly sampled in the range (0, 0.5). The variance $\sigma ^2$ and scale parameter $\gamma$ are varied as

$$\begin{aligned} \sigma ^2=\gamma =F_{\min } +( {\Delta F})\cdot \frac{\Delta f_i }{1+\Delta f_i } \end{aligned}$$

(25)

where $\Delta f_i =\left| {f(\vec {X}_i )-f(\vec {X}_{best} )} \right|$, and $F_{\min }$ and $\Delta F$ have been set to 0.2 and 0.8 respectively. As clear from equation (25), the factor ${\Delta f_i } / {( {1+\Delta f_i })}$ can be modified to $1/( {1+1 / {\Delta f_i }})$. For a target vector if $\Delta f_i$ is large $1/{\Delta f_i }$ decreases, so the factor $1/( {1+1/{\Delta f_i }})$ and accordingly $\sigma ^2$ and $\gamma$ increases, so $F_G$ and $F_C$ gets enhanced and the particle will be subjected to larger perturbation so that it can jump to a favorable region in the landscape. For the best individual $\Delta f_i =0$, so the best vector is required to undergo a lesser perturbation such that it can perform a fine search within a small neighborhood of the suspected optima. Thus the particles which are distributed away from the current fittest individual have large $F$ values and keeps on exploring the search space, maintaining sufficient population diversity. Gradually the value of $\sigma ^2$ and $\gamma$ decreases in the later stages of the run and exploration is carried out in the feasible region.

4.3.2 Crossover probability adaptation (Cr )

The adaptation of Cr is based on the concept that a search process in a population-based model cannot proceed efficiently relying only on the information contained in the elite individuals of the population or the newly generated individuals. Rather a recombination of their genetic materials can produce an effective solution point. Depending on the given logic, we make use of two crossover rates Cr $_{1}$ and Cr $_{2}$ and adaptation scheme is given below:

$$\begin{aligned} { Cr}_2 ={ Cr}_1 +( {\Delta { Cr}})\cdot (1-\mathrm{e}^{-\Delta f_i }) \end{aligned}$$

(26)

where $\Delta f_i =\left| {f(\vec {X}_i )-f(\vec {X}_\mathrm{best} )} \right|$, ${ Cr}_1$ and $\Delta { Cr}$ are set to 0.2 and 0.8 respectively. As evident from Eqs. (26), Cr $_{i}$ depends on the factor $( {1-\mathrm{e}^{-\Delta f_i }})$. If $\Delta f_i$ is large, the factor $( {1-\mathrm{e}^{-\Delta f_i }})$ attains a higher value resulting in larger crossover probability values.

The aim is that an offspring vector that has components of the target vector, its mutant vector and most importantly the top ranking individuals of the current generation. Now if the solution of the target vector is better, the chances of a randomly picked up number lying in the range of $\left[ {{ Cr}_1 ,{ Cr}_1 +( {\Delta { Cr}})} \right]$ is high and thus the offspring vector has more components of its corresponding parent. Otherwise if it is below the value of ${ Cr}_1$, the components of the mutant vector is incorporated while that of elite members are inserted if it exceeds the value of ${ Cr}_1 +( {\Delta { Cr}})$ which is ${ Cr}_2$. To assist the convergence of the target vector, the value of Cr controls the flow of genetic information to the trial vector.

Suppose that a particle is situated in an adverse region of the fitness-space. During the crossover operation the donor vector created by perturbing the target particle should inject information to the trial vector to a greater extent so that it can switch to a favorable area in the fitness landscape. So the value of Cr should be relatively high in accordance with the binomial crossover scheme ensuring more contribution of genetic information from the donor vector. For the best member, the value of ${ Cr}_1$ and ${ Cr}_2$ will coincide, i.e., ${ Cr}_2 ={ Cr}_1$ and thus it will either include information from its mutant vector or other elite members rather than itself. Note that in the end stages of the run, there will be a primary focus on the information from the best member thereby invoking exploitation.

4.4 Putting it all together

A complete pseudo-code of the MSeDE algorithm composed of DE/current-to-constrbest/1 mutation, $p$-BCX crossover and the proposed parameter adaptation schemes is presented in Table 1.

Table 1 Pseudo-code representation of the MSeDE algorithm

5 Handling constraints

The combined routing and Sleep scheduling problem considered here has equality and inequality constraint. Due to the presence of the equality constraint we have opted for the $\varepsilon$-constraint handling technique as it becomes particularly useful in presence of active constraints (Takahama and Sakai 2006). The $\varepsilon$-constraint handling method was proposed in Takahama and Sakai (2006) in which the relaxation of the constraints is controlled by using the $\varepsilon$ parameter. The $\varepsilon$-constraint technique is capable of converting a constrained optimization problem into an equivalent unconstrained one by doing $\varepsilon$-level comparisons (Takahama and Sakai 2006). So by incorporating this method in unconstrained optimization algorithms like MSeDE, SaDE, JADE and CLPSO, constrained optimization problem can be solved. As solving a constrained optimization problem becomes tedious when active constraints are present, proper control of the $\varepsilon$ parameter is essential (Takahama and Sakai 2006) to obtain high-quality solutions for problems with equality constraints. The $\varepsilon$ level is updated until the generation counter $k$ reaches the control generation $T_\mathrm{c}$. After the generation counter exceeds $T_\mathrm{c}$, the $\varepsilon$ level is set to zero to obtain solutions with no constraint violation.

$$\begin{aligned} \begin{array}{l} \varepsilon \left( 0\right) =\nu \left( {X_\theta }\right) \\ \varepsilon \left( k\right) =\left\{ {\begin{array}{ll} \varepsilon \left( 0\right) \left( {1-\frac{k}{T_\mathrm{c} }}\right) ^\mathrm{cp},&{} 0<k<T_\mathrm{c} \\ 0&{}k>T_\mathrm{c} \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(27)

where $X_{\theta }$ is the top $\theta$th individual and $\theta = (NP/20)$. The recommended parameter ranges are (Takahama and Sakai 2006): $T_\mathrm{c}\, \epsilon \, [0.1\,G_\mathrm{max}$, 0.8 $G_\mathrm{max}$] and $\mathrm{cp} \,\epsilon \,[2, 10]$. Here we have kept $T_\mathrm{c}= \mathrm{ceil}\, (0.3\,G_\mathrm{max})$ and $\mathrm{cp}=3$ and these parameter settings have given a perfect balance between robustness and celerity. In this technique a solution is considered as feasible if its overall constraint violation is less than $\varepsilon$($k$).

6 Experimental study and discussion

In this section, the performance of the proposed MSeDE algorithm has been illustrated through various simulations. The performance of MSeDE has been compared with state-of-the-art EAs like SaDE, JADE and CLPSO which themselves are very powerful optimization techniques. We also have compared our results with a famous DE-based dedicated constrained optimizer, namely $\varepsilon$DEag which came 1st in the CEC 2010 competition on constraint handling techniques. We have also included the results of S-RS method to show the effectiveness of the considered optimization framework. Finally, we have performed comparisons using the contender algorithms on the CEC 2010 constrained benchmark set to depict the applicability of MSeDE to an extended set of benchmark problems and also shown convergence profile of MSeDE against that of a very powerful, recently proposed optimizer called MDEpBX (Islam et al. 2012) from which the mutation and crossover is inspired from. Note that for the proposed algorithm MSeDE and also for SaDE, JADE and CLPSO, we have applied the same constraint handling technique, namely $\varepsilon$-constraint method which has been described in Sect. 5.

In this section, three network simulation setups has been considered with 25, 50 and 75 randomly placed nodes in a 75 m by 75 m area. The gateway node lies in the centre of the square or the area. As far as the nodes are concerned, we have used the power consumption model of Mica2mote and CC1000 transceiver the specifications of which are summarized in Table 2. The nodes which have been deployed in the field for all the three cases (25, 50 and 75) are operating in the radio frequency (RF) transmission power and also in each of the cases the RF range of the node is 20 meters. For the initial node battery capacity we have assumed a Gaussian distribution $( {\mu ,\delta ^2})$ of mean $\mu$ and standard deviation $\delta$ with $\mu =2{,}500$ mAh and $\delta =25$ mAh.

Table 2 System power and time parameters

For all the cases of 25, 50 and 75 nodes in the field we have assumed that in the network all the nodes have same packet generation rate of $4.19 \times 10^{-3}$ packet/s. Again for all the cases, we randomly generate 50 different network topologies according to the above set up. For each network topology, the initial sleep time of nodes is randomly picked from an interval [$10 \times \,T_\mathrm{det}, 1{,}000 \times \,T_\mathrm{det}$]. For the termination of each algorithm we have assumed $G_\mathrm{max}$ as 15 for each case. The population size for all the evolutionary algorithms is kept at a moderate value 75. For MSeDE, the parameters $p$ in $p$-best crossover and $q$ in DE/current-to-constr_best/1 are kept at 25 and 10 % of population size $N_p$, i.e., $\left\lceil {{N_p}/4} \right\rceil$and $\left\lceil {{N_p}/10} \right\rceil$ respectively. The reason for setting these parameter values is discussed elaborately in Sects. 6.1, 6.2 and 6.3. The final mean network lifetime and the standard deviations obtained at the end of the performance of the algorithms using the three different node numbers (25, 50 and 75) for those different 50 network topologies is listed in Table 3.

In order to evaluate the statistical significance of the end results obtained by an algorithm, we perform two sided Wilcoxon’s rank sum test (Wilcoxon 1945) between the MSeDE and other competing algorithms. This test is based on null hypothesis which states that for every test is the samples considered for comparison are independently taken from identical continuous distributions having same medians. The end result is marked by using three different symbols. We use + for the cases when the null hypothesis is rejected at the 5 % significance level and the MSeDE is statistically superior performing than the competitor. Similarly, “$-$” sign indicates rejection of the null hypothesis at the same significance level with the MSeDE exhibiting inferior performance and with “$=$” no statistically significant difference in performance between the MSeDE and other algorithm is observed.

Table 3 Mean network lifetime (standard deviation and Wilcoxon’s rank sum test are given in braces)

Next part of the simulation shows four performance criteria used for the analysis of the results given by MSeDE.

• 1. Generation wise network lifetime variation, i.e., the convergence profile.

• 2. Network lifetime variation with the node packet generation rate.

• 3. Network lifetime variation with different initial node sleep time and.

• 4. Effectiveness of different components of MSeDE.

6.1 Generation wise network lifetime variation (convergence profile)

In this section we have demonstrated the calculated network lifetime variation which has been obtained at every generation through runtime performance of MSeDE with respect to the competitor algorithms. The obtained results are also shown explicitly when the parameters such as, $p$-value in $p$-best crossover, $q$-value in the mutation scheme DE/current-to-constr_best/1 and the population size associated with MSeDE are varied to find out the optimal parameter settings. Figure 4 shows the network lifetime achieved by using MSeDE for different generations against its competitor algorithms and also with the variation of its parameters like $p$-value, $q$-value and population size Np. In Fig. 4a–c, for comparison of MSeDE with its competitor algorithms, the parameters used in different algorithmic components of MSeDE are set to their optimal values which will be discussed more elaborately in the current ongoing section.

Fig. 4

Network lifetime achieved by using MSeDE for different generations against its competitor algorithms

Figure 4a–c shows the network lifetime profile with different generations for MSeDE and its competitor algorithms for 25, 50 and 75 nodes respectively. In each case, the node packet generation rate has been kept at $4.19 \times 10^{-3}$ packet/s. Each point in the graph is the mean of 20 network topologies. From these figures it can be seen that the network lifetime obtained for MSeDE is best as compared to the $\varepsilon$DEag, JADE, SaDE, CLPSO and the S-RS method.

Tables 4, 5 and 6 show the performance of MSeDE by varying its parameter values, such as population size, $p$-values and $q$-values respectively for 75 nodes. From Table 4, it is evident that with increase in population size, the performance of MSeDE improves as the number of search particles increase in the fitness space leading to an increment in population diversity. As the population size gets lower the population diversity reduces which leads to premature convergence. So, in those cases, the network lifetime is lower. But the computational cost associated with the wireless sensor system also increases as a function of the population size. In order to ensure that we do not incur any extra computational burden, we adopt a moderate population size of value 75. Table 5 shows the performance of MSeDE with a variation of $p$-values in the novel $p$-best crossover scheme. It shows the optimum results when the value of $p$ is equal to 25 % of the population size. As the value of $p$ gets lowered, say 10 % of population size the algorithm suffers from a tremendously greedy exploitation and thus it shows good results at the initial stages but ultimately premature convergence takes place due to lack of exploration and as a consequence it shows a lesser network lifetime at the later generations. Again, at a $p$-value $>$25 the exploitation power of MSeDE is decreased because if the value of $p$ is taken too large (near about population size), the concept of $p$-best crossover is violated and it becomes ineffective as the randomly selected $p$-best vector with whom the donor vector exchanges its components may not be a top-ranking individual of the population and the proposed algorithm may fail to converge properly. Table 6 shows the performance of MSeDE with variation in $q$-values.

Table 4 Mean network lifetime and standard deviation for different values of population size

Table 5 Mean network lifetime and standard deviation for different $p$ values

Table 6 Mean network lifetime and standard deviations for different $q$ values

The performance of MSeDE is dependent on the selection of group size $q$. If the value of $q$ is large (near about population size), the proposed mutation scheme DE/current-to-constr_best/1 basically becomes identical to the current-to-best scheme. This hampers the explorative power and the algorithm may be trapped at some local optimum that is not the actual global optimum. The reason is that if $q$ is on par with population size, the probability that the best of randomly chosen $q$ % vectors is similar to the globally best vector of the entire population will be high. This drives most of the vectors towards a specific point in the search space resulting in premature convergence. Again, too small a value of $q$ runs the risk of losing the exploitative capacity of the algorithm. This is due to the fact that the value of $q$ being small the best of randomly chosen $q$ % vectors may not be a fitter agent of the population resulting in creation of poor donor vectors and the convergence performance may get hampered. It is seen that keeping the group size $q$ equal to 10 % of the population size offers the best performance of MSeDE.

6.2 Network lifetime variations with different initial node sleep time

In this section, the variation of the network lifetime with the different initial node sleep time has been shown with the help of bar diagram for 25, 50 and 75 nodes and also with varying the parameters. Since the problem is a non-convex optimization problem with two constraints it is very difficult to locate the global optimal solution for a simple EA and it is liable to be trapped in local optima that are present in the fitness landscape. Subsequently, here we use the global optimum solution to denote the particular solution that has the maximum lifetime obtained from simulations with several different initializations. To observe this phenomenon, we pick a definite network topology as an example and run the corresponding algorithms with 7 different initializations. Each initialization randomly picks an initial sleep time within an interval.

In Fig. 5a–c, the performance of MSeDE has been compared with $\varepsilon$DEag, SaDE, JADE, CLPSO and the S-RS method to figure out the superior convergence performance of the proposed MSeDE with respect to the contestant algorithms for 25, 50 and 75 nodes. In all 7 initializations, the proposed MSeDE converges towards the global optimum more prominently and therefore gives much superior network lifetime outperforming the rest of the algorithms. The competitor algorithms are unable to converge properly only getting stuck in a local optimum as the combined routing and sleep scheduling problem considered here is a non-convex one.

Fig. 5

Variation of Network lifetime with different initial node sleep-time for 25, 50 and 75 nodes, and for different values of parameters

The Fig. 5d–f shows the performance of the MSeDE with the variation of the parameters like the $p$-values, $q$-values and the population size for a 75 node network topology. The Fig. 5d shows the variation of the network lifetime with all 7 initializations with different population size $N_p$. A close scrutiny reveals that the convergence performance of MSeDE improves with increasing $N_p$ due to the reason that an increase in number of population agents assists an EA to explore the fitness space in a much better manner. So the population diversity gets enhanced improving the convergence speed of the algorithm. But on increasing the population size a problem arises that the computational complexity of the system also gets elevated at the same time. Keeping all these factors in mind, value of $N_p$ is set to a moderate value 75. Figure 5e shows the network lifetime variation with variation of the $p$-values in $p$-best crossover operation. Again for the reason stated above in Sect. 6.1 the best result comes at the value of $p$ at 25 % of Np. In Fig. 5f the network lifetime variation with variation of $q$-values in DE/current-to-constr_best/1 is portrayed where the proposed algorithm performs the best when $q$ is set to be 10 % of $N_p$ and the reason behind it is already discussed in the Sect. 6.1.

6.3 Network lifetime variation with the node packet generation rate

In this section we have compared the performance of the MSeDE algorithms stated above under different network traffic density by changing the node packet generation rate. Tables 7, 8 and 9 show the superiority of performance of the MSeDE with different node packet generation rate ranging from $7\times 10^{-4}$ packet/s to $4\times 10^{-2}$ packet/s for 25, 50 and 75 nodes respectively. Tables 7 shows the network lifetime achieved by using MSeDE for different node packet generation rate (npgr) against its competitor algorithms and also with the variation of its parameters like $p$-value, $q$-value and population size.

Table 7 Mean network lifetime and standard deviations (given in braces) of MSeDE and the competitor algorithms for different node packet generation rate (25 nodes)

Table 8 Mean network lifetime and standard deviations (given in braces) of MSeDE and the competitor algorithms for different node packet generation rate (50 nodes)

Table 9 Mean network lifetime and standard deviations (given in braces) of MSeDE and the competitor algorithms for different node packet generation rate (75 nodes)

Tables 7, 8 and 9 shows the average network lifetime (and the standard deviations) profile with the variation of npgr for MSeDE and its competitors for 25, 50 and 75 nodes respectively. The Node packet generation rate has been varied from $7\times 10^{-4}$ packet/s to $4\times 10^{-2}$ packet/s. From the figure it can be seen that the network lifetime obtained for MSeDE is best as compared to the $\varepsilon$-DEag, SaDE, JADE, CLPSO and the S-RS method in all node packet generation. It can be clearly seen that as the packet generation rate gets higher, it takes more energy for transmitting the generated packet to the gateway and as a consequence the network lifetime gets shorter. Here, the important thing is to note that all the performance of the proposed MSeDE is accomplished with default parameters of $p$-value at 25 % of population size, population size at 75 and $q$-value at 10 % of population size and whenever a particular parameter is varied, the remaining two parameters are kept fixed.

6.4 Performance of MSeDE on constrained optimization problem

In this section we have compared the performance of the MSeDE algorithm have been compared with different real-parameter constrained optimizers on the benchmark problems proposed for CEC 2010 Special Session/Competition on Evolutionary Constrained Real Parameter single objective optimization (Mallipeddi and Suganthan 2010). Three contending algorithms—infeasibility empowered memetic algorithm (IEMA) Singh et al. (2010), multiple trajectory search algorithm (MTS) Tseng and Chen (2010) and the winner algorithm $\varepsilon$DEag (Takahama and Sakai 2006) have been considered and compared for 10$D$ problems. In Table 10, MSeDE has been compared with results of three other state-of-the-art algorithms used for constrained optimization for the same test environment for 10-dimensional problems. Wilcoxon’s rank sum statistical test has been done.

Table 10 Performance of MSeDE and competitor algorithms for 10-D problems for functions C01–C18

The results in bold letters indicate the best result obtained which may not necessarily be the least since infeasible solutions may have less fitness value. The table shows that MSeDE outperforms the algorithms, namely $\varepsilon$DEag in 4 cases, IEMA in 12 cases and MTS in all 18 cases. This establishes MSeDE as statistically superior to the state-of the-art algorithms compared and also accounts for its versatile nature. These simulations have been performed using their standard parametric setups suggested in literature and the default configuration for our MSeDE algorithm. The outcome also validates that the parametric settings for our MSeDE is optimal.

6.5 Performance of MSeDE vs MDEpBX

The use of $F$ and Cr adaptation in our proposed MSeDE algorithm have been inspired from MDEpBX which was originally designed for real-parameter unconstrained (bound-constrained only) optimization. The entire search space formed its domain without the need for checking feasibility. However the conditions becomes somewhat varied in the constrained optimization problem. The concept of DE/current-to-constrbest/1 mutation and the $p$-BCX crossover are modified versions tailored particularly with respect to the problem type. The comparison with MDEpBX, as highlighted through Fig. 6a–c, reflects that the combined advantage of the constrained versions of DE/current-to-grbest/1 and $p$-best crossover implemented in MSeDE aided by the semi-adaptive variation of control parameters help to improve the search behavior of MSeDE. It can be said that the search move of MSeDE excels that of MDEpBX in constrained domain by generating better end results in feasible portion of the search space.

Fig. 6

Network lifetime achieved by using MSeDE for different generations against MDEpBX for different nodes

6.6 Suitability of MSeDE to proposed benchmark problem

The usage of varying network topologies causes random placement of the node without concern for the RF range of each node. Such random placement imparts sharp difference in the cardinality of the set $N_i$ used in Eq. (1). This in turn affects the power expended by the nodes as is evident from Eqs. (11) and (13). When the set $N_i$ becomes null, the power consumption is minimum since the first two terms in Eq. (11) equal 0. But such occurrences are rare. The inequality constraint (line 2 of Eq. 14) becomes difficult to satisfy due to the non-linear nature of the relation and the range of values it can take. It should be noted that we have specifically ensured random topologies to complexity to an otherwise separable, multimodal but highly constrained benchmark problem (from Eqs. 8, 11, 14, 15) in the form of sharp local optima and ill-conditioning (sharp change in value). Additionally the routing matrix satisfies a flow conservation constraint which is very hard to satisfy for being an equality constraint (line 3 of Eq. 14). Due to this difficulty, we have normalized the value of the constraints to 1 by modifying it (line 2 and 3 of Eq. 15). This helps in adding the constraint violations to constitute $\varepsilon (0)$ of Eq. 26 for implementing the constraint handling. But in spite of the normalization, as is evident from the experimental results, some well-known state-of-the-art search methods have failed to perform appreciably within a limited generation ($G_\mathrm{max}$ being 15) which is needed for online optimization algorithms. We opine that the main problem here is reaching the feasible space by nullifying the violations and successfully guiding the search agents towards the optimal region.

The aforesaid observation brings into picture an important problem associated with the control algorithm of our choice, i.e., DE. Although the differential nature of mutation in DE seems an efficient search mechanism, it suffers from an intrinsic limitation. The use of constant values of scale factor $F$ and crossover rate Cr needs fine tuning to suit the problem landscape otherwise a situation called stagnation Weber et al. (2011); Feoktistov (2006) is reached where the algorithm is not able to reach even a sub-optimal solution in spite of maintaining threshold population diversity. This has been subjected to detailed investigations, e.g., see (Zaharie 2009; Weber et al. 2011), and is also the reason behind parameter adaptation (Qin et al. 2009; Brest et al. 2006; Islam et al. 2012). We have adopted a similar approach here. But real-world problems are seldom well-behaved as standard benchmarks and operate within a limited feasible domain of decision space without providing any a priori knowledge of the fitness landscape to the practitioner. The main motivation behind the design of MSeDE lies in the attention paid to the feasible search space, which is critical in constrained optimization, in addition to parameter adaptation.

An important feature of the problem definition here is that it is lower bounded, i.e., $r_{ij} \ge 0\;\forall i,j,T_s^i >0$, unlike bounded problems. Thus the search range is vast and makes the algorithm wandering in the space unless some restriction is imposed. The inequality and equality constraints play an important role in attaining our objective of efficient routing and lifetime maximization. This was one of our main concerns since the MDEpBX was designed for bound-constrained global optimization process without consideration for feasibility. This is overcome through the modification of the DE/current-to-gr_best/1 mutation and the $p$-best crossover employed MDEpBX through the enhanced DE/current-to-constrbest/1 mutation and $p-$BCX crossover proposed here. The difference in performance in observed through the plots shown in Fig. 6. Likewise the details of parameter adaptation of $F$ and Cr are detailed in Sect. 4.3. Note that we have set $\mu =x_0 =0$ so that the values of $F_G$ and $F_C$ are appreciably less as the value of $\sigma$and $\gamma$approaches$F_{\min }$during the end stages of the run. The relation $\sigma ^2=\gamma <1$ensures that the value of $\sigma >\gamma$. We would like to point out that MDEpBX has a strong affinity for exploitation since it uses the information from top ranking individuals both during the mutation and crossover operation. Unlike MDEpBX, in the proposed $p-$BCX strategy the value of ${ Cr}_1$ has been kept 0.2 and ${ Cr}_2 \sim 1$. This limits the transfer of genetic information from parents since low value of Cr is favorable for separable functions as in classical DE. The information from the top-ranking (feasible) individuals are inherited when the value of ${ Cr}_2$ starts falling from 1. The mutation already ensures that population members are attracted towards a feasible region so the need to include them initially in the crossover is relaxed. This philosophy is quite different from that of MDEpBX. Besides, MSeDE has also been able to maintain its robustness when tested on the constrained benchmark problems proposed for the CEC 2010 Special Session/Competition which attests to its versatility.

Memory management is another important issue in real-life applications that require results in a short interval of time. The time expended in information storage and retrieval can be a serious limitation to the applicability of an algorithm. We would like to note that MSeDE does not require historical memory like some high performing adaptive DE variants like JADE, SaDE, MDEpBX. The variation of the control parameters is independent of past success of the parents. In this regard, it will be interesting to implement compact version (Neri et al. 2011; Mininno et al. 2011) in relation to MSeDE as a future work since they are capable of performing efficiently under limited memory requirement.

7 Conclusion

Most of the works previously in the field of maximizing lifetime for the battery powered wireless sensor network treated the concept of energy efficient routing and periodic sleep scheduling separately, i.e., till date for designing Wireless Sensor Networks one of the above component had been kept fixed while the other is optimized. Such designs give rise to practical difficulty in determining the appropriate routing and sleep scheduling schemes in the real deployment of sensor networks, as neither component can be optimized without pre-fixing the other one.

In this paper, we have focused on an all embracing approach to network life time maximization of wireless sensor networks that encompasses both efficient routing and sleep scheduling. This optimization framework for combined routing and sleep scheduling is especially difficult for its non-convex nature. The non-convex optimization is a very difficult optimization problem to solve with the help of traditional linear programming and gradient based approach. As a result, we tackle the problem by an evolutionary algorithm in the form of Differential Evolution. We have modified the mutation strategy and also adapted the scale factor and the crossover probability constant and synergized with an improved version of recent crossover strategy ($p$-best crossover). Then this modified version of DE algorithm has been used to solve the non-convex optimization problem. Our work in this paper has demonstrated the importance of combined routing and sleep scheduling by comparing with a separate routing and sleep scheduling (S-RS) technique. The proposed MSeDE algorithm drastically outperforms the performance of SaDE and JADE which are two famous variant of differential evolution algorithm and also shows far superior performance as compared to CLPSO and S-RS method.

The superior performance of MSeDE can be attributed to the balanced ratio of exploration and exploitation achieved throughout the evolutionary stages. This balance is accomplished through the synergized functioning of the modifications proposed in MSeDE that help to harmoniously boost up the performance of the algorithm. In fact comparison with some well known optimizers in the domain of constrained optimization reveals the novel nature of our algorithm. Our assumption is a collision-free system due to the light traffic in sensor networks. In our future work, we will extend this model to take into account the effect of collisions on routing and sleep scheduling decisions. Also the memory management issue in compact EAs is an interesting topic that requires further investigation.