Conditions for the arrest of a vertical propagating dyke

Abstract

Magma ascent towards the Earth’s surface occurs through dyke propagation in the vast majority of cases. We investigate two purely mechanical effects unrelated to cooling or solidification that lead to the arrest of propagation, so that no eruption occurs. The first is that the input of magma from the source is not maintained continuously, such that a fixed volume of magma is released. Laboratory experiments show that, in this case, the dyke stops at a finite distance from the source. This behaviour is specific to the fracturing process in 3-D. We derive a relationship for the minimum magma volume required for an eruption as a function of magma buoyancy and source depth. When large magma volumes are available, eruption may also be prevented by a thick low density layer in the upper crust. Numerical studies of dyke propagation show that the dyke continues to rise even though it is negatively buoyant. Magma accumulates in a swollen nose region at the interface between the low density layer and the dense basement. Magma overpressure is largest at this interface and increases with increasing penetration into the upper layer. It may become large enough to induce horizontal fractures in the dyke walls and lateral intrusion of a sill, which prevents eruption. This requires that the thickness of the low density layer exceeds a threshold value that depends on the density contrast between magma and host rock. If the magma volume is smaller than a threshold value, neither sill intrusion nor eruption are possible and magma gets stored in a horizontal blade-shaped dyke straddling the interface. Scaling laws for variations of ascent rate and for the minimum magma volume allow diagnosis of a failed eruption.

Introduction

The general question of what determines whether or not a buoyant magma-filled crack actually reaches the Earth’s surface or halts as a shallow intrusion is an intriguing one. Drawing constraints from geophysical or geological studies is difficult. Observations of frozen dykes exposed by erosion contain little dynamic information (Delaney and Pollard 1981; Jolly and Sanderson 1995). Geophysical monitoring is associated with large uncertainties and cannot specify how the width and shape of a dyke evolve during ascent (Brandsdóttir and Einarsson 1979; Battaglia and Bachèlery 2003). Some progress has recently been made using the rate of seismicity (Traversa and Grasso 2009; Traversa et al. 2010) but we are still far from reliable diagnostic tools. From a theoretical standpoint, the subject is complex, involving fluid mechanics, solid deformation, fracture mechanics, thermodynamic aspects of magma solidification and host rock softening due to heating by magma (Lister and Kerr 1991; Rubin 1995). Laboratory experiments can bridge the gap between field observations and theory because both dynamic and geometric information can be acquired during crack propagation subject to a range of boundary conditions. For complicated configurations involving vertical variations of the physical properties of host rocks, however, they require large set-ups and imaging systems. Thus, it is also useful to develop numerical tools to study the dynamics of flow and deformation within a dyke for a range of conditions. In the present paper, we will use both experiments and numerical calculations to investigate mechanisms that provoke the arrest of vertical magma propagation.

One problem in nature is that the boundary conditions of magma supply from a source may vary considerably. When supply is long-lived, a reasonable model approximation may be a constant flux. Traversa et al. (2010) have found that, in some cases, the rate of induced seismicity remains constant as magma rises towards Earth’s surface, suggesting a steady input of magma from the source. Alternatively, supply may be cut off well before magma has reached the surface, in which case, one must consider a dyke of fixed volume, and the details of establishing the fracture are secondary. In this paper, we refer to laboratory experiments, which are described in Taisne and Tait (2009), on the propagation of cracks filled with a fixed volume of buoyant liquid in a homogeneous gelatine host. We find that 3-D hydraulic fractures driven by buoyancy may only rise over a finite distance and hence may not feed an eruption if they come from a deep source. An eruption may also be prevented by a low density horizon which impedes magma ascent. This situation is investigated with a numerical model of dyke ascent through a density stratified medium in 2-D (Taisne and Jaupart 2009).

In this paper, we recapitulate the main results from earlier studies (Taisne and Tait 2009; Taisne and Jaupart 2009) and evaluate the conditions for an eruption to occur. We present new laboratory results as well as a new analysis of the behaviour of cracks with a finite magma volume with and without a density interface. We find that, depending on the magma volume and the thickness of low density rocks in the upper crust, the magma-filled fracture may stall at depth as a vertical dyke or a horizontal sill. The numerical model relies on a 2-D formulation and we discuss the implied limitations. This study emphasizes that dyke behaviour is controlled in large part by conditions at the source and in particular by the breadth of the source in the horizontal direction.

Ascent of a fixed magma volume in 3-D: laboratory experiments

For practical reasons, we have studied the downward propagation of a dense liquid through a lighter elastic-brittle medium made of gelatin. A fixed volume was injected in a small pre-existing cut at the top of a large tank. The initial cut was deep enough to be unstable, such that the buoyancy force was sufficient to induce fracturing at the tip (see Taisne and Tait 2009 for details). We took special care to ensure that crack propagation and arrest were not affected by the finite size of the tank. The crack breadth was less than 1/3 of the tank width in all experiments and was typically much smaller. Taisne and Tait (2009) showed that the dimensions of all the experimental cracks could be collapsed onto dimensionless curves independently of the ratio between crack breadth and tank width. By design, the experiments were focussed on cracks issuing from a source of small breadth B _o in the horizontal direction, such that the crack extended both horizontally and vertically. We return to the issue of the initial source breadth at the end of the section.

General features of crack propagation

We have identified different phases of crack propagation from our experimental data. An initial phase is associated with the filling of the pre-existing cut with a known volume of liquid, which depends on the injection technique and hence is not of interest for geological applications. In a first propagation phase, the crack grows larger in both breadth and length, maintaining an approximately circular shape. In a second phase, the crack maintains a constant breadth and extends only in the vertical direction with a parabola-shaped nose region. The final phase sees a rapid decrease of velocity and the arrest of propagation. As already discussed in Taisne and Tait (2009), we did not observe fractures that progagate at a constant velocity, in contrast to earlier studies (Takada 1990; Heimpel and Olson 1994; Dahm 2000). In these studies, the experimental fractures adopted a steady-state shape and rose through the solid through rupture at the tip and closure at the tail. Working fluids were hydrophobic liquids that are unable to wet thin tail regions, such that surface tension acts to retract fluid into the crack at the inlet. We reproduced the same behaviour in a series of experiments with oil (Taisne and Tait 2009), but this is not relevant to geological cases. We therefore focus on fluids that are miscible in water and wet the gelatin surface, so that the crack remains connected to the inlet at all times through a thin tail region.

The different propagation phases can be identified in a plot of crack length l as a function of time (Fig. 1). Measurements conform to power-law relationships as a function of time in the first and second propagation phases with exponents of 1/5 and 1/3, respectively. We later propose simple scaling arguments to support these values. We also determined the thickness of fluid in the crack through a light absorption technique (Fig. 2). This technique is based on the attenuation of transmitted light at wavelengths that are absorbed by the liquid within the crack. The attenuation to thickness conversion was derived from the Beer–Lambert law and the volume constraint. As shown in Fig. 2, propagation is characterized by continuous thinning of the nose region because of loss of liquid to the growing tail region. We found that, during the first propagation phase, most of the fluid is confined to a penny-shaped region at the tip that segues into a thin tail region that gets narrower towards the inlet. In the second and third phases, the crack maintains an approximately constant maximum breadth (within measurement error) and tends towards a blade-shape fracture elongated in the vertical direction. Such changes of shape constitute a challenge for scaling analyses that typically rely on self-similarity.

Fig. 1

Length of buoyancy-driven experimental fractures in gelatin as a function of time. Dashed lines show power-law relationships with exponents of 1/5 and 1/3 that are predicted by simple scaling arguments (Eqs. 6 and 8)

Fig. 2

Downward propagation for a crack filled with dense viscous liquid in gelatin. Top images: raw photographs with no vertical exaggeration at different times (in minutes). For each photograph, the field of view is limited to the crack and omits the much larger expanse of gelatin in the tank. Bottom images: maps of liquid thickness deduced from light absorption. The maximum liquid thickness δ _M is indicated below each photograph. Note that the crack thins as it extends in the vertical direction. Note also the penny-shaped nose region at early times

Scaling analysis: propagation

In all the experiments, propagation is driven by buoyancy and resisted by forces associated with fracturing at the tip, elastic deformation and viscous flow through the thin crack aperture. We introduce scales for the crack length in the vertical direction, noted L, crack breadth in the horizontal direction, noted B, and thickness of fluid within the crack, noted δ. The relevant physical properties are the fracture toughness K _c and shear modulus G of the host solid on the one hand, and the buoyancy Δρ and viscosity μ of the liquid on the other hand.

It is convenient to evaluate the different processes through their respective pressure scales (Lister 1990a; Lister and Kerr 1991). Thus, buoyancy is associated with pressure scale ΔP _b :

$$ \Delta P_b = \Delta \rho g L \, . \label{eq:Pb} $$

(1)

During propagation, this pressure may be balanced by the normal stress required to open the crack, which can be scaled as follows in an elastic deformation regime:

$$ \Delta P_e \sim \frac{G}{1 - \nu} \frac{\delta}{\min[L,B]} \, . \label{eq:Pe} $$

(2)

where we specify that the thickness of fluid is controlled by the smallest fracture dimension. Buoyancy can also be balanced by viscous stresses due to flow through the aperture of width δ, which scale with:

$$ \Delta P_v \sim \frac{\mu H U}{\delta^2} \, , $$

(3)

where H can be either L or B depending on the flow direction and U is the corresponding velocity scale. We further write that U ∼ dH/dt ∼ H/t, so that:

$$ \Delta P_v \sim \frac{\mu H^2}{\delta^2 t} \, . \label{eq:Pv} $$

(4)

We add that the total volume in the fracture is constant and equal to the liquid volume V, such that V ∼ B L δ.

In the first phase of propagation, crack growth in the horizontal direction is driven by a lateral pressure gradient, which is itself due to the liquid overpressure, so that:

$$ \frac{\mu B^2}{\delta^2 t} \sim \Delta \rho g L \, . $$

(5)

In this phase, we observe that B ∼ L. Eliminating δ using the volume equation, we find that:

$$ L \sim \left( \frac{\Delta \rho g V^2}{\mu} t \right)^{1/5} \, \, \, \mathrm{for \, phase \, \, 1} \, . \label{eq:phase2_1} $$

(6)

This is consistent with our measurements (Fig. 1). In the second propagation phase, the crack breadth B no longer increases and stabilizes at some value B _f and the crack extends only in the vertical direction. In this case, the balance between buoyancy and viscous forces is written as:

$$ \frac{\mu L^2}{\delta^2 t} \sim \Delta \rho g L \, . $$

(7)

Eliminating δ again, we find that:

$$ L\sim \left( \frac{\Delta \rho g V^2}{4\mu B_f^2} t \right)^{1/3} \, \, \, \mathrm{for \, phase \, \, 2} \, , \label{eq:phase2_2} $$

(8)

which is also consistent with the experimental data (Fig. 1).

Scaling analysis: fracture dimensions

It would be useful to derive an equation for the shape of the nose region and for the liquid volume within it. Simple arguments proved ineffective, however, and indicate the fundamentally 3-D character of the deformation. For example, one could argue that, for a crack that is elongated in the vertical direction, one can use a local 2-D analysis in the horizontal plane at height z above source, such that the fracture thickness is due to the local magma overpressure ΔP acting on a horizontal crack of breadth B. In this framework, the largest fracture breadth is such that the stress intensity factor at the lateral tips is just below the fracture toughness of the host, noted K _c , so that $\Delta P B^{1/2} \sim K_c$. At a fixed distance z from the source, the magma overpressure is largest when the crack nose goes through this location and decreases as the crack moves past it (Lister 1990a). This explains why the fracture breadth does not extend further as the dyke continues to rise. In the local horizontal 2-D approximation, one could write that the local overpressure is set by hydrostatics, such that ΔP ∼ Δρ g z. Thus, the criterion for marginal fracturing is written as $\Delta \rho g z B^{1/2} \sim K_c$, which specifies B as a function of z. This may serve to explain why the crack breadth decreases towards the crack tip but it provides a poor fit to the experimental data. One reason is that we have neglected curvature of the lateral edges of the crack, which invalidates the local 2-D approximation. The other reason is that we have not accounted for viscous stresses due to flow.

Due to the lack of a comprehensive physical model of fracturing in 3-D, we resort to simple scaling arguments and refer to the final static crack configuration. In this case, there is no flow, so that viscous forces need not be accounted for and the internal pressure distribution is hydrostatic, such that ΔP(z) = Δρ g z. Within the framework of linear elastic fracture mechanics, the stress intensity factor at the edges of a crack, K, is equal to the fracture toughness of the host medium during crack propagation. Fracturing is not possible if K < K _c so that, by continuity, the final crack configuration when flow stops is such that K = K _c . Theoretical calculations of the stress intensity factor are available for penny-shaped cracks in an infinite solid and two-dimensional fractures (Sneddon and Das 1971; Lawn 1993; Zhou et al. 2005), but not for the crack shapes of the present experiments. The stress intensity factor at the leading edge of the crack is K = γΔρg L ^3/2 , where γ is a coefficient which depends on the shape of the crack. We assume that, for all our experiments, the crack shape depends on a single parameter, the aspect ratio L/B, where L is the crack length. Theory for a two-dimensional crack with a linear internal pressure variation shows that $\gamma = \gamma_o = \sqrt{\pi}/2$ (Sneddon and Das 1971). For an edge crack (as opposed to a crack in an infinite medium), one must add a correction factor of 1.12 (Lawn 1993). This specifies the asymptotic value of γ in the limit of L/B →0. Starting from a crack with some initial aspect ratio, extension in the vertical direction implies an increase of the buoyancy force acting on the crack. The criterion that K = K _c thus implies that γ must decrease with increasing aspect ratio. Such behaviour is well established for fractures in an infinite medium. In this case, one finds indeed that, for uniform internal loading, $\gamma = \sqrt{\pi}$ for a 2-D crack (L/B → 0) and $\gamma = 2/\sqrt{\pi}$ for a penny-shaped one (L/B = 1) (Lawn 1993).

According to above arguments, the final crack length L _f is such that:

$$ \label{eq:ScalL} K_c = \gamma \Delta \rho g L_f^{3/2} \, . $$

(9)

where γ, the shape coefficient, depends on the aspect ratio, L _f /B _f . We have determined the value of this coefficient for many different experiments involving liquids with different densities and solids with different elastic properties. Figure 3 shows how γ varies as a function of the final crack aspect ratio. Note that, within experimental uncertainty, all the data can be collapsed onto a single curve independently of the material properties and the liquid volumes. We find that this coefficient is always less than for a 2-D fracture, as expected. γ decreases with increasing values of L _f /B _f and does not vary significantly for values of L _f /B _f that are larger than 4.

Fig. 3

Geometrical shape factor γ for the stress intensity factor of experimental cracks in gelatin as a function of the crack aspect ratio, L _f /B _f . In the limit of L _f /B _f →0, one retrieves the 2-D crack theory, such that $\gamma_o =1.12\ \sqrt{\pi}/2$, which is indicated by the thick bar at the left of the plot. The dashed curve was drawn through the data for illustration purposes

At this stage, it is interesting to digress on 2-D cracks briefly. Within the same theoretical framework, a 2-D crack cannot stop once it is initiated. For such a crack to start propagating, it must extend over length L _i such that $\gamma_o \Delta \rho g L_i^{3/2} \ge K_c$. As this crack propagates in the vertical direction, the buoyancy force continuously increases and the stress intensity factor also keeps on increasing, so that fracturing cannot cease. For a 2-D crack with a finite fluid volume, one can use the same dynamical balance as before in the thin liquid-filled sheet below the tip. Combining Eqs. 1 and 4, with H = L and δ = V _2D /L, where V _2D is now the volume per unit breadth of the crack, we obtain:

$$ L\sim \left( \frac{\Delta \rho g V_{2D}^2}{\mu}t \right)^{1/3}\, . $$

(10)

This is verified by theory and numerical calculations (Roper and Lister 2007). For a 2-D crack in the laboratory, arrest will occur when the liquid region is so thin that short-range molecular forces take over. In geological cases, however, the limiting mechanism is likely to be magma solidification.

To obtain a scale for B _f , we focus on the first propagation phase because it is in this phase that the crack achieves its final breadth. In this phase, the crack aspect ratio remains close to 1 and most of the liquid volume is in a penny-shaped region that grows in both the horizontal and vertical dimensions such that L ∼ B. A balance between elastic and buoyancy forces leads to the following equation for the liquid thickness:

$$ \frac{G}{1-\nu}\frac{\delta}{B_f}\sim \Delta \rho g B_f \, . $$

(11)

Using $V\sim \delta B_f^2$, we find that:

$$ B_f\sim \left( \frac{GV}{(1-\nu)\Delta \rho g}\right)^{1/4} \, , \label{eq:ScalB} $$

(12)

which is in reasonable agreement with the experimental data (Fig. 4). The experimental data indicate that the proportionality constant in this relation is ≈ 1.5.

Fig. 4

Measurements of the final fracture breadth as a function of values predicted by a simple balance between buoyancy and elastic stresses in a penny-shaped crack, which is appropriate for the first propagation phase (Eq. 12)

The final crack must be such that it is stable, which requires that the stress intensity factor is just equal to the host toughness, and also such that it contains the liquid volume V, which is achieved by elastic deformation of the host. For a crack elongated in the vertical direction, we may expect that the liquid thickness at height z is δ ∼ Δρ g B _f z (1 − ν)/G. Over the whole length of the crack, L _f , this implies that $V \sim \Delta \rho g B_f^2 L_f^2 (1-\nu)/G$. As in the above expression for the crack breadth, this relationship involves a coefficient of proportionality that depends on the crack shape. This coefficient is expected to be of order 1 (one may for example consider a penny-shaped crack and a blade-shaped fissure with a blunt termination). These simple scalings therefore imply that the crack aspect ratio L _f /B _f must also be of order 1. In our experiments, the liquid volume and the elastic modulus of the host were varied by factors of about 30 and 7, respectively (Taisne and Tait 2009), and yet the final crack aspect-ratios were found to be within a rather restricted 2–6 range.

Controls on the final crack dimensions

At this stage, it is worth recapitulating the experimental results. We have found that, for given liquid and elastic host, the final crack breadth increases with the liquid volume available (Eq. 12). Estimating the final crack length must be done in two steps. One may first assume that the final aspect ratio is large, and more specifically larger than about 4, in which case our data indicate that coefficient γ for the stress intensity factor does not vary significantly and is close to a limit value noted γ _∞. In this case, Eq. 9 allows an estimate of L _f independently of volume V. Combining Eqs. 9 and 12, the final aspect ratio is:

$$ \frac{L_f}{B_f}=\left(\frac{K_c}{\gamma_\infty}\right)^{2/3}\left(\frac{1-\nu}{GV}\right)^{1/4}\frac{1}{(\Delta \rho g)^{5/12}}\,. $$

(13)

In this limit, therefore, the final crack aspect ratio decreases with increasing magma volume. It may perhaps be more surprising that the aspect ratio also decreases with increasing buoyancy. One might have expected instead that buoyancy favors the lengthening of the crack in the vertical direction. This result stems from the fact that buoyancy is also responsible for the internal overpressure that opens up the crack. This is why the crack breadth B _f decreases with increasing buoyancy, as shown by Eq. 12. The stress intensity condition also implies that L _f decreases with increasing buoyancy, but the dependence is stronger, so that the end result is that the aspect ratio decreases with increasing magma buoyancy.

The above calculation for the crack aspect ratio becomes invalid for values of the aspect ratio that are smaller than a value of about 4. For smaller values of the aspect ratio, the available data do not allow a precise determination of the final crack length L _f . According the current experimental data, however, the implied uncertainty does not exceed a factor of 2 because the aspect ratio must be within a 2–4 range.

Minimum volume required for an eruption

For a magma source that lies at depth D, we use our experimentally derived scaling laws (Eqs. 12 and 9) to estimate the dimensions and volume of the largest dyke that can stall below Earth’s surface. In the experiments, cracks first go through a phase of lateral growth and tend to a penny-shape with an aspect ratio of about 1. They then extend in the vertical direction and their aspect ratios increase to values that were within a 2–6 range. As discussed in a separate section below, such behaviour is not possible for all values of the initial crack breadth at the magma source.

One condition for the stalling of a dyke below Earth’s surface is that L _f  ≤ D . The maximum stable crack length is:

$$ L_{\rm max} = \left( \frac{K_c}{\gamma_{\infty} \Delta \rho g} \right)^{2/3} $$

(14)

The largest crack that does not allow eruption is thus such that L _max ≈ D. Values of the fracture toughness have been measured on rock samples in the laboratory (Atkinson and Meredith 1987) and deduced from the dimensions of dykes (breadth and thickness) in the field (Delaney and Pollard 1981). The two methods indicate values of about 1 and 100 MPa m^1/2, respectively. This large discrepancy has not been explained, unfortunately, which prevents accurate calculations. Taking values of magma buoyancy in a 10–100 kg m^− 3 range, we deduce that L _max lies in a 700 m – 70 km range depending on the rock toughness, which is not very helpful. Fortunately, a stronger constraint on eruption comes from the magma volume available.

For a given aspect ratio, we can calculate the length of the crack as a function of the magma volume. For given source depth D, eruption can only occur if L _f  ≥ D. We therefore write that the smallest crack that allows eruption is such that:

$$ \frac{D}{B_f} = \frac{L_f}{B_f} $$

(15)

Using α = L _f /B _f and the equation for the crack breadth (Eq. 12), this can be recast as an equation for the minimum volume of magma that allows an eruption:

$$ V_{\rm min} = \left( \frac{D}{\alpha} \right)^4 \frac{(1-\nu) \Delta \rho g}{G} $$

(16)

For the sake of example, we use α = 4. As discussed above, the crack aspect ratio may in fact be smaller than this value, but the factor of 2 change is not significant for the purposes of this discussion. The minimum magma volume that is required for an eruption is shown as a function of source depth D in Fig. 5. For an upper crustal source (a magma reservoir, for example) at depths between 5 and 10 km, say, eruption requires magma volumes that are larger than about 10⁵ m³. This may be compared to the eruption record at Piton de la Fournaise volcano, Reunion Island. Peltier et al. (2009) have summarized volume data for 65 eruptions and found that the smallest volume erupted in one eruption is 6 10⁴ m³. The volume is even smaller (2 10⁴ m³) if we consider independently individual eruption phases. Eight eruptions emitted less than 5 10⁵ m³.

Fig. 5

Relationship between the volume of magma and the vertical length of a buoyancy-driven crack that stalls beneath Earth’s surface (values for the physical properties are listed in Table 1). This relationship can be understood as the minimum magma volume that is required for an eruption as a function of the depth of the magma source. The two curves were drawn for the two extreme values of ratio Δρ g /G that are indicated

The breadth of the magma source

We have found that the successful propagation of a dyke to the surface requires that the magma volume exceeds a threshold value. This result is only valid for cracks that initially expand in both the horizontal and vertical directions into a penny-shape, as in the experiments. For a given magma volume V, this requires that the initial crack breadth at the source, noted B _o , is smaller than the value of B _f from Eq. 12. For a given source depth D, this also requires that B _o  ≤ D. If these conditions are not met, the scalings are not valid and the crack aspect ratio is likely to remain smaller than 1 during ascent. In this case, lateral extension has a limited impact on crack propagation and it is reasonable to use the 2-D approximation.

In the 2-D limit, we have already seen that propagation cannot stop if the initial crack is unstable. Thus, the threshold magma volume for eruption corresponds to that of the largest stable crack at the source. The length of such a crack, L _o , is such that $\gamma_o \Delta \rho L_o^{3/2} = K_c$ and the thickness of liquid within it is $\delta_o \sim \Delta \rho g L_o^2 (1-\nu)/G$. If the initial crack breadth is B _o , the threshold volume is therefore V _min = C _o B _o L _o δ _o , where C _o is some proportionality coefficient of order 1. We can turn this argument around and start with a given magma volume V. In this case, the initial crack breadth must be smaller than B _max = V/(C _o L _o δ _o ) for propagation to occur. All these arguments rely on a 2-D configuration and require that B _o  ≫ L _o .

These arguments emphasize the importance of conditions at the source: dyke behaviour depends not only on the history of magma input but also on the horizontal extent of the source. To illustrate the quantitative aspects of this issue, we use data from Table 1 and calculate typical values for the variables, which must be regarded as order of magnitude estimates only. For a 10 km source depth and a crack that stalls beneath Earth’s surface, B _f  ≈ 1 km. This suggests a critical value for the initial crack breadth B _o of about 1 km, such that 3-D effects are dominant for smaller cracks. Furthermore, L _o  ≈ 1 km and δ _o  ≈ 1 m. Thus, a magma volume of 10⁵ m³ can be stored in a stable crack at the source with B _o  = 1 km and L ≈ 500 m. If B _o  < ≈ 500 m, such a magma volume cannot be maintained in the source region and the initial crack must propagate upwards.

Table 1 Value of the physical properties used for calculations

Arrest due to a buoyancy inversion in an upper crustal horizon

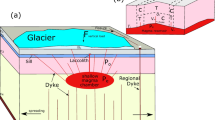
The experimental results and analysis of the previous sections tell us that a constant magma volume may stall before reaching the surface unless that volume is greater than a threshold value. However, even if the amount of magma available does surpass this threshold, an eruption might still be prevented if a low density crustal layer lies in the path of the dyke. In this section we show by a series of numerical calculations and accompanying analysis that such a layer can be an effective barrier if certain conditions are met. We shall also calculate the maximum volume of magma that can be accumulated at an interface between a lower medium where the magma is positively buoyant, and an upper medium where the magma becomes negatively buoyant. Depending on the depth of the interface, magma volumes that are larger than this threshold value allow the intrusion of a sill or eruption at Earth’s surface.

Governing equations

We recapitulate briefly the main steps in the calculation of dyke ascent and refer the reader to Taisne and Jaupart (2009) for further details. We treat the opening of a fracture in 2-D, with vertical coordinate z positive upwards (z = 0 at Earth’s surface) and we neglect atmospheric pressure. The lithostatic pressure in encasing rocks of density ρ _s is P _Lith = − ρ _s g z. Within the magma, pressure P may be decomposed into an overpressure P _e , which drives deformation of the fracture walls, and a lithostatic component:

$$ P = P_{\rm Lith} + P_e \, . $$

(17)

We assume that magma behaves as an incompressible fluid with density ρ _m and viscosity μ. For a thin and vertical fracture of half-width h, flow occurs at small Reynolds number and one can use lubrication theory, which leads to the following equation for the vertical flux of magma (Lister 1990a; Lister and Kerr 1991):

$$ \phi=-\frac{2}{3\mu}h^3\left(\frac{\partial P_e}{\partial z}-\Delta \rho g \right) \, , \label{eq:phi_dim} $$

(18)

where Δρ = ρ _s  − ρ _m is the magma buoyancy. Volume conservation (equivalent to mass conservation for the incompressible fluid) is written as:

$$ 2\frac{\partial h}{\partial t} = -\frac{\partial \phi}{\partial z} \, . \label{eq:cons_vol} $$

(19)

For a dike extending from a distant source (z→ − ∞) to a tip located at z = z _f , h and P _e are related to one another through the following equation (Muskhelishvili 1953; Weertman 1971; Spence et al. 1987):

$$ h(z) = \frac{1-\nu}{G}\frac{1}{\pi}\int_{-\infty}^{z_f} k(z_f,z,\xi) P_e(\xi)d\xi \, , \label{eq:h_pe} $$

(20)

where G is the shear modulus and ν is Poisson’s ratio and kernel k(z _f , z, ξ) is such that:

$$ k(z_f,z,\xi)=\ln\left|\frac{\sqrt{z_f-z}+\sqrt{z_f-\xi}}{\sqrt{z_f-z}-\sqrt{z_f-\xi}}\right| \, . \label{eq:kern_pe} $$

(21)

Ahead of the dike tip, the normal elastic stress has a singularity related to the stress intensity factor, such that:

$$ P_e(z) \sim -\frac{K}{2\sqrt{z - z_f}} \, \, \, , \mathrm{for } \, z > z_f \, . $$

(22)

For a propagating dike, the stress intensity factor is set equal to the fracture toughness. This specifies the shape of the dike near the tip (Muskhelishvili 1953; Weertman 1971):

$$ h \sim \frac{1-\nu}{G}K_c\sqrt{2(z_f-z)} \, \, \, , \mathrm{for } \, \, z \to z_f \, . \label{eq:h_tip} $$

(23)

These equations have been integrated numerically and were checked carefully against the analytical solutions of Lister and Kerr (1991).

Dimensional analysis

We consider that magma is fed into the dike at a constant volumetric flux Q (in the present 2-D framework, we refer to a volumetric rate per unit fissure breadth, expressed in units of m³ s^− 1m^− 1, i.e. m² s^− 1). Far from the tip, the dominant force balance in the thin tail region is between magma buoyancy and viscous head loss. This defines scale h ^* for the dike half width (Lister and Kerr 1991):

$$ h^* = \left[ \frac{3\mu Q}{2 \Delta \rho g} \right ]^{1/3} \, . \label{eq:hc} $$

(24)

This argument also leads to a velocity scale:

$$ c^* = \frac{Q}{2h^*} \, . $$

(25)

As shown by Lister and Kerr (1991) the dominant dynamical balance in the nose region is between buoyancy and the magma overpressure driving elastic deformation (see also Appendix A of Taisne and Jaupart (2009)). This introduces length scale L ^*, such that buoyancy applied over L ^* acts to open a fracture of width h ^*:

$$ \Delta \rho g L^* = \Delta P^*= \frac{G}{1-\nu}\frac{h^*}{L^*} \, , \label{eq:pc} $$

(26)

which defines pressure scale ΔP ^*. Solving for L ^* yields:

$$ \begin{array}{rll} L^*&=&\left[ \frac{G h^*}{(1-\nu)(\rho_s-\rho_m)g} \right]^{1/2} \nonumber\\ &=& \left(\frac{3 \mu Q}{2}\right)^{1/6}\left(\frac{G}{1-\nu}\right)^{1/2}\left(\Delta \rho g\right)^{-2/3} \, . \label{eq:lc} \end{array}$$

(27)

Combining these pressure and length scales (Eqs. 26 and 27), one obtains a scale for the stress intensity factor, Lister and Kerr (1991):

$$ K^* = \Delta P^*\sqrt{L^*} = \Delta \rho g \left( L^* \right)^{3/2} \, . \label{eq:Kstar} $$

(28)

In dimensionless form, solutions depend on the dimensionless toughness, $K_c/K^*$. As shown by Lister (1990b), Lister and Kerr (1991) and Taisne and Jaupart (2009), the dimensionless fracture toughness takes small values in geological conditions and has little influence on the dyke characteristics. Numerical results were therefore obtained in this limit and will be presented in dimensionless form, such that the dyke length and width are scaled by L ^* and h ^*, respectively.

Dyke penetration through a low density layer

Here, we describe how a dike rises through a two-layer system involving two different densities. In the lower part, magma is buoyant with density contrast Δρ _o . In the upper layer, the density of the host rock is smaller than that of the magma and the buoyancy force becomes negative. The upper crustal environment is likely to be stratified and dyke ascent may be affected by the thicknesses of individual strata, as discussed extensively by Taisne and Jaupart (2009). For example, vertical propagation can resume at a normal pace once the dyke has gone through a thin low density horizon. We shall assume here that the low density layer extends to the surface, so that the final phase of vertical propagation occurs with a negative buoyancy at all times. In a stratified upper crust, the upper layer density may be calculated as an average of the various density values weighted by stratum thickness.

Calculations show that the dike rises past the base of the low density layer, even though its upper part is no longer buoyant, because buoyancy in the lower layer continues to drive the flow of magma. Due to the negative buoyancy, dyke propagation slows down and the nose region swells markedly as it continues to be fed from below (Fig. 6).

Fig. 6

A dike penetrating into a layer with negative buoyancy (Δt _1 − 2 = Δt _2 − 3 = Δt _3 − 4 = 14.364). The base of the low density layer lies at z = z _inter. Note that the dike is able to overshoot the interface and that it swells markedly due to the sustained input of magma from below

The numerical results can be accounted for by simple physical arguments that can be used for arbitrary density values. For illustration purposes, we first consider that the density contrast just changes sign at the interface between the two layers, i.e. Δρ ₊ = − Δρ _o .

The inflated nose region extends over a total length L, and over lengths L _m and L _p below and above the interface, respectively, such that L = L _m  + L _p . In this region, the viscous head loss rapidly becomes negligible, so that the magma overpressure and the deformation characteristics can be determined by a local hydrostatic balance (Taisne and Jaupart 2009). This allows straightforward calculations of the propagation rate and nose dimensions. To proceed further, we use the fact that the nose region is fed from below at rate Q. We can also relate the dike maximum width (h _M ) to the magma overpressure at the interface:

$$ G \frac{h_M}{L} \sim \Delta \rho_o g L_m \sim | \Delta \rho_+ | g L_p \ . \label{eq:Pe_Pbm_Pbp} $$

(29)

We thus obtain:

$$ V = Q (t-t_o) \propto h_ML_p\left(1+\left| \frac{\Delta \rho_+}{\Delta \rho_o} \right| \right) \, , \label{eq:volp} $$

(30)

$$ G \frac{h_M}{L_p\left(1+\left| \frac{\Delta \rho_+}{\Delta \rho_o} \right| \right)}\sim | \Delta \rho_+ | g L_p \, , \label{eq:Pep_Pbp} $$

(31)

so that:

$$ L_p\sim \left[\frac{Q G}{|\Delta \rho_+| g}\frac{1}{\left(1+\frac{|\Delta \rho_+|}{\Delta \rho_o}\right)^2} (t-t_o)\right]^{1/3} \, , \label{eq:l_DRG_neg} $$

(32)

or,

$$ \frac{d L_p}{dt}\sim \frac{1}{3}\frac{Q G}{|\Delta \rho_+| g}\frac{1}{\left(1+\frac{|\Delta \rho_+|}{\Delta \rho_o}\right)^2} L_p^{-2} \, . \label{eq:dldt_l} $$

(33)

Numerical results tend towards these predictions (Figs. 7 and 8). The calculations show that the dike penetrates well above the interface, driven by the buoyancy of the lower half of the nose region below the interface. Magma buoyancy in the long and thin tail region is balanced by viscous stresses and hence does not contribute to the driving force for country rock deformation in the vicinity of the interface.

Fig. 7

Vertical extents of the upper and lower parts of the nose region of a dike that penetrates into a layer with negative buoyancy, as a function of time (in dimensionless values). For these calculations, buoyancy changes sign at the interface, such that Δρ ₊ = − Δρ _o . Both lengths tend to the limit values predicted by a simple local hydrostatic balance in the inflated nose region of the dyke (Eq. 29)

Fig. 8

Velocity of a dike penetrating into a layer with negative buoyancy, as a function of distance above the interface. The dashed line has a slope of −2 and stands for the prediction of a simple hydrostatic model for the nose region (Eq. 33)

As the pressure builds up at the interface a threshold value can be exceeded such that the walls of the dyke in the nose region rupture and induce the intrusion of a horizontal magma sheet. In this case, magma propagation will switch to the horizontal direction and proceed at the interface in the form of a sill (Taisne and Jaupart 2009). Two other outcomes are possible depending on the breadth of the dyke and on the cohesion of the host rock. The former involves 3-D effects on propagation and discussion is postponed to a separate section below. The latter outcome is due to stresses at the dyke walls becoming greater that cohesive forces in the encasing rocks. In this case, faulting occurs in a graben-like structure, which induces magma storage at shallow depth. Eruption is prevented by the deviation of the dyke trajectory rather than by an arrest of vertical propagation. Such effects have been studied numerically by Agnon and Lyakhovsky (1995) and have been documented in the Inyo volcanic chain, California (Mastin and Pollard 1988). As illustrated by the laboratory experiments of Mastin and Pollard (1988), such faulting occurs when the dyke tip is close to the surface, and hence is not relevant to dykes that are confined to the vicinity of a deep density interface, as studied here.

Minimum volume for sill inception or eruption

Considering a single pulse of magma accumulating at a density interface, we may estimate the minimum volume of magma required for either an eruption or a horizontal intrusion in the form of a sill. To estimate the volume, we take a hydrostatic pressure distribution within the fissure (Fig. 9) and use Eqs. 20 and 21. We consider that the swollen nose region ruptures when the hoop stress at the walls exceeds a threshold value, which occurs when the magma overpressure reaches a critical value noted ΔP _c . Using the above equations for the nose dimensions, we deduce that the critical length of dyke penetration that must be achieved for sill inception is:

$$ L_c = \frac{\Delta P_c}{\left| \Delta \rho_+ \right| g} \, . $$

(34)

Fig. 9

Schematic diagram illustrating the method used for calculating the volume of magma that accumulates at a density interface

Two different situations arise depending on the thickness of the low-density upper layer, noted D (Fig. 10). If D > L _c , no eruption is possible but there are two possible outcomes depending on the maximum magma overpressure that is reached. For small magma volumes, the overpressure is lower than the strength of encasing rocks and no sill is generated: storage occurs in a dyke configuration. For large magma volumes, the magma pressure is sufficiently large to induce a sill. On the other hand, if D < L _c , the magma overpressure cannot reach the rupture threshold and no sill can be generated. In this case, we may observe an eruption if there is enough magma in the crack.

Fig. 10

Behaviour of a finite amount of magma at a negative buoyancy interface depending on the depth of the interface, D. The interface is indicated by the horizontal dashed line. Left hand panel: shallow interface at a depth that is less than the penetration length of a dyke (D < L _c ). No sill can be generated in this case. If the magma volume is smaller than a critical value, the dyke stalls beneath Earth’s surface and no eruption is possible. Right hand panel: deep interface at a depth that is larger than the penetration length (D > L _c ). In this case, no eruption is possible regardless of the magma volume. A sill can be generated if the volume of magma is sufficiently large

Using these results, we can calculate the penetration length as a function of the magma volume, and hence also the magma overpressure, and evaluate the different possibilities in geological settings. We fix values of elastic modulus of G = 10¹⁰ Pa and Poisson’s ration ν = 0.25 as well as the critical overpressure for wall rupture $\Delta P_c = 5 \times 10^6$ Pa (Table 1). We distinguish between two cases, depending on the depth of the interface.

Deep interface: minimum magma volume for sill inception

In this case, eruption is not possible independently of the magma volume available. Depending on the magma volume, magma gets stored in either a dyke or a sill configuration. Figure 11 shows the relationship between the magma overpressure at the base of a density interface as a function of magma volume. Specifying the rupture threshold at some value (taken here to be 5 × 10⁶ Pa), we obtain the minimum magma volume that is required for the formation of a sill. For such 2-D calculations, the volumes are expressed per unit fracture breadth. For a representative dyke breadth of 10 km, minimum magma volumes are in a 10⁷ − 10⁸ m³ range. Note that these volumes are larger than those of a crack that stalls because of its finite volume. Results are illustrated for a large range of density contrasts in Fig. 12 (top panel).

Fig. 11

Internal overpressure as a function of the volume of the nose region of a dyke at a density interface. Calculations were made for $\left| \Delta \rho_+ \right| = 300$ kg m^− 3 and two different values for the density contrast in the lower medium Δρ _o  = 100 and 300 kg m^− 3. Other physical properties are given in the Table. The horizontal dotted line corresponds to the critical value of the magma overpressure for sill inception

Fig. 12

Top panel: minimum volume needed for a sill as a function of the thickness of low density rocks and density contrast between magma and host. Due to the negative buoyancy of magma, a dyke can only penetrate over a finite distance before reaching the rupture threshold for intrusion of a horizontal magma sheet. The blank region on the left is such that the interface is not deep enough to allow sufficient pressure build-up within the dyke. The two black horizontal lines correspond to volumes of 10⁴ and 10⁵ m³/m. Bottom panel: minimum magma volume for an eruption. The blank region on the right is such that the dense basement is too deep for the dyke to extend to the surface. Calculation for a value Δρ _o  = 100 kg m^− 3 of magma buoyancy below the interface. Black curves correspond to 10^− 4, 10^− 2, 10⁰, 10², and 10⁴ m³/m

The overpressure at the interface is specified and hence we can also estimate the thickness of the horizontal intrusion that develops as a function of its lateral extent. For a sill that extends over a few kilometers, we find that a thickness of a few meters.

Shallow interface: minimum magma volume for an eruption

If D < L _c , sill formation cannot occur and an eruption is possible if the magma volume is sufficiently large (calculated per unit dyke breadth). Figure 12 (bottom panel) shows how the minimum magma volume varies as a function of the depth to the interface and density contrast between magma and host rock. If the magma volume is smaller than this minimum value, storage occurs in a dyke configuration.

Limitations of the 2-D model

In the real world, dykes have finite breadths and extend in both the horizontal and vertical directions as they rise. A 2-D model is accurate if lateral propagation has a small impact on the mass balance for propagation, such that the horizontal flux of magma is much smaller than the vertical one. This requires that B ≫ L. In a uniform host, this only depends on the initial breadth of the crack in relation to the depth of the source. With a negative buoyancy upper layer, the lateral spreading of magma is enhanced at the base of the layer, as illustrated in the experiments of Lister and Kerr (1991). Vertical propagation also proceeds, however, so that one may still achieve the required overpressure for a horizontal sill. The robust result is the thickness of the low density upper layer that prevents eruption, which is calculated using a hydrostatic balance and hence does not depend on the total magma volume. In contrast, volume estimates that are made in the 2-D approximation are only accurate if the initial crack breadth B _o is large, as discussed previously.

Discussion and conclusions

Our results show how natural magmatic dykes may be stopped in the crust before arriving at the Earth’s surface, depending on the relative magnitudes of buoyancy, fracture toughness and magma volume. These results will be quantitatively modified by thermal effects and changes of buoyancy that occur due to processes such as vesiculation, however these differences will not alter the fundamental prediction that dykes may stall despite a phase of propagation driven by buoyancy. All else being equal, the smaller the volume of magma, the more likely it is that the dyke will stall.

Figure 5 gives the final maximum vertical extension that a dyke can attain given a finite amount of magma. If the value found is smaller than the depth of the source, the magma cannot reach the surface and there is no eruption. The presence of a stratification of density will reinforce this arrest. A dyke cannot penetrate through a low density environment over a distance that is larger than penetration length L _p , regardless of the magma volume. Thus, the penetration length must be greater than the depth of the dense basement for an eruption to occur. On an active volcano, analysis of the eruption record may yield much useful information on both the shallow environment and the volumes of magma that are required for an eruption.

Other mechanisms can affect vertical dyke propagation and prevent eruptions. For example, a compressive stress field in the upper crust, due to either large-scale tectonic forcing or loading by a tall volcanic edifice, acts to impede ascent and to enhance lateral spreading (Pinel and Jaupart 2004). Another possibility is that pre-existing fractures in the host rock act to divert the dyke from its initial trajectory (Baer et al. 1994; Ziv et al. 2000). All these mechanisms get reinforced by the physical effects that have been studied in this paper.

One interesting question that has received scant attention in the literature deals with the lateral extent of the magma source and of the initial fracture that feeds a dyke. This determines whether or not propagation can be treated in the 2-D approximation or requires a 3-D model. As shown in this paper, this issue is not of a purely academic nature and determines the dyke behaviour.