Introduction

Drained lava channels provide an excellent opportunity to complete morphological and numerical analyses of lava flow dynamics and rheology (e.g. Borgia et al. 1983; Kilburn and Guest 1993; Naranjo et al. 1992; Jurado-Chichay and Rowland 1995; Cashman et al. 1999; Harris and Neri 2002). We can, for example, draw on the engineering literature and apply equations that allow constraint of the rheology and velocity of a fluid flowing in a channel of known depth and slope (e.g. Jeffreys 1925; Baloga et al. 1995; Harris and Neri 2002). Dimensional and velocity measurements made at lava channels and flow units also, for example, allow lava rheology, e.g. viscosity and yield strength, to be calculated (e.g. Walker 1967; Hulme 1974; Fink and Zimbelman 1986; Moore 1987; Wadge and Lopes 1991). Such insights increase our ability to understand and model lava flow morphologies, dynamics and emplacement (e.g. Cigolini et al. 1984; Fink and Zimbelman 1986; Lipman and Banks 1987; Ishihara et al. 1990; Wilson and Parfitt 1993; Cashman et al. 1999; Harris and Rowland 2001; Rowland et al. 2003).

To date, most analyses have considered conditions at a fixed point in a lava channel where the channel depth and slope are known and constant (e.g. Walker 1967; Cigolini et al. 1984; Moore 1987; Wadge and Lopes 1991). Here, however, we consider the flow dynamics and rheological regime in a channel that experiences an abrupt change in slope. This builds on work by Heslop et al. (1989) who considered the rheology of lava during banking around sharp bends and Wilson and Parfitt (1993) who modelled the formation of lava ponds at the mouths of channels that experience stagnation as they move from steep to shallow slopes.

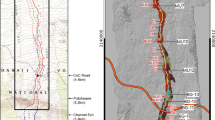
In carrying out our analysis we further develop the preliminary analysis of Woodcock (2003) and consider the fluid dynamics of basalt flowing in a length of channel emplaced on the flank of the Pico Partido cone (Lanzarote, Canary Islands). This channel was emplaced during a series of historical eruptions on Lanzarote that occurred between 1730 and 1736. During this period, over a quarter of the island was covered by lava flows and volcanic cones, where a large part of this area now comprises the Timanfaya National Park (Fig. 1; Scarth and Tanguy 2001; Carracedo and Rodriguez Badiola 1991). Pico Partido is a large volcanic cone that was formed early during this eruptive episode (Carracedo et al. 1992), where the cloven profile of Pico Partido, together with a prominent channel-fed lava flow on its northern flank, make it one of the most distinctive volcanoes on Lanzarote (Fig. 2).

Fig. 1
figure 1

Map of Lanzarote with location of Pico Partido. Area affected by the 1730-1736 eruptions is given in grey

Full size image
Fig. 2
figure 2

Sketch map of the Pico Partido area

Full size image

This paper is primarily concerned with the dynamics of the channelized lava and its behaviour at the break in slope near the channel exit. First, however, it is necessary to describe the morphology of the channel, and to provide an interpretation of the observed features, before modelling the flow dynamics that built these features.

Description of the channelized flow section

Scarth and Tanguy (2001) consider that the flow was sourced by overflow of a lava lake that developed in a small vent immediately to the north of the main edifice, the lower lava lake in Fig. 2. There is evidence that this lake was fed by eruption of lava from the main edifice of Pico Partido, with lava flowing down the steep slope of the cone to accumulate in the lower lake. An additional upper lava lake, sourced by flows moving east from the main edifice, may have overflowed to provide a further source of lava to the lower lake.

The main channel section (Figs. 3 and 4) is approximately 100 m long. It emerges from an upstream lava tube that is ~1 m high and 3 m wide and flows northwards down an 11° slope. The channel is 1–2 m wide with walls that range in height from less than 0.5 m to ~2.0 m. The floor of the channel is now covered with a thin layer of scoria. The location of the lower end of the main section coincides with a marked break of slope. At this point, the slope decreases to ~6° and the flow widens considerably to become somewhat dispersed, lacking the well-defined channel of the upper section. After a further 30 m, the slope increases again and the flow becomes channellized once more for a short section before roofing over and eventually running out into an 'a'a flow field.

Fig. 3
figure 3

View down channel towards break in slope. View shows examples of sheets of pahoehoe over-flow, drain-back veneers and superelevation at a bend. Length of hammer is 280 mm

Full size image
Fig. 4
figure 4

View west across channel from the slopes of a scoria cone immediately to the east. The smooth sheets of pahoehoe over-flow, the sinuous nature of the channel and superelevation at several bends are clearly visible

Full size image

The channel outer banks and inner walls reveal over-flow, drain-back and high-stand features, indicating that flow levels in the channel were highly variable. Over-flow units have a smooth pahoehoe surface (Fig. 3) and were no doubt emplaced as sheet flow during periods when high-volume flux pulses overwhelmed the channel to cause over-bank flow. At the end of such a pulse, the volume flux could once more be accommodated within the channel, starving the over-bank sheet flow of supply and causing near-channel lava to flow back into the channel. Back-flow into the channel built drain-back features marked by smooth pahoehoe veneers draping the banks and dipping into the channel (Fig. 3). This is in contrast to pahoehoe sheets emplaced on the outer-banks during over-flow that dip away from the channel.

A period during which the flow surface within the channel remains at a constant level results in the construction of subhorizontal benches, in this case protruding outwards into the channel by a few centimetres (Fig. 5). These mark stable flow levels where pasty lava rolling along the slow moving flow margin becomes annealed to the bank to form a train of blebs aligned down flow, both level with and parallel to the flow surface. Further decreases in flow level leaves the construct as a hanging, bulbous protrusion marking a former high stand. At least 11 such stands are evident in Fig. 5, suggesting that flow in the channel waned somewhat sporadically; the flow level decreasing suddenly by a few centimetres to become stable at a new lower level before declining again.

Fig. 5
figure 5

Details of the outside (superelevated) wall of the upper bend. Flow direction was to the left, with hammer for scale (length = 280 mm). Subhorizontal benches are apparent marking levels at which flow was relatively stable for a period of time. Counting the undrained flow on the floor of the channel and the top-most unit (the overflow unit that veneers the channel rim) these provide evidence for at least 11 flow levels. Benches bound subvertical driblet ridges

Full size image

Sudden decreases in the flow level, due to decreases in the volume flux or removal of a down-flow blockage to drain backed-up volume, are also revealed by subvertical drain-back ridges on the channel inner walls (Fig. 5). The drain-back ridges are comprised of subvertical driblet trains orientated at an angle of 20–30° from the original flow surface and pointing down-flow. The ridges are a few centimetres high and wide, and show a bulbous-to-rough form, but are covered by a smooth glaze (Fig. 5). These ridges were formed during sudden decreases in flow level, by a few centimetres to a few tens of centimetres, such that pasty, molten lava was left veneered to the channel wall. Drooling of this veneer back into the flowing lava resulted in ridge construction. On encountering the moving flow surface, the driblet would be dragged down-channel to give the down-flow pointing direction.

The drain-back driblet ridges could also be formed by bank melting to cause melted material to dribble downwards into the flow. However, that each ridge is bounded by an upper and lower high-stand bench suggests that they were formed by the drain back of lava that was left veneered to the bank when the flow level dropped from the height marked by the higher bench to that marked by the lower bench (Fig. 5). This, along with the overflow units, indicates that flow in the channel was not steady. The series of benches and driblet train features apparent in Fig. 5, for example, indicate that termination of flow was not sudden, but instead was represented by a phase of waning flow during which supply declined sporadically rather than steadily.

In addition, there has been no remelting or erosion of the driblet features. This can be used to make the following inferences. First, radiative heat loss from the flowing channel surface was insufficient to destroy the features by melting, implying that the surface was either heavily crusted or that flow was not maintained for a sufficient amount of time to heat the walls to melting temperature. Second, all driblets must reflect the final rise-and-fall event. If, for example, the flow surface rose and fell between the lowest level and bank rim on multiple occasions, each event would destroy/cover the previous event, over-plastering the previous features with a new veneer of lava. Thus, each set of features must mark the last time that lava attained the given level, and may not record all level-change events.

One striking feature of the lava channel is the difference in height between the inner and outer banks of the channel wherever the lava has flowed around a bend (Figs. 3 and 4). In all cases, the lava has banked up against the outside bend so that accretion of lava to the bank rim is greatest on the outside bank. This causes preferential construction of the outer bank to result in an asymmetric profile with a higher outer bank. This superelevation effect provides a means by which the velocity and rheology of the lava flowing in the channel may be estimated (Heslop et al. 1989). The superelevation in the Pico Partido channel is, however, not mentioned by Scarth and Tanguy (2001) or by Carracedo and Rodriguez Badiola (1991); in fact the only reference to it found to date appears in a Spanish field guide (Arana 1997). The channel has six bends showing superelevation, of which two were examined in detail (Table 1).

Table 1 Field data for the two superelevated bends. See Fig. 10 for definition of mean depth and wetted perimeter
Full size table

Where the channel encounters the break of slope, the flow bends to the right and then sharply to the left (Fig. 6). At this location an elongate mound or ridge juts out into the channel. This ridge resembles a cone cut lengthways along its axis and then laid on its cut surface, so that it tapers and slopes down-wards across the channel with a steep up-channel face and a shallower down-channel slope (Figs. 6 and 7). Smooth surfaced pahoehoe drain-back units veneer the surface of this enigmatic feature, as at the channel banks. However, the cross-channel orientation of this feature suggests a mode of formation different to levee (bank) forming mechanisms, where levees are typically formed by lava emplacement during overflow, drain back and accretion at the channel margins (e.g. Sparks et al. 1976; Lipman and Banks 1987). In the final section of the paper, we speculate on the origin of this enigmatic feature.

Fig. 6
figure 6

Terminus of steep, upper channel section showing the cross-channel ridge

Full size image
Fig. 7
figure 7

Close up view of cross-channel ridge encountered at the break in slope. Length of hammer 280 mm

Full size image

Preamble: flow dynamics within a channel

The Reynolds number is a dimensionless number that can be used to identify the dominant forces controlling the flow dynamics. Conceptually it can be considered as the ratio of inertial forces to viscous forces. In a low Reynolds number flow, the viscous forces are the dominant means by which the fluid balances the external forces such as the force of gravity in the sloping channel. The viscous forces tend to suppress turbulence so that laminar flow is associated with low Reynolds numbers. High Reynolds number flows correspond to flows in which the external forces are balanced by fluid inertial forces that are manifest as turbulent drag forces adjacent to the boundary of the flow. Outside of this boundary layer, the flow may be modelled to good accuracy using the classical hydraulic theory of steady inviscid flow. The Reynolds number (Re) can be calculated from:

$$\operatorname{Re} = {\text{v}}\;{\text{ $ \rho $ }}\;{\text{D}} \mathord{\left/ {\vphantom {{\text{D}} {\text{ $ \mu $ }}}} \right. \kern-\nulldelimiterspace} {\text{ $ \mu $ }}$$
(1)

in which v, ρ, D and μ are flow velocity, density, depth and viscosity. For flow in open semicircular channels, flow is laminar if the Reynolds number is less than ~2,000 (Heslop et al. 1989).

The viscosity of the lava flow in the channel is unknown at the outset, so it is difficult to state a priori whether the flow will be laminar or turbulent. Figure 8 shows a plot of lava volumetric flow rate against lava viscosity for a series of different Reynolds numbers—drawn for a channel cross-section and depth of flow typical for this case, i.e. deduced from measurements made for the Pico Partido channel. We observe that lavas with small volumetric flow rates and/or relatively high viscosity will be viscously controlled while larger volume fluxes and/or less viscous lavas will be controlled by turbulent drag. Figure 8 also shows the range of viscosities encountered for komatiitic and basaltic lavas (from Spera 2000). Because the lavas erupted by Pico Partido are basaltic in composition, it would seem likely that the flow was controlled by viscosity (Fig. 8).

Fig. 8
figure 8

Flow regime for a range of volumetric flow rates and lava viscosities typical of komatiites and basalts, with the likely range of values, and hence flow regime, encountered for the Pico Partido channelized lava flow

Full size image

Estimation of flow velocity within the channel

Superelevation in a curved channel may be related to curvature of the channel and flow velocity by considering the dynamic equilibrium of a mass of fluid (m) moving at velocity v on a circular path of radius r (Fig. 9). In this case, the centripetal acceleration required for circular motion is provided by a radial pressure gradient obtained from the surface sloping, at angle θ, inwards towards the axis of rotation. Following Heslop et al. (1989), we estimate flow velocity from angle θ using:

$${\text{v}} = {\left( {{\text{g}}\;{\text{r}}\;\tan \;{\text{ $ \theta $ }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} $$
(2)

in which g is acceleration due to gravity.

Fig. 9
figure 9

Flow dynamics for an element of liquid of mass m and velocity v flowing around a bend of radius r

Full size image

In our case, to obtain velocity, radius of curvature (r) was measured along a line parallel to the channel walls and which followed the median line of the bend. The superelevation angle (θ) was then estimated using simple trigonometry from the maximum and minimum lava levels in the channel, i.e. the outer and inner bank heights, and the channel width. This estimate was subsequently checked by measurements from photographs (Fig. 10). Measurements were made at two bends where superelevation was particularly well developed. The data obtained are summarized in Table 1. Calculated flow velocities and cross-sectional areas (a), together with the volumetric flow rates (Q) that these give (Q=va), are given in Table 2.

Fig. 10
figure 10

Photograph of superelevated upper bend used to estimate channel dimensions (top). The lower tip of the stick is at the lowest point on the inside wall of the bend and approximates the inferred angle of the flow surface when the channel was active. Stick length is 1,220 mm. Sketch of idealized channel geometry for the same bend (bottom)

Full size image
Table 2 Parameters calculated from field data given in Table 1, where volumetric flow rate (Q)=av, and hydraulic diameter (D)=4a/P
Full size table

The flow velocity of around 8 m s–1 (Table 2) compares with values of between 7.2 and 9.3 m s−1 obtained from the superelevation features in a lava channel on Kilauea (Hawai’i) by Heslop et al. (1989). Volume fluxes are between 7 and 12 m3 s−1. However, we obtain a higher volumetric flow rate for the lower bend than for the higher bend (Table 2). For steady flow, the mass entering the channel (m 1) must be equal to the mass leaving the channel (m 2), where the rate of mass transport through a cross-section is described by the continuity equation:

$${\text{m}} = {\text{ $ \rho $ }}_{1} a_{1} {\text{v}}_{1} = {\text{ $ \rho $ }}_{2} {\text{a}}_{2} {\text{v}}_{2} = {\text{constant}}$$
(3)

where ρ is density. Thus, if density is constant, volumetric flow rate (Q x =a x v x ) should be constant at all points down channel. Our down-flow difference in calculated Q is probably due to a combination of variable bulk density, measurement error and the limitations of the analysis leading to Eq. (2). In the last case, the derivation of Eq. (2) is based on the assumptions that viscous effects can be neglected, that the radius of curvature is large compared to the channel width and that flow in the channel was steady.

Heslop et al. (1989) considers the effect of viscosity on velocities obtained from superelevation measurements in an appendix to their paper. Using the criteria that they develop, it can be shown that the effect of viscosity on the development of the superelevation in the Pico Partido channel can be neglected. It may seem surprising that we can calculate the flow velocity from the superelevation using standard inviscid theory, given that the down-channel flow is controlled by viscosity. The crux of the argument developed in Heslop et al. (1989) is that, as far as superelevation is concerned, the viscous forces are determined by velocity gradients in directions at right angles to the direction of flow, and that these velocity gradients are much lower than those in the down-channel direction. Thus locally, the centripetal acceleration forces dominate the viscous shear forces. Once the flow leaves a bend, the centripetal acceleration forces vanish and the down channel flow velocity is determined by a balance of gravity forces and viscous shear forces.

More accurate equations are available to obtain estimates of velocity from superelevation. These are applicable to steady, inviscid flows and relax the assumption of large radius of curvature compared with channel width. In addition, they make allowances for changes in flow velocity due to changes in depth round the bend (Chow 1959). Thus, we next explore the error introduced by the assumption of large radius of curvature on the flow velocity and volumetric flow rate.

The assumption that the radius of curvature is large compared with channel width may be explored using the superelevation equation of Grashof (Chow 1959). By applying a differential form of Eq. (1) to each streamline and then integrating across the channel width, Grashof showed that the superelevation (Δh) is given by:

$$\Delta {\text{h}} = {\left( {{{\text{v}}^{2} } \mathord{\left/ {\vphantom {{{\text{v}}^{2} } {\text{g}}}} \right. \kern-\nulldelimiterspace} {\text{g}}} \right)}\ln {\left( {{{\text{r}}_{{\text{o}}} } \mathord{\left/ {\vphantom {{{\text{r}}_{{\text{o}}} } {{\text{r}}_{{\text{i}}} }}} \right. \kern-\nulldelimiterspace} {{\text{r}}_{{\text{i}}} }} \right)}$$
(4)

where r o and r i are the radii of curvature of the outer and inner banks of the channel, respectively. The transverse profile of the superelevation surface is thus a logarithmic curve, rather than linear as assumed in Eq. (2). Figure 11 shows a schematic of the corresponding profiles, drawn so that they coincide at the channel centre line. If the logarithmic curve were an exact representation of the superelevation profile in the field, then the observed superelevation (Δh) would be the difference in vertical heights between locations A and B, situated on the inner and outer banks respectively. If Eq. (2) were then used to evaluate the velocity then Tan(θ) would be equal to Δh/w, where w is the channel width. Table 3 shows the difference between the results of the two equations as a function of the ratio of channel width to radius of curvature (w/r).

Fig. 11
figure 11

Schematic comparison of transverse surface profiles of a superelevation feature. See Fig. 10 for profile notation

Full size image
Table 3 Error on calculated flow velocity (v) and cross-sectional area (a) if Eq. 2 is used for a range of widths (radius of curvature, r, is 10 m)
Full size table

On Pico Partido, the channel width is 1–2 m. This compares with a radius of curvature of ~8 m. Thus the appropriate value of w/r is thus around 0.2. The corresponding error on the velocity is thus around 0.3% (Table 3).

Volumetric flow rate is the product of the average velocity (v) and the cross-sectional area of the flow (a). Figure 11 shows that the logarithmic profile lies above the linear profile at all points across the channel. Assumption of a linear profile thus underestimates the flow cross-sectional area. We evaluate the associated error induced by this area assumption using the linear profile as a function of w/r in Table 3. For w/r =0.2, which is appropriate for the channel geometry considered here, the error on a is 3.3%. Taken together, the errors in v and a combine to give an error in volumetric flow rate of 3.6%. We conclude that, for the channel geometry observed at Pico Partido, the errors are small compared with the likely field-measurement errors and other limitations of the analysis. This leaves variations in flow rate and/or density as possible causes for the difference in Q derived at the two points.

Departures from steady flow are discussed in Heslop et al. (1989). They point out that the superelevation angle is determined from the highest and lowest levels of lava observed on a bend. Unsteady flow, where the volume flux in the channel varies through time, may have the effect of producing these maximum and minimum levels at different times and thus at different flow rates. In addition, the maximum elevation of the lower bend may have been obtained at a different time, and at a different flow rate, than the higher bend. The greater depth at the lower bend compared with the higher bend could be consistent with construction during a higher flow rate, where increased volumetric flow rates would favour higher flow levels and velocities to induce construction of higher banks than during low-volume flux periods (Tables 1 and 2).

Such temporal variation in the volume flux is consistent with variations in flow level indicated by the levee and channel wall structures described above. These show outer-bank (constructional levee) features consistent with construction during periods of over-flow caused by high-volume flux pulses. They also show inner-channel-wall structures consistent with formation during periods when the channel was flowing at several different below-bank levels during lower, but variable, flow rates. In this regard, the two calculated values of volumetric flow rate differ by less than a factor of two and compare favourably with a variation from 100 to 300 m3 s–1 for the much larger Kilauea channel studied by Heslop et al. (1989). Such short-term variation in volume flux is not uncommon (e.g. Harris et al. 2000). For example, during the 1984 Mauna Loa (Hawai’i) eruption Lipman and Banks (1987) observed that short-term surges in the erupted flux, lasting from minutes to hours, could increase the volume flux of lava flowing in the channel by 50%.

Down-channel increases in volume flux may result from decreases in density due to down-flow vesiculation to bulk up the flow. In this case, following Eq. (3), the bulk density of the flow would have to decrease by ~42% to balance the increase in bulk volume flux. This could be achieved by a 42% increase in vesicularity, a bulk effect that would also serve to increase the flow level and hence the height at which bank construction could occur with distance from the vent. This would thus also square with an increase in channel depth at the down-flow location. Again, such down-flow variations may not be uncommon, where Lipman and Banks (1987) observed that near vent variations in the bulk volume flux of 5–40% resulted from variations in flow vesicularity and density. The upper bound of this range compares with the 42% down-channel increase in bulk volume flux required here. No doubt, the down-channel difference in our bulk volume-flux estimates may result from both unsteady flow and down-flow vesiculation.

Estimation of lava viscosity

To estimate flow viscosity (μ), we need to consider the laminar flow of a viscous fluid on a sloping surface. The simplest analysis assumes that the fluid is Newtonian, in which case the viscosity of the fluid is the same at all points within the flow. For a flow of given geometry, an equation can be derived for the velocity distribution in the channel. The resulting equations can be solved for one-dimensional cases of semicircular and infinitely wide channels. For more complex geometries, velocity varies in more than one direction and the solution of the resulting partial differential equations is more difficult (e.g. Tallarico and Dragoni 1999). However the equations for all geometries have a similar form, being constrained by the requirements of dimensional consistency.

For our analysis, it is convenient to follow Heslop et al. (1989) and replace the real geometry of the channel with a hydraulically equivalent semicircular channel, using the established concept of hydraulic diameter (Massey 1970). The hydraulic diameter (D) is defined as D=4a/P (Table 1 and Fig. 10). For a semicircular channel of width w and depth h (=w/2), the ratio of hydraulic diameter to depth (D/h) is 2. For the two bends studied here, the values of D/h are 1.9 (upper) and 1.7 (lower). The departures from semicircularity can be compared with the bends studied by Heslop et al. (1989) that had values of D/h in the range 2.2 to 2.8. Thus, we use a channel radius and depth (t) that is half the hydraulic diameter (t=D/2). This gives a radius of 0.7 and 0.9 m for our two channel profiles, respectively (Table 2).

For a semicircular channel of radius t, if y is the distance to the surface centre line of the channel, the velocity at depth y is given by:

$${\text{v}}{\left( {\text{y}} \right)} = {\text{ $ \rho $ }}\,{\text{g}}\sin {\text{ $ \alpha $ }}{{\left( {{\text{t}}^{2} - {\text{y}}^{2} } \right)}} \mathord{\left/ {\vphantom {{{\left( {{\text{t}}^{2} - {\text{y}}^{2} } \right)}} {{\left( {4{\text{ $ \mu $ }}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {4{\text{ $ \mu $ }}} \right)}}$$
(5)

in which α is the angle of the underlying slope. Velocity increases from zero at the channel base to a maximum on the surface at the channel centre line (Cigolini et al. 1984; Dragoni et al. 1986; Harris et al. 2002). Following Eq. (5), the maximum surface velocity at this centre-point (v max) is obtained from the case where y=0, i.e.

$${\text{v}}_{{\max }} = {\text{ $ \rho $ g}}\,\,\sin {\text{ $ \alpha $ }}{{\text{t}}^{2} } \mathord{\left/ {\vphantom {{{\text{t}}^{2} } {4{\text{ $ \mu $ }}}}} \right. \kern-\nulldelimiterspace} {4{\text{ $ \mu $ }}}$$
(6)

Now volumetric flow rate in the semicircular channel can be obtained from:

$${\text{Q}} = \pi {\text{ $ \rho $ g}}\sin \alpha {{\text{t}}^{4} } \mathord{\left/ {\vphantom {{{\text{t}}^{4} } {{\left( {16{\text{ $ \mu $ }}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {16{\text{ $ \mu $ }}} \right)}}$$
(7)

and the average velocity (v mean) from:

$${\text{v}}_{{{\text{mean}}}} = {2\,{\text{Q}}} \mathord{\left/ {\vphantom {{2\,{\text{Q}}} {{\left( {\pi {\text{t}}^{2} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {\pi {\text{t}}^{2} } \right)}} = {{\text{v}}_{{{\text{max}}}} } \mathord{\left/ {\vphantom {{{\text{v}}_{{{\text{max}}}} } 2}} \right. \kern-\nulldelimiterspace} 2$$
(8)

Thus, from Eqs. (6) and (8), the average velocity in the equivalent semicircular channel is given by:

$${\text{v}}_{{\operatorname{m} {\text{ean}}}} = {\text{ $ \rho $ }}\,{\text{g}}\sin {\text{ $ \alpha $ }}{{\text{t}}^{2} } \mathord{\left/ {\vphantom {{{\text{t}}^{2} } {{\left( {8{\text{ $ \mu $ }}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {8{\text{ $ \mu $ }}} \right)}}$$
(9)

This is the familiar Jeffreys equation (Jeffreys 1925) which following, for example, Walker (1967) can now be used to obtain flow viscosity (μ) from:

$${\text{ $ \mu $ }} = {\text{ $ \rho $ }}\,{\text{g}}\sin {\text{ $ \alpha $ }}{{\text{t}}^{2} } \mathord{\left/ {\vphantom {{{\text{t}}^{2} } {{\left( {8{\text{v}}_{{{\text{mean}}}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {8{\text{v}}_{{{\text{mean}}}} } \right)}}$$
(10)

To solve Eq. (10) we assume that the average velocity is approximated by the velocity calculated from the superelevation measurements (i.e. 7.7–8.0 m s–1). We use these values with the average slope of the channel (11°) and a density of 1,700–2,480 kg m–3. This density (ρ) is obtained using the dense rock value (ρ DRE) of 2,500–2,700 kg.m–3 given by Spera (2000) for undegassed basalt at eruption conditions and a vesicularity (ϖ) of 8–32% (Harris et al. 2000), where ρ=(1−ϖ) ρ DRE. This gives a viscosity in the range 25 to 60 Pa s. This compares with viscosities in the range 30 to 150 Pa s obtained for the Kilauea flow by Heslop et al. (1989) using a similar methodology.

The calculated viscosity is based on the assumption of laminar flow. It is now possible to check that the flow was indeed laminar by calculating the Reynolds number. We obtain a Reynolds number in the range 610–730, confirming that the laminar flow analysis is appropriate.

The formation of the enigmatic feature

As already mentioned, an enigmatic feature is located at the break in slope where the flow widens considerably (Figs. 6 and 7). In this section, we speculate on possible modes of formation for this feature. We expect a reduction in velocity immediately below the break in slope because the gravitational force is reduced down-slope and the flow is no longer confined to a channel. A reduction in velocity would allow the deposition of any entrained material such as a lava-veneered chunk of levee torn from the bank in the proximal section and then rafted or tumbled down-flow. Dropping of this chunk at the break of slope and subsequent veneering of lava could explain the formation of the cross-channel ridge. Alternatively, the ridge may have formed by accretion of lava to the channel floor where the lava was undergoing a change in flow regime or depth. Woodcock (2003) suggested that the break in slope might be occupied by a hydraulic jump, where the flow regime changes abruptly from supercritical to subcritical (Massey 1970). Application of standard inviscid flow theory indicates that the lava flow is supercritical above the break in slope; however, we are unsure of the relevance of inviscid theory to flows of high viscosity.

It is possible that the ridge is an expression of a change in depth of the flow that is imposed by volumetric flow conservation as the velocity is reduced at the break of slope. For a channelled flow, Eq. (7) indicates that, for constant volumetric flow and lava properties, the flow depth is inversely proportional to the fourth root of the slope (sin α). For the change in slope from 110 to 60, the flow depth increases by around 15%. An unchannelled flow can be modelled as the laminar flow of a thin planar sheet with a width (w) that is much greater than its depth (h). For this case, volumetric flow rate per unit width (at right angles to the flow direction) is given by (e.g. Dragoni et al. 1986)

$${\text{Q}} \mathord{\left/ {\vphantom {{\text{Q}} {\text{w}}}} \right. \kern-\nulldelimiterspace} {\text{w}} = {\text{ $ \rho $ }}\,{\text{g}}\,{\text{h}}^{3} \sin {\text{ $ \alpha $ }} \mathord{\left/ {\vphantom {{\text{ $ \alpha $ }} {{\left( {3{\text{ $ \mu $ }}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {3{\text{ $ \mu $ }}} \right)}}$$
(11)

In this case, the flow depth is inversely proportional to the cube root of the slope (sin α). For the change in slope from 110 to 60, the flow depth increases by around 22%.

Conclusions

We have considered the flow dynamics for lava flowing in a channel that extends over an abrupt change in slope. In the upper section of well-defined channel, lava with a viscosity of 25–60 Pa s moved over an 11° slope at a velocity of ~8 m s–1. The upper channel terminus is coincident with a sudden decrease in slope to ~6°. At this point, the channel becomes less well defined, and the flow widens. Lava advancing into this less steep, wider section would have experienced a deceleration. We suggest that an elongate feature extending across the Pico Partido channel at a break of slope formed as a result of such a flow deceleration. It may result from the dropping of entrained debris, lava accretion to the channel base or a combination of the two processes.