Study on the mechanical properties and energy absorption of Gyroid sandwich structures with different gradient rules

Abstract

In the present study, a series of lattice structures with Gyroid minimal surfaces were meticulously designed to incorporate linear density gradients and two distinct trigonometric function-based density gradients. These advanced architectures were subsequently compared and contrasted with a uniform lattice sandwich structure. The mechanical behavior and energy absorption characteristics of the four lattice sandwich structures were rigorously investigated through a combination of experimental testing and finite element analysis (FEA). The results of this comprehensive analysis revealed that during compression, all four gradient lattice structures exhibited varying degrees of shear slip, which manifested as discernible discrepancies in their respective stress–strain curves. Relative to the uniform lattice structure, the linear gradient lattice sandwich structure exhibited an enhancement in elastic modulus by 1.69%, while the square sine function gradient lattice sandwich structure showed a significant increase of 14.45% in elastic modulus. Conversely, the square cosine function gradient lattice sandwich structure experienced a reduction in elastic modulus by 9.61%. Employing either a linear gradient or a square sine function density gradient design was found to augment the load-bearing capacity of the uniform lattice structure. Notably, when the strain in the uniform structure reached densification strain, it absorbed energy exceeding 5.842 MJ/m³, indicating superior energy absorption capabilities among the four structures examined, thus rendering it particularly suitable for applications where high energy absorption is imperative. Furthermore, finite element simulations were conducted to validate the experimental findings, and the simulation results demonstrated a high degree of correlation with the experimental data, with discrepancies less than 6%, thereby confirming the reliability of the FEA model in predicting the performance of these intricate lattice structures.

1 Introduction

Lattice structures, characterized by their lightweight, superior mechanical properties, biocompatibility, and permeability, have garnered increasing attention in recent literature [1, 2]. Functionally graded (FG) lattice structures, when designed judiciously, can optimize weight reduction to decrease costs and achieve performance characteristics unattainable by uniform lattice configurations. These structures hold potential industrial applications in sectors such as aerospace, transportation, and biomedical scaffolds. Traditional fabrication techniques for porous structures predominantly include methods such as gas foaming, investment casting, polymer sponge replication, and physical vapor deposition [3,4,5,6]. However, these conventional methodologies fall short in fabricating complex lattice geometries with highly controllable pore shapes and distributions. The advent and progression of additive manufacturing (AM) technologies have enabled the fabrication of diverse lattice architectures through precise control over the lattice parameters to meet more advanced requirements and applications [7, 8]. Selective laser melting (SLM) [9], a quintessential representative of AM techniques, demonstrates a capacity for controlling lattice configurations due to its layer-by-layer processing principle [10], rendering it an ideal process for the fabrication of lattice structures.

Uniform lattice structures consist of a multitude of identical unit cells arranged periodically in a specific manner. In contrast, FG lattice structures are obtained by varying the geometric configuration of the unit cells within a spatial region. For instance, Bai et al. [11] designed FG body-centered cubic (BCC) lattice structures with strut lengths that gradually change along the loading direction. Compression tests revealed that vertical gradient (VG) structures exhibited superior mechanical performance and energy absorption capabilities; compared to uniform structures, their elastic modulus and energy absorption increased by 17.53 and 59.43%, respectively. Aboulkhair et al. [12] investigated the mechanical behavior of uniform and gradient density SLM Al-Si10-Mg lattices under quasi-static loading conditions. The results indicated that graded lattices collapsed layer by layer with identifiable compaction at each level. A progressive mechanical response to static or dynamic loads can be achieved through appropriate material distribution selection. Similar phenomena were observed in helical lattice structures with three-periodic minimal surfaces (TPMS) [12].

Yang et al. [8] designed and manufactured graded Gyroid cell structures (GCS) with different gradient orientations using selective laser melting (SLM), alongside uniform structures for reference. They studied the surface morphology and mechanical response of these structures under compressive loads. It was found that SLM-fabricated GCS exhibited high manufacturability and repeatability; gradients perpendicular to the loading direction enhanced the Young's modulus, plateau stress, and energy absorption capabilities of the porous structure. Optimized density distribution allowed for novel deformation behaviors and mechanical properties in the cell structure. Zhong et al. [13] examined the deformation mechanisms and energy absorption behavior of 316L TPMS structures with uniform wall thicknesses and gradient variations fabricated using SLM2. Results showed that cell fracture in gradient TPMS structures initiated within thinner sections before propagating to thicker areas; stress–strain responses exhibited distinct dual stress plateaus. Compared to uniform TPMS structures, gradient TPMS absorbed more total energy. Zhou et al. [14] proposed design methodologies for network-based functionally graded gyroscopes (N-FGG) and sheet-based functionally graded gyroscopes (S-FGG). Mechanical properties were measured using Ti–6Al–4 V powder specimens manufactured by selective laser melting followed by quasi-static compression testing. The results demonstrated that S-FGG-based structures also exhibited higher ultimate stress and greater total energy absorption per unit volume as well as higher energy efficiency.

Current research reveals significant disparities in mechanical performance and energy absorption capabilities among different gradient patterns. On the basis of a uniform lattice sandwich structure, this study explores the mechanical properties and energy absorption characteristics of a skin lattice structure with a gradient law of first and second power functions, using the order of RG expression as the grading strategy for the lattice sandwich structure, this study introduces a design methodology for trigonometric functionally graded cladding lattice structures. Designs for uniform and linear gradient cladding lattices with equivalent volume fractions were proposed, generating three-dimensional models through parametric design modeling methods. Four samples were prepared using Al-Si10-Mg powder via SLM and subjected to compression testing to investigate their mechanical performance and deformation behavior. Concurrently, finite element method (FEM) simulations employing Johnson–Cook plasticity and damage models were conducted to emulate the compression characteristics of the samples. Finally, an analysis and discussion regarding the energy absorption properties of the four samples were presented. This work provides an effective approach for controlling the mechanical performance and energy absorption of functionally graded lattice structures in engineering applications.

2 Materials and methods

2.1 Design of lattice structure

Gyroid is a well-known member of TPMS, characterized by excellent self-supporting and geometric isotropy [15]. The Gyroid cell structure described in this article was obtained from the TPMS formula. Based on previous research [16], considering the morphology of single cells, this study modified the shape and size of pores by adjusting parameters. Taking Gyroid-type crystal cells as an example, the expression for Gyroid type three period minimum surfaces with adjustable parameters can be described by the following equation:

$$\begin{aligned}{\varphi _G}\left( {x,y,z} \right) = & cos\left( {\alpha x} \right)sin\left( {\beta y} \right) + cos\left( {\beta y} \right)sin\left( {\gamma z} \right) + cos\left( {\gamma z} \right)sin\left( {\alpha x} \right) \\ & + 0.08\left[ {cos\left( {2\alpha x} \right)cos\left( {2\beta y} \right) + cos\left( {2\beta y} \right)cos\left( {2\gamma z} \right) + cos\left( {2\gamma z} \right)cos\left( {2\alpha x} \right)} \right] \\ & + {R_G} = 0 \\\end{aligned}$$

(1)

The parameters α, β, and γ are intricately associated with the unit cell dimensions along the x-, y-, and z-axes, respectively. G represents a helical cellular structure. An inverse relationship is observed, wherein an augmentation of these parameters results in a diminution of the unit cell dimensions. Consequently, the selection of disparate values for α, β, and γ permits the attainment of crystallographic cells of varying dimensions. Additionally, the parameter R_G is employed to modulate the relative density of the triply periodic minimal surface (TPMS) lattice structures.

In the majority of instances, cellular architectures derived from triply periodic minimal surface (TPMS) equations manifest as mere smooth surfaces devoid of volumetric substance. To facilitate the materialization of TPMS cellular structures, a relative density function is employed. The quantification of relative density can be executed through the application of the triple integral method, as delineated in Eq. (2) [17].

$$\rho * = \frac{{\iiint {\Omega dv}}}{{(x_{\max } - x_{\min } )(y_{\max } - y_{\min } )(z_{\max } - z_{\min } )}} = 1 - p$$

( 2)

$$\Omega = \{ (x,y,z)|\varphi (x,y,z) \le 0,x_{\min } \le x \le x_{\max } ,y_{\min } \le y \le y_{\max } ,z_{\min } \le z \le z_{\max }$$

( 3)

In the context of triply periodic minimal surface (TPMS) lattice structures, the parameter 'p' denotes the porosity of the configuration. Within the domain where the level-set function φ(x, y, z) is less than or equal to zero, the relative density of TPMS unit cells is constrained within the interval of 0–50%. The extremal values are annotated with footnotes to delineate the spatial regions of the structure. For homogenous lattice structures, the gradient ratio (R_G) remains invariant. In contrast, for functionally graded lattice structures, the relative density (ρ*) exhibits a linear dependence on R_G. The relative density ρ* can be computed for varying values of R_G. The computational relationship between these two parameters is encapsulated by Eq. (4).

$${\rho }^{*}=-31.93{R}_{\text{G}}+49.19$$

(4)

For Gyroid cell, there is a linear relationship between R_G and ρ*, as shown in Fig. 1. Defining R_G as a function of position vector not only yields a uniform lattice structure, but also generates a functional gradient lattice structure.

Fig. 1

Linear relationship of Parameter R_G and Relative Density ρ*

In the context of the manuscript, it is pertinent to elucidate that the manipulation of the parameters α, β, γ, and R_G within Eq. (1) facilitates the generation of honeycomb lattice structures characterized by variable cell dimensions and relative densities. Concurrently, the adoption of distinct expressions for R_G enables the synthesis of functionally graded lattice structures with varying relative densities. Specifically, for linear functionally graded lattice structures, the governing expression is delineated as Eq. (5).

$${R}_{\text{G}}=kz+{R}_{0}$$

(5)

The parameter k is intimately associated with the rate of variation in the crystal cell density gradient. An increase in the magnitude of k correlates with an accelerated change in this density gradient. Furthermore, the variable R₀ is indicative of the absolute crystal cell density; by modulating R₀, one can achieve crystal cell structures with varying densities. Additionally, this study introduces a novel sinusoidal squared density functional lattice structure, which is mathematically articulated as Eq. (6).

$${R}_{\text{G}}=k{\text{sin}}^{2}\left(\delta z\right)+{R}_{0}$$

(6)

In the context of crystallographic analysis, the parameter δ is intimately associated with the periodicity of the lattice density gradient. A diminutive value of δ corresponds to an extended periodicity in the variation of the lattice density gradient. Equation (6) delineates the radial distribution function R_G as a function of the positional vector z, facilitating the establishment of a lattice structure characterized by a sinusoidal square modulation of density gradient along the z-axis. This modulation is predicated on the controlled manipulation of both the rate and periodicity of changes in the lattice density gradient.

Building upon Eq. (6), it becomes feasible to construct a three-dimensional lattice structure wherein the density gradient undergoes modulation in accordance with a sinusoidal pattern along the x-, y-, and z-axes. Analogously, by substituting the square of a cosine function for that of a sine function, one can derive a lattice structure that exhibits a cosine-modulated density gradient along these axes. The mathematical representation of such a structure is encapsulated in Expression (7):

$${R}_{\text{G}}=k{\text{cos}}^{2}\left(\delta z\right)+{R}_{0}$$

(7)

In this study, the parameters and physical meanings used in formulas (5), (6), and (7) are shown in Table 1.

Table 1 The parameters used in the expressions of three gradient lattice structures

In Table 1, the parameter k governs the rate of gradient variations in cellular density, while δ modulates the frequency of these gradient fluctuations within the crystalline cell structure. R₀ serves as a parameter influencing the density of crystal cells, maintaining a proportional relationship with R_G, which is utilized to regulate the relative density denoted by ρ*.

2.2 Establishment of lattice structure model

In the present study, we have delineated the implicit function representation of minimal surfaces within a lattice structure, predicated on the squared sine and cosine functions as per the gradient of the aforementioned functions. Utilizing MATLAB R2019b, we have meticulously generated models of Gyroid lattice structures characterized by two distinct trigonometric function-based functional gradients. To conduct a comprehensive analysis of the mechanical properties inherent to these trigonometric function gradient lattice structures, we have concurrently established models with uniform and linear functional gradients for comparative scrutiny. Subsequent to the construction of four variant Gyroid lattice models, each model was imported into Materialise Magics software to facilitate the creation of a 1-mm-thick shell. This shell was subsequently amalgamated with the lattice structure through Boolean operations to yield an integrated shell-lattice configuration. The resultant quartet of shell-lattice structure models is exemplified in Fig. 2, providing a visual representation of the intricate geometries achieved through this process:

Fig. 2

Gyroid single cell model and four types of sandwich lattice structure models

Figure 2b through e depicts the architectural models of Gyroid lattice structures with functional gradients of uniform, linear, squared sine, and squared cosine distributions, respectively. Each of these Gyroid-based functional gradient lattice structures maintains a consistent volume fraction of 0.15. As illustrated in Fig. 2a, the minimal bounding cube encapsulating a single Gyroid unit cell measures 5 mm × 5 mm × 5 mm. Upon arraying, the minimal bounding cube encompassing the entire Gyroid lattice structure extends to dimensions of 20 mm × 20 mm × 20 mm, comprising four unit cells along the x-axis, four along the y-axis, and four along the z-axis, culminating in a total of 64 unit cells.

Figure 2 further elucidates the geometric characteristics inherent to the four lattice configurations under investigation: The uniform gradient lattice structure exhibits a homogenous relative density of 0.15 across all regions, signifying uniformity in cell wall thickness throughout. In contrast, the functional gradient lattice structures demonstrate a variation in cell wall thickness corresponding to their relative densities; regions with lower relative densities possess thinner cell walls, whereas those with higher relative densities exhibit thicker cell walls. The STL format models of these lattices were subjected to pre-processing and mesh generation using Hypermesh software, laying the groundwork for subsequent finite element analysis.

2.3 Finite element analysis

In order to elucidate the mechanical properties and deformation behavior of functionally graded lattice sandwich structures under compression, simulations were conducted using the ABAQUS/Standard 2019 software to model the compression of lattice sandwich structures. Initially, the lattice structure was discretized into a tetrahedral (C3D10M) mesh model within the Hypermesh software. During mesh configuration, an unstructured mesh was employed for mesh generation. To enhance computational precision, a finer mesh was generated in regions corresponding to the lattice structure. Conversely, for the upper and lower portions of the sandwich region of the model, a coarser mesh was created to economize on computational time and resources. The details of the Gyroid structure's mesh are depicted in Fig. 3, with an average orthogonal quality of 0.726, a maximum skewness of 0.68, an average skewness of 0.2059, an aspect ratio of 2.6874, and an average warpage factor of 0.021.

Fig. 3

Grid Details Display

An independent mesh validation was performed by selecting a Gyroid lattice structure model with a linear density gradient and comparing the first peak load (σ_f) and initial failure strain (ε_b) at varying mesh densities of 0.78 × 10⁶, 1.17 × 10⁶, 2.01 × 10⁶, and 2.63 × 10⁶ elements. The results are presented in Table 2. Comparative analysis indicated that the adjacent data error for σ_f and ε_b was less than 1% when the mesh densities were 2.01 × 10⁶ and 2.63 × 10⁶ elements. To ensure accuracy of computational outcomes while conserving computational resources, subsequent calculations for other models adopted mesh sizes and settings consistent with those of the Gyroid lattice structure model at a mesh density of 2.01 × 10⁶ elements.

Table 2 Grid Independence Verification

We employed a finite element analysis (FEA) model characterized by a uniform sandwich-lattice structure, as depicted in Fig. 4. The sandwich and lattice of the structure were fabricated from Al–Si10–Mg alloy, exhibiting a Young's modulus of 70,000 Pa and a Poisson's ratio of 0.33. Discrete rigid planes measuring 15 mm by 15 mm were established on the upper surface of the top sandwich and the lower surface of the bottom sandwich. The geometric centers of these two discrete rigid planes served as reference points for data output at corresponding locations (Fig. 5).

Fig. 4

Finite element analysis model of uniform sandwich lattice structure

Fig. 5

Four types of additive manufacturing samples for sandwich lattice structures

A uniformly distributed load was applied to the top sandwich, utilizing an explicit dynamics simulation approach with a step time duration set at 0.00024 s. The simulation was configured to record stress and strain outputs over time. Contact between the discrete rigid planes and their respective sandwich surfaces was defined as general contact, with tangential behavior governed by a friction coefficient of 0.3 and normal behavior defined by hard contact constraints. The lower discrete rigid plane was fully constrained, while a displacement load was applied to the upper plane with a boundary condition specifying a displacement of 10 mm.

All simulations were conducted on an Intel Core i7-8750H CPU equipped with 10 cores and 16 GB RAM, with computational times for each FEA model averaging approximately 20 h. The FEA results yielded stress–strain curves from which the maximum permissible loads at failure for both types of sandwich-lattice structures could be ascertained.

In the finite element simulation analysis, the plastic deformation behavior of the material under investigation is characterized by the Johnson–Cook plasticity model [18]. This constitutive model encapsulates the phenomena of strain hardening, strain rate sensitivity, and thermal softening effects, rendering it particularly suitable for dynamic response analyses. The yield stress within this framework is quantitatively described by Eq. (8), which provides a comprehensive mathematical representation of the aforementioned material response attributes under varying conditions of stress and temperature.

$${\upsigma }_{\text{s}} = \left[ {A + B\left( {\varepsilon_e } \right)^N } \right] \cdot \left[ {1 + Cln\left( {\frac{\varepsilon^p }{{\varepsilon^0 }}} \right)} \right] \cdot \left[ {1 - \left( {\frac{{T - T_{room} }}{{T_m - T_{room} }}} \right)^M } \right]$$

(8)

In the context of Eq. (8), the constants A, B, N, C, and M are material-specific parameters derived from rheological stress data obtained through mechanical testing. The variable ε_e denotes the equivalent plastic strain, ε^p represents the rate of equivalent plastic strain, ε⁰ is the reference rate of equivalent plastic strain, T_room signifies ambient temperature, and T_m corresponds to the melting temperature.

To ascertain the fracture behavior of the crystalline lattice structure, the Johnson–Cook damage model is employed. Upon exceeding a critical threshold of failure in an element, it is subsequently excised from the analysis. The fracture strain is articulated by Eq. (9).

$${\upsigma }_{\text{f}} = \left[ {d_1 + d_2 exp\left( {d_3 \sigma^* } \right)} \right] \cdot \left[ {1 + d_4 ln(\frac{\varepsilon^p }{{\varepsilon^0 }})} \right] \cdot \left[ {1 + d_5 \left( {\frac{{T - T_{room} }}{{T_m - T_{room} }}} \right)} \right]$$

(9)

The parameters d₁, d₂, and d₃ are identified as damage constants that correlate with the relationship between the triaxiality of stress and strain-induced damage. Constants d₄ and d₅ are contingent upon strain rate and temperature, respectively. The stress triaxiality, denoted as σ*, is defined as the ratio of hydrostatic stress to equivalent stress. All compression tests within this study were conducted at a constant strain rate and ambient temperature; consequently, the constants C, M, d₄, and d₅ were deemed negligible for the purposes of this analysis. Drawing upon prior research [19], the constitutive parameters for the Johnson–Cook model are delineated in Table 3.

Table 3 Constitutive parameters of Johnson–Cook model

2.4 Sample preparation

In the initial phase of the experimental procedure, Standard Tessellation Language (STL) files corresponding to four distinct lattice structures were generated utilizing MATLAB R2019b software. Subsequent to their creation, these STL files underwent a series of preprocessing steps, including model defect inspection and rectification, facilitated by the application of Materialise Magics software. The fabrication of the lattice specimens, with dimensions of 20 mm × 20 mm × 22 mm, was executed using an AFS-M120XT metal additive manufacturing system. The specimens were composed of an aluminum alloy, Al–Si10–Mg, with the primary elemental chemical composition delineated in Table 4. The feedstock powder featured a particle size distribution ranging from 15 to 53 μm. The AFS-M120XT system operates with an IPG fiber laser, delivering a laser power output of 500W. In the winding scanning mode, the laser scans the parts with a profile line spacing of 130 μm, a point spacing of 80 μm, and an exposure time grating of 140 μs.

Table 4 Chemical Components

To maintain an optimal processing atmosphere, positive pressure argon gas was employed to sustain oxygen concentrations below 500 ppm. Prior to each laser pass, a layer of Al–Si10–Mg powder with a thickness of 25 μm was deposited. Throughout the production process, the build platform temperature was maintained at 180 °C. Post-fabrication, the specimens were subjected to thermal treatment to alleviate internal stresses and remove any loose residual powder. To facilitate a comparative analysis of mechanical properties across the four lattice structures on an equal mass basis, each design was calibrated to achieve an average relative density of 0.15. The additive manufacturing process enabled continuous variation in cell structure thickness, thereby providing a smoother gradation in structural density distribution.

Compression experiments were conducted utilizing a universal testing machine, designated as WDW-100, which is capable of exerting a maximum experimental load of 100KN. The experimental protocol involved the controlled displacement of the central compression platen at a constant loading rate of 1 mm/min until the specimen underwent a cumulative compression height of 11 mm, at which point the experiment was terminated. High-resolution videography was employed to document the entire experimental procedure, thereby facilitating subsequent analysis of the specimen's deformation behavior under compressive stress. Data acquisition systems interfaced with sensors and computational units automatically recorded the variations in load and displacement throughout the compression test, enabling the construction of stress–strain curves. The strain (ε) and stress (σ) parameters were computed using the following relationships:

As depicted in Fig. 4, the SLM-fabricated lattice specimens exhibited high fidelity to their respective design models. Despite some partially melted powder adhering to the surfaces—resulting in a degree of roughness—all manufactured specimens consistently matched the target relative density value of 0.15. Furthermore, measurements obtained from photographs of the cell structures corroborated the thickness values predicted by CAD models. This concordance between manufactured samples and anticipated design geometries underscores the precision achieved in fabricating the lattice structures under investigation.

2.5 Performance testing

The WDW-100 universal testing machine is utilized for conducting compression experiments, with a maximum experimental load of 100KN. During the compression experiment, the displacement of the control center pressure head is regulated, and the loading is executed at a speed of 1 mm/min. The experiment is terminated when the compression height of the sample reaches 11 mm. The entire experiment process is captured by a camera to observe the deformation behavior of the sample during the experiment. Simultaneously, sensors and computers automatically record the changes in load and displacement data during the compression experiment and generate the stress–strain curve. Strain (ε) and stress (σ) can be computed using Eqs. (10) and (11).

$$\sigma =\frac{F}{{L}_{x}{L}_{y}}$$

(10)

$$\varepsilon =\frac{S}{{L}_{z}}$$

(11)

In the context of a crystal lattice with dimensions Lx, Ly, and Lz, the elastic modulus (El) is defined as the slope of the linear portion of the strain–stress curve, while the yield stress (σl) corresponds to the stress value at 0.2% plastic strain. The compressive strength (σc) is the first peak stress on the stress–strain curve. The efficiency η(ε) of the lattice sample under compression can be calculated using Eq. (12).

$$\eta (\varepsilon ) = \frac{\smallint_0^\varepsilon \sigma (\varepsilon )d\varepsilon }{{\sigma (\varepsilon )}}$$

(12)

The definition of strain hardening (ε_D) is the strain at the maximum point on the stress–strain curve, and η(ε_D) satisfies Eq. (13)

$$\frac{d\eta (\varepsilon )}{{d\varepsilon }}{\rm{}}_{\varepsilon = \varepsilon_D } = 0$$

(13)

The accumulated energy absorbed per unit volume during the compression process is calculated according to Eq. (14):

$$W_v = \mathop \smallint \limits_0^\varepsilon \sigma (\varepsilon )d\varepsilon$$

(14)

The total absorbed energy per unit volume (W_vt) of a lattice sample during compression is W_v at time of ε = ε_D.

The effect of density gradient on mechanical properties can be described by the Gibson–Ashby Eqs. (15), (16) and(17):

$$\frac{{E}_{l}}{{E}_{s}}={C}_{1}{({\rho }^{*})}^{{n}_{1}}$$

(15)

$$\frac{{\sigma }_{l}}{{\sigma }_{s}}={C}_{2}{({\rho }^{*})}^{{n}_{2}}$$

(16)

$$\varepsilon_D = 1 - \alpha \rho^*$$

(17)

E_S and σ_S represent the elastic modulus and yield strength of the solid material, which are set as 70 GPa and 245 MPa, respectively. The constants C₁, C₂, n₁, n₂, and α can be calculated based on the results of compression tests. Here, n1 and n2 are set as 2 and 1.5, respectively [20]. Subsequently, the Gibson–Ashby coefficients C₁, C₂, and α are calculated by setting ρ* = 0.15.

3 Results and discussion

3.1 Weight difference of sandwich structure

In order to compare the load-bearing performance of sandwich structures with four different core structures, it is necessary to ensure that sandwich structures with the same volume fraction have the same weight. Table 5 lists the theoretical weight, weight obtained from the finite element simulation model, and actual weight of the specimens for the four sandwich structures. For models with different structures, the numerical difference in the total weight obtained by the above three methods is < 2%, indicating that the dimensions and shapes of the finite element simulation model and the size of the additively manufactured samples are accurate, which ensures the accuracy of the finite element analysis results and the compression test results. From the data in Table 5, it can be found that the simulated total weight is slightly smaller than the theoretical value, while the experimental value is the largest. This is because some areas in the finite element model are difficult to generate meshes due to their small size and complex shape and are therefore optimized and omitted, resulting in a reduced weight. The experimental value is the largest because there is adhesion of aluminum alloy powder during the specimen processing, resulting in a weight higher than the theoretical value.

Table 5 Total weight of four types of skin lattice structures

3.2 Deformation characteristics of sandwich lattice structures

The load–displacement curves obtained from the compression tests of four specimens are shown in Fig. 6. The compression process of the Gyroid lattice structure exhibits three distinct stages: elastic–plastic stage, undulation stage, and densification stage. For the four gradient density Gyroid lattice structures, a significant decrease in the load value is observed after the first load peak (σ_f). This trend is attributed to the sudden failure of the lattice structure, i.e., for the uniform, linear, sine function squared, and cosine function squared density gradient Gyroid lattice structures, the initial failure strain (ε_b) occurs at 0.090, 0.089, 0.091, and 0.094, respectively.

Fig. 6

Stress–strain curves of four types of specimens

During the elastoplastic regime, the stress–strain curves for all specimens exhibited a progressive augmentation in stress values concomitant with increasing strain. Upon reaching a zenith in the elastoplastic domain, an abrupt diminution in stress was observed across all specimens, indicative of a compromised load-bearing capacity. The magnitude of stress reduction (f_d) for the four types of specimens was quantified as 83.24, 80.88, 86.62, and 76.96%, respectively. Subsequent to this phase, the specimens entered a fluctuation stage characterized by multiple stress peaks, attributable to damage, collapse, and densification phenomena occurring during the compression process. The number of stress peaks was consistent across the four specimen types, suggesting uniformity in the frequency of failure and densification events; however, variations in internal structure among the specimens resulted in disparate locations of these stress peaks throughout the compression sequence. In the densification phase, the internal structures of all specimens were compacted under compressive loads, leading to increased structural density. The strain values at the onset of densification (ε_D) for Gyroid lattice structures with linear, squared sine function, and squared cosine function density gradients were recorded at 0.472, 0.422, and 0.418, respectively. In contrast, specimens with a uniform lattice structure entered the densification phase later than their counterparts due to more severe disruption of their cellular layers; collapse of the cell structure rendered overall compaction more arduous, necessitating a greater strain to initiate densification.

The significant decrease in the load-bearing capacity of the uniform sandwich lattice structure specimens is attributed to the localized shear failure. As shown in Fig. 7, triangular shear bands appear in the uniform specimens at a strain of 0.12, leading to the fracture of some unit cell structures; at a strain of 0.30, the specimen exhibits double triangular shear bands, and the damaged structures detach; at a strain of 0.45, further detachment occurs in the shear region of the specimen. Under compressive loading, the double triangular region in Fig. 7 reaches densification first. The load-bearing capacity of the specimen decreases as the stress drops rapidly three times in the stress–strain curve of the uniform specimen. The failure of the diagonal shear band in the uniform sandwich lattice structure specimen leads to the cracking of part of the unit cell structure [7, 21]. After the detachment of the damaged unit cell structure, with an increase in strain, the uniform sandwich lattice structure specimen gradually densifies, causing an increase in stress and leading to a new round of collapse. After complete densification of the specimen, the stress continues to increase.

Fig. 7

Experimental and simulated deformation behavior of four samples under different compressive strains

The linear sandwich lattice structure specimen exhibits triangular shear bands when the strain reaches 0.12, and the crystal cell structure on the shear bands fractures, leading to a decrease in stress. When the strain reaches 0.30, due to the higher volume fraction on the left side, the triangular area in Fig. 7 of the specimen becomes denser first. After this area becomes denser, the less deformed crystal cell structures will further deform, causing an increase in stress and resulting in a third stress peak. At a strain of 0.40, the uniform loading on the upper surface causes the less dense crystal cell structures on the right side to deform more, leading to the formation of double triangular dense areas. The areas that are not compacted experience increased force and collapse, resulting in a decrease in stress as the damaged structures fall off. The stress increases after the specimen is completely compacted. The first stress peak of the linear sandwich lattice structure specimen is larger than that of the uniform sandwich lattice structure specimen, indicating an improved load-bearing performance after linear density variation.

The sine function squared sandwich lattice structure specimen exhibits diagonal shear bands when the strain reaches 0.12, and its load-bearing capacity decreases significantly due to local shear failure, with a decrease of 86.62%, which is the largest among the four specimens. At a strain of 0.30, double triangular shear bands similar to those of the uniform sandwich lattice structure specimen appear, as the deformation process in the direction parallel to the loading direction is similar to that of the uniform sandwich lattice structure specimen due to equal volume fractions in adjacent layers parallel to the loading direction. At a strain of 0.45, crystal cell structures below the edges of the shear bands deform successively from top to bottom, leading to an increase in specimen density and the formation of new double triangular dense areas. Meanwhile, the specimen as a whole enters a dense stage with continuously increasing stress. The first stress peak of the sine function squared sandwich lattice structure specimen is larger than that of the linear sandwich lattice structure specimen, indicating further improved load-bearing performance under density variation according to a sine function squared pattern.

The cosine function squared sandwich lattice structure specimen exhibits shear bands consistent with those of the sine function squared sandwich lattice structure specimen when the strain reaches 0.12, resulting in reduced stress due to slip. The shear failure and degree of slip are most severe among the four structures, resulting in all three stress peaks being smaller than those of other three structures. At a strain of 0.30, crystal cell structures below the diagonal shear bands are further compressed and deformed, leading to an increase in density and gradual reaching of a second peak in stress. At a strain of 0.45, as densification progresses, accompanied by damage and collapse of crystal cell structures, a third stress valley appears before entering a densification stage with increasing stress.

The mechanical properties of the four lattice structures are listed in Table 6. The cosine function squared density gradient Gyroid sandwich lattice structure exhibits minimal stress at first failure, at 16.053 MPa. This is because the crystal unit structures with larger volume fractions on both sides have fewer contact points with upper and lower skin and are unable to withstand large loads, while those with smaller volume fractions in the middle are more susceptible to failure due to shear band effects. However, this structure undergoes significant elastic deformation before failure, resulting in a maximum initial failure strain (ε_b) of 0.094. The sine function squared density gradient Gyroid sandwich lattice structure exhibits maximum stress at first failure, at 19.226 MPa. This is because the middle part with more contact points with upper and lower skin consists of crystal unit structures with larger volume fractions, resulting in better load-bearing performance. Additionally, the linear density gradient Gyroid sandwich lattice structure has an initial failure strain of 0.089, which is the smallest among all four structures. This is because it has crystal unit structures with maximum volume fractions on its left side and is more prone to deformation due to lattice compression under external loads, resulting in minimal failure displacement among all four specimens.

Table 6 Analysis values of stress–strain curves for four types of sandwich lattice structure samples

3.3 Mechanical properties

The mechanical properties and energy absorption of four types of sandwich lattice structures are listed in Table 7. It can be observed that the sine function squared gradient sandwich lattice structure sample has the highest elastic modulus, yield strength, and compressive strength. In contrast, the cosine function squared gradient sandwich lattice structure sample has the lowest elastic modulus, yield strength, and compressive strength. The stress–strain curves of the four sandwich lattice structures exhibit multiple peaks, which is attributed to the multiple collapses during compression, and after each collapse, the internal structure of the sandwich lattice interacts with each other, leading to densification. The densification process is the interaction between the unit cell structures. Therefore, each peak on the stress–strain curve signifies the end of a stable deformation process and the destruction, collapse, and densification of the lattice structure. The value of ε_D can be determined from the energy absorption efficiency curve, as shown in Fig. 8. The densification strain value can be calculated using Eq. (13) and is listed in Table 7. The calculated value has an error of less than 8% compared to the experimental value, indicating a good agreement between the calculated and experimental values.

Table 7 Mechanical properties and energy absorption of four types of sandwich lattice structure samples

Fig. 8

Stress distribution of four sandwich structures at a strain of 0.1

Since the gradient directions of the established four sandwich lattice structures are perpendicular to the loading direction of the compression test, both the linear and sine function squared gradient sandwich lattice structures exhibit higher elastic modulus and compressive strength compared to the uniform sandwich lattice structure. Compared to the uniform sandwich lattice structure, the elastic modulus of the linear sandwich lattice structure increases by 1.69%, while that of the sine function squared gradient sandwich lattice structure increases by 14.45%. Although the gradient direction of the cosine function squared gradient sandwich lattice structure is also perpendicular to the loading direction, its elastic modulus is 9.61% lower than that of the uniform sandwich lattice structure. This is because during compression, the volume fraction of unit cells on both sides of the cosine function squared gradient sandwich lattice structure is larger, with fewer contact points with the upper and lower Skin, making it unable to withstand large loads. On the other hand, the volume fraction of unit cells in the middle with more contact points with Skin is smaller and is easily damaged by diagonal shear bands.

Figure 8a–d shows the equivalent stress distribution diagrams of uniform, linear, square of sine function, and square of cosine function sandwich structures at a strain of 0.1, respectively. The stress distribution of the model is also gradient-varying. The stress distribution of the four gradient design models is highly correlated with the gradient design method. The stress concentration degree is high in the region with a large volume fraction, and the stress is concentrated in the upper part of the structure at a strain of 0.1. It can be judged from Fig. 8 that the linear structure and the square of sine function structure have larger stresses and a larger stress distribution range, and the force is more uniform, which makes the load-bearing capacity of the linear structure and the square of sine function structure better. Compared with the linear structure, the stress distribution of the square of sine function structure is more continuous, which indicates that the square of sine function structure can better disperse the load to the surrounding cells. Therefore, the square of sine function structure has the best load-bearing performance. This is consistent with the conclusion in Fig. 6.

To more fully demonstrate the superior performance of the sine-squared sandwich structure in this study, this paper compares its performance with the G1 gradient structure [22] with a volume fraction of 0.15. The G₁ gradient structure follows a gradient variation of 0.1–0.2–0.1, which, although having the same numerical values as the gradient variation in this study, differs in the variation pattern. Compared with the uniform sandwich structure, the elastic modulus of the G₁ structure is increased by 10%, while in this study, the elastic modulus of the sine-squared gradient lattice sandwich structure is increased by 14.45%. Therefore, when the volume fraction values follow the same trend, the sandwich structure with a sine function variation exhibits better mechanical properties.

Gibson–Ashby coefficients C₁, C₂, and α Determine through Eqs. (15–17). The Gibson–Ashby coefficients for four types of sandwich lattice structures are listed in Table 8.

Table 8 Gibson–Ashby coefficients for four types of sandwich lattice structures

The determined values of C₁ for the four sandwich lattice structures are 0.195, 0.199, 0.223, and 0.178, respectively. These values fall within the specified range of the Gibson–Ashby coefficient (0.1–4) and are close to the conclusions of other researchers. For example, Yan et al. [23] reported C₁ values of 0.17 and 0.19 for two Ti6Al4V metal porous structures. The α values for the four sandwich lattice structures are 4.25, 3.51, 3.75, and 4.16, which are not significantly different from the results of Gibson [24]. However, the C₂ values for the four sandwich lattice structures are 1.18, 1.24, 1.35, and 1.14, slightly higher than the specified range of the Gibson–Ashby coefficient (0.1–1), due to the different lattice types corresponding to different values of the Gibson–Ashby coefficient. For example, Maskery et al. [25] used BCC and BCCz lattice structures, with corresponding C₂ values of 0.202 and 0.285, indicating that Gyroid-type minimal surface lattice structures have higher yield strength than many traditional lattice structures. The C₂ values of the four sandwich lattice structures vary slightly, and the magnitude of C₂ is positively correlated with the yield strength of the four structures; that is, the maximum yield strength of the sine function squared gradient sandwich lattice structure corresponds to the maximum C₂ value, while the minimum yield strength of the cosine function squared gradient sandwich lattice structure corresponds to the minimum C₂ value. Furthermore, materials also affect the C₂ value of lattice structures. For example, the C₂ value for a helical lattice structure manufactured from polymer is 0.135 [20], while for a 316L helical lattice structure it is 1.29 [26]. Therefore, C₂ can be used as a parameter to characterize the magnitude of yield strength. By adjusting the geometric configuration of sandwich lattice structures and changing the lattice material, it is possible to adjust the yield strength of sandwich lattice structures.

The α values of the four sandwich lattice structures are slightly higher than the range of 1.4–2 given by Gibson and Ashby [24]. This indicates that densification begins at a lower strain than the predicted value for the volume fraction structure. This is due to the smaller volume fraction of the sandwich lattice structure model in this study, resulting in a larger calculated α value. Maskery et al. established a gradient FGS lattice structure with a volume fraction of 0.2 in different directions, and its α value was 2.47 ± 0.01. This is reasonably consistent with this study [27].

Among the four sandwich lattice structures, the sample with a uniform sandwich lattice structure has the largest α, indicating that densification begins at the smallest strain among the four samples. For the uniform sandwich lattice structure, the densification point is mainly determined by the volume fraction, and lattice structures with high volume fractions usually have lower densification strains [24]. For gradient sandwich lattice structures, although three types of gradient sandwich lattice structure samples have the same volume fraction, the densification strain varies with the gradient. The densification strain of linear sandwich lattice structure is the largest among the three density gradient sandwich lattice structures, because the linear structure has the deepest shear slip, resulting in an increase in strain under load but little change in densification level. The sine function squared sandwich lattice structure undergoes almost no shear slip during compression, and the degree of cell deformation deepens as strain increases, thus entering the densification stage first.

3.4 Energy absorption

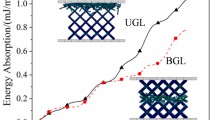
The energy absorption performance of lattice structures determines their potential applications in energy absorption and encapsulation protection. The total absorption energy W_vt per unit volume of the compressed samples is shown in Table 7. It can be seen that the energy absorption performance of lattice samples can be altered through gradient design of the sandwich lattice structure. The improvement in energy absorption performance is attributed to the difference in average volume fraction between adjacent layers, leading to changes in mechanical properties parallel to the loading direction during compression. Therefore, the layer-by-layer deformation behavior gradually enhances the mechanical properties, allowing the lattice samples to absorb more energy. The cosine squared gradient sandwich lattice structure sample absorbs the least energy before densification, indicating its weakest energy absorption capacity. The uniform structure densifies at a strain greater than 0.5, but it already absorbs 5.842 MJ/m³ of energy at a strain of 0.5. The energy absorbed when the uniform structure reaches densification strain exceeds 5.842 MJ/m³, making it the strongest in energy absorption capacity and suitable for applications requiring higher energy absorption (Fig. 9).

Fig. 9

Energy absorption efficiency strain curves of four types of sandwich lattice structures

To further elucidate the energy absorption process, the energy absorption curves of the four samples during compression are shown in Fig. 10. The results indicate that although the cosine squared gradient sandwich lattice structure sample absorbs a higher amount of energy at ε = 0.16, its rate of increase in energy absorption is lower than that of other samples, resulting in the lowest W_vt for this sample. The energy absorption curves for all four structures can be fitted with a power law Wv = aε^b, where the value of exponent b represents the rate of increase in Wv under compression load for sandwich lattice structures [28]. The fitting curve data are shown in Table 8, and due to the similarity in deformation behavior of cell layers along the loading direction where adjacent layers have the same volume fraction, Wv for all four samples almost exhibits a linear relationship with ε. The uniform sandwich lattice structure has the highest b value of 1.10593, indicating that its energy absorption performance rapidly increases with an increase in ε, resulting in the highest energy absorption before densification. Furthermore, the results indicate that gradient patterns will affect the b value of sandwich lattice structures, as different contact positions and quantities of contact points between cell lattice structures and sandwich lead to differences in volume fractions at contact points among the four structures. Changes in gradient patterns result in different average volume fractions for different layers, leading to differences in mechanical properties between adjacent layers and affecting the energy absorption process. Therefore, altering the volume fraction of cell contacts provides an effective method for adjusting the energy absorption process of lattice structures for practical applications (Table 9).

Fig. 10

Energy absorption curves of four structures

Table 9 Fitting curve data for four types of sandwich lattice structures

3.5 Simulation verification

In order to verify the reliability of FEM in predicting the deformation behavior of four sandwich lattice structure samples, Fig. 7 shows the plastic strain distribution of lattice samples under different strains. According to the observation, the local shear and deformation behavior of the sandwich lattice structure successfully simulated the sandwich lattice structure samples. The simulated and experimental strain–stress curves for the four sandwich lattice structures with uniform, linear, sine function square, and cosine function square are shown in Fig. 11a–d, respectively. Overall, all simulated curves are consistent with the experimental results and correctly simulate the different load-bearing capacities due to different gradient rules. In order to evaluate the reliability of FEM in predicting the mechanical properties of sandwich lattice structure samples, Table 10 compares the elastic modulus, yield strength, and compressive strength of experiments and finite element analysis. The deviation between the simulation results and the experimental results is 1.99–5.86%. The deviation between experimental and finite element analysis results can be attributed to the ideal geometric shapes and perfect elastoplastic material models used in finite elements, as well as the presence of internal defects and stress concentration in samples during additive manufacturing process, and surface morphology of specimens affected by sandblasting and other treatments [29], which lead to higher elastic modulus, yield strength, and compressive strength in the finite element analysis model than in the experimental results.

Fig. 11

Comparison of experimental and simulated strain stress curves for four types of sandwich lattice structures

Table 10 Mechanical performance experiments and finite element analysis of four types of sandwich lattice structure samples

4 Conclusion

This study designed a three-dimensional model of uniform, linear function, and quadratic function gradient lattice structures using parameter equation modeling method. Four sandwich lattice structures were generated, and four density gradient sandwich lattice structure samples were prepared using Al-Si10-Mg powder. The mechanical properties, deformation behavior, and energy absorption characteristics of the four gradient sandwich lattice structures were analyzed by finite element analysis and experimentally verified. The following conclusions were drawn:

• (1) Among the four sandwich lattice structures, the Gyroid sandwich lattice structure with cosine function square density gradient has the weakest load-bearing capacity at 16.053 MPa due to the large volume fraction of unit cells with fewer contact points between the upper and lower Skin. The Gyroid sandwich lattice structure with sine function square density gradient has the best load-bearing performance among the four structures at 19.226 MPa, as it has more contact points between the upper and lower skin in the middle part with a larger volume fraction of unit cells. The initial failure strain of the linear density gradient Gyroid sandwich lattice structure is 0.089, and the leftmost unit cell structure is more prone to deformation due to lattice compression under external loads, resulting in the smallest initial failure displacement.

• (2) Compared to the uniform sandwich lattice structure, the elastic modulus of the linear sandwich lattice structure increased by 1.69%, while the elastic modulus of the sine function square gradient sandwich lattice structure increased by 14.45% and that of the cosine function square gradient sandwich lattice structure decreased by 9.61%. This is because the cosine function square gradient sandwich lattice structure has a smaller volume fraction of unit cells in the middle part with more contact points between the upper and lower Skin during compression, making it susceptible to failure due to diagonal shear bands.

• (3) The energy absorbed by the cosine function square gradient sandwich lattice structure sample before densification is 3.997 MJ/m³, indicating its weakest energy absorption capacity. The uniform sandwich lattice structure has the strongest energy absorption capacity, absorbing more energy than 5.842 MJ/m³ at densification strain. In this loading direction, the uniform sandwich lattice structure is suitable for places with higher energy absorption requirements.

• (4) When the volume fraction is constant, the load-bearing capacity of the sandwich lattice structure can be altered by designing density gradient patterns. By designing linear and trigonometric function square density gradients for the uniform sandwich lattice structure, its load-bearing capacity can be enhanced to achieve optimization effects.