A new numerical approach to the solution of PDEs with optimal accuracy on irregular domains and Cartesian meshes—part 2: numerical simulations and comparison with FEM

Abstract

A new numerical approach for the time-dependent wave and heat equations as well as for the time-independent Poisson equation developed in Part 1 is applied to the simulation of 1-D and 2-D test problems on regular and irregular domains. Trivial conforming and non-conforming Cartesian meshes with 3-point stencils in the 1-D case and 9-point stencils in the 2-D case are used in calculations. The numerical solutions of the 1-D wave equation as well as the 2-D wave and heat equations for a simple rectangular plate show that the accuracy of the new approach on non-conforming meshes is practically the same as that on conforming meshes for both the Dirichlet and Neumann boundary conditions. Moreover, very small distances ($0.1 h - 10^{-9}h$ where h is the grid size) between the grid points of a Cartesian mesh and the boundary do not decrease the accuracy of the new technique. The application of the new approach to the 2-D problems on an irregular domain shows that the order of accuracy is close to four for the wave and heat equations and is close to five for the Poisson equation. This is in agreement with the theoretical results of Part 1 of the paper. The comparison of the numerical results obtained by the new approach and by FEM shows that at similar 9-point stencils, the accuracy of the new approach on irregular domains is two orders higher for the wave and heat equations and three orders higher for the Poisson equation than that for the linear finite elements. Moreover, the new approach yields even much more accurate results than the quadratic and cubic finite elements with much wider stencils. An example of a problem with a complex irregular domain that requires a prohibitively large computation time with the finite elements but can be easily solved with the new approach is presented.

1 Introduction

In Part 2 of the paper, we show the application of the new numerical approach (developed in Part 1; see [12]) to the time-dependent wave and heat equations as well as to the time-independent Poisson equation on regular and irregular domains with Cartesian meshes; see “Appendix A” for the summary of the stencil equations of the new approach derived in Part 1 in the 1-D and 2-D cases. There is a significant number of publications related to the numerical solution of different PDE on irregular domains with uniform embedded meshes. For example, we can mention the following fictitious domain numerical methods that use uniform embedded meshes: the embedded finite difference method, the cut finite element method, the finite cell method, the Cartesian grid method, the immersed interface method, the virtual boundary method, the embedded domain method, etc; e.g., see [1,2,3,4,5,6,7,8,9,10,11, 16,17,18,19,20,21,22,23,24,25,26, 28,29,32] and many others. Finally, all these approaches reduce to a system of stencil equations with given coefficients. The approach developed in Part 1 is based on postulating a system of stencil equations with unknown coefficients that are found from the minimization of the order of the local truncation error. Therefore, the proposed new technique provides the optimal order of accuracy that cannot be improved without changing the widths of stencil equations.

The numerical study of the accuracy of the new technique on conforming and non-conforming meshes for the 1-D wave equation with the Dirichlet and Neumann boundary conditions is considered in Sect. 2.1. The detailed study of the new approach for 2-D problems with the Dirichlet and Neumann boundary conditions on regular and irregular domains with Cartesian meshes as well as the comparison of the accuracy of the new technique with the linear and high-order quadrilateral and triangular finite elements is considered in Sect. 2.2 for the Poisson equation, in Sect. 2.3 for the wave equation, and in Sect. 2.4 for the heat equation. The commercial finite element software ‘COMSOL’ is used for the finite element simulations.

2 Numerical examples

In this section, the computational efficiency of the new approach developed in Part 1 of the paper will be demonstrated and compared with the 2-D conventional linear (Q3 and Q4), quadratic (Q6 and Q9) and cubic (Q10 and Q16) finite elements. Similar to the finite element terminology, a grid point of a Cartesian mesh will be called a node. In order to compare the accuracy of the new technique with FEM, the following errors are considered in the sections below. The relative errors $e_{u}^{j}$ for the function and $e_{v}^{j}$ for its first time derivative at the jth node are defined as:

$$\begin{aligned} e_{u}^{j} = \frac{\mid u_j^{\mathrm{num}} - u_j^{\mathrm{exact}} \mid }{ u_{\mathrm{max}}^{\mathrm{exact}}} \quad \text {and} \quad e_{v}^{j} = \frac{\mid v_j^{\mathrm{num}} - v_j^{\mathrm{exact}} \mid }{ v_{\mathrm{max}}^{\mathrm{exact}}} , \qquad j=1,2,\ldots ,N. \end{aligned}$$

(1)

The maximum relative errors $e_{u}^{\mathrm{max}}$ for the function and $e_{v}^{\mathrm{max}}$ for its first time derivative are defined as:

$$\begin{aligned} e_{u}^{\mathrm{max}} = \max \limits _{j} e_{u}^{j} \quad \text {and} \quad e_{v}^{\mathrm{max}} = \max \limits _{j} e_{v}^{j}, \quad j=1,2,\ldots ,N. \end{aligned}$$

(2)

In Eqs. (1)–(2), the superscripts ‘num’ and ‘exact’ correspond to the numerical and exact solutions, N is the total number of grid points used in calculations, $u_{\mathrm{max}}^{\mathrm{exact}}$ and $v_{\mathrm{max}}^{\mathrm{exact}}$ are the maximum absolute value of the exact solution over the entire domain for the function and its first time derivative, respectively. For the time-dependent wave and heat equations, the errors given by Eqs. (1)–(2) are evaluated at the final observation time T. The errors $e_{v}^{j}$ and $e_{v}^{\mathrm{max}}$ are used for the wave equation only. For the time integration, the trapezoidal rule is used for the wave equation and the backward difference method is used for the heat equation. A sufficiently small size of time steps is used in calculations. In this case, the error in time can be neglected and the numerical error is related to the space-discretization error only. For convenience, the function u is called ‘temperature’ for the heat and Poisson equation and ‘displacement’ for the wave equation. The method of manufactured solutions (see [27]) is used to construct the exact solution $u^{\mathrm{exact}}$ for the test problems solved below. The Neumann or Dirichlet boundary conditions as well as the initial conditions are applied according to the exact solutions.

2.1 1-D wave equation

Let us consider an elastic bar of length $L=1$ discretized with conforming and non-conforming uniform meshes of size h; see Fig. 1. The wave velocity is selected to be $c=1$. Two test problems are considered. As the first test problem, a standing wave in the 1-D bar is selected with the following smooth exact solution:

$$\begin{aligned} u (x , t) =\sin (\beta x)\cos (\beta t) \end{aligned}$$

(3)

with the observation time $T=0.25$, zero loading function $f=0$ and $\beta =5\pi$. The initial displacements and velocities at time $t=0$ as well as the Dirichlet or Neumann boundary conditions at both ends of the bar are applied according to the exact solution (Eq. (3)).

Fig. 1

The spatial locations of the degrees of freedom $u_{i}$ ($i = 1, 2, 3, 4,\ldots$) for a non-conforming uniform mesh in the vicinity of the left end of the 1-D domain

As the second test problem, velocity $v(x=0,t)=1$ is instantaneously applied at the left end of the bar (impact loading). The initial displacements and velocities at time $t=0$ are zero, the right end is free of forces, and the observation time is selected to be $T=0.5$. This problem has the following continuous solution for the displacement and the discontinuous solution for the velocities:

$$\begin{aligned} u (x , t)= & {} t - x , \; t \ge x , \quad \text {and} \quad u (x , t) = 0 , \; t \le x , \end{aligned}$$

(4)

$$\begin{aligned} v (x , t)= & {} 1 , \; t \ge x , \quad \text {and} \quad v (x , t) = 0 , \; t \le x . \end{aligned}$$

(5)

2.1.1 Dirichlet boundary conditions

Let us consider the first test problem with the smooth exact solution (Eq. (3)). In order to study the effect of conforming and non-conforming uniform meshes on the accuracy of the numerical results obtained by the new approach, we create a non-conforming mesh of size h by shifting a conforming mesh of size h to the left with respect to the physical domain by a distance $\xi h$ where $0 \le \xi \le 1$. According to the new approach with the Dirichlet boundary conditions, the node outside the physical domain that is the closest node to the boundary is moved to the boundary; i.e., the distance between the first two nodes is $\xi h$. The distances between other internal nodes of the mesh are the same and equal h; see Fig. 1.

The effect of the varying coefficient $\xi$ of the non-conforming mesh on the maximum relative error in displacement $e_{u}^{\mathrm{max}}$ and in velocity $e_{v}^{\mathrm{max}}$ of the numerical results obtained by the new approach is shown in Fig. 2a–d. It can be seen that the errors $e_{v}^{\mathrm{max}}$ and $e_{u}^{\mathrm{max}}$ remain almost constant in the range $0 \le \xi \le 1$ for the selected mesh sizes h; see curves 1, 2 and 3 in Fig. 2a and b. This means that the new approach yields practically the same results for the conforming ($\xi =1$) and non-conforming ($\xi \ne 1$) meshes at the same h. Moreover, this is valid even for a very small coefficient $\xi$ with $10^{-9} \le \xi \le 10^{-1}$; see Fig. 2c and d.

Let us also consider the case of non-conforming meshes with $\xi >1$; i.e., the distance between the left boundary and the first internal grid point is greater than the mesh size h. This can be implemented by removing the first internal grid point from a non-conforming mesh. As can be seen from Fig. 2e and f, there is only a slight increase in the errors $e_{v}^{\mathrm{max}}$ and $e_{u}^{\mathrm{max}}$ at $1 \le \xi \le 1.5$; i.e., the new approach retains the accuracy of the numerical results even for the coefficient $\xi$ as large as 1.5.

Fig. 2

The logarithm of the maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a, c, e) and in velocity $e_{v}^{\mathrm{max}}$ (b, d, f) at the final time $T=0.25$ as a function of $\xi$ (a, b, e, f) and $Log_{10} \xi$ for small $\xi$ (c, d) for the 1-D wave equation with the Dirichlet boundary conditions at both ends. The new approach with uniform Cartesian meshes of size $h=1/20$ (curve 1), $h=1/40$ (curve 2) and 1/80 (curve 3) is used. c, d Zoom (a, b) along the x-axis for $0 \le \xi \le 0.1$. Symbols $\bigcirc$, $\square$ and $\bigtriangledown$ correspond to the numerical results for the different $\xi$ used in the calculations

Fig. 3

The maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a) and in velocity $e_{v}^{\mathrm{max}}$ (b) at the final time $T=0.25$ as a function of the number N of degrees of freedom in the logarithmic scale for the 1-D wave equation with the Dirichlet boundary conditions at both ends. The new approach with conforming ($\xi =1$, curve 3) and non-conforming ($\xi =0.1$ (curve 1), $\xi =0.5$ (curve 2) and $\xi =1.2$ (curve 4)) meshes is used at mesh refinement. Symbols $\square$, $\bigcirc$, $\bigtriangledown$ and $\times$ correspond to the results for the different N used in the calculations

Next, let us analyze the rate of convergence (the order of accuracy) of the numerical results obtained by the new approach at mesh refinement on non-conforming meshes with constant $\xi$. In order to keep $\xi$ constant for non-conforming meshes at mesh refinement, a conforming mesh of size h is moved to the left by a distance $\xi h$ with respect to the physical domain. The results at mesh refinement with $\xi =0.1$, $\xi =0.5$, $\xi =1$ and $\xi =1.2$ are presented in Fig. 3 where the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ are plotted as a function of the number N of degrees of freedom in the logarithmic scale. The slopes of the curves at large N in Fig. 3 correspond to the order of accuracy of the new approach; i.e., for the considered $\xi$, the order of convergence of the new approach for the displacement and for the velocity is close to four. The errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ for $\xi =0.1$, $\xi =0.5$ and $\xi =1$ are close to each other and are slightly bigger for $\xi =1.2$ at the same h. This is in agreement with the results in Fig. 2 showing a very weak dependence of the numerical results on $\xi$ for $0 \le \xi \le 1$.

Fig. 4

The velocity distribution along the bar at time $T=0.5$ after basic computations (a, c ,e, g) and after the filtering stage (b, d, f, h) for the 1-D impact problem. Conforming [$\xi =1$ (a, b)] and non-conforming [$\xi =0.5$ (c, d), $\xi =0.1$ (e, f) and $\xi =10^{-5}$ (g, h)] meshes with 101 degrees of freedom are used. Curves 1 and 2 correspond to the numerical results obtained by the new approach and by the linear finite elements. Curve 3 corresponds to the exact solutions

The second test problem with the discontinuous solution for the velocity [see Eq. (5)] is solved by the new approach and by the linear finite elements with the same meshes. It is known that the accurate time integration of the semidiscrete systems for impact problems may lead to large spurious oscillations in numerical results. Therefore, the two-stage time integration procedure with the basic computations and the filtering stage (that has been developed in our papers [13, 14]) is used to obtain accurate and non-oscillatory numerical results. The basic calculations in this procedure correspond to the accurate time integration of the semidiscrete system and are equivalent to the time integration procedure of the first test problem. The velocity distribution along the bar at time $T=0.5$ after the stage of basic computations and after the filtering stage is shown in Fig. 4 for the new approach with conforming ($\xi =1$) and non-conforming ($\xi =0.5$, $\xi =0.1$ and $\xi =10^{-5}$) meshes and for the linear finite elements on the same meshes. As can be seen, two considered approaches yield large spurious oscillation after basic computations. However, it is very easy to compare the numerical results after the filtering stage. As can be seen from Fig. 4b, d, f, h after the filtering stage the new approach yields more accurate results compared with the linear finite elements and these results are practically independent of parameter $\xi$ that is related to conforming and non-conforming meshes. We should also mention that a comprehensive study of the numerical solutions of this problem obtained by the high-order elements on conforming meshes is considered in our paper [15].

2.1.2 Neumann boundary conditions

Similar to the Dirichlet boundary conditions, the effect of the varying coefficient $\xi$ on the maximum relative error in displacement $e_{u}^{\mathrm{max}}$ and in velocity $e_{v}^{\mathrm{max}}$ of the numerical results obtained by the new approach with the Neumann boundary conditions can be analyzed. The numerical results show that the errors $e_{v}^{\mathrm{max}}$ and $e_{u}^{\mathrm{max}}$ remain almost constant in the range $0 \le \xi \le 1$ (including very small coefficients $\xi$, $10^{-9} \le \xi \le 10^{-1}$) and only slightly increase at $1 \le \xi \le 1.5$. This behavior is similar to that shown in Fig. 2 for the Dirichlet boundary conditions.

Fig. 5

The maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a) and in velocity $e_{v}^{\mathrm{max}}$ (b) at the final time $T=0.25$ as a function of the number N of degrees of freedom in the logarithmic scale for the 1-D wave equation with the Neumann boundary conditions at both ends. The new approach with conforming ($\xi =1$, curve 3) and non-conforming [$\xi =0.1$ (curve 1), $\xi =0.5$ (curve 2) and $\xi =1.2$ (curve 4)] meshes is used at mesh refinement. Symbols $\square$, $\bigcirc$ , $\bigtriangledown$ and $\times$ correspond to the results for the different N used in the calculations

In order to analyze the order of accuracy of the new approach on conforming and non-conforming meshes, Fig. 5 shows the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale at $\xi =0.1$, 0.5, 1 and 1.2. The slopes of the curves at large N in Fig. 5 correspond to the order of accuracy of the new approach; i.e., for the considered $\xi$, the order of convergence of the new approach for the displacement and for the velocity with the Neumann boundary conditions is close to four. Similar to the Dirichlet boundary conditions in Sect. 2.1.1, with the Neumann boundary conditions the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ are close to each other for $\xi =0.1$, $\xi =0.5$, $\xi =1$ and slightly greater for $\xi =1.2$ at the same h.

It can be concluded that for the 1-D wave equation with the Dirichlet and/or Neumann boundary conditions, the new approach yields very close results on conforming and non-conforming meshes with the same grid size h and provides the 4th order of accuracy.

2.2 2-D Poisson equation

The application of the new approach to irregular domains with Cartesian meshes is considered to the test problems with the following exact solutions to the Poisson equation:

$$\begin{aligned} u(x, y)=\eta \sin (\beta x) \mathrm{e}^{\beta (y-y_{\mathrm{max}})} \end{aligned}$$

(6)

with $\beta =4\pi$ and zero loading function $f=0$, and

$$\begin{aligned} u(x, y)=\eta _1 \sin (\beta _1 x -\beta _2 y) \cos (\beta _3 x -\beta _4 y) \qquad \end{aligned}$$

(7)

with $\beta _1=2 \pi$, $\beta _2=3 \pi$, $\beta _3=4 \pi$, $\beta _4=5 \pi$ and nonzero loading function $f (x, y) = \eta _1 (-(\beta _1^2 +\beta _2^2+\beta _3^2+\beta _4^2) sin(\beta _1 x -\beta _2 y) cos(\beta _3 x -\beta _4 y)+2(-\beta _1 \beta _3+\beta _2 \beta _4) cos(\beta _1 x -\beta _2 y) sin(\beta _3 x -\beta _4 y))$. In Eqs. (6) and (7), $y_{\mathrm{max}}$ is the maximum y coordinate of the domain and the coefficients $\eta = 100$ and $\eta _1 = 50$ are used.

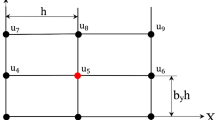
In order to study the effect of conforming and non-conforming meshes on the accuracy of the new approach in the 2-D case, first a simple rectangular plate with the dimensions $1 \times 0.8$ is considered on rectangular and square Cartesian meshes where $b_y$ is the aspect ratio of rectangular meshes ($b_y=1$ for the square meshes); see Fig. 6a. Then, the new approach is applied to a 2-D complex irregular domain presented by a trapezoidal plate OPQR with a circular hole. The angle $\theta =40^{\circ }$ of the trapezoidal plate is considered in calculations; see Fig. 9a.

For the finite element solution of the test problems by the commercial software COMSOL, quadrilateral (Fig. 11a) and triangular (Fig. 11b) meshes generated by COMSOL are used in calculations.

2.2.1 Dirichlet boundary conditions

For the two problems considered in this section, the Dirichlet boundary conditions are applied along the entire boundaries according to the exact solutions (Eqs. (6) and (7)).

First, let us analyze the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical solutions obtained by the new approach for the rectangular plate; see Fig. 6a. For this problem, we use the exact solution given by Eq. (7). In order to create a simple non-conforming Cartesian mesh of size h, we use a conforming Cartesian mesh of size h for the plate with the dimensions $1 \times 0.8$ and then move the upper boundary QR of the plate in the vertical direction by a distance $\xi h$ ($0 \le \xi \le 1$) with respect to the fixed mesh; see Fig. 6b, c. In this case, the height H of the plate is changed from 0.8 to $0.8+\xi h$. The stencils for the non-conforming meshes include the grid points inside the plate and the boundary points (Fig. 6b, c). The boundary points are obtained by the intersection of the boundary with the horizontal, diagonal and vertical grid lines of the Cartesian mesh; see Part 1 of the paper for more details. The corresponding coefficients $d_i$ ($i=1,2,\ldots ,8$) used for the nonuniform stencils close to the upper boundary QR are: $d_1=d_2=d_3=d_4=d_5=1$ and $d_6=d_7=d_8=\xi$ with $0 \le \xi \le 1$; see Fig. 6c and Part 1 for more details.

Remark: Despite the fact that for the conforming and non-conforming meshes we consider the plates with slightly different heights, the exact solutions for these plates are the same and are given by Eq. (7). This allows us to estimate the effect of parameter $\xi$ of the non-conforming meshes with the selected element size h on the accuracy of numerical results.

Figure 7a shows the logarithm of the maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of $\xi$ at the selected mesh sizes h. As can be seen from Fig. 7a, $e_{u}^{\mathrm{max}}$ is almost constant in the range $0.1 \le \xi \le 0.9$ and becomes smaller in the ranges $0 \le \xi \le 0.1$ and $0.9 \le \xi \le 0.1$. Then, at very small $10^{-9} \le \xi \le 10^{-3}$ the error $e_{u}^{\mathrm{max}}$ is almost constant (Fig. 7b) and has the minimum value. This means that the new approach yields accurate numerical results at small $\xi$; i.e., large difference in distances between the points included into a non-uniform stencil does not decrease the accuracy of the new approach. A better accuracy for the conforming meshes at $\xi = 1$ in Fig. 7a is explained by the fact that for square meshes the order of the local truncation error of the uniform stencils for conforming meshes is three orders higher than that of the non-uniform stencils for non-conforming meshes; see Part 1 of the paper.

Fig. 6

The rectangular plate OPQR with conforming (a) and non-conforming (b) rectangular Cartesian meshes of size h and the aspect ratio $b_y$. c Zooms region 1 of b of the non-conforming mesh located close to the upper boundary QR with the Dirichlet boundary conditions

Fig. 7

The logarithm of the maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of the coefficient $\xi$ (a) and $Log_{10} \xi$ for small $\xi$ (b) for the rectangular plate (Fig. 6a). The numerical solutions of the 2-D Poisson equation with nonzero loading function and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes of size $h=1/12$ (curve 1), $h=1/24$ (curve 2) and $h=1/48$ (curve 3). b Zooms a along the x-axis for $0 \le \xi \le 0.1$. Symbols $\bigcirc$ ,$\diamond$ and $\bigtriangledown$ correspond to the results for the different coefficients $\xi$ used in the calculations

Next, the difference in the accuracy of the new approach on uniform square and rectangular meshes for the rectangular plate with the fixed dimensions $1 \times 0.8$ is studied. For the rectangular meshes, at mesh refinement we use the aspect ratio $b_y=0.8$ for conforming meshes and $b_y=0.7$ for non-conforming meshes. (The non-conforming meshes are non-conforming with the upper boundary QR of the plate only.) Figure 8 shows the errors $e_u^{\mathrm{max}}$ for zero and nonzero loading as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. Similar to Fig. 7, the new approach on conforming square meshes yields more accurate results than those obtained on non-conforming square meshes at the same N; compare curves 1 and 2 in Fig. 8. This is in agreement with the theoretical results. (See the comments about Fig. 7.) It can also be seen from Fig. 8 that the results obtained by the new approach on the conforming and non-conforming rectangular meshes are close and are less accurate than those on conforming and non-conforming square meshes at the same N; see curves 1–4. This is in agreement with the theoretical results for the new approach in Part 1 related to the same order of accuracy of the results on conforming and non-conforming rectangular meshes and a higher order of accuracy of the results on conforming and non-conforming square meshes.

The slopes of the curves in Fig. 8 at large N approximately describe the order of accuracy of the numerical techniques because $\sqrt{N}$ is approximately proportional to the mesh size h. (This is strictly valid for conforming meshes.) As can be seen from Fig. 8, at mesh refinement the order of accuracy of the new approach is close to six for conforming square meshes and to five for non-conforming square meshes; see curves 1 and 2 at large N. In contrast to the square meshes, the order of accuracy of the new approach is close to four for both conforming and non-conforming rectangular meshes; see curves 3 and 4 at large N. This is in agreement with the theoretical results reported in Part 1 of the paper.

Fig. 8

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale where N is the number of degrees of freedom. The numerical solutions of the 2-D Poisson equation with zero (a) and nonzero (b) loading functions for the rectangular plate (Fig. 6a) with the Dirichlet boundary conditions are obtained by the new approach. The conforming (curve 1) and non-conforming (curve 2) square meshes with $b_y =1$ as well as the conforming ($b_y =0.8$, see curve 3) and non-conforming ($b_y =0.7$, see curve 4) rectangular meshes are used. Symbols $\square$, $\bigcirc$, $\bigtriangledown$ and $\diamond$ correspond to the results for the different N used in the calculations

Fig. 9

A 2-D trapezoidal plate OPQR with a circular hole of radius 0.25 centered at S(0.6, 0.35) (a) and the Cartesian mesh (b). c and d Zoom regions 2 and 3 of b of the non-conforming mesh located close to the boundary with the Dirichlet boundary conditions

Next, let us analyze the application of the new approach to a more complicated irregular domain represented by a trapezoidal plate OPQR with a circular hole; see Fig. 9a. Due to a higher accuracy of the new approach on square meshes, this problem is solved on square Cartesian meshes; e.g., see Fig. 9b–d. Similar to the previous problem, we consider that the boundaries OP, PQ and OR are always conforming with the Cartesian mesh (Fig. 9b). For the non-conforming meshes, the boundary nodes for the trapezoidal plate in Fig. 9b–d are selected similar to those for the rectangular plate. (See also Part 1 of the paper for more details.) Figure 9c and d zooms Fig. 9b in the vicinity of the upper boundary (see region 1 in Fig. 9a) and the circular boundary (see region 2 in Fig. 9a) in order to show the locations of the boundary nodes on the non-conforming mesh for the new approach. Figure 10 shows the distributions of temperature $u^{\mathrm{exact}}(x, y)$ and the relative error in temperature $e_u(x, y)$ in the trapezoidal plate for zero and nonzero loading functions. As can be seen from Fig. 10a and b, the maximum temperature and the maximum relative error in temperature for the zero loading function are located close to the right upper corner of the plate.

Fig. 10

The distributions of the temperature $u^{\mathrm{exact}}(x, y)$ (a, c) and the relative error in temperature $e_u(x, y)$ (b, d) for the trapezoidal plate with the circular hole; see Fig. 9a. The numerical solutions of the 2-D Poisson equation with zero (b) and nonzero (d) loading functions and the Dirichlet boundary conditions are obtained by the new approach on the square ($b_y=1$) Cartesian mesh of size $h=1/96$

Fig. 11

Examples of meshes with quadrilateral (a) and triangular (b) linear finite elements that are generated by the commercial software COMSOL for the discretization of the 2-D plate OPQR shown in Fig. 9a

Fig. 12

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D Poisson equation with zero (a), nonzero (b) loading functions and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements (curves 2–4) and by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements (curves 5–7). Symbols $\square$, $\bigcirc$, $\times$, $*$, $+$, $\bigtriangledown$ and $\diamond$ correspond to the results for the different N used in the calculations

In order to compare the accuracy of the new approach with FEM, Fig. 12 shows the error $e_{u}^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. (See Fig. 11 for examples of quadrilateral and triangular finite element meshes.) As can be seen from Fig. 12, at the same N the new approach yields more accurate results than those obtained by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements as well as by the conventional linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements. (The quadratic and cubic finite elements have much wider stencils and require more computation time compared to the linear finite elements at the same N.) It can be also seen that at the same accuracy the new approach requires a smaller number N of degrees of freedom compared to those for linear and high-order (up to the third order) finite elements; see Fig. 12.

As we mentioned earlier, the slopes of the curves at large N in Fig. 12 approximately describe the order of accuracy of the numerical techniques because $\sqrt{N}$ is approximately proportional to the mesh size h. According to Fig. 12, for the irregular domain the order of accuracy of the new approach is almost constant at mesh refinement and is close to five; see Fig. 12. This is in agreement with the theoretical results reported in Part 1 of the paper.

Fig. 13

The logarithm of the maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of the coefficients $\xi$ (a) and $Log_{10} \xi$ for small $\xi$ (b) for the rectangular plate (Fig. 6a). The numerical solutions of the 2-D Poisson equation with zero loading function and the combined Neumann and Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes of size $h=1/12$ (curve 1), $h=1/24$ (curve 2) and $h=1/48$ (curve 3). b Zooms a along the x-axis for $0 \le \xi \le 0.1$. Symbols $\bigcirc$, $\diamond$ and $\bigtriangledown$ correspond to the results for the different coefficients $\xi$ used in the calculations

2.2.2 Neumann boundary conditions

Here, we consider the same two problems as those in Sect. 2.2.1. The Poisson equation with zero loading function is considered below. The combined Neumann and Dirichlet boundary conditions are applied as follows: for the rectangular plate (Fig. 6a), the Neumann boundary conditions are imposed along QR and the Dirichlet boundary conditions are imposed along the remaining boundary; for the trapezoidal plate with the circular hole (Fig. 9a), the Neumann boundary conditions are imposed along QR and the circular hole as well as the Dirichlet boundary conditions is imposed along the remaining boundary. All boundary conditions are applied according to the exact solution (Eq. (6)). The grid points located close to the boundary with the Neumann boundary conditions have stencils that include 8 internal grid points along with 4 boundary points with the Neumann boundary conditions. (See Fig. 29 and Part 1 of the paper.)

First, let us analyze the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical solutions obtained by the new approach for the rectangular plate. Figure 13a shows the logarithm of the maximum relative error $e_{u}^{\mathrm{max}}$ as a function of the coefficients $\xi$ for the new approach. (See Fig. 6b, c and Sect. 2.2.1 for the explanation of $\xi$; however, the boundary points for the stencils are selected according to Fig. 29.) The error $e_{u}^{\mathrm{max}}$ on non-conforming meshes ($0 \le \xi < 1$) is always smaller than that on conforming meshes ($\xi =1$) at the same mesh size h; see Fig. 13a. Moreover, at very small $10^{-9} \le \xi \le 10^{-1}$ the error $e_{u}^{\mathrm{max}}$ is almost constant and is also smaller than that for $\xi =1$ (Fig. 13b); i.e., for the combined Neumann and Dirichlet boundary conditions, the new approach yields more accurate results on non-conforming meshes compared to those on conforming meshes. The difference in the accuracy of the new approach on non-conforming and conforming meshes for different boundary conditions (see Sect. 2.2.1) is explained by the different stencils used for the different boundary conditions. For the Neumann boundary conditions, the 8-point stencils used provide the same order of accuracy on non-conforming and conforming meshes. For the Dirichlet boundary conditions, the 9-point stencils used yield a higher order of accuracy on conforming meshes compared to that on non-conforming meshes; see Part 1 of the paper.

Next, let us consider the application of the new approach to the irregular domain represented by the trapezoidal plate with the circular hole; see Fig. 9a. The distribution of temperature $u^{\mathrm{exact}}(x, y)$ for this problem is shown in Fig. 10a. The numerical results show that the maximum relative error in temperature is located close to the right upper corner of the plate similar to that shown in Fig. 10b.

Fig. 14

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D Poisson equation with zero loading functions and the combined Neumann and Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4 and quadratic Q9 quadrilateral finite elements (curves 2 and 3) and by the conventional linear Q3 and quadratic Q6 triangular finite elements (curves 4 and 5). Symbols $\square$, $\bigcirc$, $\times$, $\diamond$ and $\bigtriangledown$ correspond to the results for the different N used in the calculations

In order to compare the accuracy of the new approach with FEM, Fig. 14 shows the error $e_{u}^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. Similar to the Dirichlet boundary conditions in Sect. 2.2.1, at the same N the new approach with the combined Neumann and Dirichlet boundary conditions yields more accurate results than those obtained by the conventional linear Q3 and quadratic Q6 triangular finite elements as well as by the conventional linear Q4 and quadratic Q9 quadrilateral finite elements. (The quadratic finite elements have wider stencils and require more computation time compared to the linear finite elements at the same N.) As we mentioned earlier in Sect. 2.2.1, the slopes of the curves at large N in Fig. 14 approximately describe the order of accuracy of the numerical techniques because $\sqrt{N}$ is approximately proportional to the mesh size h. According to Fig. 14, the order of accuracy of the new approach is almost constant at mesh refinement and is close to five. This is in agreement with the theoretical results reported in Part 1 of the paper.

It can be concluded that at the computational costs of the linear elements, the new approach for the 2-D Poisson equation with the Dirichlet and/or Neumann boundary conditions yields much more accurate results than those obtained by the linear and quadratic finite elements on irregular domains.

2.3 2-D wave equation

The application of the new approach to irregular domains with Cartesian meshes is considered to the test problems with the following exact solutions to the 2-D wave equation:

$$\begin{aligned} u(x, y, t)=sin(\beta x)sin(\beta y)cos(\sqrt{2}\beta t) \end{aligned}$$

(8)

with $\beta =5\pi$ and zero loading function $f=0$, and

$$\begin{aligned} u(x, y, t)=\sin (\beta _1 x)\sin (\beta _2 y)\cos (\beta _3 t) \end{aligned}$$

(9)

with $\beta _1=5 \pi$, $\beta _2=4 \pi$, $\beta _3= 2 \pi$ and nonzero loading function $f (x, y, t) = (-\beta _3^2-c^2(\beta _1^2+\beta _2^2))\sin (\beta _1 x)\sin (\beta _2 y)\cos (\beta _3 t)$. The wave velocity $c=1$ and the observation time $T=0.2$ are chosen. The initial conditions are applied according to the exact solutions (Eqs. (8) and (9)) at time $t=0$.

Similar to the Poisson equation, to study the effect of conforming and non-conforming meshes on the accuracy of the new approach for the wave equation, first a simple rectangular plate with the dimensions $1 \times 0.8$ is considered; see Fig. 6a. Then, the new approach is applied to a 2-D complex irregular domain presented by a trapezoidal plate OPQR with a circular hole. The angle $\theta =40^{\circ }$ of the trapezoidal plate is considered in calculations; see Fig. 9a.

2.3.1 Dirichlet boundary conditions

For the two problems considered in this section, the Dirichlet boundary conditions are applied along the entire boundaries according to the exact solutions (Eqs. (8) and (9)).

First, let us analyze the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical solutions obtained by the new approach for the rectangular plate; see Fig. 6a. The wave equation with nonzero loading function and the exact solution given by Eq. (9) is used. For non-conforming meshes, the stencils with the same grid and boundary points as those for the Poisson equation in Sect. 2.2.1 are used; see Part 1 of the paper for more details.

Figure 15a and c shows the logarithm of the maximum relative errors in velocity $e_{v}^{\mathrm{max}}$ and in displacement $e_{u}^{\mathrm{max}}$ as a function of the coefficient $\xi$ at the selected mesh sizes h for the new approach. (See Fig. 6b, c and Sect. 2.2.1 for the explanation of $\xi$.) As can be seen from Fig. 15a and c, the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ are practically constant in the range $0 \le \xi \le 1$. This means the new approach yields numerical results with the same accuracy for conforming ($\xi =1$) and non-conforming ($\xi \ne 1$) Cartesian meshes. Moreover, at very small $10^{-9} \le \xi \le 10^{-1}$ the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ are almost constant and have the same values as those in the range $0.1 \le \xi \le 1$; see Fig. 15. This means that large difference in distances between the nodes included into a stencil does not decrease the accuracy of the new approach.

Fig. 15

The logarithm of the maximum relative errors in velocity $e_{v}^{\mathrm{max}}$ (a, b) and in displacement $e_{u}^{\mathrm{max}}$ (c, d) at the final time $T=0.2$ as a function of the coefficient $\xi$ (a, c) and $Log_{10} \xi$ for small $\xi$ (b, d). The numerical solutions of the 2-D wave equation for the rectangular plate (Fig. 6a) with nonzero loading function and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes with size $h=1/6$ (curve 1), $h=1/12$ (curve 2) and $h=1/24$ (curve 3). b, d Zoom a, c along the x-axis for $0 \le \xi \le 0.1$. Symbols $\bigcirc$, $\square$ and $\bigtriangledown$ correspond to the results for the different coefficients $\xi$ used in the calculations

Fig. 16

The distributions of the displacement $u^{\mathrm{exact}}(x, y, T)$ (a), the velocity $v^{\mathrm{exact}}(x, y, T)$ (d), the relative errors in displacement $e_u(x, y, T)$ (b) and in velocity $e_v(x, y, T)$ (e) obtained by the new approach with 1829 degrees of freedom as well as the relative errors in displacement $e_u(x, y, T)$ (c) and in velocity $e_v(x, y, T)$ (f) obtained by the conventional linear triangular elements with 1831 degrees of freedom at the final time $T=0.2$. The 2-D wave equation with zero loading function and the Dirichlet boundary conditions is considered for the trapezoidal plate with the circular hole; see Fig. 9a. The square ($b_y=1$) Cartesian mesh of size $h=1/48$ is used with the new approach

Next, let us consider the application of the new approach to the irregular domain represented by the trapezoidal plate with the circular hole; see Fig. 9a. Figure 16a, b, d, e shows the distributions of the displacement $u^{\mathrm{exact}}(x, y, T)$, the velocity $v^{\mathrm{exact}}(x, y, T)$ as well as the relative errors in displacement $e_u(x, y, T)$ and in velocity $e_v(x, y, T)$ in the plate at the final time $T=0.2$ for zero loading functions; see Fig. 16a, b, d, e. As can be seen from Fig. 16a, b, d, e, the error distribution resembles the solution of the wave equation with multiple minimum and maximum. (For example, compare (a) and (b) for the displacements as well as (d) and (e) for the velocities in Fig. 16.) This means that the Dirichlet boundary conditions on irregular domains are accurately met by the new approach and the error distribution is mainly affected by the accuracy of the regular internal stencils inside the domain.

In order to compare the accuracy of the new approach with FEM, Fig. 17 shows the errors $e_{u}^{\mathrm{max}}$ and $e_{v}^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. As can be seen from Fig. 17, at the same N the new approach yields more accurate results than those obtained by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements as well as by the linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements. (The quadratic and cubic finite elements have much wider stencils and require more computational time compared to that of the linear finite elements at the same N.) The distribution of the relative errors in displacement $e_u(x, y, T)$ and in velocity $e_v(x, y, T)$ in the plate with zero loading function at the final time $T=0.2$ is shown in Fig. 16c, f for the linear triangular finite elements with 1831 degrees of freedom. As can be seen from Fig. 16b, c, at approximately the same numbers of degrees of freedom, the distributions of the errors in displacement obtained by the new approach and by the conventional linear triangular elements are similar and approximately differ in amplitudes by a factor of 500 for all points; i.e., the new approach yields much more accurate results at all points.

As we mentioned in Sect. 2.2.1, the slopes of the curves at large N in Fig. 17 approximately describe the order of accuracy of the numerical techniques because $\sqrt{N}$ is approximately proportional to the mesh size h. As can be seen from Fig. 17, the order of accuracy of the new approach is almost constant at mesh refinement and is close to four for the displacement and for the velocity. This is in agreement with the theoretical results reported in Part 1 of the paper.

Currently, we analyze and improve the space-discretization error with the use of the new approach. Below, we also show the effect of the size $\Delta t$ of time increments used for time integration of the new approach (with the implicit second-order trapezoidal rule) and the conventional finite elements (with the implicit second-order BDF method implemented in COMSOL). Figure 18 shows the errors in displacement and velocity for the new technique and finite elements as a function of the size of time increments for the selected space discretization meshes (e.g., we selected the meshes that provide approximately the same error in displacement for the new approach and for the different order finite elements; see Fig. 18a at small $\Delta t$ ). As can be seen, all approaches yield stable and convergent results at time refinement. At large $\Delta t$, the error in time is much larger than the error in space and the slopes of the curves at large $\Delta t$ in Fig. 18 correspond to the second order of convergence in time. The larger error in time for the finite elements in Fig. 18a compared to that for the new approach is explained by the use of the BDF method that has significant damping. At small $\Delta t$, the error in time becomes small and the total error is related to the error in space for the numerical approaches used. (See the horizontal parts of the curves in Fig. 18 at small $\Delta t$.) For all time-dependent problems considered in the paper, small time increments are used in calculations in order to exclude the error in time.

Fig. 17

The maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a, c) and in velocity $e_{v}^{\mathrm{max}}$ (b, d) at the final time $T=0.2$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D wave equations with zero (a, b) and nonzero (c, d) loading function and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements (curves 2–4) and by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements (curves 5–7). Symbols $\square$, $\bigcirc$, $\times$, $+$, $\bigtriangledown$, $\diamond$ and $\star$ correspond to the results for the different N used in the calculations

Fig. 18

The maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a) and in velocity $e_{v}^{\mathrm{max}}$ (b) at the final time $T=0.2$ as a function of the size of time increments $\Delta t$ in the logarithmic scale. The trapezoidal plate with the circular hole (Fig. 9a) is considered. The numerical solutions of the 2-D wave equation with zero loading functions and the Dirichlet boundary conditions are obtained by the new approach on the square ($b_y=1$) Cartesian mesh with $N=1408$ (curve 1), and by the linear finite elements with $N=365{,}158$ (curve 2), the quadratic finite elements with $N=9813$ (curve 3), the cubic finite elements with $N=5265$ (curve 4) on triangular meshes; N is the number of degrees of freedom. Symbols $\bigcirc$, $\bigtriangledown$, $\diamond$ and $\square$ correspond to the results for the different $\Delta t$ used in the calculations

Fig. 19

The distributions of the displacement $u^{\mathrm{exact}}(x, y, T)$ (a), the relative error in displacement $e_u(x, y, T)$ (b), the velocity $v^{\mathrm{exact}}(x, y, T)$ (c) and the relative error in velocity $e_v(x, y, T)$ (d) at the final time $T=0.2$. The trapezoidal plate with the circular hole (Fig. 9a) is considered. The numerical solutions of the 2-D wave equation with zero loading function and the combined Neumann and Dirichlet boundary conditions are obtained by the new approach on the square ($b_y=1$) Cartesian mesh of size $h=1/60$

Fig. 20

The maximum relative errors in displacement $e_{u}^{\mathrm{max}}$ (a) and in velocity $e_{v}^{\mathrm{max}}$ (b) at the final time $T=0.2$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D wave equation with zero loading function and the combined Neumann and Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4 and quadratic Q9 quadrilateral finite elements (curves 2 and 3) and by the conventional linear Q3 and quadratic Q6 triangular finite elements (curves 4 and 5). Symbols $\bigcirc$, $\bigtriangledown$, $\times$, $\diamond$ and $\square$ correspond to the results for the different N used in the calculations

2.3.2 Neumann boundary conditions

Here, we consider the same two problems as those in Sect. 2.3.1. The wave equation with zero loading function is considered below. The combined Neumann and Dirichlet boundary conditions are applied as follows: For the rectangular plate (Fig. 6a), the Neumann boundary conditions are imposed along QR and the Dirichlet boundary conditions are imposed along the remaining boundary; for the trapezoidal plate with the circular hole (Fig. 9a), the Neumann boundary conditions are imposed along QR and the circular hole as well as the Dirichlet boundary conditions are imposed along the remaining boundary. All boundary conditions are applied according to the exact solution (Eq. (8)). The grid points that are close to the boundary with the Neumann boundary conditions have stencils that include 8 internal grid points along with 3 boundary points with the Neumann boundary conditions. (See Fig. 29 and Part 1 of the paper.)

First, let us analyze the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical results obtained by the new approach for the rectangular plate; see Fig. 6. The errors $e_{v}^{\mathrm{max}}$ and $e_{u}^{\mathrm{max}}$ are practically independent of $\xi$ in the range $0 \le \xi \le 1$ as well as for small $\xi$, $10^{-9} \le \xi \le 10^{-1}$. This behavior is similar to that shown in Fig. 15 for the Dirichlet boundary conditions. This means the accuracy of the new approach is not affected by large difference in distances between the nodes included into a stencil.

Next, let us consider the application of the new approach to the irregular domain represented by the trapezoidal plate with the circular hole; see Fig. 9a. Figure 19 shows the distributions of displacement $u^{\mathrm{exact}}(x, y, T)$ and velocity $v^{\mathrm{exact}}(x, y, T)$ as well as the relative errors in displacement $e_{u}(x, y, T)$ and in velocity $e_{v}(x,y, T)$ in the trapezoidal plates at the final time $T=0.2$. It can be seen from Fig. 19 that the maximum relative errors are located close to the boundaries with the Neumann boundary conditions; i.e., in the vicinity of the upper boundary (QR) and the circular hole. In contrast to the Dirichlet boundary conditions in Sect. 2.3.1 (see also Fig. 16), the accuracy of the 8 nodes stencils used for the grid points close to the Neumann boundaries is lower than that of the stencils used for the grid points inside the domain.

In order to compare the accuracy of the new approach with FEM, Fig. 20 shows the errors $e_u^{\mathrm{max}}$ and $e_v^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. As can be seen from Fig. 20, at the same N the new approach yields more accurate results than those obtained by the conventional linear Q3 and quadratic Q6 triangular finite elements as well as by the linear Q4 and quadratic Q9 quadrilateral finite elements. (At the same N, the quadratic finite elements have wider stencils which require more computational time compared to that of the linear finite elements.)

As we mentioned in Sect. 2.2.1, the slopes of the curves at large N in Fig. 20 approximately describe the order of accuracy (convergence) because $\sqrt{N}$ is approximately proportional to the mesh size h. Similar to Sect. 2.3.1 with the Dirichlet boundary conditions, the order of accuracy (convergence) of the new approach is almost constant at mesh refinement and is close to four for the displacement and for the velocity; see curves 1 in Fig. 20. This is in agreement with the theoretical results presented in the Part 1 of the paper.

It can be concluded that at the computational cost of the linear elements, the new approach for the 2-D wave equation with the Dirichlet and/or Neumann boundary conditions yields more accurate results than those obtained not only by the conventional linear finite elements but also by the conventional quadratic finite elements on irregular domains.

2.3.3 Highly oscillatory waves on a complex irregular domain

Let us consider a trapezoidal plate OPQR with a quadrilateral hole ABCD and a 4-sector hole that is symmetric with respect to the horizontal and vertical axes passing through its center S; see Fig. 21a. For the test problem, we select the following highly oscillatory exact solution:

$$\begin{aligned} u(x,y,t)=\sin (25\pi x) sin(25 \pi y) \cos (25\sqrt{2} \pi t) \end{aligned}$$

(10)

with zero loading function $f(x,y,t)=0$. This solution has many local minima and maxima for the displacement and for the velocity on the considered irregular domain; see Fig. 21b and c. The wave velocity c and the observation time T are selected to be $c=1$ and $T=2$. The initial conditions over the entire domain at time $t=0$ and the Dirichlet boundary conditions along the entire boundaries are calculated according to the exact solution (Eq. (10)).

Fig. 21

a A 2-D trapezoidal plate OPQR ($\theta =40^{\circ }$) with a quadrilateral hole ABCD (A(0.2, 0.95), B(0.8, 0.75), C(0.75, 1.05), D(0.35, 1.2)) and 4-sector hole centered at S(0.6, 0.35) with F(0.6, 0.3), G(0.65, 0.35), H(0.6, 0.4), E(0.55, 0.35) and $\alpha =30^{\circ }$. b, c The distribution of the displacement $u(x, y, T=2)$ (b) and the velocity $v(x, y, T=2)$ (c) for the exact solutions

Fig. 22

The distribution of the relative errors in displacement $e_u(x, y, T=2)$ (a, b) and in velocity $e_u(x, y, T=2)$ (c, d) of the numerical solutions obtained by the new approach with 48210 degrees of freedom (a, c) and by the linear triangular finite elements with 652,462 degrees of freedom (b, d). The square ($b_y=1$) Cartesian mesh of size $h=1/200$ is used for the new approach

The problem was solved by the new approach as well as by the linear Q3 and quadratic Q6 triangular finite elements. First, we compare the results for the new approach and for linear finite elements because they have the similar widths of the stencil equations. The computation time on the desktop computer (Intel(R) Core(TM) i7-4790 CPU @ 3.60GHz with 16.0 GB RAM) was about 17 min for the new approach with 48,210 degrees of freedom (using our non-optimized MATLAB code) and about 11 h for the linear finite elements with 652,462 degrees of freedom by the modern commercial code COMSOL.

Figure 22 shows the distribution of the relative errors in velocity and in displacement of the numerical solutions for these two techniques. As can be seen from Fig. 22a and c, the maximum error for the numerical results obtained by the new approach is close to $15 \times 10^{-3}$ (or $1.5 \%$) for both displacements and velocities. On the other hand, with approximately 14 times more degrees of freedom compared to that for the new approach, the linear finite elements yield the numerical results with about the 30$\%$ error for the displacements and for the velocities; see Fig. 22b and d; i.e., this error is about 20 times greater than the error for the new approach.

For linear finite elements with the second order of convergence, we can predict that for the maximum error of 1.5$\%$ (the same as for the new approach) we need to increase the number of degrees of freedom for the linear elements to approximately 13,000,000 (Table 1). In this case, we are not able to solve this problem by the finite elements on our desktop computer due to a prohibitively large computational time.

Table 1 Comparison of number of degrees of freedom N for different numerical techniques

The numerical results also show that in order to obtain the accuracy of 1.5% with the quadratic Q6 finite elements, the increase in the number of degrees of freedom by approximately five times is required compared to that for the new approach; see Table 1. (Quadratic finite elements also have wider stencils compared to those for the new approach.) We should mention that this increase in the number of degrees of freedom is greater if a higher accuracy is necessary. Moreover, in contrast to the complicated mesh generators used for the finite elements, the new approach uses trivial Cartesian meshes for complex irregular domains.

2.4 2-D heat equation

The application of the new approach to irregular domains with Cartesian meshes is considered to the test problems with the following exact solutions to the 2-D heat equation:

$$\begin{aligned} u (x, y, t) = \eta e^{\beta _2 (y-y_{\mathrm{max}}) - a(\beta _1^2 - \beta _2^2)t} \sin (\beta _1 x ) \end{aligned}$$

(11)

with $\beta _1= 4 \pi$, $\beta _2=12$, $\eta =1000$ and zero loading function $f=0$, and

$$\begin{aligned} u (x, y, t) = e^{\beta _4 (y-y_{\mathrm{max}}) + \beta _5 t} \sin (\beta _3 x ) \end{aligned}$$

(12)

with $\beta _3= \frac{7 \pi }{2}$, $\beta _4=\frac{5 \pi }{2}$, $\beta _5= \pi$ and nonzero loading function $f (x, y, t) = (\beta _5 - a(\beta _4^2 - \beta _3^2 ))e^{\beta _4 (y-y_{\mathrm{max}}) + \beta _5 t} sin(\beta _3 x )$. In Eqs. (11) and (12), $y_{\mathrm{max}}$ is the maximum y coordinate of the domain and the coefficient $a=100$ is used. The observation times for the heat equation with zero and nonzero loading functions are chosen to be $T=0.002$ and $T=1$, respectively. The initial conditions are applied according to the exact solutions (Eqs. (11) and (12)) at time $t=0$.

Similar to the Poisson and wave equations, the effect of conforming and non-conforming meshes on the accuracy of the new approach for the heat equation is first analyzed for a simple rectangular plate with the dimensions $1 \times 0.8$; see Fig. 6a. Then, the new approach is applied to a 2-D complex irregular domain presented by a trapezoidal plate OPQR with a circular hole. The angle $\theta =40^{\circ }$ of the trapezoidal plate is considered in calculations; see Fig. 9a.

2.4.1 Dirichlet boundary conditions

For the two problems considered in this section, the Dirichlet boundary conditions are applied along the entire boundaries according to the exact solutions (Eqs. (11) and (12)).

First, the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical solutions obtained by the new approach for the rectangular plate (Fig. 6) is analyzed. The error $e_{u}^{\mathrm{max}}$ is practically constant in the range $0 \le \xi \le 1$ as well as for small $10^{-9} \le \xi \le 10^{-1}$. This behavior is similar to that shown in Fig. 15c and d for the wave equation with the Dirichlet boundary conditions. This means the accuracy of the new approach is not affected by large difference in distances between the nodes included into a stencil.

Next, let us consider the application of the new approach to the irregular domain represented by the trapezoidal plate with the circular hole; see Fig. 9a. The distributions of temperature $u^{\mathrm{exact}}(x, y, T)$ as well as the relative error in temperature $e_u(x, y, T)$ for the trapezoidal plate are shown in Fig. 23a and b for zero loading function at the final time $T=0.002$ and in Fig. 23c and d for nonzero loading function at the final time $T=1$. As can be seen from Fig. 23, the maximum temperature and the maximum relative error in temperature are located close to the right upper corner of the plate.

In order to compare the accuracy of the new approach with FEM, Fig. 24 shows the errors $e_{u}^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. As can be seen from Fig. 24, at the same N the new approach yields more accurate results than those obtained by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements as well as by the linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements. (The quadratic and cubic finite elements have much wider stencils and require more computational time compared to that of the linear finite elements at the same N.)

As we mentioned in Sect. 2.2.1, the slopes of the curves at large N in Fig. 24 approximately describe the order of accuracy of the numerical techniques because $\sqrt{N}$ is approximately proportional to the mesh size h. According to Fig. 24, except the first coarse mesh the order of accuracy of the new approach is almost constant at mesh refinement and is close to four. This is in agreement with the theoretical results reported in Part 1 of the paper.

Fig. 23

The distributions of the temperature $u^{\mathrm{exact}}(x, y, T)$ (a, c) and the relative error in temperature $e_u(x, y, T)$ (b, d) at the final times $T=0.002$ (a, b) and $T=1$ (c, d) for the trapezoidal plate with the circular hole (Fig. 9a). The numerical solutions of the 2-D heat equation with zero (b) and nonzero (d) loading function and the Dirichlet boundary conditions are obtained by the new approach on the square ($b_y=1$) Cartesian mesh of size $h=1/48$

Fig. 24

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ at the final times $T=0.002$ (a) and $T=1$ (b) as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D heat equation with zero (a) and nonzero (b) loading functions and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4, quadratic Q9 and cubic Q16 quadrilateral finite elements (curves 2-4) and by the conventional linear Q3, quadratic Q6 and cubic Q10 triangular finite elements (curves 5–7). Symbols $\bigcirc$, $\times$, $\bigtriangledown$, $\diamond$, $\square$, $+$ and $*$ correspond to the results for the different N used in the calculations

Fig. 25

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ at the final time $T=0.002$ as a function of the number $N_x$ of grid points along the x-axis (a) and as a function of the mesh size h (b) at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a). The numerical solutions of the 2-D heat equation with nonzero loading function and the Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes. b Zooms curve 1 in a for the interval $17 \le N_x \le 19$ and shows curve 1 as a function of the mesh size h. Symbol $\bigcirc$ corresponds to the results for the different $N_x$ (a) or the different h (b) used in the calculations

In order to study the convergence of the new approach in more detail, Fig. 25 analyzes the curve 1 in Fig. 24b at small changes of the mesh size h. (Curve 1 in Fig. 25 corresponds to curve 1 in Fig. 24b.) Figure 25a shows the convergence of the numerical results given by curves 1 in Fig. 24b when the mesh size h of the square Cartesian grids decreases as $h = 1/(N_x-1)$ with the unit increments for $N_x$. ($N_x$ is the number of grid points along the x-axis for the considered domain; see Fig. 9a.) In this case, the vertical and horizontal boundaries are conforming and the upper boundary as well as the circular boundary id non-conforming with the Cartesian grids (Fig. 9b). As can be seen, the new approach converges even at small variations of the grid size h. However, small oscillations may occur. These oscillations become smaller with the decrease in h. One of the oscillations of curve 1 between $N_x=17$ and $N_x=19$ is shown in Fig. 25b in more detail using smaller increments $\Delta h$ between the mesh sizes $h_1= 1/(17-1)=0.0625$ and $h_2 = 1/(19-1) \approx 0.0555$. The small oscillations of curve 1 are explained by the complicated dependence of the leading terms of the local truncation error on the coefficients $d_i$ of nonuniform stencils for the grid points close to the boundary (see Part 1 of the paper and Fig. 28) because the coefficients $d_i$ vary with small variations of the grid size h. This is a typical behavior of the numerical techniques for irregular domains at a relatively large h. For example, the changes in the angles of finite elements at small variations of the element size h also lead to small oscillations in the convergence of the finite element techniques. We should also mention that the detailed study of convergence of the new approach (similar to that in Fig. 25) was also applied to all numerical examples considered in this paper and showed that the new approach yields stable and convergence results.

Fig. 26

The maximum relative error in temperature $e_{u}^{\mathrm{max}}$ at the final time $T=0.002$ as a function of $\sqrt{N}$ at mesh refinement in the logarithmic scale for the trapezoidal plate with the circular hole (Fig. 9a); N is the number of degrees of freedom. The numerical solutions of the 2-D heat equation with zero loading function and the combined Neumann and Dirichlet boundary conditions are obtained by the new approach on square ($b_y=1$) Cartesian meshes (curve 1), by the conventional linear Q4 and quadratic Q9 quadrilateral finite elements (curves 2 and 3) and by the conventional linear Q3 and quadratic Q6 triangular finite elements (curves 4 and 5). Symbols $\bigcirc$, $\times$, $\bigtriangledown$, $\diamond$ and $\square$ correspond to the results for the different N used in the calculations

2.4.2 Neumann boundary condition

Here, we consider the same two problems as those in Sect. 2.4.1. The combined Neumann and Dirichlet boundary conditions are applied as follows: For the rectangular plate (Fig. 6a), the Neumann boundary conditions are imposed along QR and the Dirichlet boundary conditions are imposed along the remaining boundary; for the trapezoidal plate with the circular hole (Fig. 9a), the Neumann boundary conditions are imposed along QR and the circular hole as well as the Dirichlet boundary conditions are imposed along the remaining boundary. All the boundary conditions are applied according to the exact solution (Eq. (11)). Similar to Sect. 2.3.2, the grid points located close to the boundary with the Neumann boundary conditions have the stencils with 8 internal grid points along with 3 boundary points with the Neumann boundary conditions. (See Fig. 29 and Part 1 of the paper.)

First, the effect of conforming and non-conforming square ($b_y=1$) Cartesian meshes on the accuracy of the numerical results obtained by the new approach for the rectangular plate (Fig. 6) is analyzed. The numerical results show that the error $e_{u}^{\mathrm{max}}$ on non-conforming meshes ($0 \le \xi < 1$) is smaller than that on conforming meshes ($\xi =1$) and is practically constant for small $\xi$, $10^{-9} \le \xi \le 10^{-1}$. This behavior is similar to that shown in Fig. 13 for the Poisson equation with the Neumann boundary conditions. This means the accuracy of the new approach is not affected by large difference in distances between the nodes included into a stencil.

Next, let us consider the application of the new approach to the irregular domain represented by the trapezoidal plate with the circular hole; see Fig. 9a. Figure 23a shows the distributions of the exact solution for the temperature $u^{\mathrm{exact}}(x,y, T)$ at the final time $T=0.002$. The distribution of the relative errors in temperature $e_{u}(x, y, T)$ in the trapezoidal plate at the final time $T=0.002$ is similar to that shown in Fig. 23b for the Dirichlet boundary conditions; i.e., the maximum relative error in temperature is located close to the right upper corner of the plate.

In order to compare the accuracy of the new approach with FEM, Fig. 26 shows the error $e_u^{\mathrm{max}}$ for these techniques as a function of the number N of degrees of freedom at mesh refinement in the logarithmic scale. As can be seen from Fig. 26, at the same N the new approach yields more accurate results than those obtained by the conventional linear Q3 and quadratic Q6 triangular finite elements as well as by the conventional linear Q4 and quadratic Q9 quadrilateral finite elements. (The quadratic finite elements have wider stencils and require more computational time compared to that of the linear finite elements at the same N.)

As we mentioned in Sect. 2.2.1, the slopes of the curves at large N in Fig. 26 approximately describe the order of accuracy (convergence) because $\sqrt{N}$ is approximately proportional to the mesh size h. According to Fig. 26, the order of accuracy for the temperature of the new approach is almost constant and is close to four. This is in agreement with the theoretical results reported in Part 1 of the paper.

It can be concluded that at the computational cost of the linear elements the new approach for the 2-D heat equation with the Dirichlet and/or Neumann boundary conditions yields more accurate results than those obtained not only by the conventional linear finite elements but also by the conventional quadratic finite elements at mesh refinement on irregular domains.

3 Concluding remarks

In the considered paper, the new numerical approach developed in Part 1 of the paper has been applied to the time-dependent wave and heat equations as well as to the time-independent Poisson equation on regular and irregular domains with Cartesian meshes. Three-point stencils in the 1-D case and 9-point stencils in the 2-D case that are similar to those for the linear quadrilateral finite elements are considered in the paper. The main numerical results can be summarized as follows:

• The numerical solutions of the 1-D wave equation as well as the 2-D wave and heat equations for a simple rectangular plate show that the accuracy of the new approach on non-conforming meshes is practically the same as that on conforming meshes for both the Dirichlet and Neumann boundary conditions. Moreover, very small distances ($0.1 h - 10^{-9}h$ where h is the grid size) between the grid points of a Cartesian mesh and the boundary do not decrease the accuracy of the new technique.

• For the Poisson equation with the Dirichlet boundary conditions, the new approach for regular domains and conforming meshes yields the sixth order of accuracy on square Cartesian meshes and the fourth order of accuracy on rectangular Cartesian meshes. Therefore, the accuracy of numerical results on conforming square meshes is higher than that on non-conforming square meshes. Nevertheless, even on non-conforming square meshes the new technique yields much more accurate results compared to those obtained by the linear and quadratic finite elements at the same number of degrees of freedom. Similar to the wave and heat equations, very small distances ($0.1 h - 10^{-9}h$ where h is the grid size) between Cartesian grid points and the boundary do not decrease the accuracy of the new technique for the Poisson equation.

• The application of the new approach to the 2-D problems on an irregular domain shows that the order of accuracy is close to four for the wave and heat equations and is close to five for the Poisson equation. This is in agreement with the theoretical results of Part 1 of the paper. The detailed numerical study shows stable and convergent numerical results obtained by the new approach.

• The comparison of the numerical results obtained by the new approach and by FEM shows that at similar 9-point stencils, the accuracy of the new approach on irregular domains is two orders higher for the wave and heat equations and three orders higher for the Poisson equation than that for the linear finite elements. Moreover, the new approach yields even much more accurate results than the quadratic finite elements as well as the cubic finite elements (with the Dirichlet boundary conditions) with much wider stencils. The new technique will allow the solution of new real-world problems that cannot be solved by FEM due to a prohibitively large computation time; e.g., see Sect. 2.3.3.

• The wave and heat equations can be uniformly solved with the new approach. The order of the time derivative in these equations affects the time integration scheme but does not affect the coefficients of the stencil equations of the semidiscrete systems.

The application of the new approach to 3-D problems will be considered in the future.

Appendix A. The summary of the new numerical approach developed in Part 1 of the paper.

The wave and heat equations in domain $\Omega$ can be uniformly written as:

$$\begin{aligned} \frac{\partial ^n u}{\partial t^n} - \bar{c} \nabla ^2 u = f , \end{aligned}$$

(A.1)

where $n=2$ and $\bar{c}=c^2$ for the wave equation as well as $n=1$ and $\bar{c}=a$ for the heat equation, c is the wave velocity, a is the thermal diffusivity, $f (\mathbf{x}, t)$ is the loading term and u is the field variable. The Poisson equation in domain $\Omega$ has the following form:

$$\begin{aligned} \nabla ^2 u = f . \end{aligned}$$

(A.2)

The Neumann boundary conditions $\mathbf{n} \cdot \bigtriangledown u = g_1$ on $\Gamma ^t$ and the Dirichlet boundary conditions $u=g_2$ on $\Gamma ^u$ are applied where $\mathbf{n}$ is the outward unit normal on $\Gamma ^t$ and $\Gamma ^t$ and $\Gamma ^u$ denote the boundaries with the Dirichlet and Neumann boundary conditions, respectively. The initial conditions are $u (\mathbf{x}, t=0) =g_3$, $v (\mathbf{x}, t=0) =g_4$ in $\Omega$ for the wave equation and $u (\mathbf{x}, t=0) =g_3$ in $\Omega$ for the heat equation where $g_i$ ($i=1,2,3,4$) are the given functions.

1.1 Appendix A.1. The stencil equations for the 1-D wave equation

The following 3-point stencils on conforming and non-conforming uniform meshes are used:

$$\begin{aligned} h^2 ({m_1} {\ddot{u}^{\mathrm{num}}_{A-1}}+{m_2} {\ddot{u}^{\mathrm{num}}_{A}}+{m_3}{\ddot{u}^{\mathrm{num}}_{A+1}}) + c^2({k_1} {u^{\mathrm{num}}_{A-1}}+{k_2} {u^{\mathrm{num}}_{A}}+{k_3}{u^{\mathrm{num}}_{A+1}}) = \bar{f} + \bar{f}^{Neum} , \end{aligned}$$

(A.3)

where the case of zero loading $f = \bar{f} = 0$ is considered below, $A=2,\ldots ,N-1$, N is the total number of grid points (Fig. 1). The coefficients $m_j$ and $k_j$ ($j=1,2,3$) are determined in Part 1 from the minimization of the local truncation error and are given: a) by Eq. (15) of Part 1 for the internal nodes $A=3,\ldots ,N-2$ located far from the boundary ($\bar{f}^{Neum} =0$); b) by Eq. (14) of Part 1 for the nodes $A=2,N-1$ located close to the boundary with the Dirichlet boundary conditions ($\bar{f}^{Neum} =0$); c) by Eq. (29) of Part 1 for the nodes $A=2,N-1$ located close to the boundary with the Neumann boundary conditions (for the Neumann boundary conditions, $\bar{f}^{Neum} = f_1$ where $f_1$ is determined by Eq. (30) of Part 1). The coefficients $m_1=k_1=0$ are zero in Eq. (29) of Part 1; i.e., the 2-node stencils, Eq. (A.3) with $m_1=k_1=0$, are used for the points located close to the boundary with the Neumann boundary conditions.

1.2 Appendix A.2. The stencil equations for the 2-D wave and heat equations

Fig. 27

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point uniform stencil for the internal degree of freedom $u_{A,B}$ located far from the boundary

Fig. 28

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point nonuniform stencil for the internal degree of freedom $u_{A,B}$ located close to the boundary with the Dirichlet boundary conditions

The following 9-point stencils on Cartesian meshes are used:

$$\begin{aligned}&h^2 \left\{ m_1 \frac{d^n u^{\mathrm{num}}_{(A-1),(B-1)}}{dt^n} + m_2 \frac{d^n u^{\mathrm{num}}_{A,(B-1)}}{dt^n} + m_3 \frac{d^n u^{\mathrm{num}}_{(A+1),(B-1)}}{dt^n} + {m_4} \frac{d^n u^{\mathrm{num}}_{(A-1),B}}{dt^n} + {m_5} \frac{d^n u^{\mathrm{num}}_{A,B}}{dt^n}\right. \nonumber \\&\quad \left. + m_6 \frac{d^n u^{\mathrm{num}}_{(A+1),B}}{dt^n} + m_7 \frac{d^n u^{\mathrm{num}}_{(A-1),(B+1)}}{dt^n} + m_8 \frac{d^n u^{\mathrm{num}}_{A,(B+1)}}{dt^n} + m_9 \frac{d^n u^{\mathrm{num}}_{(A+1),(B+1)}}{dt^n} \right\} \nonumber \\&\quad +\bar{c} \{ k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\quad + k_6 u^{\mathrm{num}}_{(A+1),B} + k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} \} = \bar{f}_{A,B} + \bar{f}_{A,B}^{Neum} , \end{aligned}$$

(A.4)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ and $\bar{f}_{A,B}$ is defined by Eq. (45) of Part 1 for nonzero load $f \ne 0$, the superscript n in the time derivative in Eq. (A.4) and the material parameter $\bar{c}$ are $n=1$ and $\bar{c}=a$ for the heat equation as well as $n=2$ and $\bar{c}=c^2$ for the wave equation. The coefficients $m_j$ and $k_j$ ($j=1,2,\ldots ,9$) along with the coefficients $l_i$ ($i=1,2,3,4$) used for the Neumann boundary conditions (see below) are determined from the minimization of the local truncation error and are: a) given by Eq. (39) of Part 1 for the internal nodes located far from the boundary (Fig. 27) and $\bar{f}_{A,B}^{Neum} =0$; b) calculated by the solution of 17 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 11,13,14,15,17,20,26$ ($b_p$ are given by Eq. (C.1) of Part 1) for the nodes located close to the boundary with the Dirichlet boundary conditions (see Fig. 28) and $\bar{f}_{A,B}^{Neum}=0$; c) calculated by the solution of 6 linear algebraic equations given by Eq. (52) of Part 1 (as well as Eqs. (C.2) and (A.2) of Part 1) for the nodes located close to the boundary with the Neumann boundary conditions and $\bar{f}_{A,B}^{Neum}=\bar{c} h (l_1 g_1(x_1,y_1,t)+l_2 g_1(x_2,y_2,t)+l_3 g_1(x_3,y_3,t))+ h^3 l_4 \frac{\partial ^n g_1(x_2,y_2,t) }{\partial t^n}$ where $x_i, y_i$ ($i=1,2,3$) are the coordinates of 3 boundary points (Fig. 29) and $g_1(x_i, y_i, t)$ expresses the Neumann boundary conditions. The coefficients $m_7=k_7=0$ for the stencil in Fig. 29 are zero; i.e., the 8-node cut stencils, Eq. (A.4) with $m_7=k_7=0$, are used for the points located close to the boundary with the Neumann boundary conditions.

Fig. 29

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 8-point cut stencils for the internal degrees of freedom $u_{A,B}$ and $u_{A,B+1}$ located close to the boundary with the Neumann boundary conditions. $\bullet$ designates the 8 nodes contributing to the stencil equation

1.3 Appendix A.3. The stencil equations for the 2-D Poisson equation

Nine-node stencils for the degree of freedom $u^{\mathrm{num}}_{A,B}$ of the time-independent Poisson equation can be obtained from Eq. (A.4) with $\bar{c}=1$ and $m_j= 0$ ($j=1,2,\ldots ,9$) as follows:

$$\begin{aligned}&k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\quad + k_6 u^{\mathrm{num}}_{(A+1),B} + k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} = \bar{f}_{A,B} + \bar{f}_{A,B}^{Neum} , \end{aligned}$$

(A.5)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ and $\bar{f}_{A,B}$ is defined by Eq. (D.1) of Part 1 for nonzero load $f \ne 0$. The coefficients $k_j$ ($j=1,2,\ldots ,9$) along with the coefficients $l_i$ ($i=1,2,3,4$) used for the Neumann boundary conditions (see below) are determined from the minimization of the local truncation error and are: a) given by Eq. (58) of Part 1 for the internal nodes located far from the boundary (Fig. 27) and $\bar{f}_{A,B}^{Neum} =0$; b) calculated by the solution of 8 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 8$ ($b_p$ are given by Eq. (C.3) of Part 1) for the nodes located close to the boundary with the Dirichlet boundary conditions (see Fig. 28) and $\bar{f}_{A,B}^{Neum}=0$; c) calculated by the solution of 11 linear algebraic equations $b_p=0$ for $p=1,2,\ldots , 11$ ($b_p$ are given by Eq. (C.4) of Part 1) for the nodes located close to the boundary with the Neumann boundary conditions and $\bar{f}_{A,B}^{Neum}=\bar{c} h (l_1 g_1(x_1,y_1)+l_2 g_1(x_2,y_2)+l_3 g_1(x_3,y_3))+ +l_4 g_1(x_4,y_4)$ where $x_i, y_i$ ($i=1,2,3,4$) are the coordinates of 4 boundary points (Fig. 29), and $g_1(x_i, y_i)$ expresses the Neumann boundary conditions. The coefficients $k_7=0$ for the stencil in Fig. 29 are zero; i.e., the 8-node stencils, Eq. (A.5) with $k_7=0$, are used for the points located close to the boundary with the Neumann boundary conditions.