1 Introduction

Stochastic micromechanical approaches are usually adopted to predict the material’s probabilistic behavior [1,2,3,4,5,6,7,8,9]. As one of the promising techniques for repairing concrete cracks in a water environment or the underground conditions, the electrochemical deposition method (EDM) has been developed in the past 20 years [10,11,12,13,14,15]. Many deterministic micromechanical models were presented to investigate the healing mechanism of EDM from the microscale level [16,17,18,19,20,21,22,23,24]. They do not consider the inherent randomness among the material’s microstructures before healing and during the healing process [10,11,12,13]. Recently, stochastic micromechanical models were proposed for saturated concrete repaired by EDM to incorporate the randomness during the healing process [2].

However, the concrete specimen in the water conditions is usually unsaturated even for a long time [25,26,27]. Meanwhile, the biased results will be led when different assumptions are adopted to represent the real distributions with the common probability density functions (PDFs) [3, 4]. To address these issues, by extending our presented deterministic model [20], a Legendre polynomial-based stochastic micromechanical framework is proposed to quantitatively characterize the unbiased probabilistic behavior of the unsaturated concrete healed by the EDM. The presented stochastic framework is made up of the deterministic micromechanical model for the repaired unsaturated concrete, the stochastic descriptions for the material’s microstructures and the Legendre polynomial-based characterization for the probabilistic behavior. As to the deterministic framework, instead of the effective medium methods, the direct inter-particle interaction micromechanical approach-based multilevel homogenization scheme is employed to obtain the effective properties of the repaired unsaturated concrete. Random vectors are employed for the stochastic descriptions of the repaired concrete’s microstructures. New stochastic simulation framework is proposed to arrive the moduli’s unbiased PDFs by incorporating the Legendre polynomial approximation and Monte Carlo simulations. The outline of this paper is as follows: Section 2 introduces the Legendre orthogonal polynomial, which will be employed to approximate the PDFs of the repaired concrete’s properties in Sect. 4. In Sect. 3, the deterministic micromechanical framework is proposed for the unsaturated concrete repaired by EDM, which is the micromechanical basis for the stochastic framework in Sect. 4. The stochastic micromechanical framework is attained through the incorporations of the stochastic representations, the deterministic models, the Legendre polynomial-based approximations and the Monte Carlo simulations in Sect. 4. Numerical examples including experimental validations and comparisons with existing micromechanical models are presented in Sect. 5, which also discusses the influences of the saturation degrees, the equivalent aspect ratios and the properties of deposition products based on our proposed stochastic micromechanical framework. And some conclusions are reached in the final section.

It is noted that similar limitations exist in this work as many previous stochastic micromechanical models for the composite material, where the random morphologies of the microstructures are not fully taken into considerations [2,3,4,5,6]. More attention is paid on the quite specific microstructures with uncertain quantities, such as the linear elastic constituents, the volume fractions and the aspect ratios.

2 Legendre polynomial

2.1 The orthogonal polynomial

The target PDFs are unknown for the material’s properties. To approximate these unknown PDFs, many orthogonal series, which include the Legendre polynomials (LP), Bessel functions and Fourier series, can be utilized. In this paper, instead of discussing the difference among these orthogonal series, we pay more attention to the unbiased approximations for the unknown target PDFs. Hence, the LP, which is a commonly used decomposing approach, is adopted herein.

Suppose a family of orthogonal polynomial functions \(\varphi \left( x \right) \subset {\mathbf{C}}[a,b]\) and \(\omega \left( x \right) \) is the weight function on [a, b]. The interior product of \(\left\{ {\varphi \left( x \right) } \right\} \) is

$$\begin{aligned} \left( {\varphi _{m} ,\varphi _{n} } \right) =\int _a^b {\omega \left( x \right) } \varphi _{m} \left( x \right) \varphi _{n} \left( x \right) \mathrm{d}x \end{aligned}$$
(1)

where \({\mathbf{C}}[a,b]\) denotes a space composed by all functions that are continuous on real set. An orthogonality relation can be expressed as

$$\begin{aligned} \left( {\varphi _{m} ,\varphi _{n} } \right) =\left\{ {\begin{array}{l} 0,\quad m\ne n \\ H_{n} >0,\quad m=n \\ \end{array}} \right. \; \end{aligned}$$
(2)

where \(H_{n} \) is a constant or a specific function of integer \(\mathrm{n}\)\((\mathrm{n} = 0,1,\ldots )\). If a function f(x) can be expanded by the orthogonal polynomial \(\left\{ {\varphi (x)} \right\} \) with the weight function \(\omega \left( x \right) \) on [a, b], it can be defined as Eq.(3):

$$\begin{aligned} f(x)\approx \omega \left( x \right) \sum \limits _{i=0}^n {\alpha _{i} \varphi _{i} \left( x \right) } \quad \left( {i=0,1,\ldots ,n} \right) \end{aligned}$$
(3)

With the orthogonal relation, the coefficients \(\alpha _{i} \) can be obtained as:

$$\begin{aligned} \alpha _{i} =\frac{\int _a^b {\varphi _{i} \left( x \right) f\left( x \right) \mathrm{d}x} }{\int _a^b {\omega \left( x \right) \varphi _{i}^{2} \left( x \right) \mathrm{d}x} } \end{aligned}$$
(4)

2.2 The Legendre polynomial

As one of the most widely used orthogonal polynomials, Legendre polynomials can be defined by recursive expressions as below:

$$\begin{aligned} \left( {n+1} \right) P_{n+1} \left( x \right) =\left( {2n+1} \right) xP_{n} \left( x \right) -nP_{n-1} \left( x \right) ,\,x\in [-1,\;1] \end{aligned}$$
(5)

with

$$\begin{aligned} P_{0} \left( x \right) =1,\;\;P_{1} \left( x \right) =x \end{aligned}$$
(6)

The first few Legendre polynomials can be expressed as below using the above recursive expressions:

$$\begin{aligned} P_{2} \left( x \right)= & {} \frac{1}{2}\left( {3x^{2}-1} \right) ,\; P_{3} \left( x \right) =\frac{1}{2}\left( {5x^{3}-3x} \right) \end{aligned}$$
(7)
$$\begin{aligned} P_{4} \left( x \right)= & {} \frac{1}{8}\left( {35x^{4}-30x^{2}+3} \right) ,\;P_{5} \left( x \right) =\frac{1}{8}\left( {63x^{5}-70x^{3}+15x} \right) \end{aligned}$$
(8)

The orthogonal condition for Legendre polynomials can be expressed as follows:

$$\begin{aligned} \int \limits _{-1}^1 {P_{n} \left( x \right) P_{m} \left( x \right) \mathrm{d}x} =\frac{2}{2n+1}\delta _{mn} \end{aligned}$$
(9)

where \(\delta _{mn} \) denotes the Kronecker delta, which is equal to 1 if \( m = n\) and to 0 otherwise.

3 Deterministic micromechanical framework for unsaturated concrete repaired by EDM

3.1 Micromechanical representation for the unsaturated concrete repaired by EDM

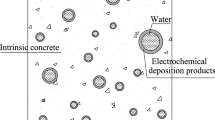
At the microlevel, the concrete repaired by EDM is composed of the pores, the water, the deposition products and the intrinsic concrete [16,17,18,19,20]. By following our previous works [16,17,18,19,20], the micromechanical model for the repaired unsaturated concrete is presented in Fig. 1, where the matrix phase is the intrinsic concrete and the inclusion phases are the pores, the water and the deposition products. The fully saturated (micro-)cracks and (micro-)voids inside the concrete element are assumed to be spherical, and the unsaturated pores are supposed to be ellipsoidal [20].

Fig. 1
figure 1

Multiphase micromechanical model for unsaturated concrete healed using EDM [20]

Full size image

Meanwhile, to illustrate the healing mechanism conveniently, the effective porosity \(\phi _{\mathrm{eff}} \) and the effective saturation degree \(S_{\mathrm{eff}} \) are employed to characterize the deposition process [20]. They can be defined as [20]:

$$\begin{aligned} \phi _{\mathrm{eff}}= & {} m(k_{p} ,t,v)\phi \end{aligned}$$
(10)
$$\begin{aligned} S_{\mathrm{eff}}= & {} \frac{V_{P-\mathrm{sat}} }{V_{P} }=h(k_{p} ,t)S_{w} \end{aligned}$$
(11)

where \(\phi \) refers to the porosity of dry concrete, m is a function of seepage rate \((k_{p})\), seepage time (t) and effective viscosity of water (v), and \(m < 1\) for wet concrete [28, 29]. \(V_{P-\mathrm{sat}} \) is the volume of pores which are fully filled with water; \(V_{P}\) is the total volume of pores in concrete; \(S_{w}\) is the general saturation degree; h is less than 1 [29].

3.2 The multilevel homogenization scheme

Multilevel homogenization scheme has been proved to be effective to obtain the properties of the multiphase composite, such as the shale rock [30, 31], fiber-reinforced composite [32,33,34], mental matrix composite [35,36,37] and particle-reinforced composite [38,39,40,41]. By extending our previous work [20], a similar but different multilevel homogenization scheme based on the direct inter-particle interaction solution is presented to attain the effective properties of the repaired unsaturated concrete. As Fig. 2 illustrates: (i) first, the equivalent inclusion is obtained by the homogenization of the two-phase composite consisting of the water phase and the EDM deposition products. (ii) Second, the equivalent matrix can be reached by the homogenization of the two-phase composite composed of the intrinsic concrete (matrix) and the equivalent inclusion. (iii) Third, the equivalent composite for repaired unsaturated concrete can be attained by the homogenization of the two-phase composite composed of the equivalent matrix and the unsaturated pores.

Fig. 2
figure 2

The multilevel homogenization procedures [20]: a the first level: homogenization of the deposition products and water; b the second level: homogenization of the intrinsic concrete and equivalent inclusion; c the third level: homogenization of the pores and equivalent matrix

Full size image

3.3 The effective properties of equivalent inclusion

According to the three-phase sphere model presented by Christensen and Lo, the effective bulk modulus and shear modulus for the equivalent inclusion can be calculated as [42]:

$$\begin{aligned}&K_{FF} =K_{2} +\frac{\phi _{F} (K_{1} -K_{2} )\;(3K_{2} +4\mu _{2} )}{3K_{2} +4\mu _{2} +3\;(1-\phi _{F} )\;(K_{1} -K_{2} )} \end{aligned}$$
(12)
$$\begin{aligned}&A\left( {\frac{\mu _{FF} }{\mu _{2} }} \right) ^{2}+B\left( {\frac{\mu _{FF} }{\mu _{2} }} \right) +C=0 \end{aligned}$$
(13)
$$\begin{aligned}&\phi _{F} =\text{1 }-\phi _{F\text{ D }} \text{=1 }-\frac{V_{\mathrm{dep}} }{V_{\mathrm{wat}} +V_{\mathrm{dep}} } \end{aligned}$$
(14)

where \(K_{FF}\) and \(\mu _{FF} \) (\(K_{1}{} \textit{ and }\mu _{1}\)) are the bulk modulus and shear modulus of the equivalent inclusion (water); \(\mu _{2} \) is the shear modulus of the deposition product; \(\phi _{FD} \) and \(\phi _{F}\) are, respectively, the volume fraction of the water phase and deposition products in the two-phase composite composed by these two components; \(V_{\mathrm{wat}}\) denotes the volume of the water; and \(V_{\mathrm{dep}}\) signifies the volume of the deposition product. The parameters A, B, C are defined by the properties of the water and deposition products. See details for our previous work [16].

3.4 The effective properties of equivalent matrix

Based on the micromechanical framework, the effective stiffness tensor of two-phase composite considering the inter-particle interaction effects can be derived through [43,44,45]:

$$\begin{aligned} {\mathbf{C}}_{*}= & {} \left[ {{\mathbf{C}}_{0} +\phi _{1} \left( {{\mathbf{C}}_{1} -{\mathbf{C}}_{0} } \right) :{\mathbf{B}}} \right] \end{aligned}$$
(15)
$$\begin{aligned} {\mathbf{B}}= & {} {\varvec{\Gamma } \mathbf{A}}_{1} (\mathbf{A}_{1} +{\mathbf{S}}-\phi _{1} {\mathbf{S}{\varvec{\Gamma }}})^{-1} \end{aligned}$$
(16)

where \({\mathbf{C}}_{*} \) is the effective elastic stiffness tensor of the composite; \({\mathbf{C}}_{0} \) and \({\mathbf{C}}_{1}\) are the elastic stiffness tensor of the matrix phase and the inhomogeneity, respectively; \(\phi _{1} \) is the volume fraction of the inhomogeneity; and \({\mathbf{B}}\) is the strain concentration tensor. The definitions of \({{{\varvec{\Gamma }}}}\) and \({\mathbf{S}}\) can be found in [44].

By substituting the stiffness tensor of the intrinsic concrete and the equivalent inclusion into Eqs. (15)–(16), the effective bulk modulus and shear modulus of the equivalent matrix considering the inter-particle interaction are as follows [44]:

$$\begin{aligned} K_{S}= & {} K_{3} \left\{ {1+\frac{30\left( {1-\nu _{3} } \right) \phi _{\text{ S }} (3\gamma ^{1}+2\gamma ^{2})}{3\alpha +2\beta -10(1+\nu _{3} )\phi _{\text{ S }} (3\gamma ^{1}+2\gamma ^{2})}} \right\} \end{aligned}$$
(17)
$$\begin{aligned} {\mu }'_{S}= & {} \mu _{3} \left\{ {1+\frac{30(1-\nu _{3} )\phi _{\text{ S }} \gamma ^{2}}{\beta -4\left( {4-5\nu _{3} } \right) \phi _{\text{ S }} \gamma ^{2}}} \right\} \end{aligned}$$
(18)
$$\begin{aligned} \phi _{\text{ S }}= & {} \frac{V_{\mathrm{wat}} +V_{\mathrm{dep}} }{V_{\mathrm{wat}} +V_{\mathrm{dep}} +V_{\mathrm{int}} }=\frac{S_{\mathrm{eff}} \phi _{\mathrm{eff}} }{(1-(1-S_{\mathrm{eff}} )\phi _{\mathrm{eff}} )} \end{aligned}$$
(19)

where \(V_{\mathrm{int}} \) defines the volume of the intrinsic concrete matrix; \(S_{\mathrm{eff}} \) is the effective saturation degree; and \(\phi _{\mathrm{eff}} \) is the effective porosity. \(\nu _{3} K_{3}, \mu _{3}\) are, respectively, the Poisson’s ratio, bulk modulus and shear modulus of the intrinsic concrete. \(K_{S} \) and \(\mu _{S} \) are the bulk modulus and shear modulus of the equivalent matrix, respectively. \(\gamma ^{1}\) and \(\gamma ^{\text{2 }}\) are parameter dependent on the material’s properties. See details for [44].

With regard to the effect of water viscosity in pores, we use the effective saturation degree to modify the shear modulus, as described by the following expression [20]

$$\begin{aligned} \mu _{S} =[1+f_{1} (S_{\mathrm{eff}} \phi )^{2}+f_{2} S_{\mathrm{eff}} \phi ]{\mu }'_{S} \end{aligned}$$
(20)

where \(\mu _{S}\) is the effective shear modulus of the equivalent matrix considering the effect of water viscosity and \(f_{1}\) and \(f_{2}\) are parameters investigated by the experiment [20].

3.5 The effective properties of equivalent composite

In the third-level homogenization process, the effective properties of the unsaturated healed concrete (i.e., the equivalent homogenous composite) can be obtained by replacing its matrix phase [46] with the equivalent matrix calculated in the second-level homogenization. The resulting iteration schemes are described by the expressions below:

$$\begin{aligned} (K^{*})_{n+1}= & {} \frac{(1-\phi _{\text{ T }} )K_{S} (P^{*2})_{n} }{(\phi _{\text{ T }} )(P^{*1})_{n} +(1-\phi _{\text{ T }} )(P^{*2})_{n} } \end{aligned}$$
(21)
$$\begin{aligned} (\mu ^{*})_{n+1}= & {} \frac{(1-\phi _{\text{ T }} )\mu _{S} (Q^{*2})_{n} }{(\phi _{\text{ T }} )(Q^{*1})_{n} +(1-\phi _{\text{ T }} )(Q^{*2})_{n} } \end{aligned}$$
(22)
$$\begin{aligned} \phi _{\text{ T }}= & {} (1-S_{\mathrm{eff}} )\phi _{\mathrm{eff}} \end{aligned}$$
(23)

where \((K^{*})_{n+1} \), \((\mu ^{*})_{n+1}\) and \((K^{*})_{n} \), \((\mu ^{*})_{n} \) are the \((n+1)\)th and nth approximations of \(K^{*}\) and \(\mu ^{*}\), respectively; the first approximations are \((K^{*})_{1} =K_{S} \) , \((\mu ^{*})_{1} =\mu _{S}\); \(\phi _{\mathrm{T}} \) is the volume fraction of pores that are not healed. \((P^{*1})_{n} \),\((P^{*2})_{n} \), \((Q^{*1})_{n} \), \((Q^{*2})_{n} \) are coefficients defined by the nth approximations to \(K^{*}\) and \(\mu ^{*}\), i.e., \((K^{*})_{n}\) and \((\mu ^{*})_{n} \). They are dependent on the material’s properties and the equivalent aspect ratio. See details for [46]. When the difference of the value between these two successive approximations is small enough (in the present case, this value is 0.0001), the effective properties of the unsaturated healed concrete can be expressed as follows:

$$\begin{aligned} K_{T}= & {} (K^{*})_{n+1} \end{aligned}$$
(24)
$$\begin{aligned} \mu _{T}= & {} (\mu ^{*})_{n+1} \end{aligned}$$
(25)

where \(K_{T} \) and \(\mu _{T}\) are the effective bulk modulus and shear modulus of the equivalent homogenous composite (i.e., the healed unsaturated concrete). Furthermore, the Young’s modulus of unsaturated concrete can be obtained based on the theorem of elastic mechanics, provided that the bulk modulus and shear modulus are known

$$\begin{aligned} E_{T} =\frac{9K_{T} \mu _{T} }{3K_{T} +\mu _{T} } \end{aligned}$$
(26)

where \(E_{T}\) is the Young’s modulus of the equivalent homogenous composite (i.e., the healed unsaturated concrete).

Considering that the above predictions are based on the assumptions that all pores in the saturated concrete are spherical, the modification coefficients should be introduced when the specimen is dried. See details for [16].

4 Stochastic micromechanical framework for unsaturated concrete repaired by EDM

4.1 Stochastic descriptions for the microstructures of unsaturated concrete repaired by the EDM

According to the deterministic framework in Sect. 3, the macroscopic properties of the repaired concrete are dependent on the components’ properties, the volume fractions and the aspect ratios. Let \(E_{{3}},\nu _{{3}} (E_{{2}} ,\nu _{{2}}\), \(E_{{1}} ,\nu _{{1}} \) and \(E_{{0}}, \nu _{{0}} )\) be the elastic modulus and Poisson’s ratio of the intrinsic concrete matrix (electrochemical deposition product, water and air), respectively. Therefore, the random vector \(\left\{ {E_{{3}} ,E_{{2}} ,E_{{1}} ,E_{{0}} ,\nu _{{3}} ,\nu _{{2}} ,\nu _{{1}} ,\nu _{{0}} } \right\} ^{T}\in {\mathbf{R}}^{8}\) describes stochastic elastic properties of all constituents, where \({\mathbf{R}}^{{8}}\) is an 8-dimensional real vector space. The probability density function of constituent material properties is either assumed or derived from available material characterization data.

During the healing process, the volume fraction of the deposition products will increase with fluctuations and the volume fraction of the matrix phase and unsaturated pores remains constant [2]. Let \(\phi _{m} \), \(\phi _{uns} \) , \(\phi _{sa-w}\) and \(\phi _{sa-d} \) denote the volume fractions of the matrix, unsaturated pores, water in the saturated pores and deposition products in the saturated pores, each of which is bounded between 0 and 1, and satisfy the constraint \(\phi _{m} +\phi _{uns} +\phi _{sa-d} +\phi _{sa-w} =1\), where \(\phi _{uns} =(1-S_{\mathrm{eff}} )\phi _{\mathrm{eff}} \), \(\phi _{sa-d} +\phi _{sa-w} =S_{\mathrm{eff}} \phi _{\mathrm{eff}}\) and \(\phi _{FD} =V_{\mathrm{wat}} /\left( {V_{\mathrm{wat}} +V_{\mathrm{dep}} } \right) =\phi _{sa-w} /\left( {\phi _{sa-d} +\phi _{sa-w} } \right) \). Therefore, the random vector \(\left\{ {S_{\mathrm{eff}} ,\phi _{\mathrm{eff}} ,\phi _{FD} } \right\} ^{T}\) represents the randomness of the different components’ volume fractions in the unsaturated concrete repaired by EDM. In addition, the aspect ratio of unsaturated pores should be described by a random variable \(\alpha _{a} \).

From the above, an input random vector \(\left\{ {E_{{3}}, E_{{2}} ,E_{{1}} ,E_{{0}} ,\nu _{{3}} ,\nu _{{2}} ,\nu _{{1}} ,\nu _{{0}} ,S_{\mathrm{eff}} ,\phi _{\mathrm{eff}} ,\phi _{FD} ,\alpha _{a} } \right\} ^{T}\) characterizes uncertainties from all sources in the unsaturated concrete repaired by EDM based on our proposed micromechanical model. The elastic moduli and the Poisson’s ratios are supposed to follow the lognormal distribution for different components. Since the values of the parameters \(S_{\mathrm{eff}} ,\phi _{\mathrm{eff}} ,\phi _{FD} ,\alpha _{a}\) are between 0 and 1, they are assumed to follow the beta distribution in this paper.

4.2 The moments of the effective properties

Through the stochastic descriptions of the material’s microstructures, the effective properties of the repaired concrete turn to the random functions with multiple random variables according to our proposed deterministic micromechanical model. By employing the Monte Carlo simulations, the different statistics of the effective properties can be obtained with Eqs. (27)–(29):

$$\begin{aligned} \text {mean}\left( {K^{*}} \right)= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {K_{q}^{*} } \right) } ,\;imom\left( {K^{*}} \right) \nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {K_{q}^{*} } \right) ^{i}} \;,sd\left( {K^{*}} \right) =\sqrt{\left( {\frac{1}{M}\sum \limits _{q=1}^M {\left( {K_{q}^{*} -\text {mean}\left( {K^{*}} \right) } \right) }^{2}} \right) ^{1/2}} \end{aligned}$$
(27)
$$\begin{aligned} \text {mean}\left( {\mu ^{*}} \right)= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {\mu _{q}^{*} } \right) } ,\;imom\left( {\mu ^{*}} \right) \nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {\mu _{q}^{*} } \right) ^{i}} \;,sd\left( {\mu ^{*}} \right) =\sqrt{\left( {\frac{1}{M}\sum \limits _{q=1}^M {\left( {\mu _{q}^{*} -\text {mean}\left( {\mu ^{*}} \right) } \right) }^{2}} \right) ^{1/2}} \end{aligned}$$
(28)
$$\begin{aligned} \text {mean}\left( {E^{*}} \right)= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {E_{q}^{*} } \right) } ,\;imom\left( {E^{*}} \right) \nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {E_{q}^{*} } \right) ^{i}} \;,sd\left( {E^{*}} \right) =\sqrt{\left( {\frac{1}{M}\sum \limits _{q=1}^M {\left( {E_{q}^{*} -\text {mean}\left( {E^{*}} \right) } \right) }^{2}} \right) ^{1/2}} \end{aligned}$$
(29)

where M is the sample size; \(\text {mean}\left( \right) \), \(imom\left( \right) \) and \(sd\left( \right) \), respectively, represent the mean, the ith-order moment and the standard deviation for the effective properties; \(K_{q}^{*}\) ,\(\mu _{q}^{*} \) and \(E_{q}^{*} \) are the qth sample of the effective bulk modulus, shear modulus and Young’s modulus.

4.3 The Legendre polynomial-based probability density function

The Legendre polynomials are utilized to approximate the unknown probability density function of the repaired concrete’s properties. For the probability density function (PDF) \(g(x)\subset {\mathbf{C}}[-1,1]\), with Eqs. (3)–(9), the approximation for g(x) can be expressed using the Legendre polynomial (\(\omega \left( x \right) =1\)) as below:

$$\begin{aligned} g(x)\approx \sum \limits _{i=0}^n {\alpha _{i} P_{i} \left( x \right) } \quad \left( {i=0,1,\ldots ,n} \right) \end{aligned}$$
(30)

with

$$\begin{aligned} \alpha _{i} =\frac{\int _{-1}^1 {P_{i} \left( x \right) g\left( x \right) \mathrm{d}x}}{\frac{2}{2i+1}} \end{aligned}$$
(31)

where \(P_{i} \left( x \right) \) is the Legendre polynomial.

According to Eqs. (5)–(8), \(P_{i} \left( x \right) \) can be expressed as:

$$\begin{aligned} P_{i} \left( x \right) =\beta _{i0} +\beta _{i1} x+\beta _{i2} x^{2}+\cdots \beta _{ii} x^{i} \end{aligned}$$
(32)

With Eq.(32)

$$\begin{aligned} \int _{-1}^1 {P_{i} \left( x \right) g\left( x \right) \mathrm{d}x}= & {} \int _{-1}^1 {\left( {\beta _{i0} +\beta _{i1} x+\beta _{i2} x^{2}+\cdots \beta _{ii} x^{i}} \right) g\left( x \right) \mathrm{d}x} \nonumber \\= & {} \beta _{i0} +\beta _{i1} m_{1} +\beta _{i2} m_{2} \cdots \beta _{ii} m_{i} \end{aligned}$$
(33)

where \(m_{1} ,m_{2} \) and \(m_{i} \) are the first-, second- and ith-order moments of random variable x. The coefficients \(\beta _{i0}\), \(\beta _{i1} \), \(\beta _{i2}\) and \(\beta _{ii}\) are available according to the definition of Legendre polynomial. For example, \(\beta _{50} =0,\beta _{51} =\frac{15}{8},\beta _{52} =0;\beta _{53} =-\frac{70}{8},\beta _{54} =0,\beta _{55} =\frac{63}{8}\). By substituting Eq.(33) into Eq.(31), the coefficient \(\alpha _{i} \) can be calculated by Eq.(34):

$$\begin{aligned} \alpha _{i} =\frac{1}{2}\left( {2i+1} \right) \sum \limits _{j=0}^i {\beta _{ij} m_{j} } \end{aligned}$$
(34)

4.4 The PDFs of the effective properties based on Legendre polynomial approximations

Since the values for the effective properties are not between -1 and 1, the linear transformations are adopted herein to meet the conditions of the Legendre polynomial approximations. Let \(\min \left( \right) \) and \(\max \left( \right) \) represent the minimum and maximum values of the effective properties in the samples. Through the linear transformations for the sample of the effective properties with Eqs. (35)–(37), \(K^{*},\mu ^{*}\) and \(E^{*}\) turn to the random variable \(\bar{{K}}^{*},\bar{{\mu }}^{*}\) and \(\bar{{E}}^{*}\) , which are in the region between \(\text{-1 }\) and \(\text{1 }\).

$$\begin{aligned} \bar{{K}}^{*}= & {} \left[ {K^{*}-\frac{1}{2}\left( {\min \left( {K_{q}^{*} } \right) +\max \left( {K_{q}^{*} } \right) } \right) } \right] \big /\max \nonumber \\&\left| {K^{*}-\frac{1}{2}\left( {\min \left( {K_{q}^{*} } \right) +\max \left( {K_{q}^{*} } \right) } \right) } \right| \;\text {with}\;q=1,2,\ldots ,M \end{aligned}$$
(35)
$$\begin{aligned} \bar{{\mu }}^{*}= & {} \left[ {\mu ^{*}-\frac{1}{2}\left( {\min \left( {\mu _{q}^{*} } \right) +\max \left( {\mu _{q}^{*} } \right) } \right) } \right] \big /\max \nonumber \\&\left| {\mu ^{*}-\frac{1}{2}\left( {\min \left( {\mu _{q}^{*} } \right) +\max \left( {\mu _{q}^{*} } \right) } \right) } \right| \text {with}\;q=1,2,\ldots ,M \end{aligned}$$
(36)
$$\begin{aligned} \bar{{E}}^{*}= & {} \left[ {E^{*}-\frac{1}{2}\left( {\min \left( {E_{q}^{*} } \right) +\max \left( {E_{q}^{*} } \right) } \right) } \right] \big /\max \nonumber \\&\left| {E^{*}-\frac{1}{2}\left( {\min \left( {E_{q}^{*} } \right) +\max \left( {E_{q}^{*} } \right) } \right) } \right| \text {with}\;q=1,2,\ldots ,M \end{aligned}$$
(37)

Suppose \(\bar{{g}}()\) is the PDF for the effective properties after linear transformations using Eqs. (35)–(37). According to Eqs. (30)–(34), the Legendre polynomial approximation for \(\bar{{g}}()\) can be obtained with the following expressions:

$$\begin{aligned} \bar{{g}}_{k} (x)\approx & {} \sum \limits _{i=0}^n {\alpha _{i}^{k} P_{i} \left( x \right) } \;\;\left( {i=0,1,\ldots ,n} \right) \,\text { with } \,\alpha _{i}^{k} =\frac{1}{2}\left( {2i+1} \right) \sum \limits _{j=0}^i {\beta _{ij} \bar{{m}}_{j}^{k} } \;\text { and }\;\bar{{m}}_{j}^{k}\nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {\bar{{K}}_{q}^{*} } \right) } ^{j} \end{aligned}$$
(38)
$$\begin{aligned} \bar{{g}}_{\mu } (x)\approx & {} \sum \limits _{i=0}^n {\alpha _{i}^{\mu } P_{i} \left( x \right) } \;\;\left( {i=0,1,\ldots ,n} \right) \;\text { with }\;\alpha _{i}^{\mu }=\frac{1}{2}\left( {2i+1} \right) \sum \limits _{j=0}^i {\beta _{ij} \bar{{m}}_{j}^{\mu } } \;\text { and }\;\bar{{m}}_{j}^{\mu }\nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {\bar{{\mu }}_{q}^{*} } \right) } ^{j} \end{aligned}$$
(39)
$$\begin{aligned} \bar{{g}}_{E} (x)\approx & {} \sum \limits _{i=0}^n {\alpha _{i}^{E} P_{i} \left( x \right) } \;\;\left( {i=0,1,\ldots ,n} \right) \;\text { with }\;\alpha _{i}^{E} =\frac{1}{2}\left( {2i+1} \right) \sum \limits _{j=0}^i {\beta _{ij} \bar{{m}}_{j}^{E} } \;\text { and }\;\bar{{m}}_{j}^{E}\nonumber \\= & {} \frac{1}{M}\sum \limits _{q=1}^M {\left( {\bar{{E}}_{q}^{*} } \right) } ^{j} \end{aligned}$$
(40)

With \(\bar{{g}}()\), the PDF g() of the effective properties can be obtained as follows:

$$\begin{aligned} g_{K} \left( x \right)= & {} \frac{1}{\max \left| {K^{*}-\frac{1}{2}\left( {\min \left( {K_{q}^{*} } \right) +\max \left( {K_{q}^{*} } \right) } \right) } \right| }\bar{{g}}\nonumber \\&\left( {\frac{\left[ {x-\frac{1}{2}\left( {\min \left( {K_{q}^{*} } \right) +\max \left( {K_{q}^{*} } \right) } \right) } \right] }{\max \left| {K^{*}-\frac{1}{2}\left( {\min \left( {K_{q}^{*} } \right) +\max \left( {K_{q}^{*} } \right) } \right) } \right| }} \right) \;\;\left( {q=1,2\ldots ,M} \right) \end{aligned}$$
(41)
$$\begin{aligned} g_{\mu } \left( x \right)= & {} \frac{1}{\max \left| {\mu ^{*}-\frac{1}{2}\left( {\min \left( {\mu _{q}^{*} } \right) +\max \left( {\mu _{q}^{*} } \right) } \right) } \right| }\bar{{g}}\nonumber \\&\left( {\frac{\left[ {x-\frac{1}{2}\left( {\min \left( {\mu _{q}^{*} } \right) +\max \left( {\mu _{q}^{*} } \right) } \right) } \right] }{\max \left| {\mu ^{*}-\frac{1}{2}\left( {\min \left( {\mu _{q}^{*} } \right) +\max \left( {\mu _{q}^{*} } \right) } \right) } \right| }} \right) \; \left( {q=1,2\ldots ,M} \right) \end{aligned}$$
(42)
$$\begin{aligned} g_{E} \left( x \right)= & {} \frac{1}{\max \left| {E^{*}-\frac{1}{2}\left( {\min \left( {E_{q}^{*} } \right) +\max \left( {E_{q}^{*} } \right) } \right) } \right| }\bar{{g}}\nonumber \\&\left( {\frac{\left[ {x-\frac{1}{2}\left( {\min \left( {E_{q}^{*} } \right) +\max \left( {E_{q}^{*} } \right) } \right) } \right] }{\max \left| {E^{*}-\frac{1}{2}\left( {\min \left( {E_{q}^{*} } \right) +\max \left( {E_{q}^{*} } \right) } \right) } \right| }} \right) \;\left( {q=1,2\ldots ,M} \right) \end{aligned}$$
(43)

where \(g_{K} \left( x \right) \), \(g_{\mu } \left( x \right) \) and \(g_{E} \left( x \right) \) are the PDFs for the effective bulk modulus, shear modulus and Young’s modulus.

5 Verification and discussions

5.1 Verification for the stochastic micromechanical framework

The proposed stochastic micromechanical framework is made up of the deterministic micromechanical model for unsaturated concrete repaired by EDM, the stochastic description of the material’s microstructures and the Legendre polynomial-based PDFs.

The results of the proposed deterministic micromechanical model are compared with those of the previous model [20]. Figure 3a exhibits the comparisons between the predicted shear modulus obtained by the proposed model and those of the existing model [20]. It can be found that the maximum difference between these two results is less than 10%. With the decrease in the effective saturation degrees, the relative differences diminish. With the increase in the deposition products, these two predicted results are almost the same with each other. When the effective bulk modulus is considered, the similar conclusions can be reached as Fig. 3b displays.

Fig. 3
figure 3

Comparisons between the predicting properties obtained by the proposed model and those of the existing model [20]

Full size image

If the effective saturation degree is 100% and all these defects are totally repaired, the proposed micromechanical model can obtain the properties of the particle-reinforced composite. As Fig. 4 illustrates, our predictions correspond well with the experimental data of particle-reinforced composite [47]. When the particle volume fraction increases, our predictions are better than those of the existing model, including the Hashin–Shtrikman (H–S) bounds [45] and the results of Yan et al. [20].

Fig. 4
figure 4

Comparisons among predictions herein, those of the previous work [20], Hashin–Shtrikman (H–S) bounds [45] and the experimental data [47] for the Young’s modulus

Full size image
Fig. 5
figure 5

Comparison between the results obtained with the proposed model and theoretical results for the commonly used probability density function

Full size image

The two commonly used probability distributions, including the normal distribution and lognormal distribution, are utilized to test the effectiveness of the Legendre polynomial-based PDFs, which are distribution-free. As Fig. 5a shows, when the 8th-order moments are used, the results of our proposed method are acceptable compared with the theoretical solutions for the normal distribution. With the higher-order moments, the Legendre polynomial-based PDFs are more accurate. Similarly, the proposed Legendre polynomial-based approach is also capable of representing the Lognormal distribution without any premise, which is displayed in Fig. 5b.

Fig. 6
figure 6

Comparisons among the results obtained with the proposed model and those obtained experimentally [13] for the Young’s modulus

Full size image

The proposed stochastic micromechanical framework is further verified by the experimental data for the same batch of concrete specimens repaired by EDM [13]. Figure 6 shows the comparisons of our results and the experimental data. It can be found that the distributions obtained using the stochastic framework herein are acceptable compared with the histogram of the experimental data before healing, as Fig. 6a shows. After healing, the predicting results with the saturation degree being 90% correspond better with the experimental data than those with the saturation degree as 100%, which is exhibited in Fig. 6b. There are some deviations between our predicting results and the experimental data. The reasons may include: Firstly, the input data for the intrinsic concrete in the proposed model are based on the linear regression results of the limited experimental data [13], since it is hard to produce the concrete specimen with the zero porosity. Secondly, the exact saturation degrees are difficult to be tested [13]; the input data for the effective saturation degree are assumed to be 100% and 90% in this numerical example. Thirdly, the interface effects between the deposition products and the intrinsic concrete are not considered in this model. The interface will degrade the healing effects of the EDM [19, 22].

5.2 Discussions on the influence of the saturation degrees and the deposition products

The effective saturation degrees, the equivalent aspect ratios and the properties of deposition products play important roles in determining the properties of the repaired concrete. Based on our proposed stochastic framework, the statistical influence of these factors can be quantitatively reached on the macroscopic properties of the repaired concrete.

Figure 7a and b presents the comparisons among the PDFs of the properties of the repaired concrete obtained with different saturation degrees and aspect ratios. The mean values for the saturation degrees are, respectively, 0.6 and 0.9, and those for the aspect ratios are 0.2 and 0.8, respectively. The coefficient of variation for these variables is 0.1 in this numerical case. From Fig. 7a, with the increase in the mean value of the saturation degrees, the repaired concrete demonstrates greater shear modulus statistically. Meanwhile, the shear modulus increases statistically when the mean values of the equivalent aspect ratio raise. For the effective bulk modulus, similar results can be obtained from Fig. 7b.

Fig. 7
figure 7

Influence of the saturation degrees and aspect ratios on the property distributions for the repaired concrete

Full size image
Table 1 Properties of three types of deposition products
Full size table
Fig. 8
figure 8

Influence of deposition products on the property distributions for the repaired concrete

Full size image

The properties of deposition products are influenced by many factors, such as the type of the solution, the microstructure of the specimen and the density of the current. The repairing effects will differ when the properties of the deposition products change. Figure 8 displays the probability density functions of the effective properties of the repaired concrete with three different deposition products, whose properties are from [13] as Table 1 shows. It is observed from Fig. 8a that the repaired concrete demonstrates greater shear modulus statistically when the mean values for the properties of the deposition products increase. As to the bulk modulus, similar conclusions can be reached from Fig. 8b.

6 Conclusions

Based on our previous works [16,17,18,19,20], a stochastic micromechanical framework is proposed to quantitatively characterize the probabilistic behavior of the unsaturated concrete healed by the EDM. Meanwhile, instead of the effective medium methods, the direct inter-particle interaction micromechanical approach is employed to obtain the effective properties of repaired concrete. The unbiased probability density functions (PDFs) of the effective properties are reached by incorporating the Legendre orthogonal polynomial approximation and Monte Carlo simulations. Meanwhile, numerical examples are conducted including experimental validations and comparisons with existing micromechanical models. And some conclusions can be reached as follows:

  1. (1)

    The proposed stochastic micromechanical frameworks are effective to obtain the unbiased PDFs for the effective properties of the unsaturated concrete repaired by EDM.

  2. (2)

    The multilevel homogenization scheme herein predicts more accurate results when the particle volume fraction increases.

  3. (3)

    The presented Legendre orthogonal polynomial-based stochastic simulation program can approximate the commonly used PDFs without any assumptions.

  4. (4)

    The statistical effects of the saturation degrees and the deposition products can be quantitatively reached with the proposed framework.

In our future work, the interface effects between the deposition products and the intrinsic concrete will be considered for the repaired concrete, and much more experiment will be performed to improve the accuracy of the input data. Meanwhile, the additional modeling of epistemic uncertainty for the input variables will be included.