On optimality of column geometry

Abstract

Critical loads of columns under compressive follower forces have been widely discussed in the literature. By means of shape optimization, improvements by factors of more than eight could be achieved. However, the obtained solutions turn out to be not robust against perturbations of shape or material parameters. The aim of this paper is to explain this sensitivity effect, basing on a study of eigenforms. Further, a robust alternative to the classical optimization approach is proposed.

1 Introduction

The study of critical loads of constructions has a long tradition, it goes back to L. Euler [17, 18], and is still of ongoing interest [10, 12], due to new designs and new challenges as, e.g., in jet propulsion or wind turbines. In particular, variable forcing, coupling effects, passive and active control [13] are important issues. The maximization of critical loads, but also the avoidance of certain undesirable eigenfrequencies, earns a lot of attention. In this context—as well as in numerous others—it was observed that the optimization of shape and other construction parameters frequently leads to negative effects. In particular, the robustness against perturbations of design variables and of the loading conditions, considered for an optimized column, may turn out to be unsatisfactory. Several authors obtained astonishing critical loads for Beck’s column, see Fig. 1, middle, but the results could not be confirmed by different numerical methods, see, e.g., [14].

In [2] we reported a severe drop in the critical load after (accidentally) rounding profile data from double to single floating point numbers, compare Fig. 2.

Fig. 1

Euler’s, Beck’s and Reut’s columns

Fig. 2

Catastrophic change in root curve topology in $P-\omega$-plane, stepped Beck’s column

In this analysis, Fig. 2, the critical load of a Beck’s column was studied for two almost identical geometries. One of the columns stays stable for much larger loads. Since the linear elastic case was studied, this means that a tiny initial displacement or velocity causes a superposition of periodic oscillations. An analysis of the expansion of a small perturbation to the equilibrium state in the system of eigenforms shows that, once the critical load is exceeded, some contributions start growing exponentially. In Fig. 2, this happens at a lower load in the case represented on the lower part than on the upper part. This behavior is typical of non-conservative problems, to which the Beck’s and Reut’s columns belong. In that, they differ from conservative, self-adjoint problems, where instead of flutter, a divergent loss of stability is observed. We concentrate here on the non-conservative case, i.e., constructions and loading conditions featuring follower or circular forces.

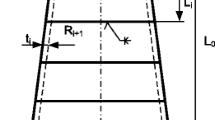
In general, in optimization of parameters of this class of constructions, not only a non-convex, but even a discontinuous dependence of the critical load on parameters may be observed. In the case of columns, this may include the shape or make, including the thickness and mass density as functions of the length variable as well as internal joints with their stiffness and damping parameters, cf. Fig. 3.

The key to an understanding of the mentioned effects lies in the analysis of eigenforms of the considered constructions under loads close to the critical one. As a rule, the characteristic curves in the $P-\omega$-plane become not only higher but also more and more slender during the optimization process. Typically, in the vicinity of maximizers, one can find configurations, where neighboring branches touch, see Fig. 8 in the next section. This leads to catastrophic changes in the topology of root curves, where a new, considerably lower, local maximizer appears, with the corresponding eigenfrequency jumping and a different eigenform at the new critical point. This discontinuous behavior is presented in Fig. 2.

Notice that in the classical Euler case, Fig. 1, left, for dead load at a certain low and constant level, with frequency increasing from zero, one passes through consecutive resonances, where the number of nodes of the eigenforms, cf. Fig. 4, is always the same as their counter indicates. The change in the eigenmodes is visualized in Fig. 5. However, this counter-mode relation is violated, if shapes are modified and loads are increased, with different thresholds for other kinds of loading, e.g., the Beck, Reut or Lipmann cases. On this issue, see also [7].

Fig. 3

Discontinuous critical load as function of shape parameters (width of upper segment, position of interface between two segments)

An example is shown in Fig. 4. The characteristic root curves corresponding to Euler, Beck and Reut conditions intersect for a load close to 80% of the critical Beck load. Close to this point, the unstable second eigenform of the Euler column has only one root. However, it has a change in the sign of curvature, i.e., a zero of the second derivative. For this reason, we propose to consider it a second, not first, mode of oscillation.

Fig. 4

Characteristic curves (left), first and second Euler eigenforms near triple point (right)

This effect becomes more evident, when the shape of the column, i.e., its thickness profile function, is optimized, so that the critical load of a column with uniform thickness is by far exceeded, as in Fig. 8. Hence, we propose a modification of the way nodes are defined and hence calculated. In fact, we look at changes in the sign of the curvature instead of the sign of the displacement itself. This definition is consistent with the classical approach, since in the Euler case the eigenforms are sinusoidal, and zeros of the function and its second derivatives are identical. However, in general, despite the fact that we have only one point with zero displacement, there may be nonetheless two arcs with opposite signs of curvature. This classifies those eigenforms as second modes.

Fig. 5

Changing eigenforms with load parameter (displacements exaggerated. Sign of $u\left( x \right)$ near the clamped end is assumed positive, which leads to jump at top end)

A chart, mapping the location of certain modes for Beck’s column in the $P-\omega$-plane, is shown in Fig. 6.

Fig. 6

Map of eigenmodes according to node count

Load versus frequency, numbers of nodes of eigenforms of Beck’s column

The discontinuities of the objective, as shown in Fig. 3 on a low-dimensional example, are related to changes in the responsible unstable mode. The drop of the critical load coincides also with a jump in the frequency of the flutter mode that shows an exponentially growing amplitude.

This means that for a shape-optimized Beck’s column—and in generalization any other non-conservative construction—a perturbation of displacement and velocity does not ensue growth of the disturbance. Indeed, the stability of the dynamical system as a constraint is respected during optimization. However, the tiniest variation of the mass distribution, or the angle between force and tangent, or damping by friction or weakening of a support, may change drastically eigenmode and eigenfrequency. If, in the consequence of a small disturbance of the system configuration, such an eigenfrequency moves into the complex plane, with a positive imaginary part, then flutter type instability occurs.

Now, by robustness we understand a column design that not only ensures stability of the dynamical system for the given set of geometrical and material properties, but also in the case of any variations in a certain neighborhood of the considered original configuration.

In order to obtain practically applicable results for critical loads, we propose hence to evaluate the worst case load (WCL). Assuming a maximal tolerable measure of deviation from the given shape, parameters and loading conditions, each given configuration is assigned the least critical load over all neighboring configurations within this tolerance. This approach makes optimization more expensive, and it gives considerably smaller optimal loads. The results, however, are robust to (sufficiently small) manufacturing errors and disturbances during the utilization of the considered construction.

2 Model equations

We denote by $u=u\left( {x,t} \right)$ the lateral displacement of the middle line of the considered column, and position $x\psi$ and time $t\psi$ are the independent variables. Partial derivatives we indicate by subscripts, sub $t\psi$ for the time derivative, sub x for the space derivative.

Knowing the limitations of the theory, we follow Euler and Bernoulli and consider in (1) only the balance of momentum in the lateral direction, see also [3, 7, 8].

$$\begin{aligned} \left( {S\left( x \right) u_{xx} \left( {x,t} \right) +Pu\left( {x,t} \right) } \right) _{xx} +\rho \left( x \right) u_{tt} \left( {x,t} \right) =0 \end{aligned}$$

(1)

We assume clamped conditions at the bottom, $u\left( {0,t} \right) =u_x \left( {0,t} \right) =0$. At the tip of the column, $x=L>0$, one may impose a variety of conditions. However, later on we will focus our attention on the Beck case. In the Euler case, moment and lateral force are assumed to vanish, (2, 3).

$$\begin{aligned}&\displaystyle u_{xx} \left( {L,t} \right) =0 \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \left( {S\left( x \right) u_{xx} \left( {x,t} \right) +Pu\left( {x,t} \right) } \right) _x |_{x=L} =0 \end{aligned}$$

(3)

For Beck’s column, the bending moment is supposed to be zero as well, but the lateral force is set proportional to the inclination $u_x \left( {L,t} \right)$. This leads to a reduced form of (3), where the term with P drops out, (4),

$$\begin{aligned} \left( {S\left( x \right) u_{xx} \left( {x,t} \right) } \right) _x |_{x=L} =0 \end{aligned}$$

(4)

So the external force is always tangential to the center line of the deformed column at its upper end point, $x=L$. The modulus P of the compression force, which is constant in (1), plays the role of a loading parameter in the stability analysis.

The conditions imposed by Reut consist of a zero lateral force component; therefore, a bending moment equal to $-u\left( L \right) P\psi$ is applied in order to bring the column back to its straight upward position. A variational formulation reveals that the Beck and Reut cases are adjoint to each other. Hence none of the two problems is self-adjoint, and both have identical eigenvalues. The eigenmodes, of course, look quite different. The critical load is several times higher than in the pure Euler case, where there is just a dead load, while here a restoring force appears, respectively, a restoring moment, giving a stabilizing effect.

By $S\psi$, the bending stiffness is abbreviated. Notice that the mass density, which is related to the length measure, $\rho \left( x \right) =\rho _\mathrm{mat} \left( x \right) A_\mathrm{cross} \left( x \right)$ as well as the stiffness $S=S\left( x \right) \psi$ depends on the location x, but not on time t. On the other hand, $P\psi$ is a concentrated force; hence, it does not depend on the space variable x. While it might be a function of time t, for this paper, we assume it constant. Of course, $P\psi$ is just the modulus—the direction of the force is variable in Beck’s case; thus the system (1, 2, 4) is a special case of a problem with a follower force. Analogous problems may be considered for other choices of (2, 4), e.g., the Reut case is very similar and in the same class. Here, the modulus of the force is constant, the direction is unchanged as well—but the force is applied at a variable point on a lever. The Euler case, on the other side, is distinguished by a constant force, acting always at the same material point and in the same direction. For this reason it called a dead load.

For better comparison, the variables in (1, 2, 4) are assumed to be dimensionless. Division by a suitable characteristic length, density and stiffness eliminates the coefficients. Then the load is measured in multiples of $S^{-1}L^{-2}$, where $L\psi$ denotes the true physical length of the column, and S is a typical value of the bending stiffness.

Inserting $u\left( {x,t} \right) =w\left( x \right) \sin \left( {\omega t} \right)$ into the equation of motion (1) for the inviscid case, gives

$$\begin{aligned} \left( {S\left( x \right) w_{xx} \left( x \right) +Pw\left( x \right) } \right) _{xx} =\rho \left( x \right) \omega ^{2}w\left( x \right) \end{aligned}$$

(5)

which is a fourth-order linear ordinary differential equation.

Fig. 7

Complex root curves in Beck’s case

Since the boundary value problem (1, 2, 4) is non-self-adjoint, non-real complex eigenvalues may occur. Figure 7 shows that this happens, indeed. For a column of uniform width (density and bending stiffness all constant and equal to 1, since we consider the dimensionless case), the onset of a non-vanishing imaginary part of a characteristic root happens at $P\approx 20$.

Fourth-order Eq. (5) can be rewritten as a first-order system for the vector-valued function y comprising four scalar variables $\left( {w,\alpha ,M,Q} \right) ^\mathrm{T}=:y$

$$\begin{aligned} {y}'(x)=Ay(x) \end{aligned}$$

(6)

with the matrix

$$\begin{aligned} A(x)=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}1&{}0&{}0\\ 0&{}0&{}S^{-1}(x)&{}0\\ 0&{}0&{}0&{}1\\ \rho (x)\omega ^{2}&{}0&{}P&{}0\\ \end{array}\right] \end{aligned}$$

(7)

A general solution can be expressed by the formula

$$\begin{aligned} y\left( x \right) =\hbox {exp}\left( {\mathop \int \limits _{x_0 }^x A\left( \xi \right) \mathrm{d}\xi } \right) y\left( {x_0 } \right) \end{aligned}$$

(8)

Here, the matrix exponential function may be defined by the power series

$$\begin{aligned} \exp \left( B \right) =I+B+\frac{1}{2!}B^{2}+\frac{1}{3!}B^{3}+\ldots \end{aligned}$$

(9)

However, when eigenvectors or main vectors of $\hbox {B}\psi$ are known, a finite representation of the solution in terms of scalar exponential functions can be given.

The aim of this paper is to find optimal shapes of columns, in a sense to be specified later, and hence a high number of evaluations of problem (1, 2, 4), with variations to its parameters, will be required. For this reason, it is essential to find a possibly convenient equivalent re-formulation. The first-order linear system (6) with solution (8) turns out to serve this purpose very well.

We assume, as before, the lower end to be at $x_0 =0$, and the boundary condition there is $w\left( x \right) =u\left( {x,t} \right) ={w}''$, i.e., the column is clamped at the lower end. In general, two independent quantities at each of the ends $x=x_0 =0$ and $x=L=1$ are given as boundary conditions. These may be any suitable independent combinations of the components of the vector y. The boundary value problem can now be stated as

$$\begin{aligned} RY\left( L \right) =RY\left( {L,P,\omega ,S,\rho } \right) \Pi z_0 =0 \end{aligned}$$

(10)

For example, in the case of a Beck’s column, $z_0$ is the vector of unknown bending moment and lateral force at the foundation, the prolongation operator $\Pi$ fills in zeros for the lateral displacement and angle of inclination at the foundation. The solution operator of the initial value problem Y, depending on the length of the column and its parameters like thickness profile and material modulus E, returns the state value at the tip. Finally, this four-component vector is mapped by a matrix R onto the bending moment and the third derivative of the displacement. Equation (10) represents a two-dimensional linear homogeneous system of equations for the unknown vector $z_0$. Non-trivial solutions exist if and only if

$$\begin{aligned} \hbox {det}\left( {RY\left( {L,P,\omega ,S,\rho } \right) \Pi } \right) =0 \end{aligned}$$

(11)

Often this condition is studied under assumptions like $L = 1$, $S\psi$ and $\rho \psi$ being constants or— in the case of so-called stepped columns—piecewise constant functions,. In any case, (11) is a non-polynomial equation in $\omega \psi$ with a parametric dependence on P. However, since all coefficients in the problem are real-valued, all complex quantities that appear during the evaluation of the matrix exponential (9) are pairwise conjugate complex numbers.

Fig. 8

Root curves poorly separated, shape-optimized Beck’s stepped column

In the externally damped versions of the equation of motion, cf. [5], we have

$$\begin{aligned} \left( {Su_{xx} +S^{\prime }u_{txx} +Pu} \right) _{xx} +\mu u_t +\rho u_{tt} =0 \end{aligned}$$

(12)

which, with the substitution $u\left( {x,t} \right) =w\left( x \right) \hbox {sin}\left( {i\omega t} \right)$, leads to the perturbed condition on the form of the oscillation

$$\begin{aligned} \left( {Sw_{xx} +i\omega S^{\prime }w_{xx} +Pw} \right) _{xx} +i\omega \mu w-\rho \omega ^{2}w=0 \end{aligned}$$

(13)

Equation (13) features a term with coefficient $\omega \psi$ and another one with $\omega ^{2}$, furthermore, it is complex from the start. The quantity $S^{{\prime }}$ denotes the dimensionless damping.

In the case of a real frequency $\omega \in R$ , solutions of the form $u\left( {x,t} \right) =w\left( x \right) \hbox {exp}\left( {i\omega t} \right)$ are periodic in time. For positive damping, we expect a decreasing amplitude; hence, a positive imaginary part $\hbox {re}\left( \omega \right) >0$ is desirable. We have to see whether all solutions have non-negative imaginary parts—otherwise instability of the trivial solution follows. This is usually the case, when a critical load $P_\mathrm{cr}\psi$ is exceeded.

The real part of the equation becomes

$$\begin{aligned} \left( {Sw_{xx} +\mathrm{im}\left( \omega \right) S^{\prime }w_{xx} +Pw} \right) _{xx} -\mathrm{im}\left( \omega \right) \mu w+\rho \left( {\mathrm{re}\left( \omega \right) ^{2}-\mathrm{im}\left( \omega \right) ^{2}} \right) w=0 \end{aligned}$$

(14)

while the imaginary contributions amount to

$$\begin{aligned} \mathrm{re}\left( \omega \right) S^{\prime }w_{xxxx} +\mathrm{re}\left( \omega \right) \mu w+2\rho \, \mathrm{im}\left( \omega \right) \mathrm{re}\left( \omega \right) =0 \end{aligned}$$

(15)

In order to find out, whether the state of rest of an undeformed column under a compressive load P is stable, solutions to Eq. (11) have to be studied. The configuration, i.e., the length of the domain $L=1$ and the parameter functions $\rho$ and $S\psi$ are frozen. They will be varied later, in the optimization procedure. The dependence on $P\psi$ and ${\omega }\psi$ is represented in plots like Figs. 2, 7 or  8. The root curves are evaluated numerically—on a certain rectangle in $R^{+}\times R^{+}$—and the critical force $P_\mathrm{cr}\psi$ calculated at a moderate (but not really low) numerical cost. Needless to say that in the case of positive damping, the numerical cost of following the root curves of (13), or (14, 15) in 3d, as in Fig. 7, is much higher.

3 Numerical study

In the previous section, we have outlined the derivation of the objective function in shape optimization of Beck’s column. Typically, the total mass (16) is used as a constraint, representing the cost of the construction. For a given depth of a column with a rectangular cross section, the stiffness is proportional to the third power of the width. Stepped columns, with a piecewise constant width, hence also piecewise constant mass density $\rho \psi$ and stiffness S, are particularly attractive to study. This is because there are closed formulas at least for the calculation of the left-hand side of (11). For this reason, in this study we ignore the limitations of the Bernoulli–Euler theory for this type of profile functions. In any case, a numerical approach is needed in order to find the smallest local maximum of all of the calculated root curves—which defines $P_\mathrm{cr}$. Even for piecewise linear width profile, already the evaluation of the operator (8) requires numerical evaluation, which drives up the CPU time.

Now, we consider the maximization of the objective function $f=f\left( \rho \right)$, i.e., the critical load $P_\mathrm{cr}$, $f=P_\mathrm{cr}$, under the chosen constraint

$$\begin{aligned} g\left( \rho \right) =\mathop \int \nolimits _0^1 \rho \left( x \right) \mathrm{d}x=1 \end{aligned}$$

(16)

Notice that for given geometry of the cross sections, e.g., rectangular with constant depth, stiffness S and density $\rho$ are in one-to-one correspondence, and $\rho$ is proportional to the width. In order to ensure meaningful results, a minimum thickness is added as a unilateral constraint. This constraint turns out to be not active in the optimizer, as long as the number of segments remains small.

Alternatively, one can prescribe a certain value of $f=P_\mathrm{cr}$ and minimize g, i.e., find the cheapest column fulfilling a stability requirement. Here we present some results on the optimization of Beck’s column in the primary case. The dual problem,

Minimize $g\left( \rho \right)$ under the constraint $f=P_\mathrm{cr}$,

can be solved in an analogous way. Compare on that topic also the papers [4, 6, 15, 16].

Bearing in mind the lack of useful properties of the objective, and the high cost of function evaluations, two strategies have proven most successful. The first is a brutal evolution algorithm followed by a derivative-free method of ascent. The second is a sequence of refinements, where again on each level a derivative-free ascent is started. The first one was implemented in Matlab, making use of the built-in ga-function followed by a run of fminsearch. While straightforward and easy to implement, this turned out very time-consuming. Thus we developed the alternative multiscale approach.

For this, we first divide the column in two segments. We remove material from the upper part, adding it to the lower part. Depending on the ratio between the width of the end segment to the original uniform width, different eigenforms and eigenfrequencies are obtained. The critical load is increased. Then, in the next refinement step, each segment is split again. Now, maximization is repeated in four variables. The widths, or equivalently the mass densities per unit of length of the four segments $\left[ {\rho _1 ,\rho _2 ,\rho _3 ,\rho _4 } \right]$, are the design variables. The constraint—constant total mass—takes the form of a sum of segment lengths times densities, so it is a linear functional. Next, in a loop, on each level the last maximizer serves as starting point for the next maximization. Hence on level k, we have $2^{k}$ decision variables, or design parameters, and we start from pairwise equal values. These are taken from the optimizer at level $k-1$. Finally, when increasing k does not give significantly higher critical load, we switch from the ultimate stepped column to one with a continuous density function, and hence a continuous width. Using an interpolation method on the highest level piecewise constant profile with $2^{k}$ equidistant nodes, Eq. (6), now featuring variable entries in the matrix $\hbox {A}\left( x \right)$, given by (7), has to be integrated numerically. In that last step, optimization is done with respect to the grid values $\left[ {\rho _1 ,\rho _2 ,\rho _3 ,\ldots ,\rho _n } \right]$, $n=2^{k}$, of the interpolating function $\tilde{\rho }$. The equality constraint is still given by (16), with $\tilde{\rho }$ substituted for $\rho$. On each level, optimization is performed locally, using a Nelder–Mead algorithm.

The total computation time depends on a sensitive choice of accuracy settings and stopping criteria. On the one hand, this concerns the optimization, on the other hand the evaluation of the objective via numerical integration of an ODE-system. Given the present computer power, configurations with $P_\mathrm{cr}\psi$ higher than six times the value for a homogeneous column are easy to achieve. A typical run for a column with 64 segments takes up to one hour, depending on processor and implementation. However, the results are not very useful. This is revealed in the transition step from the finest stepped column to a continuous profile, modeled on the same x-grid —which leads to a drastic drop of the objective. This drop comes with considerable changes in critical frequency and corresponding eigenmode.

Fig. 9

Regularized objective for optimizing shape of Beck’s column. Critical load vs width of upper segment and position of interface

Fig. 10

Optimal robust shape of Beck’s column

In order to overcome this problem, we formulate the following modified objective:

$$\begin{aligned} f_\varepsilon =\min \left( {\left( {\left\{ {f\left( {\tilde{\rho }} \right) :\tilde{\rho }-\rho <\varepsilon \wedge g\left( {\tilde{\rho }} \right) =g\left( \rho \right) } \right\} } \right) } \right) \end{aligned}$$

(17)

Here the distance between width functions is measured in a suitable norm. The set of neighboring configurations may be extended by allowing for modified material parameters, including even the damped version according to (12).

The problem now is, obviously, that the evaluation of the new objective function becomes even more expensive than the whole optimization problem was before.

Thus, the maximization of $f_\varepsilon \psi$ for any given positive $\varepsilon \psi$ becomes not implementable. As a workable version, we estimate $f_\varepsilon \psi$ by evaluating a given number of random configurations on the $\varepsilon$-sphere around $\omega \psi$ and taking the worst obtained value as an approximation for the wanted $f_\varepsilon$.

The objective in a low-dimensional test case is shown in Fig. 9, compare Fig. 3.

We conclude this section with a figure representing a continuous width function, yielding a critical value of around $P_\mathrm{cr} \approx 100$, robust against changes of $\rho \psi$ up to 5% in maximum norm, Fig. 10.

4 Conclusions

The classical method for the study of slender columns assumes a time dependence of displacements in sine or exponential form. Substitution into the equation of motion leads to an eigenvalue problem for a fourth-order differential operator under specified boundary conditions. Analytical solutions can be found in certain special cases, in general; however, a numerical approach has to be taken.

The introduction of damping terms leads to qualitative changes in the root curves of the characteristic equation. We are interested in the lowest value of a compression force that gives complex (not real valued) frequencies, which correspond to exponential growth of oscillations, i.e., a flutter instability. The search for shape and material parameters, which yield a possibly high value of a feasible compressive force, is an expensive optimization problem. It turns out that the optimizer, although defining a stable dynamical system, is much too sensitive with respect to small perturbations in configuration space to be of practical use.

We propose and test on the example of Beck’s column that an optimization problem with modified objective allows to find a compromise between the requirements of high critical load and sufficient robustness against deviations from the assumed system specification.