Introduction

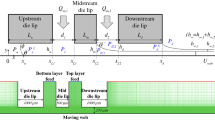
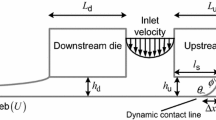
Slot coating is a pre-metered coating process in which the final thickness of a wet coating layer on a moving web is pre-determined by the relationship between the inlet flow rate of a coating liquid and the web speed, despite the characteristics of coating liquids (Schweizer and Kistler 1997). This can produce a uniform, thin-coated film with precision at high speeds by simply manipulating operating conditions. Therefore, it is widely applied in industrial fields including displays, secondary batteries, and functional films, all of which require uniform thickness and a high level of coating quality. As depicted in Fig. 1a, a pre-metered coating liquid enters the slot die through the feed. It is distributed and metered inside the die manifold consisting of chamber and slit channel (Sartor 1990; Jin et al. 2016). Once the coating liquid is discharged from the slot die, it forms a coating bead (Fig. 1b) encompassed by upstream and downstream die lips, menisci at both sides, and a moving web (Higgins and Scriven 1980), which is mainly governed by capillary pressure and viscous forces.

Fig. 1
figure 1

Schematic diagrams of (a) overall slot coating process and (b) coating bead region used in this study. Notations and geometrical dimensions are indicated in figures

Full size image

A liquid entering the coating bead finally exits the system in the form of a uniform thin film, unless coating defects occur. Therefore, using a simple mass balance relation, the final coating thickness of the film (h ∞) can be easily calculated from q/U W , where q is the inlet flow rate per width and U W is the web speed. In some cases, a vacuum box can be implemented upstream to stabilize the coating bead by counter-balancing the dragging force of the moving web, particularly when the final wet thickness is less than half of the downstream coating gap (Carvalho and Khesghi 2000; Lee et al. 2011).

The operability of a slot coating process is largely dependent on the stability of a coating bead. Coating defects such as bead break-up and leaking can arise from unstable coating beads, which are significantly linked to the position of the upstream meniscus (Nam and Carvalho 2010; Lee et al. 2014). A web speed that is too fast or a low bead pressure (or flow rate) condition can break the formation of the coating bead. Break-up of the coating bead can lead to failures in film formation, like ribbing, rivulets, air entrainment, or barring.

On the other hand, a liquid can leak beyond the upstream die at slow web speeds or excessive bead pressures (or flow rate), resulting in uncontrollable film thickness and the accumulation of particles in suspensions near the far upstream die (Schmitt et al. 2013). The operability window provides a favorable range of practical operating conditions for defect-free and stable coating by examining the status of the coating bead (Ruschak 1976; Gates 1999).

Ruschak (1976) first introduced the operability window by expanding the Landau and Levich (1942) approach in dip coating flow to a pre-metered coating system to address the limitations of operating conditions. Higgins and Scriven (1980) defined the coating bead and formulated the operability window using a one-dimensional (1D) visco-capillary model for a Newtonian liquid by combining the capillary pressure force and viscous force within and around the coating bead. Following these studies, Tsuda (2010), Gates (1999), Lee et al. (2011), and Koh et al. (2012) further developed visco-capillary models for non-Newtonian coating liquids (not viscoelastic). Lee et al. (2011) also predicted changes in the final coating thickness with respect to periodic disturbances imposed on the system. Ji et al. (2016) recently reported that such a simplified model could usefully be applied to construct operability windows in dual-layer slot coating systems for Newtonian liquids. The simplified visco-capillary models of slot coating flows offered reasonable and reliable results, agreeing with experimental observations or higher-dimensional models and simulations.

There have been many endeavors to explore the dynamics and windows in slot coating processes. For example, Silliman (1979) introduced an interpretation of the liquid flow with free surfaces using a two-dimensional (2D) Navier-Stokes model. Saito and Scriven (1981) scrutinized the shape of the downstream meniscus at a high capillary number through the same method. Carvalho and Khesghi (2000) elucidated the minimum coating thickness or the low-flow limit in the slot coating process.

Rheologically complex coating liquids with viscoelasticity have become more attractive in many coating processes, taking into account environmental and economic issues. However, there have been few reports dealing with theoretical approaches in viscoelastic coating applications. Romero et al. (2004, 2006) and Brethour (2005) explored the downstream low-flow limit for weakly viscoelastic liquids in 2D slot coating flows. Several experimental results addressed the role of viscoelastic nature in coating liquids on windows in slot coating processes (Ning et al. 1996; Chu et al. 2010). To our knowledge, it is a very challenging task to incorporate viscoelastic dynamics into higher-dimensional coating flow models with free surfaces.

In this study, a simple viscoelastic-capillary model derived via a lubrication approximation was tested to interpret the flow characteristics inside the coating bead region and to establish operability windows in slot coating processes involving viscoelastic liquids. The Oldroyd-B and Phan-Thien-Tanner (PTT) models were employed for viscoelastic fluids. The effects of viscoelasticity and solvent portion on the velocity and pressure profiles in the coating bead region and corresponding operability windows were mainly investigated. Finally, the ranges for uniform coating operations of viscoelastic coating liquids were compared with experiments using a laboratory-scale slot coater.

Derivation of flow equations and numerical methods

Simplification of the equation of motion

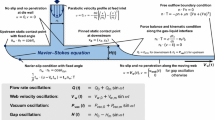
Obtaining the flow field for a viscoelastic liquid in the coating bead region is the first step in determining the operability window. There are two main forces acting on the coating flow in the coating bead: viscoelastic force and capillary pressure force. The coating bead region is characterized by a combination of pressure-driven flow and drag-driven flow by the moving web (i.e., Couette-Poiseuille flow). Capillary pressure force is naturally related to approximations near the free surfaces. A schematic diagram for the flow and pressure distribution in the coating bead is portrayed in Fig. 1b. The lubrication approximation was applied to simplify a 2D model for weakly viscoelastic flows in the coating bead under the low capillary number condition, by assuming steady, incompressible, and rectilinear flow states. The momentum equation in the x-flow direction (Eq. 1b) can be simplified from the full equation (Eq. 1a), considering no change of variables with respect to x, i.e., \( \frac{\partial }{\partial x}\left(\right)=0 \), v y  ≈ 0, and \( \frac{\partial {\tau}_{xy}^s}{\partial y}={\eta}_s\frac{\partial^2{v}_x}{\partial {y}^2} \)

$$ \rho \left(\underline{v}\cdot \underline{\nabla}\underline {v}\right)=-\underline{\nabla}P+\underline{\nabla}\cdot \left({\underline {\underline{\tau}}}^s+{\underline {\underline{\tau}}}^p\right) $$
(1a)
$$ 0=-{P}_x+{\eta}_s\frac{\partial^2{v}_x}{\partial {y}^2}+\frac{\partial }{\partial y}{\tau}_{xy}^p $$
(1b)

where P x (≡dP/dx) is the pressure gradient, η s is the Newtonian solvent viscosity, v x and v y are the x- and y-component velocities, and \( {\tau}_{xy}^s \) and \( {\tau}_{xy}^p \) are the Newtonian and polymeric shear stresses, respectively (the superscript p will be omitted for convenience). Note that the stress of a coating liquid contains contributions of a Newtonian solvent (\( {\underline {\underline{\tau}}}^s \)) and a polymer (\( {\underline {\underline{\tau}}}^p \)). The integrated form of Eq. 1b along the y-height direction is required to solve the relationship between the pressure gradient and the velocity profile, as shown in Eq. 2,

$$ 0=-{P}_xy+{\eta}_s\frac{\partial {v}_x}{\partial y}+{\tau}_{xy}+{\tau}_0, $$
(2)

where τ 0 is an integration constant.

Velocity-solving equation for viscoelastic fluids

In this study, we employed a linear PTT fluid model to study coating bead dynamics (Phan-Thien and Tanner 1977; Sibley 2010).

$$ \left[1+\left(\frac{\varepsilon \lambda }{\eta_p}\right)tr\left(\underline {\underline{\tau}}\right)\right]\underline {\underline{\tau}}+\lambda \overset{\nabla }{\underline {\underline{\tau}}}=2{\eta}_p\underline {\underline{D}} $$
(3)

where ε denotes the PTT material parameter that shows the maximum extension length of the long-chain polymer, η p is the polymeric viscosity, \( \underline {\underline{D}} \) is the rate of the deformation tensor \( \left(\equiv \frac{1}{2}\left(\underline{\nabla}\underline {v}+{\left(\underline{\nabla}\underline {v}\right)}^T\right)\right) \), λ is the material relaxation time, and the superscript ∇ represents the upper-convected time derivative \( \left(\overset{\nabla }{\underline {\underline{\tau}}}=\frac{\partial \underline {\underline{\tau}}}{\partial t}+\left(\underline{v}\cdot \underline{\nabla}\right)\underline {\underline{\tau}}-{\left(\underline{\nabla}\underline {v}\right)}^T\cdot \underline {\underline{\tau}}-\underline {\underline{\tau}}\cdot \left(\underline{\nabla}\underline {v}\right)\right) \). Note that the PTT model is equal to the Oldroyd-B model when ε = 0. It is known that the Oldroyd-B liquid with no solvent viscosity (i.e., upper-convected Maxwell fluid) exhibits constant shear viscosity regardless of shear rate, whereas the PTT liquid with non-zero ε shows shear-thinning behavior; shear thinning increases with ε or λ. The combination of solvent viscosity and polymeric viscosity terms gives total zero-shear viscosity (η 0 = η s  + η p ) and the ratio of the solvent viscosity to the total zero-shear viscosity is defined as the solvent viscosity parameter, β = η s /η 0. In uniaxial extensional flow, the tensile stress level evolves into infinity at a finite extension rate for the Oldroyd-B case and is kept at a finite value with increasing extensional rate in the PTT case (Song et al. 2010).

Polymeric stress components in the PTT model for the analysis of coating bead dynamics reduce to,

$$ {\tau}_{yy}=0, $$
(4a)
$$ \left(1+\left(\frac{\varepsilon \lambda }{\eta_p}\right){\tau}_{xx}\right){\tau}_{xx}=2{\lambda \tau}_{xy}\frac{\partial {v}_x}{\partial y}, $$
(4b)
$$ \left(1+\left(\frac{\varepsilon \lambda }{\eta_p}\right){\tau}_{xx}\right){\tau}_{xy}={\eta}_P\frac{\partial {v}_x}{\partial y}. $$
(4c)

Note that τ yy component in Eq. 3 will be zero, following aforementioned assumptions for a lubrication approximation. The relationship between τ xx and τ xy is obtained from Eqs. 4b and 4c.

$$ {\tau}_{xx}=\frac{2\lambda }{\eta_p}{\tau_{xy}}^2 $$
(5)

This cubic equation has a real solution given by (Cruz et al. 2005),

$$ {\tau}_{xy}=\sqrt[3]{\left(Cy-D\right)+\sqrt{A^3+{\left(Cy-D\right)}^2}}+\sqrt[3]{\left(Cy-D\right)-\sqrt{A^3+{\left(Cy-D\right)}^2}}, $$
(7)

where \( A=\frac{{\eta_p}^2}{6{\varepsilon \lambda}^2}\left(1+\frac{\eta_p}{\eta_s}\right) \), \( C=\left(\frac{\eta_p^3}{4{\eta}_s{\varepsilon \lambda}^2}{P}_x\right) \), and \( D=\left(\frac{\eta_p^3}{4{\eta}_s{\varepsilon \lambda}^2}{\tau}_0\right) \).

Using the explicit form of τ xy (Eq. 7), the equation for the velocity gradient (Eq. 2) is reformulated as follows:

$$ \frac{\partial {v}_x}{\partial y}=\frac{P_xy}{\eta_s}-\frac{1}{\eta_s}{\tau}_0-\frac{1}{\eta_s}\left(\sqrt[3]{\left(Cy-D\right)+\sqrt{A^3+{\left(Cy-D\right)}^2}}+\sqrt[3]{\left(Cy-D\right)-\sqrt{A^3+{\left(Cy-D\right)}^2}}\right) $$
(8)

The velocity profile equation (Eq. 9) for viscoelastic PTT fluids in Couette-Poiseuille flow is finally derived by integrating Eq. 8 along the y-height direction, incorporating two no-slip boundary conditions: v x (y) = 0 at y = H and v x (y) = U W    at y = 0.

$$ \begin{array}{l}{v}_x(y)=\left(-\frac{P_x{H}^2}{2{\eta}_s}\right)\left(1-{\left(\frac{y}{H}\right)}^2\right)+\left(\frac{\tau_0H}{\eta_s}\right)\left(1-\frac{y}{H}\right)\\ {}\kern2.2em +\frac{3}{8C{\eta}_s}\left[{F}^{+}(H){G}^{-}(H)-{F}^{+}(y){G}^{-}(y)+{F}^{-}(H){G}^{+}(H)-{F}^{-}(y){G}^{+}(y)\right]\end{array} $$
(9)

where \( {F}^{\pm }(X)={\left\{\left(CX-D\right)\pm \sqrt{A^3+{\left(D-CX\right)}^2}\right\}}^{\frac{1}{3}} \), \( {G}^{\pm }(X)=3\left(CX-D\right)\pm \sqrt{A^3+{\left(D-CX\right)}^2} \).

Note that τ 0 is a still unknown constant. τ 0 at a given pressure gradient is numerically obtained using the bisection method satisfying the boundary condition at the moving web (y = 0). For the Oldroyd-B liquid, the shear stress, τ xy , is equal to that of the Newtonian liquid with the exception of the shear viscosity for a polymeric solution.

$$ {\tau}_{xy}={\eta}_p\frac{\partial {v}_x}{\partial y} $$
(10)

Therefore, the velocity profile for this liquid is exactly the same as the Newtonian case having zero-shear viscosity, η 0.

$$ {v}_x(y)=\left(-\frac{P_x{H}^2}{2{\eta}_0}\right)\left(1-{\left(\frac{y}{H}\right)}^2\right)+\left(\frac{\tau_0H}{\eta_0}\right)\left(1-\frac{y}{H}\right) $$
(11)

The same boundary conditions and numerical method for determining the constant τ 0 are adopted for the Oldroyd-B liquid. Representative velocity profiles inside both the upstream and downstream die lip regions of coating bead, which mainly features Couette-Poiseuille flow, are described later in the “Results and discussion” section.

Pressure distribution inside the coating bead

In the slot coating process, volumetric flow rates per width \( \left(={\int}_0^H{v}_x(y)\;\mathrm{d}y\right) \) in the upstream and downstream coating bead regions become 0 and U W  ⋅ h ∞, respectively (Gates 1999; Tsuda 2010). The flow rate per width is evaluated by integrating the velocity equation (Eqs. 9 or 11) over the y-direction via the fourth-order Simpson’s method, guaranteeing numerical accuracy. To satisfy the flow rate conditions (0 or U W  ⋅ h ∞) in both upstream and downstream regions, the pressure gradient, P x , should be adjusted via Newton’s method under the given inlet flow rate and web speed conditions. Pressure distribution will be involved in deciding the position of the upstream meniscus as an indicator of the operability coating window. Total pressure differences in the upstream and downstream regions complying with the boundary conditions are expressed below:

$$ {\left.\frac{\mathrm{d}{P}^L}{\mathrm{d}x}\right|}_{\mathrm{up}}=\frac{P_F^L-{P}_U^L}{x_F-{x}_U}\kern0.5em \mathrm{and}\kern0.5em {\left.\frac{\mathrm{d}{P}^L}{\mathrm{d}x}\right|}_{\mathrm{d}\mathrm{own}}=\frac{P_D^L-{P}_F^L}{x_D-{x}_F}=\frac{P_D^L-{P}_F^L}{L_D} $$
(12)

The subscripts U and D represent the upstream and downstream die lip regions (Fig. 1b), respectively, and the subscript F is the feed region where the coating liquid first enters the coating bead.

Determination of the position of the upstream meniscus, x U

It is assumed that the downstream meniscus is pinned at the end of the downstream die lip (Carvalho and Khesghi 2000) and the upstream meniscus in an arc-of-circle shape is placed within the upstream die region, which is freely movable according to the process conditions (Higgins and Scriven 1980). The position of the upstream meniscus can be correlated with the bead pressure \( \left(\Delta {P}^{vac}={P}_D^{Atm}-{P}_U^{Vac}\right) \), i.e., the pressure difference between the ambient pressure \( \left({P}_D^{Atm}\right) \) at the downstream meniscus and the applied vacuum pressure \( \left({P}_U^{Vac}\right) \) at the upstream meniscus. Pressure jumps between the gas and liquid phases at both menisci are approximated by the arc-of-circle relation at the upstream (Higgins and Scriven 1980; Gates 1999) and the meniscus form for a viscoelastic fluid, suggested by Ro and Homsy (1995), at the downstream.

$$ {P}_U^L={P}_U^{Vac}-\frac{\sigma }{h_U}\left( \cos \theta + \cos \phi \right), $$
(13a)
$$ {P}_D^L={P}_D^{Atm}-\left[\left(1.337-0.08346{m}^2\right){Ca}^{2/3}-\left(0.12-0.027{k}^2\right)\left(1-\beta \right){De}_R{Ca}^{1/3}\right]\frac{\sigma }{h_{\infty }}, $$
(13b)

where \( m=k=\frac{De_R}{Ca^{2/3}} \).

Here, σ is the surface tension of a coating liquid, Ca is the capillary number \( \left(\equiv \frac{\eta_0{U}_W}{\sigma}\right) \), and De R is the modified Deborah number \( \left(\equiv \frac{\lambda }{t^{\ast }}=\frac{\lambda {U}_{\mathrm{avg}}}{L_D+{L}_U}\right) \), where t * is the characteristic flow residence time inside the coating bead and U avg is the average velocity. θ and ϕ are respectively the dynamic (120°) and static (60°) contact angles at the upstream meniscus (Lee et al. 2011). In Eq. 13b, the first and second terms inside the square bracket on the right hand side represent the viscous and elastic contributions of a liquid, respectively (Ro and Homsy 1995). Normal stress generated by a polymeric contribution in a coating liquid causes resistance to the flow direction and increases the pressure at the downstream meniscus (Lee et al. 2002; Romero et al. 2006). m and k denote the degrees of shear thinning and normal stress thinning of a liquid, respectively. Note that the liquid with m = 0 and k = 0 is regarded as an Oldroyd-B liquid. When the relaxation time reduces to zero, the elastic effect disappears at the downstream meniscus, yielding the pressure jump approximation for a Newtonian fluid (Landau and Levich 1942; Ruschak 1976; Gates 1999; Lee et al. 2011).

$$ {P}_D^L={P}_D^{Atm}-1.34{Ca}^{2/3}\frac{\sigma }{h_{\infty }} $$
(14)

It should be mentioned that Eq. 13b or 14 is limited to low Ca (Higgins and Scriven 1980; Weinstein and Ruschak 2004) or low De R numbers. To achieve a thinner coating film, \( {P}_U^{Vac} \) lower than the ambient pressure can be applied in the vacuum box beyond the upstream region (Schweizer and Kistler 1997; Koh et al. 2012).

The position of the upstream meniscus, x U , is calculated from pressure jumps at menisci and pressure distributions inside the upstream and downstream coating bead regions.

$$ {x}_U={x}_F-\frac{\left({P}_D^{Atm}-{P}_U^{Vac}\right)-\left(\left[\begin{array}{l}\left(1.337-0.08346{m}^2\right){Ca}^{2/3}\\ {}-\left(0.12-0.027{k}^2\right)\left(1-\beta \right){De}_R{Ca}^{1/3}\end{array}\right]\frac{\sigma }{h_{\infty }}\right)-{\frac{\mathrm{d}P}{\mathrm{d}x}}_{down}{L}_D+\left(\frac{\sigma }{h_U}\left( \cos \theta + \cos \phi \right)\right)}{{\frac{\mathrm{d}P}{\mathrm{d}x}}_{up}} $$
(15)

The position of the upstream meniscus plays an important role in determining the operating limits such as leaking (at x U  = 0) and bead break-up (at x U  = L U ) for viscoelastic coating flows by altering the flow rate and web speed or the bead pressure and web speed, under low-speed coating conditions (Nam and Carvalho 2010; Lee et al. 2014). The die geometries incorporated in computations and experiments are 1000 μm for upstream and downstream die lip lengths, 500 μm for the slit gap, 0.05 m for die width, and 250 μm for the coating gap (Lee et al. 2011) (Fig. 1a).

Experiments

Laboratory-scale slot coating experiments using three different coating liquids (one Newtonian liquid and two viscoelastic liquids) were carried out to validate the numerical predictions on operability windows. We tried to produce coating liquids with the same zero-shear viscosity value but different rheological behaviors. A mixture of glycerin (84 wt.%) and distilled water (16 wt.%) was used as the Newtonian liquid. A polymer solution containing 35 wt.% poly(ethylene glycol) (PEG, M n  = 6000), 0.3 wt.% poly(ethylene oxide) (PEO, M w  = 1 M), and 64.7 wt.% distilled water was selected as the Oldroyd-B viscoelastic liquid, which is like a Boger fluid with constant shear viscosity. An aqueous polymer solution including 3 wt.% PEO was used for the PTT viscoelastic liquid. All coating liquids were prepared by stirring for 24 h at room temperature.

The rheological properties of the liquids such as shear viscosity and elastic/viscous moduli were measured via a stress-controlled rheometer (AR-2000; TA Instruments) equipped with a cone-plate fixture with diameter of 40 mm at room temperature. Their surface tension data were measured using a surface tension meter (DCAT11; Dataphysics). The properties of the coating liquids used for experiments are presented in Fig. 2 and Table 1. Note that the relaxation time data for two viscoelastic liquids were decided at the intersection of the elastic and viscous modulus curves with respect to the input frequency (Fig. 2b). ε and β for the PTT liquid were found to be 0.8 and 0.25 and β for the Oldroyd-B liquid was 0.74 from the best-fit curves of the real viscosity.

Fig. 2
figure 2

Rheological properties of coating liquids in experimental tests: a shear viscosities and b elastic (G’) and viscous (G′′) moduli for Newtonian, Oldroyd-B, and PTT liquids

Full size image
Table 1 Rheological and materials properties of coating liquids for experiments
Full size table

The slot die geometry is identical to that adopted in the numerical simulation, as mentioned before. A CCD camera is placed laterally between the slot die lips and roll to capture the coating bead flow. The position of the upstream meniscus is observed by changing the inlet flow rate and the roll speed to determine operation limits, under no bead pressure conditions. Operability windows built through experiments were averaged by performing three triplicate tests.

Results and discussion

Operability windows and flow characteristics from the simplified model under no bead pressure condition

Effects of viscoelastic coating liquids on the operability windows and flow characteristics in slot coating flows are examined using the viscoelastic-capillary model derived in this study. Operability windows for Newtonian, PTT, and Oldroyd-B liquids under no bead pressure condition, i.e., same ambient pressures beyond the upstream and downstream menisci, are compared in Fig. 3 by changing both the inlet flow rate and web speed. For theoretical calculations, material data selected for the coating liquids were different from the experiments, as a model case (Romero et al. 2006; Lee et al. 2011): 0.45 Pa⋅s for the zero-shear viscosity, 66 mN/m for the surface tension, and 0 for the solvent viscosity parameter. The values of other material parameters such as λ, ε, and β are labeled in the figures. Based on the limits for the Newtonian liquid (solid lines), limits for Oldroyd-B liquids were shifted to the right in the window map as the relaxation time increased (Fig. 3a). This is due to the elastic effect at the downstream meniscus, drawing its meniscus inwards opposite to the direction of the moving web (Romero et al. 2006). The Oldroyd-B liquid exhibits the same velocity profile as the Newtonian liquid inside the coating bead region (Eq. 11) and thus the difference between two liquids arises from the existence of elasticity at the downstream free surface. The elastic force induces a normal stress in the Couette-Poiseuille flow inside the coating bead and exerts resistance to the flow (Lee et al. 2002). Therefore, such a resistance by the Oldroyd-B liquids draws the downstream meniscus inside the coating bead region in contrast to the Newtonian case, requiring a stronger drag force (or web speed) to desirably deposit the coating liquid in the web direction. The noticeable change in limits to the right occurs with increasing flow rate and web speed because of the increased viscoelasticity or De R .

Fig. 3
figure 3

Effects of material parameters for viscoelastic liquids on the operability window under no bead pressure conditions: a relaxation time (λ) of Oldroyd-B liquids, b relaxation time of PTT liquids, c PTT parameter (ε), and d solvent viscosity parameter (β) of PTT liquids

Full size image

For PTT fluids, the combined elastic and shear-thinning contributions of the liquids shifted the window to the left (Fig. 3b). As the relaxation time or web speed increases, the viscoelasticity or De R of the liquids increases, inducing reduction to the drag force due to the decreasing shear viscosity with shear rate. The shear-thinning feature makes the coating liquid move more easily in the coating bead region. The elastic force of a PTT liquid also exerts flow resistance at the downstream meniscus, as will be shown in the pressure profiles. Figure 3c and d exhibits the effects of the PTT material parameter, ε, and the solvent viscosity parameter, β, on the operability windows in the PTT case. Increasing ε and decreasing β significantly promote the shear-thinning behavior of liquids inside the coating bead, further shifting the window to the left in the map. Such a change is intensified with increasing flow rate and web speed owing to the generation of a greater shear rate.

The velocity (Fig. 4) and pressure profiles (Fig. 5) of the PTT and Oldroyd-B liquids in the coating bead are compared with those of a Newtonian liquid in a specified uniform coating state (point A designated in Fig. 3a and b): inlet flow rate of 0.4 × 10−6 m3/s and web speed of 0.04 m/s. Figure 4a and b shows velocity profiles of the viscoelastic coating liquids with different relaxation times in the upstream and downstream bead regions, respectively. Note that these profiles ensure zero flow rate at the upstream and outgoing flow rate at the downstream. Oldroyd-B liquids show exactly the same velocity profiles as the Newtonian case in the coating bead, irrespective of the relaxation time. For PTT liquids, the velocity pattern becomes blunter in the middle and displays a higher velocity change near the wall with increasing relaxation time, in accordance with typical shear-thinning behavior (Morrison 2001).

Fig. 4
figure 4

Velocity profiles of Newtonian, Oldroyd-B, and PTT liquids with different relaxation times in a upstream and b downstream coating bead regions at a specified operation state (point A in Fig. 3, inlet flow rate = 0.4 × 10−6 m3/s and web speed = 0.04 m/s) without bead pressure

Full size image
Fig. 5
figure 5

Pressure distributions of a PTT and b Oldroyd-B liquids inside the coating bead at a specified operation state (point A in Fig. 3, inlet flow rate = 0.4 × 10−6 m3/s and web speed = 0.04 m/s) without bead pressure

Full size image

Local pressure values for PTT and Oldroyd-B liquids with different relaxation times are evaluated at five positions inside the coating bead (Fig. 5). Pressure distributions of PTT liquids generally show negative and positive contribution with respect to drag flow, based on the feed position (Fig. 5a). The pressure level reduces as the relaxation time increases because of the noticeable shear-thinning effect inside the coating bead. The position of the upstream meniscus moved forward, as expected from the change of the operability window. On the other hand, the pressure around the downstream meniscus increased with increasing relaxation time owing to the build-up of elastic stress exerted at the downstream meniscus. Figure 5b represents the pressure profiles of Oldroyd-B liquids. Unlike the PTT case, the global level of local pressures increases with increasing relaxation time. This is because the main factor altering the pressure level of Oldroyd-B liquids is the elastic force exerted downstream.

Operability windows and flow characteristics from the simplified model under the existence of bead pressure

The bead pressure controlled by the vacuum box implemented at the outside of upstream die lip can be beneficial in stabilizing the coating bead by counteracting the drag force, particularly for the manufacture of thin-layered coating products (Lee et al. 2011; Koh et al. 2012). Figure 6 shows the operability windows of various coating liquids obtained by changing the bead pressure and web speed under a constant final wet thickness condition (h ∝ = 100 μm). The flow rate of the inlet coating liquid is calculated via a mass balance relation for the production of a wet film with a 100 μm thickness at a given web speed. As the relaxation time increases, uniform operating regimes for both the Oldroyd-B and PTT liquids become narrower and shift to the right in the map, relative to the Newtonian case. At the specified web speed, both viscoelastic liquids require lower bead pressure ranges for stable operation than the Newtonian liquid because the elastic contribution exerted on the downstream meniscus was enhanced in the same direction as the bead pressure. The lower level of the uniform bead pressure range in the PTT case relative to the Oldroyd-B case can be explained by the shear-thinning effect in the former. The same phenomenon was corroborated in previous studies on operability windows for generalized Newtonian fluids in slot coating processes (Tsuda 2010; Lee et al. 2011).

Fig. 6
figure 6

Effects of relaxation time for a Oldroyd-B and b PTT liquids on the operability window under bead pressure conditions

Full size image

The pressure and velocity profiles of the PTT and Oldroyd-B liquids inside the coating bead are shown in Figs. 7 and 8, respectively, at the state (point B) specified in Fig. 6: a bead pressure of 850 Pa and a web speed of 0.04 m/s. The pressure gradient is opposite to the web direction in the entire coating bead region under the existence of the bead pressure condition because \( {P}_U^{Vac} \) at the upstream is lower than \( {P}_D^{Atm} \) at the downstream. Negative pressure contributions (Fig. 7a, b) with respect to drag force by the moving web create more drag-dominant velocity profiles in the downstream region (Fig. 8b), which are similar for all the coating liquids considered in this study, despite occurring at different relaxation times. Velocity profiles (Fig. 8a) of PTT liquids in the upstream coating bead region are affected by the change in relaxation time, as in cases without bead pressure.

Fig. 7
figure 7

Pressure distributions of a PTT and b Oldroyd-B liquids inside the coating bead at a specified operation state (point B in Fig. 6, bead pressure = 850 Pa and web speed = 0.04 m/s) with bead pressure

Full size image
Fig. 8
figure 8

Velocity profiles of Newtonian, Oldroyd-B, and PTT liquids with different relaxation times in a upstream and b downstream coating bead regions at a specified operation state (point B in Fig. 6, bead pressure = 850 Pa and web speed = 0.04 m/s) with bead pressure

Full size image

Comparison of operability windows by models and experiments

The operability windows predicted from the viscoelastic-capillary model, based on Table 1, are compared with those obtained by experiments using a laboratory-scale slot coater (Fig. 1a). As mentioned in the “Experiments” section, an Oldroyd-B liquid with constant viscosity and a PTT liquid with shear-thinning behavior are used in the experiments. Figure 9 shows operating limits obtained by the model (lines) and experiments (symbols), which were determined from the change in the flow rate and web speed. Experimentally observed limits of coating liquids for the bead break-up defect matched the simulation results fairly well; however, those for leaking were barely distinguishable. As predicted from the simplified model, it is demonstrated that the uniform coating regime for the PTT liquid evidently shifted to the left of the map, relative to the Newtonian case. However, the uniform range for the Oldroyd-B liquid seldom or very slightly moved to the right relative to the Newtonian case because of its low viscoelasticity. It was actually difficult to prepare the Oldroyd-B liquid with highly increased elasticity, while maintaining the same zero-shear viscosity value as the Newtonian and PTT liquids. From these results, the viscoelastic-capillary model seems to be a useful tool for reliably establishing operating limits in the viscoelastic slot coating process. It is worth mentioning that its performance must be verified using more rigorous, fuller models.

Fig. 9
figure 9

Comparison of operability windows obtained from the viscoelastic-capillary model and experiments for Newtonian, Oldroyd-B, and PTT liquids. Model and experimental results are depicted in lines and symbols with error bars, respectively

Full size image

Conclusions

Flow features and operability windows for viscoelastic coating liquids with different rheological characteristics in slot coating flows have been examined using the simplified viscoelastic-capillary model derived from the fuller equations. This model considered the Couette-Poiseuille flow inside the coating bead region, together with approximations of pressure differences at the upstream and downstream menisci or free surfaces. Employing this model with the viscoelasticity effect, coating bead dynamics including velocity and pressure distributions in the coating bead region were analyzed and also the corresponding operating limits, which demarcate leaking and bead break-up defects, were suitably predicted for Oldroyd-B liquids with constant viscosity and PTT liquids with shear-thinning behavior. Limit curves for the Oldroyd-B case are more shifted to the right in the flow rate and web speed maps relative to the Newtonian case, as the relaxation time increases, resulting from the elasticity at the downstream meniscus. The limits for the PTT case moved further to the left in the map with increasing viscoelasticity, owing to the increased shear-thinning effect. The operability windows obtained using the viscoelastic-capillary model were reasonably supported by experimental results, demonstrating its effectiveness as a fast and reliable tool in determining operation limits for slot coating processes with viscoelastic liquids.