Introduction

Crude oil is a primary and essential energy source throughout the world. Waxy crude oils represent about 20 % in the world petroleum reserves produced and pipelined amongst various non-conventional oils nowadays (Vinay et al. 2007). In China, more than 80 % of crude oil produced is waxy crude oil. Waxy crude oil shows complex temperature-dependent rheological behaviors. At temperatures above the so-called wax appearance temperature (WAT) or cloud point, waxes are dissolved into the oil matrix, and waxy crude oil behaves like Newtonian fluid. When the temperature falls down to the WAT, molecules of wax start to precipitate and form solid wax crystals in the oil (Rønningsen et al. 1991). As the temperature further decreases, the amount of precipitated wax crystals increases, and the crude oil becomes a pseudoplastic fluid and begins to exhibit thixotropic behavior. When the temperature decreases to the gelation temperature, the precipitated wax crystals start to form a three-dimensional sponge-like interlock network, completing the transition from sol to colloidal gel (Visintin et al. 2005). The gelled crude oil shows complex rheological behaviors, such as thixotropy and yield stress (Visintin et al. 2005; Magda et al. 2009).

Thixotropic behaviors of materials including waxy crude have been extensively studied, and many thixotropic models have been proposed (Mujumdar et al. 2002; Mewis and Wagner 2009). For waxy crude, the mostly used thixotropic model is the Houska model (Houska 1981). While for the Houska model and other thixotropic models, such as the Moore model (Moore 1959) and Alexandrou model (Alexandrou et al. 2009), it has been demonstrated that after a sudden change in shear rate, the structural parameter changes exponentially to its equilibrium value (Kirkwood and Ward 2008), thus the shear stress of waxy crude predicted by those models decreases to its equilibrium value more quickly than the measured data (Zhang et al. 2010).

To solve this problem, a new thixotropic model is proposed in this paper. In the kinetic equation for the structural parameter, a new pre-factor, which contains shear strain as variables, is introduced for the buildup and breakdown terms, and the breakdown term is assumed to be dependent on the rate of energy dissipation. The model was validated by stepwise shear rate test and hysteresis loop test. Moreover, we checked the validity and applicability of the model by predicting the thixotropic behavior of one type of measurement using the model parameters obtained from another type of measurement, i.e., we predict the stress transient of hysteresis loop test with the model parameters fitted from the stepwise shear rate measurement. Furthermore, the new thixotropic model was compared with the Houska model. And the proposed kinetic equation was compared with the other three kinetic equations, whose pre-factor takes time as variable and/or whose breakdown term is assumed to be dependent on shear rate.

Theory

This section describes the assumptions and gives the equations that compose the proposed thixotropic model. As a common practice, this paper only considers one-dimensional version of the model.

Most of the existing thixotropic models belong to the class of structural kinetics model. It uses a scalar structural parameter λ to characterize the instantaneous level of microstructure, and its value varies between the values of 0 for the totally broken-down structure and 1 for the fully developed structure. The inelastic general structural thixotropic model is composed of an equation of state and a kinetic equation, and their general formats are shown as follows (Cheng and Evans 1965).

$$\tau =\tau (\lambda ,\dot{{\gamma }}) $$
(1)
$$\frac{\mbox{D}\lambda }{\mbox{D}\,t}=g(\lambda ,\dot{{\gamma }}) $$
(2)

In literatures, various thixotropic models of this type have been put forward (Moore 1959; Cheng and Evans 1965; Houska 1981; Lacuna et al. 1996; Toorman 1997; Coussot et al. 2002). Some were introduced in the reviews of Cheng (1987) and Barnes (1997), and an extensive list of available models has been compiled by Mujumdar et al. (2002) and Mewis and Wagner (2009).

As for the equation of state, it usually uses a yield stress to account for the plastic behavior. The Houska model and others (Carleton et al. 1974; Zhao 1999; Chen 2002) assume that the yield stress comprises a residual, permanent component τ y0 when the thixotropic structure is completely broken down (λ = 0) and a structural contribution part λτ y1. While for waxy crude, it has been found that after shearing under a high shear rate for a period of time, the waxy crude behaves as a shear thinning fluid with the residual yield stress negligible, therefore the permanent part τ y0 can be neglected for waxy crude. As for the apparent viscosity, it is usually characterized by a structure-parameter-dependent consistency Δk (the so-called structural consistency) and a completely unstructured consistency k, as some of the thixotropic models do (Houska 1981; Zhao 1999; Chen 2002). The shear thinning behavior can be described by a kinetic index n 1. Consequently, we developed the equation of state shown as follows:

$$ \tau =\lambda \tau_{y} +(k+\Delta k\lambda )\dot{{\gamma }}^{n_{1} } $$
(3)

As for the structural parameter, some authors argued that for some materials with separate static and dynamic yield stresses, such as bentonite, paints, and waxy crude (Rønningsen 1992; Visintin et al. 2005), there can be two types of structure:reversible and irreversible (Cheng 1986; Toorman 1997; Mewis and Wagner 2009). The irreversible structure is very sensitive, and a very small disturbance will readily break it down. And it recovers very slowly or only under specific ambient conditions, while the reversible structure is more robust and can survive high shear rate. From this viewpoint, several thixotropic models with two structural parameters have been proposed (Toorman 1997; Zhao 1999). And the secondary structural parameter is also described by a kinetic equation similar to that of the primary structural parameter. The secondary structural parameter improves the models’ accuracy of describing the thixotropic behavior, especially for the shear stress’s fast decay period after the yield point, but it also makes the model numerically more complex and less practical to use. Whether there exists more than one type of structure still needs further experimental validation; therefore, most models still use only one structural parameter.

As to the structural parameter’s kinetic equation, in analogy with chemical reaction kinetics, it is usually assumed that its time evolution is controlled by the combined result of structure buildup and breakdown rate. So far, many kinetic equations have been put forward, and some of those have been summarized by Mewis and Wagner (2009). Yziquel et al. (1999) as well as Mewis and Wagner (2009) have reviewed that the kinetic equations can be categorized into the following three types. The mostly used ones assume that the structure change is due to shear rate (Houska 1981; Toorman 1997; Coussot et al. 2002; Dullaert and Mewis 2006), and some suppose that the structure evolution is associated with shear stress (Mendes 2009, 2011), while rare kinetic equations assume that the variation of structure is related to a combination of the two, e.g. the rate of energy dissipation (Yziquel et al. 1999; Fredrickson 1970). Thus, the kinetic equation for structural parameter can be summarized as the following general form:

$$ \frac{\mathrm{d}\lambda}{\mathrm{d}t}=g({\lambda,\dot{{\gamma}}})-\lambda f({\tau ,\dot{{\gamma}}}) $$
(4)

in which \(g( {\lambda ,\dot {{\gamma }}} )\) and \(f\left ( {\tau , \dot {{\gamma }}}\right )\) are two material functions. The first term on the right-hand side expresses the structure buildup rate, while the second term represents the structure breakdown rate.

Some models introduce a common pre-factor, which contains shear rate, structure, and/or time as variable, for the buildup and breakdown terms (Mewis and Wagner 2009). From the phenomenological point of view, the pre-factor generates stretched exponentials for the evolution of structural parameter. The pre-factor does not change the equilibrium value of structural parameter at each shear rate, but it changes the rate at which the structural parameter comes to its equilibrium value. For the start-up flow, the shear strain increases with time and the value of dλ/dt decreases with time. If the pre-factor takes time as variable as the model proposed by Dullaert and Mewis (2006) do, that is \(1/t^{n_{2} }\), at the same time point, the value of pre-factor is the same no matter what the shear rate of start-up flow is. Nevertheless, the structural parameter at a high shear rate is different from that at a lower shear rate and so is the descending rate of structural parameter. Therefore, it seems somewhat not consistent with the actual evolution of structural parameter. To solve this problem, we introduce here a new pre-factor \(1/( {1+\gamma ^{n_{2} }} )\), which takes shear strain as variable. At the same time point, as the shear rate of start-up flow increases, the shear strain γ gets a larger value; hence, the value of pre-factor becomes smaller. Therefore, the descending rate under a higher shear rate is different from that under a lower shear rate, which complies with the structural parameter’s actual evolution. In this sense, the pre-factor that takes shear strain as variable seems more plausible than that takes time as variable.

Here, we assume that the breakdown term of kinetic equation is a function of energy dissipation rate ϕ. The energy dissipation rate is the product of shear stress and shear rate, that is ϕ = τ :D, where τ is the stress tensor, and D is the rate of deformation tensor. For simple shear flow, it becomes \(\phi =\tau {\kern 1pt}\dot {{\gamma }}\). Based on the above analysis, we assume that the structural parameter λ is assumed to obey the following kinetic equation, named kinetic Eq. I in this paper:

$$ \frac{\mathrm{d}\lambda }{\mathrm{d}t}=\frac{1}{1+\gamma^{n_{2} }}\left[ {a\left( {1-\lambda } \right)-b\lambda \phi^{m}} \right] $$
(5)

where γ is the total shear strain; a is a rate constant for structure buildup; b is a rate constant for structure breakdown; and m as well as n 2 are positive dimensionless material parameters.

To estimate the assumptions made in the kinetic equation, in this paper, the new proposed kinetic equation is compared with the other three kinetic equations, whose pre-factor contains shear strain and/or time as variable and whose breakdown term is assumed to be a function of energy dissipation rate and/or shear rate, which are summarized as the following three kinetic equations:

  • Kinetic Eq. II:the kinetic equation whose pre-factor contains shear strain as variable and whose breakdown term is assumed to be related with shear rate:

    $$ \frac{\mathrm{d}\lambda }{\mathrm{d}t}=\frac{1}{1+\gamma^{n_{2} }}\left[ {a\left( {1-\lambda } \right)-b\lambda \,\dot{{\gamma }}^{m}} \right] $$
    (6)

  • Kinetic Eq. III:the kinetic equation whose pre-factor contains time as variable and whose breakdown term is assumed to be a function of energy dissipation rate:

    $$ \frac{\mathrm{d}\lambda }{\mathrm{d}t}=\frac{1}{t^{n_{2} }}\left[ {a\left( {1-\lambda } \right)-b\lambda \,\phi^{m}} \right] $$
    (7)

  • Kinetic Eq. IV:the kinetic equation whose pre-factor contains time as variable and whose breakdown term is assumed to be a function of shear rate:

    $$ \frac{\mathrm{d}\lambda }{\mathrm{d}t}=\frac{1}{t^{n_{2} }}\left[ {a\left( {1-\lambda } \right)-b\lambda \,\dot{{\gamma }}^{m}} \right] $$
    (8)

In summary, the proposed thixotropic model is composed of the equation of state (Eq. 3) and the kinetic Eq. I (Eq. 5). The new model contains eight adjustable model parameters:τ y , k, Δk, n 1, n 2, a, b, and m. In principle, via substituting the equilibrium structural parameter obtained from the kinetic equation into the equation of state, the constants of the equation of state ( τ y , k, Δk, and n 1), the ratio of b/a and m can be determined through a least square fitting to the steady-state flow curve. And the values of the remaining parameters (and/or all of the model parameters) can be determined via fittings to transient data. In this work, the values of all model parameters are obtained via fittings to the data pertaining to transient flow through a computer program with the nonlinear least square method. The kinetic equation is solved numerically by the fourth-order Runge–Kutta discretization method.

Materials and experimental methods

Material

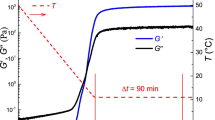
To validate the proposed model, a waxy crude oil from China, i.e., Daqing waxy crude, is used. This waxy crude has a wax content of 24.1 %, a WAT of 39.0 °C and a specific gravity of 0.8624 at 20 °C. The gelation point (at which G′ = G″) is 35.0 °C when heated to 50 °C. In consideration of the thermal and shear history dependence of rheological behaviors of the waxy crude, the oil specimens were pretreated to a temperature of 80 °C to resolve all wax crystals and to remove the “memory” of the oil, and then placed at room temperature statically for 48 h before test, for the better repeatability and comparability of experimental data.

Rheological measurements

All measurements were performed with the coaxial cylinder sensor system (Z41Ti) of HAAKE MARS III rheometer, and the temperature of the sample was controlled by a programmable water bath (AC 200) with temperature control accuracy of 0.01 °C. Pretreated oil specimen was heated to 50 °C and held at that temperature for 20 min. Then they were loaded into the measuring cylinder preheated at 50 °C and then isothermally held for 10 min; after that, the specimen was statically cooled to the test temperature at a cooling rate of 0.5 °C/min. Finally, the oil specimen was isothermally held for 45 min before test to let the wax crystal structure fully develop. After that, the thixotropic measurements, stepwise shear rate and hysteresis loop tests were performed isothermally at the test temperatures. In this work, the chosen test temperatures are 32, 33, 34, and 35 °C. And for each test, a fresh specimen was used.

Thixotropic behavior of waxy crude

The experimental data and the fitted results of the proposed model to the stepwise increases and decreases in shear rate for Daqing waxy crude at 33 °C are shown in Fig. 1. It can be observed that the transient flow curves after the maximum shear rate (128 s−1) are nearly parallel with the X-axis, which confirms that the structure buildup rate is very small and even negligible compared with the structure breakdown rate (Visintin et al. 2005). And this phenomenon is also confirmed by the hysteresis loop tests shown later in Fig. 3. Moreover, it can be observed that after the maximum shear rate, the shear stresses at the end of each shear rates are less than those under the same shear rates before the maximum shear rate. This phenomenon suggests that the thixotropy of waxy crude is partially reversible, which was also demonstrated by other researchers (Rønningsen 1992; Visintin et al. 2005). Therefore, in this work the model validation is mainly focused on the structure breakdown conditions. And the stepwise shear rate test does not contain the stepwise decrease in the shear rate procedure; it only considers the stepwise increase in shear rate procedure.

Fig. 1
figure 1

Stepwise changes in shear rate and model fitting results of proposed model with kinetic Eq. 1 for Daqing waxy crude at 33 °C

Full size image

One thing needed to note is that in Fig. 1, the shear stress vs. time curves for the stepwise decrease in shear rate from 128 down to 1 s−1 are not fitted; they are predicted by the model with the model parameters fitted from the experimental data of shear rate 1–128 s−1. It can be observed in Fig. 1 that the predicted shear stresses of shear rate 128–1 s−1 are very close to the measured data. Thus, it can be summarized that for the waxy crude, the model parameters can be fitted from the test of the stepwise increases in shear rate.

Results and discussion

The purpose of this section is to discuss the predictive capabilities of the proposed model. In this paper, the model was validated by the stepwise shear rate test and the hysteresis loop test, and the proposed kinetic Eq. I was compared with the other three kinetic Eqs. II–IV. And the validation and applicability of the model was checked by predicting the transient shear stress of hysteresis loop test with the model parameters fitted from the stepwise shear rate measurement.

Stepwise changes in shear rate

Thixotropic behavior is best studied by the test of stepwise changes in shear rate or shear stress, since the coupled effects of time and shear rate/stress can be clearly separated in such experiments (Barnes 1997). In this study, the stepwise increases in shear rate test is adopted, and the shear rates used are 1, 2, 4, 8, 16, 32, and 64 s−1; each shear rate lasts for 450 s. For Daqing waxy crude at 32 °C, the experimental data and model fittings of the Houska model and the proposed equation of state with the kinetic Eqs. I–IV are shown in Fig. 2. Table 1 lists the model parameters fitted from the stepwise shear rate test and the hysteresis loop test for the proposed model with kinetic Eq. I at the four test temperatures. It can be seen form Table 1 that the values of τ y , Δk, and k increase, while the value of n 1decreases with the decrease of temperature. This is because the gel strength and the non-Newtonian characteristic of waxy crude get stronger as the temperature decreases. The parameters a and b should decrease with the decrease of temperature, since the structural parameter is a relative parameter, and it ranges from 0 to 1. While the fitted value of parameter a is very small and shows little function with temperature, which is maybe attributed to the fact that for waxy crude, the structure buildup rate is very small, and the thixotropy shows some extent of irreversibility.

Fig. 2
figure 2

Model fittings of stepwise shear rate test for Daqing waxy crude at 32 °C

Full size image
Table 1 Fitted model parameters of the proposed model with kinetic Eq. I from stepwise shear rate (corresponding to the upper four rows) and hysteresis loop tests (corresponding to the lower four rows) of Daqing waxy crude
Full size table

From Fig. 2, it can be found that the fitting results of the Houska model is not satisfactory, and the average absolute deviations (AADs) between the fitted values and the measured data range from 4.8 to 8.1 % for the four test temperatures. And it can be observed that the Houska model’s fitted shear stress at each shear rate reduces to its equilibrium value more quickly than the measured data, which is related with the fact that the structural parameter of the Houska model decays exponentially after the stepwise change in shear rate. While for the proposed equation of state with kinetic Eqs. I–IV, it can be seen in Fig. 2 that the fitted flow curves are very close to the measured flow curve. And the AADs are all within 3 % for the four test temperatures, which is surprisingly good considering that the data includes seven shear rates. There is nearly no difference between the fitted results of the four kinetic equations.

For the Houska model, after a sudden change in shear rate, the structural parameter changes exponentially to its equilibrium value with the characteristic time of \(1/( {a+b\,\dot {{\gamma }}^{m}} )\) (Kirkwood and Ward 2008). The characteristic time only depends on the final shear rate and varies inversely as the value of the final shear rate. The property that the characteristic time varies inversely as the final shear rate has been validated by some papers, that is, the time required to reach a steady state is much shorter when increasing the final shear rate (Dullaert and Mewis 2005; Grillet et al. 2009). However, some papers also reported that when applying a sudden change in shear rate, the characteristic time of the subsequent stress transient is affected not only by the final shear rate, but also by the initial structure before the change of shear rate (Dullaert and Mewis 2005; Grillet et al. 2009).

For the proposed kinetic Eq. I, when the structure buildup and breakdown reaches a dynamic equilibrium, the equilibrium structural parameter λ e has λ e = 1 / [1 + (b / a) ϕ m]. Consequently, the kinetic Eq. I (Eq. 5) can be changed to the following form:

$$ \frac{\mathrm{d}\lambda }{\mathrm{d}{\kern 1pt}t}=-\frac{1}{1+\gamma^{n_{2} }}(a+b\,\phi ^m)(\lambda -\lambda_{e} ) $$
(9)

If the initial structural parameter (before applying a sudden change in shear rate) is higher (in other words, the previous shear rate is small), usually the shear strain is smaller, and after a sudden change in shear rate, the shear stress is larger. Thus, it can be deduced implicitly that the proposed kinetic equation predicts the structural parameter with a varying, non-exponential shape. And the effect of the initial structure level on the characteristic time of structural change implicitly appears in the pre-factor and the breakdown term.

Hysteresis loop test

This section shows the model’s predictive capability for hysteresis loop test. Hysteresis loop measurement is a common method to demonstrate the thixotropic behavior of complex fluids, and it is best used as a qualitative measure of thixotropy (Barnes 1997). The hysteresis loop test here consists of two cycles of linear increase of shear rate from 0 to 50 s−1 in 200 s and then linear decrease to 0-1 for the same time period. Figure 3 shows the fitted results of the Houska model and the proposed equation of state with the kinetic Eqs. I–IV for the hysteresis loop test of Daqing waxy crude at 32 °C. The fitted model parameters of the proposed model with kinetic Eq. I are listed in Table 1. In Fig. 3, it can be observed that for the proposed equation of state with kinetic Eqs. I–IV, the fitted flow curves are nearly superposed with the measured flow curve. And the average AADs are all within 5.0 % for the four test temperatures. While for the Houska model, the fitted results are not very good, especially for the shear stress’s fast decay period after the yield point. And the AADs are about 8.0 % for the four test temperatures.

Fig. 3
figure 3

Model fittings of hysteresis loop test for Daqing waxy crude at 32 °C:a Shear stress vs. time and b shear stress vs. shear rate

Full size image

In Fig. 3b, it can also be found that there is a large hysteresis in the first thixotropic loop, while the second consecutive thixotropic loop shows little hysteresis. And the shear stresses in the increasing rate ramp of the second loop are nearly identical with the shear stresses in the decreasing rate ramp of the first loop. This suggests that the microstructure must have been broken down in the initial increasing rate ramp and have not recovered in the decreasing rate ramp, in line with the fact that, at constant temperature, the structure buildup rate of waxy crude is relatively smaller compared with its breakdown rate.

It was found that the hysteresis loop test alone is somewhat not suitable to be used to determine the values of model parameter (Baravian et al. 1996). For the hysteresis loop test, due to the simultaneous change of two variables of shear rate and time during the experiment, the structural parameter, apparent viscosity, and other parameters do not arrive at their equilibrium values at each shear rate, which may lead to the fact that the fitted values of the model parameter may deviate from their true values, especially for the model parameters (a, b, and m) related with the structural kinetic equation. From Table 1, it can be found that the model parameters fitted from the hysteresis loop test differ from those fitted from the stepwise shear rate test, especially for the parameters a and b. The fitted structure buildup constant a is greater than that fitted from the stepwise shear rate test, and it is ever greater than the structure breakdown constant b. This is not consistent with the fact that the structure buildup rate is relatively smaller compared with the breakdown rate, as demonstrated above. To test the model parameters fitted from the hysteresis loop test, we used them to predict the transient flow curve of stepwise shear rate test. The predicted results are not good. Taken the proposed model with kinetic Eq. I as an example, the AADs are about 40 % for the four test temperatures. However, for the stepwise shear rate test, the apparent viscosity at each shear rate nearly reaches its equilibrium value, so are the structural parameter and other parameters. In this aspect, the stepwise shear rate test seems more suitable than the hysteresis loop test for fitting the values of model parameter. To check this, we used the model parameters fitted from the stepwise shear rate test to predict the transient flow curve of hysteresis loop test. For the four test temperatures, the AADs of kinetic Eq. I range from 11 to 15 %. Therefore, it can be summarized that the model parameters should be fitted from the stepwise shear rate test and should not be fitted from the hysteresis loop test. This is because that the transient data of stepwise shear rate test contain the steady-state information, for the steady-state values of stress at different shear rates can be extracted from the stepwise shear rate test, while the transient data of hysteresis loop test do not contain the steady-state information. For Daqing waxy crude at 32 °C, the predicted results of the Houska model and the proposed equation of state with kinetic Eqs. I–IV are shown in Fig. 4.

Fig. 4
figure 4

Model predictions of hysteresis loop test for Daqing waxy crude at 32 °C, using the model parameters fitted from stepwise shear rate test

Full size image

It can be observed in Fig. 4 that the Houska model provides the worst predicted results, and the discrepancy between the predicted shear stress and the measured value is large. While for the kinetic Eqs. III and IV whose pre-factor contains time as variable, it can be found that the fitted results are also not good, especially for the first hysteresis loop. For the pre-factor taken time as variable, as analyzed in the “Theory” section, at the same time point, the value of pre-factor is all the same no matter what the shear condition is. This leads to the abnormal evolution of structural parameter for hysteresis loop test when using the model parameters fitted from stepwise shear rate test. Therefore, for the kinetic Eqs. III and IV, although the fitting results of one type of measurement are as good, their predictive capabilities are bad. While the pre-factor with shear strain as variable overcomes this problem. It can be found in Fig. 4 that the predicted results of kinetic Eqs. I and II, whose pre-factor takes shear strain as variable, are much better than those of kinetic Eqs. III and IV. The best predicted result is provided by the proposed kinetic Eq. I, whose breakdown term is assumed to be related with the rate of energy dissipation. This may be explained as follows. Under constant shear rate condition, the shear stress gradually decays to its equilibrium value, and in this process, the structure breakdown rate decreases. If the breakdown term is assumed to be related with shear rate, the kinetic equation only takes account of the effect of shear rate on the breakdown rate. While if the breakdown term is assumed to be related with the rate of energy dissipation, the kinetic equation takes account of not only the effect of shear rate but also the effect of shear stress on the breakdown rate. Therefore, it can be concluded that the assumption that the breakdown term of structural kinetic equation is a function of energy dissipation rate is better than the assumption that the breakdown term is related with shear rate. As a result, the predictive ability of kinetic Eq. I is little better than that of kinetic Eq. II.

Concluding remarks

In this paper, we proposed a new viscoplastic thixotropic model. For the kinetic equation for the structural parameter, a new pre-factor, which contains shear strain as variable, is introduced for the structure buildup and breakdown term. And the kinetic equation’s breakdown term is assumed to be a function of energy dissipation rate. It has demonstrated that after a sudden change in shear rate, the proposed kinetic equation predicts the structural parameter with a varying, non-exponential shape.

The fitting and predictive capability of the proposed model is shown to be excellent for the stepwise shear rate test and hysteresis loop test. The proposed model was compared with the Houska model, and the proposed equation of state with the kinetic Eq. II whose breakdown term is assumed to be related with shear rate and the other two kinetic Eqs. III and IV, whose pre-factor contains time as variable. The results showed that the fitting capabilities of the four kinetic Eqs. I–IV are almost the same. However, when using the model parameters fitted from the stepwise shear rate test to predict the stress transient of hysteresis loop test, the predicted results of the kinetic Eqs. III and IV, whose pre-factor takes time as variable are bad, caused by the fact that the pre-factor cannot take account of the effect of flow condition on its value. While the proposed pre-factor with shear strain as variable overcomes this problem, the predictive capabilities of kinetic Eqs. I and II are better. For the breakdown term of structural kinetic equation, the assumption that it is a function of energy dissipation rate is proved to be better than the assumption that the breakdown term is related with shear rate, for it takes account of not only the influence of shear rate but also the influence of shear stress on the breakdown rate of structural parameter.

Although the proposed model shows substantial improvement over the previous Houska model, it is also phenomenological in nature, and the pre-factor and the breakdown term as a function of energy dissipation rate are introduced, to some extent, on empirical basis. Besides, the prediction capability, i.e., the result of using model parameters fitted from the stepwise changes in shear rate to predict the hysteresis loop test, is not very satisfactory, which may be attributed to some complicated reasons including the repeatability of experiments, the physical and mathematical difficulties in the prediction based on one type of transient flow behavior to another type, and the possible imperfectness of the model itself. Finally, the proposed model in this work is validated with waxy crude which shows some extent of irreversible thixotropy. As a result, the structure buildup aspect of the model is actually not fully validated in this work.