Introduction

A magneto-rheological fluid (MRF) essentially is a concentrated suspension of magnetizable particles in a low viscosity Newtonian liquid. Upon application of a magnetic field, the mostly ferromagnetic particles form string-like structures parallel to the magnetic flux lines, thus creating a distinct yield stress in the system (Schulman and Kordonski 1982; Bossis and Lemaire 1991; Felt et al. 1996; Ginder et al. 1996; Laun et al. 1996). As the flowability of the MRF is reversibly controllable by an external magnetic field, it is used for mechanical devices like dampers, clutches, actuators, etc. (Rabinow 1948; Jolly et al. 1996; Klingenberg 2001). A recent estimate gives a number of 250,000 devices currently in use, although a strong growth in number and additional applications is anticipated (Carlson 2006).

The switching time of a mechanical device from the off-state to the activated state and vice versa is an important performance property in practical use. Noteworthy, this property is controlled by two different response times: on one hand, the switching time of the MRF itself and on the other hand, the time constant of the electromagnetic circuit necessary to create the field in the MRF. In general, it is not possible to achieve a real step in magnetic flux density due to the inductance of the coil-yoke arrangement and the occurrence of eddy currents.

Several attempts to characterize the response time of a MRF are described in the literature. So far, however, no generally accepted procedure has been developed. Reported response times cover a broad range from 0.1 up to 100 ms, depending on the method applied. In most cases, the device response time was determined rather than that of the MR fluid itself. In general, the mechanical compliance of the torque measurement system could also contribute. This part is neglected in this paper because it will not play a role in the experimental section due to the high stiffness of the shaft.

Weiss et al. (1993) measured the response time by using a controllable damper. They found that the damper was able to reach 90% of its maximum force output in less than 6.5 ms at a 2 Hz stroke rate. A commercially available damper from Lord Corporation was used by Koo et al. (2006). They found that the response time of the system was dependent upon piston velocity, operating current (i.e., magnetic flux), and time constant of the electronics. Reported are 25 ms to achieve 95% of the maximum damping force. As with the work of Weiss et al. (1993), no response time of the MR fluid itself was determined.

With a disk-type MR fluid damper, Zhu (2005) used a step current mode to determine the response time. Whereas the step current reaches 90% of its final value in less than 2 ms, the response time of the damper is reported to fall into a regime between 0.08 and 0.4 s, depending on the type of MR fluid and the rotational speed of the disk. The response time was distinctly longer when switching the current off again. This result indicates that inertia effects may not have been carefully considered. For a MR fluid containing 50 vol.% of magnetic particles, Böse et al. (2006) found in “preliminary measurements”, using a disk type device, a response time of 30 ms at a shear rate of 26 s−1. An increase in rotational speed is reported to decrease the response time. For step currents from 2.4 to 0 A, the time-dependence of the torque signal was found not to depend on the shear rate, however. The rise times of the magnetic flux density in the device are not addressed.

Goncalves et al. (2006) investigated the response time at high shear rates in the order of 105 s−1 using a slit device. The authors determine the yield stress as a function of the average residence time (dwell time) of the MRF in the magnetic field, which decreases for increasing flow velocities. Maximum yield stress of 63.2% is attained at dwell times as low as 0.45 to 0.6 ms. The data evolution, however, ignores the shear rate and residence time distribution across the slit and thus rather represents a hydraulic time constant of the device.

Kormann et al. (1996) investigated the dynamic response of a nano-sized MRF at 60 wt% in concentric cylinder flow applying a sinusoidal flux density but steady shear rate. The modulation of the resulting periodic shear stress was used as a measure to identify the maximum frequency of switching. A switching time of less than 5 ms was estimated. We will apply a similar technique but in a much more quantitative way as one of the methods to be introduced below.

In the following, we consider the switching behavior in steady simple shear, as for instance relevant in disc or concentric cylinder clutches (Kieburg et al. 2006). We focus on the determination of the MRF switching time and demonstrate how this property may be measured in a commercial magneto-rheometer if the relevant signals are detected adequately. It is shown how to overcome some of the experimental challenges if the MRF switching time is in the range of a few milliseconds. In addition, we demonstrate that different modes of measurement give agreeing results within experimental accuracy.

Theory

Relation between shear stress and flux density

We consider simple shear of the MRF at a constant shear rate \( {\mathop \gamma \limits^. } \). The resulting shear stress τ will depend on the absolute value of the magnetic flux density B. For mathematical simplicity, the steady-state shear stress τ s is assumed to be proportional to the absolute value of the imposed flux density, where p is the slope of the linear characteristic (shear stress vs flux density):

$$ \tau _{{\text{s}}} = p{\left| B \right|} $$
(1)

Modifications introduced by a non-linear characteristic are addressed in the Appendix.

The effect of a magnetic flux density change on the shear stress response is described by a simple Maxwell model in which a switching time λ plays the role of the material specific parameter:

$$ \tau + \lambda {\mathop \tau \limits^. } = p{\left| B \right|} $$
(2)

It is not clear a priori whether the Maxwell type equation is pertinent to describe the MRF behavior and needs to be justified by experiments.

Measurement modes and expected MRF response

Step flux density

For a step in magnetic flux density, either from B = 0 to B = B 0 at t = 0 after a field-free period much longer than λ or from the steady-state at B = B 0 to zero at time t′ = 0, the expected shear stress response would respectively be given as:

$$ \tau {\left( t \right)} = pB_{0} {\left[ {1 - \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} \lambda }} \right. \kern-\nulldelimiterspace} \lambda } \right)}} \right]} $$
(3)
$$ \tau {\left( {t'} \right)} = pB_{0} {\left[ {\exp {\left( {{ - t'} \mathord{\left/ {\vphantom {{ - t'} \lambda }} \right. \kern-\nulldelimiterspace} \lambda } \right)}} \right]} $$
(4)

In reality, however, it will not be feasible to realize this test because the inductance of a magneto-cell (see below) does not allow a step-like change in flux density.

Experimentally, a step coil current test would be the best approximation of a step flux density test. However, as the challenge of a delayed flux density increase remains, we prefer to start with the response to step voltage, which treats such a situation. The results are pertinent to be applied to an imposed coil current step (see below).

Step coil voltage

To impose a step voltage to the coil (U = 0 to U = U 0 or vice versa) is experimentally simple. The time response of the current J is

$$ J + \Lambda {\mathop J\limits^. } = U \mathord{\left/ {\vphantom {U R}} \right. \kern-\nulldelimiterspace} R. $$
(5)

In this equation, Λ stands for the time constant of the electro-magnetic circuit, and R represents the Ohmic resistance of the coil. For a step-up voltage at t = 0 or step-down voltage at t′ = 0, the respective current response is

$$ J{\left( t \right)} = {U_{0} } \mathord{\left/ {\vphantom {{U_{0} } {R{\left[ {1 - \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]}}}} \right. \kern-\nulldelimiterspace} {R{\left[ {1 - \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]}} $$
(6)
$$ J{\left( {t'} \right)} = {U_{0} } \mathord{\left/ {\vphantom {{U_{0} } {R{\left[ {\exp {\left( {{ - t'} \mathord{\left/ {\vphantom {{ - t'} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]}}}} \right. \kern-\nulldelimiterspace} {R{\left[ {\exp {\left( {{ - t'} \mathord{\left/ {\vphantom {{ - t'} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]}} $$
(7)

As long as neither eddy currents in the yoke of the magnetic circuit are relevant nor magnetic saturation effects of the yoke material come into play, the resulting magnetic flux density is proportional to the coil current (parameter c being a constant):

$$ B = cJ $$
(8)

As a consequence, the transient magnetic flux density after a coil voltage step follows single exponentials with B 0 = cU 0/R:

$$ B{\left( t \right)} = B_{0} {\left[ {1 - \exp {\left( {{ - t} \mathord{\left/ {\vphantom {{ - t} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]} $$
(9)
$$ B{\left( {t'} \right)} = B_{0} {\left[ {\exp {\left( {{ - t'} \mathord{\left/ {\vphantom {{ - t'} \Lambda }} \right. \kern-\nulldelimiterspace} \Lambda } \right)}} \right]} $$
(10)

Inserting Eqs. (9, 10) into Eq. (2) yields analytic expressions for the transient shear stress:

$$ \tau {\left( t \right)} = pB_{0} {\left[ {1 - \frac{\lambda } {{\lambda - \Lambda }}\exp {\left( {\frac{{ - t}} {\lambda }} \right)} - \frac{\Lambda } {{\Lambda - \lambda }}\exp {\left( {\frac{{ - t}} {\Lambda }} \right)}} \right]} $$
(11)
$$ \tau {\left( {t'} \right)} = pB_{0} {\left[ {\frac{\lambda } {{\lambda - \Lambda }}\exp {\left( {\frac{{ - t'}} {\lambda }} \right)} + \frac{\Lambda } {{\Lambda - \lambda }}\exp {\left( {\frac{{ - t'}} {\Lambda }} \right)}} \right]} $$
(12)

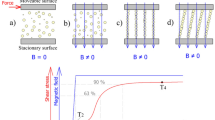
As an example, Fig. 1 shows the normalized transients of both magnetic flux density and shear stress for λ/Λ = 0.15 and λ/Λ = 0.5, respectively, as a function of the normalized times t/Λ or t′/Λ. Although the switching time is much smaller than Λ, the additional delay of the shear stress compared to the magnetic flux density rise is clearly seen. Thus, if the time constant of the electromagnetic circuit is known, it should be feasible to determine the switching time by a fit of Eqs. (11, 12) to the shear stress transients. In reality, the finite value of the off-state shear stress needs to be considered as an additional bias shear stress.

Fig. 1
figure 1

Normalized transients of flux density B and shear stress τ for a step coil voltage test for two ratios of λ/Λ. a Start-up. b Shutdown

Full size image

Sine voltage

Applying a sine voltage in the regime where Eq. (8) is valid causes a sinusoidal magnetic flux density (\( {\mathop B\limits^ \wedge } \)amplitude, ω angular frequency):

$$ B{\left( t \right)} = {\mathop B\limits^ \wedge }\sin \omega t $$
(13)

Noteworthy, the resulting shear stress does only depend on the absolute value of B. The latter may be expressed as a Taylor series (Ruge 1991):

$$ {\left| {B{\left( t \right)}} \right|}\left. { = {\mathop B\limits^ \wedge }} \right|\left. {\sin \omega t} \right| = \frac{{2{\mathop B\limits^ \wedge }}} {\pi }{\left[ {1 - 2{\sum\limits_{n = 1}^\infty {\frac{{\cos {\left( {2n\omega t} \right)}}} {{{\left( {2n - 1} \right)}{\left( {2n + 1} \right)}}}} }} \right]} $$
(14)

Taking into account that the solution of Eq. (2) for a single cosine flux density \( {\mathop B\limits^ \wedge }\cos \omega \,t \) is

$$ \tau {\left( {t,\omega } \right)} = p{\mathop B\limits^ \wedge }{\left[ {\frac{1} {{1 + \omega ^{2} \lambda ^{2} }}\cos \omega \,t + \frac{{\omega \lambda }} {{1 + \omega ^{2} \lambda ^{2} }}\sin \omega \,t} \right]}, $$
(15)

the solution for the time dependent flux density as in Eq. (14) follows as a linear superposition:

$$ \tau {\left( {t,\omega } \right)} = \frac{{2p{\mathop B\limits^ \wedge }}} {\pi }{\left[ {1 - 2{\sum\limits_{n = 1}^\infty {\frac{{\cos {\left( {2n\omega \,t} \right)} + \omega \,\lambda \sin {\left( {2n\omega \,t} \right)}}} {{{\left( {2n - 1} \right)}{\left( {2n + 1} \right)}{\left( {1 + \omega ^{2} \lambda ^{2} } \right)}}}} }} \right]} $$
(16)

As long as ωλ ≪ 1, the cosine terms dominate, and the transient shear stress remains proportional to the sine half waves expressed by Eq. (14). This means a full modulation of the shear stress, reaching τ = 0 at the instant where B changes its sign.

For growing ωλ, the sine contributions increase and only a partial modulation is obtained, as demonstrated in Fig. 2.

Fig. 2
figure 2

Transient shear stress for a sinusoidal flux density—normalized to the maximum value τmax(0) at low angular frequencies—at various values of normalized angular frequency ωλ

Full size image

It turns out that the ratio of the minimum and maximum shear stress (τ min/τ max) in a cycle may be regarded as characteristic for a given angular frequency. It follows from Eq. (16), that this ratio is solely a function of ωλ (Fig. 3). Thus, if the ratio has been determined for a given angular frequency, it should be possible to extract the corresponding value of the switching time from Fig. 3. In reality, the finite value of the off-state shear stress (bias shear stress) needs to be taken into account (see “Experimental”).

Fig. 3
figure 3

Modulation depth characterized by the ratio τmin/τmax as function of the normalized frequency ωλ

Full size image

For convenience, one may approximate the curve in Fig. 3 by an analytic relation:

$$ y = a{\left[ {\exp {\left( {\frac{{ - x}} {c}} \right)} - 1} \right]} + bx. $$
(17)

The fit parameters are a = 0.1448, b = 0.5443, and c = 0.3472.

Experimental

Rheometer

Geometry with on-line flux density measurement

Measurements were made in a Physica MCR501 rheometer equipped with a Physica MRD180/1T magneto-cell as described by Laeuger et al. (2004) and manufactured by Anton Paar GmbH. The geometry was plate–plate with radius R G = 10 mm and gap h G = 0.3 mm. As depicted in Fig. 4a, the vector of flux density B is perpendicular to the plane of shear. In this geometry, a flux density above 1 T is obtained for the maximum allowed coil current.

Fig. 4
figure 4

a Schematic of the magneto-cell modified for an online measurement of the magnetic flux density. b Photograph of the magneto-cell with Hall probe (front half of top yoke and rotor removed)

Full size image

One of the challenges of magneto-rheology is the knowledge of the magnetic flux in the gap with sample, which depends on the magnetization of the MRF. An on-line measurement of the true flux density in the sample was achieved by a Hall probe (F.W. Bell probe 1X and Model 9500 Gaussmeter) attached to the magneto-cell (Fig. 4b): The probe is located in the rectangular horizontal channel of a non-magnetic disk. The disk is located directly above the bottom yoke of the magneto-cell and plays the role of the stationary plate of the gap. The thickness of this additional plate is 1.5 mm. The Hall probe strip with cross-section of 1 × 4 mm may be placed at various radial positions to determine the radial flux density profile. The flux-sensitive part of the probe has a diameter of about 3 mm. At fixed position, the Hall probe monitors the flux density for various coil currents or the time-dependence of flux density transients (see below).

Electromagnetic circuit

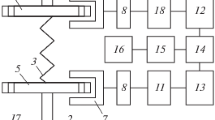
In the following, the MRD180 will be applied for tests using magnetic flux density transients, although the soft iron yoke was not designed for such measurements. The coil-yoke arrangement is schematically depicted in Fig. 5a. To study the response to a transient coil voltage or current, respectively, the electric schematic in Fig. 5b is used.

Fig. 5
figure 5

a Schematic for magnetic circuit with coil, yoke, and gap filled by MRF. b Corresponding electrical circuit

Full size image

The coil is represented by an inductance L = 0.136 Henry in series with an Ohmic resistance R = 2.18 Ohm. An input voltage U in is applied to the series arrangement of coil and Ohmic resistor R s = 0.26 Ohm to create an output voltage U out, being proportional to the coil current J.

For a sinusoidal voltage of angular frequency ω, the complex resistance R* of the coil is given by

$$ R^{ * } = R + i\omega L $$
(18)

The frequency dependence of absolute value of the ratio of output and input voltage follows as

$$ {\left| {\frac{{U_{{{\text{out}}}} }} {{U_{{{\text{in}}}} }}} \right|} = \frac{{R_{{\text{s}}} }} {{{\sqrt {{\left( {\omega L} \right)}^{2} + {\left( {R + R_{{\text{s}}} } \right)}^{2} } }}}. $$
(19)

The behavior corresponds to a low pass filter with cut-off frequency ω 0:

$$ \omega _{0} = \frac{{R + R_{{\text{s}}} }} {L}. $$
(20)

Whereas R and R s were directly measured using an ohmmeter, the inductance L was obtained by determining the cut-off frequency (Fig. 6) of ω 0 = 20 rad/s and applying Eq. (19). It should be noted that the inverse of the cut-off frequency is the time constant Λ = 50 ms of the electromagnetic circuit in Fig. 5b.

Fig. 6
figure 6

Frequency response of the coil-resistor arrangement from Fig. 5b

Full size image

Realization of test modes

A schematic of the electrical circuits is given in Fig. 7a,b. A KEPCO bipolar operational power amplifyer BOP 20-10 M was used to create the coil input voltage U in or current J, respectively. Square wave or sine wave input signals for the operational amplifier were generated by a HP 3325A digital synthesizer/function generator, whereas the output voltage U out was recorded by a Tektronics TDS 5032B digital phosphor oscilloscope (350 MHz). In addition to U out, the transient flux density signal (from the Gaussmeter analog output) was recorded by the oscilloscope. Compared to the empty gap, the MRF in the magneto-cell causes an increase in the true flux density of about 15% at constant coil current. The frequency response shown in Fig. 6, however, does not change significantly with and without sample.

Fig. 7
figure 7

a Circuit for voltage imposition. b Circuit for current imposition

Full size image

The circuit in Fig. 7a simply amplifies and inverts the voltage signal from the function generator and feeds it as input voltage U in (20 V max) directly into the series arrangement of coil and resistor R s (voltage imposition). To impose the coil current, the circuit in Fig. 7b was used. Here, the output current J of the power operational amplifier (5 A max) is controlled such that the output voltage U out, being proportional to the coil current J, equals the function generator voltage at any time (deviations being due to the time constant of the control loop).

The magneto-rheological measurements were performed at a constant rim shear rate 100 s−1. Noteworthy, the Physica MCR501 is torque-controlled. The shear stress output signal reflects the torque, necessary to maintain the constant shear rate. It was therefore checked that in spite of large torque variations caused by changing flux density, the shear rate was kept sufficiently constant (compare Fig. 10).

Initially, the transient shear stress was taken directly from the MCR501 software (compare Fig. 10). However, this caused erroneously large apparent switching times because of a low pass filter in the torque signal. The effect was confirmed by Dr. Huck of Anton Paar GmbH, who kindly provided us with a firmware, allowing to record the shear stress and shear rate signals (using the oscilloscope) from the MCR analog outputs at 0.1 ms sampling rate! All results presented in the following are based on this firmware, unless otherwise stated.

Sample

The MRF investigated is a high performance MRF developed for use in an automotive drive-train clutch (Kieburg et al. 2006). It consists of magnetizable spherical carbonyl iron powder particles (size range several micrometers) suspended in a mixture of mineral oils. Several additives are needed to prevent sedimentation due to the large density mismatch of particles and base oil and to ensure easy redispersibility after centrifugation or long-term rest. The steady shear rheology of the sample is characterized by the flow curves shown in Fig. 8a, the shear stress vs flux density relation by the characteristic in Fig. 8b.

Fig. 8
figure 8

a Steady-state flow curves of the MRF over a wide range of shear rates at various flux densities at room temperature. b Characteristic of the MRF derived from the flow curves at shear rates 1, 10, 100, and 1,000 s−1 (symbols)

Full size image

The shear rate given is the shear rate \( {\mathop \gamma \limits^ \cdot }_{R} \) at the rim of the plate-plate gap, whereas the Newtonian shear stress is evaluated from the torque by assuming a Newtonian fluid in the gap (Bird et al. 1987). The true shear stress τ follows from the Newtonian shear stress τ N as

$$ \tau = \tau _{{\text{N}}} \frac{{3 + n}} {4} $$
(21)

with a power law index defined by

$$ n \equiv \frac{{d\log \tau _{{\text{N}}} }} {{d\log {\mathop \gamma \limits^ \cdot }_{R} }}. $$
(22)

At high flux density, the shear stress is independent of the shear rate (n = 0), thus τ = τ N 3/4. Noteworthy are the low shear stresses without magnetic field, which allow a magnetic control of the true shear stress at the highest applied shear rate by a factor >50.

Results

Sinusoidal coil current

A sinusoidal coil current may be imposed by either imposing the coil voltage (Fig. 7a) or the coil current (Fig. 7b), respectively. The latter version has the advantage that the current amplitude remains fixed if the frequency is changed, whereas voltage imposition yields an amplitude decrease above the cut-off frequency. The oscilloscope screenshot in Fig. 9 compares the transient coil current (determined via the output voltage U out) and resulting magnetic flux density for a frequency of 8 Hz and current amplitude 1 A. The negative sign of B for positive current has been chosen by the orientation of the Hall probe. Both signals are detected with a time resolution of better than 0.1 ms. Noteworthy is the about 2 ms delay of B compared to J at the zeropoint, indicating a measurable effect of eddy currents. However, as long as the flux density signal remains sinusoidal, this phase shift of 6° should not have an effect on the measurement of the shear stress ratio introduced in Fig. 2.

Fig. 9
figure 9

Oscilloscope screenshot of coil current and magnetic flux density for current imposition (1 A amplitude) at 8 Hz

Full size image

Shear stress response from standard MCR501 software

Figure 10a,b shows the resulting periodic shear stress for steady shear at \( {\mathop \gamma \limits^ \cdot }_{R} = 100\,s^{{ - 1}} \) and sinusoidal flux density of 0.4 T amplitude due to current imposition at frequencies 0.5 and 5 Hz, respectively. The shear rate remains fairly constant during these cycles. At 0.5 Hz, a full modulation is observed: The maximum shear stress corresponds to that expected from the characteristic in Fig. 8b, whereas the minimum shear stress reaches practically zero, taking into account the off-state shear stress of about 0.1 kPa at 100 s−1 (Fig. 8a). This example represents the case of full modulation. Yet the shape of the shear stress half wave deviates distinctly from symmetry. This indicates some hysteresis of the transient characteristic, not further investigated in this paper.

Fig. 10
figure 10

MCR501 software output of transient shear stress and shear rate (controlled to 100 s−1) measured for a flux density amplitude of 0.4 T. a Frequency 0.5 Hz. b Frequency 5 Hz

Full size image

In contrary, the modulation is only partial for 5 Hz (Fig. 10b). Here, the sampling rate for the data points was set to 5 ms. The experimental ratio τ min/τ max = 0.12 (neglecting the off-state shear stress) yields ωλ = 0.40 from Fig. 3 or Eq. (17), which finally gives a switching time of λ = 13 ms. This value is an artifact, however, because of a low pass filter in the MCR501 shear stress signal. This becomes obvious if the unfiltered torque signal is accessible at 0.1 ms sampling rate.

Unfiltered torque from analog output (MCR501 firmware)

Figure 11a,b shows for the same measurement conditions as above (5 Hz and 0.4 T amplitude, shear rate 100 s−1) the transient flux density as well as the unfiltered torque at higher time resolution. In the oscilloscope screenshot (Fig. 11a), the zero point of the torque has been set to −2 scale divisions. Whereas the flux density signal is smooth and sinusoidal, the torque signal exhibits distinct noise. In spite of the latter, however, it is clearly seen that the torque signal reaches zero when the flux density changes its sign. Whereas the decreasing branch of the torque shows a smooth descent, strong fluctuations of the torque are observed in the start-up branch, presumably caused by the torque imposition control.

Fig. 11
figure 11

Same measurement conditions as in Fig. 10b but torque signal from firmware at 0.1 ms sampling rate. a Oscilloscope screenshot of flux density and torque signal. b Torque signal after 0.5 ms floating average

Full size image

For a more quantitative representation, the digital oscilloscope data were submitted to a digital smoothening by using a floating average over 0.5 ms (Fig. 11b). The torque noise is distinctly reduced, whereas the torque fluctuations remain visible. The key result is confirmed: A full modulation is observed at 5 Hz if the unfiltered torque signal is used! For an estimate for the upper bound of the switching time from this experiment, one could assume a ratio τ min/τ max < 0.02. This corresponds to ωλ < 0.10 or λ < 3.2 ms. This switching time is much shorter compared to the result from the original software signal!

In principle, one could try to use higher frequencies to see a partial modulation of the unfiltered torque signal, thus allowing the determination of the switching time more accurately. However, this is not feasible with the current magneto-cell. A frequency of 5 Hz (31.4 rad/s) is more than 50% above the cut-off frequency of the electro-magnetic circuit. This means that larger currents—outside the range of the present power amplifier—are required to reach the same level of flux density amplitude. In addition, interferences with eddy currents and saturation magnetization of the yoke come into play.

A possible way to overcome this limit would be to operate at lower flux density amplitudes and to use a lock-in technique to detect the transient torque signal from the resulting distinct noise level. Such an approach is outside the scope of this paper.

Step coil voltage

Imposition of a step voltage was accomplished by using the circuit depicted in Fig. 7a. Figure 12 shows a screenshot for a square wave voltage imposition (alternating between 0 and 4.4 V at frequency of 8 Hz). The current signal (U out) follows exactly the transients expected from Eqs. (6, 7) with time constant Λ = 51 ms and 1.8 A in the activated state. The flux density signal (plateau value of 0.36 T) is essentially proportional to the coil current. However, a distinct bias flux density in the order of 0.02 T is observed, caused by the remanence of the yoke. Because a switching time in the order of a few milliseconds is too short compared to Λ = 51 ms to cause a distinct effect on the transient torque (compare Fig. 1), it was not tried to use this kind of test for a switching time determination.

Fig. 12
figure 12

Oscilloscope screenshot for coil current and flux density for a square wave voltage imposition of 4.4 V at 8 Hz

Full size image

Step coil current

Imposition of a step current was accomplished by using the circuit depicted in Fig. 7b. Figure 13 compares the step-up transients of current, i.e., U out and magnetic flux density B for a square wave current imposition (alternating between 0 and 4.5 A at frequency 8 Hz). Due to the coil inductance, only a steep current ramp over 19 ms is achieved at maximum voltage output of the power operational amplifier. After a significant overshoot (due to the time constant of the operational amplifier’s feedback loop), a coil current plateau of 4.5 A is reached. The transient flux density also shows a steep increase, albeit somewhat delayed compared to the current. It does not exhibit an overshoot and gradually reaches a flux density of about 0.9 T after 50 ms. This example clearly demonstrates the effect of eddy currents and yoke saturation magnetization on the transient of B. As a consequence, a reliable determination of switching times at high flux density changes requires a direct measurement of the transient flux density.

Fig. 13
figure 13

Transient coil current and corresponding flux density for a step coil current imposition (4.5 A plateau current)

Full size image

A comparison of the transient flux density and resulting torque for steady shear at 100 s−1 is shown in Fig. 14 for a step current of 5 A that creates a flux density of about 1.05 T over 500 ms, both for the start-up and shutdown phase. The transients have been recorded by the digital oscilloscope and have then been transferred to Excel. To reduce the noise from the original screenshot (compare Fig. 11a), a digital floating averaging over 0.25 ms has been applied. It is clearly seen that the torque signal transients are delayed compared to the flux density by a few milliseconds.

Fig. 14
figure 14

Transient flux density and resulting shear stress for a step coil current test at shear rate 100 s−1 and fit by Eqs. (9, 11) and (10, 12), respectively. a Start-up (Λ = 35 ms, B 0 = 2.08 T). b Shutdown (Λ = 49 ms, B 0 = 3.6 T)

Full size image

For a quantitative analysis, we fitted the monotonously increasing and decreasing parts of the flux density transients by Eqs. (9) and (10), respectively. An excellent fit is obtained if both B o and Λ are considered as adjustable parameters. In this case, Λ may deviate from the time constant of the electromagnetic circuit determined by Fig. 6 but still remains in the right order of magnitude. The fits are represented in Fig. 14 by the smooth lines.

The transient torque shows distinct fluctuations. For a fit of the transient torque by means of Eqs. (11, 12), we require the slope of the (linear) characteristic p = 75 kPa/T and the relation between torque M D and Newtonian shear stress for 10 mm radius disks: M D = 1.6 × 10–3 Nm/kPa. The only remaining parameter for the fit is the switching time λ. As seen from the figures, a switching time of 2.8 ms is pertinent to describe two third of the start-up transition, whereas a value of 1.8 ms is more pertinent for the shutdown transient. The estimated uncertainty for the fit is about ±0.5 ms. It should be noted that these values are in agreement with the estimate from the 5 Hz sinusoidal flux density test.

Conclusions

Although not developed for rapid flux density changes, we could demonstrate that the commercial 1 T magneto-cell MRD180 may be used to impose flux density transients by means of a power operational amplifier. The preferred circuit (Fig. 7b) imposes the coil current. Sine wave and nearly square wave flux densities could be created. The bulky soft iron joke is responsible for the relatively long time constant Λ = 50 ms of the electromagnetic circuit. To detect the true flux density transients in the MRF, an additional non-magnetic disk was introduced, which acts as the housing of a hall probe. The Hall probe allows an online measurement of the flux density during the rheological measurement. The phase shift between oscillating coil current and flux density, as well as the time delay of the flux density compared to a steep coil current ramp, was demonstrated for large changes of flux density (magnitude of 0.4 to 1 T). This is a clear indication that a reliable switching time determination requires the online flux density measurement.

Analytic expressions for the transient shear stress at constant shear rate are derived, assuming a Maxwell behavior of the MRF with switching time λ as well as a linear characteristic (shear stress vs magnetic flux density). For a sine wave flux density, the switching time may be derived from the ratio τ min/τ max of the periodic shear stress. For a step voltage test, the flux density exhibits single exponential behavior scaled by the time constant Λ of the electromagnetic circuit. In the shear stress response, both the circuit time constant and the MRF switching time show up, allowing a determination of the switching time from the shear stress transient, as long as the switching time is not much shorter than about Λ/10. In a step current test, an analogous treatment of the transient shear stress is pertinent as long as the flux density transient may be approximated by a single exponential.

The test modes described above were applied for a constant shear rate at room temperature. The rheometer MCR501 was found capable to maintain fairly well the programmed shear rate in spite of large and rapid changes of the shear stress. The theoretically expected behavior for a sine wave flux density was verified: Full modulation of the shear stress for ωλ ≪ 1 and distinct partial modulation for ωλ > 0.1. However, the original MCR501 software output contains a low pass filter (time constant > 10 ms), which yields an erroneously long switching time of 13 ms. With the help of a special firmware, kindly provided by the instrument manufacturer, unfiltered access to the torque signal at 0.1 ms sampling rate was possible. From the full (unfiltered) torque modulation at 5 Hz, a switching time of less than 3 ms could be estimated. Measurements at large flux density amplitude but higher frequency were restricted by the cut-off frequency of the electromagnetic circuit.

A step voltage test was not suited to determine the switching time because 3 ms would be too small compared to the 50 ms time constant to cause a distinct deviation of the shear stress compared to the flux density transient. The step current test was found to be most suitable for the switching time determination. The major part of the flux density start-up and shut-down regimes could be approximated by single exponential functions. The fit of the corresponding shear stress transients yields a switching time of 2.8 ms (start-up) and 1.8 ms (shutdown), in agreement with the estimate from the sine wave experiment, fitting two third of the transient. This supports the concept of a Maxwell-like switching behavior.

Finally, the effect of a sigmoidal characteristic is addressed by two simple approximations for start-up and shutdown, respectively. In both cases, the shear stress transients exhibit an additional delay. A fit by the linear model will in part compensate the non-linearity effect by an increased switching time. The effect is less pronounced for the shut-down case. To quantify the possible experimental error, a more realistic description of the whole characteristic would be required.