1 Introduction

In many devices, the flow control is of key importance for their hydrodynamic performance, and a century long research on flow control methods has resulted in very high performing systems [1]. Meanwhile, the usage of renewable energies is sharply increasing in all industrial and developing countries, and the wind energy has had a very high contribution in this trend. This is partly due to its global distribution and the sense of reliability in usage of this energy source [2,3,4,5,6,7]. Recent research has shown great potential for improving the performance of wind energy harvesting by aerodynamic optimization of the flow field around turbine blades [8, 9]. The flow control technology has significantly contributed to the blade aerodynamic performance, especially to improve the performance at low speed winds [5]. Strong flow control around turbine blades, may retard the performance deterioration due to the flow separation when the blade is highly loaded. This will result in a higher generated lift and aerodynamic efficiency for a constant wind speed, which produces higher mechanical and electrical power. The other advantage of flow control is to increase the availability by reducing the limiting conditions and flow regimes in which the turbine may not generate any mechanical power [5, 6].

The plasma physics is known for a long time [10, 11], and in recent years, many industrial applications has benefited from this technology. Recently usage of dielectric discharge barrier (DBD) plasma actuators for different applications [12, 13] including flow control, has attracted many researchers. This is partly due to their low cost and ease of applicability. To design application of these actuators for real wind turbine blades, one needs to engineering data or tools to select appropriate values for different physical or operational parameters. For this reason, one of the main lines of research in this field is devoted to parametric study to optimize the efficiency and performance of a wind turbine blade by embedding a DBD actuator. The parametric study may include geometrical, physical and operational parameters. This may result in a knowledge of the sensitivity of performance criteria to different design parameters, and to evaluate their effective range of variation, and how to constrain them in design. Finally, one may analyze effect of each parameter variation on performance indices [14,15,16,17,18,19,20,21].

These parametric studies may be categorized to three sections: pure experimental, pure computational, and hybrid methods. The initial research in this line was devoted to experimental parametric study of the application of a DBD actuator on a flat plate. Effect of the geometrical and operational parameters where experimentally investigated by Fort et al. [22]. In another study, the physical parameters including the ambient gas combination and pressure, the applied voltage waveform, the shape of the electrodes and the dielectric material were considered by Abe et al. [23] to improve the induced jet momentum. Robert Van Dyken et al. [24] used a flat plate in a still air environment to find optimum parameter’s value. To compare active and passive flow control strategies, Thomas et al. [25] used an array of plasma vortex generators for production of body forces to be compared by passive vortex generators introduced by Wicks et al. [26]. Jukes et al. [27] performed a similar investigation. Erfani et al. [28] studied the applied voltage and frequency parameters effect on performance, and used multi-encapsulated DBD electrodes to induce a stronger induced jet in their experiments.

A main challenge to the experimental studies is the excessive number of effective parameters. This makes the experimental work very slow and expensive. Neretti et al. [29] investigated effect of different electrode geometries. In an experimental parametric study, the geometrical and operational parameters were optimized by Taleghani et al. [30] to increase the induced wall jet velocity. Greenblatt and Wygnanski [31] experimentally investigated the periodic excitations due to the cyclic pitch in a low speed flow over a rotorcraft NACA0015 airfoil, and optimized the lift coefficient while the moment was restricted to its pre-stall condition. The power flow structure in a DBD actuator was analyzed by Roth and Dai [32] and was optimized by identifying different actuator power sinks.

To improve the aerodynamic performance of a NACA0015 airfoil, Jolibois et al. [33] use experimental modification of the boundary layer velocity profile. A circumferential configuration for a micro DBD actuator was introduced by Ozturk et al. [34] to improve the quality of an internal duct flow. For experimental optimization of operational and geometrical parameters of the DBD actuator electrodes, Corke et al. [35] used models for time and space dependence of the induced body force.

The expense and complexity of pure experimental work have led many people to hybrid numerical-experimental analysis to decrease the expense of the experimental investigations. A genetic algorithm was used by Benard et al. [36] to control the size of the separation zone of a backward stepping flow. They also used a multi-variable single objective optimization algorithm to optimize operational parameters like the amplitude, frequency and the duty cycle of the high voltage bursts [37]. To estimate the electro-hydro-dynamic body forces, they use experimental velocity measurements [38].

The general trend in the scientific research is towards computational analysis instead of experimentation. The DBD plasma actuators design and optimization is no exception. Here we review a few of these numerical and optimization studies, and how they have improved during recent years. In a low Reynolds number flow with an adverse pressure gradient on a flat plate, Regis de Quadros et al. [39] used numerical optimization to cancel wave generation made by flow separation. Similarly effect of different flow kinematic and thermodynamic parameters on the performance of DBD actuators were investigated by Kriegseis et al. [40].

To control the wake at high dynamic pressure conditions, Matsuno et al. [41, 42] applied a robust design algorithm for design of a DBD actuator and to optimize the driving conditions used an optimization scheme. Similarly, Sulaiman et al. [43] used a multi-objective design optimization algorithm to find the optimum DBD actuator design over an airfoil. Large eddy simulations were used by Sato et al. [44] for flow separation control over a NACA0015 airfoil, and power reduction, by application of optimum geometrical and operational parameters, including the burst frequency and actuation ratio. For DBD performance improvement, Watanabe et al. [45] used a multi-objective evolutionary scheme based on a non-dominated sorted genetic algorithm. A quantitative design optimization was applied by Williams et al. [46] by coupling the geometric changes and the actuator design, to control the boundary layer flow. Foe wind energy harvesting applications, Batlle et al. [47] investigated design of airfoils with a suitable DBD actuator by introducing a design methodology, evaluated by an experimentation.

Despite the increasing number of numerical analysis, there is still a far more left to reach a reasonable situation. The structure of the flow field around a DBD plasma actuator is complex and involves different interacting physics. Firstly, it includes plasma generation, which is a chaotic phenomenon with a nano-second time scale. The variations in the electrical field, which drives the motion of the plasma particles, has a millisecond time scale, while we typically have a time scale of the order of one second for flow parameters. This makes the modelling very complicated and for real industrial applications the perfect computational simulation is still out of reach. Many mathematical and physical modellings are introduced to remove this complexity. One strategy is to use empirical models for the electro-static field based on physical equations. This was improved by Yoon and Han [48], and was followed by Seth et al. [49] to analyze how different geometrical and electrical parameters affect performance.

For a perfect computational analysis of a plasma induced jet in a boundary layer, one needs to simultaneous solutions of the electrical field Maxwell equations and the flow field Navier Stokes equations. Computation of this complex non-linear system for a real industrial system is prohibitively expensive. A waterfall of numerical schemes are suggested to decrease this complexity [50,51,52,53,54,55,56,57]. Suzen and Huang [53, 54] used the formulation suggested by Enole [58, 59] to introduce their electrostatic S–H model. Many people have improved this formulation, including Bouchmal [55], Skote et al. [56], Abdollahzadeh et al. [57]. To propose a new model based on S–H model, authors considered the effects of the applied voltage amplitude and frequency, and applied this by integrating different numerical models [51]. Further, to make the model independent of the experimental data, they introduced a new phenomenological model [52]. This formulation was used in an optimization procedure for a few thin and thick airfoils suited for wind energy harvesting in large wind turbines. To improve the performance of these airfoils, the location and configuration of twin DBD actuators installed on blades of the high-Megawatt Dutch Offshore Wind Energy Converter (DOWEC 6 MW) turbine with a collective pitch mechanism were optimized [52].

One observes the evident need for more efficient numerical analysis methods for design of optimum application of DBD actuators for wind turbine blades. In this article, a parametric study on operational design parameters of a DBD actuator, including the applied voltage waveform, amplitude and frequency, is presented. To enhance performance of a real wind turbine blade by installation of a DBD actuator, for modeling of the plasma region, we have used the phenomenological model formulated by ourselves [52], which is validated by a wind turbine application [21].

Main contributions of this article include definition of a parametric study on operational parameters. This is used to have an optimized design for installation of a DBD actuator on a DU21 wind turbine blade. At stall conditions, the interaction of the induced wall jet and the boundary layer in the separation zone is analyzed. The main contributions follow:

  • A parametric study on operational parameters (including the applied voltage waveform, amplitude, and frequency) is defined, and their effect on the blade aerodynamic performance are studied.

  • The usage of the electrostatic model developed by authors for operational parameters is validated.

  • The fully stalled boundary layer enhanced by wall induced jet under different operational parameters are analyzed.

  • An engineering design formula derived for optimum selection of operational parameters.

2 The governing equations

2.1 Electrostatic model

The S–H model [53, 54] is one of the most robust physical approximations of the DBD plasma actuator effects [60, 61]. In this model, the body force is computed by solving two elliptic equations independent from the fluid flow equations. This body force is added as a source term to the Navier–Stokes equations. By imposing a high AC voltage on the arrangement of two electrodes separated by a dielectric layer, the air starts to ionize unsteadily and the plasma is formed. This periodic plasma formation happens in a time scale of 10–9–10–8 s [55] while the response time of the neutral flow field induced by the plasma generation is in the order of 10–2 s. The time scale of the electrical field is of the order of 10–4 s. Presence of ionized particles in the electrical field results in a body force that acts on the flow in a quasi-steady manner. This body force can be incorporated into the flow governing Navier–Stokes equations as a source term.

The momentum transfer during collision of accelerated charged particles and low speed neutral particles is like a body force on the medium. Assuming that particles 1 lose their momentum when elastically colliding particles 2, the lost momentum per unit volume and time is \(\overrightarrow{{P}_{1}}=-{m}_{1}{n}_{1}{\vartheta }_{12}(\overrightarrow{{V}_{1}}- \overrightarrow{{V}_{2}})\) [60]. Here, for particle 1, \({m}_{1}\), \({n}_{1}\), and \(\overrightarrow{{V}_{1}}\) denote, respectively, mass, density, and velocity (and similarly \(\overrightarrow{{V}_{2}}\) is the velocity of type 2). \({\vartheta }_{12}\) is the collision frequency between particles. One may neglect the velocity of the neutral particles, and the total equivalent force of this momentum transfer by positively and negatively charged particles to the neutral medium is equivalent to

$$\overrightarrow{{f}_{\mathrm{b}}}={m}_{\mathrm{e}}{n}_{\mathrm{e}}{\vartheta }_{\mathrm{en}}\overrightarrow{{V}_{\mathrm{e}}}+{m}_{\mathrm{i}}{n}_{\mathrm{i}}{\vartheta }_{\mathrm{in}}\overrightarrow{{V}_{\mathrm{i}}}$$
(1)

Here we have used subscripts e, i, and n to refer to electrons, ions, and neutral particles, respectively. If we define the pressure of electron and ion by \({p}_{\mathrm{e}}={n}_{\mathrm{e}}{k}_{\mathrm{B}}{T}_{\mathrm{e}}\) and \({p}_{\mathrm{i}}={n}_{\mathrm{i}}{k}_{\mathrm{B}}{T}_{\mathrm{i}}\), The velocity of the electron and ion particles at steady state is defined as [61]:

$$\overrightarrow{{V}_{\mathrm{e}}}=-\frac{e}{{m}_{\mathrm{e}}{\vartheta }_{\mathrm{en}}}\overrightarrow{E}-\frac{1}{{m}_{\mathrm{e}}{n}_{\mathrm{e}}{\vartheta }_{\mathrm{en}}}\overrightarrow{\nabla }{p}_{e}$$
(2)
$$\overrightarrow{{V}_{i}}=+\frac{e}{{m}_{\mathrm{i}}{\vartheta }_{\mathrm{in}}}\overrightarrow{E}-\frac{1}{{m}_{\mathrm{i}}{n}_{\mathrm{i}}{\vartheta }_{\mathrm{in}}}\overrightarrow{\nabla }{p}_{\mathrm{i}}.$$
(3)

Velocities are made up of two terms. The first term is called drift, and the second term is a diffusion term. The electro-hydro-dynamic body force induced by the electrical field is then estimated by substituting Eqs. (2–3) into Eq. (1), which gives the induced body force per unit volume exerted on the flow field:

$$\overrightarrow{{f}_{\mathrm{b}}}=e\left({n}_{\mathrm{i}}-{n}_{\mathrm{e}}\right)\overrightarrow{E}-{k}_{\mathrm{B}}{T}_{\mathrm{e}}\nabla {n}_{\mathrm{e}}-{k}_{\mathrm{B}}{T}_{\mathrm{i}}\nabla {n}_{\mathrm{i}}.$$
(4)

The body force is made up of three terms. The first term is the conduction of the current densities. The other terms are related to the diffusion. For a thin layer adjacent to the DBD electrodes discharging in an atmospheric ambient, this force is significant and produces a so called “induced wall jet”. Usually we assume \({T}_{\mathrm{e}}\gg {T}_{\mathrm{i}}\) therefore the term \({k}_{\mathrm{B}}{T}_{\mathrm{i}}\nabla {n}_{\mathrm{i}}\) may be neglected. Close to the cathode (negative electrode), we have a region of discharge with a large electric field and EHD body force, while we have a quasi-neutral plasma region close to the anode, where the EHD force (the first term) is close to zero. The body force ratio in these two regions is of the order of 10–4 [61, 62]. Therefore, defining the net charge density in \(\mathrm{C}/{\mathrm{m}}^{3}\) by \({q}_{\mathrm{c}}\), and the electric field vector by \(\overrightarrow{E}\), the body force equation could be simplified to:

$$\overrightarrow{{f}_{\mathrm{b}}}={e\left({n}_{\mathrm{i}}-{n}_{\mathrm{e}}\right)\overrightarrow{E}=q}_{\mathrm{c}}\overrightarrow{E},$$
(5)

where \(\overrightarrow{{f}_{\mathrm{b}}}\) is the body force vector per unit volume, \({q}_{\mathrm{c}}\) is the net charge density in \(\mathrm{C}/{\mathrm{m}}^{3}\), and \(\overrightarrow{E}\) is the electric field vector.

The basic equations for the electrostatic model to simulate the effect of the plasma actuator on the fluid flow are the Maxwell’s equations written as follows:

$$\nabla .\overrightarrow{\mathrm{D}}={q}_{\mathrm{c}}$$
(6)
$$\nabla .\overrightarrow{B}=0$$
(7)
$$\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$$
(8)
$$\nabla \times \overrightarrow{H}=\overrightarrow{J}-\frac{\partial \overrightarrow{D}}{\partial t},$$
(9)

where \(\overrightarrow{D}\) is electrical induction, \(\overrightarrow{B}\) is magnetic induction \(\overrightarrow{E}\) is electrical field, \(\overrightarrow{H}\) is magnetic field, and \(\overrightarrow{J}\) is electric current. Assuming that there is enough time to charge the plasma in the redistribution process as well as the whole system is almost quasi-steady, magnetic induction, magnetic field, electric current, and also the time derivatives in Maxwell's equations become zero. Thus Maxwell's equations will be simplified to the following two equations:

$$\nabla .\overrightarrow{\mathrm{D}}={q}_{\mathrm{c}}$$
(10)
$$\nabla \times \overrightarrow{E}=0.$$
(11)

Ignoring the temporal changes of the magnetic field in this model is almost a correct assumption for plasma actuator phenomena [53]. It should be noted that the relationship between electric induction and electric field is as follows:

$$\overrightarrow{D}=\varepsilon .\overrightarrow{E},$$
(12)

where ε is the electrical permittivity and is defined as ε = ε0εr and ε0 is free permittivity and εr is relative permittivity. With this definition, Eq. (10) is as follows:

$$\nabla .\upvarepsilon \overrightarrow{\mathrm{E}}={q}_{\mathrm{c}}.$$
(13)

Also, according to Eq. (11), we can say that the electric field can be a gradient of a scalar potential function Φ, so we can write:

$$\overrightarrow{E}=-\nabla \Phi .$$
(14)

Equation (13) can now be rewritten as follows:

$$\nabla .\left({\varepsilon }_{r}\nabla \Phi \right)=-\frac{{q}_{\mathrm{c}}}{{\varepsilon }_{0}}.$$
(15)

On the other hand, Boltzmann’s relation to charged plasma particles is written as follows [58]:

$$\frac{{q}_{c}}{{\varepsilon }_{0}}=\frac{e}{{\varepsilon }_{0}}\left({n}_{\mathrm{i}}-{n}_{\mathrm{e}}\right)=-e\frac{{n}_{0}}{{\varepsilon }_{0}}\left[\mathrm{exp}\left(\frac{e\varphi }{{K}_{\mathrm{b}}{T}_{\mathrm{i}}}\right)+\mathrm{exp}\left(\frac{e\varphi }{{K}_{\mathrm{b}}{T}_{\mathrm{e}}}\right)\right],$$
(16)

where \(\varphi\) is the local electric potential, \({K}_{\mathrm{b}}\) is the Boltzmann constant, \({T}_{\mathrm{i}}\) and \({T}_{\mathrm{e}}\) are the temperatures of ions and electrons, \({n}_{\mathrm{i}}\) and \({n}_{\mathrm{e}}\) are the charged particles density, and \({n}_{0}\) is the base plasma density. The Boltzmann relation can be transformed by extending the Taylor series for exponential functions, assuming \(\varphi \ll T\):

$$\frac{{q}_{\mathrm{c}}}{{\varepsilon }_{0}}\approx -{e}^{2}\frac{{n}_{0}}{{\varepsilon }_{0}}\varphi \left[\left(\frac{1}{{K}_{\mathrm{b}}{T}_{\mathrm{i}}}\right)+\left(\frac{1}{{K}_{\mathrm{b}}{T}_{\mathrm{e}}}\right)\right].$$
(17)

Also, the Debye length \({\lambda }_{\mathrm{d}}\), which is the characteristic length of the produced plasma thickness in neutral gas, is defined as follows:

$${\lambda }_{\mathrm{d}}={\left[{e}^{2}\frac{{n}_{0}}{{\varepsilon }_{0}}\left[\left(\frac{1}{{K}_{\mathrm{b}}{T}_{\mathrm{i}}}\right)+\left(\frac{1}{{K}_{\mathrm{b}}{T}_{\mathrm{e}}}\right)\right]\right]}^{-0.5}.$$
(18)

According to the definition of the Debye length, Eq. (17) can be written as follows:

$${q}_{\mathrm{c}}=-\frac{{\varepsilon }_{0}}{{\lambda }_{\mathrm{d}}^{2}}\Phi .$$
(19)

The experimental results show that the direction of the generated body force and consequently the direction of the induced velocity to the fluid flow is independent of the electrode to which the voltage is applied. It is also independent of the polarity that the electrode with voltage finds at any given moment. The results show that the direction of the generated body force component is always from the exposed electrode to the embedded electrode [54].

Suzen and Huang proposed that the electric potential field could be divided into two parts using the principle of superposition of the field [54]. Because the gas particles are poorly ionized, it can be assumed that Φ is composed of two parts. An electric potential due to electric field \(\phi\) and another one due to net charge density \(\varphi\):

$$\Phi =\phi +\varphi$$
(20)

Assuming that the Debye length is very small, the charge thickness on the dielectric surface will be small and it can be assumed that the distribution of charged particles in the domain is more affected by the potential of the charged particles on the wall and receives less impact from the external electric field. Therefore, for the electric field potential, we arrive at a Poisson equation:

$$\nabla .\left({\varepsilon }_{\mathrm{r}}\nabla \phi \right)=0$$
(21)

And for the potential due to the total charge concentration we get a Helmholtz equation:

$$\nabla .\left({\varepsilon }_{\mathrm{r}}\nabla \varphi \right)=-\frac{{q}_{\mathrm{c}}}{{\varepsilon }_{0}}.$$
(22)

Using Eq. (19), the Helmholtz equation can be written in terms of the charge concentration variable:

$$\nabla .\left({\varepsilon }_{\mathrm{r}}\nabla {q}_{\mathrm{c}}\right)=-\frac{{q}_{\mathrm{c}}}{{\lambda }_{d}^{2}}$$
(23)

The two Eqs. (21) and (23) are the basic equations used for electrostatic modeling of the plasma operator.

There are two different Eqs. (21) and (23) that need to be solved (see Fig. 1c). They need to two different sets of boundary conditions. Electric potential Eq. (21) is solved in both the dielectric and the fluid domain. Boundary conditions are defined as: \(\partial \phi /\partial {n}_{\mathrm{i}}= 0\) on outer boundaries, \(\phi =\phi (t)\) on the exposed electrode, and \(\phi =0\) on the embedded electrode. Here, \({n}_{\mathrm{i}}\) is the unit normal vector of the surface and \(\phi \left(t\right)={\phi }^{\mathrm{max}}f(t)\) denotes the applied voltage. \({\phi }^{\mathrm{max}}\) refers to the amplitude of the AC voltage applied. The wave form function \(f(t)\) is a time-dependent function and can be used to model both steady and unsteady actuators. Details for the boundary condition for the charge density are given in Ref. [52].

Fig. 1
figure 1

The schematics of the DBD plasma actuator a model using capacitors, b the equivalent electrical circuit, c boundary conditions for the electrical field and the density charge

Full size image

The net charge density Eq. (23) is solved only on the fluid flow side of the domain (Fig. 1c). Boundary conditions for solution of this equation are given as: \({q}_{\mathrm{c}}=0\) on outer boundaries, \({q}_{\mathrm{c}}={q}_{\mathrm{c}}^{\mathrm{max}}G\left(x\right)f\left(t\right)\) for downstream of the exposed electrode, on the surface of the dielectric above the embedded electrode, and \(\partial {q}_{\mathrm{c}}/\partial {n}_{\mathrm{i}}= 0\) on the solid walls except the region of the lower electrode. \({q}_{\mathrm{c}}^{\mathrm{max}}\) refers to the maximum charge density of the applied AC voltage on the dielectric surface. Based on the experimental results [58], Suzen et al. [53, 54] suggested a half Gaussian distribution \(G\left(x\right)=\mathrm{exp}(-\frac{{\tilde{x }}^{2}}{2{\sigma }^{2}})\) to simulate the variation of the charge density on the wall over the embedded electrode in the stream-wise direction. \(\tilde{x }\) is the chord-wise length measured from the leading edge of the embedded electrode, and \(\sigma\) is a scale parameter for the Gaussian distribution. \({\lambda }_{\mathrm{d}}\) and \({q}_{\mathrm{c}}^{\mathrm{max}}\) remain to be determined later by an empirical or phenomenological model.

Ibrahim and Skote [56] implemented the following boundary condition for the electric potential field equation.

$${\nabla }_{\mathrm{n}}\, \phi ={\nabla }_{\mathrm{t}}.\left({\lambda }_{\mathrm{d}}{\varepsilon }_{\mathrm{r}}{\nabla }_{\mathrm{t}}\phi \right),$$
(24)

where \({\nabla }_{\mathrm{n}}\) and \({\nabla }_{\mathrm{t}}\) describe the normal and tangential derivatives. In our previous publication [51, 52], we introduced a new boundary condition on the charged surface to be used instead of the Gaussian distribution to remedy the poor performance of the S–H model. After solution of the electric potential Eq. (21) and finding the potential electric field distribution on the charged surface, this value is used in Eq. (25) to find the boundary condition of the net charge density Eq. (23) along the plasma extent:

$${0<x<17\% \,\,q}_{c}\left(x\right)={q}_{\mathrm{c}}^{\mathrm{max}}{\left(\frac{{\phi }_{\mathrm{max}}^{\mathrm{local}}-\phi }{{\phi }_{\mathrm{max}}^{\mathrm{local}}-{\phi }_{{17}_{\%}}}\right)}^{2.0}$$
(25)
$${17\%<x<100\% \,\,q}_{c}\left(x\right)={q}_{\mathrm{c}}^{\mathrm{max}}{\left(\frac{\phi -{\phi }_{\mathrm{min}}^{\mathrm{local}}}{{\phi }_{{17}_{\%}}-{\phi }_{\mathrm{min}}^{\mathrm{local}}}\right)}^{0.6}.$$

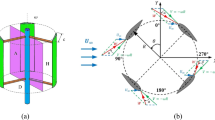
The thrust induced by a DBD plasma actuator could be assumed to be proportional to the electric energy consumption of the DBD actuator [57]. This provides a well accurate method to estimate the plasma actuator performance by calculating the energy consumption of the AC circuit. Yoon and Han [48] considered the dielectric barrier plasma actuator as an AC circuit having two capacitors connected serially, and used the consumed energy of the capacitors to calculate the thrust value (see Fig. 1b). \({C}_{\mathrm{d}}\) is the capacitance of the lower electrode and the dielectric barrier, while \({C}_{\mathrm{g}}\) is the capacitance of the upper electrode and the generated plasma over the electrodes (see Fig. 1a). The capacitance of the capacitors can be expressed in terms of the geometric and material properties of the actuator components as [57]:

$${C}_{\mathrm{g}}=2\pi {\varepsilon }_{0}\frac{{l}_{\mathrm{p}}}{\mathrm{ln}\left(\frac{0.5{t}_{\mathrm{e}}+{\lambda }_{\mathrm{d}}}{0.5{t}_{\mathrm{e}}}\right)}$$
(26)
$${C}_{\mathrm{d}}=2\pi {\varepsilon }_{\mathrm{d}}\frac{{l}_{\mathrm{e}}}{\mathrm{ln}\left(\frac{0.5{t}_{\mathrm{e}}+2{t}_{\mathrm{d}}}{0.5{t}_{\mathrm{e}}}\right)}.$$
(27)

Here, \({t}_{\mathrm{e}}\) is the thickness of the exposed electrode, \({t}_{\mathrm{d}}\) is the thickness of the dielectric barrier, \({l}_{\mathrm{p}}\) is the length of the plasma extent on the dielectric surface, \({l}_{\mathrm{e}}\) is the length of the embedded electrode, \({\varepsilon }_{0}\) is the permittivity of the free space and \({\varepsilon }_{\mathrm{d}}\) is the dielectric permittivity.

The maximum charge concentration is a very important parameter in the present model, and a modified equation is used to estimate the maximum charge density in terms of the induced thrust:

$${q}_{\mathrm{c}}^{\mathrm{max}}={\alpha }_{\mathrm{corr}}\frac{\mathrm{Thrust}}{{\lambda }_{\mathrm{d}}({V}_{\mathrm{app}}-{V}_{\mathrm{bd}})}.$$
(28)

Here \({V}_{\mathrm{bd}}\) is the breakdown voltage, i.e., the least voltage required to start the ionization process [48, 52].

2.2 The non-dimensionalized form and the numerical simulation process

The normalized parameters are defined as relations (29). Using these non-dimensionalized variables in equations governing the electrostatic model, the non-dimensionalized Eqs. (30) and (31) are obtained.

$${\phi }^{*}=\phi /{\phi }^{\mathrm{max}}f(t)$$
(29)
$${q}_{\mathrm{c}}^{*}={q}_{\mathrm{c}}/{q}_{\mathrm{c}}^{\mathrm{max}}f(t)$$
$${\overrightarrow{E}}^{*}=\frac{\overrightarrow{E}}{{E}_{0}}={l}_{\mathrm{p}}\nabla {\phi }^{*},$$
$${E}_{0}=\frac{{V}_{\mathrm{app}}-{V}_{\mathrm{bd}}}{{l}_{\mathrm{p}}}$$
$$\nabla .({\varepsilon }_{\mathrm{r}}\nabla {\phi }^{*})=0$$
(30)
$$\nabla .\left({\varepsilon }_{\mathrm{r}}\nabla {q}_{\mathrm{c}}^{*}\right)=\frac{{q}_{\mathrm{c}}^{*}}{{\lambda }_{\mathrm{d}}^{2}}.$$
(31)

Two-dimensional incompressible Reynolds-averaged Navier–Stokes (RANS) equations are employed for fluid flow simulation [51]. Since most of the energy given to the plasma actuator is consumed to accelerate the fluid particles and only a negligible part is contributed to the fluid warming [63], the flow field energy equation is ignored. The fundamental equations of mass and momentum conservation that are used to simulate the fluid flow are as follows:

$$\nabla .\overrightarrow{u}=0$$
(32)
$$\left(\overrightarrow{u}.\nabla \right)\overrightarrow{u}=-\frac{1}{\rho }\nabla P+\upsilon {\nabla }^{2}\overrightarrow{u}+\overrightarrow{{f}_{\mathrm{b}}}$$
(33)

in which \(\overrightarrow{{f}_{\mathrm{b}}}\) is the body force per unit volume in \(\mathrm{N}/{\mathrm{m}}^{3}\) due to the effect of the plasma actuator. \(\overrightarrow{u}\), \(\rho\), \(P\) and \(\upsilon\) are respectively, the velocity, density, static pressure and kinematic viscosity. As seen in Eq. (33), the body force generated by the plasma actuator is added to the right hand side of the momentum equation.

2.3 Numerical procedure

The solution algorithm starts with solution of the potential Eq. (30). The boundary condition (25) is applied to solve the Poisson Eq. (31) in the flow field to find the charge density distribution over the dielectric surface, as explained in Sect. 2.1. The body force in normal and tangential directions are found using the Lorentz equations:

$$\overrightarrow{{f}_{\mathrm{b}}}(x,t)=\left(\left({V}_{\mathrm{app}}-{V}_{\mathrm{bd}}\right)f\left(t\right){q}_{\mathrm{c}}^{\mathrm{max}}f\left(t\right)\right){q}_{\mathrm{c}}^{*}(x)(-\nabla {\phi }^{*}(x))$$
(34)

and finally this is used in solution of the Navier–Stokes Eqs. (32) and (33). The above algorithm is iterated in a loop, until satisfactory convergence (five orders of magnitude) is achieved.

A computer program is developed in MATLAB to compute the electrical parameters and to solve and the electrical Eq. (31). The electrical parameters include the maximum charge density, the maximum electrical potential (i.e., the difference of the break down and the applied potentials), the Debye length and the plasma extent length over the airfoil surface.

To solve the Navier–Stokes Eqs. (32) and (33) for the domain around the DBD actuator, the commercial fluid solver ANSYS Fluent 15.0 is used. The scalar transport equations of \({\rho }_{\mathrm{c}},\upphi\) are simulated and user defined scalars (UDS) are used to apply the electrostatic equations. User defined functions (UDFs) are also used to include the source term \(\frac{{\rho }_{\mathrm{c}}}{{\lambda }_{\mathrm{d}}^{2}}\) into the scalar transport equation of \({\rho }_{\mathrm{c}}\) and to compute the body forces, and also the body force is added to the momentum equations as a source term. To save the components of the body force computed by the UDFs, we have used user defined memories (UDMs) in the solution of the electrical equations.

The boundary conditions are shown in Fig. 2. On the airfoil surface the no slip condition is set, and a uniform flow is set at the upstream condition. The pressure condition is used for the outflow boundary condition. The inflow turbulence intensity is assumed 0.02% while the outflow intensity is set to 4.0%. Another UDF is used for application of the boundary condition of the scalar transport equation of charge density (Eq. (25)).

Fig. 2
figure 2

The multi-block C-type grid around the DU21 airfoil. The central zone includes the actuator electrodes

Full size image

2.4 Problem description

The main purpose of this article is to study the effects of different operational parameters of a DBD actuator on the aerodynamic performance of a wind turbine blade, and to find the optimum conditions. The study parameters include the applied alternating voltage amplitude, waveform and frequency. The actuator is installed on a DU21 wind turbine section [64]. The main contribution of the DBD actuators installed on large wind turbines at sea level conditions happens at low speeds of 5–10 m/s, therefore a Reynolds number of 106 is selected for this study [52]. At this Re number, the maximum lift is achieved at 9° angle of attack, therefore, based on our previous experience [51], we selected a fully stalled condition which happens at a 16° angle of attack. At this point, the lift and drag coefficients of the airfoil are respectively 1.28 and 0.08. In fact, the actuator effect on the aerodynamics of the airfoil before the stall condition is negligible.

Based on our previous experience [52], we selected the configuration used in experiments of Forte et al. [22] as the base or reference design. Since at the angle of attack of 16 degrees, the flow is separated from the surface at the middle of the airfoil chord length, based on our previous experience [52], the actuator was located at 16% of the chord length from the leading edge. The exposed and embedded electrodes lengths are respectively 0.032 and 0.04 times the chord length (c), with similar thickness of 0.00015c. The selected dielectric has a thickness of 0.006c, and a relative permittivity of 3. The base applied voltage is 12 kV with a frequency of 5 kHz. The range of parameters of the applied voltage studied here are:

  • \(7000\le {V}_{\mathrm{app}}\le \mathrm{18,000} \mathrm{V}\)

  • \(1000\le f\le \mathrm{14,000} \mathrm{Hz}\)

  • \(\mathrm{Waveforms}:\mathrm{Rectangular},\mathrm{ Sinusoidal},\mathrm{ and Triangular}\)

The grid for this simulation needs special treatment. To resolve the plasma extent and its interactions with the flow field, special grid treatment in the vicinity of the electrical electrodes is required. The flow is a low speed incompressible flow, but the Reynolds number is fairly high, therefore we have assumed that a transition to turbulence happens over the airfoil suction side, and the flow may be separated at the adverse pressure gradient region. The grid should be suitable for these conditions as well. To consider effects of the wake region on the flow field, the grid is extended to 20c (chord length) in all upper, lower and upstream directions, and to 40c in the downstream direction.

Table 1 shows results of the grid study. A clean DU21 airfoil (i.e., with no active actuator) at 8° angle of attack with a C-type grid is used for this study, and the area-weighted average of Cp at the trailing edge is studied. Finally a grid with 60,300 cells is used for this study, shown in Fig. 2. One observes that the grid around the electrodes, and the leading and trailing edges are quite fine. For the transition SST turbulence model, the maximum and minimum Y + are respectively, 0.89 and 0.43, and the average Y + over the airfoil is 0.51 which is quite enough for this study [65].

Table 1 Grid independency study
Full size table

3 Validation of the electro-hydro-dynamic (EHD) computational model

3.1 The flat plate test case

Two test cases are used to validate the usage of the proposed model under different operational conditions. First we use experimental data of Durscher and Roy [66] which is also used in simulations by Abdollahzadeh et al. [57] and Yoon and Han [48]. This test case involves the stagnant atmospheric air over a flat plate. A DBD actuator derived by a 10 kV voltage at a frequency of 14 kHz is inducing a wall jet in the flow field. The length of the external electrode is 5 mm, the internal electrode is 20 mm long, and the electrodes are made of copper with a thickness of 70 μm. The dielectric is made of Acrylic with 3-mm thickness, and has a relative electrical diffusivity of 3. The length and width of the computational domain are respectively 1 and 0.5 m. No-slip boundary condition is applied to the flat plate, symmetry condition is applied to the upper surface, and zero velocity is applied at the left boundary.

The experimental velocity contours and vectors measured by the PIV method [66] is shown in Fig. 3 down, and may be used as reference for comparison of this simulation (Fig. 3 up right) with the numerical simulation of Abdollahzadeh et al.[57] (Fig. 3 up left). The maximum velocity in our simulation is 5.8 m/s, about 3% less than the measured value of 6 m/s [66], and much better than the predicted value of 4.6 m/s in Ref. [57].

Fig. 3
figure 3

The velocity magnitude and vectors around and downstream the DBD actuator. Up left: simulation data [57], Up right: the current simulation, down: the reference experimental data [66]

Full size image

To analyze details of the boundary layer profile, the x-component of the boundary layer velocity distributions at two different sections of 25 and 35 mm downstream of the exposed electrode are compared in Fig. 4. Experimental results [66] are used as the reference, and the current simulation data are compared with the numerical results of Yoon and Han [48]. The maximum velocity error predicted by our model at the first section is about 10.3%, which is much better than results reported by Yoon and Han [48] which is about 38.4% off. At the second section, the error of the current simulation is less than 1%, while it is still more than 31% for simulations of Yoon and Han. We conclude that our model is well reliable and accurate for simulation of the interactions of the induced wall jet and the boundary layer in an electrostatic field.

Fig. 4
figure 4

The x-velocity distribution at two sections. Left: at 25 mm downstream the exposed electrode. Right: at 35 mm. Circles show the experimental data [66] and the lines show simulations results presented in Ref. [66] and the current computations

Full size image

3.2 The airfoil test case

To study the accuracy and reliability of the presented model in a closer physical case, the boundary layer around a NACA0015 airfoil at fully stalled condition, with and without a DBD actuator was considered. The experimental results for this case are reported by Wang et al. [67], who used an airfoil with a chord of 10 cm with a freestream velocity of 20 m/s. The exposed electrode installed at the leading edge, had a length of 44 mm and thickness of 0.05 mm. The dielectric was made of Kapton and had a thickness of 0.1 mm. They had grounded the airfoil to zero voltage as the embedded electrode, and the driving voltage of 2.4 kV and 3 kHz frequency was applied to the exposed electrode.

The flow streamlines for the stalled airfoil at 16 degrees angle of attack, with and without the DBD actuator, and the velocity distributions at two different sections, 10% and 40% of the chord, are shown in Fig. 5. One observes that the actuator has effectively controlled the boundary layer separation, and only a small detached region is remained over the suctions surface. In fact, if they have installed the actuator further downstream at about 30% of the chord, the detached region would have almost diminished. The velocity distribution predicted by the numerical simulation follows very closely the experimental results, and the small difference in the maximum speed could be due to the lack of resolution in the experimental data.

Fig. 5
figure 5

The streamlines around a NACA0015 airfoil at a fully stalled condition, with and without a DBD actuator. Bottom compares the velocity distribution predicted by the current simulation and the experimental data [67], at two sections 10% and 40% of the chord from the leading edge. The actuator is installed at the leading edge

Full size image

4 Results

4.1 Voltage effect

One of the most important operational parameters effective in the performance of a DBD actuator, i.e., the linear momentum of the generated plasma wall jet, is the amplitude of the voltage applied to the actuator electrodes. Here we have applied a sinusoidal voltage with an amplitude in the range of 7–18 kV, and a frequency of 5 kHz. According to Ref. [52] for the geometry and operating conditions of this study, the breakdown voltage is close to 7 kV, so we do not expect generation of the plasma wall jet below this voltage.

Figure 6 shows distribution of density charges and body force vectors for four different applied voltages. One expects to see two different effects due to the increase of the applied voltage amplitude. The first is an increase in the charge density distribution along the embedded electrode, which implies a larger plasma extent on the dielectric surface [22], as observed in Fig. 6 (left). This higher charge density results in generation of more active ions in the fluid field. The second is a higher acceleration of ions in a stronger potential field, which results in a higher achieved linear momentum for the plasma wall jet. The increase in the mass and velocity of the energized ions results in a higher body force in the boundary layer region, shown in Fig. 6 (right). The Debye length parameter which shows the penetration depth of the plasma wall jet in the boundary layer has also increased, which is again clearly seen in Fig. 6 (right).

Fig. 6
figure 6

Density charge distribution contours (left) and the body force vectors (right) near the plasma actuator for different applied voltages a 7 kV, b 12 kV, c 15 kV, and d 18 kV

Full size image

Components of the generated body forces in both horizontal and vertical directions are affected by the increase in the applied voltage. Figure 7 shows variations of the integral of the body forces in the boundary layer region due to the increase in the input voltage. We expect an increase in both the number of active ions and their acceleration in this potential field. This increase in the horizontal body force is almost proportional to \({V}^{2.5}\). The sign of the body force in the normal direction is negative, which helps to generate an inflow of energetic particles out of the boundary layer into the sub layers of the boundary layer.

Fig. 7
figure 7

The generated body force for different applied voltages

Full size image

As discussed earlier, a higher horizontal body force energizes the boundary layer, which is otherwise prone to detachment from the surface in the adverse pressure gradient field over the airfoil upper surface. Figure 8 shows the distribution of streamlines close to the airfoil trailing edge for different applied voltages of 11, 13.5 and 16 kV, and compares them with the flow field over the clean airfoil (Fig. 8a). One observes a large separation bubble spread over the whole second half of the airfoil surface. The airfoil is in an angle of attack of 16 degrees, which brings the airfoil to a complete stall condition. Generation of the plasma jet helps to delay the separation, and decreases the size of the separation bubble. As observed in Fig. 8b–d as the applied voltage is increased, the size of the separation zone is decreased to a region about 32% of the chord size for an applied voltage of 11 kV, and it is almost disappeared for an applied voltage of 16 kV. It means that we have an almost full pressure recovery, which shall result in a higher lift and a lower drag coefficient.

Fig. 8
figure 8

Flow streamlines around the trailing edge of DU21 airfoil for three different applied voltages in comparison with the clean airfoil a clean, b 11 kV, c 13.5 kV, and d 16 kV

Full size image

To show this more clearly, the velocity profiles in the boundary layer for three different sections located at respectively, 50, 70, and 90% of the chord from the airfoil leading edge are illustrated in Fig. 9a–c. Velocity profiles for the same three different applied voltages are compared with the velocity profile of the boundary layers of the clean airfoil, at three sections. Figure 9a shows the velocity profiles at the 50% section, which shows that all boundary layers are attached, and generation of the plasma wall jet is also completely visible. Figure 9b could be compared with Fig. 8a to see how a large separation bubble is generated, and a strong vortex is established in the boundary layer. The reverse flow is extended to a distance of about 6% of the chord length in the normal direction. Figure 9b shows that for the case of the applied voltage of 11 kV the size of the separation zone is very small (about 1% of the chord length) and there is almost no separation for higher applied voltages at this 70% chord-wise section. Finally Fig. 9c shows the structure of the boundary layers at a 90% chord-wise section. The size of the separation bubble of the clean airfoil in this section is about 20% of the chord length (also see Fig. 8a), while we have almost no separated boundary layer for the 16 kV applied voltage.

Fig. 9
figure 9

Velocity profiles in different boundary layer sections of 50, 70, and 90% of the chord length from the leading edge for clean, and actuated airfoils with three different applied voltages a 11 kV, b 13.5 kV, and c 16 kV

Full size image

The improvement in the boundary layer structure of the stalled flow field shall result in a better pressure recovery over the upper airfoil surface, which has a twofold effect of increase in the lift coefficient, and a decrease in the pressure drag coefficient. The drag force consists of two components: the pressure drag and the skin or friction drag. Although the skin drag component increases locally by the formation of a wall jet which results in an increase in the velocity gradient over the surface, the control of the pressure drag by the pressure recovery is so effective that the overall drag coefficient is significantly decreased. Figure 10 shows an almost linear improvement of the lift coefficient with the applied voltage, while Fig. 11 shows a similar almost linear decrease in the total drag coefficient. Finally Fig. 12 shows a similar linear improvement in the lift to drag ratio. From an energy harvesting view point, the lift increase is a very valuable parameter, while the drag decrease is valuable form a structural view point to decrease the bending moment in the rotating wind turbine blade.

Fig. 10
figure 10

Lift coefficient for different applied voltages

Full size image
Fig. 11
figure 11

Drag coefficient for different applied voltages

Full size image
Fig. 12
figure 12

Lift to drag ratio for different applied voltages

Full size image

4.2 The frequency effect

The other important parameter considered in this study is the frequency of the applied voltage. The impact of the frequency on the actuator performance and the generated body force is very significant. Here, fourteen different frequencies in the range of 1–14 kHz is applied. This range is the range mostly used in experimental works [48]. The frequency effect in the basic electrostatic model is modified in previous authors’ works [51, 52]. Figure 13 shows results for the integral of the generated body force in both horizontal and vertical directions, and a steady increase of the body force by increase in the frequency is observed.

Fig. 13
figure 13

The generated body force for different applied frequencies

Full size image

Due to the increase in the frequency, the phenomenon of charging and discharging of the actuator happens more in a time unit, and this causes more ions to accumulate on the dielectric surface [22]. Therefore, despite the constant amplitude of the potential field generated by the actuator, more ions are accelerated in the boundary layer, and the plasma wall jet gains a higher momentum, which is transferred to the boundary layer. This results in the increase of the induced body force in both directions. Figure 14 shows the plasma density contours produced on the dielectric surface for four different frequencies of 1, 5, 6, and 13 kHz. The increase in the thickness of the plasma region as well as its further longitudinal extension on the dielectric surface due to the increase in the frequency is clearly visible.

Fig. 14
figure 14

Charge density contours around the plasma actuator for different frequencies a 1 kHz, b 5 kHz, c 9 kHz, and d 13 kHz

Full size image

To see how frequency variation affects the hydrodynamic field, the distribution of the pressure coefficient over the airfoil surface is plotted in Figure 15. Four different frequencies of 2, 4, 9 and 11 kHz are applied to the actuator and results are compared with the clean airfoil. This figure also shows the location of the separation point for each case. At 16 degrees angle of attack this airfoil is in complete stall condition, and the length of the separated region is about 52% of the chord length. After separation, a uniform high pressure is maintained over the airfoil. This uniform pressure region is gradually decreased by increase in the applied frequency, and has reached to 7% for the 11 kHz applied frequency. It is very interesting to observe that the lower airfoil surface pressure distribution is also improved, and having a higher pressure distribution contributes to a higher lift coefficient. The increase in the enclosure surface between the lower and upper surface pressures with the increase of the frequency is significant. This could be attributed to a more fluent flow over the upper surface, which helps to decrease the mass flux and the flow velocity under the lower surface and results in a higher pressure. One also observes that there is a limit for pressure recovery over the upper surface, which is almost achieved at a frequency of 9 kHz, and most of the separation bubble is controlled by this applied frequency. Further increase in the frequency will increase the plasma extent and will strengthen the wall jet and the integral induced body force, but it could not contribute to a much increase in the lift coefficient. One observes that only 2 kHz increase of the applied frequency at initial frequency of 2 kHz has delayed the separation point by 13% of the chord length, while in 9 kHz it is only 5% of the chord length, and there is almost no room for extra improvement.

Fig. 15
figure 15

Pressure coefficient distributions around the DU21 for four different applied frequencies in comparison with that of a clean airfoil

Full size image

Figure 16 shows the boundary layer profile close to the separation point. One readily observes that a higher frequency has retarded the separation, which results in a much smaller separation bubble, and a better pressure recovery. The point where the velocity gradient over the surface reaches zero is called the separation point, and the pressure distribution after this point reaches to the high pressure value of the stagnation point at the trailing edge.

Fig. 16
figure 16

Velocity vectors in the separation zone over the airfoil for three different applied frequencies, a 2 kHz, b 4 kHz, and c 8 kHz

Full size image

Figures 17 and 18 show variations of the aerodynamic coefficients by increase in the applied frequency. One observes that by increase in the applied frequency, the lift coefficient initially experiences an almost linear improvement, and after an applied frequency of about 8 or 9 kHz, the improvement reduces to zero. This is about the maximum lift coefficient achievable at this angle of attack. Similarly, due to the pressure recovery in the upper airfoil surface, the pressure drag is significantly decreased which initially results in an almost linear decrease in the total drag coefficient in Fig. 18. The skin friction should have increased in higher applied frequencies, since the velocity gradient over the airfoil surface has increased by a delay in the separation point, but contribution of the pressure drag is more significant. Finally, Fig. 19 shows the lift to drag ratio, which shows similar improvements for higher applied frequencies.

Fig. 17
figure 17

Lift coefficient for different applied frequencies

Full size image
Fig. 18
figure 18

Drag coefficient for different applied frequencies

Full size image
Fig. 19
figure 19

Lift to drag ratio for different applied frequencies

Full size image

4.3 Waveform effect

Another important operational condition is the waveform of the electrodes applied voltage. A few people (e.g., Refs. [25, 68]) have studied this effect. Benard and Moreau [68] have experimentally shown that a rectangular pulse has a better performance in generation of the magnitude of the body force and the wall jet thrust on a flat plate, but a sinusoidal wave results in a higher variation (amplitude) in the body force values (although its mean magnitude is less) and have expected that this may be manipulated by a control system to achieve a better control of the velocity fluctuations in a turbulent boundary layer.

To study this parameter numerically, we may use the function \(f(t)\) in the boundary condition equation for the potential over the exposed electrode \(\phi \left(t\right)={\phi }^{\mathrm{max}}f(t)\) to find the new body forces and then solve the flow field equations. Here we select a frequency of 1 kHz and an amplitude of 12 kV for the applied voltage, and consider application of three different waveform functions (respectively rectangular, sinusoidal and triangular) described by Eqs. (35)–(37). These temporal functions are shown in Fig. 20.

Fig. 20
figure 20

Three different applied voltage waveforms

Full size image
$$f\left(t\right)=+1 \,\,t\in [0, T/2 ]$$
(35)
$$f\left(t\right)=-1 \,\,t\in [T/2, T]$$
$$f\left(t\right)=\mathrm{sin}\left(\frac{2\pi t}{T}\right) \,\,t\in [0, T]$$
(36)
$$f\left(t\right)=4\left(\frac{t}{T}\right) \,\,t\in [0, T/4]$$
(37)
$$f\left(t\right)=2\left(1-\frac{2t}{T}\right) \,\,t\in [T/4, 3T/4]$$
$$f\left(t\right)=4\left(\frac{t}{T}-1\right) \,\,t\in [3T/4, T]$$

Figure 21 shows the mean integral of the body forces, in both horizontal and vertical direction, for these three cases. The rectangular waveform has generated higher horizontal and vertical body forces. A similar experiment is performed by Benard and Moreau [68], in which they have measured the thrust generated by a DBD actuator installed on a flat plate and operated at a voltage range of 14–20 kV and a frequency range of 0.3–1.6 kHz. Their measured thrust at a relatively similar operating condition (13 kV, 1.5 kHz) shows a 22% higher thrust for the rectangular waveform, which is qualitatively similar to our simulation results. Also our triangular waveform, although some how different from positive or negative ramp of reference [68], follows the experimental results in producing a lower thrust. Figure 22 shows the resulting aerodynamic forces for these three cases. As expected, the rectangular, sinusoidal and triangular waveforms generate a lift coefficient of, respectively, 2.82, 2.00, and 1.50, and drag coefficients of 0.015, 0.026, and 0.041. Finally, the corresponding lift to drag ratios are, respectively, 188, 76.9, and 36.6.

Fig. 21
figure 21

Generated body force for different applied voltage waveforms

Full size image
Fig. 22
figure 22

Lift and drag coefficients for different applied voltage waveforms

Full size image

The velocity contours are plotted in Fig. 23. As expected, the rectangular waveform has resulted in a better control of the boundary layer and has resulted in a smaller separated zone. As discussed by Benard and Moreau [68] the dynamic features of the generated body force could be used to actively damp the main oscillating vortical flow structure in the separation zone. This effect is different from the mean hydrodynamic mechanism studied here, and is an open subject to be studied numerically later. For this purpose, the variation (amplitude) of the body force (and not its mean value which is studied here) is the most important parameter, which is experimentally shown to be higher for the sinusoidal waveform. To complete this study, we need to know the consumed energy for the unit generated body force or the lift coefficient, which we have not been able to compute in our simulation. Benard and Moreau [68] have shown that the specific generated thrust (i.e., the thrust per unit consumed power) is the highest for the sinusoidal case.

Fig. 23
figure 23

Velocity magnitude contours for different applied voltage waveforms

Full size image

4.4 Discussion

One observes that the applied voltage, the frequency and the waveform have significant effects on the boundary layer control and the resulting aerodynamic forces. However, the effect of the applied frequency is less than the applied voltage, and its resulted increase in the charge density distribution over the dielectric surface is also less. Among three different waveforms with similar amplitudes studied here, the generated body force and the resulting lift coefficient is higher for a rectangular waveform. However one shall note that if two waveforms have similar root mean square (RMS) values, the resulting body force of the sinusoidal waveform is expected to be higher, which is in line with the main conclusion of Benard and Moreau [68] regarding observation of a quasi-linear electromechanical conversion phenomenon.

One concludes that, at least for the range of parameters studied here, the increase of the lift coefficient with the applied voltage is linear, but it asymptotically converges to a limit with the applied frequency increase. We believe study of higher voltages shall show similar performance as well. The behavior of the lift coefficient respect to the frequency change can be modeled by an exponential trend line. Equations (38) and (39) are proposed here to model the behavior of the lift coefficient with respect to the changes in the applied voltage (kV) and frequency (kHz):

$${C}_{\mathrm{l}}=0.16\mathrm{V}+0.16 \,\,7\mathrm{ kV}\le V\le 18\mathrm{ kV}$$
(38)
$${C}_{\mathrm{l}}=2.7-2.0{\mathrm{e}}^{-0.2\left(f+1.7\right)}.$$
(39)

5 Conclusion

Plasma actuators have been used to control the boundary layer and to improve actively the energy harvesting performance of wind turbine blades at low airspeeds. In this study, to improve the aerodynamic performance of a DU21 wind turbine blade, the effect of the applied voltage, frequency and waveform parameters of the DBD plasma actuator on the generated body force was studied.

A range of 7kV–18 kV for voltage and 1 kHz–14 kHz for frequency was studied. For a Reynolds number of one million which corresponds to an air speed of 6.7 m/s for a chord of unit length, it was shown that both increase in the voltage and frequency of the actuator improve its performance. Initial increase of the applied frequency improves the aerodynamic performance of the airfoil, and after reaching a certain limit (about 8 kHz), more increase in the frequency has little more improvement. Increasing the applied voltage is continuously effective in improving the aerodynamic performance in the range studied here. The final improvement in the lift coefficient is about 100% for frequency increase and is about 131% for the applied voltage. Two equations are proposed to show variation of the lift coefficient with the applied frequency and voltage. For an operating condition of an applied voltage of 12 kV and 1 kHz frequency, three different waveforms for the applied voltage were studied, and it was shown that the rectangular waveform produces a 41% higher lift with respect to the sinusoidal waveform, and produces an 88% higher lift in comparison with the triangular waveform. These results show that how the improved electrostatic model can be effectively used as a powerful tool to model the effects of different operational parameters and to optimize the performance of DBD actuators.