A reliable algorithm to determine the pollution transport within underground reservoirs: implementation of an efficient collocation meshless method based on the moving Kriging interpolation

Abstract

The pollution propagation within the underground water reservoirs is a challenging and important phenomenon. In the current work, the numerical simulation of pollution transport in an underground channel is performed using the meshless method. To account the anomalous dispersion in a general case, the variable order fractional mass transfer equation is utilized for a rectangular channel. The clean fluid stream enters the channel and due to several phenomenon including the leakage of pollution from the channel walls, the internal pollution source, and the occurrence of the chemical reactions, the pollution content is affected. The non-dimensional form of the governing equation is derived to introduce the dominant dimensionless group numbers. The numerical solution of the obtained equation is established based on the meshless local Petrov–Galerkin method using the moving Kriging interpolation. The Dirac delta function is used as a test function over the local sub-domains. To discretize the present formulation in space variables, we apply the moving Kriging shape functions. Also, to estimate the fractional-order versus the time, finite difference relation is utilized. Using Kronecker’s delta property of moving Kriging interpolation shape functions the boundary conditions in the final system are imposed automatically. The main aim of this technique is to investigate a global estimation for the model, which consequently decrease such problems to those of solving a system of algebraic equations. To determine the accuracy and efficiency of the present method on regular and irregular domains, an example is given in various domains and with regular and irregular distributed points. Also, the effect of major parameters including the fractional order exponent, leakage velocity, chemical reaction rate constant, diffusion coefficient in addition to the stationary/moving pollution source is also examined. It will be shown that, by enhancement of the diffusivity from 0.1 to 20, the outlet concentration reduces by 25.1%, while diffusivity increase from 20 to 50 affects the exiting pollution by merely 7.0%.

1 Introduction

Recently, fractional calculus has absorbed developing attentions [1,2,3,4], because it was used to model unusual behaviors appreciated in various types of science and engineering issues. The fractional differential equations (FDEs) have many applications in physical and chemical processes, biological systems, etc. Because finding the analytical solution of the FDEs is difficult or impossible [5], obtaining their approximate solution received much attentions. Based on this fact, several numerical methods were proposed to solve these equations e.g [2, 6,7,8,9] and references therein.

The anomalous diffusion occurs in several fields including chemistry, physics and biology [10]. Up to now several methods are proposed to mathematically simulate the dispersion mechanism such as the variable diffusion coefficient [11]. However, recently the utilization of the fractional order derivatives is proved to be promising and compatible with the physical nature of the phenomena especially in sub/super diffusion circumstances [12]. Besides, in several cases the variations of the domain structure or diffusivity with time for heterogeneous processes dictates the necessity of implementation of variable order fractional derivatives [13].

One of the most important applications of the anomalous dispersion occurs for simulation of pollution propagation in underground water resources [14]. The distribution of the pollution in underground reservoirs is affected by many factors including the rate of pollution generation, the leakage of polluted water from the reservoir peripheral walls, the main flow velocity for the underground streams as well as removal/generation of pollutants by chemical reactions [15]. Recently several studies have focus on the solution of the anomalous fractional dispersion to propose novel and efficient methods for realistic problems using a wide variety of numerical algorithms [16].

In 2014, Atangana and Kilicman [17] proposed a generalized form of the mass transfer equation based on the implementation of the variable order fractional derivatives. The discretization was performed using the Crank–Nicholson scheme and several numerical for its solutions were examined. The proposed methodology was proved to be useful for pollution transport in underground resources, specifically for the deformable aquifers. In 2019, Aslefallah et al. [18] utilized the meshless singular boundary method to simulate the anomalous diffusion problem. To solve the mentioned problem with nonlinear source terms, they implement the Riemann–Liouville fractional derivatives. Method of particular solutions (MPS) and Singular boundary method (SBM) were employed to determine the particular and homogeneous solutions, respectively. It was found that the proposed method has sufficient accuracy in comparison to the analytical solutions. The multi-dimensional anomalous diffusion for a moving media was numerically simulated by Liu et al. [19]. To examine the long range transport in complex geological structures, they utilized the super-diffusion model based on the Kansa solver which is meshless and appropriate for multi-dimensional cases. The proposed method was tested for natural scenarios and it was proved to be useful in the simulation of non-local transport problems.

In this work, we study a fractional model as

$$\begin{aligned}&D^{\alpha }_{t}C(\mathbf{x} ,t)+A(\mathbf{x} )\frac{\partial C(\mathbf{x} ,t)}{\partial x}+B(\mathbf{x} )\frac{\partial C(\mathbf{x} ,t)}{\partial y}\nonumber \\&\quad =D(\mathbf{x} )\left( \frac{\partial ^{2}C(\mathbf{x} ,t)}{\partial x^{2}}+\frac{\partial ^{2} C(\mathbf{x} ,t)}{\partial y^{2}}\right) \nonumber \\&\qquad +k(\mathbf{x} )C(\mathbf{x} ,t)+f(\mathbf{x} ,t),\qquad \mathbf{x} \in \Omega \subset {\mathbb {R}}^2,t\in [0,T], \end{aligned}$$

(1.1)

with the initial condition

$$\begin{aligned} C({\mathbf {x}},0)=g({\mathbf {x}},0), \end{aligned}$$

(1.2)

and sufficient boundary conditions. In Eq. (1.1) A, B, D, k and f are known functions and $\mathbf{x} =(x,y)$. Also, $D^{\alpha }_{t}$ is the time fractional derivative in the Caputo sense as follows

$$\begin{aligned} D^{\alpha }_{t}C(\mathbf{x} ,t)= \left\{ \begin{array}{ll} \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}\frac{1}{(t-\eta )^{\alpha }}\frac{\partial C({\mathbf {x}},\eta )}{\partial \eta }d\eta , &{} 0<\alpha <1,\\ \frac{\partial C({\mathbf {x}},t)}{\partial t},&{} \alpha =1. \end{array}\right. \end{aligned}$$

(1.3)

Here, we use a meshless method for solving this equation.

Over the past years, many researchers have studied the meshless methods, since they are efficient and accurate. Some numerical meshfree schemes have been used for solving partial differential equations (PDE) such as the reproducing kernel particle method (RKPM) proposed by Liu et al [20], element-free Galerkin (EFG) method proposed by Belytschko et al [21], meshless radial basis functions [22,23,24], point interpolation method (PIM) by Liu et al [25], radial point interpolation method (RPIM) by Liu and Gu [26], smooth particle hydrodynamics (SPH) scheme by Gingold and Monaghan [27], the meshless local Petrov–Galerkin (MLPG) technique by Atluri and Zhu [28, 29], Wang and Liu [30], Liu et al [31] and etc.

The MLPG scheme is truly a meshfree scheme, since mesh division is not required in its analysis. This method was proposed by Atluri and Shen [28, 32, 33] and Atluri [34] which is usually created by moving least square (MLS) approximation [35]. In this case, the MLS shape functions don’t have delta function property and building the products of essential boundary conditions is hard. To remove this difficulty of MLS shape functions, authors of [36] used the moving Kriging interpolation to form shape functions of MLPG with the Kronecker delta function possession. In this work, we use the moving Kriging interpolation (MK) instead of MLS approximation to form MLPG shape function which has the Kronecker delta function property.

In the current work, the numerical simulation of pollution transport in an underground channel is performed using this meshless method. To account the anomalous dispersion in a general case, the variable order fractional mass transfer equation is utilized for a rectangular channel. The clean fluid stream enters the channel and due to several phenomenon including the leakage of pollution from the channel walls, the pollution source within the channel and the occurrence of the chemical reactions, the pollution content is affected. The non-dimensional form of the governing equation is derived to introduce the dominant dimensionless group numbers. The effect of major parameters including the fractional order exponent, leakage velocity, chemical reaction rate constant, diffusion coefficient in addition to the stationary/moving pollution source is also examined.

This paper is constructed from the following sections: In Sect. 2, we give a brief review of the MK interpolation. In Sect. 3 , we explain the time discretization and numerical performance of the MLPG technique for the anomalous diffusion equation. A numerical experiment is performed for the mentioned equation in Sect. 4. The pollution propagation is simulated in Sects. 5 and 6. Finally, a brief conclusion is given in Sect. 7.

2 A short review of moving Kriging interpolation

In this section, we briefly describe the structure of moving Kriging (MK) interpolation shape functions. At first, the Gaussian or Kriging methods regression were used in geostatistics for spatial interpolation [37, 38]. This section has been derived from [36, 37, 39, 40]. Let that the global domain $\Omega \subseteq {\mathbb {R}}^2$ is discretized by a class of random scattered points ${\mathbf {x}}_i,\ i=1,2,\ldots ,n_{1}$ and $C({\mathbf {x}})$ is an arbitrary function defined in $\Omega$.

Fig. 1

Global domain $\Omega$ and sub-domains with distributed points

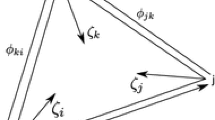
Also, suppose that just $N_{1}$ points are in the neighborhood of a point ${\mathbf {x}}$ (i.e $\Omega _{{\mathbf {x}}}$ see Fig. 1) have effect on $C({\mathbf {x}})$. The MK interpolation $C^{h}({\mathbf {x}})$ is a linear combination of shape functions as follows

$$\begin{aligned} C^{h}({\mathbf {x}})=\sum _{j=1}^{N_{1}} \phi _{j}({\mathbf {x}})C_{j}=\Phi ({\mathbf {x}}){\mathbf {C}}, \quad {\mathbf {x}}\in \Omega _{{\mathbf {x}}}, \end{aligned}$$

(2.1)

where

$$\begin{aligned} \Phi ({\mathbf {x}})={\mathbf {p}}^T({\mathbf {x}})\Xi + {\mathbf {r}}^T({\mathbf {x}})\Upsilon . \end{aligned}$$

(2.2)

Matrices A and B are known as follows:

$$\begin{aligned} \Xi = (P^TR^{-1}P)^{-1}P^TR^{-1}, \qquad \Upsilon = R^{-1}(I-P\Xi ), \end{aligned}$$

(2.3)

where I is an $N_{1}\times N_{1}$ unit matrix and ${\mathbf {p}}({\mathbf {x}})$ is a vector of the m basis functions as follows

$$\begin{aligned} {\mathbf {p}}^T({\mathbf {x}}) = [p_1({\mathbf {x}})\ldots p_m({\mathbf {x}})], \end{aligned}$$

(2.4)

In the present work, we will use the following cubic polynomial expressed as

$$\begin{aligned} {\mathbf {p}}^T({\mathbf {x}}) =[1,x,y,x^2,xy,y^2,x^3,x^2 y,xy^2,y^3]. \end{aligned}$$

in our computations. Also, ${\mathbf {r}}({\mathbf {x}})$ in (2.2) is as follows

$$\begin{aligned} {\mathbf {r}}^T({\mathbf {x}}) = \left[ \begin{array}{ccc} \gamma ({\mathbf {x}},{\mathbf {x}}_1)&\cdots&\gamma ({\mathbf {x}},{\mathbf {x}}_{N_{1}}) \end{array}\right] , \end{aligned}$$

(2.5)

where $\gamma ({\mathbf {x}},{\mathbf {x}}_j)$ is a correlation function. Many functions such as thin plat splines, multi-quadrics, Gaussian, etc. can be applied to construct MK interpolation. In the current study, the following weight function is used

$$\begin{aligned} \gamma ({\mathbf {x}},{\mathbf {x}}_j) = \left\{ \begin{array}{ll} 1-6d_j^2+8d_j^3-3d_j^4 ,&{} d_j\le 1,\\ 0, &{} d_j> 1, \end{array}\right. \end{aligned}$$

(2.6)

where $d_j=\frac{\Vert {\mathbf {x}}-{\mathbf {x}}_j\Vert }{r_j}$, in which $r_j$ is the size of support in correlation function (2.6). Moreover, two matrices R and P are given as :

$$\begin{aligned} R= & {} \left[ \begin{array}{ccc} \gamma ({\mathbf {x}}_1,{\mathbf {x}}_1) &{} \cdots &{} \gamma ({\mathbf {x}}_1,{\mathbf {x}}_{N_{1}})\\ \cdots &{} \cdots &{} \cdots \\ \gamma ({\mathbf {x}}_{N_{1}},{\mathbf {x}}_1) &{} \cdots &{} \gamma ({\mathbf {x}}_{N_{1}},{\mathbf {x}}_{N_{1}})\\ \end{array}\right] , \nonumber \\ P= & {} \left[ \begin{array}{ccc} p_1({\mathbf {x}}_1) &{} \cdots &{} p_m({\mathbf {x}}_1)\\ \cdots &{} \cdots &{} \cdots \\ p_1({\mathbf {x}}_{N_{1}}) &{} \cdots &{} p_m({\mathbf {x}}_{N_{1}})\\ \end{array}\right] . \end{aligned}$$

(2.7)

The partial derivatives of the MK shape function $\Phi ({\mathbf {x}})$ with respect to ${\mathbf {x}}_{i}$ from (2.2) are taken as follows

$$\begin{aligned} \frac{\partial \Phi ({\mathbf {x}})}{\partial {\mathbf {x}}_{i}} n&=\frac{\partial {\mathbf {p}}^T({\mathbf {x}})}{\partial {\mathbf {x}}_{i}}\Xi + \frac{\partial {\mathbf {r}}^T({\mathbf {x}})}{\partial {\mathbf {x}}_{i}}\Upsilon , \end{aligned}$$

(2.8)

$$\begin{aligned} \frac{\partial ^{2} \Phi ({\mathbf {x}})}{\partial {\mathbf {x}}_{i}^{2}}&=\frac{\partial ^{2} {\mathbf {p}}^T({\mathbf {x}})}{\partial {\mathbf {x}}_{i}^{2}}\Xi + \frac{\partial ^{2} {\mathbf {r}}^T({\mathbf {x}})}{\partial {\mathbf {x}}_{i}^{2}}\Upsilon . \end{aligned}$$

(2.9)

The MK interpolation shape functions $\Phi ({\mathbf {x}})$ given in (2.2) satisfy the delta function property. One can see more details about this concept in [37, 38, 40].

3 Mathematical modeling

In this section, we illustrate a meshless method based on MK interpolation for solving Eq. (1.1).

3.1 MLPG2

Suppose that $\Omega$ is the problem domain and $\mathbf{X} ^{*}=\left\{ \mathbf{x} _{1}, \mathbf{x} _{2},\mathbf{x} _{3},\ldots , \mathbf{x} _{n_{2}} \right\}$ be an arbitrary sufficient scattered nodes in this global domain. In the MLPG scheme, instead of calculation global weak form, we construct weak form over a local subdomain like the $\Omega _\mathbf{x }$ which is a small region environment over each node in the general domain $\Omega$. These subdomains can have any arbitrary geometric shapes and size [28] which overlap each other and cover entire domain $\Omega$. In our study, we take them as circle shape in $\Omega$. Now, for every random point $\mathbf{x} _{i}\in \mathbf{X} ^{*} (1\le i\le n_{2})$ we introduce the local weak form of (1.1) in associated subdomain $\Omega _\mathbf{x }^{i} \subset \Omega$ to $\mathbf{x} _{i}$. Really, among the six diverse types of MLPG, the MLPG2 is a collocation method. Because, in this technique the Dirac delta function $\delta (\mathbf{x} -\mathbf{x} _{i})$ is the test function in every local subdomain. So, for every point $\mathbf{x} _{i}$, the local weak form of Eq. (1.1) in $\Omega _\mathbf{x }^{i}$ is as follows

$$\begin{aligned}&D^{\alpha }_{t}C(\mathbf{x} _{i},t)+A(\mathbf{x} _{i})\frac{\partial C(\mathbf{x} _{i},t)}{\partial x}+B(\mathbf{x} _{i})\frac{\partial C(\mathbf{x} _{i},t)}{\partial y}\nonumber \\&\quad =D(\mathbf{x} _{i})\left( \frac{\partial ^{2}C(\mathbf{x} _{i},t)}{\partial x^{2}}+\frac{\partial ^{2} C(\mathbf{x} _{i},t)}{\partial y^{2}}\right) +k(\mathbf{x} _{i})C(\mathbf{x} _{i},t)+f(\mathbf{x} _{i},t). \end{aligned}$$

(3.1)

Let only $N (N<n_{2})$ nodes have influence on the numerical solution in subdomain $\Omega _\mathbf{x }^{i}$. So, using (2.1), we get

$$\begin{aligned} C^{h} (\mathbf{x} ,t)=\sum _{j=1}^{N}\phi _j(\mathbf{x} ) {\hat{C}}_j(t). \end{aligned}$$

(3.2)

Substituting the MK interpolation (3.2) in the local weak form (3.1), one obtains the following discrete equation for all points

$$\begin{aligned} {\mathfrak {I}}D^{\alpha }_{t}C(t)+{\mathfrak {A}}C(t)={\mathfrak {K}}C(t)+F(t), \end{aligned}$$

(3.3)

in which

$$\begin{aligned}&{\mathfrak {I}}_{ij}=\phi _j(\mathbf{x} _i)=\left\{ \begin{array}{ll} 1 ,&{} i=j,\\ 0, &{} i\ne j, \end{array}\right. ,\quad {\mathfrak {K}}_{ij}=k(\mathbf{x} _{i})\phi _j(\mathbf{x} _{i}),\qquad F_{i}=f(\mathbf{x} _{i},t),\\&{\mathfrak {A}}_{ij}=A(\mathbf{x} _{i})\frac{\partial \phi _j(\mathbf{x} _{i})}{\partial x}+B(\mathbf{x} _{i})\frac{\partial \phi _j(\mathbf{x} _{i})}{\partial y}-D(\mathbf{x} _{i})\left( \frac{\partial ^{2} \phi _j(\mathbf{x} _{i})}{\partial x^{2}}+ \frac{\partial ^{2} \phi _j(\mathbf{x} _{i})}{\partial y^{2}}\right) . \end{aligned}$$

To introduce a fully discrete version of Eq .(3.3), suppose $\tau =\frac{T}{n}$ be the step time. So, we take $t_k=k\tau , k=0,1,2,\ldots ,n$, which n is a nonnegative integer. Using the following technique [41] to approximate the fractional derivative

$$\begin{aligned} \small D^{\alpha }_{t}C(\mathbf{x} ,t_{n+1})=a\left[ C_{n+1}-C_{n}+\sum _{k=1}^{n}b_{k}\left( C_{n-k+1}-C_{n-k}\right) \right] +O\left( \tau ^{2-\alpha }\right) , \end{aligned}$$

(3.4)

in which $a=\frac{\tau ^{-\alpha }}{\Gamma (2-\alpha )} , b_{k}=(k+1)^{1-\alpha } -(k)^{1-\alpha }$ and $C_{n} =C(\mathbf{x} ,n\tau )$. Moreover,

$$\begin{aligned} \small C=\frac{1}{2}(C_{n+1}+C_n). \end{aligned}$$

(3.5)

Substituting Eqs. (3.5) and (3.4) in (3.3), the following discrete scheme in time variable is resulted

$$\begin{aligned} &\left( a {\mathfrak {I}}+\frac{{\mathfrak {A}}-{\mathfrak {D}}}{2}\right) C_{n+1} \\&\quad =\left( a {\mathfrak {I}}-\frac{{\mathfrak {A}}+{\mathfrak {D}}}{2}\right) C_{n}-a {\mathfrak {I}}\sum _{k=1}^{n}b_{k}\left( C_{n-k+1}-C_{n-k}\right) +F_{n}. \end{aligned}$$

(3.6)

Therefore, the complete discrete form of Eq. (1.1) will be obtained.

4 Numerical example

In this section, we report the numerical results of our method for 2D anomalous pollution transport on one example. Here, we present the $L_{\infty }$ norm as follows

$$\begin{aligned} L_\infty = \big \Vert C^\mathrm{exact}-C^\mathrm{numerical}\big \Vert _\infty = \ \max _{i}\big |C^\mathrm{exact}_i-C^\mathrm{numerical}_i\big |\ . \end{aligned}$$

Also, we consider the fractional equation (3.1) as

$$\begin{aligned}&D^{\alpha }_{t}C(\mathbf{x} ,t)+\frac{\partial C(\mathbf{x} ,t)}{\partial x}+\frac{\partial C(\mathbf{x} ,t)}{\partial y}\\&\quad = \frac{\partial ^{2}C(\mathbf{x} ,t)}{\partial x^{2}}+\frac{\partial ^{2} C(\mathbf{x} ,t)}{\partial y^{2}} +C(\mathbf{x} ,t)+\exp (-t+x+y)\left( t^{-\alpha }E_{1,1-\alpha }(-t)-1\right) , \end{aligned}$$

in which $E_{1,1-\alpha }(-t)$ is the two parameters Mittag–Leffer function defined in [42] and the exact solution $\exp (-t+x+y)$. Moreover, the Dirichlet boundary and initial conditions can be obtained from the analytical solution.

Fig. 2

$\Omega _{i}, i=1,\ldots ,4,$ Uniform and nonuniform distributed points

Figure 2 shows different types of domains with uniform and nonuniform scattered points. We solve this example by our scheme in rectangular domains $\Omega _{1}$ and $\Omega _{2}$ and report the associated results in Table 1.

Table 1 The $L_\infty$ errors of the current scheme over $\Omega _1$ and $\Omega _2$ for Example 1 with $T=1$

Here, $T=1$ and $\Omega _1=\Omega _2=[0,1]\times [0,1]$. Also, we choose $31\times 31$ uniform nodes in $\Omega _1$. The first column is time step and the next three columns of this table are $L_\infty$ errors of the presented method for three different values of $\alpha$ for solving this example. Also, we use 961 nonuniform nodes (Halton nodes) in $\Omega _2$. The last three columns show $L_\infty$ errors in this domain. This table reveals that our scheme is accurate and efficient for solving this problem in uniform and nonuniform distributed points. one can see that by decreasing the time step, the errors will be decreased.

Table 2 The $L_\infty$ errors of the current scheme over $\Omega _3$ and $\Omega _4$ for Example 1 in different final times $T=1,3,5$

An important property of the meshless methods is their efficiency on irregular domains. We show this feature on $\Omega _3$ and $\Omega _4$.

Table 2 indicates the results for this example on $\Omega _3$ and $\Omega _4$ for different values of $\alpha$. The boundary of these domains ($\partial \Omega _3,\partial \Omega _4$) have the following polar relation

$$\begin{aligned} \Omega _{3},\Omega _4=\left\{ (x,y)\in {\mathbb {R}}^2:x=r\cos (\theta ),y=r\sin (\theta ),~ \theta \in [0,2\pi ]\right\} , \end{aligned}$$

in which $r=\frac{1}{2} \sqrt{\sin ^2(5\theta )+\cos ^2(2\theta )+cos^2(\theta )}$. We use 629 points in each boundary. Also, we apply 441 uniform nodes in $\Omega _3$ and 456 irregular points in $\Omega _4$.

Column one of this table shows different final times. Columns two, three and four report computations of our method on $\Omega _3$. Also, the last three columns illustrate $L_\infty$ errors of the presented method on $\Omega _4$. This table indicates that our scheme has a good efficiency in irregular domain with regular and irregular distributed points. Moreover, it has capability in the large final time.

Fig. 3

The figures of present approximate solution and absolute error dependent on Example 1 in $\Omega _3$ at $T = 1$ with $\tau = 0.001$

Fig. 3 shows the estimate solution (left) and behavior of absolute error for Example 1. Hence, the time step size and final time are $\tau =0.001$ and $T=1$, respectively. Also, this figure is plotted for the domain $\Omega _3$. Tables 1, 2 and Fig. 3 illustrate that presented technique is accurate and efficient to obtain numerical solution of this example.

5 Pollution transport simulation

5.1 Velocity field

The pollution propagation within the channel is simulated using the solution of the Navier-Stokes and mass transfer equations. The contaminant is assumed to be penetrated into the domain from the peripheral channel wall, so the injection velocity is implemented at those boundaries. The schematic of the simulated problem in addition to the operating condition specifics and boundary conditions are illustrated in Fig. 4.

Fig. 4

The schematic of the anomalous diffusion problem

The analytic form of the velocity profile is determined based on the solution of the Poiseuille flow [43] with blowing/suction at side faces as:

$$\begin{aligned}&\frac{\partial U_{i}}{\partial x_{i}}=0, \end{aligned}$$

(5.1)

$$\begin{aligned}&\frac{\partial U_{i}}{\partial t}+U_{j}\frac{\partial U_{i}}{\partial x_{i}} = -\frac{1}{\rho }\frac{\partial P}{\partial x_{i}}+\vartheta \frac{\partial ^{2} U_{i}}{\partial x_{k}\partial x_{k}}, \end{aligned}$$

(5.2)

where i, j and k are the direction indices, U is the velocity, P is the pressure, $\rho$ is the fluid density and $\vartheta$ is the kinematic viscosity. The transient propagation of the pollution is assumed to be occurred inside a 2D channel with steady velocity field. Therefore, it can be assumed that $U_i=(u(y),\nu _0,0)$ according to the assumption of fully developed (FD) has laminar flow with blowing/suction component of $\nu _0$. Based on the mentioned assumption, Eqs. (5.1) and (5.2) can be simplified to:

$$\begin{aligned} \nu _0\frac{\partial u}{\partial y}-\vartheta \frac{\partial ^{2} u}{\partial y^{2}}=-\frac{1}{\rho }\frac{\partial P}{\partial x}. \end{aligned}$$

(5.3)

The right hand side of Eq. (5.3) represents the pressure drop through the channel, which is constant according to the FD assumption. Moreover, at the upper and lower boundaries we have:

$$\begin{aligned} u(y=0)=0 \qquad \text {and} \qquad u(y=H)=0. \end{aligned}$$

(5.4)

The solution of Eq. (5.3) subject to the boundary conditions (5.4) is:

$$\begin{aligned} u(y)=\frac{H}{\nu _{0}\rho }\frac{\partial P}{\partial x}\left( \frac{\exp (\frac{\nu _{0}y }{\vartheta })-1}{\exp (\frac{\nu _{0}H }{\vartheta })-1}-\frac{y}{H}\right) . \end{aligned}$$

(5.5)

The velocity profile of (5.4) can become non-dimensional by using the following dimensionless parameters (Eq. (5.6)):

$$\begin{aligned} U= & {} \frac{u}{U_0},Y=\frac{y}{H}, Re=\frac{U_0 H}{\vartheta }, V_0=\dfrac{\nu _{0}}{U_0}, \end{aligned}$$

(5.6)

$$\begin{aligned} U(Y)= & {} \frac{H}{\rho V_{0}U_{0}}\frac{\partial P}{\partial x}\left( \frac{\exp (V_{0}Y Re)-1}{\exp (V_{0} Re)-1}-Y\right) , \end{aligned}$$

(5.7)

where, $U_0$ is the velocity magnitude at the entrance of the channel. Moreover, the magnitude of the pressure gradient can be estimated based on the balance between the shear stress at the channel walls and the pressure drop gradient. So, the dimensionless velocity profile for implementation in the pollution transfer equation can be expressed as:

$$\begin{aligned} U(Y)=-\frac{4}{ Re V_{0}}\left( \frac{\exp (V_{0}Y Re)-1}{\exp (V_{0} Re)-1}-Y\right) . \end{aligned}$$

(5.8)

The velocity profiles for some values of Re and $V_0$ are illustrated in Fig. 5.

5.2 Pollution transport equation

The pollution concentration distribution is governed by the mass transfer law. Several mechanisms affect the distribution of the penetrated pollution within the examined channel such as diffusion, convection and chemical reaction. The mentioned mechanisms can be included in the fractional mass transfer equation as:

$$\begin{aligned}&D_{t}^{\alpha }C+u(y)\frac{\partial C}{\partial x}+\nu _{0}\frac{\partial C}{\partial y}\nonumber \\&\quad =D(x,y)\left( \frac{\partial ^{2} C}{\partial x^{2}}+\frac{\partial ^{2} C}{\partial y^{2}}\right) -k_\mathrm{reac}(x,y)(C-C_{0})+Q(x,y), \end{aligned}$$

(5.9)

where C(x, y, t) is the pollution concentration, D(x, y, t) is the diffusivity coefficient which is assumed to be a function of the channel location (non-homogenous medium), $k_\mathrm{reac}$ is the first order reaction rate of removal chemical mechanism, Q is the source pollution term and $C_0$ is the reference concentration. Moreover, the fractional order of time derivative is represented by $\alpha$. Besides, four boundary conditions for the concentration at inlet, outlet and side walls in addition the initial condition is required to determine the pollution distribution as:

Boundary condition:

$$\begin{aligned}&C(0,y,t)=C_{i},\qquad \qquad \qquad \text {uniform inlet},\nonumber \\&\frac{\partial C(L,y,t)}{\partial x}=0,\qquad \qquad \qquad \text {fully developed outlet},\nonumber \\&\frac{\partial C(x,0,t)}{\partial y}=b_{1}C(x,0,t)+b_{2},\qquad \qquad \text {lower channel wall},\nonumber \\&\frac{\partial C(x,H,t)}{\partial y}=b_{3}C(x,H,t)+b_{4},\qquad \qquad \text {upper channel wall}. \end{aligned}$$

(5.10)

Also, the initial condition is

$$\begin{aligned} C(x,y,0)=C_0,\qquad \qquad \text {uniform initial condition}. \end{aligned}$$

(5.11)

Regarding the simulated chemical reaction, it should be stated that the removal of the pollutant is proportional to its concentration which is a common assumption for the first order reaction kinetics [44]. Additionally, at the upper and lower channel surfaces, it is assumed that a combination of convection and diffusion mechanisms are affecting the net pollution flux into the domain. It should be noted that to prevent unnecessary complexity in the physical explanation of the simulated problem, simple case of iso-value pollution concentration at the upper and lower walls is assumed as the boundary condition. However, the proposed mathematical method is applicable to the general case explained by Eq. (5.10).

To obtain the main non-dimensional affecting groups of parameters, the following dimensionless variables are introduced:

$$\begin{aligned}&X=\frac{x}{H},\quad Y=\frac{y}{H},\quad {\bar{C}}\nonumber \\&\quad =\frac{c-c_{0}}{c_{\omega }-c_{0}},\quad \theta =\frac{t}{t^{*}},\quad t^{*}=\frac{H^{2}}{D}. \end{aligned}$$

(5.12)

Substitution (5.12) in Eqs. (5.9 - 5.11), the non-dimensional form of mass transfer equation is obtained as:

$$\begin{aligned}&D_{\theta }^{\alpha }{\bar{C}}+\left( \frac{H^{2}}{D}\right) ^{\alpha } \frac{Re\vartheta }{H^{2}}\left[ U(\eta )\frac{\partial {\bar{C}} }{\partial X}+V_{0}\frac{\partial {\bar{C}} }{\partial Y} \right] \nonumber \\&\quad =\left( \frac{H^{2}}{D}\right) ^{\alpha } \frac{D}{H^{2}}\left( \frac{\partial ^{2}{\bar{C}} }{\partial X^{2}} +\frac{\partial ^{2}{\bar{C}} }{\partial Y^{2}} \right) -k_\mathrm{reac}(x,y)\left( \frac{H^{2}}{D}\right) ^{\alpha }{\bar{C}} +{\bar{Q}}(X,Y). \end{aligned}$$

(5.13)

This equation is subjected to the following simplified initial and boundary conditions:

Boundary conditions:

$$\begin{aligned}&{\bar{C}}(0,Y,\theta )=0,\qquad \qquad \text {uniform inlet},\nonumber \\&\frac{\partial {\bar{C}}(L/H,y,\theta )}{\partial X}=0,\qquad \text {fully developed outlet},\nonumber \\&{\bar{C}}(X,0,\theta )=0,\qquad \qquad \text {constant concentration at the lower wall},\nonumber \\&{\bar{C}}(X,1,\theta )=1,\qquad \qquad \text {constant flux at the upper wall}. \end{aligned}$$

(5.14)

Initial condition:

$$\begin{aligned} {\bar{C}}(X,Y,0)=0,\qquad \qquad \text {Uniform initial condition}. \end{aligned}$$

(5.15)

Moreover, to account for the pollution generation mechanisms, two cases of stationary and moving pollution generator source are assumed using the sigmoid function as:

$$\begin{aligned}&{\bar{Q}}(X)=\frac{a_{0}}{1+e^{-a_{1}(X-x_{1})} }-\frac{a_{0}}{1+e^{-a_{1}(X-x_{2}) }},\nonumber \\&\qquad \qquad \text {Stationary source}, \end{aligned}$$

(5.16)

$$\begin{aligned}&{\bar{Q}}(X,\theta )=\left( \frac{a_{0}}{1+e^{-a_{1}(X-x_{1})} }-\frac{a_{0}}{1+e^{-a_{1}(X-x_{2}) }} \right) \nonumber \\&\quad \times \left( STP(\theta _{1})-STP(\theta _{2}) \right) ,\quad \text {Moving source,} \end{aligned}$$

(5.17)

where, $a_0=2000, a_1=20, x_1=1.0$ and $x_2=1.5$. The variables of $\theta _{1}$ and $\theta _{2}$ in Eq. (5.17) are set to 0.1 and 0.2 of $\theta _\mathrm{final}$ which is defined as the dimensionless form of the final simulation instance. Moreover, the STP denotes the step function which is implemented to denote the presence of the pollution generation pulse between $\theta _{1}$ and $\theta _{2}$ time instances.

6 Results and discussion

6.1 Velocity profiles

In the first step, the effect of Re and suction/blowing velocity on the velocity profile is examined (Fig. 5). The results are obtained for $Re=1, 20, 100$ and 200 subjected to cross velocity of $V_0=0.0005, 0.05, 0.1$ and 0.2 to determine the streamwise component of the velocity (U) . According to the obtained results for the lowest examined Re, the effect of suction velocity is almost negligible (i.e. all of the velocity profiles are nearly coincident for $Re=1$). However, as the Re increases, the effect of suction velocity becomes more obvious. By enhancement of the suction strength, the location of the velocity profile is shifted toward the upper channel wall and its magnitude reduces. For example, by increasing of the suction velocity from 0.0005 to 0.2 the velocity peak reduces by 38.5, 82.4 and $90.7 \%$ for Re of 20, 100 and 200, respectively. The effect of velocity suction magnitude on the pollution dispersion will be investigated in the following sections.

Fig. 5

The effect of Re and $V_0$ on the velocity profile: a) $Re=1$, b) $Re=20$, c) $Re=100$ and d) $Re=200$

6.2 Pollution distribution

As the propagation of the pollution within the domain is governed by several interconnected parameters, to assess the effect of individual parameters the following procedure is implemented. A case with specified operating conditions are assumed as the benchmark case and at each phase only one parameters is varied by freezing the other involving parameters. So, at each phase merely the effect of an individual parameter is studied. The following dimensionless parameters are set for the benchmark case: $Re=20$, $V_0=0.2$, $\alpha =0.7$, $k_\mathrm{reac}=50$, $D=10$ as well as stationary pollution generator. For simplicity the $\bar{()}$ symbol is omitted for non-dimensional variables.

The pollution distribution contours are depicted in Fig. 6 for three various cases at the final simulation time. The contours of Fig. 6a reveal the pollution distribution for the benchmark case. As it is obvious, several points can be determined from the contours of Fig. 6a including: the pollution increase around the generation region (between $X=1.0$ and 1.5), the iso-value at the inlet and upper/lower boundaries, reduction of concentration beyond $X=1.5$ (due to removal mechanism) and zero gradient along channel length near the outlet. By reduction of the diffusion coefficient (Fig. 6b), the pollution enhancement at the generation region becomes more obvious. Moreover, the case with the moving pollution source is illustrated in Fig. 6c for which the concentration is increased near the end of the channel due to the presence of the moving source at that point at the final simulation instance.

Fig. 6

The contours of pollution distribution at the final simulation instance for: a benchmark case, b $D=1$ and c moving pollution generation source

6.3 The effect of fractional order ($\alpha$)

To examine the effect of fractional order on the propagation of the pollution, $\alpha$ is increased from 0.4 to 1 by an incremental step of 0.1. The variations of the pollution mass fraction along the channel width, height and through time is illustrated in Fig. 7. The mass fraction profiles along X and Y axis are obtained at the steady state condition, while the variations through time is determined at the vertical line passing through the peak values of mass fraction (i.e. $X=1.25$). As it is presented in Fig. 7a, by increasing the fractional order value from 0.4 to 1.0 the pollution propagation behavior is altered substantially. In other words, referring to Eq. (5.13), for lower values of $\alpha$, the diffusion is more effective in comparison to the highest $\alpha$ value of 1 which resembles the conventional non-fractional diffusion. Due to the enhanced artificial diffusion for low values of $\alpha$, the pollution is distributed smoothly into the field and non-local aggregation is observed. At the channel midline, the peak value of the pollution concentration is increased by $232 \%$ as a results of fractional order increase from 0.4 to 1.0. Also, the same results are observable for variations along the channel length (see Fig. 7b). According to the results, due to the artificial enhancement of diffusion for lower values of fractional order, the presence of a concentrated pollution source between $X=1$ and $X= 1.5$ is not detectable for $\alpha =0.4$.

In contrary, by increasing the fractional order toward one, a local peak in the amount of pollution concentration is observed. To make a better understanding of the system response to a pollution generation pulse between $X=1.0$ and 1.5, the variations of the concentration at $X=1.25$ for various time instances is reported in Fig. 7c. Based on the results, due to the uniform mass generation between $\theta =0.1\theta _\mathrm{final}$ and $0.2 \theta _\mathrm{final}$, a high concentration is achieved at early stages. However, passing through time due to the diffusion at the lower and upper channel walls as well as the convection mechanism, which sweeps the pollution downstream, the mass fraction is reduced. Moreover, as the gradient (slope) of mass fraction at the lower and upper walls denotes the outward flux, it is concluded that the pollution extraction especially at the upper channel walls reduces significantly during the wash away of the generation pollution (at the final time the impermeable condition is achieved at the upper surface).

Fig. 7

Examination of the effect of fractional order $(\alpha )$ at: a $X=1.25$ and $\theta _\mathrm{final}$, b $Y=0.5$ and $\theta _\mathrm{final}$ and c $X=1.25$ at various instances

6.4 The effect of blowing/suction velocity

The effect of the blowing/suction velocity on the pollution propagation is revealed in Fig. 8. The velocity component perpendicular to the main stream direction (known as the blowing/suction velocity) can affect the distribution of the pollution within the channel significantly. It is worth noting that the $V_0$ sign determines the characteristics of the upper and lower channel walls regarding the blowing or suction behavior (e.g. a positive $V_0$ sign determines the blowing at the lower and suction at the upper face). To be more specific, by increasing the velocity magnitude in both directions of upward and downward, the convection of the boundary concentration of lower and upper channel walls into the domain is enhanced, respectively. For example at the maximum simulated downward velocity (i.e. $V_0 = -50$), the concentration of the upper wall (${\bar{C}}=1$) is propagated into a major portion of the channel width, while for the other extreme case ($V_0 = 50$), the channel is highly affected by the concentration at the lower surface (${\bar{C}}= 0$). Additionally, it should be noted that the variations of the concentration profile is insignificant while the blowing/suction velocity is altered in the range of $-10$ to 10. Also, the similar results are obtained for variations of the pollution mass fraction across the channel length (Fig. 8b).

Fig. 8

Examination of the effect of blowing/suction velocity ($V_0$) at: a $X=1.25$ and $\theta _\mathrm{final}$ and b $Y=0.5$ and $\theta _\mathrm{final}$

6.5 The effect of diffusion coefficient

The effect of diffusion coefficient is depicted in Fig. 9. The dimensionless diffusion coefficient is examined in the range of 0.1–50. As the diffusion coefficient is reduced the generated pollution can not be effectively propagated within the domain and consequently the local concentration is enhanced (see Fig. 9b). On the other hand, for higher values of the diffusion coefficient, the effect of chemical reaction, convection and other involving parameters are faded and a smooth Laplacian distribution is achieved (e.g. for $D=50$, ${\bar{C}}$ is varied linearly between the channel boundaries). Furthermore, it is worth noting that the effect of diffusion coefficient is nearly similar to the fractional order parameter (see Fig. 7). So, in some cases for which the variable diffusion coefficient is applicable, the utilization of fractional order operator in conjugation with constant diffusion coefficient might leads to the same results with more physical validity.

Fig. 9

Examination of the effect of diffusion coefficient (D) at: a $X=1.25$ and $\theta _\mathrm{final}$ and b $Y=0.5$ and $\theta _\mathrm{final}$

6.6 The effect of reaction rate constant

The effect of reaction rate constant on the pollution distribution within the channel is shown in Fig. 10. The reaction rate constant determines the speed of chemical reaction as well as the removal or generation nature of the reaction (for $+$ or $-$ sign of reaction constant, respectively according to Eq. (5.13)). The reaction rate constant is varied form 500 for abrupt removal chemical reaction to $-100$ for a high rate generating chemical reaction. It should be noted that the results for $k_\mathrm{reac} = -500$ is not presented due to the obtained high values of concentration which affects the clarity of Fig. 10 data for other $k_\mathrm{reac}$ magnitudes.

As it is obvious, by reduction of the removal reaction rate, the concentration at the channel midsection (Fig. 10a) and along the channel length (Fig. 10b) is enhanced. As the first order kinetic is incorporated in Eq. (5.13), the chemical reaction rate is proportional to both of $k_\mathrm{reac}$ and ${\bar{C}}$. So, it is expected that for a constant value of reaction rate (e.g. $k_\mathrm{reac} = 500$), the gradient of the pollution mass fraction will be higher at the upper channel wall in comparison to the lower surface due to the assigned magnitudes at the boundaries. Besides according to Fig. 10b, one can see that for a high speed removal reaction (which can be done by addition of any type of desorbing substances to the channel flow), the pollution concentration can only varied slightly from its zero value at the channel inlet.

Fig. 10

Examination of the effect of reaction rate constant $( k_\mathrm{reac})$ at: a $X=1.25$ and $\theta _\mathrm{final}$ and b $Y=0.5$ and $\theta _\mathrm{final}$

6.7 The effect of pollution source movement

The effect of movement of the pollution source along the channel is also examined and the obtained data are shown in Fig. 11 for different values of the reaction rate. The pollution source is assumed to move at constant dimensionless velocity of 6 (the source is moved from the channel entrance to nearly its exit in 0 to $\theta _\mathrm{final}$ time interval). The concentration distribution along the channel is presented at four consequential instances of $\theta =0.1$, 0.4, 0.7 and 1. As it is obvious, by passage of the pollution source across the channel, the high concentration front is moved downstream, while its effect on the mass fraction on upstream side remains during a specified time duration. By increasing the chemical reaction rate of the removal mechanism, two main phenomena occurs simultaneously. First, the peak of the moving pollution wave is reduced due to the sudden elimination of the pollution. Second the presence time of the pollution upstream of the moving wave is reduced, significantly.

Fig. 11

The effect of movement of the pollution source for $k_\mathrm{reac}$ of: a 50, b 100, c 500 and d 1000

To summarize the effect of various involving variables, the average magnitude of the concentration at the channel outlet is chosen as the assessment parameter. The pollution concentration at the channel outlet is a crucial factor in examination of the channel characteristics. The pollution enters the channel from iso-value upper wall subjected to a specified generation mechanism, flow convection and chemical reaction and finally exits the channel from the lower and outlet surfaces. The effect of fractional order on the average outlet concentration is illustrated in Fig. 9a. According to the results, by increasing the fractional order the outlet pollution is increased. This phenomenon is due to the fact that by reduction of the fractional order, the artificial diffusivity is increased (see Fig. 7) and consequently the added pollution source can be better propagated within the domain. By increasing $\alpha$ from 0.4 to 1, the outlet pollution is increased by 122.2%. Likewise, by increasing the actual diffusivity, the outlet mass fraction is reduced due to the same mechanism (Fig. 12b). The rate of variations of the outlet concentration is not linearly dependent to the actual diffusion. In other words, by enhancement of the diffusivity from 0.1 to 20 the outlet concentration reduces by 25.1%, while diffusivity increase from 20 to 50 merely affect the exiting pollution by 7.0 %.

The reaction rate constant as a major parameter for removal/generating pollution plays an important role in determination of the averaged leaving contaminant. To be more specific, by increasing the $k_\mathrm{reac}$ from 500 (for a rapid removal reaction) to $-100$ (for a fast generation chemical reaction), the pollution mass fraction at the exit surface grows by 425.1%. It is worth noting that as the assumed kinetic rate is proportional to the concentration, the removal performance doesn’t improve beyond a specific reaction rate (i.e. variation of the reaction rate from 500 to 100 only increase the output pollution by 49.6%). Finally, the effect of the blowing/suction velocity is depicted in Fig. 12d. As it is expected by enhancement of the blowing velocity at the lower face with zero concentration magnitude, the prevention of the pollution entrance from the upper face intensifies and consequently the outlet concentration is reduced. The correlation between the cross velocity component $(V_0)$ and the pollution removal is almost linear. By enhancement of the blowing velocity at the lower face from $-50$ to 50, the pollution removal performance is improved by 34.1%.

Fig. 12

The effect of various involving parameters on the average magnitude of concentration at the channel outlet: a $\alpha$, b D, c $k_\mathrm{reac}$ and d $V_0$

7 Conclusion

The pollution propagation inside underground reservoirs was numerically examined using an efficient meshless scheme for fractional-order mass transport equation. Also, the effect of major parameters including the fractional-order exponent, leakage velocity, chemical reaction rate constant, diffusion coefficient in addition to the stationary/moving pollution source were examined. According to the results, by enhancement of the diffusivity from 0.1 to 20 the outlet concentration reduced by 25.1%, while diffusivity increased from 20 to 50 affects the exiting pollution by merely 7.0%. Therefore, by enhancement of the suction velocity from 0.0005 to 0.2, the velocity peak reduced by 38.5 , 82.4 and 90.7% for Re of 20, 100 and 200, respectively. Due to the enhanced artificial diffusion for low values of $\alpha$, the pollution was distributed smoothly into the field and non-local aggregation was observed. At the channel midline, the peak value of the pollution concentration was increased by 232% as a results of fractional order increase from 0.4 to 1.0. Besides, it was observed that for a high speed removal reaction (which could be done by addition of any type of desorbing substances to the channel flow), the pollution concentration could only be varied slightly from its zero value at the channel inlet. In this scheme, to apply the essential boundary conditions automatically, we used moving Kriging interpolation in the MLPG scheme. Since the moving Kriging interpolation shape functions have Kronecker’s delta properties. Also, we used finite difference relations to approximate the time fraction derivative order. We indicated the capability and accuracy of the presented method were shown through an example.