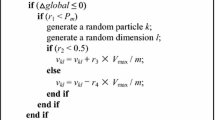Finite element model updating of a multispan bridge with a hybrid metaheuristic search algorithm using experimental data from wireless triaxial sensors

Abstract

The Guadalquivir bridge is a large-scale twin steel truss bridge located in Spain that opened to traffic in 1929. Since the bridge has come into operation for a long time, structural health monitoring (SHM) is strictly necessary to guarantee safety and avoid serious incidents. This paper proposes a novel approach to model updating for the Guadalquivir bridge based on the vibration measurements combined with a hybrid metaheuristic search algorithm. Cuckoo Search (CS) is an evolutionary algorithm derived from global search techniques to look for the best solution. Nevertheless, CS contains some fundamental defects that may reduce its effectiveness in dealing with optimization issues. A main drawback of CS arises in the low convergence level because CS applies fixed values for parameters when looking for the optimal solution. In addition, CS relies a lot on the quality of original populations and does not have the capability to enhance the quality of the next generations. If the position of the original particles is far from the optimal places, it may be challenging to look for the best solution. To remedy the shortcomings of CS, we propose a hybrid metaheuristic algorithm (HGAICS) employing the advantages of both Genetic Algorithm (GA) and Improved Cuckoo Search (ICS) to solve optimization problems. HGAICS contains two outstanding characteristics as follows: (1) GA is employed to create original particles with the best quality based on the capacity of crossover and mutation operators and (2) those particles are then applied to look for the global best derived from the flexible and global search ability of ICS. This paper also presents the application of wireless triaxial sensors (WTSs) taking the place of classical wired systems (CWSs) to the measurements. The use of WTSs increases dramatically the freedom in setting up experimental measurements. The results show that the performance of the proposed hybrid algorithm not only determines uncertain parameters of the Guadalquivir bridge properly, but also is more accurate than GA, CS, and improved CS (ICS). A MATLAB package of the proposed method (HGAICS) is available via GitHub: https://github.com/HoatranCH/HGAICS.

1 Introduction

SHM for large-scale structures has attracted special attention of researchers and the scientific community in recent decades [1,2,3,4,5]. Numerous large-scale structures worldwide are established monitoring systems to assess health conditions and ensure operational safety. Among solutions to SHM, model updating based on vibration measurements seems to bring considerable benefits to structures because it is nondestructive, effective, and able to detect damages located deeply in structures. This approach overcomes the drawbacks of other methods, e.g., magnet field methods, acoustic methods, ultrasonic methods, and visual inspection. Magnet field methods, acoustic methods, and ultrasonic methods need to get prior information of damage locations, whereas visual inspection is impossible to detect damages that are invisible to human eyes. In order to obtain the structural dynamic characteristics, in the last decades, CWSs were applied commonly. However, these systems still have major drawbacks e.g., the difficulties with equipment installation, requiring a huge time for test setup. To remedy the shortcomings of CWSs, WTSs are employed and has become popular in civil engineering practice due to their enormous advantages. The use of WTSs can cover the whole length of large structures without cables. This helps experimental measurements becoming more convenient, decreases equipment setup time on the field [6, 7].

Over the last decades, vibration-based SHM has been commonly applied to identify the physical characteristics of large-scale structures [8,9,10,11,12]. For example, Kao et al. [13] proposed a novel method based on the artificial neural networks to detect structural damages. The objective function consisted of free vibration of intact and damaged structures. Ashebo et al. [14] used field measurements to judge the impacts of the skewness on the load distribution in the transversal direction of a skew box-girder bridge. Both static and dynamic behaviors were selected as an objective function. The authors concluded that the impacts of inclination angle on static and dynamic characteristics of the bridge are insignificant within an inclination of 0°–$30^{0}$. Jin et al. [15] determined structural damages employing adaptive principal component analysis. The results showed that the proposed method outperformed conventional principal component analysis in terms of accuracy and computational cost. Wu et al. [16] updated a finite element model (FEM) of a highway bridge using spatially distributed optical fiber sensors in the field. The objective function consisted of the first order modal macro-strains and static long-gauge strains. Minshui and Hongping [17] identified the physical characteristics of a highway bridge using the first-order method. The theoretical and experimental natural frequencies were selected as an objective function. After model updating, the discrepancy of natural frequencies between numerical and experimental modal analysis results reduced from 8.77 to 4.56% for the largest difference. Tran-Ngoc et al. [18] employed experimental measurements carried out under excitation sources of wind, micro-tremors, and train passage combined with a finite element (FE) model to identify the stiffness conditions of truss joints of a large-scale truss bridge. The result indicated that the assumption of semi-rigid links using rotational springs could reflect the dynamic behavior of the tested bridge most properly. Deng and Cai [19] employed response surface methods coupled with GA to obtain a close correspondence of updated parameters between analytically predicted and experimentally measured responses of a prestressed concrete highway bridge. The results showed that the proposed approach possibly provides reasonable physical explanations for the uncertain parameters of the considered bridge. Rao et al. [20] combined a self-adaptive differential evolution algorithm with model reduction methods (proper orthogonal decomposition) to identify damage in a cantilever beam. Feng et al. [21] updated a short-span steel railway bridge applying a time–domain finite element model updating approach based on the field measurements. They pointed out that it was unfeasible to identify dynamic behaviors of short-span railway bridges based on model updating methods since the natural frequencies of such bridges were higher than those of trainload’s excitation. El-Borgi et al. [22] used the enhanced frequency domain decomposition technique and the Femtools software to update a reinforced concrete bridge in Tunisia. The objective function comprised natural frequencies and mode shapes. The results indicated that approximately 25% of concrete elements of the bridge suffer reductions in Young's modulus of elasticity during its service life (20 years). A modified constitutive relation error (CRE) technique derived from the energy-based function was proposed by Marchand et al. [23] to update structures with nonlinear mechanical behaviors. Goller et al. [24] proposed the underlying distribution used commonly for the field of statics to deal with insufficient information and to update the structures based on dynamic characteristics. Bayraktar et al. [25] updated a balanced cantilever concrete bridge employing a manual method based on peak picking technique in the frequency domain. The objective function consisted of natural frequencies of the first ten modes used to minimize the difference between experimental and theoretical modal analysis.

It is commonly acknowledged that evolutionary algorithms consisting of the Jaya algorithm [26, 27], Tree-seed algorithm [28], and hybrid algorithms [29,30,31,32], etc.… have played a vital role in SHM in this day and age. CS is a meta-heuristic algorithm based on the global search techniques to look for the best solution. This algorithm has been effectively used for a wide range of optimization problems in recent decades [33]. Khatir et al. [34] applied CS algorithm to determine the discrepancy of natural frequencies between experimental and theoretical analysis of Timoshenko beams based on the Isogeometric Analysis (IGA). The outcomes indicated that CS provided a very high degree of accuracy to identify the best IGA parameters of Timoshenko beams. Yildiz [35] employed CS to tackle manufacturing optimization problems. In order to compare with CS in terms of solving a milling optimization problem, other optimization algorithms consisting of hybrid particle swarm optimization (PSO), ant colony (AC) algorithm, and immune algorithm were applied. The results showed that CS was superior to the aforementioned algorithms. Xu et al. [36] used CS to identify damage locations and severity of a dual-span supported beam and a truss structure based on a nonlinear objective function of natural frequencies and modal assurance criterion (MAC). The results demonstrated that CS could detect damages in the considered structures accurately even when the effect of noise was fully assessed. However, the main drawback of the traditional CS algorithm is the application of fixed values for its parameters during the search process. This not only makes the performance of CS less accurate but also leads to a massive increase in computational cost.

Recently, many researchers have proposed different types of ICS to deal with the issues of low convergence level of CS reported in the literature [37, 38]. A major discrepancy between the ICS and CS is in the way of using search parameters to find the global best. ICS employs flexible search parameters, which not only helps it become more varied but also increases the opportunity for looking for the best solution. Marichelvam et al. [39] employed ICS to deal with the multistage hybrid flow shop (HFS) scheduling problems. ICS was applied to minimize the discrepancy between the start time and finish time of sequential tasks for the HFS scheduling problems. Simulations and comparison indicated that ICS was superior to simulated annealing, GA, PSO, and AC algorithms in terms of accuracy and the speed of convergence. Mohapatra et al. [40] combined ICS with machine learning techniques to classify binary medical datasets. ICS was employed to determine training parameters of machine learning consisting of input weights and hidden biases. The results demonstrated that the proposed approach outperformed online sequential extreme learning algorithm (OSELM), multilayered perceptron (MLP), and radial basis function neural network (RBFNN) in terms of accuracy, sensitivity, and specificity. Zhou et al. [41] used ICS applying swap and inversion strategy, and greedy strategy to solve planar graph coloring problems. The results showed that ICS made a higher correction to the coloring rate and requires less computational time than PSO.

Nevertheless, ICS still has fundamental shortcomings because it relies strongly on the quality of the original populations. If the position of original particles is far from the optimal places, it may be challenging to look for the best solution. Therefore, we propose HGAICS employing the advantages of both GA and ICS to deal with optimization problems. First, mutation and crossover features of GA are used to create populations with the best quality and then utilizing those populations to seek the global best derived from the global search ability of ICS. This strategy overcomes the problems of low convergence level and enhances the quality of new generations. To assess the efficiency of the proposed algorithm, a large-scale railway bridge is applied for model updating. To compare with HGAICS, GA, CS, and ICS are also considered.

The paper is organized as follows. The methodology of GA, CS, ICS, and HGAICS is presented in Sect. 2. Section 3 describes the calibration of FEM using experimental data of the Guadalquivir bridge. Model updating is introduced in Sect. 4. Finally, the highlighted conclusions are presented.

2 Hybrid GAICS

2.1 GA

GA is a global search method derived from the concept of Darwin’s theory of evolution [42]. This algorithm applies a combination of natural selection (crossover operators and random mutations) to look for the optimal solution based on the objective function. Although crossover operations are employed to generate the next generations, mutation operators are used to improve the quality of new ones. The objective function is applied to lower the discrepancies between calculated and desired results. There are different kinds of GA utilizing for optimization issues, e.g., real-coded or binary coded, etc. In this paper, we use real-coded GA for model updating of Guadalquivir bridge due to its simplicity and efficiency.

3 CS

CS is a kind of bionic optimization algorithm inspired by the obligate brood parasitism of cuckoo birds. Basically, cuckoos often choose the nests of other birds to spawn their eggs. If the host birds discover the eggs are not their own, they may either leave their nest or throw parasite eggs away. CS algorithm is formed based on the following three idealized rules [43].

• 1. The cuckoos select a stochastic nest to lay their eggs and only one egg is spawned at a time.

• 2. The nests with the highest quality of eggs will be carried over into the next steps.

• 3. The number of available host nests is fixed, whereas there is a 0–100% probability (${P}_{a}$) that the host possibly discovers the parasite eggs. If the host birds detect parasite eggs, they may either abandon their own nest or throw the eggs away.

The best solution is based on the objective function Eq. (1):

$$\varvec{ }X^{i + 1} = X^{i} + {\text{levy}}\left( \lambda \right)*\alpha$$

(1)

where

$$X^{i} = \left[ {x_{1}^{i} , x_{2}^{i} , \ldots , x_{m}^{i} } \right],$$

and

$$\varvec{ }x_{j}^{i} = \left[ {x_{1j}^{i} , x_{2j}^{i} , \ldots , x_{nj}^{i} } \right]^{T} ,\;\;\;j = 1, 2, \ldots , m.$$

where $x_{j}^{i}$ and $x_{j}^{i + 1}$ are solutions of cuckoo j at $i{\text{th}}$ and $i + 1{\text{th }}$ iteration, respectively, and α represents the step size. While n indicates the number of populations and m is the number of uncertain parameters that need to be sound. $\left( . \right)^{T}$ denotes transpose operation. Lévy flight (λ) is step length drawn from the following probability distribution (2):

$$levy \left( \lambda \right) = \frac{1}{{\delta^{\beta } }}$$

(2)

$\beta {\text{is the coefficient of Levy flight}}:{ }1 < \beta < 3$ [43] and parameter (δ) is determined based on a random walk via probability distribution function. Step length (levy (λ)) should be selected according to the scale of the problem of interest. If step length (levy (λ)) is chosen too short, the new generation may be very close to the previous one. If ʎ is too long, the next generation may jump extremely far from the old one.

3.1 ICS

The difference between the ICS and CS is in the way of using search parameters consisting of ${P}_{\mathrm{a}}$ and α. The search parameters are vital to enhance the convergence rate and improve the accuracy of the algorithm. A main drawback of the traditional CS algorithm is the application of fixed values for its parameters during the search process. If the value of α is large, and the value of ${P}_{\mathrm{a}}$ is small, the performance of CS is not only less accurate, but also leads to a massive increase in computational cost. In contrast, the speed of convergence will increase if the value of α is small and the value of ${P}_{\mathrm{a}}$ is large. However, it may fail to look for the best solution. In order to enhance the accuracy and the convergence rate of the algorithm, the ICS applies flexible parameters $({P}_{\mathrm{a}}$ and α). The values of search parameters (α and ${P}_{\mathrm{a}}$) must be big enough in the early steps to increase the diversity of solutions. In contrast, in the final steps, the values of α and ${P}_{\mathrm{a}}$ should follow a downward trend to avoid missing the best solution. The values of α and ${P}_{\mathrm{a}}$ are changed after each iteration based on Eqs. 3–5 [44].

$$\varvec{ \alpha }_{{\varvec{l}}} = \alpha_{{{\text{max}}}}^{{\text{c*l}}}$$

(3)

$$p_{{\text{a}}}^{{\text{l}}} = p_{{\text{a}}}^{{{\text{max}}}} - \frac{{p_{{\text{a}}}^{{{\text{max}}}} - p_{{\text{a}}}^{{{\text{min}}}} }}{N} \times l$$

(4)

$$c = \frac{1}{N} \times {\text{Ln}}\left( {\frac{{\alpha_{{{\text{min}}}} }}{{\alpha_{{{\text{max}}}} }}} \right)$$

(5)

where l represents the number of the current iteration, l ∈ [0, N], N indicates the total number of iteration, ${\alpha }_{\mathrm{max}}$, and ${\alpha }_{\mathrm{min}}$ indicate the maximum and minimum values of step length and ${p}_{\mathrm{a}}^{\mathrm{max}}$, ${p}_{\mathrm{a}}^{\mathrm{min}}$ are the maximum and minimum probability of detecting a parasite egg.

3.2 HGAICS

ICS has already demonstrated its ability to deal with optimization problems based on flexible global search techniques. Nevertheless, ICS still relies strongly on the quality of its original populations and does not have the capability to enhance the quality of the next generations. If the position of original particles is far from the optimal places, it may be challenging to look for the best solution. In order to overcome this drawback of ICS, in this present paper, we propose HGAICS employing the advantages of both GA and ICS to deal with optimization problems. First, crossover and mutation features of GA is used to generate the initial elite populations, and then those populations are employed to look for the best solutions based on the global search capacity of ICS. The application of HGAICS to model updating of Guadalquivir bridge is conducted as follows:

Step 1 Creating the initial positions of particles.

$$X^{0} = \left[ {x_{1}^{0} , x_{2}^{0} , \ldots , x_{m}^{0} } \right],$$

$$x_{j}^{0} = \left[ {x_{1j}^{0} , x_{2j}^{0} , \ldots , x_{nj}^{0} } \right]^{T} ,\user2{ }j = 1, 2, \ldots , m.$$

Step 2 Choosing the objective function $\Phi$ (x).

$$\Phi\left( x \right) = \mathop \sum \limits_{z = 1}^{t} \frac{{\left( {\tilde{f}_{z} - f_{z} } \right)^{2} }}{{\left( {\tilde{f}_{z} } \right)^{2} }} + \mathop \sum \limits_{z = 1}^{t} 1 - \frac{{\left( {{\hat{\varepsilon }}_{z}^{T} *{\upvarepsilon }_{z} } \right)^{2} }}{{\left( {{\upvarepsilon }_{z}^{T} *{\upvarepsilon }_{z} } \right)*\left( {{\hat{\varepsilon }}_{z}^{T} *{\hat{\varepsilon }}_{z} } \right)}}$$

(6)

$(f_{z} ,{ }\varepsilon_{z} ){\text{ and }}\left( {\tilde{f}_{z} ,{ }\hat{\varepsilon }_{z} } \right)$ represent numerical and experimental natural frequencies and mode shapes. “z” is the modal order and t is the number of modes. To prevent adjoining modes containing very close natural frequencies from shifting during the search for the best solution, the lower and upper bounds for the numerical natural frequencies are employed (Eqs. 7 and 8).

$$f_{z}^{i} ~ \in ~\left[ {f_{v} ,~f_{{v + 1}} } \right],~f_{{z + 1~}}^{i} \in ~\left[ {f_{{v + 1}} ,~f_{{v + 2}} } \right]~$$

$${\text{If}}\;{ }f_{z}^{i} > f_{v + 1} \;{\text{ or}}\;\; f_{z}^{i} < f_{v}$$

$$f_{z}^{i} = f_{z}^{i - 1}$$

(7)

$${\text{End}}$$

$${\text{If}}\; f_{z + 1}^{i} > f_{v + 2} \;{\text{or}}\; f_{z + 1}^{i} < f_{v + 1}$$

$$f_{z + 1}^{i} = f_{z + 1}^{i - 1}$$

(8)

$${\text{End}}$$

Step 3 Determining the values of the objective function $\Phi \left( x \right)$ of initial particles

$$\Phi\left( {x^{0} } \right) = \left[ {\begin{array}{*{20}c} {\Phi \left( {x_{1}^{0} } \right)} \\ {\begin{array}{*{20}c} {\Phi \left( {x_{2}^{0} } \right)} \\ {\Phi \left( {x_{3}^{0} } \right)} \\ {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} . \\ {\Phi \left( {x_{n}^{0} } \right)} \\ \end{array} } \\ \end{array} } \right]_{n*1}$$

(9)

Step 4 Arranging the local optimal best of each particle following an increasing order based on the values of the objective function $\Phi \left( x \right)$.

$$\varvec{ } p_{best}^{0} = \left[ {\begin{array}{*{20}c} {p_{p}^{0} } \\ {p_{u}^{0} } \\ {\begin{array}{*{20}c} . \\ . \\ {\begin{array}{*{20}c} . \\ {p_{v}^{0} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]_{n*1}$$

(10)

$$p_{p}^{0} = \left[ {x_{p1}^{0} x_{p2}^{0} \ldots x_{pm}^{0} } \right]_{1*m}$$

$$p_{u}^{0} = \left[ {x_{u1}^{0} x_{u2}^{0} \ldots x_{um}^{0} } \right]_{1*m}$$

$$p_{v}^{0} = \left[ {x_{v1}^{0} x_{v2}^{0} \ldots x_{vm}^{0} } \right]_{1*m}$$

$$\Phi\left( {x_{p}^{0} } \right) <\Phi\left( {x_{u}^{0} } \right) <\Phi\left( {x_{v}^{0} } \right)$$

p, u,…,v are the particles $p{\text{th}},{ }u{\text{th}},{\text{ and }}v{\text{th}},{\text{ respectively}}$.

Step 5 Evolution process.

Step 5.1 The number of the best parehe number of the best parents is chosen for crossover based on the crossover percentage calculated as in Eq. 11.

$$n_{{\text{c}}} = p_{{\text{c}}} *n$$

(11)

$p_{{\text{c}}}$ is the crossover percentage ($p_{{\text{c}}}$ = 0.8) [42].

Step 5.2 Crossover.

Step 5.3 The number of the best parents is chosen for mutation based on the mutation percentage calculated as in Eq. 12.

$$n_{{\text{m}}} = p_{{\text{m}}} *n$$

(12)

$p_{{\text{m}}}$ is the mutation percentage ($p_{{\text{m}}}$ = 0.1) [42].

Step 5.4 Mutation.

Step 6 Recalculating tolerance values of new particles.

$$\Phi\left( {x^{i} } \right) = \mathop \sum \limits_{z = 1}^{t} \frac{{\left( {\tilde{f}_{z}^{i} - f_{z}^{i} } \right)^{2} }}{{\left( {\tilde{f}_{z}^{i} } \right)^{2} }} + \mathop \sum \limits_{z = 1}^{t} 1 - \frac{{\left( {\hat{\varepsilon }_{z}^{iT} *\varepsilon_{z}^{i} } \right)^{2} }}{{\left( { \varepsilon_{z}^{iT} *\varepsilon_{z}^{i} } \right)*\left( {\hat{\varepsilon }_{z}^{iT} *\hat{\varepsilon }_{z}^{i} } \right)}}$$

(13)

Step 7 Selecting the best particles after the crossover and mutation process based on values of the objective function $\Phi \left( x \right)$.

$$p_{{{\text{best}}}}^{i} = \left[ {\begin{array}{*{20}c} {p_{p}^{i} } \\ {p_{u}^{i} } \\ {\begin{array}{*{20}c} . \\ . \\ {\begin{array}{*{20}c} . \\ {p_{v}^{i} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]_{n*1}$$

(14)

$$p_{p}^{i} = \left[ {x_{p1}^{i} x_{p2}^{i} \ldots x_{pm}^{i} } \right]_{1*m}$$

$$p_{u}^{i} = \left[ {x_{u1}^{i} x_{u2}^{i} \ldots x_{um}^{i} } \right]_{1*m}$$

$$p_{v}^{i} = \left[ {x_{v1}^{i} x_{v2}^{i} \ldots x_{vm}^{i} } \right]_{1*m}$$

$$\Phi\left( {x_{p}^{i} } \right) <\Phi\left( {x_{u}^{i} } \right) <\Phi\left( {x_{v}^{i} } \right)$$

Step 8 Repeating steps 5 to 7 until the number of iteration is finished.

Step 9 Getting cuckoos randomly based on Levy flights from GA

$$X^{t + 1} = p_{{{\text{best}}}}^{t} + {\text{levy}}\left( \lambda \right)*\alpha_{n}$$

(15)

where

$$p_{{{\text{best}}}}^{t} = \left[ {x_{1}^{t} , x_{2}^{t} , \ldots , x_{m}^{t} } \right],$$

and

$$\varvec{ x}_{j}^{t} = \left[ {x_{1j}^{t} , x_{2j}^{t} , \ldots , x_{nj}^{t} } \right]^{T} , \,\,\, j = 1, 2, \ldots , m.$$

where t is the number of iteration used by GA, whereas $p_{{{\text{best}}}}^{t}\varvec{ }$ is the local best of particles at $t{\text{th}}$ iteration.

Determining the random walk based on Levy flight [43].

$${\text{levy}} \left( \lambda \right) = \frac{1}{{\delta^{\beta } }}$$

(16)

Determining parameter (δ) of the random walk via a probability distribution function.

$$\delta = \left( {\frac{{\Gamma \left( {1 + \beta } \right)*\sin \left( {\frac{\Pi *\beta }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right)*\beta *2^{{\frac{{\left( {\beta - 1} \right)}}{2}}} }}} \right)^{{\frac{1}{\beta }}}$$

(17)

where Γ is the gamma function that is one of the extensions of factorial function with its variable reducing to 1 used for complex numbers. Apart from nonpositive integers, Γ is utilized for all complex numbers. For any positive integers (k), Γ is defined as in Eq. 18.

$$\Gamma \left( k \right) = \left( {k - 1} \right)!$$

(18)

For complex numbers, Γ is identified by Eq. 19:

$$\Gamma \left( y \right) = \mathop \int \limits_{0}^{\infty } w^{y - 1} e^{ - w} {\text{d}}w$$

(19)

Applying the limit for nests $\left( {x_{{{\text{min}}}} , x_{{{\text{max}}}} } \right):$

$$x_{{{\text{lower}}}} = \left[ {x_{{{\text{min}}}} } \right]_{n*m}$$

(20)

$$x_{{{\text{upper}}}} = \left[ {x_{\max } } \right]_{n*m}$$

(21)

Applying limit Position:

$${\text{ If}} \, X^{t + 1} > x_{{{\text{upper}}}} { }$$

$$\varvec{ } X^{t + 1} = x_{{{\text{lower}}}} + {\text{rand}}*x_{{{\text{lower}}}} { }$$

(22)

$$\varvec{ }{\text{ Else if }}X^{t + 1} < x_{{{\text{lower}}}}$$

$$\varvec{ }X^{t + 1} = x_{{{\text{lower}}}} + {\text{rand}}*x_{{{\text{lower}}}}$$

(23)

$${\text{End}}$$

Determining the best nest:

If $\Phi\left( {X^{t + 1} } \right) <\Phi\left( {X^{t} } \right)$

$$\Phi\left( {{\text{X}}^{t + 1} } \right) =\Phi\left( {{\text{X}}^{t + 1} } \right);{\text{X}}^{t + 1} = {\text{X}}^{t + 1}$$

(24)

Otherwise

$$\Phi\left( {{\text{X}}^{t + 1} } \right) =\Phi\left( {{\text{X}}^{t} } \right);{\text{X}}^{t + 1} = {\text{X}}^{t}$$

(25)

New solution by biased/selective random walks

$$K = {\text{ rand}} \left( {X^{t + 1} } \right) > P_{{\text{a}}}$$

(26)

where $P_{{\text{a}}}$ is the probability that the host possibly can discover the parasite eggs

$$X^{t + 2} = X^{t + 1} + \alpha_{n} *K$$

(27)

$${\text{If}} \, X^{t + 2} > x_{{{\text{upper}}}}$$

$$X^{t + 2} = x_{{{\text{lower}}}} + {\text{rand}}*x_{{{\text{lower}}}}$$

(28)

$${\text{Else if}} \, X^{t + 2} < x_{{{\text{lower}}}}$$

$$X^{t + 2} = x_{{{\text{lower}}}} + {\text{rand}}*x_{{{\text{lower}}}}$$

(29)

$${\text{End}}$$

Determining the best nest:

If $\Phi\left( {{\text{X}}^{t + 2} } \right) <\Phi\left( {{\text{X}}^{t + 1} } \right)$

$$\Phi\left( {{\text{X}}^{t + 2} } \right) =\Phi\left( {{\text{X}}^{t + 2} } \right);{\text{X}}^{t + 2} = {\text{X}}^{t + 2}$$

(30)

Otherwise

$$\Phi\left( {{\text{X}}^{t + 2} } \right) =\Phi\left( {{\text{X}}^{t + 1} } \right);{\text{X}}^{t + 2} = {\text{X}}^{t + 1}$$

(31)

Step 10 Repeat step 9 until the criteria are satisfied.

Step 11 The best solution is determined.

$$\Phi\left( {G_{best} } \right) = \min (\Phi \left( x \right))$$

(32)

$${\varvec{X}} = G_{{{\text{best}}}}$$

(33)

The approach of the proposed method of SHM for the Guadalquivir bridge is illustrated in Fig. 1.

Fig. 1

The methodological approach to SHM for the Guadalquivir railway bridge using HGAICS

4 Guadalquivir bridge

4.1 Bridge description

The Guadalquivir bridge is a large-scale twin railway bridge connecting traffic from Alcazar to Seville in Spain as shown in Fig. 2a. The bridge includes five continuous spans with almost the same length: 50.48 m + 3 × 50.94 m + 50.61 m. Two abutments are referred to $A_{1}$ and $A_{2}$, whereas four piers are labeled as $P_{1}$–$P_{4}$. The bridge was constructed in 1929 and has been maintained periodically to guarantee the operational safety. Owing to a prolonged exploitation period, visual inspection showed that some minor damages occurring at connection bolts and structural members. Fortunately, the condition of the bridge is quite good and still assures service loads. The left truss plane is located on the upstream side, whereas the right truss plane belongs to the downstream side. The axis system is selected as shown in Fig. 2b. The global X axis represents the longitudinal direction of the bridge and the Y axis is in the transverse direction—and the Z axis is in the vertical direction.

Fig. 2

The Guadalquivir railway bridge a the layout of the bridge and b the axis system of the bridge [45]

4.2 FEM of the bridge

Based on the design documents and visual inspection at the field, a FEM of the Guadalquivir is constructed using MATLAB toolbox Stabil [46] (see Fig. 3). The model consists of 3234 degrees of freedom (DOF), 1626 elements, and 564 nodes. The main truss members consisting of portal frames, lower chords, upper chords, stringers, and vertical chords are modeled using three-dimensional (3D) elements. This beam element type is also applied for transverse beams. Counter braking truss members, bracing members, and diagonal chords are modeled using bar elements. Other structures comprising rail track, handrail, maintenance path, and power line are considered as an added mass in the model.

Fig. 3

FEM of the Guadalquivir railway bridge

The cross-sections and the connections of truss members are shown in Fig. 4. The connections between counter braking truss members and main truss members are modeled as by translational constraints (all six DOFs are fixed). The portal frames and the upper transverse beam are also connected with main truss members as fully constrained, but the upper transverse beam can rotate around the global Y axis (detail C). The same type of this link is applied for the connection between the main truss members and other floor beams as shown in detail B. The stringers are discontinuous at the crossbeam positions. This connection permits the stringers to rotate around the global X direction. Those choices are based on the design documents and visual inspection. As other truss bridges, roller, and pin bearings are also applied for abutments and piers of the Guadalquivir bridge. Roller bearings permit translational and rotational displacement in longitudinal axis used for abutment $A_{1}$ and piers $P_{1}$, $P_{3} ,$ and $P_{4}$, whereas pin bearings allow rotation applied to the other remaining abutment and piers ($A_{2} , P_{2} )$. Spring elements are employed to model pin and roller bearings as described in detail in Sect. 4. Therefore, this model can represent accurately the boundary conditions of real structure.

Fig. 4

Cross-sections and connections of truss members; xyz is the local axis, whereas XYZ is the global coordinate [32]

Based on the constructed FE model, the first 22 modes with a frequency range from 2.81 Hz to 10.02 Hz are extracted as shown in Table 1 and Fig. 5. The first modes (modes 1–4) are transverse modes. Mode 1 has the largest modal deformation in span 1. Mode 2 is similar to mode 1 but its main modal displacement occurs at span 5. Transverse modes also appear at higher modes, specifically modes 6, 9–10, and modes 13–16. The shapes of modes 4 and 10 look similar in the second and the fifth span, whereas mode 3, and mode 9 have similar modal deformations in the second and the third span. Vertical modes start to appear at mode 5. Modes 7–8 and modes 11–12 are also vertical modes in which their modal displacements occur at all five spans. Mode 5 has an asymmetric shape since its maximum vertical deformation happens in the first span. The highest modes are torsional modes (from mode 17 onward). Some torsional modes (modes 21–22) are a combination of transverse and torsional frame deformation. No local modes appear in the FE model. All modes are global modes, but they have very close natural frequencies. This poses a challenging problem to separate them.

Table 1 The calculated first 22 modes

Fig. 5

Mode shapes from FEM. The global X axis is in the longitudinal direction of the bridge, the Z axis is in the vertical direction, and the Y axis is in the transverse direction [32]

4.3 The ambient vibration test

4.3.1 Instrumentation and test setup

The operational modal analysis (OMA) was carried out on the bridge located at the upstream side of the river. To reduce the time in equipment installation, WTS systems were employed instead of CWS ones. Totally, there are twelve WTS units combined with a time-synchronous Wi-Fi network to obtain vibration data. In order to monitor structural dynamic behaviors accurately, the measurement grid needs to cover the whole structure. Therefore, for the truss structures, the sensors should be put at truss joints on the top and the bottom of the bridge. Nevertheless, due to safety reasons, most sensors were used to measure truss joints on the bottom chords, and only a few truss joints (nodes 0, 86, 90 as shown in Fig. 6) belonging to the upper chords were taken into account. The vibration tests were split into 27 setups. Each setup consisted of roving and fixed reference sensors, in which fixed reference sensors played the most vital role in connecting other roving sensors. Therefore, fixed reference sensors might be put at locations containing large modal displacements that significantly affect structural dynamic behaviors. In order to seek precise locations to place fixed reference sensors on the measurement grid, a baseline FEM was first built. Based on the results obtained from the baseline FEM, four fixed reference sensors were put at nodes 9, 27, 43, and 63 on the right main truss, whereas the fifth fixed one was put at node 63 on the left main truss. The remaining seven sensors played as a role as roving ones. Roving sensors were equally distributed to five spans in which at least one roving sensor was located at each span. The measurement grid was constructed for OMA as shown in Fig. 6 and Table 2.

Fig. 6

The measurement points ( ) and the fixed sensors ( ) [32]

Table 2 Overview of the measurement setups

Table 2 shows an overview of setups 1 to 13 and setup 27. The setup 27 was not only applied to obtain the vibration data of the transversal portal frame but also was used to separate the global modes. This setup employed sensors placed at a few accessible nodes (nodes 1, 86, 90) on the upper chord. Setups 14 to 26 were similar to setups 1–13 but they were located at the left truss plane. The sampling frequency is 200 Hz. The measurement time spent for one setup lasted approximately 30 min, from which 15 min were used to obtain data and the remaining 15 min were used to relocate roving sensors and install other equipment. The train still operated normally in the measurement time. It took nearly 2 days to finish the whole in situ test.

4.3.2 Test results

4.3.2.1 System identification and modal analysis

The data from the ambient vibration test is processed utilizing the MATLAB toolbox MACEC 3.2 developed by the Structural Mechanics Section of KU Leuven [46]. In order to remove low-frequency disturbance, a high pass filtering is employed. After that, a low pass filtering is applied for measurement signals to decrease the redundant measured data. To obtain dynamic system identification from the measured data, the stochastic subspace identification (SSI) method is used. SSI method comprises the covariance-driven (SSI-cov) and the data-driven (SSI data). SSI-cov is more straightforward and outperforms than SSI-data in terms of reduction in computational time. Therefore, in this paper, we apply SSI-cov to identify the dynamic characteristics of the Guadalquivir bridge. To conduct system identification, the raw time data are split into blocks used to determine the covariance of output data. Theoretically, the number of chosen block rows (${n}_{0}$) relies on the relationship between the Nyquist frequencies and the lowest frequency of interest. In practice, the value of ${n}_{0}$ has a significant influence on the results of the system. Its value should be as large as possible. However, some factors including memory usage and computational time might be taken into account. For this case, the value of ${n}_{0}$ is chosen as 250 and the considered model order range is from 2 to 250 in steps of 2. The number of blocks was used for computing the sample covariance of the output correlation matrices. The discrepancies of damping ratios and natural frequencies in two consecutive modes are lower than 5% and 1%, respectively. Modal phase collinearity (MPC) values of mode shapes between two successive modes are higher than 0.5, whereas Modal Assurance Criterion (MAC) values are lower than 1. 36 modes within a frequency range (from 2.78 to 12.59 Hz) are determined as shown in Table 3 and Fig. 7. Almost all modes contain low damping ratios and have nearly pure real mode shapes, as evidenced by low mean phase deviation (MPD) values and high MPC ones. It can be concluded that a high estimation accuracy is achieved.

Table 3 Identified thirty-six modes 

Fig. 7

The stabilization diagram in the frequency interval between 2.5 and 14.5 Hz

The lowest modes with the frequency range (from 2.78 to 2.90 Hz) are transverse modes. Apart from mode 3, the quality of those modes is quite good, evidenced by low mean phase deviation (MPD) values and high MPC ones. Mode 3 has lower quality, possibly since it was not well stimulated. Another possible reason is that mode 3 has its largest modal displacements in the fifth span where no fixed sensors were placed. Transverse modes also appear at higher modes, specifically modes 11, 12, 14, 15, and modes 18–22. The quality of those modes is not as good as the lower ones (low MPC values and high MPD values). Modes 19, 20, and 21 have MPC values less than 0.85 and MPD values more than ${12}^{^\circ }$, indicating a lower accuracy. The appearance of vertical modes starts at the frequency range from 4.36 to 6.70 Hz with 6 vertical modes including modes 7, 8, 10, 13, 16, and 17. Those modes have the best quality demonstrated clearly through high MPD values and low MPC values. The highest modes (mode 23 onward) are torsional modes or a combination of torsional and transverse modal deformation. The values of MPC values of torsional modes are from 0.84 to 0.95, whereas MPD values are from ${6}^{^\circ }$ to ${13}^{^\circ }$.

4.3.2.2 Identified mode shapes

Figure 8 shows the mode shapes of some measured modes. Mode 1 has the maximum transverse modal displacements in the second and the third span. Mode 2 has the largest modal displacements in the first span, whereas mode 3 is similar to mode 2, but its main modal deformation appears in the fifth span. Mode 5 is a pure transverse mode with transverse vibration in both the upper chords and lower chords. Mode 2 and mode 11 have the same shapes in the lateral direction but they are different from the vertical direction. This feature is similar to the pair of modes 3 and 12. The shapes of modes 4 and 15 look similar in the second and the fifth span, whereas mode 1, mode 6 and mode 14 have similar modal deformations in the second and the third span. Mode 7 is the first vertical mode and has an asymmetric mode shape since its maximum vertical deformation happens in the first span. Modes 7, 8, 10, 13, 16, 17 are vertical modes, in which their modal displacements occurring at all five spans. Modes 21–22 are not purely transverse modes because they are a combination of transverse and vertical modal deformation. Similarly, modes 31 and 32 could be considered as combination modes of transverse and torsional modes. The modal displacements of nodes located at the bottom chords in the longitudinal direction are pretty small compared to other directions. The main reason is that roller and rocker bearings used for the bridge are hindering displacements in the longitudinal direction. The modal displacements of nodes located at the upper plane in the longitudinal direction are relatively large. Those displacements were obtained by sensors placed at nodes (nodes 0, 86, 90) on the top chords.

Fig. 8

Identified mode shapes [45]

Figure 9 indicates (MAC) values among different measured vertical and transverse modes respectively. The high MAC values close to 1 demonstrate that identified modes have similar shapes.

Fig. 9

The MAC values of identified modes: a transverse modes and b vertical modes [45]

4.4 Validation of FE model

The natural frequencies and mode shapes from the FE model are compared with those obtained from measurements. Those modes are split into three groups consisting of vertical, transverse, and torsional modes.

4.4.1 Vertical modes

Table 4 summarizes vertical modes provided by the OMA and FE analysis results. The modal order of modes obtained from measurements is different from that of the numerical model. Specifically, measured modes 8, 10, 13, 16, and 17 correspond to calculated modes 5, 7, 8, 11, and 12, respectively. Mode 7 is not found in the FE results. MAC values are close to 1 and the discrepancies of natural frequencies between the numerical model and measurements are lower than 4%. This demonstrates that measured vertical modes have a good agreement with calculated ones.

Table 4 Comparison of experimental and FE modal analysis results for the vertical modes

4.4.2 Transverse modes

Table 5 compares calculated and measured transverse modes. The modal order of measured transverse modes is also different from that of calculated ones. Modes 5, 6, 11, and 12 of the measurements are not found in the FE model. The quality of identified transverse modes is lower than that of identified vertical modes. This makes differences between calculated and measured transverse modes. However, MAC values are still higher 0.85, and the discrepancy of natural frequencies between measurements and the numerical model is lower than 10%, except for identified modes 1 and 4 (FE modes 3 and 4). Those results can be accepted and used for model updating.

Table 5 Comparison of experimental and theoretical modal analysis results for the transverse modes

4.4.3 Torsional modes

Torsional modes appear at higher modes (mode 23 onward) as shown in Table 6. Some measured torsional modes do not match very well with the corresponding calculated modes possibly because of some reasons, such as the condition of the bearings or coupling constraints between the stiffness of truss members. However, identified torsional modes including modes 23–26, and modes 29–30 have a good agreement with calculated torsional modes (modes 17–22). MAC values are higher than 0.9 and the deviation of natural frequencies is lower than 7%.

Table 6 Comparison of experimental and theoretical modal analysis results for the torsional modes

5 Model updating

In this section, HGAICS is employed to identify uncertain parameters in the Guadalquivir bridge comprising Young’s modulus (E) of truss members and the stiffness of springs (T₁, T₂, T₃, T₄, T₅, T_6, T_7, T₈) as shown in Fig. 10.

Fig. 10

Uncertain parameters for model updating

To evaluate the effectiveness of HGAICS, other algorithms including GA, CS, and ICS are also applied to update unknown parameters of the Guadalquivir bridge. For GA, crossover and mutation operators are 0.8 and 0.1, respectively. For CS, the probability of detecting parasite eggs (${P}_{\mathrm{a}}) \mathrm{is} 0.25$, and the step length (α) is 1, whereas these values used for ICS are flexible. The population size is 50 for all algorithms. The algorithms will finish and the global best will be determined if the variations of the objective function of two consecutive iterations are lower than a given tolerance ${10}^{-6}$ or the maximum number of iterations is 100. Theoretically, based on the number of DOFs, structures, as well as bridges, can provide as many vibration modes as possible but those modes do not make the same contribution to structural dynamic characteristics. Only some lower modes reflect structural behaviors most vitally. However, other modes that do not belong to the objective function are also used to assess the effectiveness of the proposed algorithm after model updating. The results after model updating are summarized in Fig. 11 and Table 7.

Fig. 11

Fitness tolerance of GA, CS, ICS, and HGAICS

Table 7 The calculated and measured natural frequencies before and after model updating

Figure 11 shows that HGAICS is superior to GA, CS, ICS in terms of convergence level. The fitness tolerance of HGAICS is the lowest, at 0.0543, whereas those of GA, CS, ICS are approximately 0.25, 0.16, and 0.075, respectively. CS and ICS converge soon (after 30 iterations), whereas GA and HGAICS need approximately 45 iterations to obtain the best solution.

• Table 7 shows that before model updating, the results of calculated and measured natural frequencies are in a good agreement, except for mode 3 and mode 4 (the difference of natural frequencies between numerical model and measurement is still higher than 10%).

• After model updating, the deviation between calculated and identified natural frequencies reduces dramatically.

• Natural frequencies of calculated and identified vertical modes have the closest correspondence.

• HGAICS outperforms better than GA, CS, and ICS in terms of accuracy. After model updating, the difference of natural frequencies between the numerical model and measurement using HGAICS is lower than 5% (except for identified modes 3 and 4).

• Fig. 12 shows that the MAC values are also improved after model updating (using HGAICS).

Fig. 12

MAC values of mode shapes a before model updating, b after model updating (HGAICS)

After model updating, the model is used to recalculate modes that do not belong to the objective function (modes 11–22). The results of those modes are also considerably improved.

Table 8 shows uncertain parameters that need to be updated.

Table 8 Values of uncertain parameters before and after updating

6 Conclusions

In this paper, we propose a novel hybrid algorithm (HGAICS) to overcome the drawbacks of the traditional CS. First, GA is applied to generate original populations with the best quality based on the crossover and mutation operators. Afterward, CS is used to seek the best solution derived from global search techniques. To demonstrate the capacity of the proposed approach, the Guadalquivir bridge is employed for model updating. The objective function consists of the first ten natural frequencies and mode shapes used to minimize the difference between calculated results from numerical analysis and measured results. Moreover, modes that are not considered for the objective function are used to assess the effectiveness of the proposed algorithm after model updating.

From the obtained results, the main conclusions can be drawn as follows:

• The appearance of WTSs makes the measurement more convenient, e.g., the avoidance of using cables, reduction in the time used for equipment installation, and possibly covering all the length of large-scale structures.

• The effectiveness of the WTSs using for OMA is demonstrated via outcomes obtained from experimental measurements.

• All considered algorithms can identify uncertain parameters in the Guadalquivir bridge accurately. However, HGAICS surpasses GA, CS, and ICS in terms of accuracy and convergence level.

• A close agreement between numerical and experimental modal analysis results is obtained after model updating.