Free-motion wind tunnel testing using a three-degree-of-freedom magnetic suspension system

Abstract

A magnetic suspension system is developed for free-motion wind tunnel testing. An external magnet-yoke open magnetic circuit produces a levitation force acting on the disk magnet in the model, and stable suspension of the model is achieved by PID feedback control using two coils. The suspended models are free from support interference and move in three degrees of freedom in the wind tunnel. The pitch rotation around the y-axis and the translational motion in the xz plane under the influence of unsteady aerodynamic forces are observed using the motion capture technique. Parameter identification methods using Fourier analysis of the motion capture data are developed to determine the moment slope $C_{\textrm{M}\alpha }$, lift slope $C_{\textrm{L}\alpha }$ and drag coefficient $C_{\textrm{D}}$. The standard deviations of the identified values of $C_{\textrm{M}\alpha }$, $C_{\textrm{L}\alpha }$ and $C_{\textrm{D}}$ are less than 5%, 8% and 6% of the respective means.

Graphical abstract

1 Introduction

The wind tunnel model supports have an impact on the flow around each model, which can hinder visualization and make it challenging to compensate for this interference in aerodynamic force measurements, particularly when the flow is highly nonlinear. Magnetic suspension and balance systems (MSBS) for wind tunnels have been developed to eliminate support interference (Chrisinger et al. 1963; Humphris et al. 1975; Sawada and Kanda 1992; Sawada and Kunimasu 2002; Kawamura 2003; Kawamura et al. 2004). A wind-tunnel model containing a permanent magnet is suspended by a magnetic field produced by electromagnets around the wind tunnel. Recently, various MSBSs (Hasan et al. 2016; Takagi et al. 2016; Lee and Han 2016; Sung et al. 2017; Nonomura et al. 2018; Okuizumi et al. 2018; Schoenenberger et al. 2018a, b; Kai et al. 2019; Tran et al. 2019; Kai et al. 2021; Yokota et al. 2021; Ramirez et al. 2023) have been developed in Japan, Korea and the United States.

Conventional MSBSs control all the three-dimensional positions and two axial attitudes with roll axis free. The wind tunnel model can move when the target value of the automatic control is a function of time. Nevertheless, this motion is a type of forced oscillation and is not directly influenced by aerodynamic force.

Dynamic wind tunnel tests in which free-rotation models were used under the influence of unsteady aerodynamic forces were conducted to study the dynamic instability of re-entry capsules (Hiraki 1999; Fujii et al. 2013; Koga et al. 2016). A pivot connects the model and the support in these experiments. The moment slope $C_{\textrm{M}\alpha }$ and dynamic properties of the re-entry capsule were obtained. The wind-tunnel models of these dynamic tests have one degree of freedom in pitch rotation. Therefore, we do not have enough knowledge of the translational motion of the capsules. Free-motion wind tunnel testing with two or three degrees of freedom, including the translational motion of the capsule models, has been attempted (Ueno et al. 2020).

Free-motion wind tunnel testing under the influence of aerodynamic forces is proposed in the present study. To realize this, a three-degree-of-freedom suspension system that contains magnets is developed. The wind tunnel model of this system moves in three degrees of freedom under the influence of unsteady aerodynamic forces and no support interference. The design and properties of the magnetic suspension system are reported in this paper. The wind tunnel airflow causes the pitch rotation and the translational motion in the lift and flow directions to oscillate in the wind tunnel. The history of the pitch rotation and translational motion is observed using the motion capture technique. Furthermore, estimation methods of the moment slope $C_{\textrm{M}\alpha }$, the lift slope $C_{\textrm{L}\alpha }$ and the drag coefficient $C_\textrm{D}$ are developed. The value of $C_{\textrm{M}\alpha }$, $C_{\textrm{L}\alpha }$ and $C_\textrm{D}$ of a reentry capsule model are identified.

2 Three-degree-of-freedom magnetic suspension system

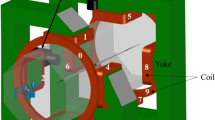
Figure 1 shows a schematic of the three-degree-of-freedom magnetic suspension system developed in the present study. It is placed adjacent to the test section of a blow-down wind tunnel. The cross-section of the nozzle exit of the wind tunnel is 100$\times$100 mm square. The air flow is in the upward vertical direction, and the x axis coincides with the central axis of the wind tunnel. Rectangular neodymium magnets are placed at $y=\pm 80$ mm and $-50\le z \le 50$ mm. The origin of x is located in the yz horizontal plane that includes the bottom surfaces of the two rectangular magnets. These two sets of magnets are connected with a yoke (external magnets–yoke open magnetic circuit), as shown in Fig. 1.

Fig. 1

Three-degree-of-freedom suspension system using magnets for free-motion wind tunnel testing under the influence of unsteady aerodynamic forces

Figures 2 and 3 show the wind-tunnel model in which a disk magnet is embedded. It is a 1/33.6 scale model of the capsule HSRC (H–II Transfer Vehicle Small Re-entry Capsule) that was launched from HTV7 (H-II Transfer Vehicle 7) on November 2018 (Haruki et al. 2019). The body of the wind tunnel model is produced by a 3D printer that laminates acrylic resin. The dimension of the disk permanent magnet is $\phi 10\times 5$ mm. The center of the disk magnet is adjusted to the center of gravity of the model. The real HSRC is a lifting capsule, and its center of gravity is off the geometric centerline of the capsule. However, the model’s center of gravity is designed to be on the centerline. The total mass of the capsule model is 7.63 g.

Fig. 2

Photograph of a wind-tunnel model of a re-entry capsule HSRC

Fig. 3

Dimension of the wind-tunnel model in which a disk magnet is embedded

The three-degree-of-freedom magnetic suspension system of this study is designed for vertical wind tunnels. The axisymmetric disk magnet permits free-rotation of the model around the y-axis (i.e., pitch), as shown in Fig. 4. Two sets of long rectangular magnets used in the external magnets–yoke open magnetic circuit permit translational motion of the model in the xz plane. Table 1 shows the motion of the model and the forces acting on the model.

In addition to its uniqueness as a free-motion wind tunnel system, this system has the advantages of a wide viewing angle for observation and a smaller coil power requirement than conventional MSBSs.

This system is not able to measure aerodynamic forces directly. However, it is possible to identify these forces by using motion capture data and the equation of motion. The method for estimating aerodynamic forces is explained in Sects. 4 and 5. Another issue is the resonance caused by the magnetic restoring forces. Under certain conditions, the model’s suspension may break down due to energy transfer from aerodynamic oscillation to the magnetic natural oscillation (e.g. Fig. 18).

Fig. 4

Three-degree-of-freedom motion of the model in the central xz-plane at $y=0$

Fig. 5

Contour of the magnetic flux density $B_{\textrm{p} y}$ obtained by a preliminary two-dimensional computation when the wind-tunnel model is absent

Table 1 Motion of the model and forces acting on the model with the built-in permanent disk magnet

Figure 5 shows the contour of the y component $B_{\textrm{p}y}$ of the magnetic flux density of the external magnets–yoke open magnetic circuit when the wind-tunnel model is absent. It is a result of a preliminary computation of a two-dimensional problem when the magnets and yoke are sufficiently long in the z-direction. Figure 6 shows the profile of $B_{\textrm{p}y}$ along the dashed-dotted line in Fig. 5.

Fig. 6

Magnetic flux density $B_{\textrm{p} y}$ along the x-axis and possible area of magnetic suspension

The force of the magnetic field of the external magnets–yoke circuit on the disk magnet in the wind-tunnel model when it is placed in the open magnetic circuit is as follows:

$$\begin{aligned} F_{\textrm{p} x} = \frac{B_{\textrm{f} y}}{\mu _0}\, \frac{\partial B_{\textrm{p} y}}{\partial x}\, V_{\textrm{f}} \nonumber \\ F_{\textrm{p} y} = \frac{B_{\textrm{f} y}}{\mu _0}\, \frac{\partial B_{\textrm{p} y}}{\partial y}\, V_{\textrm{f}} \\ F_{\textrm{p} z} = \frac{B_{\textrm{f} y}}{\mu _0}\, \frac{\partial B_{\textrm{p} y}}{\partial z}\, V_{\textrm{f}} \nonumber \end{aligned}$$

(1)

where $\mu _0$ and $V_{\textrm{f}}$ denote the space magnetic permeability and volume of the disk magnet in the model, respectively. The constant $B_{\textrm{f} y}$ denotes the surface magnetic flux density of the disk magnet when it is isolated. Equilibrium suspension of the wind tunnel model is possible when the center of gravity $x_\textrm{g}$ of the wind tunnel model is located in the area between the maximum value point and the inflection point of $B_{\text {p}y}$, as shown in Fig. 6.

In the possible area of magnetic suspension, the upward vertical component $F_{\textrm{p} x}$ is balanced with downward gravity:

$$\begin{aligned} F_{\textrm{p} x}= m g \end{aligned}$$

(2)

where m denotes the mass of the wind tunnel model and g denotes the magnitude of the gravitational acceleration. The force $F_{\textrm{p} x}$ is stable ($\partial F_{\textrm{p} x}/\partial x_\textrm{g}<0$) in this area of $x_\textrm{g}$. When the wind tunnel velocity is $U_\infty =0$, the center of gravity $x_\textrm{g}$ of the model is automatically held at the balance position $x_1$, where Eq. (2) is satisfied.

The magnetic force in the area below the inflection point in Fig. 6 is upward but unstable ($\partial F_{\textrm{p} x}/\partial x_\textrm{g}>0$). The magnetic force in the area above the maximum-value point is downward ($F_{\textrm{p} x}<0$). Thus, magnetic suspension is impossible in these areas.

The z component $F_{\textrm{p} z}$ of the magnetic force is zero in the ideal system. However, in a real system with external permanent magnets of finite length, a weak magnetic force $F_{\textrm{p} z}$ acts in the restoring direction with respect to the symmetry plane $z=0$. It is stable ($\partial F_{\textrm{p} z}/\partial z_\textrm{g}<0$). Consequently, the translational motion of the center of gravity $z_\textrm{g}$ of the wind tunnel model is affected by not only the aerodynamic force but also the restoring magnetic force.

Figure 7 shows schematics of the magnetic force in the xy-plane. The y component $F_{\textrm{p}y}$ of the magnetic force by the external magnets–yoke circuit is unstable ($\partial F_{\textrm{p} y}/\partial y_\textrm{g} >0$), as shown in Fig. 8. The y component of the magnetic force $F_{\textrm{p} y}$ is given in the following linear approximation:

$$\begin{aligned} F_{\textrm{p} y} = k_y \, ( y_\textrm{g} - y_0 ) \end{aligned}$$

(3)

where $k_y$ is a characteristic constant of the magnetic suspension system. The constant $y_0$ is the position of the magnetically symmetric plane, which is slightly different from the geometrically symmetric plane $y=0$. Figure 8 shows the results of the preliminary measurement of $F_{\textrm{p} y}$ (Supplementary file 3). The error between the measured values and the linear approximation is sufficiently small, between $y=\pm 10$ mm.

To stabilize $y_\textrm{g}$ of the model, two air-core coils are placed at $y=\pm 60$ mm (Fig. 1). Two coils are connected in series, and the directions of the coil currents $I_\textrm{c}$ are opposite to each other. This coil system generates a cusped magnetic field, as shown by the orange lines in Fig. 7.

The y component of the magnetic flux density $B_{\textrm{c} y}$ due to the coil current along the coil axis is estimated by the Biot–Savart law:

$$\begin{aligned} B_{\textrm{c} y} =\ {}&\frac{\mu _{0} I_\textrm{c} {R_\textrm{c}}^2 N_\textrm{c}}{2 \left( {R_\textrm{c}}^2+(y+{l_\textrm{c}}/2)^2 \right) ^{3/2}} \nonumber \\&-\frac{\mu _{0} I_\textrm{c} {R_\textrm{c}}^2 N_\textrm{c}}{2 \left( {R_\textrm{c}}^2+(y-{l_\textrm{c}}/2)^2 \right) ^{3/2}} \end{aligned}$$

(4)

where $R_\textrm{c}$, $l_\textrm{c}$, and $N_\textrm{c}$ denote the radius of the coils, the distance between the two coils and the turn number of a coil, respectively. The gradient of the magnetic field produces the y component $F_{\textrm{c} y}$ of the magnetic force of the coil:

$$\begin{aligned} F_{\textrm{c} y} = \frac{B_{\textrm{f} y}}{\mu _0}\, \frac{\partial B_{\textrm{c} y}}{\partial y}\, V_{\textrm{f}} = - c\, I_\textrm{c} \end{aligned}$$

(5)

$$\begin{aligned} c \simeq \frac{3 {R_\textrm{c}}^2 l_\textrm{c} N_\textrm{c}}{2 \left( {R_\textrm{c}}^2+{l_\textrm{c}}^2/4 \right) ^{5/2}} \, B_{\textrm{f} y} V_{\textrm{f}} \end{aligned}$$

(6)

where c is a characteristic constant of the magnetic suspension system. The coil magnetic force $F_{\textrm{c} y}$ is proportional to the coil current $I_\textrm{c}$.

Fig. 7

Schematics of the magnetic force in the xy-plane. $F_{\textrm{p}x}$: stable levitation force by the external magnets–yoke open magnetic circuit, $F_{\textrm{p}y}$: unstable side force by the magnets–yoke circuit, $F_{\textrm{c}y}$: side force by the control coils, mg: gravity

Figure 9 shows a feedback control system for the center of gravity $y_\textrm{g}$ of the wind tunnel model. Two laser displacement sensors measure $y_\textrm{g}$, as shown in Fig. 10, and the PID feedback control module commands the coil current as follows:

$$\begin{aligned} I_\textrm{c} = K_\textrm{P}\cdot ( y_\textrm{g}-y_0 ) +K_\textrm{I} \int ( y_\textrm{g}-y_0 ) \,\textrm{d} t +K_\textrm{D} \dot{y}_\textrm{g} \end{aligned}$$

(7)

The y component of the equation of motion of the wind tunnel model is

$$\begin{aligned} m \ddot{y}_\textrm{g} = F_{\textrm{p} y} + F_{\textrm{c} y} \end{aligned}$$

(8)

where $\ddot{y}_\textrm{g}$ denotes the acceleration of the center of gravity of the model. The stabilization period of $y_\textrm{g}-y_0$ is inversely proportional to $K_\textrm{D}$. After determining the value of $K_\textrm{D}$, we can obtain the values of $K_\textrm{P}$ and $K_\textrm{I}$ as follows:

$$\begin{aligned} K_\textrm{P} = \frac{k_y}{c} + \frac{c {K_\textrm{D}}^2}{3 m}, \qquad K_\textrm{I} = \frac{c^2 {K_\textrm{D}}^3}{27 m^2} \end{aligned}$$

(9)

These relations give triple roots of the characteristic equation of Eqs. (5)–(8). The control parameter $K_\textrm{D}$ has an upper limit because a large $K_\textrm{D}$ causes saturation of the power supply. The value of $K_\textrm{D}$ was decided by the preliminary simulation of Eqs. (5)–(8), as shown in Fig. 11.

Fig. 8

Preliminary measurement values of the y component $F_{\textrm{p} y}$ of the magnetic force by the external magnets–yoke open magnetic circuit. This force is unstable ($\partial F_{\textrm{p} y}/\partial y_\textrm{g} >0$) with respect to the position $y_{\textrm{g}}$ of the wind tunnel model

Fig. 9

Feedback control system for position $y_\textrm{g}$ of the wind tunnel model

Fig. 10

Position detection using a pair of laser displacement meters

Fig. 11

Displacement of the model center in the y direction under PID feedback control ($K_\textrm{D}=140$)

Stable suspension of the capsule model at the target position $(x_\textrm{g}, y_\textrm{g}, z_\textrm{g})=(x_1, y_0, 0)$ has been successfully achieved by PID control of $y_\textrm{g}$, as shown in Fig. 12. Figure 11 shows an example of the displacement of the suspension experiment. The time history of the experiment in wind-off testing is consistent with the preliminary simulation (a solution of Eq.(8) in case of $K_\textrm{D}=140$). The standard deviation of error between the controlled $y_\textrm{g}$ and the target value $y_0$ is 0.024 mm in typical wind-off testing. This is a sufficiently small value compared with the capsule diameter of 25 mm.

Fig. 12

Magnetically suspended wind-tunnel model under PID feedback control in the target xy plane at $y_\textrm{g}=y_0$

The laser displacement meters are set on a moving stage driven by a linear actuator, as shown in Fig. 1. This stage tracks the mean displacement $\bar{x}_{\textrm{g}}$ of the wind tunnel model in the x direction when the flow velocity of the wind tunnel increases.

3 Free-motion wind tunnel testing

It was confirmed that the suspended wind-tunnel model freely rotates around the y-axis (pitch rotation). On the other hand, the rotation of the model around the x-axis and z-axis is strongly restrained by the magnetic torque caused by the magnets–yoke open magnetic circuit, as mentioned in Table 1. The suspended wind-tunnel model easily moves in the lift direction (z direction), although it is not free from the weak restoring magnetic force in the z direction. It also moves in the x direction around the position $x_1$, where gravity and the upward magnetic suspension force balance each other. The translational motion of the wind tunnel model in the y direction is restrained by PID control using two coils within 0.1 mm.

Air flow causes oscillation of the pitch angle $\theta$ and translational motion of $x_\textrm{g}$ and $z_\textrm{g}$ in the flow and lift directions, respectively. Drag causes a certain shift in the time average $\bar{x}_\textrm{g}$ of the suspension position.

In-house motion capture software with ARToolkit (Kato et al. 2001) is used for the observation of $x_\textrm{g}$, $z_\textrm{g}$ and $\theta$. This software detects a square marker, as shown in Fig. 13. Figure 14 shows sequence photographs of the free-motion wind tunnel testing of the capsule model (Supplementary movie file 1 when U_∞ = 5 m/s, and file 2 when U_∞ = 3 m/s). The frame rate of the camera is 120 fps, and the motion capture software is used to analyze the recorded video during postprocessing. The bright red short line at the center of the frames is the reflection of the laser of the displacement meter. A green filter is attached to the camera to prevent the motion capture from being affected.

Fig. 13

A marker for motion capture in the xz plane

Fig. 14

Sequence of the pitch rotation and translational motion of the wind tunnel model in the xz plane when the air flow velocity is $U_\infty =5$ m/s. The bright red short line at the center of frame is the reflection of the laser of the displacement meter

Figures 15 and 16 show the typical time history of the pitch angle $\theta$ when the flow velocity $U_\infty$ of the wind tunnel is 3 m/s and 5 m/s, respectively. The model starts to levitate without wind at $t=0$, while the airflow in the wind tunnel starts at $t=30$ s. The small disturbance at $t=0$ depends on coincidence. The amplitudes of the $\theta$ oscillations are less than 6 and 11 degrees, respectively. Continuous oscillations are observed, and fluctuations in the amplitudes occur.

Fig. 15

Pitch angle $\theta$ of the wind tunnel model around the y-axis when the air flow velocity is $U_\infty =3$ m/s

Fig. 16

Pitch angle $\theta$ of the wind tunnel model around the y-axis when the air flow velocity is $U_\infty =5$ m/s

Figures 17 and 18 show the typical time history of translational motion $z_\textrm{g}$ in the lift direction when $U_\infty =3$ and 5 m/s, respectively. The amplitude of the $z_\textrm{g}$ oscillation grows in the case of a 5 m/s air flow. As a consequence, laser beams of the displacement meters lost sight of the capsule at $t=155$ s.

Fig. 17

Translational motion $z_\textrm{g}$ of the wind tunnel model in the lift direction when the air flow velocity is $U_\infty =3$ m/s

Fig. 18

Translational motion $z_\textrm{g}$ of the wind tunnel model in the lift direction when the air flow velocity is $U_\infty =5$ m/s

Figures 19 and 20 show the typical time history of translational motion $x_\textrm{g}$ in the flow direction when $U_\infty = 3$ and 5 m/s, respectively. A jump in the data is found at the time of acceleration of the flow velocity of the wind tunnel. At that moment, the camera installed on the moving stage was driven upward by the linear actuator. The red lines in Figs. 19 and 20 show the initial position of the model whose apparent position decreases due to the camera stage displacement.

Fig. 19

Translational motion $x_\textrm{g}$ of the wind tunnel model in the flow direction when the air flow velocity is $U_\infty =3$ m/s. The red line shows the initial position of the model whose apparent position decreases due to the camera stage displacement

Fig. 20

Translational motion $x_\textrm{g}$ of the wind tunnel model in the flow direction when the air flow velocity is $U_\infty =5$ m/s. The red line shows the initial position of the model whose apparent position decreases due to the camera stage displacement

Figures 21 and 22 show examples of the power spectra of $\theta$, $z_\textrm{g}$ and $x_\textrm{g}$. The dominant frequencies of the three kinds of oscillations are different from one another. The dominant frequencies $f_{\theta 1}$ of the pitch angle oscillation and $f_{x1}$ of the flow-directional oscillation depend on the flow velocity $U_\infty$, as shown in Fig. 23. On the other hand, the dominant frequency $f_{z1}$ of the lift-directional oscillation hardly depends on the flow velocity. These facts suggest that the aerodynamic moment is dominant in pitching motion. In contrast to the moment, the lift force in this velocity range is suggested to be smaller than the magnetic restoring forces in the z-direction.

Fig. 21

Typical power spectra of the pitch angle $\theta$, translational motion $x_\textrm{g}$ and $z_\textrm{g}$ when $U_\infty = 3$ m/s

Fig. 22

Typical power spectra of the pitch angle $\theta$, translational motion $x_\textrm{g}$ and $z_\textrm{g}$ when $U_\infty = 5$ m/s

Fig. 23

Dominant frequencies $f_{\theta 1}$ of the pitching oscillation and $f_{x1}$, $f_{z1}$ of the translational oscillations

4 Identification of the moment slope

The conservation equation of the angular momentum of the capsule model around the y-axis is

$$\begin{aligned} I \ddot{\theta } = q_\gamma S d\, C_\textrm{M} -F_{\textrm{p} x}\, \delta _\textrm{og}\sin \theta -F_{\textrm{p} z}\, \delta _\textrm{og}\cos \theta \end{aligned}$$

(10)

where I, $q_\gamma$, $C_\textrm{M}$, S and d denote the inertia moment around the rotation axis, dynamic pressure $\frac{1}{2} \rho _\infty {U_\gamma }^2$, pitching moment coefficient, cross-sectional area and diameter of the shoulder of the capsule model, respectively. The constant $\delta _\textrm{og}$ denotes the distance between the rotation axis (the center of gravity) and the center of the disk magnet (Fig. 24). The designed value of $\delta _\textrm{og}$ is 0. However, the best resolution of our 3D printer gives $\delta _\textrm{og}\sim 0.05$ mm.

Figure 24 shows the relation between the translational velocity $(\dot{x}_\textrm{g},\,0,\,\dot{z}_\textrm{g})$ and flight-path angle $\gamma$. The sum of $\gamma$ and the attack angle $\alpha$ is equal to the pitch angle $\theta$. When both $\dot{x}_\textrm{g}$ and $\dot{z}_\textrm{g}$ are much smaller than the flow velocity $U_\infty$ of the wind tunnel, the following approximations are valid:

$$\begin{aligned} U_\gamma =\sqrt{(U_\infty -\dot{x}_\textrm{g})^2+{\dot{z}_\textrm{g}}^2}\simeq U_\infty , \quad q_\gamma \simeq q_\infty =\frac{1}{2} \rho _\infty {U_\infty }^2, \quad \alpha =\theta -\gamma \simeq \theta -\frac{\dot{z}_\textrm{g}}{U_\infty } \end{aligned}$$

(11)

Considering $F_{\textrm{p} x}\sim mg$ and $|F_{\textrm{p} z}|\ll mg$, Eq. (10) is reduced to

$$\begin{aligned} I \ddot{\theta } = q_\infty S d\, C_{\textrm{M}\alpha }\cdot \left( \theta -\frac{\dot{z}_\textrm{g}}{U_\infty }\right) +q_\infty S d\, C_{\textrm{Mdyn}} -mg \delta _\textrm{og}\theta \end{aligned}$$

(12)

Here, the moment coefficient is separated into a linear static part $C_{\textrm{M}\alpha } \cdot \alpha$ and a nonlinear dynamic part $C_{\textrm{Mdyn}}$:

$$\begin{aligned} C_\textrm{M}\simeq C_{\textrm{M}\alpha } \cdot \alpha +C_{\textrm{Mdyn}} \end{aligned}$$

(13)

where the moment slope $C_{\textrm{M}\alpha }$ is a constant and the nonlinear dynamic part $C_\textrm{Mdyn}$ is a variable.

Fig. 24

Deviation value $\delta _\textrm{og}$ between the centers of gravity and the magnet, and the flight-path angle $\gamma$, attack angle $\alpha$ and pitch angle $\theta$ of the moving capsule in the air flow velocity $U_\infty$ of the wind tunnel

The dynamic part $C_\textrm{Mdyn}$ affects the long-term behavior of the pitch angle $\theta$ (Takeda et al. 2020), while it is not dominant with regards to the short-term behavior. Moreover, the peaks of the power spectrum of $\theta$ at frequencies $f_{z1}$ and $f_{x1}$ are much weaker than those at $f_{\theta 1}$ in Figs. 21 and 22. Therefore, the following approximation of Eq. (12) for short time behavior can be obtained:

$$\begin{aligned} I \ddot{\theta } = q_\infty S d\, C_{\textrm{M}\alpha }\theta -mg \delta _\textrm{og}\theta \end{aligned}$$

(14)

The solution of this equation is

$$\begin{aligned} \theta =A_{\theta 1}\, \sin (2\pi f_{\theta 1} t+\varphi _{\theta 1}) \end{aligned}$$

(15)

By substituting this solution into Eq. (14), we obtain

$$\begin{aligned} (2\pi f_{\theta 1})^2 I=q_\infty S d\, (-C_{\textrm{M}\alpha })+mg \delta _\textrm{og} \end{aligned}$$

(16)

The free-motion wind tunnel testing of the capsule model is performed to obtain the dominant frequency $f_{\theta 1}$. The small deviation $\delta _\textrm{og}$ between the centers of gravity and the disk magnet is obtained from Eq. (16):

$$\begin{aligned} \delta _\textrm{og}=\frac{(2\pi f_{\theta 1})^2 I}{mg} \qquad \text{ when } U_\infty =0 \end{aligned}$$

(17)

Furthermore, we obtain $C_\mathrm {M\alpha }$ by substituting $f_{\theta 1}$ of the free-motion wind tunnel testing into Eq. (16) as follows:

$$\begin{aligned} C_{\textrm{M}\alpha } =-\frac{(2\pi f_{\theta 1})^2 I-mg \delta _\textrm{og}}{q_\infty S d} \qquad \text{ when } U_\infty >0 \end{aligned}$$

(18)

The small deviation $\delta _\textrm{og}$ for the capsule model of the present study is identified to be 0.039 mm from Eq. (17) and the experimental data at $U_\infty =0$. The mean value of the moment slope $C_\mathrm {M\alpha }$ is identified to be $-0.111$ rad$^{-1}$ from Eq. (18) and the experimental data for $2\le U_\infty \le 5$ m/s. The standard deviation is 0.005 rad$^{-1}$, as shown in Table 2. The green line in Fig. 23 shows the theoretical curve of Eq. (16) when $C_\mathrm {M\alpha }=-0.111$. This value of $C_\mathrm {M\alpha }$ is roughly consistent with the value $-0.148$ rad$^{-1}$ read from the graph in Fujii et al. (2013), although the Reynolds number and Mach number of their experiments are different from those of the present study.

Table 2 Aerodynamic coefficients derived from the time-history of free-motion wind tunnel testing using the magnetic suspension system of the present study (Reynolds number: $3.3\times 10^3$–$8.2\times 10^3$, Mach number $<0.02$)

5 Identification of the lift slope and drag coefficient of the capsule model

The equation of the translational motion of the capsule model is

$$\begin{aligned} m \ddot{x}_\textrm{g} = q_\gamma S C_\textrm{D} \cos \gamma +q_\gamma S C_\textrm{L} \sin \gamma +F_{\textrm{p} x}-mg \end{aligned}$$

(19)

$$\begin{aligned} m \ddot{z}_\textrm{g} =-q_\gamma S C_\textrm{D} \sin \gamma +q_\gamma S C_\textrm{L} \cos \gamma +F_{\textrm{p} z} \end{aligned}$$

(20)

where $C_\textrm{D}$ and $C_\textrm{L}$ denote the drag and lift coefficients of the capsule, respectively. When both $\dot{x}_\textrm{g}$ and $\dot{z}_\textrm{g}$ are much smaller than the flow velocity $U_\infty$ of the wind tunnel, Eq. (11) is also valid for translational oscillation. In this case, Eqs. (19) and (20) are reduced to

$$\begin{aligned} m \ddot{x}_\textrm{g} =&\ q_\infty S C_\textrm{D} +q_\infty S C_\mathrm {L\alpha } \cdot \left( \theta -\frac{\dot{z}_\textrm{g}}{U_\infty }\right) \, \frac{\dot{z}_\textrm{g}}{U_\infty } \nonumber \\&+q_\infty S C_\textrm{Ldyn}\, \frac{\dot{z}_\textrm{g}}{U_\infty } -\int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x \nonumber \\&-k_x(\bar{x}_\textrm{g}) \cdot (x_\textrm{g}-\bar{x}_\textrm{g}) \end{aligned}$$

(21)

$$\begin{aligned} m \ddot{z}_\textrm{g} =&\, -q_\infty S C_\textrm{D}\, \frac{\dot{z}_\textrm{g}}{U_\infty } +q_\infty S C_\mathrm {L\alpha } \,\theta -q_\infty S C_\mathrm {L\alpha } \,\frac{\dot{z}_\textrm{g}}{U_\infty } \nonumber \\&\, +q_\infty S C_\textrm{Ldyn} -k_z(\bar{x}_\textrm{g}) \cdot z_\textrm{g} \end{aligned}$$

(22)

Here, the lift coefficient is separated into a linear static part $C_\mathrm {L\alpha } \cdot \alpha$ and a nonlinear dynamic part $C_\textrm{Ldyn}$: $C_\textrm{L}\simeq C_\mathrm {L\alpha } \cdot \alpha +C_\textrm{Ldyn}$. Approximations (11) and the following linear approximation of the magnetic restoring force are applied in the derivation of Eqs. (21) and (22):

$$\begin{aligned}&F_{\textrm{p} x}=mg-\int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x -k_x(\bar{x}_\textrm{g}) \cdot (x_\textrm{g}-\bar{x}_\textrm{g}) \nonumber \\&F_{\textrm{p} z}=-k_z(\bar{x}_\textrm{g}) \cdot z_\textrm{g} \end{aligned}$$

(23)

where $\bar{x}_\textrm{g}=\bar{x}_\textrm{g}(U_\infty )$ denotes the time average value of $x_\textrm{g}$, and $x_1=\bar{x}_\textrm{g}(0)$ denotes the balance point of suspension when $U_\infty =0$.

5.1 Lift slope

The second peak $f_{z2}$ of the power spectrum of $z_\textrm{g}$ is identical to $f_{\theta 1}$, as shown in Figs. 21 and 22. Accordingly, we simplify the momentum equation (22) as follows:

$$\begin{aligned} m \ddot{z}_\textrm{g} =q_\infty S C_\mathrm {L\alpha } \,\theta -k_z(\bar{x}_\textrm{g}) \cdot z_\textrm{g} \end{aligned}$$

(24)

The solution of this equation is

$$\begin{aligned} z_\textrm{g}=A_{z1}\,\sin (2\pi f_{z1} \, t+\varphi _{z1}) +A_{z2}\,\sin (2\pi f_{\theta 1} t+\varphi _{z2}) \end{aligned}$$

(25)

The leading term of the right-hand side represents the natural oscillation by the magnetic restoring force, and the second term represents the forced oscillation by the aerodynamic force caused by the pitching of the capsule model.

By substituting the leading term of the right-hand side of Eq. (25) into Eq. (24), we obtain

$$\begin{aligned} k_z(\bar{x}_\textrm{g})=\{2\pi f_{z1}(\bar{x}_\textrm{g})\}^2 m \end{aligned}$$

(26)

The natural frequency $f_{z1}$ is obtained in free-motion wind tunnel testing. Figure 25 shows $k_z$ identified by substituting $f_{z1}$ into Eq. (26). The least-squares fitting curve is

$$\begin{aligned} k_z(\bar{x}_\textrm{g})= 1.31+27.0\, (\bar{x}_\textrm{g}-x_1) -6.65\times 10^2\, (\bar{x}_\textrm{g}-x_1)^2 \end{aligned}$$

(27)

The square of a correlation coefficient $R^2$ is 0.949. This curve is less dependent on $\bar{x}_\textrm{g}$.

Fig. 25

Coefficient $k_z(\bar{x}_\textrm{g})$ of the restoring magnetic force in the z direction

The relation between $k_z$ and $\bar{x}_\textrm{g}-x_1$ does not depend on the aerodynamic force but on the magnetic restoring force. This fact is confirmed by the wind tunnel testing of a sphere model. The area of the cross section S, the mass m, and a built-in disk magnet of the sphere model are identical to those of the capsule model. The restoring coefficient $k_z(\bar{x}_\textrm{g})$ of both the capsule and the sphere models shown in Fig. 25 are in the same relation, although each model gives different $\bar{x}_\textrm{g}(U_\infty )$.

By substituting the solution (15) and the second term of the right-hand side of Eq. (25) into Eq. (24), we obtain the following relations:

$$\begin{aligned} C_{\textrm{L}\alpha } = \frac{(2\pi )^2 \,({f_{z1}}^2-{f_{\theta 1}}^2)\, m}{q_\infty S} \ \frac{A_{z2}}{A_{\theta 1}}\ \cos (\varphi _{z2}-\varphi _{\theta 1}) \end{aligned}$$

(28)

$$\begin{aligned} q_\infty S C_{\textrm{L}\alpha } A_{\theta 1} \sin (\varphi _{z2}-\varphi _{\theta 1}) =0 \end{aligned}$$

(29)

The amplitude ratio ${A_{z2}}/{A_{\theta 1}}$ and phase difference $\varphi _{z2}-\varphi _{\theta 1}$ are calculated from the Fourier coefficients of $z_\textrm{g}(t)$ obtained by free-motion wind tunnel testing. The results of the Fourier analysis show $\varphi _{z2}-\varphi _{\theta 1}\simeq \pi$ in the conditions of the present study. The mean value and the standard deviation of the lift slope $C_{\textrm{L}\alpha }$ are identified to be $-0.81$ and 0.06 rad$^{-1}$, respectively, from Eq. (28) and the experimental data for $3\le U_\infty \le 5$ m/s, as shown in Table 2.

The value of $C_{\textrm{L}\alpha }$ is roughly consistent with the reference value $-1.04$ read from the graph in Fujii et al. (2013). One of the causes of this difference is the small Fourier coefficient $A_{z2}$ compared with the dominant Fourier coefficient $A_{z1}$. Further development of an experimental system for a higher flow velocity $U_\infty$ is required to increase reliability. Figure 23 suggests that $f_{\theta 1}$ exceeds $f_{z1}$ for larger $U_\infty$. Considering the resonance of natural oscillation, $A_{z2}$ is presumed to be greater than $A_{z1}$ when $f_{\theta 1}>f_{z1}$. Unfortunately, free-motion wind tunnel testing for $f_{\theta 1}>f_{z1}$ has not yet been realized using the system of the present study.

5.2 Drag coefficients

We assume that the second and third terms of Eq. (21) are negligible for short-term behaviors:

$$\begin{aligned} m \ddot{x}_\textrm{g} =q_\infty S C_\textrm{D} -\int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x -k_x(\bar{x}_\textrm{g}) \cdot (x_\textrm{g}-\bar{x}_\textrm{g}) \end{aligned}$$

(30)

The solution of this equation is

$$\begin{aligned} x_\textrm{g} =\bar{x}_\textrm{g}&+\frac{q_\infty S C_\textrm{D}-\int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x}{k_x(\bar{x}_\textrm{g})} \nonumber \\&+A_{x1}\,\sin (2\pi f_{x1} t+\varphi _{x1}) \end{aligned}$$

(31)

where the amplitude $A_{x1}$ and the initial phase $\varphi _{x1}$ are constants.

In the same way as in the process of deriving Eqs. (26) and ( 27), we obtain

$$\begin{aligned} k_x(\bar{x}_\textrm{g})=\{2\pi f_{x1}(\bar{x}_\textrm{g})\}^2 m \end{aligned}$$

(32)

$$\begin{aligned} k_x=0.367 +1.01\times 10^2\, (\bar{x}_\textrm{g}-x_1) +8.55\times 10^2\, (\bar{x}_\textrm{g}-x_1)^2 \end{aligned}$$

(33)

The square of a correlation coefficient $R^2$ is 0.993. Figure 26 shows $k_x$ calculated by substituting dominant frequency $f_{x1}$ in free-motion testing into Eq. (32). By integrating this function, we can obtain the following:

$$\begin{aligned} \int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x =&\ 0.367\,(\bar{x}_\textrm{g}-x_1) +50.5\, (\bar{x}_\textrm{g}-x_1)^2 \nonumber \\&+2.85\times 10^2\, (\bar{x}_\textrm{g}-x_1)^3 \end{aligned}$$

(34)

The time average of Eq. (31) can be used to determine the drag coefficient of the capsule model as follows:

$$\begin{aligned} C_\textrm{D} =\frac{\int _{x_1}^{\bar{x}_\textrm{g}} k_x(x)\,\textrm{d} x}{q_\infty S } \end{aligned}$$

(35)

The drag coefficient $C_\textrm{D}$ is almost constant within the Reynolds number $3.3\times 10^3$ – $8.2\times 10^3$ (2 – 5 m/s in the present study), although $\bar{x}_\textrm{g}$ depends on $q_\infty =\frac{1}{2}\rho _\infty {U_\infty }^2$.

Fig. 26

Coefficient $k_x(\bar{x}_\textrm{g})$ of the magnetic force in the vertical direction

The mean value and standard deviation of the drag coefficient $C_\textrm{D}$ of the capsule model for $2\le U_\infty \le 5$ m/s are estimated to be 0.83 and 0.04, respectively, for Reynolds numbers $3.3\times 10^3$ – $8.2\times 10^3$ (Table 2).

This evaluation method of $C_\textrm{D}$ is applicable to other wind-tunnel models. The validity and accuracy of this method is confirmed using a sphere model. The disk magnet in the sphere model is identical to that in the capsule model. Therefore, the values of $k_x(\bar{x}_\textrm{g})$ obtained for the capsule model are also valid for the sphere model, although the relation $\bar{x}_\textrm{g}=\bar{x}_\textrm{g}(U_\infty )$ of the sphere model is different from that of the capsule model.

The mean value and standard deviation of the drag coefficient $C_\textrm{Dsp}$ of the sphere model for $3\le U_\infty \le 7$ m/s are estimated to be 0.39 and 0.02, respectively, as shown in Table 2. The value of $C_\textrm{Dsp}$ is close to the reference value in Morrison (2013). This fact shows the validity of the drag estimation method of free-motion wind tunnel testing in the present study.

6 Conclusions

A three-degree-of-freedom magnetic suspension system for free-motion wind tunnel testing is developed. Wind tunnel models containing a disk permanent magnet move under the influence of unsteady aerodynamic forces. Stable suspension of the capsule model at the target plane $y=y_0$ was successfully achieved by PID feedback control of the model position $y_\textrm{g}$. It was confirmed that the suspended wind-tunnel model rotates freely around the y-axis (pitch rotation). The suspended wind-tunnel model moves easily in the lift and flow directions (z and x directions), while it is not free from the weak restoring magnetic force caused by the external magnets–yoke open magnetic circuit.

The wind tunnel airflow causes the pitch rotation and the translational motion in the lift and flow directions to oscillate in the wind tunnel. The history of the pitch rotation and translational motion in the xz plane was observed using the motion capture technique.

The relation between the pitching moment slope $C_{\textrm{M}\alpha }$ and the dominant frequency of the rotational oscillation $f_{\theta 1}$ is derived from the conservation of the angular momentum. The value of the pitching moment slope $C_{\textrm{M}\alpha }$ was identified by substituting $f_{\theta 1}$ of the motion capture data into this relation. The standard deviation of $C_{\textrm{M}\alpha }$ is less than $5\%$ of its mean.

The relation between the lift slope $C_{\textrm{L}\alpha }$ and the second peak $f_{z2}$ of the power spectrum of the translational motion $z_\textrm{g}$ is derived from the conservation of momentum. The value of the lift slope $C_{\textrm{L}\alpha }$ was identified by substituting $f_{z2}$ of the motion capture data into this relation. The standard deviation of $C_{\textrm{L}\alpha }$ is less than $8\%$ of its mean.

The drag coefficient value $C_\textrm{D}$ was identified using the magnetic restoring coefficient $k_x(x)$, which was obtained through the momentum equation and the measured dominant frequencies $f_{x1}$ of the flow directional oscillations for various $U_\infty$. The standard deviation of $C_\textrm{D}$ is less than $6\%$ of its mean.

The next issue to address is the increase in airflow velocity of the wind tunnel. Currently, the aerodynamic oscillation frequency is lower than the natural frequency of the magnetic restoring force. However, increasing the airflow velocity will cause an increase in the aerodynamic oscillation frequency. If this frequency is sufficiently higher than the magnetic natural frequency, the wind tunnel model will become free from magnetic resonance.

By reducing the influence of magnetic resonance, it becomes possible to study the dynamic stability of the capsule using motion capture data and conservation of kinetic energy. The kinetic energy may have a long-period component compared to the dominant frequency of oscillation.