1 Introduction

Steady jets issuing into a crossflow—sometimes referred to as transverse jets—have been extensively studied due to their natural/industrial occurrences including hydrothermal plumes (Lupton 1995), wildfires (Kahn et al. 2008), and smokestacks (Hewett et al. 1971). Additionally, jets in a crossflow are utilized as flow control devices (List 1982; Gutmark and Grinstein 1999), typically for separation control (Smith 2002; Shun and Ahmed 2011), though also for improved heat transfer (Kamotani and Greber 1972), enhanced mixing (Broadwell and Breidenthal 1984), and even thrust vectoring (Chandra Sekar et al. 2017). While a circular jet is most common, rectangular shaped orifices are often used in application (Strykowski et al. 1996), though less rigorously studied. We aim to characterize the resulting flow field of rectangular orifice jets issuing into a laminar boundary layer for a variety of orifice geometries and orientations.

The salient features of transverse circular jets are their four types of vortex structures: counter-rotating vortex pairs, shear-layer vortices, horseshoe vortices, and wake vortices (Fric and Roshko 1994). Counter-rotating vortex pairs form behind the jet that are generated at the orifice during jet formation (Kamotani and Greber 1972). Additionally, horseshoe vortices form when the crossflow encounters the adverse pressure gradient upstream of the jet (Mahesh 2013); i.e., the boundary layer bends around the jet and a portion of the vorticity is re-oriented into the streamwise direction. Shear layer instabilities between the jet and the crossflow generate a hovering vortex that envelops the jet and augments the counter-rotating vortex pair (Kelso et al. 1996). Finally, wake vortices are generated between the counter-rotating vortex pair and the wall due to interactions with the crossflow boundary layer and the jet exit boundary layer (Fric and Roshko 1994). One of the dominating features of these jets is the streamwise vortex generation and evolution downstream. The strength of these longitudinal vortices vary with pitch and skew angles of the jet orifice (Compton and Johnston 1992). Another major feature of these jet flows is their wake deficit due to the virtual blockage they impose on the crossflow, typically characterized in development via the jet trajectory or penetration (Smith and Mungal 1998).

Rectangular jets have critical differences compared to circular jets. They often produce non-axisymmetric flow fields (Miller et al. 1995; Plesniak and Cusano 2005) characterized by steady streamwise vortex structure downstream of the orifice. The interaction of the flow field with the jet relies heavily on the geometric features of the rectangular orifice, including the aspect ratio (slot length divided by the width), the pitch angle (angle between the orifice-normal centerline and the flat plate surface) and skew angle (varying from parallel or perpendicular to the crossflow). The asymmetry in the axial direction of a rectangular orifice gives rise to instabilities like “axis switching” (Ho and Gutmark 1987), where the jet cross-sectional shape oscillates between the long and short cross-sectional axis.

The most traditional jet orientation is wall-normal and perpendicular to the flow. When the jet ejects from the orifice, the cross-sectional profile immediately deforms due to the nearby vortex structure, yielding a saddle-back or kidney-shaped profile (Humber et al. 1993; Vouros et al. 2015). This jet axial velocity field then develops downstream, sometimes characterized into the following development regions: potential core, two-dimensional, and axisymmetric (Krothapalli et al. 1981). The jet also influences the crossflow, leading to an upstream separation region dominated by blockage and a downstream counter-rotating streamwise vortex pair (Krothapalli et al. 1990). Less traditionally, the orifice can have different orientations. Changing the pitch and skew angle of the jet can significantly impact the jet trajectory (Weston and Thames 1979), penetration (Pokharel and Acharya 2021), and the downstream mixing (Plesniak and Cusano 2005) (which we will further substantiate in this work). While these works individually explored important aspects of rectangular jets, none to our knowledge have completely characterized the flow field and statistics of a steady rectangular jet with varying aspect ratios, blowing ratios, and especially orifice orientation; all of which have a major impact on their interaction with the flow fields.

With this work, our focus is on the vortex structure and flow field generated by rectangular orifice steady jets issued into a laminar boundary layer. We systematically vary the orifice aspect ratio, the blowing ratio (i.e., the velocity ratio between the jet and the crossflow), and the orifice orientation defined by the pitch (angle between the orifice-normal centerline and the flat plate surface) and skew (varying from parallel or perpendicular to the crossflow) angles. First we characterize the vortex and velocity fields, then make scaling arguments on the vortex trajectory and vorticity production, and finally consider statistics that have flow control implications like added boundary layer momentum and flow mixing.

2 Methods

We study steady jets with a rectangular orifice issuing into a laminar boundary layer on a flat plate where the wind tunnel and experimental methods are the same as those in Van Buren et al. (2016) and Tricouros et al. (2022). The average jet output velocity at the orifice is termed \(U_\textrm{o}\). All quantities are presented dimensionless unless otherwise stated. Length scales are normalized by the orifice width \(h_\textrm{o} = 1\) mm and velocities are normalized by the crossflow freestream velocity \(U_\infty = 10\) m/s.

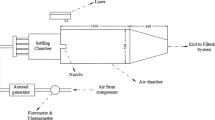
Data were collected in a custom open return suction wind tunnel with a 0.1 m \(\times 0.1\) m cross section \(\times 0.61\) m test section length. The wind tunnel speed was measured with a differential pressure transducer, OMEGA PX653-0.5BD5V (accuracy of \(\pm \,0.3\%\) corresponding to velocity errors of \(\pm \,0.78\) m/s), comparing the pressure at the inlet and exit of the contraction section, from this point the velocity can be calculated using the Bernoulli equation. The contraction section had an area ratio of 9:1 and a length to diameter ratio of 1.5. This facility had a freestream turbulence intensity of \(0.5\%\), and the tunnel ceiling was contoured so that there was no streamwise pressure gradient. The boundary layer on the floor of the tunnel was laminar with a height of \(\delta _{0.95} = 3\) mm at the jet location. The housing for the jet mounts into the wind tunnel floor as shown in Fig. 1.

Fig. 1
figure 1

Jet mounting system used to house the steady jet in the floor of the wind tunnel

Full size image

The steady jet is driven by a constant pressure source where pressure is evenly distributed and disturbances are cleaned by a steel wool inlet section. The jet flow rate was measured using an OMEGA FLMG-series volumetric flow rate transducer, corresponding to a velocity uncertainty of \(\pm \,0.75\) m/s. The flow rate transducer provided us with the approximate average flow from the orifice, this flow was validated using particle image velocimetry in a quiescent study (Van Buren and Amitay 2016). The orifice is rectangular with lengths of \(l_\textrm{o} = 3, 6\), and 9 mm and width of a fixed \(h_\textrm{o} = 1\) mm, resulting in aspect ratios \(\text {AR} = 2l_\textrm{o}/h_\textrm{o} = 6,\) 12, and 18. Our orifice geometry features sharp edges, potentially leading to separation and increased turbulence. Sharp-edged rectangular orifice jets are not uncommon in literature (Tsuchiya and Horikoshi 1986; Pollard and Iwaniw 1985; Humber et al. 1993). This facility design has previously been used in a study between steady and unsteady jets issued into a quiescent fluid (Van Buren and Amitay 2016), the effect of flow separation or higher turbulence levels at the orifice were negligible. The jet was found to behave as a traditional laminar jet with no significant asymmetry, lending confidence to the flow cleaning section and orifice inlet geometry yielding a quality jet. However, true self-similarity studies for this orifice setup have not been conducted. Given that the thickness of the orifice plate is fixed at 6 mm, the orifice neck height is dependent on the pitch angle, \(h_n = 6/\sin {(\alpha )}\) mm. The apparatus allows various pitch angles \(\alpha = 45^\circ , 65^\circ , 90^\circ\) and skew angles \(\beta = 0^\circ , 45^\circ , 90^\circ\). The quality of the jet at the various pitch angles has not been evaluated but we do not expect orifice angle to have a large impact. Blowing ratios ranged from \(C_\textrm{b} = U_\textrm{o}/U_\infty = 0.5{-}3.0\). Vector components highlighting the noted direction are denoted by subscripts x, y, and z. The complete set of parameters are in Table 1.

Table 1 Jet geometry, orifice orientation, and blowing ratio for all cases
Full size table

Stereoscopic particle image velocimetry (SPIV) was used to gather two-dimensional planes with three component velocity measurements along the span of the wind tunnel. A commercial LaVision system was used, featuring a dual-head double-pulsed 120 mJ Nd:YAG laser with two \(1376 \times 1040\) pixel resolution 12-bit Imager Intense CCD cameras. The cameras had a pixel pitch of 6.45 \(\upmu\)m \(\times\) 6.45 \(\upmu\)m on the CCD sensor. The original image sizes from the camera were 63 mm \(\times\) 40 mm, corresponding to 0.046 mm/pixel in the horizontal direction and 0.038 mm/pixel in the vertical direction. The cameras were equipped with 105 mm focal length lenses with 532 nm ± 10 nm band-pass filters. The cameras were oriented \(60^\circ\) from each other on one side of the wind tunnel while the laser emitted from the opposite side. To seed the flow, a Martin Magnum 850 smoke machine was used, generating particles 2–4 pixels in diameter. The particle size was chosen to avoid pixel locking, following the guideline of 3–5 pixels per particle image diameter (Prasad et al. 1992). Particle images were diffraction-limited, an f-stop number of 11 was used to compensate for this effect. Data were taken upstream and downstream of the orifice in \(y{-}z\) planes, with variable spacing, from \(x = -10\) to 20 every 1 orifice width, \(x = 20\) to 40 every 2 orifice widths, and \(x = 40\) to 90 every 5 orifice widths. With our data acquisition orientation where every plane is taken at inherently a different time, we do not have the capability to see the spanwise structures that can exist in the shear layers along the jet centerline as well as the finger-like wall-normal vortex structures that can connect the wall to the jet wake as seen in other studies. Data were processed using LaVision DaVis software. Cross-correlations of successive image pairs were computed with 50% overlap interrogation regions. A multi-pass technique was used where our initial pass consisted of 32 \(\times\) 32 pixel windows and our final pass was 16 \(\times\) 16 pixel windows. The result of these correlations generated windows with \(209 \times 103\) velocity vectors with a resolution of 0.61 mm \(\times 0.7\) mm in the y and z directions, respectively. Time-averaged data were taken from an ensemble average of 500 image pairs. Statistical convergence time averages were performed to ensure all average quantities were sufficiently converged to within the uncertainty of the experiment. To minimize measurement uncertainty, the steps outlined by Adrian and Westerweel (2011) were followed. A spatial error of 0.1 pixels was assumed, resulting in velocity measurement errors of \(\pm 0.2{-}0.6\) m/s that correspond to time delays of \(\Delta t = 1{-}10\,\upmu\)s (Adrian and Westerweel 2011). The reported SPIV accuracies are idealized and experimental setup specific. Our focus is on the large scale structures and area-averaged statistics, conclusions would not be dramatically changed by small changes in measurement accuracy. For additional details on the experimental apparatus, see Van Buren et al. (2016).

3 Results and discussion

3.1 Flow field characterization

We begin by looking at a representative flow field to become familiar with the salient features of a rectangular transverse jet. For this, we consider the case with a wall-normal orifice, \(\alpha = 90^\circ\), that is perpendicular to the flow, \(\beta = 0^\circ\). The jet blowing ratio is a moderate \(C_\textrm{b} = 1.5\) and aspect ratio \(\text {AR} = 18\). To highlight the complete effects of the jet on the velocity field, we look at the change in total velocity, \(\Delta U_\textrm{tot}\), where the baseline velocity field (i.e., no jet activated) is subtracted from when the jet was active. Isosurfaces of \(\Delta U_\textrm{tot}/U_\infty\) are shown in Fig. 2, where regions of higher velocity are colored red and regions of lower velocity are colored blue. Multiple surfaces of each are shown with higher magnitudes corresponding to deeper color shading and lower transparency. A velocity deficit region is formed around the orifice and continues downstream, throughout the entire measurement domain. This wake region is a characteristic feature of transverse jets (Fric and Roshko 1994). Initially, the wake region extends across the entire jet orifice span then coalesces toward the centerline as it develops. Along the flat plate surface, within the boundary layer, flow is accelerated.

Fig. 2
figure 2

Baseline flow field for our wall-normal, \(\alpha = 90^\circ\), and perpendicular to the flow, \(\beta = 0^\circ\), jet with a blowing ratio of \(C_\textrm{b} = 1.5\) and aspect ratio \(\text {AR} = 18\). Total velocity isosurfaces are plotted at \(\Delta U_\textrm{tot}/U_\infty = \pm \,0.1, 0.15, 0.2\), where increases are shown in red and decreases are shown in blue. Vortex structures are represented by the yellow isosurfaces at \(q_x h_\textrm{o}^2/U_\infty ^2 = 2.5, 3.7, 5.0 \times 10^{-3}\)

Full size image

With the same figure, we can also analyze the vortex structure using the \({\mathcal {Q}}\)-criterion. (Note, \({\mathcal {Q}}\)-criterion highlights the rotation-components of vorticity dominating the strain components (Hunt et al. 1988)). Typically \({\mathcal {Q}}\)-criterion is a total quantity, however here we ignore gradients in the streamwise direction to calculate \({\mathcal {Q}}\), denoted as \(q_x\), to isolate streamwise vortex structure, Eq. 1.

$$\begin{aligned} q_x = -\frac{1}{2} \frac{\partial v}{\partial y}\frac{\partial v}{\partial y} - \frac{1}{2}\frac{\partial w}{\partial z}\frac{\partial w}{\partial z} - \frac{\partial v}{\partial z}\frac{\partial w}{\partial y} \end{aligned}$$
(1)

These are represented by the yellow isosurfaces in Fig. 2. In this case, a counter-rotating vortex pair is visible on either side of the orifice in the near orifice region (we refer to these as edge vortices), whereas the jet velocity wake can be seen throughout our whole measurement domain, the stronger vortex structures quickly decay. The vortex structures last until \(x/h_\textrm{o} \approx 13\), with no visible structures after \(x/h_\textrm{o} = 15\) for these levels of \(q_x h_\textrm{o}^2/U_\infty ^2\).

Interestingly, the vorticity generated by steady jets is low compared to circular transverse jets (Di Cicca and Iuso 2007) as well as others like the unsteady rectangular jet (Tricouros et al. 2022), leading to these fleeting structures. It is likely that, given the larger virtual blockage of the rectangular jets, the horseshoe vortex is less prominent than with circular jets where the boundary layer can re-orient with less resistance. Additionally, unsteady jets naturally yield higher vorticity at the orifice and fundamentally are different—they produce a train of vortex rings instead of shear layers that break down into vortex structure. As we will show throughout this work, a surprising feature of these rectangular steady jets is often the lack of vortex prominence.

With features like the wake region, boundary layer acceleration, and streamwise vortex structure in mind, the effects of orifice orientation, aspect ratio, and blowing ratio on these features can now be explored.

3.1.1 Orifice orientation

Unsurprisingly, orifice orientation heavily impacts how the jet interacts with the crossflow. We consider when the orifice pitch is varied from being partially aligned with the flow to wall-normal, and also skewed such that the crossflow is aligned either the long or short side of the orifice. This results in nine combinations of pitch and skew angles (see Table 1).

First, we look to the vortex structures generated at the orifice, specifically focusing on the near field due to how quickly the structures decay away from the orifice. Contour slices of vortex strength \(q_x h_\textrm{o}^2/U_\infty ^2\) are shown in Fig. 3 at four downstream locations for all orientations. (Note that, in these contours, the \(q_x h_\textrm{o}^2/U_\infty ^2\) field is multiplied by the sign of the local vorticity to preserve the direction of rotation). Starting with the streamwise normal \(\beta = 0^\circ\) orifice, Fig. 3a–c, i, the vortex structures are the weakest and extend only a few orifice widths into the boundary layer. In addition to being the weakest, these structures also decay the quickest, almost entirely gone by \(x/h_\textrm{o} = 14\). An increase in pitch results in moderately stronger vortex structure. The orifice skewed to \(\beta = 45^\circ\), Fig. 3a–c, ii, produces stronger and more expansive vortex structures than for \(\beta = 0^\circ\). These structures are still confined to the near wall region but cover a wider region. Here the vortex structure is less organized because of the skew angle where neither of the orifice edges are aligned with the flow. Regardless of pitch angle, the streamwise oriented \(\beta = 90^\circ\), Fig. 3a–c, iii, orifice produced the most dominant vortex structures. In addition to having the largest magnitude, they also extended over 10 orifice widths away from the flat plate surface. This behavior is likely due to the how vorticity is generated along the orifice walls by the jet. The streamwise oriented orifice orientation has the longest sides in the streamwise direction.

In Fig. 3, we can see the characteristic counter-rotating vortex pair associated with jets. The counter-rotating vortex pair is not symmetric in the \(y{-}z\) plane in Fig. 3a, b, iii due to the jet pitch angles. For the wall-normal jet, Fig. 3c, iii, the vortex pair has some asymmetry, likely due to crossflow interaction. (Note, in quiescent studies this jet was symmetric and rectilinear (Van Buren and Amitay 2016)). Elements of upper and lower deck kidney vortices can be seen in Fig. 3c, iii as was seen in Haven and Kurosaka (1997) for a much lower aspect ratio orifice (\(\text {AR}=2.4\)). However, the existence of these vortex pairs is not as readily noticeable for all the jet orientations. Overall, wall-normal and parallel to the flow jets will produce the strongest vortex structures, with the parallel condition being the most critical.

Fig. 3
figure 3

Vortex structures produced for each jet orientation: pitch angles \(\alpha = 45^\circ , 65^\circ , 90^\circ\) (a–c), and skew angles \(\beta = 0^\circ , 45^\circ , 90^\circ\) (i–iii), where each row represents a single jet orientation at multiple streamwise locations. The jets have an orifice aspect ratio \(\text {AR} = 18\) and blowing ratio \(C_\textrm{b} = 1.5\)

Full size image

The resulting velocity field is also heavily impacted by orifice orientation. The downstream development of the change in streamwise velocity field \(\Delta U_x/U_\infty\) is shown in Fig. 4.

Fig. 4
figure 4

Changes in streamwise velocity for each jet orientation: pitch angles \(\alpha = 45^\circ , 65^\circ , 90^\circ\) (a–c), and skew angles \(\beta = 0^\circ , 45^\circ , 90^\circ\) (i–iii). The jets have an orifice aspect ratio \(\text {AR} = 18\) and blowing ratio \(C_\textrm{b} = 1.5\). This data first appeared in Tricouros et al. (2022) but have been re-plotted for this manuscript

Full size image

Consider only the effects of adjusting the jet pitch. For the traditional zero-skew \(\beta = 0^\circ\) cases, Fig. 4i, at the lowest pitch angle the jet is most aligned with the flow and directly adds momentum into the boundary layer near-wall region. As the pitch is increased, the jet becomes more transverse and the virtual blockage is increased resulting in a larger velocity deficit region. Notably, even with the larger blockage there is still considerable near-wall acceleration. The impact of pitch angle becomes less pronounced at nonzero skew angles. For \(\beta = 45^\circ\), Fig. 4ii, there is a growing blockage region with increased pitch, though the flow field is more chaotic and asymmetric. For \(\beta =90^\circ\), Fig. 4iii, the impact of pitch is minimized, where the wake and acceleration regions are similar in size but the trajectory changes with pitch angle.

Next, consider the effects of changing skew angle for given pitch angles. Generally, as the skew angle increases from \(\beta =0^\circ - 90^\circ\), the long dimension of the jet orifice becomes more aligned with the flow and the blockage is minimized. As a result, we see that the jet penetrates the furthest into the crossflow and is least impacted by the surrounding flow field. This is most pronounced across all pitch angles for \(\beta = 90^\circ\), Fig. 4iii. When the skew angle is low, as in \(\beta = 0^\circ\) Fig. 4i, the blockage is highest and the jet trajectory is most compressed into the near-wall region.

3.1.2 Aspect ratio

For our jet, aspect ratio changes the distance between the orifice long edges, as our orifice width is held constant. Note that our exploration of aspect ratio is limited to only the more traditional zero-skew \(\beta =0^\circ\) case. As before, we start with comparing the vortex structures in Fig. 5. For all aspect ratios, counter-rotating vortex pairs are shed from the orifice along the streamwise edges. The distance between the counter-rotating vortex pairs increases proportionally with aspect ratio, however the vortex field is largely similar between aspect ratios. Generally, higher aspect ratios led to slightly stronger edge vortices structures but they decay more rapidly. For the highest aspect ratio case, secondary vortex structures faintly appear between the edge vortices.

In a paired study looking at unsteady jets of the same geometry (Van Buren et al. 2016), it was found that in the AR \(= 6\) close proximity of the edge vortices led to earlier vortex liftoff from the surface and more rapidly decaying structures. However, we do not see that for the steady jet, likely because the vortex structures are not strong enough to produce this liftoff [unsteady jets produce much stronger vortex structures (Tricouros et al. 2022)].

Fig. 5
figure 5

Vortex structures produced for each jet aspect ratio \(\text {AR} = 6, 12, 18\) (a–c), where each row represents a single jet aspect ratio at multiple streamwise locations. The jets are wall-normal \(\alpha = 90^\circ\) and perpendicular to the flow \(\beta = 0^\circ\) with a blowing ratio of \(C_\textrm{b} = 1.5\)

Full size image
Fig. 6
figure 6

Changes in streamwise velocity for each jet aspect ratio: \(\text {AR} = 6, 12\), and 18. The jets are pitched at \(\alpha = 90^\circ\) and skewed to \(\beta = 0^\circ\) with blowing ratio \(C_\textrm{b} = 1.5\). These data first appeared in Tricouros et al. (2022) but have been re-plotted for this manuscript

Full size image

Aspect ratio effects on the velocity field are primarily due to the changing orifice area. The principal feature shared for all jet aspect ratios is the velocity deficit region, Fig. 6. The blockage forms near the orifice and extends downstream. The size of this negative streamwise velocity region scales with orifice length. Small pockets of accelerated flow emerge along the tunnel floor, on either side of the deficit regions. These regions appear faintly for \(\text {AR} = 6\) but as aspect ratio increases, these positive velocity regions grow in size and strength. Overall, the flow fields are similar but aspect ratio scales the size and strength of the flow features.

3.1.3 Blowing ratio

Our final parameter is blowing ratio, which varied from \(C_\textrm{b} = 0.5{-}3.0\) in increments of 0.5. The blowing ratio is primarily responsible for changing the size and strength of existing structures, though sometimes impacts the organization of the flow structure itself. The streamwise vortex structures generated, Fig. 7, highlight the varying array of structures generated for these different blowing ratios.

Fig. 7
figure 7

Vortex structures produced for each jet blowing ratio \(C_\textrm{b} = 0.5{-}3.0\) in increments of 0.5 (a–f), where each row represents a single jet blowing ratio at multiple streamwise locations. The jets have an orifice aspect ratio of \(\text {AR} = 18\) and are wall-normal, \(\alpha = 90^\circ\), and perpendicular to the flow, \(\beta = 0^\circ\)

Full size image

The vortex structures increase in strength and size as blowing ratio increases. Secondary structures appear faintly for \(C_\textrm{b} = 1.0\) and become more pronounced with increasing blowing ratio. The vortices shedding off the streamwise edges of the orifice lift away from the flat plate surface, especially for \(C_\textrm{b} = 2.5, 3.0\). The secondary structures between the two main counter-rotating vortices tend to spread out along the orifice span, near the floor. Vortex structures produced are highly dependent on the blowing ratio of the jet. The main reason for this is that the blowing ratio directly affects the vorticity generation within the orifice, with higher velocity producing stronger vorticity. A secondary reason is that increases in blowing ratio correspond to more momentum interrupting the crossflow and in turn creating rotational structures due to flow interaction.

Fig. 8
figure 8

Change in streamwise velocity for \(C_\textrm{b} = 0.5{-}3.0\) in increments of 0.5 (a–f). Jet orifice has aspect ratio \(\text {AR} = 18\) and is wall-normal, \(\alpha = 90^\circ\), and perpendicular, \(\beta = 0^\circ\), to the flow. These data first appeared in Tricouros et al. (2022) but have been re-plotted for this manuscript

Full size image

Now we will look at the change in the streamwise velocity field, Fig. 8. Jet blockage causes an initial velocity deficit region near the orifice which grows away from the floor and toward the orifice centerline. The size and strength of this deficit region increases proportionally with increasing blowing ratio. The flow acceleration regions also grow in strength and size, from faint when \(C_\textrm{b} = 1.0\) to more pronounced by \(C_\textrm{b} = 2.0\). Despite being largely similar, there are notable differences for the different jet velocities. For the lowest blowing ratios, \(C_\textrm{b} = 0.5, 1.0\), the jets are relatively weak, unable to penetrate further into the crossflow and maintaining their original shape. Comparatively, the velocity structures from the stronger blowing ratios (\(C_\textrm{b} \ge 1.5\)) extend away from the floor and encounter resistance from more of the crossflow, causing the jets to coalesce to the center. Finally, a region of velocity increase appears above the deficit core at \(C_\textrm{b} = 1.5\) and grows for larger blowing ratios. The larger velocity gradients between the jet and the crossflow result in stronger shear layers that contribute to these accelerated flow regions.

3.2 Scaling considerations

In the previous section, it is clear that certain steady jet characteristics, like the aspect ratio and blowing ratio, produce fairly similar flow fields. It stands to reason that we might be able to develop scaling arguments for various flow statistics and remove the aspect ratio and blowing ratio dependence. In this section, we will make theoretical arguments for scaling the steady jet impact on the crossflow and see how scaling impacts specifically the jet trajectory and area averaged streamwise vorticity. Note that, given the complexity that orifice orientation has on the jet interaction with the crossflow and the downstream development, we were unable to find sufficient scaling parameters to sufficiently capture the impact of these parameters.

We begin with the jet trajectory, which has already had a number of scaling studies in the past with circular (Keffer and Baines 1963; Kamotani and Greber 1972; Chassaing et al. 1974; Hasselbrink and Mungal 2001; New et al. 2006), elliptical (Lim et al. 2006), and planar jets (Huang et al. 2005). A collection of the studies, the orifices used, blowing ratios, and scalings used have been summarized in Table 2.

Table 2 Collection of different methods in the literature to scale transverse jet trajectories
Full size table

In this study, trajectory was calculated using the wall-normal centroid approach using the change in spanwise-averaged streamwise velocity,

$$\begin{aligned} y_c = \frac{\sum \nolimits _{y=0}^{y=y_{\text {max}}} y \left\langle \Delta U_x \right\rangle _z}{\sum \nolimits _{y=0}^{y=y_{\text {max}}} \left\langle \Delta U_x \right\rangle _z}, \end{aligned}$$
(2)

where spanwise-averaged streamwise velocity is denoted by \(\langle \Delta U_x \rangle _z\). Note, the trajectory for other studies are often defined slightly differently depending on measurement availability; for example, in Smith and Mungal (1998) the trajectory was calculated based upon concentrations of flow seeding. We do not anticipate these differences to have major influences on the scaling strategy. The jet trajectories are shown in Fig. 9a for all aspect ratios and blowing ratios. Note here that, in this section the jet orientation is consistently wall-normal (\(\alpha =90^\circ\)) and perpendicular to the flow jet orientation (\(\beta =0^\circ\)). Generally, higher blowing ratio yields jet trajectories further away from the wall because increasing the jet velocity allows the jet to better overcome the crossflow and extend further from the wall. Alternatively, the trajectory is largely unaffected by aspect ratio (for our limited range of geometries) indicating that we are at a sufficiently high aspect ratio with \(\text {AR}=6\) such that there are limited finite-span influences.

Fig. 9
figure 9

Trajectories for the wall-normal \(\alpha = 90^\circ\) and perpendicular to the flow \(\beta = 0^\circ\) jet orientation. Colors correspond to the six blowing ratios while line styles correspond to the three aspect ratios. The trajectories represented are the: no scaling applied (\(C_\textrm{b} = 0.5{-}3.0\)) (a), normalized by the blowing ratio squared (\(C_\textrm{b} = 1.0{-}3.0\)) (b)

Full size image

Now, we consider a scaling method to collapse the jet trajectory behavior. Looking at Table 2, traditionally the streamwise and wall-normal distances are divided by some length scale associated with the orifice and the blowing ratio to some exponent between 1 and 2. In the simplest interpretation, the physical argument here is that the jet trajectory dependence is on the jet velocity, \(\sim C_\textrm{b}^1\), or the jet momentum, \(\sim C_\textrm{b}^2\). (Note that, for low blowing ratio jets the role of the boundary layer is more important and this physical interpretation my be too simplistic). The jets in this study have moderate aspect ratio, sitting somewhere between the behavior of circular jets [for example, New et al. (2006)] and two-dimensional planar jets [for example, Huang et al. (2005)] We find that the trajectory is largely aspect ratio independent, which indicates we are toward two-dimensional behavior. For our data set, the best scaling fit was to divide the streamwise and wall-normal distances by \(h_\textrm{o}\;C_\textrm{b}^{2}\) [which most closely follows the strategy of Keffer and Baines (1963), Smith and Mungal (1998), and Huang et al. (2005)]. Figure 9b shows the scaled trajectory for \(C_\textrm{b} = 1.0\) to 3.0. For this range of blowing ratios, the scale of \(h_\textrm{o}\;C_\textrm{b}^{2}\) sufficiently collapses the jet trajectory. Note here that, we have ignored the blowing ratio \(C_\textrm{b}=0.5\) because it is both problematic to quantify downstream with such low velocities and also the traditional scaling methods become undefined as \(C_\textrm{b}\) trends toward zero.

Next, we seek a method to normalize the streamwise vorticity generation due to the jet presence. Here, we follow a scaling argument used in Tricouros et al. (2022) which ties the streamwise vorticity to the vorticity produced within the orifice on the side walls, evaluated at the orifice wall. We model the streamwise orifice edges as flat plates. This allows us to use the Blasius boundary layer solutions and directly derive the expected wall vorticity,

$$\begin{aligned} \omega _{z^*_B} = 0.332\sqrt{\frac{U_\textrm{o}^3}{\nu x^*}}, \end{aligned}$$
(3)

Here, \(\cdot ^*\) denotes that we are in the reference frame of the orifice flow where \(x^*\) is the jet direction, \(y^*\) is wall normal to the local orifice side wall, and \(z^*\) is tangential to the side wall. Thus, \(\omega _{z^*_B}\) is the vorticity for a Blasius boundary layer developing on the orifice side wall evaluated at the wall, \(\nu\) is the kinematic viscosity of air, and \(x^*\) is the development length. For us, \(x^*\) becomes the neck height of our orifice, \(h_n\) because we are looking for a scale factor representing the approximate vorticity at the orifice exit where \(x^*=h_n\). We take the absolute value of our streamwise vorticity and then area average it at each streamwise location (area averaging denoted by \(||\cdot ||\)):

$$\begin{aligned} ||\omega _x ||= \frac{1}{(2l_\textrm{o})h_\textrm{o}}\iint |\omega _x |{\textrm{d}y} {\textrm{d}z}. \end{aligned}$$
(4)
Fig. 10
figure 10

Area average of the absolute value of streamwise vorticity (a), and the area average normalized by the theoretical vorticity production (b). Jets are wall-normal, \(\alpha = 90^\circ\), and perpendicular to the flow, \(\beta = 0^\circ\). Changes in aspect ratio are represented through the different line styles while changes in blowing ratio are shown by varying color. In b, for \(C_\textrm{b} = 0.5, 1.0\), the lines are semi-transparent to highlight that they differ compared to the other blowing ratios. Legend as in Fig. 9

Full size image

The unscaled and scaled area averaged streamwise vorticity are shown in Fig. 10. In the unscaled case, a trend emerges where higher blowing ratios lead to increased average streamwise vorticity. This behavior is expected, higher jet velocities lead to higher velocity gradients. Generally the vorticity peaks shortly downstream from the orifice and then gradually decays. Normalizing by the Blasius vorticity primarily collapses the majority of our cases with the lowest blowing ratios (\(C_\textrm{b}=0.5\), in particular) responding the worst to the scaling. This indicates that for the majority of the jet velocities, the added streamwise vorticity was dependent primarily on the vorticity generated within the orifice during jet formation. However, there are other physical mechanisms for generating streamwise vorticity due to the jet and crossflow interaction. For example, the horseshoe vortices that are more prominent in circular jets (Kelso and Smits 1995) that are a result of the boundary layer vorticity bending around the jet and reorienting in the streamwise direction. For our lowest blowing ratio cases, it could be that these secondary forms of vorticity generation are relatively more important and not captured by our simplified scaling argument. From a more numerical perspective, our scaling argument is problematic as the jet velocity trends toward zero (as with the jet trajectory scaling).

3.3 Flow control implications

Impinging jets on a surface is a common strategy for active flow control, primarily utilized for separation control in adverse pressure gradients (Smith 2002). In this study, we introduce the jet to an attached laminar flat plate boundary layer and are not controlling separation. However, we can still assess important aspects of the flow interaction to glean out possible flow control performance implications. In this section we use two flow statistics: added (1) boundary layer momentum and (2) streamwise enstrophy, as conduits for separation control effectiveness. The former directly prevents separation through boundary layer reenergization, and the latter is more useful in large-scale separation where mixing over a large area benefits flow reattachment.

First, we look at the added momentum near the wall, \({\overline{P}}_{\delta _{0.95}}\) calculated by

$$\begin{aligned} {\overline{P}}_{\delta _{0.95}} = \frac{1}{(2 l_\textrm{o}) h_\textrm{o}} \int \limits _{\text {z}_{\text {min}}}^{\text {z}_{\text {max}}}\int \limits _0^{\delta _\text {0.95}} \frac{U_x^2}{U_{x_b}^2} {\textrm{d}y} {\textrm{d}z}, \end{aligned}$$
(5)

We normalize the streamwise velocity by the baseline velocity field, \(U_b\), from when the jet was not active to see how the jet alters near-wall the momentum. Our y limits of integration are restricted to the boundary layer height based on the baseline case. The baseline cases are specific to each case where we compare the same setup (i.e., geometry, pitch, and skew angles) for when the jet is active or inactive.

In Fig. 11 we show the effects of aspect ratio and blowing ratio on added boundary layer momentum. Regardless of blowing ratio, the lowest aspect ratio jet (Fig. 11a) decreases the momentum within the boundary layer, making the boundary layer more susceptible to an adverse pressure gradient. At higher aspect ratios, we start to see acceleration within the boundary layer that directly correlates to the jet blowing ratio. At the highest aspect ratio (\(\text {AR}=18\)) and blowing ratio (\(C_\textrm{b}=3\)), we see over 200% the original boundary layer momentum. This correlates well with what we saw in the flow field characterization (Fig. 6). All jet aspect ratios generate the velocity deficit core emanating from the orifice. However, the lower aspect ratio jet orifices showed smaller and weaker positive velocity regions along the wall. As aspect ratio increases, these acceleration pockets grow, supporting what we see here for added boundary layer momentum.

Fig. 11
figure 11

Baseline normalized boundary layer momentum for \(\text {AR} = 6\) (a), 12 (b), and 18 (c). Jets are wall-normal, \(\alpha = 90^\circ\), and perpendicular to the flow, \(\beta = 0^\circ\), for all blowing ratios. A faint red region indicates decreases in boundary layer momentum

Full size image

Interestingly, the added boundary layer momentum takes time to grow downstream of the orifice. When utilized as a separation control device, the location of the orifice relative to potential separation points may be critical. Special care must be taken as the negative momentum regions may cause the flow to separate prematurely.

Now let us consider the effect of orifice orientation on the added boundary layer momentum, as shown in Fig. 12. Note that we show only \(C_\textrm{b}=1.5\) as they are the best case scenarios and the highest blowing ratios we tested for these orifice orientations. Here, the trends are not as clear as they were with blowing ratio and aspect ratio. At lower pitch angles, the jet is more aligned with the freestream velocity and less transverse. This results in added boundary layer momentum just downstream of the orifice, in contrast to the wall-normal cases where there was first a momentum deficit in the near-orifice region. This is because the jet momentum directly contributes to the boundary layer momentum at lower pitch angles. However, this benefit is lost in downstream development as the jet penetrates into the freestream. The wall-normal cases \(\alpha =90^\circ\) yield the best downstream benefit to the boundary layer momentum. Generally, for all pitch angles the skew angle has the same effect—larger skew angle (becoming more aligned with the flow) results in reduced boundary layer momentum addition. This is because the jet has less virtual blockage to the crossflow and penetrates into the freestream more easily, quickly moving away from the boundary layer region.

Fig. 12
figure 12

Effect of orifice orientation on baseline normalized boundary layer momentum. Fixed aspect ratio \(\text {AR} = 18\) and blowing ratio \(C_\textrm{b} = 1.5\) for all pitch and skew angles presented. A faint red region indicates decreases in boundary layer momentum

Full size image

Now we move on to the added streamwise enstrophy (i.e., the energy in vorticity) as being representative of the jet induced mixing. This is calculated as

$$\begin{aligned} \varepsilon _x = \frac{1}{2}\iint \omega _x^2 {\textrm{d}y} {\textrm{d}z} \end{aligned}$$
(6)

We do not have measures of vorticity in y- or z-directions due to measurement limitations. However, our primary concern is the streamwise mixing, which we were able to calculate. As before, we start by looking at the effects of blowing ratio and aspect ratio, as shown in Fig. 13. Note here that we effectively show the enstrophy per unit length to more genuinely compare the different sized orifices (i.e., from an applied perspective it is helpful to know whether to have one big jet or to have an array of smaller jets). Generally for all cases, the enstrophy peaks just downstream of the orifice and then decays. Higher blowing ratios correspond to higher streamwise enstrophy, as expected because the higher velocity corresponds to more generation of vorticity at the orifice. The aspect ratio has a relatively weak impact on the enstrophy production, with the lowest aspect ratio case providing a bit higher peak enstrophy. (It is important here to note that vorticity and enstrophy are not the same as rotational vortex structure, as we explored in Sect. 3.1).

Fig. 13
figure 13

Streamwise evolution of enstrophy, \(\varepsilon _x/(U_\infty ^2 \text {AR})\). Orifice orientation is wall-normal, \(\alpha = 90^\circ\), and perpendicular to the flow, \(\beta = 0^\circ\). Aspect ratios are represented through the line styles while blowing ratios are represented by the different colors

Full size image
Fig. 14
figure 14

Streamwise evolution of enstrophy, \(\varepsilon _x/(U_\infty ^2 AR)\). The orifice has a fixed aspect ratio, \(\text {AR} = 18\), and blowing ratio, \(C_\textrm{b} = 1.5\). Orifice orientation is represented through line style for pitch angles (\(\alpha\)) and color for skew angles (\(\beta\))

Full size image

The impact of jet orifice orientation on streamwise enstrophy is more complex, as we see in Fig. 14. Across the entire plotted domain, the jet orientation with the longest edge parallel to the streamwise direction \(\beta = 90^\circ\) produces the largest enstrophy, regardless of pitch angle. This is because this jet skew orientation has the longest vortex structure producing edges aligned with the streamwise direction. Beyond that, the medium skew angles \(\beta = 45^\circ\) are generally the second most powerful group, for similar reasons. Comparing Figs. 13 and 14, we see that orifice orientation plays a larger role in the amount of enstrophy produced than aspect ratio. At the same blowing ratio, adjusting the orifice orientation can produce almost four times the enstrophy. This relationship can be important for mixing applications where higher or lower enstrophy may be desired to alter the mixing strength, or if the incoming flow to the orifice might be variable (e.g., on a maneuvering vehicle or in gusty environments).

4 Conclusion

Rectangular orifice steady jets were issued into a laminar boundary layer crossflow. The resulting flow fields were explored using stereoscopic particle image velocimetry. The jet orifice had variable aspect ratios, blowing ratios, and orifice orientation through pitch and skew angles.

First, we characterized the streamwise vortex structures and velocity field produced by the jet interaction with the crossflow. Orifice orientation heavily impacted both, altering both the strength and locations of these structures. Vortex structures were comparatively much weaker for cases where the jet was more aligned with the freestream (low \(\alpha\)). For skew angles where the orifice was across the flow (\(\beta =0^\circ\)), the edge vortices were far apart and relatively weak. Conversely, when the orifice was aligned with the flow (\(\beta =90^\circ\)) the edge vortices were stronger and penetrated further into the flow. Generally, the jets produced a large wake-like region downstream of the blockage, which was minimized at low pitch angles and high skew angles. The wall-normal jet aligned across the flow produced the largest velocity deficit region but also the largest acceleration within the boundary layer downstream. Aspect ratio and blowing ratio had less of an impact on the flow organization, and merely correlated to the strength of the structures.

Through theoretical scaling arguments, we were able to collapse the behavior of the jet trajectory and added streamwise vorticity. The trajectory is directly impacted by the ratio of the jet to crossflow momentum (\(C_\textrm{b}^2\)), where both the wall-normal and downstream coordinates were normalized by this quantity. The vorticity added to the flow is physically tied to the vorticity on the orifice walls during jet formation, and normalizing the vorticity statistics by the theoretical Blasius boundary layer vorticity at the orifice edge sufficiently collapsed the majority of cases. In both trajectory and streamwise vorticity, the lowest blowing ratio \(C_\textrm{b}=0.5\) behavior was not sufficiently captured by the scaling arguments.

Finally we considered flow separation control implications as they are a common application of steady jets in a crossflow. This was done by looking at boundary layer acceleration and added mixing statistics. Perhaps most surprising, the aspect ratio played a critical role in whether there was boundary layer acceleration or not. For the lowest aspect ratio (\(\text {AR}=6\)) the boundary layer became weaker and more susceptible to separation, however the highest aspect ratio (\(\text {AR}=18\)) led to a more resilient and energetic boundary layer. Blowing ratio served to only strengthen or weaken the jet impact. Considering the jet orientation, the lower pitch angles directly added momentum to the boundary layer and briefly energized it near the orifice, but this impact decayed quickly downstream. Higher pitch angles initially slowed the boundary layer, but recovered downstream and eventually led to added momentum near the wall for the longest lasting and greatest impact. Generally, the skew angles that had the orifice crossing the flow instead of aligned with it led to the greatest boundary layer acceleration. For added mixing (studied via streamwise enstrophy), the aspect ratio had little impact and increases in blowing ratio increased added mixing. Skew angles aligned with the flow led to the largest induced mixing (a consequence of the reduced blockage and longer orifice walls being aligned with the streamwise direction), and pitch angle had only a minor influence.

In using jets as separation control devices, these results indicate a few important guidelines. For direct boundary layer acceleration to prevent separation before it happens, a wall-normal jet with the highest feasible blowing ratio may be best, and the jet needs to be placed 30-40 orifice widths upstream of the separation to give the boundary layer energization space to develop. If the orifice is in a region of already separated flow, where deeper penetration and large-scale mixing will be more helpful, then a wall-normal jet skewed to be aligned with the flow is best. Note here that there is a configuration that is not studied where the orifice is pitched to the point that the Coandǎ effect keeps the jet attached to the wall and produces a wall jet [for an orifice geometry example, see Rathay et al. (2014), figure 3c]. This might be better at direct momentum injection into the boundary layer than the cases studied in this work.