Bubbly drag reduction accompanied by void wave generation inside turbulent boundary layers

Abstract

Frictional drag reduction, a technique by which bubbles are injected into the turbulent boundary layer surrounding the hull of a marine vessel, is now at the stage of practical applications. In achieving drag reduction, void waves often stand out naturally, the reason for which still remains unclear. The present study aims at an experimental characterization of void waves along a flat-bottom ship. A 100-m-long water reservoir is used in which a 4-m-long fully transparent experimental model ship, equipped with wall shear stress sensors and cameras, is towed by a train at speeds of up to 3 m/s. From measurements of the transition of the bubble distribution from random to wavy accumulated swarms downstream, the accompanying intrinsic passing frequency of void waves is examined. A 30% drag reduction rate was recorded with the appearance of void waves in the boundary layer at an average void fraction of 4%. This is much greater than the trivial inertia effect from drag reduction. To clarify the characteristics of the measured void waves, we compare the void wave frequency range to those of several flow instabilities that may occur in bubbly two-phase boundary layer flows.

Graphical abstract

1 Introduction

Since its first demonstration conducted by McCormick and Bhattachayya (1973), the drag reduction technique, specifically the injection of bubbles into the liquid turbulent boundary layer to reduce skin frictional drag along solid walls, has long been of interest to engineers aiming at energy savings for marine vessels. The technique is currently called bubbly drag reduction (BDR) and is distinct from the air cavity technique that separates liquid from the solid wall. Despite the 45-year history on BDR research, the technique has been applied only to a small number of vessels. One of the primary issues that is faced is the unstable performance, i.e., drag reduction is strongly non-linear and depends on many operating conditions. As in the evaluation of fuel savings or regulating CO₂ emissions, power reductions enabled by BDR must be sufficiently larger than the power consumed in injecting bubbles. A past case study by Kodama et al. (2008) using a real vessel recorded a net energy saving of 5% with a hull drag reduction of 12%, implying 7% was spent in bubble injection. Learning from their study, two development paths are suggested: one is to reduce the power for bubble injection, and the other is to amplify the effect of drag reduction per unit amount of air supply. For the former, one of the authors succeeded in minimizing the power using a hydrofoil-type high-speed bubble generator (Kumagai et al. 2015). About 10% of the net power saving was obtained for several large vessels in sea trials. For the latter, a mechanism for drag reduction, which were previously reviewed by Ceccio (2010) and Murai (2014), had to be investigated more. An inescapable feature in the pursuit of a mechanism was the appearance of void waves that stood out clearly during drag reduction (Park et al. 2016). We report in this paper how void waves expand inside a turbulent boundary layer and its relationship to drag reduction performance.

In general, void waves are associated with the wavy propagation of the bubble volume fraction at a certain speed different from the individual bubble velocity. They occur for multiple reasons such as bubble compressibility, evaporation/cavitation, plugging/slugging in bounded flow, gravity-dependent interfacial dynamics, and the variation in the drag coefficient of bubbles increasing with ambient void fraction. However, a deeper understanding is needed for void waves taking place in the two-phase boundary layer along walls. Concerning local bubble clustering initiating the elementary void wave, we find several reports such as Kitagawa et al. (2004) and Takagi and Matsumoto (2010). In their papers, bubble clustering was observed in the vertical system, i.e., the buoyancy of bubbles driving the clusters. With horizontal-wall confinement, wall shear stress plays a primary role that dominates the motion of bubbles. Murai et al. (2007) reported such a phenomenon for bubbles larger than the boundary layer thickness. In contrast, Oishi et al. (2009) found that void waves consisted of small bubbles in a 5-m-long horizontal turbulent channel flow and confirmed that the waves contributed significantly to frictional drag reduction. Following up this discovery, our group applied artificially generated void waves and proved significant improvement in the drag reduction rate in a fully developed horizontal channel flow (Park et al. 2014, 2015).

Currently, there is convincing evidence that void waves influence the performance of BDR. In horizontal channel flows, void waves inevitably accompany pressure fluctuations, which may feed back to influence void wave behavior. In an open system though, such as the external flow along a flat-bottom ship, void waves only nucleate through wall shear stress, almost free from streamwise pressure fluctuations. Therefore, the mutual relationship between void wave development and wall shear stress needs to be defined better. Park et al. (2016) reported on their investigation of void waves using optical images taken through the bottom of a fully transparent model ship as well as theory. They proposed a void wave equation derived from the volume-averaged model equation describing bubbly two-phase flows. They found mathematically that void waves occurred when drag reduction was enhanced by streamwise gradient of local void fraction. This indicates that streamwise momentum contains a double time-lag element to local void fraction inside the turbulent boundary layer; one is for the continuity equation and the other is for the momentum equation. However, the void wave equation did not give outstanding frequency but just proved the waviness in the bubbly turbulent boundary layer. Later, Qin et al. (2017) also mentioned the relationship between BDR and the spatial–temporal fluctuation in the void fraction, but the mechanism that causes the fluctuation has not been uncovered yet. In this paper, we report a quantitative void wave characterization. Based on the amplitude and natural frequency, mechanisms for void wave generation are then assessed, comparing different scales of flow instabilities.

2 Experimental method

2.1 Experimental facilities

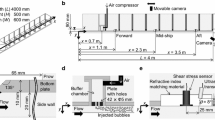
A flat-bottom model ship (Fig. 1) of total length 4.0 m and width 0.6 m was made of flat transparent acrylic plates for optical visualization. To maintain an ideal spatial development of the turbulent boundary layer over the bottom plate, the model ship has a forward-protruding bow with a sharp leading edge and two side walls of height 20 mm to prevent hydraulic wave generation on the water surface level during towing. Air was stored in a buffer chamber regulated at a constant pressure and injected beneath the hull through a porous plate located 0.7 m from the bow. Apart from the bubble injector, the model ship is the same as that used in previous experiments (Park et al. 2016). In those experiments, the air injector plate had an array of 42 5-mm-diameter holes forming two lines perpendicular to the towing direction. Hence, with increasing air volume flow rate, the air jet generated downward from each hole disturbed the turbulent boundary layer strongly (e.g., Bagheri et al. 2009). Therefore, already influenced by the additional turbulence, little could be said regarding the drag reduction performance in the upstream region or the spatial development of void waves. To prevent the jets from forming in this study, a flush-mounted porous plate of sinter aluminum with pore sizes of order 100 µm was fabricated for bubble injection. With this change, the bubbles mixed smoothly from the plate area; the initial mean bubble size decreased because of the strong shearing near the wall. To investigate the spatial development of shear stress along the wall, three measurement locations at 1.1 m, 2.3 m, and 3.5 m from the bow were selected where shear stress sensors were mounted. With a temporal resolution of 20 Hz, these sensors (S10W-02, SSK Co., Ltd., Tokyo, Japan) have a measurable range from − 25 to 25 Pa. Such sensors have been adopted in several experiments of gas–liquid two-phase flows (Guin et al. 1996; Kodama et al. 2000; Moriguchi and Kato 2002; Oishi et al. 2009; Park et al. 2015, 2016). A video camera (EX-F1, Casio Computer Co., Ltd.; frame rate 120 fps) was set at various locations inside the ship to record bubble images. In some experimental setups, we used an underwater camera to monitor the states of the injector and a high-resolution camera to take snapshots of passing bubbles.

Fig. 1

Flat-bottom model ship: a photograph, schematics of b the side view, c details of bow, and d details of bubble injector. The x, y, and z coordinates are aligned in the streamwise, vertical-downward and spanwise directions from the bow

We used a towing test facility to study the dynamics of the ship under constant speeds, located at Hiroshima University. The facility has a train and a water tank of total length 100 m, depth 3.5 m, and width 8.0 m. During experiments the water temperature in the tank was around 24 °C at which the water density and kinematic viscosity (ν) are 997 kg/m³ and 0.923 × 10⁻⁶ m²/s, respectively. The train is controlled to operate at a fixed speed (U_main) of which the maximum towing speed is 3.0 m/s. Excluding the sectors for acceleration and deceleration in the tank, the train can maintain a constant maximum towing speed for approximately 7 s in period or 21 m in distance.

2.2 Experimental conditions

To confirm the functioning of the side walls and to verify the performance of the bubble injector, images near the bubble injector were taken using the underwater camera of the bottom of the ship (Fig. 2). Bubbles are also naturally ventilated outside the side walls due to wave breaking, but we confirmed from video clips that these bubbles did not enter the target boundary layer of the flat-bottom area (Fig. 2b). Figure 2c shows bubbles injected from the whole region of the porous plate. The bubbles ventilated outside the side walls were sucked downward due to tip vortices induced by the side edges of the bow. In contrast, the bubbles injected from the porous plate travelled smoothly downstream without separating from the bottom plate.

Fig. 2

Photographs of the ship’s bottom near the bubble injector taken by an underwater camera; when the ship was a stationary, b towed without bubble injection, and c towed with bubble injection

Figure 3 plots the friction coefficient measured by the shear stress sensor in single-phase flow operation, i.e., without bubble injection. Here, the Reynolds number is defined as

$$R{e_x}=\frac{{x{U_{{\text{main}}}}}}{\nu },$$

(1)

where x, U_main, and ν denote the distance from the bow, towing speed (or outside free stream velocity), and kinematic viscosity of water. The friction coefficients for $R{e_x}$ > 2.0 × 10⁶ measured from previous and present experiments are scattered around that of turbulent flow in literature (e.g., Schlichting 1979), indicating that the boundary layer was in a fully turbulent state.

Fig. 3

Friction coefficient as a function of Reynolds number based on x, where error bars indicate standard deviations. Open symbols signify data obtained in a previous experiment (Park et al. 2016) employing an array of holes as the bubble injector. Solid symbols mark the present data obtained using the porous plate type of bubble injector. Light and dark gray lines indicate, respectively, the Blasius friction law for laminar flow and the empirical friction coefficient for turbulent flow (Schlichting 1979)

For this study, the air volume flow rate for bubble injection was set at four different values: Q_g = 1.25 × 10⁻³ m³/s, 1.67 × 10⁻³ m³/s, 2.08 × 10⁻³ m³/s, and 2.50 × 10⁻³ m³/s. From the volume flow rates of gas and liquid phases flowing inside the boundary layer, the boundary layer void fraction ${\alpha _\delta }$ is estimated to be

$${\alpha _\delta }=\frac{{{Q_{\text{g}}}}}{{{Q_{\text{l}}}+{Q_{\text{g}}}}} \approx \frac{{{Q_{\text{g}}}}}{{W\int_{0}^{{_{\delta }}} {{u_y}{\text{d}}y} }} \approx \frac{{{Q_{\text{g}}}}}{{W{U_{{\text{main}}}}\int_{0}^{{_{\delta }}} {{{(y/\delta )}^{1/7}}{\text{d}}y} }},\quad \delta =0.37{x^{4/5}}{(\nu /{U_{{\text{main}}}})^{1/5}},$$

(2)

where Q_l, W, ${u_y}$, and δ are liquid flow rate inside the boundary layer, the width of the ship, vertical profile of the streamwise liquid velocity, and 99% velocity depth of the boundary layer, respectively. Since it is difficult to predict the boundary layer thickness in bubbly flow conditions, here in the definition of ${\alpha _\delta }$, we adopt thickness and velocity profile of the boundary layer in single phase condition. Namely, the 1/7 power law is adopted for the boundary layer velocity profile to represent the liquid flow rate. Details of the experimental conditions are summarized in Table 1.

Table 1 Experimental conditions of a boundary layer

3 Results and discussions

3.1 Bubble conditions

Snapshots of bubbles were taken at the three different locations beneath the plate (Fig. 4). The bubbles are non-spherical because of the strong turbulence and cover the wall as viewed from above. As void waves are induced downstream, local bubble distribution transits from a uniform state to a wavy state of dense and sparse areas. Given the experimental conditions as in Fig. 4, the probability density functions (PDFs) for the size of bubbles were obtained (Fig. 5). The bubble size is defined as the equivalent diameter obtained from the area of each bubble; the bin size for each PDF is 0.5 mm. From these results, we confirm the following: (1) the average bubble size is around 3 mm, which coincides with the estimation formula proposed by Sanders et al. (2006). This implies that the bubbles are easily deformable in shear with high turbulence and their peak population stays closely to the critical Weber number of fragmentation. (2) The deviation in size expands with the spatial development downstream. This occurs for two reasons. One is the history of bubble fragmentation and coalescence from upstream. The other is the influence of void wave generation, which forces bubbles to coalesce in highly dense regions (see Fig. 4c) producing sizes of over 6 mm (Fig. 5c). Such large bubbles fragment immediately into small bubbles as the critical Weber number is surpassed, resulting in a broad spread in size.

Fig. 4

Sample of snapshots of bubbles moving beneath the hull with Q_g = 1.25 × 10⁻³ m³/s: a front region, b middle region and c rear region

Fig. 5

Sample of distributions in bubble size with Q_g = 1.25 × 10⁻³ m³/s at the different locations: a front region, b middle region and c rear region

In this context, when we discuss void wave generation hereafter, we need to recall that the phenomenon always takes place together with a spread in bubble size. Therefore, the void wave in this instance must be distinguished from similar structures often observed in mono-dispersion systems. More generally, the void wave treated here is not that caused by a spatially regularized interaction at the bubble–bubble distance scale, but is estimated to be that induced at length scales associated with boundary layer development.

3.2 Drag reduction by bubble injection

The results for the measured ratios of the time-averaged wall shear stress with bubble injection to that without bubbles are presented in Fig. 6 which is purposely separated according to location, i.e., front region (Fig. 6a), and the two downstream regions (Fig. 6b) because the former is influenced by the sudden impact of bubble injection. From the present data, shear stress is reduced in all regions including the front region, whereas our previous data had indicated increases in shear stress in the front region as well. The difference stems from the effect of the air jet of the previous bubble injector (see Sect. 2.1). In the case of multi-hole bubble injector, the air jet velocity of each hole to supply the boundary layer void fraction at ${\alpha _\delta }$ = 0.05 is calculated to be 0.75 m/s, which is over 25% of the ship speed. Hence, bubble injection strongly supplies additional turbulence greater than the original turbulence within a certain distance downstream from the bubble injector. In contrast, with the present bubble injector of porous plate principle, the mean air flow velocity from the plate at the same void fraction is regulated to 0.045 m/s, less than 2% of the ship speed. We therefore attribute the difference in the wall shear stress data in the front region to the boundary layer structure disturbed by the way the bubbles are injected.

Fig. 6

Wall shear stress modified by bubble injection; a front region, b middle and rear regions. The open and solid symbols are as given in Fig. 3. Error bars indicate standard deviations of data on each condition of boundary layer void fraction

In the middle and rear regions (Fig. 6b), the wall shear stress decreases with increasing void fraction regardless of the manner of injection. This implies that the method no longer influences the two-phase boundary layer structure at locations far downstream. The gain factor in drag reduction in these regions, defined by

$$G=\frac{1}{{{\alpha _\delta }}}\left( {1 - \frac{{{\tau _{\text{w}}}}}{{{\tau _{{\text{w}}0}}}}} \right),$$

(3)

is around G = 6 as read from the average descending slope of the plots. This number is much greater than the trivial inertia effect at G = 1 (which means that drag reduction occurs simply with a reduction in density), and therefore implies that the inner layer structure of the boundary layer of the present model ship is altered due to the presence of bubbles. More importantly, the structure accompanies clear void waves during drag reduction, on which we shall elaborate in the next section.

3.3 Visualization of void wave

To evaluate the spatial development of the bubble distribution, we took a timeline of bubble images from video clips (Fig. 7) obtained at the three locations. The air injection flow rate is fixed at Q_g = 1.25 × 10⁻³ m³/s. The bright areas in the images correspond to local high void fraction, as the light is scattered from individual bubbles. In the front region (Fig. 7a), the bubbles are distributed almost randomly, although some weak temporal fluctuations are already visible. In images from the downstream locations (Fig. 7b, c), void waves are clearly evident and are regarded as periodic passages of bubble swarms. The void wave has a lateral length scale of order 100 mm, much longer than the mean bubble size. The thickness of the void wave, as visualized on the temporal scale, expands gradually downstream as does the time interval between two successive waves. In the rear region, large void packets form due to further growth of the void wave (for instance, see t = 0.3 s in Fig. 7c). From watching the video, such packets are generated by the coalescence of two bubble swarms having different wave velocities. As a result, some waves change from being lateral to being irregular in shape in the region furthest downstream.

Fig. 7

Timeline images taken at different measurement locations with Q_g = 1.25 × 10⁻³ m³/s; a front, b middle and c rear locations, where bubbles appear as white areas as a result of self-reflections

According to our previous research (Park et al. 2016), a bubble swarm traveling in the turbulent boundary layer has an advection velocity of almost half the ship’s speed U_main and is maintained in whole the region. Therefore, the interval time expanding downstream indicates that the wavelength of the void wave also expands during propagation. Consequently, the void wave induced beneath the flat-bottom model ship grows continually in the downstream direction both in amplitude and wavelength.

To evaluate the periodicity of the void wave quantitatively, frequency spectra of the waves were calculated using the Walsh transform of the timeline images. Prior to the calculation, the images (Fig. 7) were binarized while subtracting the mean background image to normalize the spectral intensity; namely, liquid phase and gas phase in the binary images were expressed as 0 and 1, respectively. In comparison with the Fourier transform, the Walsh transform is suitable for frequency analysis of square wave such as binary waves (Broadbent and Maksik 1992). The spectra obtained from the void waves were averaged in the spanwise direction (Fig. 8). We then focused on the results at the lowest air injection flow rate of Q_g = 1.25 × 10⁻³ m³/s (see top panels in Fig. 8), the conditions of which are the same as given in Fig. 7. At the front region, the spectrum has almost constant intensity without significant peaks. This means that the bubbles there are distributed randomly as for white spectrum. At the middle and rear locations, several small peaks stand out as having intensities greater than the white spectrum level and are understood to correspond to the initiation of the void waves. The peaks are observed in the range 5 Hz < f_void < 30 Hz, and its central frequency decreases from 26 to 8 Hz as bubbles go downstream. This frequency shift is explained from the coalescence of thin void waves during advection downstream. As is evident, the void wave intensity is amplified at the rear location. Second, on increasing the air injection flow rate Q_g, the spectral intensity is amplified only in a limited frequency range.

Fig. 8

Linear spectra of the void wave taken at three different measurement locations and with different Q_g

Note that no significant peaks are detected in the front location even at the maximum air injection flow rate Q_g = 2.50 × 10⁻³ m³/s (we therefore did not conduct an experiment with the intermediate value of Q_g at the front location). In this analysis, the maximum detectable frequency is 60 Hz, because the frame rate was set at 120 fps. At frequencies higher than 60 Hz, the spectrum is expected to continue until the limit of the bubble–bubble spacing, which corresponds into between 300 and 500 Hz in terms of frequency as estimated from the image in Fig. 4. In contrast, the frequency of the void waves is found at f_void < 30 Hz and is distinguishable from that for the local bubble–bubble interaction by the one-order of magnitude difference in the frequency domain.

3.4 Void wave characteristics

To highlight the trend mentioned above, the peak frequencies of the void waves, f_void, at the middle and rear regions are extracted and plotted in Fig. 9a. The frequencies of the first three highest peaks and the same frequencies from the previous experiment (Park et al. 2016) are plotted for reference. A solid curve is added to the data obtained at all locations; it connects the data points of only the first peaks with a single fitted curve given by

$${f_{{\text{peak}}}}={f_0}{\left( {\frac{{{X_3}}}{{{X_2}}}} \right)^{{N_x}}}{\left( {\frac{{{Q_{\text{g}}}}}{{{Q_{{\text{g}},\hbox{min} }}}}} \right)^{{N_Q}}},$$

(4)

where X stands for the streamwise coordinate from the bubble injection point. Namely, X₂ and X₃ are the distances from the bubble injector at the middle and rear locations, respectively (X₂ = 2.3 m − 0.7 m = 1.6 m, X₃ = 3.5 m − 0.7 m = 2.8 m), Q_g,min is the lowest air injection flow rate, and f₀ is a referential frequency set to f₀ = 26 Hz and measured at X₂ under flow rate Q_g,min. By the least squares approach, the two exponents have values ${N_x}$ = − 1.9, and ${N_Q}$ = − 0.9 in the range tested. In terms of the spatial development with X, the peak frequency decreases from the middle to the rear regions by less than half. The magnitude of the exponent |N_x| = 1.9 is greater than that of the boundary layer thickness expansion that is approximately proportional to X^1/5 and is also greater than that of wall friction decay (proportional to X^−1/7) in the present range of $R{e_x}$ (see Table 1). Therefore, the generation of the void wave is not explained with such scales of a single-phase boundary layer, but should be understood as a feature of two-phase flow dynamics appearing with drag reduction.

Fig. 9

Peak frequencies of the void wave at two measurement locations for four different gas injection flow rates; a dimensional domain and non-dimensional domains normalized using b scales of the turbulent boundary layer and c a referential frequency, f_ref. The top three peak values are selected from the void wave spectra and fitted using Eq. (4) to give the solid curve

Another point we need to address is the value ${N_Q}$ = − 0.9 in Eq. (4) as an influencing factor of the air injection flow rate on the peak frequency. This negative value means that increasing the bubbles per unit wall area promotes a spatial transition of void waves to lower peak frequencies. Specifically, it is attributed to bubble coalescence due to the spaces filled up with many bubbles supplied on the wall. Because drag reduction is thus strongly promoted, it is inferred that the exponent ${N_Q}$ also influences drag reduction accompanied by void waves.

As shown in Fig. 9b, the measured void wave frequencies are re-plotted in a non-dimensional domain normalized by scales of the turbulent boundary layer mentioned in Eq. (2); the ordinate is non-dimensionalized by U_main/δ and abscissa is replaced with ${\alpha _\delta }$. Dimensionless frequencies of the first peak still scatter in the range from 0.09 to 0.31 and separate between the middle and the rear regions. We suppose that this indicates the dominance of bubble coalescence during streamwise development of void waves. Focusing only on the first peaks, we forcibly unify the measured void wave frequencies onto a single curve as shown in Fig. 9c. The curve is expressed as

$$\frac{{{f_{{\text{peak}}}}}}{{{f_{{\text{ref}}}}}}=\frac{{0.007}}{{{\alpha _\delta }}},\quad {f_{{\text{ref}}}}=\frac{{{U_{{\text{main}}}}}}{\delta }{\left( {\frac{X}{{{X_2}}}} \right)^{{M_x}}},$$

(5)

where f_ref is a referential frequency for re-normalizing the ordinate and X. Here, the exponent ${M_x}$ is obtained by the least square approach as ${M_x}$ = − 2.5. This value means that the void wave frequency sharply decreases quicker than the growth rate of the boundary layer thickness in a single-phase flow.

Finally, Fig. 10 presents the change in void wave intensity with increasing air injection flow rate. The intensity is defined as the integrated value that exceeds the white spectral level of a random bubble distribution. As the front region has no significant intensity, the void wave is amplified downstream in all cases. In contrast, the intensity measured is found to be a non-monotonic function of the air injection flow rate: at maximum Q_g, the intensity begins to decrease. This corresponds to the generation of void packets, mentioned previously, which rather breaks the periodic propagation of void waves. If Q_g increases further, then most of the wall is expected to be covered with bubbles to leave no vacant space for wave generation. Therefore, the intensity of the wave is inevitably attenuated with such a geometric constraint, and with too much supply of air the role of void waves in drag reduction is lost.

Fig. 10

Void wave intensity measured from the void wave spectra, where the intensity is calculated from the wave components, excluding the uniform random bubble distribution of the background

3.5 Discussion on initiation of the void wave

Based on the measured results, we discuss in this section which phenomenon initiatively triggers the peak frequency of void waves. We consider situations that oscillating flow structure embedded in the boundary layer in development modifies the initial bubble distributions, or interactions between injected bubbles and the boundary layer flow induce fluctuations. There are several types of possible flow instabilities that may form such periodic fluctuations in the bubbly flows downstream. One by one, we here estimate the theoretical frequency and try matching it with the present experimental data.

3.5.1 Tollmien–Schlichting (T–S) wave

The T–S wave is induced along a smooth flat plate in a Blasius-type boundary layer for a single-phase incompressible laminar flow (Schbauer and Scramstad 1947). We consider this because the present model ship has a flat smooth surface that keeps the laminar boundary layer in the front part before the bubble injection point. The standing-wave frequency obtained by linear stability analysis is given by

$$f=\frac{F}{\nu }{\left( {\frac{U}{{2\pi }}} \right)^2},$$

(6)

where U, ν and F denote the freestream velocity, the kinematic viscosity, and a dimensionless constant at which instability occurs. Here, F ranges from 0.1 × 10⁻⁴ to 0.8 × 10^− 4 at Re = 3000. In the present experimental conditions, the standing-wave frequency of the T–S wave is estimated to be in the range 2.3 Hz < f < 18.2 Hz. The central frequency at which the wave grows rapidly is around 12 Hz. Because the void wave also has a similar frequency range, the T–S wave is a candidate relevant in void wave generation. Although the dynamics associated with the T–S wave is totally different from bubble kinematics, it is inferred that a shear wave on the wall excited by the T–S wave may trigger the initial wavy bubble motion just after the bubble injection.

3.5.2 Kelvin–Helmholtz (K–H) wave

The K–H instability appears on an initially flat interface between two different co-flowing fluids with a difference in density or momentum (Helmholtz 1868; Kelvin 1871). For horizontal co-flows in a gravity environment, K–H waves occur if the following condition is satisfied,

$$k>g\frac{{{\rho _2}^{2} - {\rho _1}^{2}}}{{{\rho _1}{\rho _2}}}\frac{1}{{{{({U_2} - {U_1})}^2}}},$$

(7)

where k and g are wave number and acceleration of gravity, ρ and U represent the density and velocity of a fluid; suffixes 1 and 2 distinguish the two fluids. Since the present flow configuration consists of upper bubbly flow at a slow speed and lower water single-phase flow at a high speed, we consider the possibility of K–H instability. The following simplified relations are substituted into Eq. (7) to estimate the possible range of the K–H wave frequency,

$${\rho _1}=(1 - \alpha )\rho ,\quad {\rho _2}=\rho ,\quad {U_1}=c=\frac{1}{2}U,\quad {\text{and}}\quad {U_2}=U,$$

(8)

where c is an averaged streamwise velocity in the bubbly flow. Equation (7) is rewritten in dimensional form as a wave-passing frequency,

$$f>{f_{\hbox{min} }}=ck=2\frac{g}{U}\frac{{\alpha (2 - \alpha )}}{{(1 - \alpha )}},$$

(9)

where α and U denote the boundary layer void fraction and the free stream velocity outside the boundary layer. In the present experimental condition at α = 4% for example, f_min is estimated to be 0.06 Hz. Since there is no upper limit for the frequency of K–H waves, a wide range of frequencies may be produced over this frequency. Therefore, K–H waves remain as one of the candidates that initiate periodic fluctuation of bubble distribution.

3.5.3 Richardson wave

Dependent on the velocity gradient in a diffused density interface with a thickness of h, the wave frequency has an upper bound, over which the wave is not amplified. This is known as the Richardson wave and is regulated by the Richardson number:

$$Ri=\frac{g}{h}{\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{ - 2}}\sim \frac{g}{\delta }{\left( {\frac{U}{\delta }} \right)^{ - 2}}=\frac{{g\delta }}{{{U^2}}}=F{r^{ - 2}},\quad Fr=\frac{U}{{\sqrt {g\delta } }},$$

(10)

where h is a characteristic length that is replaced by δ for a bubbly two-phase boundary layer as a representative length scale. The Froude number Fr consequently regulates the wave. According to linear stability analysis, waves are produced around the density interface when

$$Ri<{\delta ^2}{k^2}(1 - {\delta ^2}{k^2}),\quad f=ck=\frac{{Uk}}{2},$$

(11)

where c, U, and k are the same as in Eq. (9). Waves arise only if 0 < δk < 1 (Drazin 1958) and therefore the possible frequencies under the present experimental conditions is estimated as

$$f=ck,\quad k<\frac{1}{\delta }\quad \to \quad {f_{\hbox{min} }}=0,\quad {f_{\hbox{max} }}=\frac{{cU}}{\delta }=\frac{U}{{2\delta }}.$$

(12)

Also, the upper limit frequency is estimated to be f_max = 150 Hz. Hence, the Richardson wave also corresponds with the measured peak frequencies.

3.5.4 Gravity wave

In a stationary fluid subject to vertical density stratification of dρ/dy, there is a natural frequency for the vertical motion of a fluid due to gravity given by

$$f=\frac{1}{{2\pi }}\sqrt {\left( {\frac{1}{\rho }\frac{{{\text{d}}\rho }}{{{\text{d}}y}}} \right)g} \sim \frac{1}{{2\pi }}\sqrt {\left( {\frac{1}{{{\rho _2}}}\frac{{{\rho _2} - {\rho _1}}}{\delta }} \right)g} =\frac{1}{{2\pi }}\sqrt {\frac{{\alpha g}}{\delta }} ,$$

(13)

where the density gradient is approximated using Eq. (8). Considering the present experimental conditions, the natural frequency has a range 0.5 Hz < f < 1.4 Hz for 1% < α < 10%. This range is lower than the measured peak frequencies. If the gravity wave propagates at a speed a on the interface in addition to the void advection velocity inside the boundary layer flow at U/2, the differential speed is estimated to be

$$c - a=\frac{1}{2}U - \sqrt {\left( {1 - \alpha } \right)g\delta } ,$$

(14)

where a, the second term on the right-hand side, corresponds to the propagation speed of the gravity wave. In the Lagrangian frame or at a fixed location X in the Eulerian frame, the differential speed induces during the time elapse T a Doppler shift in the frequency,

$$f=\frac{{c - a}}{{UT}}=\frac{{1 - 2\sqrt {1 - \alpha } /Fr}}{{2T}}=\frac{{1 - 2\sqrt {1 - \alpha } /Fr}}{{2X/U}},$$

(15)

where T and X are the values from the bubble injection point; Fr is the same as in Eq. (10). Under the present experimental conditions, Eq. (15) yields an estimate for the peak frequency of f = 0.4 Hz at the rear region (X₃ = 2.8 m). This value is still too low to be comparable with the measured peak frequencies, and hence this shallow wave theory can be denied as a source of void waves.

3.5.5 Renewal scale of boundary layer

As the friction coefficient of the wall is C_f, the kinetic energy of the flow inside the boundary layer is lost within a distance λ given by

$$\lambda =\frac{\delta }{{{C_{\text{f}}}}},\quad {C_{\text{f}}}=\frac{{{\tau _{\text{w}}}}}{{\rho {U^2}/2}}.$$

(16)

This length λ is interpreted as a streamwise renewal distance, over which an external force is required to maintain the boundary layer flow. The renewal distance is rewritten in frequency by

$$f=\frac{c}{\lambda }={C_{\text{f}}}\frac{c}{\delta }\sim {C_{\text{f}}}\frac{U}{{2\delta }},\quad \to \quad \frac{{f\delta }}{U}=\frac{1}{2}{C_{\text{f}}}.$$

(17)

In the present experiments, f is roughly estimated to be 0.006 × 3/(2 × 0.01) = 0.018/0.02 = 0.9 Hz, and is too low for waves to interact directly with the observed void waves. Local decrease of C_f in the bubbly region makes the frequency further lower. In dimensionless form, the renewal frequency takes fδ/U = 0.003, which is two-order lower than the measured values (Fig. 9b).

In the steady boundary layer, the growth rate of the boundary layer thickness, dδ/dx, is estimated by

$$\frac{{{\text{d}}\delta }}{{{\text{d}}x}}={\left( {\frac{{{u_\tau }}}{U}} \right)^2}=\frac{{{\tau _{\text{w}}}}}{{\rho {U^2}}}=\frac{1}{2}{C_{\text{f}}},$$

(18)

which formulation results to be the same as dimensionless frequency in Eq. (17). Therefore, eliminating C_f gives another description of the renewal frequency as

$$f=\frac{U}{\delta }\left( {\frac{{{\text{d}}\delta }}{{{\text{d}}x}}} \right)=\frac{4}{5}\frac{U}{x},$$

(19)

where Eq. (2) is used for representative δ to obtain the frequency as a function of the streamwise distance x from the front edge of the ship bottom plate. In the present experiment, the renewal frequency is estimated to be f = 3.4 Hz at the bubble injection point (x = 0.7 m, U = 3.0 m/s). Originally, Eqs. (17) and (19) tell us that all kinds of events at frequencies over f appear as unsteady states inside the boundary layer. The void waves which we observed are all above this renewal frequency and thus the phenomenon of void wave generation is regarded as a fully unsteady boundary layer structure that cannot be modeled by a steady boundary layer in an energy balance.

3.5.6 Other instabilities judged irrelevant to void waves

The Rayleigh–Taylor (R–T) instability occurs when two fluids lie horizontally with the heavier fluid on top of a lighter fluid. This situation may occur as the bubbly layer separates from the wall. However, such a condition is not observed in our experiment and can be eliminated as a candidate of wave sources. A Holmboe instability also occurs for two fluids with different viscosities co-flowing with shear. However, the present target is a flow at sufficiently high Re numbers unmodified by a small change in viscosity between the bubby and non-bubbly layers. Finally, the bubble–bubble interaction may induce local bubble clustering, and may nucleate void waves. However, as explained in the previous section using the spectral characteristics, the range of frequencies for individual bubble propagation is above 300 Hz. Furthermore, local bubble–bubble interactions induce such bubble clusters but only in mono-dispersive systems. Thus, the bubble–bubble interaction cannot be a direct activator of the void wave.

In summarizing the above scale estimations, the initiator of void wave still remains one of a multiple number of candidates and has not been uniquely determined. The T–S, K–H, and Richardson waves have wave-amplifying frequencies in the range that covers the range of measured peak frequencies. Therefore, these instabilities are not fully dismissive. In contrast, gravity, Holmboe, and R–T waves have frequencies much lower than our measured values and can be discarded as initiating void waves.

4 Conclusions

Spatially developing void waves are observed inside a bubbly two-phase turbulent boundary layer beneath a flat-bottom model ship being towed in a 100 m-long water tank. From the wall shear stress measurements at three locations downstream from the bubble injector, we found that such void waves promoted frictional drag reduction. A gain factor of 6 was obtained with void waves naturally standing out as bubbles migrated downstream. The value is much greater than that from the trivial inertia effect in drag reduction. From an analysis of local bubble images, we confirmed that the void waves take place clearly even though bubbles have a broad distribution in size. This means that void waves are not induced by a local bubble–bubble interaction (often seen in mono-dispersive systems as bubble clusters), but are generated with two-way interaction between the void and the internal turbulent boundary layer structure over a more dynamic scale. The wave amplitude increases monotonically with gas injection flow rate and streamwise distance from bubble injection point until the bubbles fully cover the wall.

A spectral analysis of the frequencies finds that the void wave has a peak frequency range of 5 Hz < f < 30 Hz. Within this range, f decreases with increasing air injection flow rate following a power-law behavior with exponent − 0.9 and also decreases with downstream distance with exponent − 1.9. Introduction of representative scales of the boundary layer to the normalization of the measured frequencies reveals the following remarks.

• 1. The void wave frequency scaled by U_main/δ ranges at 0.09 < fδ/U_main < 0.31. It is inversely proportional to the boundary layer void fraction ${\alpha _\delta }$, and decreases with streamwise distance to the power of − 2.5 [see Eq. (5)]. This explains that the void waves grow up due to coalescence of neighbor thin void waves during the downstream migration.

• 2. Renewal scale and growth rate of the boundary layer do not match the measured void wave frequencies, taking two-order lower frequencies. This proves that the void waves which we observed cannot be explained by an energy balance of quasi-steady turbulent boundary layer theories, but should be regarded as internal unsteadiness of the turbulent boundary layer.

• 3. The T–S, K–H, and Richardson waves cover the measured frequency range and therefore these kinds of instability remain as candidate factors to create initial periodic fluctuation of void distribution in the region just after the bubble injection.

As our future analysis, coalescence of bubbles during downstream migration of void waves should be analyzed more quantitatively since we obtained a high impact ${N_x}$ = − 1.9 to the downstream distance. Namely, poly-dispersed characteristics of the bubbly two-phase turbulent boundary layer enhances drag reduction via formation of void waves.