PIV-based load investigation in dynamic stall for different reduced frequencies

Abstract

Measuring the aerodynamic loads on dynamic objects in small wind tunnels is often challenging. In this regard, fast-response particle image velocimetry (PIV) data are post-processed using advanced tools to calculate aerodynamic loads based on the control-volume approach. For dynamic stall phenomena, due to the existence of dynamic stall vortices and significant load changes over a short time interval, applying the control-volume technique is difficult in particular for drag estimation. In this study, an examination of the dynamic stall phenomena of an oscillating SD7037 airfoil is reported for a reduced frequency range of $0.05\le k \le 0.12$ when $Re=4\times 10^{4}$. A numerical simulation is utilized as an alternative method for comparison and agrees well with the experimental results. The results suggest that loads can be determined accurately if the spatial resolution satisfies the reduced frequency increment. Minimizing the control-volume works best for lift determination. For the drag calculation, it was found that the location of the downstream boundary should be placed where it was not disturbed with wake vortices. The high-velocity gradients of the wake vortices increase the error level along the downstream boundary for the drag calculation but not for the lift estimation. Beside the load calculation, high-resolution PIV velocity fields also reveal insights into the effects of reduced frequency on dynamic flow behavior including the pitch angle range for vortex growth (between vortex generation and pinch-off), phase delay and number of vortices. These observations agree well with the load curve behavior.

1 Introduction

Analysis of each blade element of wind turbine rotors, maneuverable wings and helicopter rotors has shown that the angle of attack of an airfoil cross section can oscillate under some circumstances. An oscillating airfoil creates load variation which affects the controls of an operating system designed based on static loads. The airfoil can experience significantly increased or decreased loads when the angle of attack of the airfoil goes beyond the static stall angle often called dynamic stall (Cebec et al. 2005; Leishman 2006; McCroskey et al. 1976; Ko and McCroskey 1997; Martin et al. 1974; McCroskey 1981, 1982). The main features of dynamic stall are a delayed stall angle and dynamic stall vortices: a leading edge vortex (LEV) and a trailing edge vortex (TEV). Dynamic stall issues have been addressed in many recent studies utilizing numerical or experimental techniques, but all aspects of these phenomena have not been discovered yet because of many complex interactions of parameters.

In terms of experimental study, for small wind tunnel dynamic models, available conventional techniques for load calculation, pressure measurement and even visualization are quite limited and not readily applied. Conventional force measurement techniques for loads are not appropriate for small dynamic models. To measure dynamic pressure, pressure probes are intrusive and pointwise providing incomplete information. According to Rival et al. (2010), when the dynamic pressure is very low, integration of surface pressure from fast-response miniaturized pressure sensors cannot provide reliable information to determine the aerodynamic loads. Challenges regarding these methods indicate the importance of the particle image velocimetry (PIV) technique. The PIV technique is non-intrusive, gives instantaneous whole-field data, responds fast enough for high-frequency dynamic objects and is sensitive to a dynamic range of fluctuations. Advanced PIV post-processing techniques using the control-volume approach have been applied recently in PIV velocity fields to determine the loads on an object. Then a simultaneous evaluation of the calculated loads and flow field events is possible. The control-volume approach provides the opportunity to determine the loads on control-volume surfaces which are not close to the object; therefore, errors which are usually high close to the object surface do not affect the loads. Errors in PIV velocity determination and pressure-gradient integration inaccuracies result in error accumulation in the whole pressure field (van Oudheusden 2013). Thus, determining the pressure values in a limited area causes less pressure error accumulation. For load calculations in the control-volume approach, the pressure values need to be calculated only on the control-volume boundaries, and the pressure determination errors are decreased and have a reduced effect on load calculations which is one of the advantages of this technique. In 1997, Noca et al. (1997) calculated forces around a stationary circular cylinder by applying the control-volume approach while the pressure term was eliminated analytically. Unal et al. (1997) applied a momentum-based method for an oscillating circular cylinder with a fixed control volume. Because of the low accuracy of the processing algorithms at that time and the limitations of the experimental equipment, this method was not much used by other researchers. From 2006, Scarano and van Oudheusden with their colleagues at Delft University started using this technique to evaluate loads for a stationary airfoil (Casimiri 2006; Souverein et al. 2007; van Oudheusden et al. 2007, 2006a, b) and for a square cylinder (van Oudheusden et al. 2008). They also applied this approach to time-resolved PIV to evaluate unsteady aerodynamic forces on a static square cylinder (Kurtulus et al. 2007). Since 2011, they extended this technique to examine dynamic airfoils (Heerenbrink 2011; Ragni 2012; Ragni et al. 2012). Recently, David et al. (2009) and Rival et al. (2010) also calculated aerodynamic loads of dynamic airfoils based on this approach. Load calculation based on the control-volume approach of PIV velocity fields has been extensively validated for static objects. The dependency of the unsteady forces of dynamic airfoils on many parameters makes applying this technique to dynamic airfoils more complicated in particular when the airfoils experience dynamic stall as addressed here. One of the dominant motion parameters in dynamic stall phenomena is the frequency of oscillation. Increasing the oscillation frequency postpones both LEV formation and dynamic stall with increases in LEV strength and dynamic stall vortices dominating the wake and suction side of the airfoil (McCroskey et al. 1976; Carr et al. 1977; Kim and Park 1988; McAlister et al. 1978; Panda and Zaman 1994). These issues make applying the control-volume approach very challenging.

In this study, high-resolution PIV velocity fields were post-processed to determine the loads and the pressure field for the challenging case of deep dynamic stall. The effects of the reduced frequency on leading edge and rolling-up trailing edge vortices will also be discussed in detail. In this regard, the SD7037 airfoil at Reynolds number ($Re$) of $4\times 10^{4}$ was selected with $Re$ based on airfoil chord $c$ and mean freestream velocity $U_{\infty }$. Because there is no literature regarding the dynamic SD7037 airfoil, a numerical simulation is considered here as an alternative method of comparison.

2 Case studies and approaches

Sinusoidal pitch oscillation of the SD7037 airfoil is considered according to

$$\begin{aligned} \alpha = \alpha _{\rm{mean}} + \alpha _{\rm{amp}}\, \sin {(2\pi ft)}.\qquad \end{aligned}$$

(1)

The mean angle of attack, $\alpha _{\rm{mean}}$, and the pitch oscillation amplitude, $\alpha _{\rm{amp}}$, were fixed at $11^{\circ }$ for all cases. In some prior studies, the angle of attack has been modified to an effective angle of attack due to the pitch rate term ($c\dot{\alpha }/2U_{\infty }$ and variations). For the current study, the contribution of the calculated pitch rate term is negligible even for the $k = 0.12$ case. Thus, for this study, it is assumed that the effective angle of attack is equal to the pitch motion.

The oscillation frequency, $f$, is commonly presented as the reduced frequency ($k$):

$$\begin{aligned} k = \frac{\pi {fc}}{U_\infty }. \end{aligned}$$

(2)

Three reduced frequencies of $k = 0.05, 0.08$ and $0.12$ were considered in this study. The sinusoidal oscillation about the $\frac{1}{4}$ chord location provides an increasing angle of attack for half the cycle, the pitch up motion ($\uparrow$), and an angle of attack reduction for the second half, the pitch down motion ($\downarrow$).

The experimental part of the current study employed particle image velocimetry (PIV), while a computational fluid dynamics (CFD) simulation was performed for the same flow field with the transition SST method.

2.1 Experimental setup: wind tunnel, airfoil motion and PIV setup

Experiments were performed in a low-speed closed circuit wind tunnel located in the Turbulent Flow Lab of the University of Waterloo. The Reynolds number ($Re$) was fixed at $4\times 10^{4}$ with a freestream of 25.5 m/s with an uncertainty of $0.14$ m/s (Gharali 2013). The upstream turbulent intensity was measured to be $0.8\,\%$. The maximum blockage ratio was $6.4\,\%$. The two dimensionality assumption of the wind tunnel was examined by the oil film visualization technique showing that for more than $80\,\%$ of the spanwise length of the airfoil, slightly away from the wind tunnel walls, a two-dimensional flow field was indicated (Orlando 2011). Thus, in the mid-span of the airfoil where data were taken two-dimensional flow was assumed.

The airfoil with a constant chord length c ($26\,\hbox {mm}$) was attached from one end in the test section. The airfoil motion was actuated using a servo motor with 8,000 counts or 22 positions within a single degree of shaft rotation. Galil software was applied to produce the sinusoidal motion. A single axis PID controller and drive (Galil Motion Controls CDS-3310) was used to interface with the servo motor and trigger the PIV image acquisition. The triggering digital signals were sent to the PIV processor in the actual position of the shaft based on user specified angles in each oscillation cycle.

Figure 1 illustrates the current PIV setup. A dual cavity Nd:YAG laser operating at a wavelength of 532 nm was used to illuminate the flow field. A beam splitter separated the laser light into equal beams in order to illuminate the top and bottom surfaces of the airfoil equally. Light sheets from the top and the bottom overlapped in the mid-span of the test section. A Dantec Dynamics FlowSense EO 4M camera with a sensor resolution of $2{,}048 \times 2{,}048\hbox { pix}^{2}$ and a 60 mm f /2.8 Nikkor lens captured the images. The full resolution images were taken with fields of view of $\frac{x}{c}=\frac{y}{c}\approx 1.4$ and $\frac{x}{c}=\frac{y}{c}\approx 3$ while the time interval between frames was set between $4$ and $10\,\,\mu \hbox {s}$. The 80N77 Timer Box synchronized the laser and camera when triggered from the motor controller. For the highest frequency of oscillation, the maximum error of triggering is around $0.2^{\circ }$. For each phase, 500 image pairs were acquired in several sequential experimental runs. It should be noted that since the airfoil is small, one camera was sufficient to capture the whole field of view, and there was no need for additional cameras or lasers. Thus, the errors associated with multiple cameras and lasers are removed. Because of the small field of view, the spatial resolution is high.

Fig. 1

Details of the PIV setup

The PIV images were processed with the PIV adaptive method of the Dantec Dynamic Studio software. Each resultant velocity vector was validated by the universal outlier detection local neighborhood with size $3 \times 3$. Considering a well-designed PIV experiment according to Raffel et al. (2007) and van Oudheusden (2013), the PIV velocity error has been determined to be about $0.32\hbox { m/s}$ for the current setup.

2.2 Numerical setup

While not the focus of this particular study, a computational fluid dynamic (CFD) simulation was completed to aid in the understanding of some of the flow phenomena. The CFD flow solver package ANSYS Fluent version 13 (ANSYS Fluent, Academic Research, V13 2010) was employed to model a two-dimensional flow over an oscillating SD 7037 airfoil. ICEM CFD (ANSYS Fluent, Academic Research, V13 2010) was used to generate a C-type mesh around the airfoil, as shown in Fig. 2, while the computational domain boundaries were located about $20 c$ away from the airfoil surface. A grid independence study was performed, concluding that a mesh resolution of $2\times 10^{5}$ cells with 500 nodes around the airfoil was suitable. The whole computational domain was oscillated around the one quarter chord of the airfoil via a user-defined function to represent a pitch oscillating airfoil. The transition SST model was applied as the turbulence model (Menter et al. 2004, 2006). In order to render the simulation results temporally independent the time step size for the transient simulation was chosen in accordance with the characteristic time of the airfoil, $dt=\tau (c/U_\infty )$, where ($\tau$) is on the order of $10^{-2}$. All simulations were run over 16 CPUs in parallel using the Shared Hierarchical Academic Research Computing Network (SHARCNET) and Compute/Calcul Canada facilities. More details regarding the numerical setup can be found in Gharali and Johnson (2013), Gharali and Johnson (2014).

Fig. 2

C-type mesh

3 Governing equations of PIV-based load determination

3.1 Integral force calculation

Based on linear momentum, the aerodynamic loads on an object, surrounded by a control volume of unit depth fixed in space and bounded by a control surface, as shown in Fig. 3, are determined indirectly by integrating flow variables inside the control volume:

$$\begin{aligned} \varvec{F} = - \int \int \int _V \frac{d}{dt}(\rho \varvec{U})dV - \int \int _s \rho \varvec{U} (\varvec{U} \cdot \hat{n})dS - \int \int _s P \hat{n} dS + \int \int _s (\bar{\bar{\tau }} \cdot \hat{n}) dS \qquad \end{aligned}$$

(3)

where $\hat{n}$ is the unit vector, $\varvec{U}$ the velocity vector, $P$ the pressure and $\bar{\bar{\tau }}$ the viscous stress tensor. In the pitch oscillating case, loads are calculated from the phase-averaged velocity field.

Fig. 3

Sketch of the 2D control-volume and control-surface definitions for determining integral aerodynamic forces; right control-volume boundaries for a pitching airfoil during post-stall superimposed with the vorticity field

To investigate the effects of the unsteady term, two consecutive velocity fields from the numerical simulation separated by a short time step were used as time-resolved PIV data since the numerical simulation includes the unsteady term. Using linear interpolation, the velocity fields from the simulation were transferred to PIV velocity maps. Each pair of the transferred velocity maps were then post-processed using Eq. 3 for calculating the loads with and without the unsteady term. The results showed that for the selected range of the reduced frequency of this study, the load differences with and without the unsteady term were negligible; thus, for the rest of this study, the unsteady term has been eliminated.

Assumptions of a 2D domain transfers the integration of the control surface to a line or contour integration. Choosing a counterclockwise direction for the line integration, substituting the averaged values and ignoring the overbars give the total force:

$$\begin{aligned} \begin{aligned} \varvec{F} =\left[ \begin{array}{c} d \\ l \end{array} \right]&= \rho \oint \left[ \begin{array}{cc} -uu\,dy\,+\,uv\,dx \\ -uv\,dy\,+vv\,dx \end{array} \right] - \oint \left[ \begin{array}{cc} P\,dy \\ -P\,dx \end{array} \right] \\& \quad + \mu \oint \left[ \begin{array}{cc} 2{\frac{\partial {u}}{\partial {x}}}\,dy\, -\, \left( \frac{\partial {u}}{\partial {y}} + \frac{\partial {v}}{\partial {x}}\right) \,dx \\ \left( \frac{\partial {u}}{\partial {y}} + \frac{\partial {v}}{\partial {x}}\right) \,dy - \, 2{\frac{\partial {v}}{\partial {y}}}\,dx \end{array} \right] \\& \quad +\rho \oint \left[ \begin{array}{ccc} -\overline{u'u'}\, dy \,+\, \overline{u'v'}\, dx \\ -\overline{u'v'}\, dy \,+ \,\overline{v'v'}\, dx \end{array} \right] \end{aligned} \end{aligned}$$

(4)

where the flow is considered as incompressible flow and $\varvec{F} = \left[ \begin{array}{c} d \\ l \end{array} \right]$ represents the drag ($d$) and lift ($l$) forces. The aerodynamic loads based on unit span can be normalized to

$$\begin{aligned}{}[c_l, c_d]= \frac{[l,d]}{\frac{1}{2}\rho {U_\infty }^2 c}. \end{aligned}$$

(5)

3.2 Pressure determination

Integrating the phase-averaged Navier–Stokes equations determines the mean pressure. By assuming 2D incompressible flow, the planar pressure-gradient components are

$$\begin{aligned} \begin{aligned} \frac{\partial {P}}{\partial {x}}=-\rho \left( u\frac{\partial {u}}{\partial {x}} +v\frac{\partial {u}}{\partial {y}} +\frac{\partial {{\overline{{u'}{u'}}}}}{\partial {x}} +\frac{\partial {{\overline{{u'}{v'}}}}}{\partial {y}}\right) +\mu \left( \frac{\partial ^2{u}}{\partial {x^{2}}} +\frac{\partial ^2{u}}{\partial {y^{2}}}\right) \\ \frac{\partial {P}}{\partial {y}}=-\rho \left( u\frac{\partial {v}}{\partial {x}} +v\frac{\partial {v}}{\partial {y}} +\frac{\partial {{\overline{{u'}{v'}}}}}{\partial {x}} +\frac{\partial {{\overline{{v'}{v'}}}}}{\partial {y}}\right) +\mu \left( \frac{\partial ^2{v}}{\partial {x^{2}}} +\frac{\partial ^2{v}}{\partial {y^{2}}}\right) . \end{aligned} \end{aligned}$$

(6)

To integrate gradient information, a 2D surface is generated and then central difference is used on the whole body except along the surface boundaries where forward/backward difference is applied. To avoid error propagation associated with integration methods for calculating aerodynamic loads, pressure was calculated through the extended version of the Bernoulli relation corrected for the perturbations (de Kat 2012) for the upstream and the lower sides of the control surface. The Navier–Stokes equations are integrated numerically by a forward-differencing method in the x-axis direction for the suction side of the control surface. Finally, in the wake the downstream side is integrated by a second order central-differencing (standard five-point) scheme while the first and last nodes were known.

Here, the pressure coefficient is calculated based on

$$\begin{aligned} C_{P}=\frac{P-P_{\infty }}{\frac{1}{2}\,\rho \,U_{\infty }^{2}}, \end{aligned}$$

(7)

where $P_{\infty }$ is the freestream static pressure. The pressure precision error (the sensitivity to noise) from the velocity field can be estimated as van Oudheusden (2013), de Kat (2012)

$$\begin{aligned} \varepsilon _{P}\propto \varepsilon _{u}\sqrt{|\nabla u|^{2}h^{2}+\frac{|u|^{2}}{2}}, \end{aligned}$$

(8)

where $\varepsilon _{u}, h$ and $|\nabla u|$ represent velocity uncertainty, grid spacing ($\Delta x = \Delta y =h$) and magnitude of the streamwise velocity gradient, respectively.

As an example, for a case of $k=0.08$, the statistical uncertainty for velocity was calculated as $\varepsilon _{u}/U_{\infty }=0.52\,\%$ which results in pressure coefficient error of $\varepsilon _{Cp}=0.8\,\%$.

4 Results and discussion

4.1 PIV-based load determination

4.1.1 Number of sample effects

For visualization purposes, the effects of the number of samples on the resultant vorticity field are presented in Fig. 4 for the dynamic case of $k=0.08$ at $\alpha =20^{\circ }\uparrow$ with highly separated flow after dynamic stall. Although increasing the number of samples or image pairs ($N$) decreases the statistical errors, the visualized vortical structure demonstrates no significant difference by increasing the number of image pairs by twenty times and the details of the vortical structure are captured well indicating a stable, repeatable structure.

Fig. 4

Effects of the number of image pairs on visualization; vorticity field of $k=0.08$ and $\alpha =20^{\circ }\uparrow$

On the contrary, the calculated loads in Table 1 indicate the load sensitivity when the number of images is changing from 250 to 500. The effects of the number of image pairs on load calculation is more significant for dynamic cases with dominant vortices. For $N > 500$, there is no significant change in the estimated loads. It can be concluded that for visualization purposes, very low $N$ values (50 images with high-quality raw images) give satisfactory results and all the main flow structures are captured but for load calculation purposes, after 500 samples load estimates are insensitive to image number.

Table 1 Load determination sensitivity to the number of samples

4.1.2 Control-volume surface location effects

Examination of all cases shows that the loads are not very sensitive to the locations of the upstream and the lower boundary surfaces, as shown in Fig. 3. Changing the location of the top surface results in uncertainty of $\triangle C_{l}=\pm 0.05$ and $\triangle C_{d}=\pm 0.02$ for the lift and drag values, respectively. It also should be noted that the top surface should not be very close to the airfoil because the level of image noise in that area is high due to minor surface light reflection. Changing the location of the downstream surface gives $\triangle C_{l}=\pm 0.03$ uncertainty for lift values. The maximum uncertainty was observed for high angles of attack during dynamic stall regardless of the reduced frequency value.

Fig. 5

Downstream control-volume boundary locations; vorticity field of $k=0.08$ and $\alpha =20.5^{\circ }\uparrow$

Determining drag values is very challenging, and some correction methods for drag determination were introduced by van Oudheusden et al. (2006a, b), Heerenbrink (2011), Ragni (2012), van Oudheusden et al. (2007). For the dynamic case, the drag determination will be even more challenging since stronger vortices with high-velocity variation introduce significant uncertainties in the pressure field. In this study, when the effects of the control-volume surfaces were investigated and at the same time the corresponding vortical structure was examined, the trends of the results showed a significant uncertainty for the calculated drag value when a vortex center was close to the downstream control-volume surface. Figure 5 is used as an example for the case where the wake is dominated by vortices at $\alpha =20.5^{\circ }\uparrow$ for $k=0.08$. Three different locations (I, II and III) are marked in the near wake. According to the numerical simulation, $C_{d}$ for this angle is predicted as $0.48$ while the calculated PIV drag coefficients are 0.45, 1 and 1.2 when the downstream boundary is located at locations I, II and III, respectively, but the lift values do not differ. That means, closer to the center of the vortex, higher uncertainty in the drag value is expected. Hence, there is a strong dependency of the drag value to the boundary location when the vortices are present.

Fig. 6

Trailing edge vortex sheet for $k=0.05$ at $\alpha =9^{\circ } \uparrow$

All loads presented here are the averaged values from shifting the top and downstream boundaries from close to the airfoil to $\frac{c}{2}$ away from it. For the drag values, the downstream boundary is fixed where the wake is less disrupted with the vortical structures. In some cases, the whole wake inside the field of view is covered with vortices and finding a good location for the downstream boundary is impossible; then, a larger field of view would be helpful, but the effects of spatial resolution should be considered.

4.1.3 Spatial resolution effects

The spatial resolution is defined as the number of pixels over the chord length, $c$. Considering the same interrogation area and the full resolution of camera, the fields of view $\frac{x}{c}=\frac{y}{c}\approx 1.4$ and $\frac{x}{c}=\frac{y}{c}\approx 3$ result in a maximum spatial resolution of $1{,}500\hbox { pix}/c$ and a minimum spatial resolution of $700\hbox { pix}/c$, respectively.

In Table 2, for $k=0.05$ at $\alpha =9^{\circ } \uparrow$, the calculated PIV lift value is almost the same for resolutions greater than $1{,}200\hbox { pix}/c$ and agrees with the numerical lift determination within an acceptable accuracy. For the lift calculation, a higher reduced frequency requires more spatial resolution. For example, for $\alpha =9^{\circ }\uparrow$, the lift coefficient differences between the high spatial resolution PIV and the numerical approaches are $0.04, 0.07$ and $0.13$ for $k=0.05, 0.08$ and $0.12$, respectively. At high angles, because of the highly separated flow, the PIV load values from the spatial resolution of $1{,}500\hbox { pix}/c$ are closer to the numerical ones than those from the lower spatial resolution of $1{,}200\hbox { pix}/c$. Therefore, for lift calculation purposes, the minimum possible field of view will be chosen to have the maximum spatial resolution and as $k$ increases higher spatial resolution provides more accurate results.

Table 2 Load determination sensitivity to the spatial resolution

For $\alpha =9^{\circ } \uparrow$ ($k=0.05$) in Table 2, opposite to the lift value, the drag value is closer to the numerical determination when the field of view is large; i.e., the spatial resolution of $700\hbox { pix}/c$. Since this small angle of attack is located in the linear part of the load curves, as shown in Fig. 6, the near wake is occupied with a trailing edge vortex sheet (as described in Gharali and Johnson 2013). Since the vortices introduce error in the PIV drag calculation, for a large field of view, the downstream control volume can be far from the airfoil trailing edge where the effects of the vortex sheet can be ignored. At $\alpha =17^{\circ }\uparrow$ ($k=0.05$), the vortex sheet is replaced with a rolling vortex (as an example of replacing the vortex sheet by a rolling one see Fig. 8, at $\alpha =19^{\circ }\uparrow$ for $k=0.08$, when the vortex sheet at the trailing edge is visible and then the vortex sheet is replaced with a rolling-up vortex after $\alpha =20^{\circ }\uparrow$ which is after dynamic stall). At this angle, since the entire near wake is not covered with vortices, the small field of view with high spatial resolution of $1{,}500\hbox { pix}/c$ provides a reliable value for the drag. Similar to the lift calculation, the effects of the spatial resolution on drag calculation will be more important by increasing $k$. In Table 2, for $\alpha =5^{\circ }\uparrow$ ($k=0.08$), although the near wake is occupied with a trailing edge vortex sheet the large field of view does not give the correct drag value since the reduced frequency is increased compared to the previous case ($\alpha =9^{\circ }\uparrow$ and $k=0.05$). Because the load calculation of $k=0.08$ and $0.12$ requires more spatial resolution than the current one, if the spatial resolution of the large field of view was increased (e.g., by using a higher spatial resolution camera), drag values at low angles of attack would provide accurate values. For high angles of attack at $k=0.08$ and $0.12$ when the vortex sheet is replaced by a trailing edge vortex, the small fields of view (the spatial resolution of $1{,}500\hbox { pix}/c$) provide reliable drag values but they differ more from the numerical ones as k increases; see Table 2 at $\alpha =21^{\circ }$ ($k=0.12$). Thus for the drag calculation, if the wake is not covered by the vortices, the small field of view (high spatial resolution of $1{,}500\hbox { pix}/c$) similar to the lift calculation can provide reliable results. On the contrary, when the near wake is covered with vortices, increasing the field of view while the spatial resolution is decreased increases the possibility of finding a proper location for the downstream boundary which is not covered with vortices, but the low spatial resolution (such as $700\hbox { pix}/c$) will be problematic if $k$ increases ($k>0.05$).

Fig. 7

Comparison of the determined PIV and numerical lift cycles for $k=0.08$; solid line pitch up motion; broken line pitch down motion

4.1.4 Dynamic lift

Figure 7 shows a comparison between the numerical and experimental lift cycles for $k=0.08$. The linear part of the lift cycle during pitch up motion, $\alpha \, \le \, 16^{\circ }\uparrow$, from both methods almost overlap with the same overall trend. The numerical simulation underpredicts the measured lift values for the dynamic stall angle or peak lift value ($\alpha = 18.5^{\circ }\uparrow$). Both methods predict two load peaks during pitch up motion. Although there is good overall agreement between the numerical and experimental load cycles especially during pitch up motion, analyzing the details of the vortical structure can be used as another indicator to determine whether the calculated loads correspond with the nature of the vortical structures.

Fig. 8

Experimental and numerical vortical structures for a pitch cycle of $k=0.08$ ($\uparrow$: pitch up motion and $\downarrow$: pitch down motion)

The stages of the dynamic stall process from both experimental PIV and numerical methods are plotted in Fig. 8. Experimental static pressure coefficient ($C_p$) contours are also plotted in Fig. 9. During upward pitch motion ($\uparrow$), the flow is mainly attached except for a small separated flow at the trailing edge. A further increase in the angle of incidence results in LEV formation which is shown at $\alpha = 16^{\circ }\uparrow$ in Fig. 8 and then at $\alpha = 17^{\circ }\uparrow$ in Fig. 9 where the clockwise LEV with low-pressure values covers half of the suction side. Hence, the LEV causes a large pressure difference between the pressure and suction sides, resulting in high lift. The lift coefficient reaches the absolute maximum at the dynamic stall point. The stall angle is $\alpha = 18.5^{\circ }\uparrow$ according to measured PIV data and $\alpha = 18.8^{\circ }\uparrow$ by numerical prediction. The numerical approach postpones the dynamic stall about $0.3^{\circ }$. Consequently, some of the subsequent aerodynamic events are postponed. Figure 8 illustrates that at the dynamic stall point, the LEV covers the entire suction side resulting in very low-pressure values.

Fig. 9

Experimental and numerical pressure coefficients for $k=0.08$

After the airfoil stalls, a counterclockwise rotating vortex from the pressure surface gradually rolls up at the trailing edge when a rapid drop in lift is observed. At the end of full stall, this TEV reaches its maximum size and is shed into the wake. Emergence of a second LEV is evident at $\alpha = 20.5^{\circ }\uparrow$ from the PIV measurements and $\alpha = 20.7^{\circ }\uparrow$ from the numerical method, as shown in Fig. 8. The growth of the second LEV enhances the lift performance during pitch up motion though its strength subsides in comparison with the first LEV, as shown in Fig. 7, as is evidenced by the higher pressures, as shown in Fig. 9. At $\alpha = 22^{\circ }$ from the measurements and $\alpha = 21.8^{\circ }\uparrow$ from the numerical method, the second LEV reaches the end of the airfoil, corresponding with a second lift peak during the pitch up motion while slightly before it the first trailing edge vortex is shed. Although there may be other effects involved in the lift curve behavior, the results show that the formation and growth of the LEV and TEV correspond with the lift curve events.

Fig. 10

Comparison of the determined PIV and numerical drag cycles for $k=0.05$; solid line pitch up motion; broken line pitch down motion

As for the downward pitch motion, at $\alpha = 20.5^{\circ }\downarrow$ from the numerical simulation, the new LEV covers the entire suction side. The LEVs during the pitch down motion are not as strong as the pitch up motion and in turn do not significantly alter the aerodynamic loads. At $\alpha = 5^{\circ }\downarrow$, there is no sign of vortex formation, and the flow remains attached until the end of the cycle. It can be concluded that trends in the load cycle coincide with the vortical structures of the flow.

4.1.5 Dynamic drag

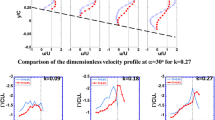
Figure 10 shows a comparison between the PIV drag cycle and the numerical drag results ($k=0.05$). To determine the drag values from the PIV velocity fields, the large field of view ($700\hbox { pix}/c$) was used for $0^{\circ }\le \alpha \le 11^{\circ }$ during pitch up motion and $0^{\circ }\le \alpha \le 5^{\circ }$ during pitch down motion and for the rest, the small field of view ($1{,}500\hbox { pix}/c$) was selected. There is good agreement between the numerical and experimental methods.

Fig. 11

Effects of the reduced frequency on determined lift coefficients from the PIV velocity fields; arrows show lift peaks during pitch up motion

4.2 Lift cycles for different $k$

Experimental lift coefficients for different reduced frequency values for complete oscillation cycles are shown in Fig. 11. Increasing the reduced frequency delays dynamic stall resulting in an augmented lift value. For $k=0.12$, the only peak in lift during pitch up motion is observed close to the end of the pitch up cycle. Decreasing $k$ to 0.08 results in two lift peaks in pitch up motion while the maximum lift magnitude is decreased compared to that of higher $k$. A similar result was observed by McCroskey et al. (1976) for a NACA0012 airfoil as $k$ varied considerably. Further $k$ reduction results in three lift peaks with much lower lift values.

Fig. 12

Circulation of dynamic stall vortices; left PIV results for k = 0.05, 0.08 and 0.12; right PIV and numerical results for k = 0.12; arrows show the dynamic stall angles; for k = 0.12, the PIV data for angles between $22^{\circ }$ and $21.8^{\circ }\downarrow$ are not available

For $k=0.12$, the first lift peak during pitch down motion is noticeable; for $k=0.08$, the magnitude of the first pitch down lift peak is decreased and for $k=0.05$ the peak has almost vanished. Based on the vortical structure discussed above, each lift peak indicates a developing LEV which meets the trailing edge of the airfoil. Since for the selected range of $k$ in this study, decreasing the reduced frequency advances dynamic stall, the boundary layer feeds low strength dynamic stall vortices (see Sect. 4.3.1); then, the results show that the PIV lift calculation method can capture the lift peaks associated with even weak vortices.

4.3 Vortex circulation

The circulation, $\varGamma$, of a targeted vortex inside the rectangular area A can be calculated according to Stoke’s theorem as

$$\begin{aligned} \varGamma = \int \int _{A}\omega _{z} dA, \qquad \end{aligned}$$

(9)

where $\omega _{z}$ is the vortex vorticity and it is made dimensionless with $U_{\infty } c$. In Fig. 12, the LEVs and TEVs have positive and negative values depending on the direction of the vortex rotation with zero threshold; for more details on the method, see Gharali and Johnson (2014), Prangemeier et al. (2010).

Comparison between Figs. 11 and 12 reveals the contribution of the LEV to the lift trend. A higher reduced frequency increases the circulation of the LEV resulting in lift augmentation. After stall, the TEV rolls up and increases in size and strength. Significant lift reduction during post-stall indicates the negative effects of the TEV. Therefore, there should be a strong correlation between the strength of the LEV and the corresponding TEV in terms of the magnitude of the circulation as is obvious in Fig. 12 which is in agreement with the results of Prangemeier et al. (2010) (for PIV data of $k =0.12$, see the next paragraph). When the TEV reaches its maximum circulation, it separates from the boundary layer and at this angle the lift value starts to increase due to the formation of the next LEV. The higher lift peak at dynamic stall results in a lower lift value at the end of the lift reduction process (Fig. 11). That means, higher TEV circulation values result in more lift drop during post-stall (Fig. 12).

For $k=0.12$, the lift drop occurs in a very short time between angles $22^{\circ }$ and $21.8^{\circ }\downarrow$ where the TEV reaches the maximum circulation. Because of the higher frequency of oscillation for this particular case, it was impossible to acquire experimental data between angles $22^{\circ }$ and $21.8^{\circ }\downarrow$. Thus, in Fig. 12, the experimental circulation values of the TEV are not available between angles $22^{\circ }$ and $21.8^{\circ }\downarrow$. To fill out this gap, the numerical circulation values of $k=0.12$ are provided in this figure. As discussed above, the numerical results slightly underpredict the lift values during stall and the corresponding vortex circulation from the numerical simulation is also lower for the LEV. The discrepancies between numerical and experimental results for vortex circulation are much higher than those of lift calculation. It should be mentioned that the LEV circulation differs from the overall circulation around the airfoil; as mentioned before, other parameters may affect the lift peak value besides the vortex circulation therefore the contribution of vortex circulation to the lift calculation may be decreased. The dynamic stall angle difference between the two methods is about $0.5^{\circ }$ which is visible as a $0.5^{\circ }$ shift between the curves of the two methods in Fig. 12-right.

4.3.1 Pinch-off and phase delay ($\Delta \alpha$)

While the LEV is fed by the boundary layer, the strength of the vortex increases. Finally, the vortex circulation reaches the maximum value and pinches off from the boundary layer. The phase difference between the dynamic stall angle and the angle corresponding to the maximum circulation of the dynamic stall LEV is the phase delay ($\Delta \alpha$). For two parallel SD7003 airfoils with pure-plunge motion ($Re=3\times 10^{4}$ and $k=0.25$), Rival et al. (2010) mentioned that for their case the TEV formed after the maximum LEV circulation with negligible phase delay. For an oscillating NACA0012 airfoil ($0\le k \le 1.6$ and Reynolds number of $2.2\times 10^{4}$ and $4.4\times 10^{4}$), Panda and Zaman (1994) showed that after vortex pinch-off, the lift drops. Gharali and Johnson reported a significant phase delay for a pitch oscillating NACA0012 and also an oscillating freestream at $\hbox {Re}\approx 10^{5}$ ($k=0.1$) (Gharali and Johnson 2013) but negligible phase delay for the pitch oscillating S809 airfoil and oscillating freestream at $Re \approx 10^{6}$ ($k=0.077$) (Gharali and Johnson 2014) using numerical simulation.

Here, with the aid of high-resolution velocity gradients from the PIV velocity field, it is possible to see a significant phase delay ($\Delta \alpha$) and the rolled-up TEV formation occurring right after the maximum lift value (dynamic stall angle). Based on the current results, as shown in Fig. 12, the LEV does not always separate immediately after stall and the delay depends on the reduced frequency. For $k=0.12, 0.08$ and $0.05, \Delta \alpha$ values of $1^{\circ }, 0.5^{\circ }$ and $0^{\circ }$ are seen, respectively, which all agree with those of the numerical results. For the first LEV, the pitch angle range for vortex growth, between vortex generation and pinch-off, shows an increase as $k$ increases. That means, as the pitch angle range for vortex growth increases, the boundary layer continues to feed the vortex resulting in higher circulation values and then a higher lift peak. In contrast, as the pitch angle range for vortex growth decreases, more LEVs are observed during pitch up motion, two LEVs for $k=0.08$ and three LEVs for $k=0.05$, as shown in Fig. 11, which agree with the numerical results as well (not shown here).

5 Conclusions

There was reasonable agreement between the numerical loads and PIV loads and the determined PIV lift loops correspond with the all vortical characteristics. It was found in this study that for a qualified PIV load determination strategy, the following points should be considered:

• Increasing the number of images above 500 does not provide more accurate loads and for visualization purposes a much lower number of images are sufficient.

• The PIV load determination accuracy improves as the spatial resolution increases especially when either the reduced frequency or the angle of attack increases.

• The PIV drag errors are mostly attributed to the high-velocity gradient from the vortical structure of the wake. In this regard, finding a location for the downstream control-volume boundary which is not disturbed with vortices is essential, but the lift coefficient is not very sensitive to the vortical structure. Thus, for calculating the drag when the angle of attack is low, a large field of view is needed since the vortex sheet covers the near wake.

• To decrease the small discrepancy coming from the varying location of the top and downstream control-volume boundaries, the resultant calculated lift was averaged for the specific domains but for calculating drag, the downstream boundary is fixed.

A low reduced frequency advances the dynamic stall and increases the number of LEVs during pitch up motion. For $k=0.05$, three LEVs form during pitch up motion, for $k=0.08$, the number of the LEVs reduces to two and finally for $k=0.12$, just one LEV is fully developed during the pitch up motion while the lift augmentation because of this one vortex is significantly higher than the others. With the aid of the calculated whole velocity field from the PIV method, calculating the vortex circulation was possible. As the reduced frequency increases, the magnitude of the vortex (both LEV and TEV) circulation increases which corresponds with the lift behavior. Higher reduced frequencies increase the phase delay showing that even with a significant lift drop after stall, the boundary layer still feeds the LEV. The PIV-based load calculation could readily predict the lift increments from the LEVs even with low circulations. The numerical simulations underpredict the circulation values of the dynamic stall vortices similar to the dynamic stall lift. It is suggested that for the numerical methods, besides load comparison with the experimental ones, as another indicator, the circulation from the vortices should be compared.