Schlieren-based techniques for investigating instability development and transition in a hypersonic boundary layer

Abstract

Three variants of schlieren techniques are employed to investigate the development of second-mode instability waves in the hypersonic boundary layer of a slender cone in a reflected shock tunnel. First, a previously proposed technique using high frame rate (i.e., at least as high as the dominant instability frequency) schlieren visualization with a continuous light source is shown to provide repeatable measurements of the instability propagation speed and frequency. A modified version of the technique is then introduced whereby a pulsed light source allows the use of a higher-resolution camera with a lower frame rate: this provides significant benefits in terms of spatial resolution and total recording time. A detailed picture of the surface-normal intensity distribution for individual wave packets is obtained, and the images provide comprehensive insight into the unsteady flow structures within the boundary layer. Finally, two-point schlieren deflectometry is implemented and shown to be capable of providing second-mode growth information in the challenging shock tunnel environment.

1 Introduction

Transition to turbulence of the boundary layers on a hypersonic vehicle can greatly increase the surface heating rates, as well as lead to elevated levels of frictional drag. Understanding and prediction of the boundary layer transition process is thus a critical problem in hypersonic flight. To simulate true hypervelocity conditions and the accompanying high-temperature effects (which may influence the growth of instabilities leading to transition—see, for example, Johnson et al. 1998 and Fujii and Hornung 2003), the use of impulse facilities such as reflected shock wind tunnels and expansion tubes is necessary. Because of the short test times and harsh flow environments typical of these facilities (as well as other factors that will be discussed shortly), however, the difficulty of making instability measurements is greatly increased compared to cold hypersonic tunnels, i.e., facilities that simulate flight Mach numbers but not velocities.

For hypersonic flows over slender two-dimensional or axisymmetric geometries, the dominant instability is typically the second or Mack mode (Mack 1975), corresponding to trapped acoustic waves within the boundary layer. These waves propagate with a speed close to the boundary layer edge velocity and have a wavelength approximately twice the boundary layer thicknesses, resulting in dominant frequencies ranging from around $100\,\mathrm{kHz}$ to over $1\,\mathrm{MHz}$, the latter for hypervelocity boundary layers in impulse facilities. The accurate measurement of instability–wave characteristics at this upper frequency limit presents a significant challenge, especially when hot wire anemometry, the traditional technique of choice for cold hypersonic flows (Demetriades 1974; Kendall 1975; Stetson and Kimmel 1992) cannot be used because of the destructive testing environment. Fast-response pressure transducers, first employed for second-mode measurements by Fujii (2006), have been used with some success in reflected shock tunnels for frequencies below $1\,\mathrm{MHz}$ (Wagner et al. 2013a, b), though earlier attempts with such sensors (Tanno et al. 2009) emphasized the importance of ensuring adequate mechanical isolation from vibrations induced in the model structure. Fast-response ALTP (atomic-layer thermopile) heat flux gages also show promise (Roediger et al. 2009), though their use has yet to be demonstrated in a high-enthalpy facility.

An attractive alternative to surface-mounted instrumentation is the use of optical or visualization-based techniques. These combine several benefits: they are nonintrusive, able to measure away from the model surface, and typically have bandwidths that are limited only by the recording electronics. An indication that such techniques might be useful for second-mode measurements was provided by early researchers who captured single-image photographs of “rope-like” wave structures in laminar hypersonic boundary layers (Potter and Whitfield 1965; Fischer and Weinstein 1972; Demetriades 1974; Smith 1994). The observed wavelengths were approximately twice the boundary layer thickness, which led to these waves being identified as second-mode disturbances. This motivated the present authors to apply image processing techniques to high-speed schlieren sequences containing such waves (Laurence et al. 2012); the dominant frequencies determined by this analysis showed good agreement with the most-amplified frequencies predicted by linear stability computations. A similar visualization-based methodology has been employed by Casper et al. (2013a, b).

Related optical techniques have been implemented recently by other researchers: VanDercreek et al. (2010) and Hofferth et al. (2013) employed focused schlieren deflectometry for second-mode measurement in long-duration hypersonic tunnels; and notably, Parziale et al. (2013a, b, 2014) obtained quantitative density disturbance measurements, including instability amplification rates, in the T5 hypervelocity shock tunnel at Caltech using focused laser differential interferometry (FLDI). One typical drawback of such optical techniques (even in focusing form), namely that they integrate along the line of sight, is of limited relevance to the measurement of second-mode disturbances, since they are primarily two-dimensional (Demetriades 1974), i.e., the wave fronts form normal to the flow direction. Furthermore, as the disturbances are fluctuations primarily in density rather than velocity, optical techniques that capture changes in the refractive index of the gas are well suited to their measurement.

In the present work, we are concerned with showing how schlieren-based visualization techniques can be employed for investigating hypersonic transition in configurations where the second mode is the dominant instability. The paper is organized as follows. In Sect. 2, we describe the experimental facility, test conditions, and model. In Sect. 3, we revisit the technique first proposed in our earlier paper and demonstrate that it is capable of providing reliable and repeatable second-mode measurements. A further development of this technique that addresses some of its more significant limitations is described in Sect. 4; then, in Sect. 5, we detail measurements using a schlieren deflectometry setup. Comparisons are made in these sections with results from fast-response pressure transducers, and one important aim throughout is to demonstrate how these techniques can be used both to provide information similar to more traditional methods and also to enable new measurement possibilities. A discussion of the relative advantages and disadvantages of the various techniques follows in Sect. 6; then, conclusions are drawn in Sect. 7.

2 Experimental setup

2.1 Facility

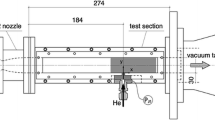
All experiments were carried out in the HEG (High Enthalpy shock tunnel Göttingen) of the German Aerospace Center (DLR). HEG is a large-scale reflected shock wind tunnel, making use of free-piston compression to generate the driver conditions necessary for simulating high-speed flows. HEG is capable of reproducing a wide range of flow conditions, but is limited in terms of test duration to at most a few milliseconds. Further information regarding the operating principle of and conditions achievable in HEG are provided, for example, in Hannemann (2003) and Hannemann et al. (2008).

The present investigation was focused on low-enthalpy conditions ($h_0=3.1-3.3\,\mathrm{MJ/kg}$), with various unit Reynolds numbers in the range from 1.4 to $6.5 \times 10^6\,\mathrm{m}^{-1}$ achieved by adjusting the reservoir pressure. These conditions are intended to simulate Mach-8 flight at different altitudes. Representative reservoir and freestream properties for the relevant conditions are provided in Table 1, and corresponding reservoir pressure traces are presented in Fig. 1. Note that the numbering convention adopted in the present article is based on the unit Reynolds number; to prevent confusion with previously published work, the internal HEG numbering convention for each condition is also provided in Table 1. The pressure traces show that, after a start-up period lasting a 2-3 milliseconds, steady conditions are attained and persist for approximately $3\,\mathrm{ms}$. The test time is terminated by the arrival of expansion waves from the diaphragm burst, resulting in a steadily decreasing reservoir pressure thereafter.

Table 1 Typical facility reservoir (subscript 0) and computed freestream (subscript $\infty$) properties from the test conditions employed in the experiments of the present study

Fig. 1

Typical reservoir pressure traces for the test conditions detailed in Table 1. The approximate test times (slightly different for each condition) are indicated by the vertical lines

2.2 Model description

The model configuration in this study was a slender $7^\circ$-half-angle cone, mounted at zero incidence ($\pm 0.01^\circ$). The nose section was interchangeable: with a sharp nose, the cone length was $1,100\,\mathrm{mm}$. Although a blunted nose of $2.5\,\mathrm{mm}$ radius was used in all experiments described here, for clarity we will refer to distances along the cone surface, $s$, measured from the extrapolated sharp nose. As shown in Fig. 2, the lower part of the cone was fitted with a surface insert constructed of a carbon-fiber-reinforced carbon ceramic material. One of the main aims of the present experimental sequence was to investigate the transition-delaying effects of such a porous material; relevant results are described in earlier publications (Wagner et al. 2013a, b). The focus of the present article is the visualization-based measurement techniques developed during the course of the investigation.

Fig. 2

Sketch of the slender cone model with porous insert (not to scale)

The cone was equipped with various surface instrumentation on both the smooth and porous sides: thermocouples to provide approximate transition locations, Kulite pressure transducers for mean measurements, and fast-response PCB pressure transducers for measuring instabilities. Blind PCB transducers were also installed to isolate the influence of mechanical vibrations. For all schlieren visualizations described herein, a conventional Z-fold schlieren arrangement was employed, with two 1.5-m-focal-length spherical mirrors collimating the light beam to pass through the test section and then refocusing it on the opposite side. A horizontal knife-edge was used in all cases. The light source and camera/imaging device varied according to the technique employed and will be described at appropriate locations in the following sections. A line of thermocouples lay along each of the two rays corresponding to the vertical plane-of-visualization of the schlieren setup. The fast-response pressure transducers were offset in the circumferential direction relative to this plane.

In Fig. 3, we show the heat flux profiles derived from thermocouple measurements for the four test conditions. For the two higher Reynolds number conditions, the visualization measurements were performed on the porous side; hence, for these two cases, the porous-side heat flux distributions are shown. For Condition I, the flow is laminar over almost the entire cone length, with perhaps the beginning of a heat flux rise indicating the onset of transition from around $s=950\,\mathrm{mm}$. Transition is clearly visible at approximately $800\,\mathrm{mm}$ for the increased Reynolds number of Condition II. In Wagner et al. (2013a, b), the porous side showed significantly delayed transition compared to the smooth side at the present conditions. Here, we see that, for Condition IV, the transition location on the porous side has reached approximately midway up the cone.

Fig. 3

Heat flux profiles derived from thermocouple measurements for the four conditions utilized in this study

3 High-speed schlieren with a continuous light source

In an earlier investigation (Laurence et al. 2012), the present authors performed high-speed schlieren visualizations of the boundary layer on a similar cone model with a continuous light source and a high-speed camera (Shimadzu HPV-1). We visualized second-mode wave packets at a sufficiently high frame rate ($500\,\mathrm{kHz}$) to be able to determine the propagation speed using image correlation techniques. This allowed inverse wavelength spectra derived from the row-wise intensity profiles to be converted into frequency spectra; the dominant frequency content showed good agreement with the most-amplified frequencies predicted by a linear stability analysis. As this earlier result came about somewhat fortuitously, however, it was desired to show in the present experiments that such a visualization technique could be employed reliably and repeatedly to derive quantitative information on instability–wave development in hypersonic boundary layers. To this end, three experiments were performed at the same nominal conditions, namely condition I in Table 1. Since this is the lowest density condition of those tested, it provides the most challenging environment for techniques such as schlieren that rely on changes of density in the flow.

The camera used in these three experiments was again a Shimadzu HPV-1, recording at a frame rate of either 250 or $500\,\mathrm{kHz}$ and with an exposure time of $0.5\,\upmu \mathrm{s}$. Although capable of high frame rates, the Shimadzu has two relative disadvantages in this context: a restriction to 102 images (meaning a maximum of $0.4\,\mathrm{ms}$ recording time at the frame rates employed here); and a limited resolution of $312\times 260$ pixels, which is not particularly suitable for visualizing a long, thin region such as a boundary layer. The effective magnification was 3.0 pixels per millimeter, meaning approximately 12 pixels across the approximately 4-mm-thick boundary layer here. The light source employed was a single blue LED, run continuously over the recording time of the camera. The sensitivity of the schlieren setup was increased successively over the three experiments by adjusting the knife-edge cutoff and the orientation of the rectangular LED.

A selected image from the sequence recorded with the highest sensitivity is shown with different degrees of image processing in Fig. 4. With linear contrast enhancement (0.05 % saturation—top image), the extent of the boundary layer is easily discernible, but the instability waves are only faintly visible, a situation only slightly helped by gamma adjustment (power 1.8) and unsharp masking (middle image). By first subtracting a reference image obtained by averaging over all images in the sequence and subsequent contrast adjustment, however, the instability wave structures are clearly revealed in the right part of the lower image. These show the same “rope-like” form as the waves visualized by the earlier researchers referred to in the Introduction.

Fig. 4

Schlieren image of a laminar boundary layer with a wave packet (condition I, smooth side, $s=743$ to $840\,\mathrm{mm}$), captured by the Shimadzu camera with a continuous LED light source: (top) with basic contrast enhancement; (center) with gamma adjustment and unsharp masking; (bottom) with reference image subtracted and subsequent contrast enhancement. Flow is left to right. Note that the periodic structures at the cone surface are artifacts of the image processing and do not represent flow features

Power spectra in terms of inverse wavelength at different heights above the cone surface can be derived by taking the Fourier transform of the row-wise intensity profiles (assuming the scale in the images is known). In each sequence, all images containing wave packets were identified by examining the reference-subtracted images and these inverse wavelength spectra. In order to convert to the frequency spectra of more interest for comparing to results from surface-mounted instrumentation and linear stability analysis, we again use image correlation techniques to determination the propagation speed of the wave packet. It was found that improved results for these correlations were possible if all rows were first filtered with a bandpass filter centered at the wavelength peak of the wave packet, thus minimizing the influence of high-frequency noise and other undesired flow features (the filter cutoffs were approximately one-half and twice the peak wavelength).

Examples of correlation curves for image pairs from the sequence of Fig. 4 with different temporal spacings are shown in Fig. 5. As discussed in Laurence et al. (2012), the present technique suffers from a frequency restriction associated with the periodic nature of the wave packets: to unambiguously resolve the motion, the recording frequency must be at least as high as the dominant frequency of the wave packet. This restriction is clearly illustrated by the correlation curves. For consecutive images (i.e., $4\,\upmu \mathrm{s}$ spacing, corresponding to a $250\,\mathrm{kHz}$ sampling rate), only a single peak occurs at the correct speed of approximately 1,950 $\mathrm{\mathrm m/s}$, but for doubly and triply spaced pairs (corresponding to frame rates of 125 and $83\,\mathrm{kHz}$, respectively), aliasing peaks appear at lower speeds. These latter two curves nevertheless demonstrate one advantage of using more widely spaced image pairs for the speed determination (assuming the closely spaced pairs are also available to avoid ambiguity): the narrower peak profile means that the speed can be determined more precisely. Since the correlation is performed in pixel increments, in order to identify the location of the correlation peak with sub-pixel resolution, a quadratic curve was fitted to the 3 points on either side of the pixel–resolution peak. The correlation speed was taken as the location of the maximum of this fitted curve.

Fig. 5

Propagation–speed correlation curves for image pairs from the sequence of Fig. 4 (condition I, smooth side, $s \approx 810\,\mathrm{mm}$) with various temporal spacings ($4\,\mu \mathrm{s}$ corresponds to two consecutive images for this sequence)

Such correlations were performed for each sequence over all images that were identified as having wave packets. The correlation region was limited to that part of the reference image containing the wave packet, again identified manually for each image. This procedure was somewhat tedious and for larger image sequences would require some form of automation. Histograms showing the distributions of measured speeds in the sequence previously referred to for both singly and doubly spaced image pairs are plotted in Fig. 6; in both, 39 image pairs are considered. The lower (doubly spaced) distribution appears regular with two outliers; the upper distribution is less regular and exhibits greater spread, as might be expected. The mean velocities show no significant difference at 1,943 ± 61 ($4\,\upmu \mathrm{s}$) and 1,948 $\pm\,54\,\mathrm{m/s}$ ($8\,\mu \mathrm{s}$), the uncertainties quoted here being 95 % confidence values. A smaller uncertainty is noted for the wider temporal spacing, but this benefit would decrease as the gap is further widened. Furthermore, we might be concerned that any development in the wave packet shape would adversely affect the correlation accuracy for large spacings. A separation of approximately two periods, which here corresponds to the $8\,\mu \mathrm{s}$ spacing, thus appears to be a good compromise and is assumed throughout the remainder of this section.

Fig. 6

Histograms of propagation speeds determined over an entire Shimadzu 102-image sequence from a condition I experiment (smooth side, in range $s=743$ to $840\,\mathrm{mm}$) using correlation with (above) singly and (below) doubly spaced image pairs

The measured correlation speeds determined in all three repeated experiments are presented in Table 2. Both conventional mean and weighted-average values (the weighting in the latter was based on the strength of the second-mode peaks) are included, together with the 95 % confidence interval. Good agreement is observed between all three experiments, though it should be noted that velocity is a relatively insensitive parameter in hypersonic flows. Not surprisingly, larger uncertainties are obtained with the less sensitive optical setups; nevertheless, with a sufficiently sensitive arrangement, measurement of the propagation speed to within around 3 % appears to be attainable with this method. The propagation speed here is approximately 83 % of the edge velocity determined from a computation of the mean cone flow (for further details of these computations, see Wartemann et al. 2013).

Table 2 Mean characteristics of the wave packets measured in three repeated experiments using condition I, varying the sensitivity in the schlieren setup. The schlieren window was centered at $s=760\,\mathrm{mm}$ in experiment 1 and $790\,\mathrm{mm}$ in experiments 2 and 3. The surface peak frequencies were as recorded by a fast-response pressure transducer located at $s=791\,\mathrm{mm}$ over the entire test time

In Fig. 7, frequency spectra at various heights, $y$, above the cone surface for the image in Fig. 4 are plotted. These are obtained from the inverse wavelength spectra derived for each row of pixels and the mean correlation speed just referred to: as the variation in the measured speed is small, using the mean value averaged over all image pairs seems reasonable. Strong peaks corresponding to the second mode are observed slightly above $200\,\mathrm{kHz}$. As in earlier hot wire measurements (see, for example, Demetriades 1974; Stetson and Kimmel 1992) as well as Laurence et al. (2012), the intensity of the second-mode disturbance reaches a local maximum within the boundary layer (here at $y=2.0\,\mathrm{mm}$), then decreases in the direction of the boundary layer edge. A strong peak is also observed here in the row closest to the cone surface. Such a feature does not appear to have been observed previously in published hot wire measurements, perhaps because of the difficulty in placing a hot wire sufficiently close to the model surface without producing wall interactions. Nevertheless, this wall peak may be expected, considering that previous theoretical analysis of second-mode disturbances, e.g., Fedorov and Tumin (2011) have shown the pressure perturbations to reach a maximum at the wall, whereas temperature perturbations necessarily go to zero. Since this wall peak will be obscured by the cone body for disturbances that are circumferentially off-axis (i.e., that lie away from the vertical imaging plane passing through the cone axis of symmetry), its presence or otherwise could be used as a criterion for determining whether wave packets lie approximately on the cone axis for non-focusing optical setups such as the present one. No harmonics are visible at this stage in the wave packet development.

Fig. 7

Frequency spectra at different heights above the cone surface for the condition I image shown in Fig. 4

The time-developing power spectrum over the entire image sequence is presented in contour plot form in Fig. 8 for two values of $y$: the height of the maximum signal level as well as the pixel row closest to the surface. Aside from low-frequency noise, which tends to be more pronounced away from the cone surface, strong second-mode peaks are present between 200 and $250\,\mathrm{kHz}$. The propagation of the most prominent wave packet is seen clearly in both plots from approximately 0.2 to $0.3\,\mathrm{ms}$. The passage of another packet at a slightly lower frequency is also apparent at close to $0.1\,\mathrm{ms}$; at least one other weaker packet is also visible in the $y=0.3\,\mathrm{mm}$ plot. These less prominent wave packets were perhaps circumferentially off-axis, which resulted in the lateral (wall-normal) profile being displaced effectively downwards.

Fig. 8

Time-developing frequency spectra at heights of (above) $y=0.3\,\mathrm{mm}$ and (below) $2.0\,\mathrm{mm}$ above the cone surface for a condition I experiment. The profiles in Fig. 7 correspond to $t=0.244\,\mathrm{ms}$ in these plots

In Table 2, we also present the mean peak second-mode frequencies for the three repeated experiments. In each case, this was obtained by, first, for each image in which a wave packet was identified, summing the spectra over all rows in the wall-normal direction within the boundary layer, then identifying the frequency in this summed spectrum at which the maximum signal was located, and finally averaging this value over all images. The quoted uncertainty is based on the standard deviation in these peak measurements rather than being any indication of the peak width (a general idea of which can be gleaned from Figs. 7,  8). Good agreement is again obtained between the experiments. The peak frequency for experiment 3 lies slightly lower than the other two (the wave packet at $0.1\,\mathrm{ms}$ in Fig. 8 is partially responsible for this; eliminating this packet from the analysis gives $f_{peak}=226\,\mathrm{kHz}$), but the discrepancy is still well within the measurement uncertainty. These peak frequencies are also compared with values recorded by a fast-response pressure transducer located at $s=791\,\mathrm{mm}$. As the transducer and the visualization plane lay on different rays of the cone, the transducer spectra were averaged using Welch’s method (Welch 1967), with the test time of $2\,\mathrm{ms}$ broken up into $50\,\upmu \mathrm{s}$ intervals with 50 % overlap, to minimize variations between individual wave packets. The full widths at half maximum of the transducer peaks were typically on the order of 70–$80\,\mathrm{kHz}$; in light of this, the agreement between the peak frequencies of the different techniques is very satisfactory.

4 Schlieren with pulsed light source

The results described in the previous section show that the visualization setup employed was capable of providing repeatable and reliable measurements of second-mode wave packets under certain conditions. Nevertheless, there were several limitations to this setup associated with both the camera and light source. First, the fixed and relatively low resolution of the Shimadzu camera is not well suited to studying a long, thin region of interest such as a boundary layer, as it means that for acceptable resolution across the boundary layer, the streamwise extent is restricted (though an anamorphic setup with a magnified wall-normal direction, as in Driest and McCauley 1960, could have mitigated this problem). This could be addressed more simply by employing a CMOS camera with an adjustable resolution, but such cameras typically have lower maximum frame rates than the Shimadzu, even at a reduced resolution. Hence, assuming a continuous light source is employed, we invariably come up against the frequency limitation described in the previous section; furthermore, the minimum exposure time will be determined by the camera and may be insufficiently short to freeze the second-mode waves, especially at higher enthalpy or Reynolds number conditions where the relevant frequencies are also higher. This latter problem can be solved, however, through the use of a short-duration pulsed light source. If the source is capable of nonuniform spacing between pulses, the frequency limitation can also be addressed as illustrated in Fig. 9. By maximizing the gate time of the camera at the given recording frequency, two closely spaced pulses can be used (similar to PIV applications), the first catching the end of one exposure window and the second the beginning of the next. In this case, the maximum frequency that can be resolved increases from the camera frame rate to the inverse of the time between the two pulses, $\Delta t_1$, and is restricted only by the inter-frame gap of the camera (or the timing accuracy of the light source).

Fig. 9

Timing diagram showing how a pulsed light source can be used to overcome the frequency limitation associated with uniform camera frame spacing

In fact, if the light source is capable of a multi-pulse burst, as illustrated in the lower part of Fig. 9, even this latter restriction can be avoided. By employing two pulse pairs with different temporal spacings, $\Delta t_1$ and $\Delta t_2$, (chosen such that neither is close to being a multiple of the other), the aliasing peaks in the correlation curves will lie at different speeds. This is demonstrated more concretely in Figs. 10 and 11, showing results from an experiment performed at Condition III of Table 1. In this experiment, we employed a Phantom v641 camera running at a frame rate of $64\,\mathrm{kHz}$, a resolution of $1408 \times 40$ pixels, and an exposure time of $12.8\,\mu \mathrm{s}$, in conjunction with a Cavilux Smart visualization laser. When slaved to the camera, this laser provides five-pulse bursts with arbitrary intervals between pulses (down to $10\,\mathrm{ns}$ resolution) and an overall repetition rate of up to $130\,\mathrm{kHz}$. Here, a four-pulse burst was used with pulse spacings of 2.8, 28, and $4.5\,\mu \mathrm{s}$. The two image pairs in Fig. 10 were recorded on the porous side of the cone. They have spacings of 2.8 and $4.5\,\mu \mathrm{s}$, respectively, and are separated by approximately $150\,\mu \mathrm{s}$. In each pair, the propagation of a wave packet is clearly visible. The image processing applied to these images consists only of basic contrast enhancement: the increased clarity of the flow structures in comparison with the continuous-light-source visualization in Fig. 4 is notable (though the higher flow density is also a factor here). These images also highlight another advantage of the Cavilux Smart over more traditional lasers used for visualization purposes: the effective incoherence of the beam provides a speckle-free image without diffraction effects.

Fig. 10

Schlieren images of a laminar boundary layer with showing the propagation of wave packets (Condition III, porous side, $s=594$ to $772\,\mathrm{mm}$), at times (top to bottom): $t, t+2.8\,\mu \mathrm{s}, t+155.8\,\mu \mathrm{s}$, and $t+160.3\,\mu \mathrm{s}$

In Fig. 11, we plot correlation curves for the two image pairs. The second-mode frequency here is approximately $400\,\mathrm{kHz}$, which means that an aliasing peak appears below the correct speed even for the $2.8\,\mu \mathrm{s}$-spaced pair. Overlapping of peaks, however, only occurs at the correct value of slightly above 2 km/s. By choosing appropriate intervals $\Delta t_1$ and $\Delta t_2$ then, the frequency limitation for this technique can be increased to much higher values than would be possible running the camera and light source at a uniform repetition rate. This pulsing technique is expected to be especially useful for investigating second-mode development under higher-enthalpy conditions.

Fig. 11

Correlation curves in terms of propagation speed obtained for the two image pairs in Fig. 10

Considering the increased clarity of the wave packets in Fig. 10 compared to that in Fig. 4, we might expect improved analysis results to be obtainable in this case. In the upper part of Fig. 12 ,we present periodograms of the signals at $y=1.4\,\mathrm{mm}$ (the height above the cone surface corresponding to the maximum disturbance intensity: approximately 50 % of the visible boundary layer thickness) for the lower image pair in Fig. 10. Welch’s method was used to reduce the spectral noise: the total length of the considered region was $88.5\,\mathrm{mm}$; the window width was $50.5\,\mathrm{mm}$ and the overlap 75 %. A strong second-mode peak near $360\,\mathrm{kHz}$ appears in both spectra, with a clearly visible first harmonic at $700\,\mathrm{kHz}$, and perhaps also the second harmonic at approximately 1,050$\,\mathrm{kHz}$ in the later-time spectrum. The propagation speed of the first harmonic was checked by changing the limits of the bandpass filter in the correlation procedure and was found to be essentially identical to that of the fundamental (2,043 vs. 2,072$\,\mathrm{m/s}$); it is thus reasonable to use a single correlation speed in the conversion from inverse wavelength to frequency. The lack of growth in the fundamental peak indicates that this wave packet is close to saturation; the next image in the sequence ($27\, \mu \mathrm{s}$ later) showed breakdown in the wave packet structure. Also plotted in Fig. 12 is the normalized power spectrum of the pressure signal measured by a PCB transducer located at $s=655\,\mathrm{mm}$ over a $0.5\,\mathrm{ms}$ interval centered around the instant of the images. The second-mode frequency shows good agreement with the image-based measurement, as does the ratio of the harmonic and fundamental strength; the first harmonic peak, however, lies at a noticeably higher frequency.

Fig. 12

(Above) Power spectra at the height of maximum signal strength ($y=1.4\,\mathrm{mm}$) and (below) time series showing the propagation of the filtered second-mode wave packet and its first harmonic for the lower image pair in Fig. 10 (condition III). The spectrum measured by a fast-response pressure transducer is also included in the upper plot

In the lower part of Fig. 12, we show intensity profiles corresponding to these two image spectra. To isolate the different components of the signals, bandpass filters centered around the fundamental and first harmonic frequencies have been applied. The wave packet profiles are very similar to those obtained with other instrumentation techniques such as hot wire anemometry and surface-mounted pressure transducers (see, for example, Stetson and Kimmel 1992; Heitmann et al. 2013). One observation here is that the harmonic energy appears to be more concentrated toward the center of the wave packet than the fundamental energy. This was confirmed by taking Fourier transforms of consecutive windowed sections of the intensity profiles and examining the spatial extents of the peaks in the two relevant frequency ranges.

The results just discussed are relevant to the behavior of wave packets close to breakdown, but less so for comparing to linear stability computations, especially since they were obtained on the porous side of the cone. As the ability to make such comparisons is one of the aims of the present work, we now concentrate on visualizations performed at a lower Reynolds number condition (II) on the smooth side. The extent of the visualized region here was $s=697$ to $812\,\mathrm{mm}$. In Fig. 3, we see that the rear part of this region coincides with the beginning of the rise in mean heat flux caused by the onset of transition. The schlieren movie revealed that the transition process was highly unsteady: at different points in time, the boundary layer could be entirely laminar and disturbance-free, laminar with instability waves, transitional, or containing turbulent spots. This observation will be discussed in more detail shortly; for now, we note that caution would have to be exercised here also in comparing results to an analysis that assumes linear growth of instabilities.

Fig. 13

Consecutive schlieren images of a laminar boundary layer with a second-mode wave packet (Condition II, smooth side, $s=697$ to $812\,\mathrm{mm}$). The image times (top to bottom, relative to the second image) are $t = -28.15, 0, 2.8$ and $30.8\,\mu \mathrm{s}$. The markers indicate the approximate extent of the wave packet in the second image, propagated with a fixed spacing for each other image by the calculated phase speed (note the upstream marker is outside the visualization region in the first image; likewise, the downstream marker in the last)

Figure 13 shows four consecutive images of a propagating wave packet; the markers indicate the approximate extent of the packet in the second image and are shifted with fixed spacing for each other image by the calculated propagation speed. Comparing the third and fourth images, we see that the extent of the disturbance is growing at the trailing end, i.e., spatial dispersion of the wave packet is occurring.

In the upper part of Fig. 14, we present a histogram of all propagation speeds determined during the test time of this experiment: this includes correlations from image pairs with both 2.8 and $4.5\,\mu \mathrm{s}$ spacing. The distribution here is somewhat less regular than in Fig. 6, with 2–3 separate peaks discernible. One possible explanation for this is fluctuations in the mean flow caused by unsteadiness in the reservoir conditions (in the earlier experiment, all wave packets were measured within a period of approximately $0.25\,\mathrm{ms}$, probably too short for such fluctuations to be registered in the histograms). To test this possibility, in the lower part of Fig. 14, we plot the measured propagation speed versus the experimental time together with a trace from a Kulite pressure transducer at approximately the same streamwise location. A substantial degree of scatter is present in the measured speeds, making it difficult to draw solid conclusions: visually, there does appear to be some link between the fluctuations in the two curves; the calculated correlation coefficient of 0.2, however, does not indicate strong evidence of a correlation. Despite the non-regularity of the distribution of the measured propagation speed, the mean value of $2039\pm 59\,\mathrm{m/s}$ (95 % confidence interval) has an uncertainty that is essentially no higher than that of the earlier experiment shown in Fig. 6.

Fig. 14

(Above) Histogram of calculated propagation speeds for all wave packets observed during the test time in a condition II experiment. (Below) Determined propagation speeds plotted versus experimental time together with the surface pressure measured at a nearby pressure transducer; the vertical dashed lines indicate the steady test time

In Fig. 15, we plot power spectra at different heights above the cone surface corresponding to the second and third images of Fig. 13. Comparing to Fig. 7, the benefit of using a camera with a higher pixel count is immediately obvious. The second-mode frequency here is approximately $260\,\mathrm{kHz}$; again the double-extremum profile is observed, with one local maximum inside the boundary layer and the other at the cone surface, but now in much improved resolution. Such a detailed picture of the evolution of an individual wave packet is not possible with any other currently available technique. In contrast to the wave packet shown in Fig. 12, here, we still see significant growth in the downstream direction (note the vertical scale is the same on the two plots), indicating that the disturbance has not yet reached the stage of saturation and breakdown. Nevertheless, the first harmonic at $520\,\mathrm{kHz}$ is already present in these spectra (although it is not clearly visible on the linear scale), indicating that the wave packet is undergoing nonlinear amplification.

Fig. 15

Power spectra at different heights above the cone surface for the second and third images shown in Fig. 13. The vertical scale is the same in both plots

Time-developing power spectra at the height above the cone surface of maximum disturbance intensity are shown in contour plot form in Fig. 16, both for the upstream and downstream halves of the visualized region. Immediately apparent is the inherently unsteady nature of the transition process, as would be expected for a boundary layer under noisy freestream conditions close to transition. In the upstream plot, second-mode wave packets with frequencies around $300\,\mathrm{kHz}$ appear intermittently. The exact frequency varies in time, which again seems to reflect fluctuations in the reservoir and cone surface pressures. Occasional bursts of turbulence can be observed by the disappearance of the second-mode peak and the shifting of the signal energy to lower frequencies (e.g., at 3.7 and $6.5\,\mathrm{ms}$); entirely disturbance-free laminar sections of flow correspond to vertical time slices with no visible energy (or only a weak signal at the lower-frequency limit).

Fig. 16

Time-developing power spectra $1.5\,\mathrm{mm}$ above the cone surface, for (above) $s=698-754\,\mathrm{mm}$ and (below) $s=755-811\,\mathrm{mm}$, derived from a condition II experiment

In the lower plot of Fig. 16, showing the downstream development, second-mode wave packets are still visible, though these are weaker in amplitude and shifted to slightly lower frequencies because of boundary layer growth. The general appearance, however, is much more scattered, with an increased tendency toward extended bursts of turbulence. This is consistent with breakdown and the onset of transition as indicated by the heat flux distribution in Fig. 3.

In order for the reader to gain clearer insight into the unsteady nature of the transition process, in the online supplementary material, we include a movie of the boundary layer development during the time period shown in Fig. 16. Each frame shows the schlieren image, three-dimensional spectra (as in Fig. 15) of the upstream and downstream halves of the visualization region, and the plots from Fig. 16 with the experimental time indicated by white vertical lines.

5 Schlieren deflectometry

Measurements were also performed using a schlieren deflectometry setup. Schlieren deflectometry was first employed in a basic form by Davis (1971) to extract information from a turbulent axisymmetric shear layer. An improved version of the technique was implemented by McIntyre and Settles (1991); localized measurements (along the line of sight) were then made possible by the introduction of a focusing schlieren setup (Alvin et al. 1993; Garg and Settles 1998). The flow investigated in all of these instances was turbulent. The first measurements of instability waves in a laminar boundary layer using schlieren deflectometry were performed by VanDercreek et al. (2010); more recently, extensive second-mode measurements were made on a flared cone in a quiet tunnel (Hofferth et al. 2013). In both of these investigations, the facility was long duration and a focusing schlieren setup was employed.

In the present experiments, performed in the more challenging flow environment of a shock tunnel, we used a non-focusing arrangement (the benefits and drawbacks of this are discussed in Sect. 6). The setup was similar to that described in Sect. 3, with a blue LED as light source, but the high-speed camera was replaced by two $200 \mu \hbox {m}$ diameter optical fibers mounted in the imaging plane at locations corresponding to two streamwise-separated points inside the cone boundary layer. As the light source was rectangular with an intensity distribution close to uniform, the schlieren response was essentially linear in the density gradient. Each optical fiber was connected to a Thorlabs avalanche photodetector, having a bandwidth of $50\,\mathrm{MHz}$, and the acquired signal was recorded by a high-speed data acquisition system at $100\,\mathrm{MHz}$. Cable lengths were minimized to prevent attenuation of the high-frequency components of the signal. This arrangement thus behaved effectively as an ultra-fast two-pixel camera, with fluctuations in density gradient being recorded as they would for a conventional schlieren arrangement, but with a much higher bandwidth.

In Fig. 17, we present periodograms of the signals recorded in three experiments. In all cases, the LED light source was pulsed for a duration of $1.2\,\mathrm{ms}$ rather than run continuously. This provided a higher luminous output and allowed a larger degree of knife-edge cutoff, improving the system sensitivity; the measurement time, however, was thereby limited even further. The power spectra shown were derived using Welch’s method: a Blackman window of $50\,\mu \mathrm{s}$ (upper plot) or $100\,\mu \mathrm{s}$ width (lower plot) with 50 % overlap was employed.

Fig. 17

(Above) Power spectra from two experiments using Condition III (porous side) as measured by schlieren deflectometry with two photodetectors; in the second experiment, the measurement points were shifted downstream so that the upstream detector was at the same location as the downstream detector in the first experiment. (Below) Power spectra measured in a turbulent boundary layer from a condition IV experiment (note the differing horizontal scales)

In the upper plot of Fig. 17, we show results from two experiments at Condition III in which the measurements were performed on the porous side, 1.2 ($\pm 0.1$) mm above the cone surface (approximately corresponding to the peak signal location determined earlier for this condition). In the first experiment, the probe separation in test section dimensions was $61\,\mathrm{mm}$; for the second, the probe locations were shifted together downstream so that the upstream probe lay now at the location of the downstream probe in the first experiment. The accuracy of the streamwise positioning of each probe in the boundary layer is estimated as $1\,\mathrm{mm}$ and the circular interrogation area had a diameter of approximately $0.8\,\mathrm{mm}$ (the image magnification was approximately 1:4). Second-mode peaks are clearly visible close to $400\,\mathrm{kHz}$ in all spectra. In the first experiment, the signal strength has grown by approximately an order of magnitude between stations, and the peak has shifted to a slightly lower frequency. No harmonics are yet visible in either signal. The power spectrum of the PCB signal at $s=655\,\mathrm{mm}$ was similar to that seen in Fig. 12: the PCB second-mode peak was at $401\,\mathrm{kHz}$, which matches well with the downstream photodiode peak ($396\,\mathrm{kHz}$); in contrast to the photodiode measurement, however, the first harmonic was clearly visible in the PCB spectrum. In the second experiment, the spectrum from the upstream photodetector shows reasonable agreement with the equivalent spectrum from the first. The small differences that are observed in peak height and location can be attributed to run-to-run variation. The second-mode growth in the downstream direction has now tapered off, suggesting that disturbances are becoming saturated and the boundary layer is close to transitioning. There are still no clear harmonics in the signal, however, which comparing to the results shown in Fig. 12, suggests the signal-to-noise ratio of the deflectometry technique to be somewhat lower than the camera-based technique.

In the lower plot of Fig. 17, we show similar results from an experiment with Condition IV. The spectral energy is now distributed over a broad range of frequencies with no significant peaks, as is typical of a turbulent boundary layer. The upstream and downstream spectra are essentially identical, indicating that the boundary layer is close to being fully developed (Fig. 3 shows that the upstream interrogation point is in the vicinity of the peak post-transitional heating location). The noise floor from a flow-off measurement is also shown; this merges with the flow-on profiles at a frequency of around $2.2\,\mathrm{MHz}$. Considering that, for a propagation speed of 2,000$\,\mathrm{m/s}$, this frequency corresponds to a wavelength of $0.9\,\mathrm{mm}$ (compared to an interrogation diameter of $0.8\,\mathrm{mm}$), spatial filtering would make measurements at these frequencies questionable for the present setup even if higher signal-to-noise levels were available.

Fig. 18

(Top) Time-developing power spectrum as measured by the photodetector located at $s=669\,\mathrm{mm}$; and bandpass-filtered time series from the first condition- II experiment shown in Fig. 17: (middle) the entire measurement period, and (below) a zoom-in of the boxed region in the upper plot

The time-developing power spectrum at the downstream detector in run 1 is presented in contour plot form in the uppermost plot of Fig. 18. This was derived from short-time Fourier transforms (using $50\,\mu \mathrm{s}$ windows) of the photodiode signal; the appearance is generally similar to earlier such plots obtained from camera measurements, with second-mode wave packets intermittently visible at approximately $400\,\mathrm{kHz}$. To illustrate how these correspond to features in the photodiode signal itself, time series of the disturbance histories for both photodiodes are shown below. Here, a bandpass filter with limits $200\,\mathrm{kHz}$ and $600\,\mathrm{kHz}$ has been applied to isolate the second-mode signals. In the middle plot, we show the entire measurement period; second-mode disturbances are visible as concentrated regions of elevated fluctuation levels. In the lowermost plot, a zoom-in of the upper boxed region shows the development of a single wave packet, centered at approximately $6.855\,\mathrm{ms}$ in the downstream signal. The delay here for a disturbance to travel between the two interrogation points is $0.03\,\mathrm{ms}$.

The approximate amplification rate, $-\alpha$, can be calculated from the upstream and downstream signals using the following equation:

$$\begin{aligned} -\alpha = \frac{\ln (a_2/a_1)}{s_2-s_1}, \end{aligned}$$

(1)

where $a_1$ and $a_2$ are the signal amplitudes at a given frequency at the locations $s_1$ and $s_2$. In Fig. 19, we present normalized amplification rates determined according to this equation from the two pairs of signals shown in the upper plot of Fig. 17 (using amplitude rather than power spectra). Note that although the measured quantity here is a density gradient, if we assume the mean flow to be parallel, i.e., negligible variation in the streamwise direction, because we are dividing the signal amplitudes by one another, the resulting amplification rate will also be that for fluctuations in the density itself. This avoids one of the drawbacks of schlieren-based techniques. For the first experiment, the maximum growth rate occurs close to the second-mode peak of the downstream photodiode, at just under $400\,\mathrm{kHz}$. There is also significant lower-frequency amplification, but little evidence of growth at frequencies above that of the second mode. In the second experiment, the main peak has shifted to a lower frequency and decreased significantly in magnitude. The growth at lower frequencies has all but disappeared, but there is now increased evidence of higher-frequency amplification (though this is broadly distributed without a clear indication of a well-defined harmonic.)

Fig. 19

Normalized amplification rates determined over the entire measurement time for the two condition- II experiments shown in the upper plot of Fig. 17

There is substantial experimental uncertainty associated with the amplification rate determination, and we conclude the present section with an attempt to characterize this. We have already noted that the uncertainty in the streamwise positioning of each sensor was approximately $1\,\mathrm{mm}$. Far more significant, however, is the uncertainty in the lateral (i.e., surface-normal) positioning: as Fig. 15 shows, there are large lateral variations in signal strength even a short distance from the peak. In hot wire experiments in continuous facilities (e.g., Stetson and Kimmel 1992), amplification rates are typically determined at the peak signal location in the lateral direction as the hot wire is traversed across the boundary layer; in a shock tunnel, the short test time excludes such a practice, so we must account for possible errors introduced if the probe locations are offset from the lateral maximum. These errors will be alleviated to some extent by the effective integration over the interrogation area: an estimate based on profiles such as those shown in Fig. 15 suggests the maximum effective lateral derivative of the signal strength to be approximately 200 % per mm, which gives a 20 % error in both $a_1$ and $a_2$ for the $0.1\,\mathrm{mm}$ accuracy assumed here. Additionally, we must account for the fact that the two probes were at nominally the same $y$ value, whereas the boundary layer thickness and thus the $y$-location of maximum signal intensity increase between stations (i.e., deviation from the parallel-flow assumption). For experiment 1, for example, we estimate a growth of 7 % based on the change in the peak second-mode frequency.

Since schlieren techniques integrate along the line of sight, a further source of error will be introduced if wave packets spread circumferentially as they propagate downstream. To the authors’ knowledge, circumferential spreading rates of second-mode wave packets have not been measured experimentally; the direct numerical simulations of Sivasubramanian and Fasel (2012), however, indicate that after a short period of rapid circumferential growth (which was most likely an artifact of the point-like initial disturbance), second-mode wave packets spread only slowly as they propagate downstream. Moreover, as the growth in disturbance amplitude is exponential in the streamwise direction, any errors introduced by circumferential spreading are likely to be minor.

We assume then that the dominant systematic-error source is the uncertainty in probe locations. To compare this error with random variation in the amplification rate profiles, in Fig. 20, we again plot the normalized average growth–rate curve from experiment 1, now with an error bar included, together with the profiles obtained by considering two isolated second-mode disturbances (those shown by arrows in the uppermost plot of Fig. 18). These two were chosen as representative of the overall variation observed in the individual wave packets. In the vicinity of peak amplification, the systematic error is seen to be comparable in magnitude to the packet-to-packet variation (note that, if anything, we are probably overestimating the systematic error by using the maximum lateral derivative in intensity). At higher frequencies, this variation is somewhat larger, most likely due to the low signal-to-noise ratio of the measurement in this region.

Fig. 20

A comparison of the normalized amplification rates averaged over the entire measurement time for shot 1 of Fig. 17 with those determined from the individual wave packets indicated by arrows in the top plot of Fig. 18. The error bar shows the estimated uncertainty due to probe alignment

6 Discussion of optical and visualization-based techniques for transition measurements

Before concluding, we provide a brief critique of the relative advantages and disadvantages of experimental techniques for second-mode measurement in light of the present exposition, without limiting the discussion solely to implementation in shock tunnels. We will restrict ourselves, however, to optical/visualization-based methods and the other commonly used technique that allows measurement away from the model surface, namely hot wire anemometry. For relevant discussions of surface-mounted instrumentation, the reader is referred to, for example, Fujii (2006) and Estorf et al. (2008) (fast-response pressure transducers), and Roediger et al. (2009) (fast-response heat flux gages).

Hot wire techniques have the singular advantage of offering localized measurements in all three spatial dimensions. Even focusing optical techniques suffer from an effective integration of the measured quantity across the line of sight, the integration depth typically being larger than the width of the second-mode disturbance. If this width grows as the disturbance propagates downstream, the integration will introduce errors in the calculation of the amplification rate (though, as discussed in Sect. 5, these errors are likely to be small). Furthermore, oblique waves that may appear during breakdown (see, for example, the DNS results of Sivasubramanian and Fasel 2012) will not be resolved. Disadvantages of hot wires are also significant, however: they are intrusive, which precludes multiple measurements directly downstream of one another; they are generally difficult to implement or impossible in the case of shock tunnels; and a number of assumptions, some questionable, are required to recover the fluctuation levels of the flow quantities of direct interest, such as pressure, temperature, and velocity, from the total temperature and mass flux fluctuations obtained from a modal analysis of the hot wire signal (see Stetson and Kimmel 1992). The limitation to a single measurement location for an individual hot wire may also be problematic, since in practice, the wire will generally need to be traversed across the boundary layer to provide the required detail of information (for example, to locate the peak energy location at a given downstream station if amplification rates are desired). This is feasible in a continuous facility, but may require an unreasonably large number of experiments in a shorter duration facility such as a Ludwieg tube.

In comparison, optical techniques are inherently non-intrusive, which allows the development of individual disturbances to be monitored at different downstream locations, rather than relying on averaged measurements as must be done with hot wires. This benefit is most pronounced for the camera-based technique variants described in Sects. 3 and 4, since measurements across the entire boundary layer are obtained simultaneously. Indeed, the combination of high spatial and temporal resolutions afforded by these variants is a powerful one and will become only more so as camera and light source technology develop. The main drawback, both here and with deflectometry, is that the measured fluctuations are in terms of a density gradient, rather than a more useful flow property. For growth rate estimates, however, this drawback is conveniently avoided, as noted in Sect. 5.

Deflectometry and laser differential interferometry (LDI) are comparable in the sense that they both provide pointwise measurements in the imaging plane, which leads to the same limitation as hot wires. Deflectometry benefits from its simplicity and the ease with which multiple measurement points can be incorporated, i.e., by simply introducing additional fibers in the imaging plane, with no modification to the remainder of the optical setup necessary (and note this setup is otherwise identical to a conventional schlieren arrangement). On the other hand, deflectometry is not immediately quantitative in any useful flow property. LDI does provide a quantitative measure of density fluctuations, which has allowed Parziale et al. (2014) to determine freestream noise levels in the T5 shock tunnel, in addition to making second-mode measurements (Parziale et al. 2013a). In general, however, the LDI optical setup needs to be duplicated for multiple-point measurements.

Finally, a brief discussion of focusing versus non-focusing optical techniques is warranted. The main advantage of focusing in the present context (considering that the focal depth is still typically larger than the circumferential extent of second-mode disturbances) is the reduced influence of freestream noise and other external disturbances on the measurements. A possible additional benefit is the exclusion of off-axis disturbances for cones and the possible ambiguity that these might bring (for example, in the surface-normal distribution of the disturbance energy), though this might also be a slight drawback if, for instance, one wished for as many measurements of the propagation speed as possible in a limited measurement time, as in Sects. 3 and 4. The disadvantages of focusing schlieren setups are that they are generally less sensitive and more difficult to implement (Settles 2006); this is not necessarily true of focused LDI setups, but these are instead afflicted by a wavelength dependence in sensitivity not typically encountered for non-focusing versions—see Parziale et al. (2014). Depending on the levels of noise coming from both the freestream and other sources, it may arise that the reduced signal-to-noise resulting from the decreased schlieren sensitivity outweighs the benefits of focusing; realistically, this could only be confirmed by performing experiments at the same conditions with both focusing and non-focusing setups. Considering that successful measurements have been carried out with both types of schlieren arrangement, however, it is likely that the benefits do not lie overwhelmingly on either one side.

7 Conclusions

A series of experiments have been carried out at low-enthalpy hypersonic conditions in the HEG shock tunnel to examine instability development and transition in the boundary layer of a slender cone at zero incidence. Three variants of schlieren-based techniques were used to measure the dominant second-mode instability waves that developed under these conditions. First, three experiments were performed at the same test conditions using a previously proposed methodology that employs image correlation to determine the disturbance propagation characteristics from high-speed sequences of regularly spaced images. Good agreement was obtained both between the various experiments and with results from a surface-mounted pressure transducer, indicating that this technique is capable of providing reliable and repeatable second-mode measurements. Second, a variant of this first technique, making use of a pulsed light source to overcome the frequency limitation that is inevitably encountered with continuous illumination, was implemented. Second-mode measurements were obtained at camera frame rates far below the dominant disturbance frequency and with a signal-to-noise ratio that allowed the detection of the first and possibly second harmonic of the second mode. These measurements provided clear insight into the unsteady nature of boundary-layer transition under the present conditions: visualizations just upstream of the transition-induced rise in surface heating level showed the boundary layer to be, at different times, fully disturbance-free, laminar with instability waves, transitional, or with passing turbulent spots. Finally, schlieren deflectometry measurements were performed. The use of two streamwise-separated interrogation points showed the growth and saturation of second-mode waves and allowed approximate amplification rates to be determined, though the latter were subject to substantial uncertainty.

In summary, these experiments have shown that the present techniques can be of considerable utility for instability measurements in hypersonic boundary layers, even in the challenging environment of a shock tunnel.