1 Introduction

Prior to fielding a munition, energetic materials must undergo a thorough characterization to quantify their damage potential/performance on a target. Performance is characterized through experimental measurement of the detonation and blast wave properties produced in air. The detonation properties of interest (i.e., pressure, velocity, particle velocity, and density) depend upon chemical composition of the energetic material and vary with pressing density. The detonation wave, upon reaching the energetic material–air interface is transferred into the surrounding air as a radially outward propagating blast wave. The outward propagating blast wave transports the mechanical energy, or damage potential, produced by the energetic material. Thus, radial measurements of the blast waves peak pressure and explosive impulse are gathered for performance characterization.

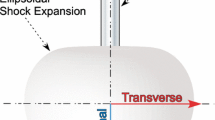
An ideal explosive pressure versus time record measured at a fixed radial standoff distance from the charge center is shown in Fig. 1. The figure identifies the important pressure regions experienced by a stationary sensor upon passage of a blast wave. Explosive impulse at the fixed sensor is defined as the area above/beneath the pressure versus time record with respect to atmospheric pressure P 0. As shown, the trace contains both a positive (pressures above atmospheric pressure) and negative (pressures below atmospheric pressure) phase of impulse. Here, only the positive phase of impulse I + is considered for characterization purposes as it is generally orders of magnitude larger than the negative phase (Baker 1973). The positive pressure phase duration T + is defined from the peak shock wave pressure P s (at the shock wave time of arrival t a) through its decay down to atmospheric pressure at time t a + T +. Thus, the positive phase of explosive impulse is defined as the integral of the positive pressure phase over its duration, Eq. (1).

$$I^{ + } = \int\limits_{{t_{\text{a}} }}^{{t_{\text{a}} + T^{ + } }} {P\left( t \right)dt}$$
(1)

These blast wave measurements are traditionally gathered from full-scale (kilogram-range) charges having masses ranging from 1 to 105 kg (Dewey 1964). Explosive scaling laws are later applied to the experimental results for comparison between charge masses. Experiments measure the temporal pressure history of the shock wave at fixed radial standoff positions using piezoelectric pressure transducers. Being mechanically actuated, these transducers possess a characteristic finite response time that inhibits their ability to accurately respond to a discontinuous signal, such as a shock wave (Ethridge 1965; Kinney and Graham 1985; Kleine et al. 2003; Rahman et al. 2007). To more easily manage these data, multiple empirical smoothing curves have been developed by previous authors (Baker 1973). However, the need for these empirically based curves only increases the experimental error in the measurement.

Fig. 1
figure 1

“Ideal” explosive pressure trace

Full size image

Recently, however, laboratory-based researchers have extended the explosive scaling laws validity from kilogram range charges down to the gram and even milligram range (Biss and Settles 2010; Hargather and Settles 2007; Kleine et al. 2003). In their research, optical flow visualization techniques (e.g., schlieren, shadowgraph, etc.) are combined with digital high-speed cameras to track the radial shock wave propagation rate, permitting a continuous, radially varying, peak shock wave pressure profile to be determined from the Rankine-Hugoniot jump equation. This extension down to the laboratory scale has been demonstrated to be a highly accurate, cost-effective supplement to the traditional air blast experiments as it provides a non-intrusive, continuous profile compared to the intrusive point measurements obtained by transducers.

Explosive impulse, on the other hand, continues to be determined from measured pressure transducer histories at both the laboratory and full scale, as no optical characterization method has been explored. In response, the present research aims to extend the utility of laboratory-scale air blast characterization by developing an optically based experimental technique to determine the explosive impulse produced by the detonation of spherical gram-range charges. Streak images are captured of the explosive event using a digital high-speed camera and schlieren flow visualization system. Images are digitally analyzed to optically determine the temporal pressure history of the explosively driven shock wave as a function of shock wave radius, yielding the explosive impulse.

2 Experimental methods

2.1 Spherical charges

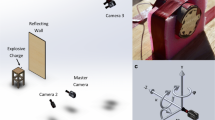
Centrally initiated laboratory-scale spherical charges are incorporated to eliminate the critical diameter effect associated with energetic material detonations (Gruschka and Wecken 1971). Spherical charges possessed a centrally positioned right-circular-cylinder void to accommodate an RP-3 exploding bridgewire (EBW) detonator [29 mg pentaerythritol tetranitrate (PETN)], Fig. 2.

Fig. 2
figure 2

Spherical charge with RP-3 EBW detonator

Full size image

Charges are composed of Class V cyclotrimethylene trinitramine (RDX) pressed to a density of 1.77 g/cm3. The assembled charge masses and their respective densities (measured using a Micrometrics AccuPyc 1330 gas pycnometer) are tabulated in Table 1.

Table 1 Experimental charges detonated
Full size table

2.2 Digital high-speed schlieren visualization

Spherical charges are detonated in the test section of a Z-type schlieren system to optically track the explosively driven shock wave radius as a function of time, Fig. 3. The schlieren system components are twin 24.75 cm f/5 parabolic mirrors, a 500-W mercury–xenon (Hg–Xe) arc-lamp light source (Newport/Oriel Instruments), a Photron SA.5 8-bit digital high-speed camera (Photron USA, Inc.), and a linearly graded filter (DSC Laboratories). A linearly graded filter is chosen for the current application in place of the traditional schlieren knife edge due to the high refractive indices expected. The graded filter provides several advantages over a knife-edge cutoff including: (1) minimal diffraction effects, (2) sharper schlieren images having increased spatial resolution, (3) extended physical cutoff range, and (4) a broader measuring range exhibiting less vibration sensitivity (Settles 2001).

Fig. 3
figure 3

Z-schlieren flow visualization system with linearly graded filter cutoff and pencil gage pressure transducer

Full size image

A pencil gage pressure transducer is placed outside the schlieren system test section to gather the side-on (static) temporal pressure history of the propagating blast wave for comparison to the optical measurement, Fig. 3. The pressure transducer is a PCB Model 137A23 with a measuring range of 345 kPa. The pencil gage is connected to a PCB signal conditioner (Model 483C) and finally to a LeCroy oscilloscope (Model 6030A) with a sample rate of 1 MHz (signal-conditioner limited).

Schlieren system calibration is performed according to the standard photometric method developed by Schardin (1947). Placing a standard lens (50.8 mm diameter, 10 m focal length) in the schlieren system test section, the image background intensity is set by adjusting the transverse position of the graded filter with respect to the optical axis. A calibration image is captured to determine the mathematical relationship between the standard lens geometry and a refracted ray of light (Bigger 2008). The image is captured with an exposure time equivalent to the exposure time for imaging the explosive event. A MATLAB script is used to calibrate the 8-bit digital intensity profile across the lens centerline. The intensity profile is generated by averaging the center three rows of pixels across the lens to minimize the presence of artifacts or noise in the image. A fourth-order polynomial is fit to this intensity profile as a function of the radial lens coordinate. The polynomial is subsequently converted to pixel intensity as a function of the refraction angle ε r thus permitting all future experimental image intensity values to be converted to refraction angles.

Due to the nature of the schlieren system’s parallel light passing though a spherical blast field, the measured refraction angles are path-integrated quantities. As such, a deconvolution of the data must be performed prior to calculating the local refractive index field generated by the blast field. The implementation of centrally initiated spherical charges and Huygens’s principle (Huygens 1690) ensure the blast field to be spherical in nature and a one-dimensional axisymmetric flow field. It should be noted that the proposed technique is limited to radial distances greater than that to which the contact surface of detonation product gases expands, to allow a proper deconvolution of the data.

Research conducted by Dasch demonstrated that the deconvolved field for path-integrated data taken at equally spaced radial positions over N intervals is producible using only weighted sums of the data divided by the spacing interval (Dasch 1992). This deconvolution is represented by Eq. (2), where δ is the normalized refractive index difference at time t m and a distance of r i (iΔr) from the center of the object of interest, D ij contains the independent data spacing linear operator coefficients (Eqs. 3 and 4), and ε mj is the refraction angle. Indices i and j correspond to the data points varying from 1 to N + 1 (Kolhe and Agrawal 2009). Kolhe and Agrawal analyzed multiple deconvolutions developed and found the two-point Abel inversion method to produce the highest accuracy measurements while minimizing experimental error propagation (Kolhe and Agrawal 2009).

$$\delta \left( {t_{\text{m}} ,r_{i} } \right) = \sum\limits_{j = i}^{N + 1} {D_{ij} \cdot \varepsilon_{mj} }$$
(2)
$$\begin{aligned} D_{ij} = & \frac{1}{\pi } \cdot \left( {A_{i,j} - A_{{i,\left( {j - 1} \right)}} - j \cdot B_{i,j} + \left( {j - 2} \right) \cdot B_{{i,\left( {j - 1} \right)}} } \right) \\ & \, if \, j > i{\text{ and }}j \ne 2, \\ \, = & \frac{1}{\pi } \cdot \left( {A_{i,j} - j \cdot B_{i,j} - 1} \right) \\ \, & if \, j > i \, {\text{ and }}j = 2, \\ = & \frac{1}{\pi } \cdot \left( {A_{i,j} - j \cdot B_{i,j} } \right) \\ \, & if \, j = i{\text{ and }}i \ne 1, \\ = \, & 0 \\ \, & if \, j = i = 1{\text{ or }}j < i \\ \end{aligned}$$
(3)

where A i,j and B i,j are.

$$ \begin{gathered} A_{i,j} = \sqrt {j^{2} - \left( {i - 1} \right)^{2} } - \sqrt {\left( {j - 1} \right)^{2} - \left( {i - 1} \right)^{2} } \hfill \\ B_{i,j} = \ln \left( {\frac{{j + \sqrt {j^{2} - \left( {i - 1^{2} } \right)} }}{{\left( {j - 1} \right) + \sqrt {\left( {j - 1} \right)^{2} - \left( {i - 1} \right)^{2} } }}} \right) \, \hfill \\ \end{gathered} $$
(4)

After deconvolution of the refraction angle data, the refractive index η is calculated from δ according to Eq. (5), where η 0 is the refractive index at ambient conditions. The Gladstone-Dale law is applied to the refractive index to determine the radial density gradient ρ of the air downstream of the shock wave, Eq. (6). The Gladstone-Dale coefficient k is 0.226 cm3/g for air at ambient conditions. Calculated densities ρ are converted to pressures P through the use of the ideal gas law, Eq. (7). Measured pressure profiles for the present research are for shock waves traveling at Mach 3 or less, thus air is assumed to behave as an ideal gas (γ = 1.4).

$$\eta \left( {t_{\text{m}} ,r_{i} } \right) = \frac{{\delta \left( {t_{\text{m}} ,r_{i} } \right) + 1}}{{\eta_{0} }}$$
(5)
$$\rho \left( {t_{\text{m}} ,r_{i} } \right) = \frac{{\eta \left( {t_{\text{m}} ,r_{i} } \right) - 1}}{k}$$
(6)
$$P\left( {t_{\text{m}} ,r_{i} } \right) = \rho \left( {t_{\text{m}} ,r_{i} } \right)T\left( {t_{\text{m}} ,r_{i} } \right)R_{\text{air}}$$
(7)

In order to calculate a pressure, a temporal temperature profile is required at each radial standoff distance. The decay profile of the temperature, however, remains an elusive experimental measurement. Thus, various assumptions have been invoked to simplify its handling. Previous research assumed the temperature profile downstream of the shock wave to be constant and equal to the shock-heated value for calculating the positive pressure phase duration from laboratory-scale PETN charges (Biss 2009; Hargather and Settles 2007). Though it turned out to be a rather good assumption for determining the positive pressure phase duration, the temperature must decay at a finite rate in order to properly calculate the pressure. As an initial estimate, a triangular temperature decay profile is assumed for the present research, Eq. (8). Where, the peak temperature T max at a given radial standoff distance is determined by the normal shock relation, Eq. (9). The shock wave Mach number M is determined by measuring the shock wave radius as a function of time and applying Dewey’s radius versus time profile to the data (Dewey 1971). The profile is differentiated with respect to time and divided by the ambient sound speed, thereby yielding the shock wave Mach number versus radius profile [for additional background, see reference (Biss and Settles 2010)]. Additionally, knowledge of the radial shock wave Mach number allows an accurate determination of the radial peak shock wave pressure profile. The minimum temperature T min is determined by forcing the pressure to atmospheric pressure at the conclusion of the positive pressure phase duration, Eq. (10). The radially varying positive pressure phase duration T + is determined according to previously published methods (Biss 2009; Hargather and Settles 2007). Finally, the spatiotemporal pressure map is calculated using the ideal gas law with the optically measured density map and calculated spatiotemporal temperature map.

$$T\left( {t_{m} ,r_{i} } \right) = \frac{{T_{\hbox{min} } \left( {r_{i} } \right) - T_{\hbox{max} } \left( {r_{i} } \right)}}{{T^{ + } \left( {r_{i} } \right)}}\left( {t_{m} - t_{a} \left( {r_{i} } \right)} \right) + T_{\hbox{max} } \left( {r_{i} } \right)$$
(8)
$$T_{\hbox{max} } \left( {r_{i} } \right) = \left[ {1 + \frac{7}{6}\left( {M\left( {r_{i} } \right)^{2} - 1} \right)} \right]\left[ {\frac{{2 + 0.4M\left( {r_{i} } \right)^{2} }}{{2.4M\left( {r_{i} } \right)^{2} }}} \right]$$
(9)
$$T_{\hbox{min} } \left( {r_{i} } \right) = \frac{{P_{0} }}{{\rho \left( {t_{a} \left( {r_{i} } \right) + T^{ + } ,r_{i} } \right)R_{air} }}$$
(10)

3 Results and discussion

3.1 Optical explosive impulse measurement

Prior to conducting each experiment, a static image of the standard lens positioned in the test section of the schlieren system was recorded to determine the radial intensity profile produced by the linearly graded filter and provide a calibration length scale. Images were captured by the Photron SA.5 at 300 kfps, 1 µs exposure, and a resolution of 832 × 16 pixels. Images possessed a spatial resolution of 2.661 e−4 m/pixel. Using the central three-row average of pixels from the calibration image, a fourth-order polynomial was fit to the lens intensity profile, Fig. 4. The profile was subsequently converted to represent intensity as a function of refraction angle. The intensity profile was found to span approximately 95 % of the cameras usable dynamic range.

Fig. 4
figure 4

Pixel intensity versus radius profile across standard lens

Full size image

It was determined that the charge needed to be positioned outside of the test section, as the test section size was limited by the mirrors. This was due to the shock wave not separating from the contact surface within the limited test section area and therefore not allowing a visualization of only the propagating shock wave in air. Thus, the explosive charge was positioned at a known standoff radius and laser aligned with the center of the mirror and pencil gage. Explosive charges were detonated, and the central row of pixels from each image was concatenated with respect to time to create a spatiotemporal intensity map of the shock wave, Fig. 5. As shown, the primary shock wave propagates from a starting radius of 0.15 m at ~0.1 ms, while the secondary shock wave becomes visible at later times. For each experiment, the shock wave radius profile was measured as a function of time. Dewey’s empirically developed radius versus time profile (Dewey 1971) was fit to the measured data and converted to a shock wave Mach number versus radius (Biss and Settles 2010).

Fig. 5
figure 5

Spatiotemporal digital intensity map

Full size image

The spatiotemporal shock wave intensity map was converted to a map of refraction angles using the calibration profile. In order to properly perform a deconvolution on the refraction angle data, it was necessary to apply padding to the image to represent the radial standoff region not visible in the schlieren test section. This was accomplished by padding the image with the background intensity value determined from the calibration image for the known radial standoff distance; the value could have just as well been padded with zeros, as the deconvolution is only affected by radial distances larger than the point of calculation. A two-point Abel deconvolution was performed on the refraction angle map according to Eqs. (2–4), yielding a map of the normalized refractive index difference δ. This was converted to an index of refraction η using Eq. (5) and subsequently to a density ρ according to Eq. (6). Peak radial temperatures were calculated at each pixel location using the previously generated shock wave Mach number versus radius profile and Eq. (9). Temporal temperature profiles were subsequently calculated at each pixel location, Eqs. (8–10). Combining these with the density map and Eq. (7), a spatiotemporal pressure map (gage pressure) was determined, Fig. 6. As shown, the primary shock wave exhibits a decaying trend, both radially outward and in time. Prior to the shock wave arrival, the ambient air is at atmospheric gage pressure or 0 kPa.

Fig. 6
figure 6

Spatiotemporal pressure map (note: all pressures are gage pressures)

Full size image

A series of pressure profiles were extracted from the pressure map at various radial standoff distances and plotted with respect to time, Fig. 7. As shown, the traces exhibit the characteristic blast wave profile: a sharp increase to peak shock wave pressure followed by an exponential decay back to atmospheric pressure and a negative phase pressure region followed by a second sharp increase and decay representing the secondary shock wave.

Fig. 7
figure 7

Optically measured temporal pressure traces at specified radial standoff distances from the charge center (note: all pressures are gage pressures)

Full size image

Optical pressure profiles for the specified pressure gage standoffs were plotted against the pencil gage traces for both experiments, Fig. 8. As shown, the calculated optical pressure profiles were in good agreement with the measured pencil gage profiles; however, both methods failed to capture the optically determined peak shock wave pressure. For the pencil gage, this was attributed to its inherent nearly 10-µs response time delay; whereas for the optical trace, it was hypothesized that this was due to inadequate camera resolution (temporal and spatial). As stated, optical pressure measurements were gathered at 300 kHz for every radial pixel location. As shown by Fig. 8, the optical pressure measurement possessed a faster response time than the pencil gage, but was slower than the generally accepted sampling rate of a MHz for blast wave pressure measurements. However, given the current Photron camera capabilities, a compromise between frame rate and spatial resolution was necessary, and therefore, 300 kHz was decided upon. Spatially, the images possessed sub-millimeter pixel resolution, 2.661 e−4 m/pixel. This was capable of being increased through use of a higher focal length camera lens; however, again, a compromise was necessary in order to capture a reasonable radial range of shock wave propagation and spatial resolution. Section 3.2 further addresses the effects of camera spatial resolution.

Fig. 8
figure 8

Temporal pressure trace comparison between pencil gages, optically calculated profiles, and the optical peak shock wave pressure for both experiments (note: all pressures are gage pressures)

Full size image

The calculated explosive impulses (Eq. 1) for the pencil gage and optical pressure measurements from experiment 14009-2 were tabulated in Table 2. A difference of only 14 % was determined between the two measurements. The experimental uncertainty was estimated to be 5 % for the pencil gage pressure measurements. The experimental uncertainty for the optical explosive impulse measurement was determined according to previous studies (Kolhe and Agrawal 2009; Moffat 1988). The average uncertainty in the calculated refraction angle was determined to be 3.4 %. This translated to a final uncertainty of 6 % for the optical explosive impulse measurements.

Table 2 Calcuated explosive impulse
Full size table

3.2 Flat-plate boundary layer

To test the previously stated spatial resolution hypothesis, a heated-flat-plate experiment was conducted to analyze the free-convective thermal boundary layer produced (Bigger 2008; Hargather and Settles 2012). Only a limited explanation is provided in the present manuscript; however, the previously mentioned references provide an in-depth and detailed experimental procedure.

The experiment consists of heating an aluminum plate (here, 0.152 m × 0.304 m × 0.013 m) to a constant temperature with a resistive heating blanket and variac controller. The heated plate was placed in the vertical orientation in the schlieren test section to image the free-convective thermal boundary layer produced. Using previously defined methods, the refraction angles across the thermal boundary layer were calculated from the pixel intensities and compared with the exact similarity solution (Ostrach 1952).

A Canon EOS Rebel T1i 8-bit handheld digital single lens reflex (dSLR) camera having a sensor resolution of 15 MPixels (4,752 × 3,168 pixels) was used to compare with the high-speed Photron sensor resolution (1,024 × 1,024 pixels). Flat-plate boundary layer schlieren images were taken and analyzed with both cameras. The plate maintained a surface temperature of 327 ± 3 K with a surrounding ambient temperature of 288 ± 1 K for the Canon image and a surface temperature of 329 ± 3 K and surrounding ambient temperature of 286 ± 1 K for the Photron image. Calibration images were taken with both cameras, refraction angles across the boundary layer were calculated, and results compared to the similarity solution. As shown in Fig. 9, the refraction angles measured by the handheld dSLR sensor compared exceptionally well (<3 % difference) with the similarity solution. The refraction angle profile measured by the Photron compared well with the similarity solution with the exception of near the surface of the plate where large thermal gradients existed. Thus, it may be concluded that the resolution of the high-speed Photron camera was inadequate for resolving the flat-plate thermal boundary layer and therefore would most certainly have been unable to resolve the peak shock wave pressure and initial decay of the explosive impulse profile.

Fig. 9
figure 9

Refraction angle versus distance comparison to similarity solution for across a flat-plate boundary layer using handheld dSLR and high-speed cameras

Full size image

4 Conclusions

An experimental technique to optically measure the explosive impulse produced by laboratory-scale spherical explosive charges detonated in air was investigated. The technique yielded two-dimensional pressure maps, from which, temporal pressure histories could be extracted at each radial pixel location. Pressure maps were developed from digital schlieren intensity maps that were converted using an Abel deconvolution, Rankine-Hugoniot jump equations, ideal gas law, triangular temperature decay profile, and Schardin’s standard photometric technique. Similar to pencil gage pressure measurements, derived impulses were found to be insufficient at resolving the peak and initial pressure decay profile. Optically derived impulses possessed a faster temporal response time than the pencil gage. It was determined that the digital high-speed camera resolution was insufficient to fully resolve the temporal pressure history near the peak pressure. However, it was shown that with increased sensor resolution, an improved impulse measurement is possible. It is proposed that the experiments be re-conducted using a digital high-speed streak camera that provides the necessary resolution (temporal and spatial) for resolving the blast wave decay.