Stereoscopic particle image velocimetry measurements of the flow around a surface-mounted block

Abstract

The advantages of 3D measurement techniques and the accuracy of the backward projection algorithm are discussed. The 3D calibration reconstruction used is based on an analytical relation between real and image co-ordinates. The accuracy of the stereoscopic particle image velocimetry (PIV) system is assessed by taking measurements of the flow in angular displacement configuration with prisms. A comparison is made with 2D PIV measurements and the accuracy of this stereo PIV algorithm is evaluated. By using this 3D measurement technique, the topology and the main 3D features of the flow around a surface-mounted block are investigated.

1 Introduction

Studies of the flow around a surface-mounted block with a free end and a finite height, for different Reynolds numbers and obstacle heights, evidenced some complex and strongly 3D topologies for these flows—Martinuzzi and Tropea (1993), Rodi et al. (1997), Calluaud et al. (2000) and Sousa (2002). In order to obtain an accurate comparison between experimental and 3D numerical results or simply to estimate the movements of the fluid and the flow organization by calculating the correlation between the various points, some reliable 3D instantaneous measurements are essential. Nowadays, 3D particle image velocimetry (PIV) measurement systems are well developed. There are different stereoscopic configurations (translation, angular or alternative systems) used for the recording of images. To reconstruct the 3D velocity fields, Prasad (2000) has classified these approaches depending on the data or the images and has evidenced three types of reconstruction: geometric, 2D calibration and 3D calibration methods. The first method is used when the geometry of the recording configuration is completely known as in Arroyo and Greated (1991) or Prasad and Adrian (1993). The 2D calibration-based reconstruction has been used for parallel or angular configuration by Willert (1997), Lawson and Wu (1997a, 1997b), Lecerf et al. (1999) and Westerweel and Van Oord (1999). Two mapping functions are calculated from a 2D grid calibration to link the two image references to the real reference. However, some knowledge of the geometry is still required. Finally, the 3D calibration method proposed by Soloff et al. (1997) does not need information about the stereoscopic geometry. The relation between the 2D image field and the 3D object field is approached by a polynomial approximation (third order terms for the in-plane direction, second or higher order terms in depth) and the 3D displacements are obtained by the resolution of a four-equation system with three unknowns using a least-square approach.

All of theses methods are now reaching maturity and give promising results.

In this context, the 3D calibration-based reconstruction suggested is a method from a real perspective camera model and without knowledge of the geometry for the calculation of the calibration matrix. The optical distortions are minimized in a first approach using prisms and large fixed focal lenses. First, the calibration technique used here and the backward projection method are explained, and then measurements from the study of the flow around a surface-mounted block are presented. The analysis of errors related to the calibration and the determination of the three velocity components is then carried out. Finally, the 3D flow topology and the main features of the flow are described.

2 The stereo PIV algorithm

2.1 The geometric back projection method

The purpose of this method is to establish the analytical relation between the object point co-ordinates and the image point co-ordinates for each camera. The calibration then consists of determining the internal and external parameters of each camera constitutive of the stereoscopic system. Whatever the selected model is, the transformation for a camera can be written:

$$ \left[ {\matrix{ {x_{\rm{i}} } \cr {y_{\rm{i}} } \cr 1 \cr } } \right] = {\bf{M}} \cdot \left[ {\matrix{ X \cr Y \cr Z \cr 1 \cr } } \right] $$

where (x _i, y _i) are the image co-ordinates corresponding to a point (X, Y, Z) of the object reference.

The selected model has been developed by Horaud and Monga (1995) and has been taken up again by Riou (1999). It is characterized by two transformations:

• A projection relationship between 3D object position (mm) and 2D image position (mm).

• A transformation of a metric reference related to the camera into a reference related to the image.

The optical distortions caused by an optical non-alignment, non-linearity of the lenses and/or optical refraction of windows, dioptres, and other optical elements of the experiment are not taken into account in this method. The real object co-ordinates can be obtained by considering the geometric transformations of the image reference into the object reference. Considering an image point (x _i, y _i) corresponding to a real point (X, Y, Z), the total transformation matrix for each camera is described as follows:

$$ {\bf{M}} = \left[ {\matrix{ {m_{11} } & {m_{12} } & {m_{13} } & {m_{14} } \cr {m_{21} } & {m_{22} } & {m_{23} } & {m_{24} } \cr {m{}_{31}} & {m_{32} } & {m_{33} } & {m_{34} } \cr } } \right] = {\bf{I}}_{\bf{c}} \cdot {\bf{A}} $$

where

$$ {\bf{I}}_{\bf{c}} = \left[ {\matrix{ {k_{\rm{u}} \cdot f} & 0 & {u_0 } & 0 \cr 0 & {k_{\rm{v}} \cdot f} & {v_0 } & 0 \cr 0 & 0 & 1 & 0 \cr } } \right]\; $$

and

$$ {\bf{A}} = \left[ {\matrix{ {r_{11} } & {r_{12} } & {r_{13} } & {t_{\rm{x}} } \cr {r_{21} } & {r_{22} } & {r_{23} } & {t_{\rm{y}} } \cr {r_{31} } & {r_{32} } & {r_{33} } & {t_{\rm{z}} } \cr 0 & 0 & 0 & 1 \cr } } \right]\; $$

are matrices expressing respectively the intrinsic parameters of the system (focal distance f, vertical and horizontal scale factors (k _u, k _v), intersection between the optical axis and the image plane (u ₀, v ₀)) and the extrinsic parameters (rotations r _ij , translations (t _x, t _y, t _z) of the CCD camera relative to the laser sheet, Scheimpflug angle β).

Knowing some object co-ordinates of reference points (target) and their respective projections in the image plane, the matrix can be obtained by numerical calculation. This 3D calibration method is based on an in-situ measurement of the target points whose co-ordinates are known.

In practice, this requires the solving of an over-determined linear system by a least squares method, without the knowledge of the experimental geometry of the device. In order to obtain a non-trivial solution, it is necessary to give at least one of the matrix coefficients. The explicit calculation of the coefficients of the matrix M, from I _c and A, particularly leads to: m ₃₁=r ₃₁, m ₃₂=r ₃₂, m ₃₃=r ₃₃, m ₃₄=t _z.

Therefore, it is easy to obtain:

$$ \left\| {m_3 } \right\| = \sqrt {m_{31} ^2 + m_{32} ^2 + m_{33} ^2 } = 1 $$

The resolution method proposed is related to this observation. The matrix is iteratively calculated in order to obtain ||m ₃|| close to unity. Thus, this iterative method does not require the introduction of a coefficient of the matrix M and makes it possible to obtain a matrix explicitly related to the geometry of the device camera/target and each parameters of the model.

The robustness and effectiveness of the method depend mainly on the calibration target point localization. This reconstruction method is simpler to implement and less subject to errors than some other reconstructions based on the knowledge of the recording geometry (geometric-based reconstruction) or using the introduction of parameters (2D calibration reconstruction).

2.2 The stereoscopic reconstruction

In the first step, the images of the flow seeded with particles are treated by cross-correlation via FFT. Thus, vector field projections on each camera are produced. In order to find the real components of the vectors in the object reference, it is necessary to determine for each vector obtained from a camera, its correspondent on the other camera. This matching can be carried out in two ways:

• By a "classical" 2D correlation of the images on a Cartesian mesh followed by an interpolation of the vector fields towards the unstructured mesh of pairing.

• By an image correlation directly carried out towards the unstructured mesh of pairing (correlation on non-rectangular interrogation areas in order to compare identical physical zones on both cameras).

Between these two matching methods, the first one has been chosen for this application. The treatment used for the cross-correlation is an adaptive multi-pass correlation on the 32×32 pixel final interrogation area with an overlap of 50%. The vectors, having a signal/noise ratio under 1.2 or filtered by the median filter, are not taken into account during the interpolations. Thus, the vector fields are calculated by the coupled method of least squares—spline thin shell, Spedding and Rignot (1992).

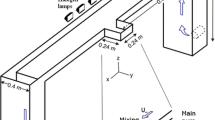
Projections of the velocity vectors on each camera, which correspond to the same real displacements, are associated. The three velocity components are given numerically with the matrices M ₁ and M ₂ of each camera. The origins of the interpolated vectors from each point of view (noted as A1 and A2, Fig. 1b) are known and located in the median plane of the laser sheet in a point A with real co-ordinates in the measurement reference (X _A, Y _A, Z _A). The ends of the homologous velocity vectors on each camera (noted as B1 and B2, Fig. 1b) correspond to a point B (X _B, Y _B, Z _B) in the object reference. The last co-ordinates are calculated numerically by solving the system (Eq. 1) and the three velocity components can then be obtained simply (Eq. 2).

Fig. 1.

a Dimension of the obstacle; b stereoscopic PIV configuration

$$ \left\{ {\begin{array}{*{20}l} {{{\left( {\begin{array}{*{20}c} {{x_{{{\text{A}}_{i} }} }} \\ {{y_{{{\text{A}}_{i} }} }} \\ {1} \\ \end{array} } \right)} = {\mathbf{M}}_{i} \cdot {\left( {\begin{array}{*{20}c} {{X_{{\text{A}}} }} \\ {{Y_{{\text{A}}} }} \\ {{Z_{{{\text{median laser sheet}}}} }} \\ {1} \\ \end{array} } \right)}\;{\text{with}}\;i = 1,\;2} \aftergroup \hfill} \\ {{} \aftergroup \hfill} \\ {{{\left( {\begin{array}{*{20}c} {{x_{{{\text{B}}_{i} }} }} \\ {{y_{{{\text{B}}_{i} }} }} \\ {1} \\ \end{array} } \right)} = {\mathbf{M}}_{i} \cdot {\left( {\begin{array}{*{20}c} {{X_{{\text{B}}} }} \\ {{Y_{{\text{B}}} }} \\ {{Z_{{\text{B}}} }} \\ {1} \\ \end{array} } \right)}\;{\text{with}}\;i = 1,\;2} \aftergroup \hfill} \\ \end{array} } \right. $$

(1)

$$\left\{ {\matrix{ {{\rm u} = \left( {{\rm X}_{\rm B} - {\rm X}_{\rm A} } \right)} \hfill \cr {} \hfill \cr {{\rm v} = \left( {{\rm Y}_{\rm B} - {\rm Y}_{\rm A} } \right)} \hfill \cr {} \hfill \cr {{\rm w} = \left( {{\rm Z}_{\rm B} - {\rm Z}_{\rm A} } \right)} \hfill \cr } } \right.$$

(2)

The accuracy of the calculated 3D fields depends mainly on the errors introduced by the 2D velocity field measurements, the interpolation of these fields and the calibration.

3 Experimental configurations

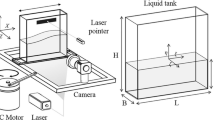
To measure the three velocity components, a stereoscopic system of PIV is developed and applied to the study of the laminar flow around a block mounted on a flat plate (Fig. 1a). Characteristic dimensions of the obstacle are its side D=60 mm and its height H=18 mm. The surface-mounted cube is placed 4 cm from the leading edge of the plate on which it is mounted. The Reynolds number, which is calculated from the block side and the uniform flow velocity U ₀, is 1,000. The experiment is performed in a fully developed hydrodynamics channel flow. The dimensions of the channel are 80 cm×16 cm×16 cm (length×width×height). Various sections of the flow are illuminated by means of a 30-mJ Mini-Yag laser. The seeding of the fluid is carried out with solid particles (hollow glass particles). Visualizations of the flow are recorded by two cross-correlation cameras with 768×484 pixel² resolution. The objectives chosen for this study are Nikon objectives of 105 mm fixed focal length with an aperture of 8. The size of the visualized zone is 86 mm in the X direction and 44 mm in the Y direction. The 2D velocity fields are measured by the flowmap software of Dantec Dynamics Company, by double frame image processing by adaptative cross-correlation via fast Fourier transform (FFT) on final size 32×32 pixels of windows with an overlap of 50%. In order to reduce the optical aberrations caused by the passage through the air–Altuglas–water dioptre as in Prasad and Jensen (1995), prisms filled with water are laid out against the faces of the hydrodynamic channel. The viewing angles of cameras 1 and 2 are fixed respectively at 45° and −45° with respect to the X axis. The Scheimpflug arrangement is used to obtain entirely focused images and small distortions (Fig. 1b). The experiments were carried out for several flow sections (Z=0, −10, −20 and −30 mm).

To compare and evaluate the stereo PIV measurements, the flow was also investigated with 2D PIV. For the 2D PIV, the prism arrangement was removed and the cameras were placed perpendicularly to the visualized section. All the others characteristics of the experimental device and hydrodynamics channel remained unchanged. The same PIV software was used and the flow was illuminated on the same Z sections.

4 Estimate of 3D measurements

In order to determine the matrix coefficients, it is essential to place in the zone to be visualized a set of points for which one knows the co-ordinates in the object reference. We therefore use a black background target on which are placed 1-mm diameter white circles spaced 1 cm apart. By moving this target in various sections Z spaced every 0.5 mm, we obtain a 3D object grid and its projections on the two cameras. The matrix coefficients for the two cameras are then calculated.

An algorithm has been developed to enable the automatic detection of the image co-ordinates of the target points. A threshold of the images is used to detect the pixels that correspond to the target points. Then, the co-ordinates (x _i, y _i) of the target point (X, Y, Z) in the image reference are identified. Those co-ordinates x _i and y _i are obtained by performing a centroid analysis, weighted by grey levels, on the detected spots. After the localization of the target points in the images of camera 1 and 2, matrices M ₁ and M ₂ are calculated.

The errors introduced by the localization technique are then quantified. The real co-ordinates of the target points are calculated by reconstruction from the matrices and the target points images co-ordinates (x ₁, y ₁) and (x ₂, y ₂). Thus, we can estimate the errors introduced by the calibration while defining the amplitudes, the averages and the RMS of the differences between the real co-ordinates (X _R, Y _R, Z _R) and the reconstructed co-ordinates (X _M, Y _M, Z _M) of the target points.

$$ \left\{ \matrix{ E_{\lambda _i } = \lambda _{{\rm{M}}_{\rm{i}} } - \lambda _{{\rm{R}}_{\rm{i}} } \hfill \cr \left\| {E_{\rm{X}} ,\;E_{\rm{Y}} ,\;E_{\rm{Z}} } \right\|_i = \sqrt {E_{{\rm{X}}_i } ^2 + E_{{\rm{Y}}_i } ^2 + E_{{\rm{Z}}_i } ^2 } \hfill \cr \overline {E_\lambda } = {1 \over N}\sum\limits_{i = 1}^N {\left| {E_{\lambda _i } } \right|} \hfill \cr E_\lambda ^\prime = \sqrt {{1 \over {\left( {N - 1} \right)}}\sum\limits_{i = 1}^N {E_{\lambda _i } ^2 } } \hfill \cr} \right. $$

with λ=X, Y, Z and N the number of localized points.

Since the matrix coefficients vary with the number of calibration planes and the adjustment of their positions, the transformation matrices between cameras and object references are robustly defined when the number of localized points is superior to 250, Riou (1999). Consequently, the target is moved through 17 sections in order to have over 400 localized points. Under these conditions the values $\overline {E_\lambda }$ and $E'_\lambda$converge.In the different sections Z=0, −10, −20 and −30 mm downstream of the obstacle, we obtain average and RMS values $\overline {E_\lambda }$ and $E'_\lambda$ varying between 16.6 and 47.4 µm, 6.3 and 12.3 µm, and 25.8 and 40.9 µm respectively for λ=X, Y, Z. The knowledge of $\overline {E_\lambda }$ and $E'_\lambda$ allows us to analyse the various errors that could be introduced during the calibration. Their values seem to be extremely low as compared with the errors obtained during the two bi-dimensional velocity field measurements and with those associated with the selected interpolation method, David et al. (2002).

The difference between the back-projected and the true positions of the target points are plotted in Fig. 2, which show that the error is smaller than to 80 µm. This difference, for the Y co-ordinate, is less than to 20 µm, which corresponds to a localization error of the target points in the images. The errors introduced in the calibration matrix correspond mainly to a dispersion of the dots in the X and Z direction.

Fig. 2.

The difference between the back-projected and the true position of the dots for the measurement in the plane Z=0 mm

The absolute value between back-projected and true position as a function of the distance from the image origin is plotted in Fig. 3. In contrast with the results obtained by Westerweel and Van Oord (1999), the error is independent of the position. The dots are concentrated in a region with an absolute error varying between 10 µm and 60 µm. The dots with an absolute error larger than 60 µm correspond to a poor localized accuracy: more than 0.8 pixels in the images of cameras 1 and 2.

Fig. 3.

Absolute difference between the back-projected and the true positions as a function of distance of the image origin for the measurement in the plane Z=0 mm

Finally, to confirm the linear camera model approach for this application, the dispersions between the projected points on a same line of the target and the nearest line defined by the points are evaluated and have a mean value of 0.13 pixels, which is the accuracy of the point detection.

In spite of the accuracy of the calibration, the stereo PIV measurements require a correct cross-correlation of the images, an accurate interpolation step of the 2D velocity fields and a precise reconstruction of those 2D velocity fields. Thus, we first compare real and stereoscopic PIV reconstructed displacements for a group of particles fixed in a block of resin. The differences between these displacements are calculated on the whole field for the three components (Table 1) and have the same order as those presented by Willert (1997) or Soloff et al. (1997).

Table 1. Variation of the 3D measured displacements for a real displacement of 1.5 mm in the three directions

Comparisons are made also between profiles of average velocity components U and V measured by 2D PIV and stereo PIV, computed by respectively 1,200 and 1,000 acquisitions (Figs. 4 and 5) with two recording rates (10 and 15 Hz). We note the correct resolution and reconstruction of the in-plane components by our stereo PIV algorithm. The results obtained by 2D PIV and stereo PIV seem similar. Nevertheless, there is a difference for the V component for Y varying between 0 mm and 15 mm for the two sections X=69.505 mm and X=78.952 mm. These differences could have several explanations. First, this flow is characterized by small displacements (0 to 7% of U ₀) in this area for Y fewer than 15 mm. The stereo PIV technique requires also the use of a large laser sheet thickness. Hence, the flow images are saturated near the flat plate and give a noisy signal.

Fig. 4.

Mean velocity component U/U ₀ measured by 3D PIV and 2D PIV in the section Z=0 mm

Fig. 5.

Mean velocity component V/U ₀ measured by 3D PIV and 2D PIV in the section Z=0 mm

5 Flow investigations by stereo PIV measurements

The stereoscopic PIV algorithm has been previously used to investigate the complex aspects of the flow around surface-mounted cubic obstacle: the existence of a horseshoe vortex upstream of the obstacle and the presence of 3D vortices have been evidenced. Downstream of the obstacle, at the interior of the horseshoe vortex separation line, a low-pressure region produces vortices with axes in the Y direction (Fig. 6a). The section Z=0 mm shows the complex flow topology behind the obstacle. A stagnation point downstream of the obstacle is apparent. Under this point, a return of fluid per aspiration on the higher part of the cube is generated. Because of the strong shearing region, which is created by interaction between an accelerated flow in the positive direction and the return of fluid in the opposite direction, some vortices are created and escape from the obstacle towards the wake (Fig. 6b).

Fig. 6.

a Particle visualization in the section Y=0 mm; b electrochemical tracer visualization in the section Z=0 mm

Figure 7 shows the mean velocity fields computed from 1,000 instantaneous velocity fields acquired by our stereo PIV technique. This figure confirms the return of fluid at the top of the obstacle for sections Z=0 mm and Z=−10 mm: some regions where the U component is negative are highlighted. In the other sections, this dynamic of the flow is not present. The absolute value of the out-of-plane component W in the section Z=0 mm, symmetric to the plane of the flow, is near zero. In sections Z=−20 mm and Z=−30 mm, this component confirms the 3D flow topology downstream of the obstacle: the vortex is illustrated by a positive W component area downstream of the cube (Fig. 7b and c) and an area with negative W component showing the presence of a detachment zone that causes the fluid coming from upstream to skirt this zone at the top of the cube. The section Z=−10 mm shows a vortex with an axis parallel to Z and a considerable negative W component zone. The latter emphasizes the form of the vortex core downstream of the cube (Fig. 8).

Fig. 7a–d.

Mean in-plane vector fields and contour plot of the mean out-of-plane velocity component in section. a Z=0 mm, b Z=10 mm, c Z=−20 mm, d Z=−30 mm

Fig. 8.

Schematic representation of the flow around a surface-mounted cube, Re=40,000, H=D, by Martinuzzi and Tropea (1993)

Being the link between spatial evolution of the vortex shedding and the velocity fluctuation, the turbulence intensity illustrates the dynamic downstream of the cube. Figure 9a and b show the turbulence intensity computed with and without the out-of-plane component W. In spite of the fact that these figures present different sections according to X where the spatial resolution is low (the acquisitions are carried out according to Z planes spaced every 10 mm), different zones where the turbulence intensity is significant have been observed. The comparison of these figures enables the observation of the out-of-plane component W contribution to the unsteady flow. Until abscissa X=100 mm, the maximum turbulence intensity zones are similar: the flow, and in particular the vortex shedding are defined by velocity fluctuations according to components u′ and v′. Beyond this abscissa, the maximum turbulence intensity areas are different: the vortex shedding seems to be defined by fluctuations according to three components and the influence of the W component becomes considerable. By the 2D turbulence intensity computation, the vortex shedding is characterized by a space evolution at a fixed altitude: at X=140 mm, the points where the turbulence intensity is maximum, are localized at Y=28 mm for the sections Z=±10 mm. The areas with important turbulence intensity described by 3D calculation characterize the 3D vortex shedding evolution and the influence of the W component on the unsteady flow. Therefore, the vortex shedding is primarily localized in sections Z=0 mm and Z=−10 mm and the out-of-plane component contribution is essential to understand the flow dynamics and the evolution of the swirling.

Fig. 9a, b.

Turbulence intensity by 3D PIV measurements. a ${It_{{2{\rm{D}}}} = {\sqrt {{\left( {({u'}^{2} + {v'}^{2} )/U_{0} } \right)}} }}$; b ${It_{{{\rm{3D}}}} = {\sqrt {{\left( {{\left( {{u'}^{2} + {v'}^{2} + {w'}^{2} } \right)}/U_{0} } \right)}} }}$

In order to study the interesting features of the flow and any coexistence of 3D vortices, we need a tool to identify coherent structures. Different quantities have been used in the past to identify the various important features of the flow. Vorticity is one such quantity that will show the presence of the swirling motion. The out-of-plane component of vorticity (ω _z) has been used to detect the interesting regions in the flow and does indeed detect regions of swirl but was unable to differentiate between straining zone and vortex structure. For that reason, the quantity Q _2D that is based on the Q criterion, defined as the second invariant of the velocity gradient tensor Jeong and Hussain (1995) has been computed in order to differentiate those two phenomena. Large positive values of Q _2D suggest the presence of a vortex and negative values indicate a straining region. It was noted that both these quantities perform well in identifying the interesting features of the flow. We will use Q _2D to illustrate the various regions of the flow field.

$$ \left\{ \matrix{ \omega _{\rm{Z}} = \left[ {{{\partial V} \over {\partial X}} - {{\partial U} \over {\partial Y}}} \right] \hfill \cr Q_{2{\rm{D}}} = - {1 \over 2}\left[ {{{\partial U} \over {\partial Y}}{{\partial V} \over {\partial X}}} \right] \hfill \cr Q = Q_{2{\rm{D}}} - {1 \over 2}\left[ {{{\partial W} \over {\partial Y}}{{\partial V} \over {\partial Z}} + {{\partial U} \over {\partial Z}}{{\partial W} \over {\partial X}}} \right] \hfill \cr} \right. $$

It is very important to note that all quantities have been computed with just the in-plane velocity gradients, and hence only the components of the 2D velocity gradient tensor have been considered.

Figures 10 and 11 illustrate the 3D degree of the flow for two flow sections and two different times. The out-of-plane component of vorticity (ω _z) and the criteria Q _2D allow the identification of the vortex structure defined by the in-plane components. The derivates ∂W/∂X and ∂W/∂Y can help for the determination of the out-of-plane component part of the coherent structure and the instantaneous flow topology downstream of the obstacle.

Fig. 10a–f.

Section Z=0 mm. a Instantaneous in-plane velocity components; b instantaneous out-of-plane velocity components; c vorticity ω _Z; d Q _2D criteria; e ∂W/∂X; f ∂W/∂Y

Fig. 11a–f.

Section Z=10 mm. a Instantaneous in-plane velocity components; b instantaneous out-of-plane velocity components; c vorticity ω _Z, d Q _2D criteria; e ∂W/∂X; f ∂W/∂Y

In section Z=0 mm, the quantities ∂W/∂X and ∂W/∂Y show the low influence of the out-of-plane component. For the vortices 1 and 2, ∂W/∂X and ∂W/∂Y reveal limited regions with negligible amplitudes. The study of vortex 2, which escapes towards the wake from the obstacle, shows the spatial evolution of the vortex shedding and the in-plane component effect and consequence.

The section Z=−10 mm, which is a region of important velocity fluctuations, allows the evaluation of the 3D flow features. The coherent structures localized by Q _2D and ω _z seem to have some relation with the W component. For vortex 3, ∂W/∂Y evidences an important zone with significant Q _2D and ω _z values. This shows the interest of the 3D measurement and the influence of the out-of-plane component. For abscissae over 100 mm, ∂W/∂X and ∂W/∂Y show a strong 3D nature of the flow. The study of those quantities for vortex 4 allows the understanding of the evolution of the flow and the flow dynamics. The coherent structure 4 moves downstream with an angle of 26° with the X axis and is characterized by a significant out-of-plane component. Zone 5, which is also characterized by significant out-of-plane component amplitude, shows the interest of an instantaneous 3D measurement and the 3D dynamics of the flow around a rectangular cylinder. Knowledge of the W component seems, for this section, to be essential for the comprehension of the dynamics of the vortex shedding. Indeed, Q _2D calculated with the U and V components reveals coherent structure 4 with low amplitude and a limited zone. Q _2D exposes the low influence of the in-plane components on vortex shedding.

6 Conclusions

To acquire information about the complex topology of the flow around a surface-mounted block, a 3D velocity measurement technique using stereoscopic PIV has been developed. It consists of a 3D calibration-based reconstruction written from a real linear camera model, and does not require the introduction of parameters nor the knowledge of the geometric configuration of the stereoscopic system in order to determine the calibration matrices. The use of a prism to mechanically reduce the distortions and other optical aberrations appears essential and simpler to implement than the compensation in the matrix calculation (which would require the solution of a non-linear system). The accuracy of the calibration step is highlighted by different criteria in an in-situ calibration. The various errors that can arise during the calibration step seem to be extremely small as compared with the errors obtained during the two bi-dimensional velocity field measurements and compared with those associated with the selected interpolation method. The velocity fields acquired by our stereo PIV algorithm appear similar to those obtained by 2D PIV acquisitions in various sections for the in-plane components. Knowledge of the three velocity components is essential for the comprehension of flows. In spite of the interest in the average quantities $\left( {\overline u {\rm{,}}\;\overline v {\rm{,}}\;\overline w {\rm{,}}\;u'{\rm{,}}\;v'{\rm{,}}\;w'{\rm{,}}\;It} \right)$, 3D instantaneous velocity field measurements have an essential advantage and enable the understanding and the study, with the use of different tools, of the flow shearing and stretching zones and the spatial evolution of the vortices. With the help of this additional and new information, quantitative investigations of real 3D flows like flow around a surface-mounted block can be supplemented.