The effect of light and heavy holes on THz radiation generation in GaAs exposed to femtosecond pulse in magnetic field

Abstract

The detailed analysis of the effect of light and heavy holes on the generation of terahertz (THz) radiation in GaAs in a magnetic field is given. It is shown that taking into account the motion of light holes leads to a relative increase in the field strength of the THz pulse by several times. Such an increase manifests itself at times comparable to or greater than the inverse plasma frequency of electrons and is accompanied by a relative increase in the spectral density of radiation at low frequencies. In the frequency range from 0.1 to 10 THz, the affect of heavy holes is weak and resulted in a small change in the spectral energy density at frequencies slightly higher than 0.1 THz, which leads to a relative increase in the THz field strength at the last stage of generation.

1 Introduction

When a semiconductor is exposed to a femtosecond laser pulse with frequency greater than bandgap, photoelectrons and holes are generated. The generation occurs in the laser field localization region and the density of photoelectrons and holes changes on the field localization scale. Subsequent redistribution of electrons and holes in space leads to a time-varying current, which is a source of THz radiation. Such radiation has been observed in many experiments, including in the presence of a constant magnetic field, which significantly affects the motion of electrons and holes. In particular, a large number of experiments have been performed using GaAs [1,2,3,4,5,6] and InAs [4, 5, 7,8,9,10,11,12] semiconductors. At photoexcitation of these semiconductors simultaneously with the generation of photoelectrons there is generation of light and heavy holes. At the same time, when interpreting most experiments, it was believed that the contribution to the THz radiation generation from holes can be neglected. The helpfulness of this approximation is due to the fact that in GaAs and InAs the light holes density is approximately three times less than the photoelectrons density [9, 12,13,14], and the affect of heavy holes is small due to relatively large value of their effective mass [1, 6, 15,16,17]. However, it is clear that due to the proximity of the effective masses of electrons and light holes, the latter can lead to noticeable quantitative changes in the generation of THz radiation. The influence of heavy holes can also manifest itself at later times, or in sufficiently strong magnetic fields [18].

Taking into account the above, in the present communication a detailed analysis of the influence of light and heavy holes on the generation of THz radiation in a semiconductor in magnetic field is given. The analysis is performed for GaAs, which is exposed to the femtosecond laser pulse with the wavelength of 800 nm. Calculations of the THz pulse shape and spectral energy density are performed for three values of magnetic field strength, when the cyclotron frequency of electrons is less than, equal to, or greater than the plasma frequency of electrons. For the selected conditions of GaAs photoexcitation, it was found that the affect of light holes is stronger in a weak magnetic field and is most pronounced at times greater than the inverse electron plasma frequency. At such times, the influence of light holes leads to a relative increase in the field strength of THz pulse by several times. Such a noticeable quantitative increase in the generated pulse is due to the fact that photoelectrons and holes move across the magnetic field in opposite directions, leading to an increase in the total current along the surface of the semiconductor. The motion of heavy holes in the considered conditions leads to insignificant changes in the pulse shape at long times and a small change in the radiation spectral density at low frequencies. However, this does not mean that situations are impossible in which the influence of heavy holes will be significant, similar to that observed in [18].

2 Generation of electrons and holes

Let us assume that a semiconductor occupying the region $x> 0$ is located in a constant magnetic field ${\textbf {B}}_0 = (0,0, B_0)$ directed along its surface (see Fig. 1). Let such semiconductor be exposed to a laser pulse propagating along ox axis and having carrier frequency $\omega _0$ greater than $E_g/\hbar$, $E_g$ is the energy band gap, $\hbar$ is Planck’s constant. Under the effect of such pulse, electrons and holes are generated. We consider the electron concentration $n_e(x,t)$ to be small, and their plasma frequency $\omega _{pe}$ to be lower $\omega _0$. Typically, the effective mass of heavy holes $m_{*h}$ is several times greater than the effective mass of electrons $m_{*e}$, and the effective mass of light holes $m_{*l}$ is slightly larger than that of electrons. Therefore, the plasma frequencies of light and heavy holes are also much less than $\omega _0$. The electric field of laser pulse can be represented as ${\textbf {E}}_ L \left( t-x/c\right) \text {cos}\left[ \omega _0 \left( t-x/c\right) \right]$, where the envelope ${\textbf {E}}_ L(t)$ is changing over time $t_p\gg 1/\omega _0$ and ${\textbf {E}}_ L \left( t\right) ||{\textbf {B}}_0$, c is the speed of light. Laser radiation penetrates into the semiconductor to a depth of $1/\alpha$, where $\alpha$ is the absorption coefficient. Usually $\omega _0 \sqrt{\varepsilon _0} \gg \alpha c$, where $\varepsilon _0$ is the permittivity in the absence of photoexcitation. Under these conditions, the electric field in the semiconductor has the form ${\textbf {E}}_ L \left( t-\sqrt{\varepsilon _0}x/c \right) \text {exp}\left( -\alpha x/2 \right) \text {cos}\left[ \omega _0 \left( t-\sqrt{\varepsilon _0}x/c \right) \right]$, where $T=2/(1+\sqrt{\varepsilon _0)}$.

Fig. 1

THz radiation generation scheme

In the case of a quadratic dependence of particle energy on momentum, the characteristic velocity of electrons arising at the absorption of photons with energy $\hbar \omega _0$ and the generation of a heavy hole is equal to $\sqrt{2(\hbar \omega _0-E_g)m_{*h}/(m_{*h}+m_{*e})m_{*e}}$. In GaAs, where $E_g =1.42$ eV, $m_{*e}=0.61\times 10^{-28}$ g and $m_{*h}=7.6 m_{*e}$, at $\omega _0=2.3\times 10^{15}\hbox {s}^{-1}$ the photoelectrons velocity is equal to $6.6\times 10^{7}$ cm/s. The heavy hole velocity is 7.6 times less. When a light hole in GaAs with $m_{*l}=1.2 m_{*e}$ is generated, the photoelectrons velocity is equal to $5.2\times 10^{7}$ cm/s. If $t_p=20$ fs, then electrons are displaced to a distance of $\sim 1.3\times 10^{-6}$ cm during the pulse impact. This distance is much less than $1/\alpha \approx 0.8 \times 10^{-4}$ cm—the penetration depth of laser radiation into GaAs at frequency $\omega _0$ [19]. The displacement of holes during the pulse impact is rather small. To describe particles generation by a short laser pulse, we use the equations for there distribution functions $f_{\beta }(x,p,t)$:

$$\begin{aligned} \frac{\partial }{\partial t}f_{\beta }(p,x,t)=\frac{\alpha _\beta I(x,t)}{\hbar \omega _0}f_{0\beta }(p). \end{aligned}$$

(1)

Here the index $\beta$ takes the values e, l, h for electrons, light and heavy holes, respectively, $f_{0\beta }(p)$ are the distribution functions normalized to unity, $\int f_{0\beta }(p)d{\textbf {p}}=1$, $I(x,t)=c|T{\textbf {E}}_{L}\left( t-x\sqrt{\varepsilon _0}/c\right) |^2\text {exp}\left( -\alpha x\right) /8\pi$, $\alpha _\beta$ is the absorption coefficient at the generation of $\beta$ type particles. Equation (1) is written under the assumption that the distribution of photoexcited particles is isotropic. Strictly speaking at photoexcitation the distribution of particles depends on both the laser radiation polarization and the semiconductor band structure. There are two reasons for using this approximation. First, we consider conditions when photoexcited particles are located near the bottom of the corresponding GaAs bands, where the influence of anisotropy on particle motion is small. Second, the currents responsible for the THz radiation generation are determined by the integrals of the particle distribution functions over all momentum directions. The latter leads to a strong smoothing of the influence of the particle distribution anisotropy. The absorption coefficients $\alpha _\beta$ depend on the reduced effective masses of electrons and holes. For light holes $\alpha _l\sim (m_{*l}m_{*e}/(m_{*e}+m_{*l}))^{3/2}$ and for heavy ones - $\alpha _h\sim (m_{*h}m_{*e}/(m_{*e}+m_{*h}))^{3/2}$. The quantities $\alpha _l$ and $\alpha _h$ obey the condition $\alpha _e=\alpha =\alpha _h+\alpha _l$, which corresponds to the electrical neutrality condition. In particular, for GaAs the number of generated heavy holes is approximately twice as large as light holes. Integrating over the time of laser pulse impact, from (1) we find the photoelectrons density after time $\sim t_p$: $n_e(x)=n \exp (-\alpha x)=(\alpha /\hbar \omega _0)\int I(x,t)dt.$ For the concentrations of light and heavy holes we have $n_l(x)=n_l \exp (-\alpha x)=\alpha _l n_e(x)/\alpha , n_h(x)=n_h \exp (-\alpha x)=\alpha _h n_e(x)/\alpha$.

3 Low frequency currents

The redistribution of electrons and holes occurs throughout the semiconductor. As a result, $\delta f_\beta (x,{\textbf {p}},t)$ appear, that are the inhomogeneous time-dependent corrections to the distribution functions of photoelectrons and holes $f_{\beta }(x,p)=n_\beta (x )f_{0\beta }(p)$ formed after the laser pulse impact. To find $\delta f_\beta (x,{\textbf {p}},t)$ we use kinetic equations of the form (cf. [20, 21]):

$$\begin{aligned} & \left( \frac{\partial }{\partial t}+\nu _\beta +\frac{q_\beta }{m_{*\beta }c}[{\textbf {p}} {\textbf {B}}_0]\frac{\partial }{\partial {\textbf {p}}}\right) \delta f_\beta (x,{\textbf {p}},t)=\nonumber \\ & \quad -\left( q_\beta {\textbf {E}}(x,t)\frac{\partial }{\partial {\textbf {p}}}+\frac{p_x}{m_{*\beta }}\frac{\partial }{\partial x}\right) f_{\beta }(x,p), \end{aligned}$$

(2)

where $q_e=e,q_l=q_h=-e$, e is the electron charge, $\nu _\beta$ is the $\beta$ type particles collision frequency, $\textbf{E}(x,t) = \left( E_x(x,t), E_y(x,t), 0 \right)$ is the low-frequency electric field arising due to the evolution of inhomogeneous distribution of photoelectrons and holes. Usually the mean free path of photoelectrons and holes is less than the function $\delta f_\beta (x,{\textbf {p}},t)$ inhomogeneity scale. Therefore in the Eq. (2) the derivative with respect to the coordinate is omitted. When the photoelectrons and holes move in the semiconductor, an electric current arises, which is a source of low-frequency electromagnetic field. To find the densities of low-frequency currents of electrons and holes $\textbf{j}_\beta (x,t) = \left( j_{x\beta }(x,t), j_{y\beta }(x,t), 0 \right)$, we integrate the Eq. (2) with the weight $q_\beta {\textbf {p}}/m_{*\beta }$ over the particle momenta. Then, taking into account the explicit form of the electron and hole densities dependence on the coordinate, we have

$$\begin{aligned} & \frac{\partial }{\partial t} \mathbf{j_\beta }(x,t)-\Omega _\beta \left[ \mathbf{j_\beta }(x,t)\textbf{b} \right] +\nu _\beta \mathbf{j_\beta }(x,t) \nonumber \\ & = \frac{q_\beta ^2n_\beta (x) }{m_{*\beta }}\left[ \textbf{E}(x,t)+\frac{1}{q_\beta } \textbf{F}_{\beta }\right] , \end{aligned}$$

(3)

where $\textbf{b}=(0,0,1)$ is the unit vector along the constant magnetic field, $\Omega _\beta =q_\beta B_0/m_{*\beta } c$ are the cyclotron frequencies, $\mathbf{F_{\beta }}=(F_{\beta },0,0)$ and

$$\begin{aligned} F_{\beta }= & \frac{1}{n_\beta (x) m_{*\beta }} \int p_x^2 \frac{\partial }{\partial x} f_{\beta }(x,p) d \textbf{p} \nonumber \\= & -\frac{\alpha }{m_{*\beta }} \int p_x^2 f_{0\beta }(p) d \textbf{p}. \end{aligned}$$

(4)

The forces $\mathbf{F_{\beta }}$ arise due to the inhomogeneous photoexcitation of electrons and holes. When calculating integrals in the expression (4), we assume that distribution functions at the end of the laser pulse impact in moment $t=0$ have the form: $f_{0e}=[\alpha _l\delta (p-p_l)+\alpha _h\delta (p-p_h)]/4\pi p^2\alpha , f_{0\gamma }=\delta (p-p_\gamma )/4\pi p^2$, where $p_\gamma =\sqrt{2(\hbar \omega _0-E_g)m_{*\gamma }m_{*e}/(m_{*\gamma }+m_{*e})}$ are particle momenta at the generation of a light and heavy holes, $\gamma =l,h$. Here and below the index $\gamma$ denotes only the holes types. In this case we have $F_{\gamma }=F_{e} m_{*e}\alpha p^2_\gamma / m_{*\gamma }(\alpha _l p^2_l+\alpha _h p^2_h)$. Further we use the Laplace transform with respect to time assuming that $\mathbf{j_\beta }(x,0)=0$. Then from (3) we find images of the low-frequency current densities $\textbf{j}_\beta (x, \omega )$:

$$\begin{aligned} j_{s\beta }(x,\omega )=\sigma _{sk\beta }(x,\omega ) \left[ \textbf{E}(x,\omega ) +\frac{i\mathbf{F_{\beta }}}{q_\beta \omega }\right] _k. \end{aligned}$$

(5)

Here $\sigma _{s k\beta }(x,\omega )$ is the conductivity tensor of the $\beta$ type particles,

$$\begin{aligned} \sigma _{sk\beta }(x,\omega )= & \frac{q_\beta ^2 n_\beta (x)}{m_{*\beta }} \frac{i(\omega +i\nu _\beta )}{(\omega +i\nu _\beta )^2-\Omega _\beta ^2} \nonumber \\ & \times\left( \delta _{sk} + \frac{i\Omega _\beta }{\omega +i\nu _\beta } \epsilon _{sk r}b_r\right) , \end{aligned}$$

(6)

$\delta _{sk}$ is the Kronecker delta, $\epsilon _{s k r}$ is the Levi-Civita symbol.

4 Low-frequency pulse field

From Maxwell’s equations for images of the electric and magnetic fields, we have the system of equations

$$\begin{aligned} \frac{\partial }{\partial x}E_y(x,\omega )= & \frac{i\omega }{c}B_z(x,\omega ), \end{aligned}$$

(7)

$$\begin{aligned} 0= & -i\omega \varepsilon _0 E_x(x,\omega )+4\pi \sum \limits _{\beta } j_{x\beta }(x,\omega ), \end{aligned}$$

(8)

$$\begin{aligned} -\frac{\partial }{\partial x}B_z(x,\omega )= & -\frac{i\omega }{c}\varepsilon _0 E_y(x,\omega )\nonumber \\ & \quad +\frac{4\pi }{c} \sum \limits _{\beta } j_{y\beta }(x,\omega ), \end{aligned}$$

(9)

where $\sum \limits _{\beta }$ denotes summation over particle types. Taking into account Eqs. (5) and (6), after excluding $E_x (x,\omega )$ and $B_z (x, \omega )$ from the Eqs. (7) to (9), we obtain equation for the image of the tangential component of electric field $E_y (x, \omega )$:

$$\begin{aligned} & \frac{\partial ^2}{\partial x^2}E_y (x, \omega )+\varkappa ^{2}(x,\omega )E_y (x, \omega ) =\frac{4\pi }{e^2c^2\varepsilon _{xx}(x,\omega )}\nonumber \\ & \quad \times \left[ \varepsilon _{xx}(x,\omega ) \sum \limits _{\beta } \sigma _{yx\beta }(x,\omega )q_\beta F_{\beta } \right. \nonumber \\ & \quad \left. -\varepsilon _{yx}(x,\omega ) \sum \limits _{\beta } \sigma _{xx\beta }(x,\omega )q_\beta F_{ \beta } \right] . \end{aligned}$$

(10)

Here $\varepsilon _{sk}(x,\omega )=\varepsilon _0\delta _{sk}+(4\pi i/\omega )\sum \limits _{\beta } \sigma _{sk\beta }(x,\omega )$ is the dielectric permittivity tensor, and the characteristic wave number $\varkappa (x,\omega )$ determines the field distribution in the semiconductor and has the form:

$$\begin{aligned} \varkappa ^{2}(x,\omega )=\frac{\omega ^2}{c^2}\frac{\varepsilon _{xx}(x,\omega ) \varepsilon _{yy}(x,\omega )- \varepsilon _{yx}(x,\omega ) \varepsilon _{xy}(x,\omega )}{\varepsilon _{xx}(x,\omega ) }. \end{aligned}$$

(11)

At frequency $\sim 1$ THz the wavelength of radiation is $\sim 3\times 10^{-2}$ cm and greater than $1/\alpha \approx 0.8\times 10^{-4}$ cm. We use this fact at calculation $E_y(0,\omega )$ on the semiconductor surface. We take into account that $\partial E_y(-0,\omega )/\partial x=-i(\omega /c)E_y(0,\omega )$ in vacuum, and $\partial E_y(+0,\omega )/\partial x \approx i\sqrt{\varepsilon _0}(\omega /c)E_y(0,\omega )$ inside the semiconductor. Then, integrating the Eq. (10) over a layer of thickness $1/\alpha$ we have approximately:

$$\begin{aligned} & E_y (0, \omega )=\frac{4\pi }{ie^2\omega \alpha c(1+\sqrt{\varepsilon _0})}\left\{ \sum \limits _{\beta }q_\beta \sigma _{yx\beta }(0,\omega )F_{\beta } \right. \nonumber \\ & \quad + \frac{\varepsilon _{yx}(0,\omega ) }{\varepsilon _{xx}(0,\omega )-\varepsilon _0}\left[ \frac{\varepsilon _0}{\varepsilon _{xx}(0,\omega )-\varepsilon _0}\text {ln}\left( \frac{\varepsilon _{xx}(0,\omega )}{\varepsilon _0}\right) -1 \right] \nonumber \\ & \times \left. \sum \limits _{\beta }q_\beta \sigma _{xx\beta }(0,\omega )F_{\beta }\right\} . \end{aligned}$$

(12)

When deriving the expression (12) it was taken into account that for all particles types the elements of the conductivity tensor are $\sim \text {exp}(-\alpha x)$. If we put $\sigma _{sk\gamma }(0,\omega ) =0$ in (12), then $E_y (0, \omega )$ contains only the term proportional to $\text {ln}$ and coincides with the expression obtained in [22], in which the influence of holes on the generation of THz radiation was not taken into account. Accounting for the holes influence leads to a relative decrease in the factor $\sum \nolimits _{\beta }q_\beta \sigma _{xx\beta }(0,\omega )F_{\beta }$ at $\text {ln}$. This decrease occurs due to the fact that the forces $F_{\beta }$ are co-directed, and the hole charges $q_{\gamma }$ have a different sign. On the contrary, the influence of the term proportional to $\sum \nolimits _{\beta }q_\beta \sigma _{yx\beta }(0,\omega )F_{\beta }$ increases, since $\sigma _{yx\beta }(0,\omega ) \propto q_\beta$. Eventually, as will be shown below, the generation of THz radiation increases. The latter is due to the fact that in the magnetic field orthogonal to forces $F_{\beta }$, electrons and holes move in opposite directions. As a result, the total current along the semiconductor surface increases. Namely this current is the source of THz radiation. The closer the effective masses of light and heavy holes to the electron effective mass, the greater the current increase.

5 Numerical calculation of low-frequency field

Now we can calculate the electric field strength on the semiconductor surface $E_y(0,t)=\int _{-\infty +i\Delta }^{+\infty +i\Delta }E_y(0,\omega )\exp (-i\omega t)d\omega /2\pi$, where $\Delta >0$. Let us present the calculation of the field strength in the case when a semiconductor is exposed to a pulse with duration of 20fs, energy flux density of $I_{L}=c|{\textbf {E}}_{L}|^{2}/8\pi =4.5\times 10 ^{7}\hbox {W/cm}^{2}$ and carrier frequency $\omega _0=2.3\times 10^{15} \, \hbox {s}^{-1}$. In this case the photoelectron density in GaAs, for which $\varepsilon _0=10.9$, is $n_e=10^{16} \, \hbox {cm}^{-3}$. The density of light holes $n_l$ is 3 times less than $n_e$, and the density of heavy holes $n_h$ is two times greater than $n_l$. Under these conditions, for plasma frequencies of electrons and holes we have: $\omega _{pe}=\sqrt{4\pi e^{2}n_e/m_{*e}\varepsilon _0} \approx 6.6\times 10^{12} \, \hbox {s}^{-1}$, $\omega _{pl}=\sqrt{4\pi e^{2}n_l/m_{*l}\varepsilon _0} \approx 3.4\times 10^{12} \, \hbox {s}^{ -1}$, $\omega _{ph}=\sqrt{4\pi e^{2}n_h/m_{*h}\varepsilon _0} \approx 2.0\times 10^{12} \, \hbox {s}^{-1}$. The electron collision frequency is $\nu _e \approx 4.1\times 10^{12} \, \hbox {s}^{-1}$. In numerical calculations we assume that $\nu _l=\nu _h=\nu _e$. This approximation gives good accuracy when calculating the generated fields for two reasons. First, under the conditions we are considering, the energy of photoexcited particles does not exceed 0.1 eV. That is, the particles energy is only 4 exceed their energy at room temperature. This increase in particle energy leads to small changes in collision frequencies. Second, a small variation of the collision frequencies in the calculations does not lead to any significant changes in the curves in the following figures. The reason for using the same collision frequencies for electrons and holes is that their scattering mainly occurs on phonons and the structures of energy bands near their bottoms are close to parabolic (see, for example, [23]). Figure 2 shows dependence of the electric field strength on the semiconductor surface versus time. The field strength is nondimensionalized to $E_m=\varepsilon _0 F_{ e} \omega _{pe}/\alpha ec(1+\sqrt{\varepsilon _0})$, which for the above-mentioned pulse and GaAs parameters is approximately equal to 80 V/cm. Calculations were performed for the constant magnetic field $B_0=7.5$ T, when $\Omega _e=3\omega _{pe},\Omega _l=4.6\omega _{pl},\Omega _h=1.3\omega _{ph}$. To identify the holes effect on the field strength Fig. 2 shows four curves.

Fig. 2

Dependence of the electric field strength $E_y(0,t)/E_m$ versus $\omega _{pe}t$. The solid, dotted, dashed and dash-dotted curves correspond to contributions to the field strength from electrons, electrons and heavy holes, electrons and light holes, electrons and all types of holes, respectively. The curves are plotted for $B_0=7.5$ T

The solid curve was obtained under the assumption that there are no holes, that is, $n_\gamma =0$. The dotted curve corresponds to the calculation for $n_l =0$, and the dashed curve corresponds to the calculation for $n_h =0$. Finally, the dash-dotted curve is obtained taking into account all particles. All curves contain oscillations at the frequency $\sim \Omega _e$. The lowest field strength values are realized for $n_\gamma =0$. Taking into account electrons and heavy holes leads to a slight field increase at times greater than $\sim 3/\omega _{pe}$ (see. Fig. 2). If we take into account electrons and light holes, then the field increase is stronger and manifests itself at earlier times $\sim 1/\omega _{pe}$. The highest field strength values are realized when the contribution of all particles to the field generation is taken into account. The relative field increase due to holes affect is most pronounced at later times, since holes are heavier than electrons. Oscillations of the generated signal, similar to those presented in Fig. 2, were observed in [24]. In [24] GaAs p-i-n diode in magnetic field was exposed to laser pulse with duration of 80 fs, energy flux density of $\sim 4\times 10^{5} \, \, \hbox {W/cm}^{2}$ and photon energy of 1.55 eV. The receiver current was recorded, which is proportional to the THz electric field. It has been established that at magnetic field strength of $\sim 2-4$ T, the receiver current has damped oscillations at frequency close to the electron cyclotron frequency during several picoseconds.

The results of similar calculations, but in the weaker magnetic field, when $B_0=2.5$ T, are presented in Fig. 3. In such magnetic field, the highest values of the THz pulse field are achieved. As the cyclotron frequencies are three times lower, then the field oscillations are practically invisible in Fig. 3. Since now $\Omega _e = \omega _{pe}$, then the maximum of the generated field on all curves is achieved at a later time moment at $t \sim 3/\omega _{pe}$. In this case the maximum field values are greater than in Fig. 2. The holes influence is also more pronounced. At times greater than $3/\omega _{pe}$, due to the affect of holes, the field increases more than twice. The main increase is due to the affect of light holes.

Fig. 3

The same dependencies as in Fig. 2, but for $B_0=2.5$ T

The tendency to increase the influence of holes on the field generation process also persists in a weaker magnetic field, when the cyclotron frequencies of particles are lower than the plasma frequencies. This can be seen in Fig. 4, which shows the results of calculations for the magnetic field $B_0=0.75$ T. As in Fig. 3, the affect of holes on the field generation is greatest at times greater than $3/\omega _{pe}$. The absolute values of the field strength are slightly less than in Fig. 2. However, the influence of holes on the generated pulse shape at moments greater than $3/\omega _{pe}$ in a weak magnetic field is even stronger. In particular, at $t>6/\omega _{pe}$, holes lead to the field strength increase by more than four times (see Fig. 4).

Fig. 4

The same dependencies as in Fig. 2, but for $B_0=0.75$ T

6 Total energy and spectral energy density of low-frequency radiation

The total energy of THz radiation emitted per unit surface area is determined by the integral

$$\begin{aligned} W_{tot}=\int _{0}^{+\infty }dt \frac{c}{4\pi }\left| E_y(0,t)\right| ^2= \int _{i\Delta }^{+\infty +i\Delta }d\omega W_{tot}(\omega ), \end{aligned}$$

(13)

where $W_{tot}(\omega )=c |E_y(0,\omega )|^2/4\pi ^2$ is the spectral energy density of THz radiation. Figure 5 shows plots of the function $W_{tot}(\omega )\omega _{pe}/W_m$.

Fig. 5

The solid, dotted, dashed and dash-dotted curves correspond to the contributions to the THz pulse spectral energy density from electrons, electrons and heavy holes, electrons and light holes, electrons and all types of holes, respectively. The curves are plotted for $B_0=7.5$ T

The laser pulse and semiconductor parameters, as well as notations in Fig. 5, are the same as in Fig. 2. Here the definition $W_m=c E_m^2/\omega _{pe}$ has been used. Using estimates for $E_m$ and $\omega _{pe}$, we have $W_m \approx 1.9 \times 10^{8}\hbox {eV/cm}^{2}$. On the solid curve corresponding to the immovable holes approximation, there is a maximum at the frequency of 3THz, corresponding to the frequency $\Omega _{e}$. In the frequency range shown in Fig. 5, the heavy holes contribution did not led to a significant change in the spectral energy density, since their mass is large. For this reason, the dotted and dash-dotted curves in Fig. 5 practically merge with the other two curves. When the light holes contribution is taken into account, the radiation spectral composition is enriched with lower frequencies. As a result, the peak at the frequency of 3THz becomes weakly pronounced (see the dashed curve in Fig. 5). The stronger light holes affect on the spectral density is due to the fact that their effective mass is close to the effective mass of electrons.

Fig. 6

The same dependencies as in Fig. 5, but for $B_0=2.5$ T

Figure 6 shows the same dependencies as in Fig. 5, but for the constant magnetic field value $B_0$ equal to 2.5T. In the case of a weaker field, the amplitude of the spectral energy density increases several times, since in the case of not very frequent particle collisions, the highest efficiency of THz radiation generation is achieved when the cyclotron frequency of electrons is $\sim \omega _{pe}$. The heavy holes motion, which manifests itself at low frequencies, leads to a slight decrease in the radiation spectral density in the frequency range shown in Fig. 6. On the contrary, light holes lead to increased generation at frequencies lower than $\omega _{pe}$ (see Fig. 6).

In a weak magnetic field, when the cyclotron frequencies of particles are lower than their plasma frequencies, the value of the spectral energy density is several times less than in the case when $\Omega _{pe}\sim \omega _{pe}$. The heavy holes motion leads to a slight decrease in the spectral density at frequencies below $\omega _{pe}$. This is demonstrated in Fig. 7, which shows the same dependencies as in Figs. 5 and  6, but for $B_0=0.75$ T. Taking the light holes into account leads to a decrease in the spectral energy density in the frequency range from $\sim 0.5 \omega _{pe}$ to $\sim \omega _{pe}$ and its increase at frequencies below $\sim 0.5 \omega _{pe }$.

Fig. 7

The same dependencies as in Fig. 5, but for $B_0=0.75$ T

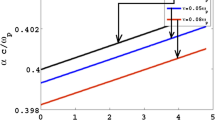
In a weak magnetic field $W_{tot} \sim B_0^2$. A similar dependence of $W_{tot} \sim E_y^2$ on $B_0$ has been observed repeatedly. For example, in [1] it was established that the amplitude of the generated THz field is proportional to $B_0$ in magnetic fields less than 0.2T. In [4] a dependence of the form $W_{tot} \sim B_0^2$ was recorded in magnetic fields less than 1.2T, as in our numerical calculations (see below). In a strong magnetic field $W_{tot}\sim 1/B_0^2$. Under the conditions considered, the function $W_{tot}$ reaches its maximum at $\Omega _{pe}\sim \omega _{pe}$. The dependence of $W_{tot}$ versus $B_0$ is presented in Fig. 8, which shows the function $W_{tot}/W_m$ graph. The notations of the curves are the same as in Fig. 2. When calculating $W_{tot}$, the spectral energy density is integrated over the frequency range 0.1–10 THz only. We do not consider radiation at frequencies below 0.1THz, which does not belong to the THz range. Note that the detectors used to register THz pulses also do not detect radiation outside the frequency range we are considering. At the same time, the above expression (12) shows that a significant part of the generated signal falls in the low-frequency region. Such low frequencies are responsible for the quasi-stationary part of the electric field, which is established at large times (see Fig. 2, 3 and 4). This quasi-stationary field, being proportional to the laser radiation intensity, is relatively small and does not affect the THz radiation generation. The quasi-stationary field strength is found from expression (12), if it is multiplied by $-i\omega$, and then put $\omega =0$. This is the contribution from the pole at the point $\omega =0$. For example, if $B=7.5$ T, then with GaAs and laser pulse parameters we assumed, the strength of this field is $0.37E_m=30$V/cm. Such a field arises due to effective charge separation only when holes are taken into account. As the concentration of electrons and holes equalizes in space, which occurs at times much longer than the generation time of the THz pulse, this field disappears. The heavy holes affect does not lead to a significant change in the total energy in the frequency range 0.1–10 THz. The light holes leads to an increase in the THz radiation total energy. Under conditions where $\Omega _{pe}\sim \omega _{pe}$ there is a relative increase in $W_{tot}$ by approximately two times. The light holes contribution to $W_{tot}$ decreases monotonically from 70 to 30% with increasing strength of the constant magnetic field. Taking the light holes into account leads to a slight shift of $W_{tot}$ maximum to the low-frequency region (see Fig. 8).

In the inset to Fig. 8 the dashed curve is the experimental data from [9], the dash-dotted curve is the same as in the main Fig. 8. In [9] GaAs sample at the temperature of 200K was exposed to the laser pulse with duration of 150fs, photon energy of 1.6eV and energy flux density of $10^7\, \hbox {W/cm}^2$. As can be seen from the inset to Fig. 8, some difference in the conditions of GaAs photoexcitation from those described by us did not lead to a large difference in the theoretical and experimental curves. This is an additional argument in favor of the justification of the approximate description of the distribution of photoexcited particles and their effective collision frequencies. In the theory presented above, the source of THz radiation is the current along the semiconductor surface. This current arises under the affect of pressure gradient of photoexcited particles directed perpendicular to the semiconductor surface and a magnetic field parallel to the surface. If the magnetic field is directed at an angle to the surface, then it has a component collinear to the pressure gradient, which does not lead to the emergence of a current along the surface. The presence of such a component reduces the generation efficiency due to a decrease in conductivity along the semiconductor surface. For this reason, without claiming on comparison of absolute values of the total energy, when comparing the theory with data from [9], where the magnetic field is directed at an angle of $45^{\text {o}}$ to the surface, we have reduced the magnetic field value from [9] by a factor of $\sqrt{2}$. Note that in another experiment [8] in the conditions when magnetic field is parallel to the semiconductor surface, the field strength at which the generation maximum is reached in InAs, which is close in its properties to GaAs, is $\simeq 3$ T. This value is close to the values given in Fig. 8.

Fig. 8

Dependence on the magnetic field $B_0$ of the contribution to the low-frequency signal total energy from the frequency range 0.1-10 THz. The inset represents the experimental data from [9] with a dotted line, the dash-dotted line is the same as in the main figure

7 Conclusion

It was shown above that to quantitatively describe the THz radiation generation in GaAs in a magnetic field, it is necessary to take into account the holes motion. The same conclusion also applies to a InAs semiconductor, since the ratio between the effective masses of electrons and holes in it is similar to that realized in GaAs. The obtained results form the basis for further development of the theory as applied to other conditions of photoexcitation of GaAs and InAs implemented in experiments, as well as to more complex geometry of experiments in which the generation dependence on polarization and exposure direction of a femtosecond laser pulse is studied.