Abstract
Nonlinear (NL) absorption and refraction are crucial optical phenomena in the development and application of optical materials. The Z-scan technique, first proposed by Bahae, is widely used to accurately measure the coefficients of NL absorption and refraction. This review presents a comprehensive overview of the most established versions of the Z-scan technique, including the transmittance closed aperture (CA) and open aperture (OA) Z-scan, reflecting CA and OA Z-scan, eclipsing Z-scan, and white light Z-scan. In each version, different sources with varying spatial and temporal intensity distributions are usually utilized. Numerical and analytical calculation results are provided for each version considering both continuous wave (CW) and pulsed laser sources. Unlike conventional reviews, which often summarize previously published results, this review primarily focuses on reproducing the findings from the literature. The analytical results, which are typically derived under specific approximations, are compared with numerical calculations to highlight the limitations of analytically derived relations. Furthermore, the necessary criteria and conditions for applying each Z-scan version are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nonlinear (NL) optics is a branch of optics in which amazing and applicable phenomena occur as a consequence of the interaction of intense electric fields with matter. When an intense electric field is applied to materials, the electron displacement from the equilibrium position is too large so that the induced polarization no longer scales linearly with the applied electric field. For nonrelativistic cases, a common way to describe the induced polarization versus applied electric field is using a power series expansion as follows:
where \(\chi^{(n)}\) is a tensor representing the \(n\)th-order susceptibility (e.g. χ(2) describes the second-order NL effects, such as second harmonic generation (SHG), sum frequency generation (SFG), difference frequency generation (DFG), optical rectification (OR) and the Pockels effect, χ(3) describes 3rd-order NL effects such as third harmonic generation (THG), the Kerr effect and two-photon absorption). In general, \({\varvec{P}}\) and \({\varvec{E}}\) are vectors, and the symbol \(\otimes\) indicates a tensor product. Even-order susceptibilities are zero for media with inversion symmetry, whereas odd-order susceptibilities have nonzero elements for media with any spatial symmetry.
The NL susceptibilities are generally complex unitless quantities. For instance, the real and imaginary parts of the 3rd- and 5th-order susceptibilities are related to the NL refraction and NL absorption coefficients through the following equations.
where \(c\) is the speed of light in free space, \(\varepsilon_{0}\) is the permittivity of free space, \(n_{0}\) is the linear refractive index, \(\omega\) is the radiation frequency, \(\alpha_{2}\) is the two-photon absorption (2PA) coefficient in units of \({\text{m}}\;{\text{W}}^{ - 1}\), \(n_{2}\) is referred to as the 3rd-order NL refractive index in units of \({\text{m}}^{2} \;{\text{W}}^{ - 1}\), \(\alpha_{3}\) is the three-photon absorption (3PA) coefficient in units of \({\text{m}}^{3} \;{\text{W}}^{ - 2}\) and \(n_{4}\) is the 5th-order NL refractive index in units of \({\text{m}}^{4} \;{\text{W}}^{ - 2}\).
An intense light beam can produce intensity- or flux-dependent changes in the refractive index and absorption coefficient of different materials through various mechanisms [1]. Many different techniques have been proposed and applied to determine the NL refractivity and absorptivity. Several methods for determining the NL refractive index, such as NL interferometry [2], four-wave mixing [3,4,5,6], ellipse rotation [7] and closed-aperture (CA) Z-scan [8, 9], have been reviewed in [10]. In [11], different techniques, including direct and indirect methods for determining the NL absorption coefficient/cross section, such as upconverted fluorescence emission [12], transient absorption [13], loss modulation [14], spectrally resolved, two-beam coupling [15], thermal lensing [16], MPA-induced photocurrent [17] and open-aperture (OA) Z-scan [18, 19], were reviewed.
Among these techniques, the Z-scan technique has become very popular since it is adequately sensitive and relatively easy to perform. It is also a technique by which both the NL refractive index and NL absorption coefficient for different orders of nonlinearities can be determined simultaneously. The Z-scan technique was first proposed by Bahae et al. [8, 9, 19].
Various modifications of the conventional Z-scan such as the two-color Z-scan [20,21,22,23,24,25,26], white light continuum (WLC) Z-scan [27,28,29,30,31,32,33,34,35,36,37,38], eclipsing Z-scan [39,40,41,42,43,44,45,46], reflection Z-scan [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61], f-scan [43, 44, 62,63,64], I-scan [46, 65,66,67,68] and spectral domain Z-scan [69], have been presented for different types of laser beams and pulse shapes [6, 18, 70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95]. The applicability of the Z-scan method goes beyond that of pure nonlinear optics. This technique is used, among other methods, to characterize cumulative thermal effects [96] or even linear optical coefficients [97].
Z-scan has been used for determining the NL optical properties of a variety of materials, including semiconductors, crystals, organic dyes and solutions. For many years, we employed a fully automatic Z-scan setup run by LabVIEW to determine the 2PA cross section of newly synthesized two-photon initiators (2PIs) used for two-photon polymerization (2PP) [35,36,37,38, 98,99,100,101,102,103,104,105,106,107,108,109]. We also developed a new version of the WLC Z-scan to determine the degenerate 2PA spectrum by running a single scan [35, 36].
The main purpose of this review is to collect the most famous and applicable versions of the Z-scan in one place and then compare their applicability for determining the different nonlinear properties of various media using different laser sources. In contrast to common review papers that very briefly report the results of published works, in this review, we attempt to reproduce the analytical and numerical results calculated for various versions of the Z-scan.
2 Introducing the Z-scan technique
Z-scan is a method in which a single tightly focused laser beam is used as the pump as well as the probe beam. The examined sample is moved in the propagation direction of the laser beam through the focal point. As the sample approaches the focal point, the beam size decreases, leading to a higher intensity within the sample, which results in the appearance of NL optical phenomena such as self-lensing, saturation of absorption and multiphoton absorption (MPA) [37, 83, 101]. Two different versions of the Z-scan, namely, CA and OA, are used to determine the NL refractivity and absorptivity. In the CA method, a small aperture is placed between the sample and the detector, whereas in the OA scheme, there is actually no aperture; the entire transmitted power must be detected. In all versions of the Z-scan, the normalized transmittance/reflectance is measured as a function of sample position. To extract the optical NL coefficients from the measured data, a proper relation of normalized transmittance versus sample position must be derived for each version of the Z-scan to determine the order of optical nonlinearity.
2.1 CA Z-scan
The CA Z-scan technique is based on the transformation of phase distortion to amplitude distortion during beam propagation through a sample. For instance, in case of positive nonlinearity, positive self-lensing (self-focusing) prior to focal point tends to increase the convergence of the beam exiting the sample, causing beam broadening on the aperture plane, which results in a decrease in the aperture transmittance (Fig. 1b). After passing through the focus, the same self-focusing tends to weaken the beam divergency, leading to beam narrowing at the aperture plane and thus resulting in an increase in the aperture transmittance (Fig. 1c); hence, there is a null point as the sample crosses the focus. Therefore, in the normalized transmittance trace, a positive NL refractivity manifests itself by the appearance of a valley followed by a peak. Conversely, a prefocus peak followed by a postfocus valley is the Z-scan signature of a negative NL refractivity. Notably, the CA Z-scan signal is affected by both the NL refractivity and absorptivity. In the presence of MPA, the peak is suppressed, and the valley is enhanced, whereas the saturable absorption (SA) results in contrary behavior.
Schematics of beam broadening and narrowing due to positive nonlinearity. a The sample is far from the focus where the intensity is not sufficient to observe the nonlinearity. b Shows the beam broadening at the aperture plane due to self-focusing prior to focus, c shows the beam narrowing at the aperture plane because the same self-focusing effect tends to reduce the beam divergence after focus, and d is similar to a, where the sample is once again far from focus
Figure 2 shows the intensity distribution on the observation plane located 100 mm from the beam waist when a Gaussian laser beam with a 20 µm waist radius travels through a NL medium. The wavelength was assumed to be 800 nm, leading to a Rayleigh length of \(z_{R} = 1.57\,{\text{mm}}\). The maximum on-focus phase shift was considered to be 1 (i.e., \(\Delta \Phi_{0} = 1\)). The dotted green curve indicates the intensity distribution when the NL sample is far from the focus, as shown in Fig. 1a and 1d. The dashed red curve shows the distribution when the sample is located prior to focusing at \(z = - 0.85z_{R}\) (Fig. 1b), leading to beam broadening at the observation plane, and the solid blue curve represents the distribution when the sample is located after the focal point at \(z = 0.85z_{R}\) (Fig. 1c), leading to beam narrowing at the observation plane.
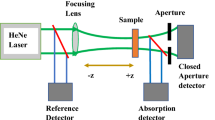
Figure 3 shows a schematic of the CA Z-scan setup. A laser beam is first divided into two parts using a beam splitter. The less intense beam is detected by a diode \(D_{r}\) to monitor the laser power fluctuations. The more intense beam is focused by a lens. The sample mounted on a motorized translation stage is moved along the laser beam propagation direction through the focus. The power transmitted through a small aperture is measured by \(D_{c}\) as a function of sample position. Finally, the signal measured with \(D_{c}\) is divided by that measured with \(D_{r}\) to eliminate the effect of laser power fluctuations. Finally, the transmittance is normalized by dividing the measured transmittance by its average value obtained at points far from the focus where the transmittance appears almost as a straight line.
Schematic diagram of the CA Z-scan setup [110]
2.2 OA Z-scan
Replacing the aperture with a large positive lens converts the CA to an OA Z-scan, as shown in Fig. 4. In this scheme, the transmittance is no longer sensitive to the NL refractivity but only to the NL absorptivity. The NL absorption is much stronger at the focus of the laser beam and decays as the sample moves away from the focus in either direction. Therefore, the OA Z-scan signal is symmetric with respect to the focal point, indicating a valley in the case of MPA and a peak in the case of SA.
Schematic diagram of the OA Z-scan [110]
Propagating a beam through a NL medium will cause changes in both the field amplitude and phase due to changes in the absorption coefficient and refractive index. Assuming a thin sample through which the diameter of the propagating beam is not altered due to diffraction or NL refraction, the amplitude and phase of the electric field of a traveling wave through the medium are governed by the following pair of equations.
where \(z^{\prime}\) is the axial coordinate within the sample, \(k\) is the wavenumber in free space, \(\Delta n(I)\) is the refractive index change, \(\alpha (I)\) is the absorption coefficient and \(I\) is the intensity with an SI unit of \({\text{W}}\;{\text{m}}^{ - 2}\).
\(\Delta n(I)\) and \(\alpha (I)\) can be expressed as a power series of intensity as follows.
where \(n_{2}\) and \(n_{4}\) are the 3rd- and 5th-order NL refractive indices related to the real parts of the 3rd- and 5th-order NL susceptibilities, respectively; \(\alpha_{0}\) is the linear absorption (i.e., 1PA) coefficient; \(\alpha_{2}\) is the 2PA coefficient related to the imaginary part of the 3rd-order NL susceptibility; and \(\alpha_{3}\) is the 3PA coefficient related to the imaginary part of the 5th-order NL susceptibility.
3 OA Z-scan transmittance
In the OA Z-scan, the entire power that is transmitted through the sample is detected; therefore, the signal is not sensitive to the NL refractivity. To determine the sample transmittance, the spatial distribution of the laser beam and the temporal distribution of the laser pulse should be known.
3.1 Circular Gaussian beam
Assuming that a circular Gaussian beam propagates in the \(z\) direction, the electric field can be written as:
where \(w\,(z) = w_{0} \left( {1 + {{z^{2} } \mathord{\left/ {\vphantom {{z^{2} } {z_{R}^{2} }}} \right. \kern-0pt} {z_{R}^{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\) is the beam radius with \(w_{0}\) the beam waist radius, \(R(z) = z + {{z_{R}^{2} } \mathord{\left/ {\vphantom {{z_{R}^{2} } z}} \right. \kern-0pt} z}\) is the wave front radius of curvature, \(z_{R} = {{kw_{0}^{2} } \mathord{\left/ {\vphantom {{kw_{0}^{2} } 2}} \right. \kern-0pt} 2}\) is the Rayleigh length and \(\phi (z,t)\) is a phase factor that is uniform in radial coordinates. \(E_{0} (t)\) contains the on-focus temporal profile.
3.1.1 Two-photon absorption (2PA)
2PA is an optical NL process in which two photons are simultaneously absorbed to excite the atom/molecule to a higher energy state. This process requires only a few femtoseconds, which is much less than the pulse duration of most laser pulses. According to [19], the intensity of a beam propagating through a medium showing 2PA is governed by
which has the following solution:
where \(I_{e}\) is the intensity at the exit surface of the sample, \(q\,(z,r,t) = \alpha_{\,2} \,I(z,r,t)\,L_{\,eff}\), \(I\) is the intensity at the entrance face of the sample, and \(L_{eff} = {{1 - e^{{ - \alpha_{0} L}} } \mathord{\left/ {\vphantom {{1 - e^{{ - \alpha_{0} L}} } {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }}\) is the so-called effective thickness, where \(L\) is the sample thickness and \(\alpha_{0}\) is the linear absorption coefficient. The power transmitted through the NL medium can be calculated by integrating the intensity over the transverse plane. For a circular symmetric intensity profile, the exit power is
Separating the axial and transverse parts of the Gaussian beam, \(I(z,r,t) = I_{0} (z,t)\exp ( - 2{{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } {\omega^{2} }}} \right. \kern-0pt} {\omega^{2} }})\), the transmitted power is obtained as
The normalized transmittance is defined as the quotient of the energy transmitted through the sample to the incident energy:
Assuming CW laser radiation or a top-hat (i.e., flat-top) pulse shape, the normalized transmittance is easily obtained as
where \(q_{0} = \alpha_{2} \,L_{eff} I_{0}\), \(I_{0}\) is the on-focus intensity and \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\).
Figure 5 shows the OA Z-scan traces for different q0. As q0 increases, the normalized transmittance decreases, approaching zero for very large values of q0.
OA Z-scan signals obtained using a CW circular Gaussian beam. They were plotted using Eq. (16) for different intensities leading to different \(q_{0}\)
Assuming a Gaussian temporal intensity distribution, the normalized transmittance can be derived by calculating the following integral over time:
where \(\tau\) is the FWHM of the Gaussian pulse.
Figure 6 shows the OA Z-scan transmittance as a result of 2PA for different laser powers (i.e., different \(q_{0}\)) when the medium is irradiated with a circular Gaussian beam of a pulsed laser emitting temporally Gaussian pulses. In the numerical calculation of Eq. (17), the integral was calculated over a time interval of \(- 5\tau\) to \(5\tau\).
OA Z-scan signals obtained using a circular Gaussian beam containing temporally Gaussian pulses. They were plotted using Eq. (17) over the time interval from \(- 5\tau\) to \(5\tau\) for different intensities leading to different \(q_{0}\)
The difference between the normalized transmittance indicated for the same \(q_{0}\) in Figs. 5 and 6 reflects the definition of \(I_{0}\) in \(q_{0} = \alpha_{2} \,L_{eff} I_{0}\). In Eq. (16), \(I_{0}\) is defined as the on-focus intensity of a CW laser beam, whereas in Eq. (17), it is defined as the peak on-focus intensity of a pulsed laser beam having temporally Gaussian pulses. \(I_{0}\) in the CW case corresponds to the time-averaged on-focus intensity for Gaussian pulses given by \(\langle I(t)\rangle = {{I_{0} } \mathord{\left/ {\vphantom {{I_{0} } {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}\). Figure 7 shows a comparison between the normalized transmittance of the OA Z-scan assuming the same \(q_{0} = 1\) obtained for the CW and pulsed lasers. This difference is understood as the consequence of the definition of \(I_{0}\) for CW and pulsed lasers.
It is not straightforward to fit Eq. (17) to the experimental Z-scan data to extract the 2PA coefficient. However, \(\ln (1 + q_{0} (z,0)\,\exp ({{ - \,4\ln 2\,\,t^{\,2} } \mathord{\left/ {\vphantom {{ - \,4\ln 2\,\,t^{\,2} } {\tau^{\,2} }}} \right. \kern-0pt} {\tau^{\,2} }}))\) can be expanded using Taylor series expansion, which converges at the limit of \(q_{0} < 1\). Therefore, the OA normalized transmittance for the 2PA process is derived as
where \(q_{0} = \alpha_{2} L_{eff} I_{0}\), \(\alpha_{2}\) denotes the 2PA coefficient and \(I_{0}\) denotes the peak on-focus intensity, which is, for temporally Gaussian pulses, given by \(I_{0} = {{4\,\sqrt {\ln 2} \,{\text{E}}_{p} } \mathord{\left/ {\vphantom {{4\,\sqrt {\ln 2} \,{\text{E}}_{p} } {\pi^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} w_{0}^{2} }}} \right. \kern-0pt} {\pi^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} w_{0}^{2} }}\tau\), with \({\text{E}}_{p}\) being the pulse energy, \(w_{0}\) being the beam waist radius and \(\tau\) being the pulse duration.
The limit of \(q_{0} < 1\) corresponds to \(T(0) > 0.765\). In other words, Eq. (18) can be used to determine the 2PA coefficient when the maximum normalized absorbance occurring at the focus, \(1 - T(0)\), is less than 0.235. Figure 8 shows how the Taylor series of \(\ln (1 + q_{0} )\) deviates from the original function (i.e., becomes divergent) as \(q_{0}\) increases to quantities greater than unity.
Figure 9 indicates the normalized transmittance given in Eq. (18) for different numbers of first terms ranging from the first 2 terms (dashed red curve) to the first 12 terms, all of which are plotted with the same \(q_{0} = 1\). The solid blue curve shows the numerical calculations acquired from Eq. (17).
Equation (18) represents an infinite summation. In practice, one has to keep a finite number of the first terms of such a summation. According to Fig. 10, in which the extracted \(q_{0}\) is shown versus different numbers of the first terms in Eq. (18), it is recommended to retain more than 10 terms of Eq. (18) to extract a precise value for \(q_{0}\) within 1% error.
Extracted value of \(q_{0}\) obtained by fitting several numbers of the first terms in the summation in Eq. (18). The \(q_{0}\) values were extracted from an OA Z-scan trace with T = 0.765 at the focal point corresponding to an actual value of \(q_{0} = 1\), as seen for a large number of terms
3.1.2 Three-photon absorption (3PA)
The 3PA process involves excitation through the simultaneous absorption of three photons. In the presence of 3PA, the intensity change versus propagation length is governed by
where \(\alpha_{3}\) is the 3PA coefficient. Integrating over the entire length of the sample will lead to
where \(I_{e}\) is the exit intensity, \(p(z,r,t) = \sqrt {2\alpha_{3} L^{\prime}_{eff} } I(z,r,t)\) and \(L^{\prime}_{eff} = (1 - e{{^{{ - \,2\,\alpha_{\,0\,} L}} )} \mathord{\left/ {\vphantom {{^{{ - \,2\,\alpha_{\,0\,} L}} )} {2\,\alpha_{\,0} }}} \right. \kern-0pt} {2\,\alpha_{\,0} }}\).
The power transmitted through the NL medium can be calculated by integrating the intensity over the transverse plane.
Assuming a CW or top-hat temporal distribution for laser pulses, the normalized transmittance, defined in Eq. (15), is derived as
where \(p_{0} = \sqrt {2\alpha_{3} L^{\prime}_{eff} \,} \,I_{0}\) and \(I_{0}\) is the on-focus intensity.
Figure 11 shows the OA-normalized Z-scan traces of a medium showing 3PA using a CW laser beam with different powers corresponding to different \(p_{0}\) values. The transmittance at the focus decreases, approaching zero, as \(p_{0}\) increases.
OA Z-scan transmittance in the case of the 3PA process for different CW laser powers corresponding to different \(p_{0}\) values according to Eq. (22)
Assuming a Gaussian temporal distribution for laser pulses, the normalized transmittance is given by
Figure 12 shows the numerical calculation of Eq. (23) for different values of \(p_{0}\). Here, the difference between the plots in Figs. 11 and 12 reflects the difference in \(I_{0}\) for CW radiation and Gaussian pulses.
OA Z-scan transmittances in the case of the 3PA process applying different laser pulse energies corresponding to different \(p_{0}\) values using Eq. (23)
The integrand in Eq. (23) can be expanded as an infinite summation via Taylor series expansion. The resultant Taylor series would be convergent if \(p_{0} < 1\). Then, the OA Z-scan normalized transmittance in the case of pure 3PA will be given by
3.1.3 Simultaneous 2PA and 3PA
To obtain the OA Z-scan transmittance of a medium showing both 2PA and 3PA simultaneously, the following differential equation must be solved:
There is no analytical solution to Eq. (25). when \(\alpha_{2}\) and \(\alpha_{3}\) are both nonzero. Solving Eq. (25) in the case of \(\alpha_{3} = 0\) leads to Eq. (18), and in the case of \(\alpha_{2} = 0\) leads to Eq. (24). Assuming weak nonlinearity, it is reasonable to retain only the first two terms of these aforementioned equations; thus, the normalized absorbance (i.e., \(A = 1 - T\)) for 2PA and 3PA are given by
Based on this approximation, Kessi and Naima [82, 111] proposed the superposition of the contributions of 2PA and 3PA. Thus, in the case of simultaneous 2PA and 3PA, the normalized transmittance can be given as
Another approximate approach was proposed by Gu et al. [80]. They introduced an empirically determined coupling equation so that the normalized transmittance for simultaneous 2PA and 3PA can be given by
where \(T_{2p} (q_{0} ,x)\,\) and \(T_{3p} (p_{0} ,x)\) are the normalized transmittances for 2PA and 3PA, respectively, and \(F(q_{0} ,p_{0} ,x)\) is introduced as the coupling factor obtained empirically as
3.1.4 Multiphoton absorption (MPA)
The OA Z-scan transmittance can be derived for higher orders of NL absorption. To do so, the following differential equation must be solved.
where \(\alpha_{M}\) is the MPA coefficient.
The irradiance at the exit surface of a thin sample is given in [11] as
As described in Sects. 3.1.1 and 3.1.2, the intensity is then integrated over space and time to calculate the total energy exiting the sample.
Correa et al. [112] derived the OA Z-scan normalized transmittance up to 5PA. Gu et al. [113] calculated the OA Z-scan normalized transmittance for higher orders of NL absorption for one MPA process (e.g., 2PA, 3PA, etc.) and for the concurrence of two consecutive processes (e.g., 2AP and 3PA). For the case when only one MPA process occurs and under the assumption of \((M - 1)\alpha_{M} I_{0}^{M - 1} L_{eff}^{(M)} < \,1\), the OA Z-scan normalized transmittance is given by
where \(L_{eff}^{(M)} = {{\left\{ {1 - \exp \left[ { - (M - 1)\alpha_{0} L} \right]} \right\}} \mathord{\left/ {\vphantom {{\left\{ {1 - \exp \left[ { - (M - 1)\alpha_{0} L} \right]} \right\}} {(M - 1)\alpha_{0} }}} \right. \kern-0pt} {(M - 1)\alpha_{0} }}\) and
and
where \(h(t)\) denotes the temporal profile of the laser pulse.
Assuming a Gaussian temporal profile, \(F_{k} = {1 \mathord{\left/ {\vphantom {1 {\left( {(M - 1)k + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {\left( {(M - 1)k + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}\). Therefore, in the case of Gaussian pulses, the OA Z-scan normalized transmittance for the 4PA and 5PA to the 3rd-order approximation can be written as
Figure 13 illustrates a comparison between the normalized transmittance of the OA Z-scan for different orders of MPA given by Eq. (33) assuming temporally Gaussian pulses. The higher the order of the MPA is, the narrower the Z-scan signal.
Comparison between the normalized transmittance of the OA Z-scan for different orders of MPA using Eq. (33) assuming temporally Gaussian pulses
3.1.5 Saturable absorption (SA)
SA describes the saturation of linear absorption leading to a decrease in the linear absorption coefficient with increasing intensity. This is considered an NL optical phenomenon since the absorption coefficient shows intensity-dependent behavior. SA occurs at the near resonance when the absorber is irradiated with high-intensity laser beams. The following equations have been used in the literature for the saturation of the first excited state [114].
where \(\alpha_{0}\) denotes the weak-field absorption coefficient and \(I_{s}\) is the saturation intensity (i.e., the intensity at which the linear absorption coefficient drops to half of its weak-field value).
Equation (38) represents the intensity dependence of the absorption coefficient for the saturation of a homogeneously broadened line [115], whereas Eq. (39) is used for the case of an inhomogeneous broadened line [116]. Equation (40) was proposed by Samoc et al. [117] since their measured results were not consistent with the models presented in Eqs. (38) and (39). They found that their experimental curves were well reproduced by Eq. (40). Later, Srinivas et al. [114] also found that Eq. (40) fits their experimental data better than Eqs. (38) and (39).
Gu et al. [118] derived the normalized transmittance of an OA Z-scan for a medium showing SA based on two models given in Eqs. (38) and (39).
where \(\rho (x,t) = {{I_{0} (t)} \mathord{\left/ {\vphantom {{I_{0} (t)} {\left[ {I_{s} (1 + x^{2} )} \right]}}} \right. \kern-0pt} {\left[ {I_{s} (1 + x^{2} )} \right]}}\), \(I_{0} (t)\) is the on-focus intensity and \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\).
In the case of CW lasers \(I_{0} (t) = I_{0}\), however, when using a pulsed laser, one must calculate the time-averaged normalized transmittance via the following equation.
The first 5 terms of \(q_{m} (\rho )\) in Eq. (41) for SA based on the model presented in Eq. (38) are given as:
The first 5 terms of \(q_{m} (\rho )\) in Eq. (41) for SA based on the model presented in Eq. (39) are given as:
Figure 14 shows OA Z-scan traces at different on-focus intensities for SA based on the model presented in Eq. (38). In this simulation, it is assumed that \(\alpha_{0} L = 1\). As the on-focus intensity increases, the SA process becomes predominant, leading to a higher transmittance; that is, the medium becomes more transparent.
OA Z-scan traces for SA at different intensities using Eq. (38). The ratio of on-focus intensity to saturation intensity was varied from 0.5 to 8
For some media at some wavelengths, SA may occur simultaneously with 2PA. For the concurrence of SA and 2PA, the optical intensity change is governed by the following differential equation.
Wang et al. [119] derived the normalized transmittance of an OA Z-scan for a medium showing simultaneous 2PA and SA, given by:
where \(\rho (x,t) = {{I_{0} (t)} \mathord{\left/ {\vphantom {{I_{0} (t)} {\left[ {I_{s} (1 + x^{2} )} \right]}}} \right. \kern-0pt} {\left[ {I_{s} (1 + x^{2} )} \right]}}\), \(I_{0} (t)\) is the on-focus intensity and \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\).
The first two terms of \(q_{m} (\rho )\) and \(q^{\prime}_{m} (\rho )\) are given as follows.
In Fig. 15, the OA Z-scan normalized transmittance for different on-focus intensities was plotted using Eq. (54). These results were obtained assuming \(\alpha_{0} L = 0.2\) and \(\alpha_{2} I_{s} /\alpha_{0} = 0.04\). In this figure, the competition between two NL phenomena is clearly demonstrated. Each trace consists of an overall peak indicating the SA behavior inside which there could be a valley as an indicative of the 2PA process. By moving the sample toward the focal point, the intensity within the focal volume increases, leading to higher saturation, which results in transmittance enhancement and thus results in a symmetric peak. For higher on-focus intensities, as the sample moves closer to the focal point, the intensity within the focal volume becomes strong enough to trigger the 2PA, leading to a decrease in the transmittance, manifesting as a valley at the focal point. This behavior is considered a switch from SA to 2PA when the intensity of radiation is increased. Performing the OA Z-scan with a higher peak on-focus intensity reveals that the 2PA monotonously overcomes the SA process around the focal point; that is, the depth of the central valley increases, and ultimately, the 2PA process becomes predominant so that the normalized transmittance drops below unity at the focal point.
OA Z-scan trace showing the competition between SA and 2PA based on Eq. (54)
The 2PA process itself could be saturated. To determine the OA Z-scan transmittance for such a process, the following differential equation must be solved. The detailed calculation can be found in [120].
Figure 16 represents the numerically calculated OA Z-scan transmittance for saturation of 2PA at different applied \(I_{0}\) values, assuming \(\alpha_{2} I_{s} = 0.1\). However, as the intensity increases, the signal becomes broader, and the depth of the trace does not increase correspondingly to that in the absence of saturation.
OA Z-scan trace for saturation of 2PA. The results were calculated numerically using Eq. (59)
The detailed calculation for the simultaneous saturation of 2PA and 3PA can be found in [121].
3.2 Astigmatic Gaussian beams
A circular Gaussian beam has the same beam waist radius in all directions and a single beam waist position. Although an elliptical Gaussian beam has a single beam waist position, the beam waist radii in two orthogonal directions (x, y) are not the same, as shown in Fig. 17. An elliptical beam may undergo stigmatism, leading to two separate foci, each corresponding to the minimum beam radius in transverse dimensions (i.e., the x- and y-axes), as shown in Fig. 18.
Beam radius of a focused elliptical Gaussian beam with an ellipticity of \({{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 2}}} \right. \kern-0pt} {w_{0x} = 2}}\) having the same foci. The dashed red curve represents the beam radius in the y direction with a Rayleigh length of 4 mm, and the solid blue curve represents the beam radius in the x direction with a Rayleigh length of 1 mm [110]
Beam radius of a focused astigmatic Gaussian beam with an ellipticity of \({{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 2}}} \right. \kern-0pt} {w_{0x} = 2}}\) and a waist separation of 4 mm. The dashed red curve represents the beam radius in the y direction with a Rayleigh length of 4 mm, and the solid blue curve represents the beam radius in the x direction with a Rayleigh length of 1 mm
The electric field of an astigmatic Gaussian beam is given by [115]
where
where \(X\) and \(Y\) are dimensionless geometric parameters defined as \(X = {{(z - z_{0x} )} \mathord{\left/ {\vphantom {{(z - z_{0x} )} {z_{Rx} }}} \right. \kern-0pt} {z_{Rx} }}\) and \(Y = {{(z - z_{0y} )} \mathord{\left/ {\vphantom {{(z - z_{0y} )} {z_{Ry} }}} \right. \kern-0pt} {z_{Ry} }}\), respectively, in which \(z_{0x,0y}\) is the location of the waist, \(Z_{Rx,Ry}\) is the Rayleigh length and \(w_{0x,\,0y}\) is the beam waist radius of the laser beam. The subscripts \(x\) and \(y\) for all parameters refer to the transverse directions of the \(x\) and \(y\) axes, respectively.
The beam waist positions of an astigmatic Gaussian beam focused by a spherical lens are given by
where \(f\) denotes the focal length of the focusing lens and the waist positions are measured with respect to the focusing lens location.
3.2.1 Two-photon absorption
The effect of beam ellipticity and astigmatism on the Z-scan trace was investigated in [70, 71, 75, 76, 82, 111]. Mian et al. [75, 76] derived the OA Z-scan transmittance for astigmatic Gaussian beams. The calculation of the power transmitted through the sample would be more convenient if the intensity is written in polar coordinates.
Then, the power is derived by calculating the following integral.
where
Thus, for the case of CW lasers or flat-top pulses, the OA Z-scan normalized transmittance is derived as
where
in which \(q_{\max } = \alpha_{2} \,L_{eff} I_{\max }\) and \(I_{\max } = {{2{\text{P}}} \mathord{\left/ {\vphantom {{2{\text{P}}} {\pi w_{0x} w_{0y} }}} \right. \kern-0pt} {\pi w_{0x} w_{0y} }}\) with \({\text{P}}\) the laser power. Note that \(I_{\max }\) is merely a definition; it does not represent the on-focus intensity.
In the general case of astigmatic beams, the on-focus intensity can be obtained from
When Gaussian pulses are used and under the assumption of \(q_{\max } < 1\), the normalized transmittance can be analytically calculated via the following summation:
In Fig. 19, the OA Z-scan transmittance for an elliptical beam with different ellipticities (\(e = {{{\text{w}}_{0y} } \mathord{\left/ {\vphantom {{{\text{w}}_{0y} } {{\text{w}}_{0x} }}} \right. \kern-0pt} {{\text{w}}_{0x} }}\)) was plotted using Eq. (73). A higher ellipticity leads to a larger beam size at the focus, resulting in less on-focus intensity and consequently weaker 2PA.
The effects of beam ellipticity on an OA Z-scan signature using Eq. (73)
In Fig. 20, the OA Z-scan transmittances for beams with different ellipticities and astigmatisms are compared. The OA transmittance is asymmetric when an astigmatic beam is used for the Z-scan experiment.
Effect of astigmatism on the Z-scan trace using Eq. (73). The solid blue curve represents the Z-scan of a circular Gaussian beam, the dashed red curve represents an elliptical beam with an ellipticity of 2, and the dotted green curve represents an astigmatic beam with an ellipticity of 2 and a beam-wait separation of 4 mm
3.2.2 Multiphoton absorption
According to the results in [82, 111], one can also use Eq. (33) for an astigmatic beam by replacing \(\left[ {(1 + X^{2} )\,(1 + Y^{2} )} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\) instead of \((1 + x^{2} )\). Hence, the normalized transmittance for the OA Z-scan using astigmatic beams with a Gaussian temporal profile under an approximation of \((M - 1)\alpha_{M} I_{0}^{M - 1} L_{eff}^{(M)} < \,1\) is given by:
where M denotes the order of the MPA and \(W_{k}\) and \(F_{k}\) are given in Eqs. (34) and (35), respectively.
4 CA Z-scan
In this section, the normalized transmittance of CA Z-scan, using various spatial profile laser beams and different temporal profile laser pulses is derived for different orders of optical nonlinearity.
To estimate the CA Z-scan trace, the far-field pattern of the beam at the aperture plane should be calculated. This can be performed through different methods, such as the zeroth-order Hankel transformation or the Fresnel diffraction integral or integral theorem of Helmholtz and Kirchhoff. The Kirchhoff diffraction integral is derived by exploiting Green’s second identity given by
The Helmholtz equation for propagation waves in free space is given by
Therefore, the Green’s function fulfilling Eq. (75) can be written as
The solution to Eq. (77) can be given by
By substituting Eq. (78) into the left side of Eq. (75), the electric field distribution on the observation plane can be calculated using the following:
Equation (79) represents the integral theorem of Helmholtz and Kirchhoff [122], which is calculated over the plane of the laser beam cross section. Henceforth, we refer to this as the Kirchhoff diffraction integral. Figure 21 schematically illustrates the diffraction and observation planes.
In the CA Z-scan experiment, \(E(r^{\prime})\) is the electric field on the exit surface of the sample (\(x^{\prime}y^{\prime}{\text{ - plane}}\)) given by Eq. (83), and \(E(r)\) is the electric field distribution on the aperture plane (\(xy{\text{ - plane}}\)), via which the intensity distribution on the aperture plane and then the power transmitted through the aperture can be calculated.
4.1 Circular Gaussian beams
The optical nonlinearity depends strongly on the laser beam intensity. The spatial distribution of the laser power determines the intensity at each point. With respect to symmetricity, it is essential to know whether the beam is circular or, to some extent, elliptical and whether it is astigmatic. The power density function should also be known, for instance, whether it is a top hat or Gaussian shape. In this section, a circular laser beam with a Gaussian spatial intensity distribution is assumed to be used for the CA Z-scan experiment to determine the nonlinear refractivity originating from pure 3rd-order, pure 5th-order or concurrent 3rd- and 5th-order nonlinearity.
4.1.1 Pure 3rd-order NL refractivity
In the case of cubic nonlinearity, the local refractive index of the medium, through which an intense laser beam is traveling, scales linearly with light intensity \(n(I) = n_{0} + n_{2} I\) with \(n_{2}\), the NL refractive index. This behavior leads to the creation of a convergent lens if n2 possesses a positive sign and, inversely, a divergent lens if n2 possesses a negative sign. These effects are known as self-focusing and self-defocusing, respectively.
If the medium length is small enough that changes in the beam diameter within the medium due to either diffraction or NL refraction can be neglected, the medium is regarded as a thin sample. In the thin sample approximation, the amplitude of the electric field changes only due to absorption, and the phase of the electric field changes due to the NL refraction governed by the following couple of equations.
In the absence of NL absorption, α(I) remains a constant equal to the linear absorption coefficient.
Assuming a spatially circular Gaussian intensity distribution, the phase shift at any point on the wave front can be derived by solving Eqs. (80) and (81).
The complex electric field on the exit surface of the sample now contains an amplitude depletion factor as well as a NL phase shift. Therefore, using the notation used in Fig. 21, the electric field on the diffracting plane (i.e., sample position) is given by:
The electric field pattern on the aperture can be numerically calculated using the Kirchhoff diffraction integral (Eq. (79)) precisely or using the Fresnel diffraction integral within the paraxial approximation given by
where \(r = \sqrt {x^{2} + y^{2} \,}\) and \(d = (z_{a} - z)\), where \(z_{a}\) is the position of the observation plane (i.e., aperture plane) and \(z\) denotes the position of the diffracting plane (i.e., sample position) in the Z-scan experiment.
A possible analytical solution to Eq. (84) proposed by Weaier et al. [123] is to decompose the complex electric field at the exit plane of the sample into a summation of Gaussian beams by expanding the NL phase term, \(e^{i\Delta \Phi }\), using Taylor series expansion. That is,
where \(\Delta \Phi_{0} (t) = k\,n_{\,2} \,I_{\,0} (t)\,L_{\,eff}\) is the on-focus phase shift with \(k\) being the wavenumber and \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\).
This method is known as Gaussian decomposition (GD) since Eq. (85) represents a summation of Gaussian beams with different complex amplitudes and different beam radii.
Using the GD approach, the electric field exiting the sample is given by
The intensity distribution on the aperture plane located at a distance \(d\) from the sample can be calculated by substituting Eq. (86) into Eq. (84) [19]. That is,
where
The normalized transmittance of the CA Z-scan is defined in [19] as
where in Eq. (94), the numerator represents the energy transmitted through the aperture in the presence of the NL medium, and the denominator represents the energy transmitted through the same aperture in the absence of the NL medium.
In terms of the electric field amplitude on the aperture plane, the normalized transmittance is given by
where \(r_{a}\) is the aperture radius.
Assuming a very small aperture centered on the optical axis (i.e., \(r = 0\)), the on-axis normalized transmittance for temporally top-hat pulses or CW laser radiation is calculated as:
In the limit of a small NL phase change, \(\Delta \Phi_{0} < 1\), only the first two terms of Eq. (96) are adequate to be retained. Therefore,
Thus, the CA Z-scan normalized transmittance as a function of the sample position is derived as:
where \(\Delta \Phi_{0} = kn_{2} L_{eff} I_{0}\), k is the wavenumber, \(L_{eff} = {{(1 - \exp ( - \alpha_{0} L))} \mathord{\left/ {\vphantom {{(1 - \exp ( - \alpha_{0} L))} {\alpha_{0} }}} \right. \kern-0pt} {\alpha_{0} }}\) is the effective length of the sample with \(L\) the sample length and \(\alpha_{0}\) the sample linear absorption coefficient, I0 is the on-focus intensity and n2 is the NL refractive index.
Instead of top-hat pulses, if Gaussian pulses propagate through an instantaneously responding NL medium, the CA-normalized transmittance is derived as
where \(\Delta \Phi_{0} (0) = kn_{2} L_{eff} I_{0} (0)\) and \(I_{0} (0)\) is the peak on-focus intensity.
According to Eqs. (98) and (99), which are derived under approximations of small apertures and small phase changes, the CA Z-scan signal is symmetric in two respects. First, the height of the peak is equal to the depth of the valley, and second, the null point (i.e., the position at which the normalized transmittance returns to unity) occurs at the focus (Fig. 22). However, the numerical calculation reveals that the signal becomes more asymmetric as the phase change increases.
The on-axis normalized transmittance of the CA Z-scan obtained from Eq. (98)
Equations (98) or (99) possess two extrema: a peak and a valley located symmetrically around the focus. The peak and valley positions and thus the peak-to-valley distance are given by
Therefore, the transmittance peak-to-valley difference is given by
Figure 23 shows the transmittance peak-to-valley difference versus the maximum on-focus phase change for very small apertures.
On-axis transmittance peak-to-valley difference versus maximum on-focus phase change. The circle points represent the data calculated numerically using the Kirchhoff diffraction integral, and the solid red curve shows a linear fit to the calculated data, with a slope of 0.406, as given in Eq. (101)
Equation (101) was derived assuming a small aperture size as well as a small phase change. Figure 24 shows the numerically calculated CA normalized transmittance using Eq. (95) assuming a phase distortion of \(\Delta \Phi_{0} = 1\) for different aperture sizes of 0.01, 0.50 and 0.80. As the aperture size increases, the transmittance peak-to-valley difference decreases and finally vanishes (i.e., \(T(z) = 1\)) for very large apertures (i.e. no aperture), indicating no sensitivity with respect to self-lensing.
CA normalized transmittance for different aperture transmittances assuming \(\Delta \Phi_{0} = 1\). The results were numerically calculated using Eq. (95)
As illustrated in Fig. 24, the coefficient in Eq. (101) in general depends on the aperture size so that it decreases with increasing aperture size according to
where \(S = 1 - \exp ( - {{2r_{a}^{2} } \mathord{\left/ {\vphantom {{2r_{a}^{2} } {w_{a}^{2} )}}} \right. \kern-0pt} {w_{a}^{2} )}}\) is defined as the aperture transmittance with \(r_{a}\) the aperture radius and \(w_{a}\) the beam radius on the aperture plane.
Figure 25 shows the transmittance peak-to-valley difference versus the aperture transmittance. The solid blue curve shows the results of the numerical calculations using the Kirchhoff diffraction integral, and the dashed red curve indicates the plot of the empirical relation given by Eq. (102) for \(\Delta \Phi_{0} = 1\).
Transmittance peak-to-valley difference versus the aperture transmittance. The solid blue curve shows the numerical calculation using the Kirchhoff diffraction integral, and the dashed red curve indicates the empirical relation given by Eq. (102)
Figure 26 illustrates the transmittance peak-to-valley difference versus the maximum on-focus phase change for different aperture transmittances. This figure reveals the linear dependency of \(\Delta T\) versus \(\Delta \Phi_{0}\) with decreasing slope as the aperture size increases.
Transmittance peak-to-valley difference versus \(\Delta \Phi_{0}\) for different aperture transmittances. The results were numerically calculated using Eq. (95)
Equation (98) reveals the effect of only the first-order of the intensity on the normalized transmittance. As the laser power increases, the effects of the second- and third-order intensities become more important. To extract the NL refractive index more precisely, higher order terms from Eq. (87) should be introduced into Eq. (96). The analytic result for the normalized transmittance of the CA Z-scan, corrected to the third-order in intensity, is found in [124] as:
According to Eq. (98), as the first-order approximation, the null position occurs at the focus regardless of the laser beam intensity. However, Eq. (103) reveals that the normalized transmittance at the waist is affected by the intensity squared, leading to a value less than unity (\(T(0) = 1 - {{20\,\Delta \Phi_{0} \,^{2} } \mathord{\left/ {\vphantom {{20\,\Delta \Phi_{0} \,^{2} } {225}}} \right. \kern-0pt} {225}}\)) for both positive and negative NL refractivity. Thus, the null position shifts toward the positive/negative direction of the z-axis in the case of positive/negative NL refractivity. Figure 27 represents the CA Z-scan traces calculated numerically using the Kirchhoff diffraction integral assuming \(\Delta \Phi_{0} = 1\) for CW radiation. This figure explicitly illustrates the shift in the null position for both positive and negative nonlinearities. Although the positions of the null, valley and peak of the Z-scan trace are shifted, the peak-to-valley separation remains nearly unchanged. For instance, in Fig. 27, the valley position is \(z_{v} = - 0.7\,z_{R}\), and the peak position is \(z_{p} = 1.02\,z_{R}\) such that \(\Delta z_{v \to p} = 1.72\,z_{R}\) is similar to that obtained for the case of a very small phase change.
CA Z-scan traces for different signs of nonlinearity illustrating the shift of the null position. The normalized transmittance at the focus is numerically calculated \(T(0) = 0.911\) based on Eq. (94) assuming a phase change of \(\Delta \Phi_{0} = 1\)
In Fig. 28, the CA Z-scan transmittances for a phase shift of \(\Delta \Phi_{0} = \pi\) are plotted using Eqs. (98) and (103) for comparison. The solid blue curve was plotted based on Eq. (98) that includes the effect of only the first-order of intensity. Within such an approximation, the null position is zero (i.e., the waist position), and the peak and valley appear symmetrically around the waist position. Furthermore, the peak height is identical to the valley depth. The dashed red curve was plotted using Eq. (103), which contains the effect of intensity up to the third-order. As shown in Fig. 28, for a larger phase change, the CA Z-scan transmittance shows two specific characteristics: first, the positions of the null, valley and peak are shifted in the positive direction for positive nonlinearity, and second, the height of the peak is less than the depth of the valley. That is, the Z-scan is not symmetric with respect to either the baseline (i.e., \(T = 1\)) or the beam waist.
Figure 29 shows the CA Z-scan on-axis transmittance calculated numerically using Eq. (96) for different phase changes. This illustrates how the symmetricity of the Z-scan decreases as the phase changes increase.
CA Z-scan on-axis transmittance for different phase changes numerically calculated using Eq. (96). The solid blue curve represents \(\Delta \Phi_{0} = 0.25\), and the dashed red curve represents \(\Delta \Phi_{0} = \pi\)
Figure 30 shows the numerical calculation using the Kirchhoff diffraction integral assuming a beam waist radius of 20 µm and that the aperture is located 100 mm from the beam waist of a laser beam with a wavelength of 800 nm. This illustrates how the self-focusing effect alters the intensity distribution on the far-field aperture by strengthening the convergence of the laser beam at the prefocal position and weakening the divergence of the laser beam at the postfocal position as the sample moves from the valley position to the null position and then to the peak position.
Intensity distribution on the aperture plane for different sample positions. The solid blue curve shows the distribution when the sample is located at the peak position, and the dotted green curve shows the distribution when the sample is located at the valley position. The dashed red curve shows the distribution when the sample is located at the null position. The results were numerically calculated based on Eq. (79)
All the relations derived for CA Z-scan using CW lasers are also valid if pulsed lasers are used instead. In fact, the time-independent phase shift \(\Delta \Phi_{0}\) can be replaced by a time-averaged phase shift, which is given by \(\langle \Delta \Phi (t)\rangle = {{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}\) for Gaussian pulses with \(\Delta \Phi_{0}\), the peak on-focus phase shift. Figure 31 illustrates the CA Z-scan normalized on-axis transmittance numerically calculated based on Eq. (94) using Gaussian pulses inducing a peak on-focus phase change of \(\Delta \Phi_{0} = \pm 1\).
CA Z-scan on-axis transmittances for cubic nonlinearity showing a peak on-focus phase shift of \(\Delta \Phi_{0} = \pm 1\) induced by temporally Gaussian pulses. The results were numerically calculated using Eq. (94)
4.1.2 Pure 5th-order NL refractivity
The real part of \(\chi^{(5)}\) gives the NL refractive index. The refractive index change arising from the 5th-order nonlinearity is proportional to the intensity squared through the following:
Under the assumption of negligible NL absorption, the following couple of differential equations give the NL phase change.
The total phase change for a beam exiting a sample of length \(L\) is derived as
where \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\) and \(\Delta \Psi_{0} (t) = kn_{4} L^{\prime}_{eff} I_{0} (t)^{2}\) in which, \(k\) is the wavenumber, \(L^{\prime}_{eff} = {{(1 - e^{{ - 2\alpha_{0} L}} )} \mathord{\left/ {\vphantom {{(1 - e^{{ - 2\alpha_{0} L}} )} {2\alpha_{0} }}} \right. \kern-0pt} {2\alpha_{0} }}\), and \(n_{4}\) is the 5th-order NL refractive index.
Now, the complex electric field exiting the sample is given by
It consists of three terms: the amplitude of the electric field at the sample position, the damping factor because of linear absorption and the term containing the NL phase distortion.
Figure 32 shows the CA normalized on-axis transmittance assuming S = 0.01 and \(\Delta \Psi_{0} = \pm 0.25\) calculated numerically using the Kirchhoff diffraction integral. In fact, the electric field distribution is first calculated numerically using Eq. (79) for the case of 5th-order nonlinearity, and then the CA normalized transmittance is calculated numerically using Eq. (94).
CA normalized on-ais transmittance calculated numerically using Eq. (94) for a medium showing 5th-order NL refractivity
Using the GD method, the electric field exiting the sample can be given by an infinite summation of Gaussian beams with different beam radii and different complex amplitudes. That is,
Now, the electric field distribution on the aperture plane can be calculated analytically using the Fresnel integral. That is,
where
In the limit of a small NL phase change induced by a Gaussian CW laser beam, the normalized transmittance for small apertures can be derived by substituting Eq. (110) into Eq. (95) and letting \(r = 0\).
Within the far-field approximation (\(d > z_{0}\)), the normalized transmittance is derived as
In the case of utilizing temporally Gaussian pulses, the time averaged \(\langle \Delta \Psi (t)\rangle\) should replace ΔΨ0; hence, the normalized transmittance is given by
where
The transmittance versus the sample position in the presence of 5th-order nonlinearity has the same qualitative features as that of the 3rd nonlinearity, namely, possessing two extrema; a peak followed by a valley indicating a self-defocusing process (\(n_{4} < 0\)); or a valley followed by a peak indicating a self-focusing process (\(n_{4} > 0\)).
Within the approximation applied to derive Eq. (118), the Z-scan trace appears to be symmetric with respect to both the baseline and the beam waist. This means that the height of the peak is identical to the depth of the valley and that the peak and valley are equidistant from the focal point. The positions of the peak and valley can be obtained by solving the differential equation \({{dT(x)} \mathord{\left/ {\vphantom {{dT(x)} {dx}}} \right. \kern-0pt} {dx}} = 0\). That is,
This gives the peak and valley positions as
Therefore, the peak-to-valley distance is calculated as
By substituting the peak and valley positions in Eq. (118), the transmittance peak-to-valley difference is obtained as
This provides a convenient estimation of the NL refractive index by measuring \(\Delta T_{p \to v}\) without any need for an arduous process of fitting the theoretical curve to the experimental data. Figure 33 illustrates the numerically calculated transmittance peak-to-valley difference versus the on-focus phase change assuming a very small aperture size, confirming the linear dependency given in Eq. (124).
The 0n-axis transmittance peak-to-valley difference versus the on-focus phase change. The circular dots were obtained numerically using Eq. (94), and the red solid line represents a linear fit with a slope of 0.205
Numerical calculations for larger apertures and greater phase changes reveal that the difference between the transmittance peak and valley scales linearly with the on-focus phase change; however, the slope of the line depends on the aperture transmittance. The coefficient in Eq. (124) decreases with aperture size so that, in the limit of small phase distortion, the aperture dependence can be approximated by multiplying the coefficient on the right-hand side of Eq. (124) by \((1 - S)^{0.25}\) [19]. Numerical calculations with more rigorous precision show that the coefficient in Eq. (124) depends, in addition to the aperture transmittance, also on the phase change. For lower phase distortion (\(\Delta \Psi_{0} = 0.25\)), Fig. 34 shows the transmittance peak-to-valley difference versus the aperture transmittance, revealing an aperture size dependence of \(\Delta T_{p \to v} = 0.205\,\Delta \Psi_{0} \,(1 - S)^{0.236}\), whereas for larger phase distortion (\(\Delta \Psi_{0} = 1\)), the transmittance peak-to-valley difference versus aperture transmittance reveals an aperture size dependence of \(\Delta T_{p \to v} = 0.212\,\Delta \Psi_{0} \,(1 - S)^{0.19}\), as shown in Fig. 35. However, the aperture size dependency suggested in [19] can be used for any aperture size within a 5% accuracy for \(\Delta \Psi_{0} < 1\).
Transmittance peak-to-valley difference versus aperture transmittance assuming a phase distortion of \(\Delta \Psi_{0} = 0.25\). The circles show the numerically calculated data using Eq. (94), in which the electric field was calculated via Eq. (79). The solid red curve indicates the best fit to the data, revealing the dependency, such as \(\Delta T_{p \to v} = 0.205\,\Delta \Psi_{0} \,(1 - S)^{0.236}\)
Transmittance peak-to-valley difference versus the aperture transmittance assuming a phase distortion of \(\Delta \Psi_{0} = 1\). The circles show the numerically calculated data using Eq. (94), in which the electric field was calculated via Eq. (79). The solid red curve indicates the best fit to the data, revealing the dependency, such as \(\Delta T_{p \to v} = 0.212\,\Delta \Psi_{0} \,(1 - S)^{0.19}\)
As mentioned earlier, the same qualitative features are observed from the Z-scan traces regardless of the order of nonlinearity. Figure 36 shows a comparison between the CA Z-scan on-axis transmittance calculated for different phase changes \(\Delta \Psi_{0} = 0.25\) and \(\Delta \Psi_{0} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\). It is illustrative that the Z-scan loses symmetricity for larger phase distortions.
CA Z-scan on-axis transmittance calculated numerically using Eq. (94) for different phase changes induced by 5th-order nonlinearity
Figure 37 shows the CA Z-scan transmittance for different aperture transmittances in the range of 0.01–0.90. Using a large size aperture leads to a smaller variation in the normalized transmittance. By enlarging the aperture size, the peak and valley both become weaker; however, the peak reduction is much more predominant, vanishing as the aperture transmittance increases to unity. Without any aperture (\(r_{a} = \infty \Rightarrow S = 1\)), the effect of NL refractivity does not appear in the Z-scan transmittance since \(T(z) = 1\) for all phase changes.
CA Z-scan in the case of 5th-order nonlinearity calculated numerically using Eq. (94) for aperture transmittance
4.1.3 Simultaneous 3rd- and 5th-order NL refractivity
Assuming simultaneous 3rd- and 5th-order NL refractivity and negligible NL absorptivity, the Z-scan trace can be derived by solving the following couple of equations.
and
Now, the total phase changes due to the 3rd- and 5th-order NL refractivity is given by
After substitution of the intensity in Eq. (127) The phase change is given as:
Thus, the complex electric field exiting the sample is given by
Using the GD method, the complex electric field exiting the sample is obtained as
where
Using the Fresnel integral, the electric field distribution in the far field is found as
where
and
Under the approximation of small phase distortion and small aperture size, the normalized transmittance of the CA Z-scan obtained by the Gaussian CW laser beam is obtained as
Within the limit of the first-order approximation (i.e., ignoring \(\Delta \Phi_{0}^{2}\), \(\Delta \Psi_{0}^{2} \,\), \(\Delta \Phi_{0} \cdot \Delta \Psi_{0}\) and higher order terms), the normalized transmittance of the CA Z-scan for the simultaneous presence of 3rd- and 5th-order NL refractivity is derived as
Within such an approximation, the Z-scan is symmetric with peak-to-valley separation given by
The transmittance peak-to-valley difference is obtained as
The numerical calculation using the Kirchhoff diffraction integral indicates that the Z-scan transmittance is never symmetric regardless of the order of the nonlinearity. Figure 38 shows the numerically calculated normalized on-axis transmittance for a small aperture size and phase changes of \(\Delta \Phi_{0} = 0.5\) and \(\Delta \Psi_{0} = 0.25\). This illustrates that the valley position is approximately \(z_{v} = - \,0.73\,z_{R}\), and the peak position is approximately \(z_{p} = \, + \,0.82\,z_{R}\), so that \(\Delta z_{p \to v} = 1.55z_{R}\). It is worth noting that the valley and peak positions shift toward the positive z-direction for positive nonlinearity (see Fig. 39) and vice versa. However, the distance between the valley and peak position remains almost constant (i.e., \(\Delta z_{p \to v} = 1.55z_{R}\)) and is independent of the amount of phase distortion.
CA Z-scan on-axis transmittance for a medium possessing both 3rd- and 5th-order nonlinearities simultaneously. Both the dashed red curve for positive nonlinearity and the solid blue curve for negative nonlinearity were calculated numerically using Eq. (94)
Figure 40 shows the CA normalized on-axis transmittance obtained for different orders of NL refractivity. The inset clearly illustrates that the peak position occurs in each case.
CA normalized on-axis transmittance for different orders of nonlinearity calculated numerically using Eq. (94). The solid blue curve represents 3rd-order nonlinearity, the dashed red curve represents simultaneous 3rd- and 5th-order nonlinearity, and the dotted green curve represents 5th-order nonlinearity
Reference [81] shows the results of the analytical calculation of the Z-scan transmittance for a medium with simultaneous 3rd- and 5th-order NL refractivity in the presence of 2PA.
4.1.4 Simultaneous 3rd-order NL refractivity and absorptivity
Depending on the laser intensity and laser wavelength used to perform the Z-scan, the NL absorption might be considerable and thus should be taken into account. The MPA leads to suppressing the peak and enhancing the valley of the CA Z-scan transmittance, and the SA results in the opposite behavior. To determine the phase change in the presence of 2PA, the following couple of differential equations must be solved [73, 74].
The solution of Eq. (139) yields the intensity within the medium given by
By substituting Eq. (141) in Eq. (140), the phase change of the electric field propagating through the medium of length L is derived as
where \(q(z,r^{\prime},t) = \alpha_{2} I(z,r^{\prime},t)L_{eff}\).
The complex electric field exiting the sample can be written as:
where \(\left| {E_{e} (z,r^{\prime},t)} \right|\) is the amplitude of the electric field exiting the sample, defined as \(\left| {E_{e} (z,r^{\prime},t)} \right| = \sqrt {{{2I_{e} (z,r^{\prime},t)} \mathord{\left/ {\vphantom {{2I_{e} (z,r^{\prime},t)} {cn\varepsilon_{0} }}} \right. \kern-0pt} {cn\varepsilon_{0} }}}\).
After substitution of the field amplitude and phase change from Eqs. (141) and (142) in Eq. (143), the exiting electric field is obtained as follows:
Using a binomial series to expand \(\left( {1 + q(z,r^{\prime})} \right)^{{i\frac{{kn_{2} }}{{\alpha_{2} }} - \frac{1}{2}}}\) leads to the following:
Using the Fresnel integral, the far-field pattern of the electric field is derived as
To calculate the on-axis (r = 0) transmittance for a small phase change (ΔΦ < 1), the first two terms in Eq. (146) are sufficient to be retained. Thus, the normalized transmittance assuming a cubic NL medium irradiated with a CW Gaussian laser beam is given by
Letting \(q_{0} = 0\) in Eq. (147), it transforms to Eq. (98) derived for pure refractivity in the case of cubic nonlinearity.
Unlike in the pure refractivity case, Eq. (147) gives, in two respects, an asymmetric trace. First, the peak height is no longer equal to the valley depth; the peak is suppressed, whereas the valley is enhanced. Second, the normalized transmittance at the focus is not unity but \(T_{0} = 1 - {{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } 3}} \right. \kern-0pt} 3}\). The latter, however, allows a readily estimation of the 2PA coefficient just by determining the normalized transmittance at the focus through \(\alpha_{2} = {{3\,(1 - T_{0} )} \mathord{\left/ {\vphantom {{3\,(1 - T_{0} )} {L_{eff} I_{0} }}} \right. \kern-0pt} {L_{eff} I_{0} }}\).
Depending on the ratio of \({{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {q_{0} }}} \right. \kern-0pt} {q_{0} }}\), there might be no null point, a single null point or even two null points observed in CA transmittance in the presence of 2PA. The critical ratio of \({{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {q_{0} = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {q_{0} = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}\) results in a situation in which only a single null point is observed at \(z = \sqrt 3 \,z_{R}\) (dashed red curve in Fig. 41). For Z-scan with the ratio \({{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {q_{0} < {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {q_{0} < {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}\), no null point is observed (dotted green curve in Fig. 41). Figure 41 shows that for a Z-scan with a ratio of \({{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {q_{0} > {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {q_{0} > {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0pt} 2}}}\), two null points occur at \(x = {{2\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{2\Delta \Phi_{0} } {q_{0} }}} \right. \kern-0pt} {q_{0} }} \pm \sqrt {({{2\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{2\Delta \Phi_{0} } {q_{0} }}} \right. \kern-0pt} {q_{0} }})^{2} - 3}\). An interesting case is \(\Delta \Phi_{0} = q_{0}\) in which the null positions occur at \(x = 1\) (i.e., \(z = z_{R}\)) and \(x = 3\) (i.e., \(z = 3z_{R}\)) (solid blue curve in Fig. 41).
The discussions above were concluded as an outcome of Eq. (147), which is valid for small values of \(\Delta \Phi_{0}\) and \(q_{0}\). Numerical calculations using the Kirchhoff diffraction integral show that the real critical ratio of \({{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {q_{0} }}} \right. \kern-0pt} {q_{0} }}\), at which only a single null point is observed, is approximately 0.63 instead of 0.86.
Figure 41 shows the Z-scan normalized on-axis transmittance of different cases showing the same \(q_{0}\) but different \(\Delta \Phi_{0}\). This figure illustrates how changing \(\Delta \Phi_{0}\) affects the Z-scan trace. A decrease in \(\Delta \Phi_{0}\) results in a V-shaped signal, which is a signature of the OA Z-scan for MPA absorption. It should be noted that for the case of \(\Delta \Phi_{0} = 0\), although the Z-scan signal is similar to that of the OA Z-scan, this transmittance was plotted assuming a small aperture; thus, the data are not expected to be exactly the same as those for the OA Z-scan transmittance.
The analytic result for the CA Z-scan transmittance corrected to the second-order of irradiance [124] (i.e., retaining more terms in Eq. (146)) is given by
\(\Delta \Phi_{0}\) and \(q_{0}\) in Eqs. (147) and (148) can be replaced by the time-averaged \(\langle \Delta \Phi_{0} (t)\rangle = {{\Delta \Phi_{0} } \mathord{\left/ {\vphantom {{\Delta \Phi_{0} } {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}\) and \(\langle q_{0} (t)\rangle = {{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}\) for the case of using temporally Gaussian pulses in the Z-scan experiment.
Figure 42 shows the normalized Z-scan on-axis transmittance of different cases showing the same \(\Delta \Phi_{0}\) but different \(q_{0}\). This illustrates how the increase in absorptivity influences the Z-scan signal. With increasing \(q_{0}\), the peak is more suppressed, and the valley becomes much deeper.
Fitting Eq. (147) to the experimental data results in attaining both the NL refractive index \(n_{2}\) and 2PA coefficient \(\alpha_{2}\) simultaneously. However, another approach for determining the optical nonlinearities of those materials showing simultaneous NL refractivity and absorptivity was suggested by Bahae [19]. The Z-scan setup can be extended to include both CA and OA. As shown in Fig. 43, the laser beam transmitted through the sample is divided into two parts using a beam splitter. One part goes through a small aperture toward the diode \(D_{c1}\) to measure the CA trace, and the other part is collected entirely by a lens and then detected by a diode \(D_{c2}\) to measure the OA trace. The simple division of CA Z-scan transmittance to OA results in a new Z-scan trace showing pure NL refractivity. In Fig. 44, the solid blue curve is the CA Z-scan transmittance, the dashed red curve indicates the OA Z-scan, and the dotted green curve represents the CA to OA trace. In conclusion, the NL refractive index \(n_{2}\) and the 2PA coefficient \(\alpha_{2}\) can be determined simultaneously by fitting Eq. (147) to the CA Z-scan (solid blue trace in Fig. 44) or separately by fitting Eq. (18) to the OA Z-scan (dashed red trace in Fig. 44) and Eq. (98) to the division of CA to OA Z-scan (dotted green curve in Fig. 44).
Schematic diagram of the Z-scan setup for measuring both CA and OA traces simultaneously [110]
4.1.5 Simultaneous 5th-order NL refractivity and absorptivity
In the presence of the 3PA, as a process of 5th-order nonlinearity, the following couple of differential equations should be solved to derive the phase change induced as a consequence of the 5th NL refractivity.
Equation (150) has already been solved in Sect. 3.1.2. Therefore, the total phase change during propagation through the medium of length L is given by
The complex electric field exiting the sample now contains the NL phase distortion and the NL absorption reduction. That is,
After substituting \(I(z,r^{\prime},t)\) and \(\Delta \Phi (z,r^{\prime},t)\) from Eqs. (20) and (151) into (152), the electric field exiting the sample is given by
The term \(\left[ {1 + p^{2} (z,r^{\prime},t)} \right]^{{(i\frac{{kn_{4} }}{{2\alpha_{3} }} - \frac{1}{4})}}\) in Eq. (153) can be expanded using a binomial series. The result is
The electric field pattern in the far field can be obtained using the Fresnel integral. That is,
All parameters, such as \(R_{m}\), \(d_{m}\), \(\theta_{m}\) and \(w_{m}\), have already been defined through Eqs. (111) to (116).
In the limit of a small NL phase change, the on-axis electric field at the aperture plane can be obtained by letting \(r = 0\) and retaining only the first two terms in Eq. (155). Following such an approximation and assuming CW radiation, the normalized transmittance for the case of CW radiation is derived as
where \(p_{0}^{2} = 2\alpha_{3} L^{\prime}_{eff} \,I_{0}^{2}\) and \(\Delta \Psi_{0} = kn_{4} L^{\prime}_{eff} I_{0}^{2}\).
By setting \(p_{0} = 0\), Eq. (156) transforms to Eq. (118), which is derived for a medium with a negligible 3PA.
Unlike in the pure refractivity case, Eq. (156) gives an asymmetric trace. In the waist position, the normalized transmittance is not unity but \(T_{0} = 1 - {{p_{0}^{2} } \mathord{\left/ {\vphantom {{p_{0}^{2} } {10}}} \right. \kern-0pt} {10}}\). This provides an opportunity to estimate the 3PA coefficient readily by determining the normalized transmittance at the focus \(\alpha_{3} = {{10\,(1 - T_{0} )} \mathord{\left/ {\vphantom {{10\,(1 - T_{0} )} {2L^{\prime}_{eff} \,I_{0}^{2} }}} \right. \kern-0pt} {2L^{\prime}_{eff} \,I_{0}^{2} }}\).
There is a critical situation introduced by \({{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} = {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}} \right. \kern-0pt} {p_{0}^{2} = {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}\) in which only a single null position is observed at \(z = \sqrt 5 \,z_{R}\)(dashed red curve in Fig. 45). For the Z-scan with a ratio of \({{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} < {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}} \right. \kern-0pt} {p_{0}^{2} < {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}\), no null position is observed (solid blue curve in Fig. 45). However, a Z-scan with a ratio of \({{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} > {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}} \right. \kern-0pt} {p_{0}^{2} > {{\sqrt 5 } \mathord{\left/ {\vphantom {{\sqrt 5 } 8}} \right. \kern-0pt} 8}}}\) possesses two null points located at \(x = 8{{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} }}} \right. \kern-0pt} {p_{0}^{2} }} \pm \sqrt {(8{{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} }}} \right. \kern-0pt} {p_{0}^{2} }})^{2} - 5}\). An interesting case is \({{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {p_{0}^{2} }}} \right. \kern-0pt} {p_{0}^{2} }} = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 3}} \right. \kern-0pt} 3}\), in which the null positions are obtained at \(x = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 3}} \right. \kern-0pt} 3}\) and \(x = 5\sqrt 3\) (dotted green curve in Fig. 45).
It is worth mentioning that the solid blue curve (\(\Delta \Psi_{0} = 0\)) in Fig. 45 is although a V-shaped signal similar to an OA Z-scan signal, it shows the normalized transmittance through a small aperture; thus, it is not expected to be exactly the same as that measured in the OA Z-scan experiment.
Figure 46 shows the CA normalized transmittance for different cases with the same \(\Delta \Psi_{0}\) but different NL absorptivity. This illustrates that 3PA affects the shape and strength of the Z-scan signal. As shown in this figure, increasing the 3PA coefficient leads to the suppression of the peak and the deepening of the valley.
When using a pulsed laser with temporally Gaussian pulses, \(\Delta \Psi_{0}\) and \(p_{0}^{2}\) in Eq. (156) should be substituted by the time-averaged \(\langle \Delta \Psi_{0} (t)\rangle = {{\Delta \Psi_{0} } \mathord{\left/ {\vphantom {{\Delta \Psi_{0} } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}\) and \(\langle p_{0}^{2} (t)\rangle = {{p_{0}^{2} } \mathord{\left/ {\vphantom {{p_{0}^{2} } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}\).
4.2 Astigmatic Gaussian beams
In this section, an astigmatic laser beam is assumed to be used for the Z-scan experiment. The electric field of an elliptic Gaussian laser beam, including the astigmatism, and the relevant parameters are given in Eq. (60) to Eq. (65).
4.2.1 Pure 3rd-order NL refractivity
Within the limit of a small phase change, the on-axis normalized CA transmittance in the case of cubic nonlinearity assuming negligible NL absorption is given by [75, 87]
where \(p_{1}\) can take the values of ± 1. It takes the value of 1 for \((X + Y)(3 + XY) > 0\). Otherwise, it takes the value of − 1 [87]. In Eq. (157), \(\Delta \Phi_{\max } = kn_{2} L_{eff} I_{\max }\) where \(n_{2}\) is the 3rd-order NL refractive index, \(L_{eff}\) is the effective length of the sample, and \(I_{\max } = {{2{\text{P}}} \mathord{\left/ {\vphantom {{2{\text{P}}} {w_{0x} w_{0y} }}} \right. \kern-0pt} {w_{0x} w_{0y} }}\) in which \({\text{P}}\) is the laser power.
By setting \(X = Y\), Eq. (157) is transformed to Eq. (98), which is derived for a spherical Gaussian beam.
The position of the nulls can be found by letting T(z) = 1 in Eq. (157). This leads to \(Y = - \,X\) or \(Y = {{ - 3} \mathord{\left/ {\vphantom {{ - 3} X}} \right. \kern-0pt} X}\) and thus to the following null positions
and
For a circular Gaussian beam, both Eqs. (158) and (159) give the same results, leading to a single null point located at the beam waist position. However, for an astigmatic beam, Eqs. (158) and (159) lead to different solutions, resulting in two or even three null points. One of the null points is always calculated from Eq. (158). According to Eq. (159), there is a critical distance for the waist separation \(\Delta z_{0xy} = \sqrt {12z_{Rx} z_{Ry} \,}\) for which the second null point occurs exactly at the middle of either focal point. For waist separations smaller than the critical distance, Eq. (159) results in a complex number, and thus, no additional null point is observed. However, for waist separations larger than the critical distance, Eq. (159) has two real answers, leading to two more null points appearing symmetrically with respect to the middle of the beam waist.
Figure 47 shows the CA Z-scan traces calculated using the Fresnel diffraction integral assuming that astigmatic laser beams have the same ellipticity of \(e = {{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 1.5}}} \right. \kern-0pt} {w_{0x} = 1.5}}\) and the same maximum phase change of \(\Delta \Phi_{\max } = 1.5\) but different waist separations. The waists are located equidistant from the origin of the z-axis. The larger beam waist is placed before the origin; thus, the sample first encounters the larger beam size and then the smaller beam size, and therefore, the depth of the valley is less than the height of the peak in all traces in Fig. 47. For an ellipticity of e = 1.5, the critical separation \(\sqrt {12z_{Rx} z_{Ry} \,}\) is approximately \(5.2\,z_{Rx}\). This value is, of course, not accurate since Eq. (157) was derived as the on-axis normalized transmittance for small phase distortion. Accurate numerical calculations show that the critical waist separation is \(5.6\,z_{Rx}\) for which two nulls are observed (dashed red curve in Fig. 47). In Fig. 47, the solid blue curve shows the Z-scan for an astigmatic beam with a waist separation of \(4\,z_{Rx}\) (less than the critical value); therefore, a single null point is observed. The dotted green curve, showing three null points, illustrates the CA Z-scan assuming an astigmatic beam with a waist separation larger than the critical value (\(\Delta z_{0xy} = 8\,z_{Rx}\)).
CA Z-scan on-ais transmittance using an astigmatic laser beam. The solid blue curve indicates the transmittance for the waist separation \(4z_{Rx}\), the dashed red curve indicates the waist separation of \(5.6z_{Rx}\), and the dotted green curve indicates the waist separation of \(8z_{Rx}\). The results were calculated numerically using Eq. (95), in which the electric field was calculated numerically using Eq. (84)
Huang [70, 71] examined a slit instead of a circular aperture to measure the CA Z-scan transmittance in the x- and y-directions. In this case, the normalized transmittance through a long slit mounted perpendicular to the y-axis (x-axis) can be defined as follows instead of Eq. (95):
where \(y_{0}\) denotes the slit width in the y-direction.
\(T_{x}\) can be defined in a similar way. For elliptical beams without astigmatism, both \(T_{x}\) and \(T_{y}\) appears to be symmetric, although they show diverse peak-to-valley differences. It is obvious that the normalized transmittance of the slit in the direction with a smaller beam waist radius shows a larger peak-to-valley difference. However, for an astigmatic beam, the transmittance of a slit, similar to the transmittance of a circular aperture, is also not symmetric. However, the slit transmittance in the direction with a smaller beam waist radius, which shows a larger peak-to-valley difference, is more symmetric than that of a circular aperture and thus more convenient and reliable for determining the NL refractive index.
Figure 48 shows the Z-scan transmittance numerically calculated using Eq. (160) for an astigmatic beam possessing an ellipticity of \({{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 4}}} \right. \kern-0pt} {w_{0x} = 4}}\) and a waist separation of \(5z_{Rx}\) assuming a maximum phase change of \(\Delta \Phi_{\max } = 1.5\). The solid blue curve shows the transmittance through a slit perpendicular to the x-axis, \(T_{x}\), and the dashed red curve indicates \(T_{y}\). The dotted green curve, denoted \(T_{c}\), represents the circular aperture transmittance for comparison.
CA Z-scan slit and aperture transmittance for an astigmatic beam possessing an ellipticity of \({{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 4}}} \right. \kern-0pt} {w_{0x} = 4}}\) and waist separation of \(5z_{Rx}\) assuming a maximum phase change of \(\Delta \Phi_{\max } = 1.5\). \(T_{x}\) and \(T_{y}\) were both calculated numerically using Eq. (160)
4.2.2 Pure 5th-order NL refractivity
Within the limit of a small phase change, the on-axis normalized CA transmittance in the case of 5th-order nonlinearity assuming negligible NL absorption is given by
where \(p_{2}\) can take the values of ± 1. It takes the value of 1 for \((X + Y)(5 + XY) > 0\). Otherwise, it takes the value of − 1 [87]. In Eq. (161)\(\Delta \Psi_{\max } = kn_{4} L^{\prime}_{eff} I_{\max }^{2}\), \(n_{4}\) is the 5th-order NL refractive index, \(L^{\prime}_{eff}\) is the effective length of the sample, and \(I_{\max } = {{2{\text{P}}} \mathord{\left/ {\vphantom {{2{\text{P}}} {w_{0x} w_{0y} }}} \right. \kern-0pt} {w_{0x} w_{0y} }}\) in which \({\text{P}}\) is the laser power.
The position of the nulls can be found by letting T(z) = 1 in Eq. (161). This leads to \(Y = - \,X\) or \(Y = {{ - 5} \mathord{\left/ {\vphantom {{ - 5} X}} \right. \kern-0pt} X}\) and thus to the following null positions:
and
Equation (162) is the same as Eq. (158), which gives a null point for any beam regardless of the degree of ellipticity or astigmatism. For the circular and astigmatism-free beams, both Eqs. (162) and (163) give the same single null point occurring at the waist position. For a stigmatic beam, depending on the waist separation, Eq. (163) may yield a different solution. For a waist separation of less than \(\sqrt {\,20\,z_{Rx} z_{Ry} \,}\), there is no real answer, so no additional null is observed. For the waist critical separation of \(\sqrt {\,20\,z_{Rx} z_{Ry} \,}\), one additional null at the middle of the two waists is observed. If the waist separation is greater than \(\sqrt {\,20\,z_{Rx} z_{Ry} \,}\), two more nulls are observed to be located symmetrically with respect to the middle of the two waists.
Figure 49 shows the CA Z-scan traces calculated using the Fresnel diffraction integral assuming that astigmatic laser beams have the same ellipticity of \(e = {{w_{0y} } \mathord{\left/ {\vphantom {{w_{0y} } {w_{0x} = 1.5}}} \right. \kern-0pt} {w_{0x} = 1.5}}\) and the same maximum phase change of \(\Delta \Psi_{\max } = 2\) but different waist separations. The waists are located equidistant from the origin of the z-axis. A larger beam waist is assumed before the origin; thus, the sample first encounters a larger beam size and then a smaller beam size; therefore, the depth of the valley is less than the height of the peak in all the traces in Fig. 49. For an ellipticity of e = 1.5, the critical separation \(\sqrt {20z_{Rx} z_{Ry} \,}\) is approximately \(6.71\,z_{Rx}\). This value is, of course, not exactly accurate since Eq. (161) is an approximate relation derived as the on-axis normalized transmittance for small phase distortion. Accurate numerical calculations show that the critical waist separation is \(6.82\,z_{Rx}\) instead of \(6.71\,z_{Rx}\) (dashed red curve shows two null points in Fig. 49). In Fig. 49, the solid blue curve shows the Z-scan for an astigmatic beam with a waist separation of \(5\,z_{Rx}\) (less than the critical value); therefore, a single null point is observed. The dotted green curve in Fig. 49, showing three null points, illustrates the CA Z-scan transmittance using an astigmatic beam with a waist separation larger than the critical value (\(\Delta z_{0xy} = 10\,z_{Rx}\)).
CA Z-scan on-axis transmittance using an astigmatic laser beam with an ellipticity of e = 1.5 and \(\Delta \Psi_{\max } = 2\) for different focus separations. The solid blue curve indicates the transmittance for the waist separation of \(5z_{Rx}\), the dashed red curve indicates the waist separation of \(6.2z_{Rx}\) and the dotted green curve indicates the waist separation of \(10z_{Rx}\). The results were calculated numerically using Eq. (95), in which the electric field was calculated numerically using Eq. (84)
4.2.3 Simultaneous 3rd- and 5th-order NL refractivity
When both the 3rd- and 5th-order of NL refractivity are responsible for the refractive index change, the normalized transmittance can be obtained by combining Eqs. (157) and (161) [87].
Equation (164) holds for small phase distortion with the same definitions presented in the previous sections.
5 Z-scan technique through beam radius measurements
In a modified version of a Z-scan, the beam radius \(r_{h}\) on the far-field plane is measured as a function of the sample position. In this method, there is no aperture or lens after the sample; thus, instead of the transmitted power, the beam radius is measured using a CCD camera.\(r_{h}\) can be defined as the distance from the beam center to the points where the intensity decreases to a specific fraction \(h\) of its on-axis (\(r = 0\)) value. (e.g., \(h = {1 \mathord{\left/ {\vphantom {1 {e^{2} }}} \right. \kern-0pt} {e^{2} }}\) corresponds to the commonly defined radius \(w(z)\) of the Gaussian beam) [83, 90,91,92, 125,126,127,128].
The radius of the beam entering the CCD camera placed in the far field can be numerically calculated through the following relationship:
where \(I(z,r_{h} ) = {{c\varepsilon_{0} \left| {E(z,r_{h} )} \right|^{2} } \mathord{\left/ {\vphantom {{c\varepsilon_{0} \left| {E(z,r_{h} )} \right|^{2} } 2}} \right. \kern-0pt} 2}\) with \(E(z,r_{h} )\) defined in Eq. (79).
For \(\left| {\Delta \Phi_{0} } \right| \le 1\), the radius peak-to-valley difference \(\Delta r_{{\text{p - v}}}\) in a Z-scan normalized radius depends almost linearly on \(\left| {\Delta \Phi_{0} } \right|\) given in [90,91,92]
This relation can be used to readily estimate the NL refractive index \(n_{2}\) by simply measuring the peak-to-valley difference in the Z-scan normalized radius.
Figure 50 shows the normalized beam radius as a function of sample position for the case of cubic nonlinearity with \(\Delta \Phi_{0} = 1\). In the numerical calculation for Fig. 50, the observation plane was placed 100 mm away from the focus, the laser wavelength was assumed to be 800 nm, and the beam waist radius was 20 µm. The self-focusing effect leads to beam broadening when the sample is located before the waist and, inversely, to beam narrowing when the sample is placed after the waist; thus, the Z-scan trace showing a peak followed by a valley is a signature of positive NL refractivity. In Fig. 50, the solid blue curve indicates the beam radius as the distance from the beam center where the intensity decreases to \(h = {1 \mathord{\left/ {\vphantom {1 e}} \right. \kern-0pt} e}\) of its on-axis value, and the dashed red curve shows the radius as the distance from the beam center where the intensity decreases to \({{h = 1} \mathord{\left/ {\vphantom {{h = 1} e}} \right. \kern-0pt} e}^{2}\) of its on-axis. As shown in Fig. 50, the sensitivity of the measurement defined as \(p = {{\Delta r_{{\text{p - v}}} } \mathord{\left/ {\vphantom {{\Delta r_{{\text{p - v}}} } {\,\left| {\Delta \Phi_{0} } \right|}}} \right. \kern-0pt} {\,\left| {\Delta \Phi_{0} } \right|}} = 0.154\,h^{ - 0.214}\) is greater for lower values of \(h\). This is because the variations in the beam radius become very large in the region of the beam wings. However, for very low values of \(h\), the beam intensity is very weak compared to the noise level, thus introducing high uncertainty into the measurements. Therefore, to achieve a reliable signal-to-noise ratio, the value of \(h\) must be kept at an optimum level, compromising between high sensitivity and low uncertainty [90,91,92].
Normalized beam radius as a function of sample position numerically calculated using Eq. (165) in the case of cubic nonlinearity with \(\Delta \Phi_{0} = 1\)
6 Two-photon spectra
In conventional OA Z-scan, the 2PA cross section is obtained for the specific wavelength delivered by the source used for the experiment. For many purposes, wavelength-resolved 2PA spectra must be obtained. For instance, the wavelength of the laser can be tuned to the peak absorption spectrum in 2PA-based applications to enhance the process efficiency. Additionally, for newly developed compounds, 2PA spectra are essentially necessary as a guideline for designing molecules with higher 2PA cross sections. To determine the 2PA spectra, a tunable laser or a high-intensity white light continuum (WLC) source should replace the single wavelength source used in conventional Z-scan. Different methods have been utilized for determining 2PA spectra, which are introduced in the following sections.
6.1 Using tunable lasers to determine the 2PA spectrum
An optical parametric amplifier (OPA) or optical parametric oscillator (OPO) can be used as a tunable laser source for determining the 2PA spectrum. The conventional OA Z-scan can be repeated at different wavelengths by tuning the central wavelength of the laser output. From each Z-scan trace, the 2PA cross section at the tuned wavelength can be extracted. Applying this method yields 2PA spectra in a point-by-point fashion [30,31,32, 129,130,131,132]. For instance, to obtain 2PA spectra in the range of 600–950 nm with a resolution of 10 nm, the Z-scan experiment must be repeated 35 times, which is cumbersome and time-consuming.
6.2 Using WLC to determine the 2PA spectrum
The WLC [133], as a broadband coherent light source, can be generated by focusing highly energetic short pulses into transparent media such as water [27], glass [134], optical fibers [135], photonic crystals [136], dielectric and semiconductors [137], crystals such as BaF2 [138] and inert gases such as Krypton or Argon [139, 140]. The WLC Z-scan is an improved version of the conventional Z-scan in which a single wavelength (i.e., narrow band) laser is replaced with a WLC source. 2PA spectral measurements using WLC have been performed in various fashions by different groups.
In [27, 28, 30,31,32, 141, 142], a series of narrow band filters with different central transmittance wavelengths were used to select a narrow range of the WLC spectrum by placing the filter in front of the WLC beam. The beam transmitted through the filter, which likely behaves as a single wavelength source, can be used to perform conventional single-beam single-wavelength Z-scan. By changing the filter and repeating the Z-scan at different wavelengths, 2PA spectra can be obtained in a point-by-point fashion, which is also cumbersome and time-consuming, as in the case of using tunable lasers.
In [33, 34, 143], the WLC beam is focused entirely in a single spot within the material using a spherical lens. In this way, the 2PA process occurs via both degenerate and nondegenerate processes since the irradiated volume of the sample receives all the entire wavelength in the WLC spectrum. In this method, the NL transmittance is measured by a spectrometer as a function of the sample position. Although the measured Z-scan show the NL transmittance for different wavelengths, they comprise both degenerate and nondegenerate 2PAs over the entire spectrum of the WLC with unknown contributions from each process. Therefore, it is not feasible to determine the pure degenerate 2PA spectra using this method. However, this method provides a simple way to obtain the wavelength-resolved nondegenerate 2PA cross section.
In [73, 144,145,146], the WLC beam is dispersed spatially and then focused by a spherical lens into the center of the sample. With this arrangement, different spectral components of the WLC beam are spatially separated from each other at the sample position, and only degenerate TPA from the same spectral component can occur. In this method, the sample is fixed at the focal point where the WLC beam is focused; thus, this technique cannot be considered a Z-scan technique. The radiation transmitted through the pure solvent as well as through the prepared sample is detected by a spectrometer. By comparing the transmission of the sample at the focus to that of the pure solvent, the attenuation of different spectral components can be determined. In this method, although the obtained spectrum is relevant to the degenerate 2PA process it represents the relative but not the absolute value of the 2PA cross section. To determine the absolute 2PA spectrum, a separate Z-scan should be performed at a single wavelength to determine the 2PA cross section required for calibration and converting the relative 2PA spectrum to absolute values.
We proposed a new method to determine the wavelength-resolved degenerate absolute 2PA spectrum by performing a single scan using WLC [35,36,37,38]. The WLC was generated by focusing 30 fs, 500 mJ Ti:sapphire laser pulses at the entrance of a hollow fiber inside a chamber filled with Ar gas at ambient pressure. The spectrally broadened light with bandwidth ranging from 500 to 1000 nm exiting the hollow fiber then travels through an ultrabroadband dispersive mirror compressor, leading to compressed pulses with a duration of less than 8 fs. The generated WLC was spatially dispersed and then collimated using a prism pair, leading to a rectangular beam cross section with a height of 10 mm and width of 30 mm. The beam was focused by a cylindrical lens to produce a focal line inside the sample. A 50 mm wide cuvette containing the sample solution mounted on a motorized translation stage was scanned along the propagation direction, similar to a conventional Z-scan. In this method, different spectral components of the WLC beam are spatially separated within the illuminated region of the sample; thus, only degenerate 2PA occur at each point of the sample. At each z-position, the transmitted intensity distribution is entirely imaged by a CCD line camera using a cylindrical lens (Fig. 51). The transmittance as a function of sample position measured by each pixel of the CCD line camera yields a Z-scan signal corresponding to a specific wavelength. This means that if the CCD camera has N pixels, N Z-scan signals are obtained by performing only a single scan along the z-axis. Thus, out of each signal measured by each pixel, the 2PA cross section can be extracted for each specific wavelength; therefore, the 2PA spectra can be determined via a single scan.
Figure 52 shows selected Z-scan signals at different wavelengths measured simultaneously via a single scan for the P2CK photoinitiator.
Figure 53 shows the 2PA spectra for three different 2PIs determined by the WLC Z-scan in the wavelength range of 680–920 nm.
2PA spectra for three different 2PIs determined by WLC Z-scan [35]
7 Eclipsing Z-scan (EZ-scan)
This modified version involves replacing the far-field aperture used in the CA Z-scan with an obscuration disk that blocks most of the beam. The resulting pattern of light that passes around the edge of the disk appears as a thin halo of light that looks like a total solar eclipse; hence, this technique is named the EZ-scan [147]. In this method, as shown in Fig. 54, the power transmitted around the edge of the disk is measured as a function of the sample position. Therefore, the EZ normalized transmittance is defined as follows:
Unlike the CA Z-scan, the eclipsing Z-scan has a more complex setup; however, it has been employed in many works [39, 40, 45, 148,149,150,151,152] due to its high sensitivity in determining the NL refractivity. In a modified version of the EZ-scan, the disk, instead of the sample, is scanned along the Z direction in the vicinity of the sample. This version is known as the disk Z-scan (DZ-scan) technique [24].
As mentioned in Sect. 4.1.1, for CA Z-scan in the case of cubic nonlinearity, the transmittance peak-to-valley difference depends linearly on the on-focus phase change obeying the relation \(\Delta T_{{({\text{p - v)}}}} = 0.406\,(1 - S_{a} )^{0.25} \Delta \Phi_{0}\) where \(S_{a} = 1 - \exp ( - {{2r_{a}^{2} } \mathord{\left/ {\vphantom {{2r_{a}^{2} } {w^{2} )}}} \right. \kern-0pt} {w^{2} )}}\) denotes the aperture transmittance with \(r_{a}\) the aperture radius. Numerical calculations show that in EZ-Scan, \(\Delta T_{{({\text{p - v)}}}}\) also has a linear dependence on \(\Delta \Phi_{0}\), which is given by
where \(S_{d} = 1 - \exp ( - {{2r_{d}^{2} } \mathord{\left/ {\vphantom {{2r_{d}^{2} } {w^{2} )}}} \right. \kern-0pt} {w^{2} )}}\) denotes the disk obscureness and \(r_{d}\) is the disk radius.
The peak-to-valley separation is empirically given by \(\Delta z_{{{\text{pv}}}} = 0.95\,z_{R}\).
As indicated in Fig. 55, the CA and eclipsing Z-scan have the same sensitivity as long as the aperture transmittance and disk obscureness are the same. It should be noted that the EZ-scan trace illustrating a peak followed by a valley is a signature of positive NL refractivity, which is opposite to that observed in a standard CA Z-scan.
Figure 56 shows a comparison between a CA Z-scan with \(S_{a} = 0.01\) and an EZ-scan with \(S_{d} = 0.99\) assuming a phase change of \(\Delta \Phi_{0} = 0.1\). The sensitivity of the EZ-scan is more than 10 times greater than that of the CA Z-scan.
In Fig. 57, the transmittance peak-to-valley difference, as a measure of sensitivity, was plotted versus the aperture transmittance (disk obscureness) for a CA Z-scan and an EZ-scan for comparison. As shown in this figure, by decreasing the aperture transmittance in the CA Z-scan, the sensitivity increases, but it is saturated to a limited value, whereas increasing the disk obscureness leads to an increase in the sensitivity almost exponentially without any limit. However, although a large disk leads to higher sensitivity, it also results in a low signal-to-nose ratio and thus a reduction in measurement accuracy.
The transmittance peak-to-valley difference versus aperture transmittance (disk obscureness) for a CA Z-scan calculated numerically using Eq. (95) (eclipsing Z-scan calculated numerically using Eq. (167)). For \(S_{d} > 0.98\), the sensitivity of the EZ-scan is approximately one order of magnitude greater than the maximum sensitivity of a CA Z-scan
8 Reflection Z-scan (RZ-scan)
In the transmittance Z-scan (TZ-scan) experiment, the light field transmitted through the sample is measured as a function of the sample as it is scanned along the propagation direction of the focused laser beam; therefore, the sample should be transparent at the wavelength of irradiation used for examination (i.e., it should show no or negligible linear absorption at the wavelength of interest). For opaque samples with high linear absorption, a modified Z-scan called the RZ-scan was introduced in 1994 [54]. In this method, instead of transmitted light, the light reflected from the surface or interface of the sample is measured as a function of the sample position. Similar to TZ-scan, the RZ-scan could be performed in different versions of CA and OA. In the CA method, the absorptive nonlinearities, which are responsible for the phase changes in the reflected beam, can be determined [47,48,49, 54,55,56,57, 85], and in the OA method, the refractive nonlinearities, which are responsible for the amplitude changes of the reflected radiation, can be determined by measuring the reflection coefficient [47,48,49, 60, 85, 153].
Figure 58 shows a schematic of the RZ-scan setup, in which the detector \(D_{c}\) measures the power reflected from the sample. Similar to TZ-scans, RZ-scans can be performed with a small aperture (CA version) or without an aperture (OA version).
The Fresnel amplitude reflection coefficient for a medium is given by [122].
where \(\theta\) is the incident angle and \(\tilde{n}\) denotes the complex refractive index defined as \(\tilde{n} = n + ik\) with \(n\) the refractive index and \(k\) the extinction coefficient.
For small changes in the complex refractive index, the reflection coefficient can be expressed as follows using Taylor expansion [85]:
where \(\Delta \tilde{n}(\rho ,z) = \tilde{n}_{2} I(\rho ,z) + \tilde{n}_{4} I^{2} (\rho ,z) + \cdots\) is the NL refractive index change and \(\tilde{r}_{0} (\theta )\) is the amplitude reflection coefficient in the linear regime.
The amplitude of the reflected field is defined as \(E_{R} (\rho ,z,t,\theta ) = \tilde{r}(\rho ,z,\theta )\,E_{in} (\rho ,z,t)\) with \(\rho\) and \(z\) the radial and axial coordinates, respectively. In the case of normal incidence (\(\theta = 0\)), the reflected wave field distribution at the interface air sample is given by [54, 55] assuming cubic nonlinearity.
where \(r_{0} = {{(n_{0} - 1 + ik_{0} )} \mathord{\left/ {\vphantom {{(n_{0} - 1 + ik_{0} )} {(n_{0} + 1 + ik_{0} )}}} \right. \kern-0pt} {(n_{0} + 1 + ik_{0} )}}\) is the linear amplitude reflection coefficient,\(r_{1} = {2 \mathord{\left/ {\vphantom {2 {(n_{0} + 1 + ik)^{2} }}} \right. \kern-0pt} {(n_{0} + 1 + ik)^{2} }}\), \(n_{2}\) is the NL refractive index and \(k_{2}\) is the NL extinction coefficient, both of which have the same unit of \({\text{m}}^{2} .{\text{W}}^{ - 1}\) in the SI system.
Using the Fresnel diffraction integral, the on-axis intensity at the far-field aperture plane can be derived [54, 55].
where \(G_{0} = 1 + {{(z + d)(z - iz_{0} )} \mathord{\left/ {\vphantom {{(z + d)(z - iz_{0} )} {(z^{2} + z_{0}^{2} )}}} \right. \kern-0pt} {(z^{2} + z_{0}^{2} )}}\) and \(G_{1} = 1 + {{(z + d)(z - i3z_{0} )} \mathord{\left/ {\vphantom {{(z + d)(z - i3z_{0} )} {(z^{2} + z_{0}^{2} )}}} \right. \kern-0pt} {(z^{2} + z_{0}^{2} )}}\), with \(d\) being the distance between the aperture plane and the beam waist.
The CA RZ-scan trace, defined as the normalized reflected power transmitted through the aperture \(R(z) = {{\int_{0}^{{r_{a} }} {I(z,\,r_{1} )\rho d\rho } } \mathord{\left/ {\vphantom {{\int_{0}^{{r_{a} }} {I(z,\,r_{1} )\rho d\rho } } {\int_{0}^{{r_{a} }} {I(z,\,r_{1} = 0)\rho d\rho } }}} \right. \kern-0pt} {\int_{0}^{{r_{a} }} {I(z,\,r_{1} = 0)\rho d\rho } }}\), is then calculated as given in [154].
The OA RZ-scan trace showing the normalized power reflection is defined as follows [60].
Figure 59 shows the OA RZ-scan traces based on Eq. (174) using data from Ref. [85] for GaAs measured at \(\lambda = 538\,{\text{nm}}\) with \(n_{0} = 4.3\), \(k_{0} = 0.363\), \(n_{2} = 7.8 \times 10^{ - 8} {\text{ cm}}^{2} .{\text{W}}^{ - 1}\) and \(k_{2} = - 2.8 \times 10^{ - 8} {\text{ cm}}^{2} \;{\text{W}}^{ - 1}\). The traces are plotted for different on-focus intensities, leading to different on-focus refractive index changes.
OA RZ-scan transmittance based on Eq. (174) for different on-focus intensities corresponding to different refractive index changes
Figure 60 shows the calculated reflectance peak versus the NL refractive index \(n_{2}\) and NL extinction coefficient \(k_{2}\) using Eq. (174), revealing that the peak reflectance increases almost linearly with \(n_{2}\), whereas its dependency on \(k_{2}\) is very weak. Therefore, the refractive nonlinearity is responsible for the amplitude of the reflected beam, so that the greater the refractive index change is, the stronger the reflated field.
Maximum reflectance change versus the NL refractive index and extinction coefficient at the on-axis surface point when the sample is located at the beam waist position. The results were numerically calculated using Eq. (174)
Figure 61 shows the normalized on-axis transmittance of the CA RZ-scan numerically calculated using Eq. (173) for different extinction coefficient changes caused by different on-focus intensities.
CA RZ-scan normalized on-axis transmittance numerically calculated using Eq. (173) for different intensities assuming \(n_{2} = 0\)
In the case of a normal incident and assuming \(n > > k\), the normalized reflectance, including the contribution of all orders of nonlinearities derived from Eq. (174), is given by
where the index \(l\) denotes the order of the nonlinearity [153].
In Fig. 62, OA RZ-scan normalized transmittances numerically calculated using Eq. (175) are compared for different orders of nonlinearity. As expected, the greater the order of nonlinearity is, the narrower the transmittance signal.
OA RZ-scan assuming different orders of nonlinearity; the solid blue curve for the 3rd-order, the dashed red curve for the 5th-order and the dotted green curve for the 7th-order. The results were numerically calculated using Eq. (175)
9 Other modified versions of the Z-scan
9.1 I-scan
This method cannot be categorized as the Z-scan method since the sample is not moved during laser beam propagation but is fixed near the focus; instead, the laser power is changed [68, 155]. However, since the Z-scan transmittance relation can be used for analyzing the I-scan experimental data here, this method is also reviewed. For the case when the sample is placed at the focus, the OA normalized transmittance in Eq. (16) derived for CW lasers can be modified by letting \(x = 0\) and expressed as a function of intensity
Figure 63 represents the numerically calculated OA normalized transmittance I-scan using Eq. (176) for a 2PA process in the intensity range leading to \(q_{0}\) in the range from 0.02 to 2.
OA normalized transmittance I-scan in the range of \(q_{0} = 0.02 \to 2\) calculated numerically using Eq. (176)
The OA normalized transmittance in Eq. (18) derived for Gaussian pulses can also be modified by letting \(x = 0\) and expressed as a function of intensity [67].
The CA normalized transmittance in Eq. (98) derived for the CW laser can also be modified by letting, for instance, \(x = \pm 0.5\) for the case when the medium is placed half a Rayleigh length away from the focus. The intensity dependance transmittance can then be expressed as
where the positive/negative sign of the second term is used for post/pre focal sample position [68, 156].
Figure 64 shows the normalized transmittance of the CA I-scan for a cubic NL medium in the intensity range leading to a maximum phase change in the range of 0.02–1 radians. The results obtained from numerical calculation (NC) and under small phase change approximation (SPCA) are compared form different prefocus and postfocus sample positions. The solid blue curve indicates the NC using the Fresnel diffraction integral and the dashed red curve shows the SPCA results based on Eq. (178) both for the same postfocus position of \(z = + 0.5z_{R}\). The dotted green curve presents the NC using the Fresnel diffraction integral and the dashed dotted brown curve shows the SPCA results based on Eq. (178) both for the same prefocus position of \(z = - 0.5z_{R}\). These comparisons reveal that placing the sample close to but after the focus leads to accurate results in the I-scan experiment.
CA normalized I-scan transmittance for different sample positions. The solid blue curve and the dotted green curve represent the numerical calculation (NC) for the postfocus and prefocus sample position respectively. The dashed red curve and the dashed dotted brown curve indicate the results obtained in small phase change approximation (SPCA) from Eq. (178) for the postfocus and prefocus sample position respectively
9.2 f-scan
An alternative method to the Z-scan is called the f-scan, in which the sample is fixed in some place but the focal point of the focused laser beam is moved instead of moving the sample. Since the movement is relative, translating the focal point against the laser propagation direction is equivalent to moving the sample in the laser propagation direction; thus, the theory and derived equations for Z-scan can be entirely employed for f-scan. Translation of the focus could be easily performed by moving the lens itself or using an electrically focus-tuneable lens [62,63,64]. In the latter case, the sample and the lens are fixed, but the focal length of the lens is changed electrically. In this case, care should be taken when calculating the on-focus intensity, as the beam waist radius changes with the focal length.
9.3 HS-scan
In this technique, instead of a detector for measuring the power transmitted through the sample, a Harman–Shack (HS) sensor is used to determine the phase of the transmitted light [157]. The main advantage of this technique is that the wavefront analyzer simultaneously measures the wavefront distortion, and the transmittance changes as a function of sample position; thus, both the NL refractivity and absorptivity can be determined using just one detector placed after the sample.
9.4 Bray scan
This technique was proposed in [158]. In this technique, the photodiode is replaced by a position sensitive detector (PSD) to detect the beam centroid. Self-focusing or self-defocusing leads to a change in the beam size, but the center of the laser spot remains unchanged if a circular symmetric beam arrives on the sensor. By placing a blade in front of the PSD so that half of the beam is truncated, any increase or decrease in the beam size leads to a change in the position of the beam centroid on the PSD. Using this technique to determine the NL refractivity, an improved sensitivity of \({\lambda \mathord{\left/ {\vphantom {\lambda {5 \times 10^{4} }}} \right. \kern-0pt} {5 \times 10^{4} }}\) was reported in [158].
10 Conclusion
The Z-scan technique, the most commonly employed method for determining the NL absorption and refraction coefficient, is well known for being used in the field of NL optics. However, a comprehensive and detailed review of all versions of the Z-scan along with the appropriate calculations is rare in the literature. This review was prepared with the purpose of presenting known versions of Z-scan to help researchers choose an appropriate version of Z-scan for the characterization of their materials. In Sect. 1, NL optics and several famous optical NL phenomena were briefly introduced. Then, the NL susceptibilities and their relationships with the NL absorption and refraction coefficients were presented, and various techniques for determining the NL absorption and refraction coefficients were described. Section 2 was devoted to a brief introduction to the Z-scan technique, illustrating the setup of the CA and OA Z-scan. In Sect. 3.1.1, the appropriate relationships for determining the 2PA coefficient were derived when a circular Gaussian beam is used in the OA Z-scan method. Similar to Sect. 3.1.1, in Sect. 3.1.2, the analysis for deriving the required relation to obtain the 3PA coefficient was performed. For simultaneous 2PA and 3PA processes, the analytical calculations were presented in Sect. 3.1.3, and for higher order MPAs, the results were presented in Sect. 3.1.4. In Sect. 3.1.5, the saturable absorption was discussed, the OA Z-scan signal for this NL process was numerically calculated, and then, the analytical relationships were obtained. In Sect. 3.2, the OA Z-scan was assumed to be performed with an astigmatic Gaussian beam. Numerical calculations were performed to determine the behavior of the OA Z-scan signal, and appropriate relationships were derived to extract the MPA coefficient from the OA Z-scan trace. In Sect. 4, diffraction integrals were introduced to calculate the CA Z-scan normalized transmittance, and in Sect. 4.1, the CA normalized transmittance was numerically calculated for different orders of nonlinearities as well as for simultaneous absorptive and refractive processes. Then, appropriate relationships were derived to obtain the NL refractive index when a circular Gaussian laser beam was used to perform the CA Z-scam experiment. All analyses and calculations presented in Sect. 4.1 were repeated in Sect. 4.2 for the case of using an astigmatic beam for the CA Z-scam experiment. In Sect. 5, it was explained that how the NL refractive index can be obtained by measuring the beam size on the far-field plain instead of measuring the power transmitted through an aperture. Section 6 was devoted to introducing different methods for determining the 2PA spectrum using a white light continuum or tunable laser sources. In Sect. 7, eclipsing Z-scan was introduced and compared with CA Z-scan. Numerical calculations showed that the sensitivity of the EZ-scan could be tens of times greater than that of the CA Z-scan. Reflection Z-scan suitable for opaque materials, in which the reflected power is measured instead of the transmitted power, was reviewed in Sect. 8. In Sect. 9, some other methods which can be categorized as the Z-scan method, were briefly introduced. Overall, we prepared a review in which information regarding the Z-scan technique, including the different methods, numerical calculation results and analytical derivations, can be found.
Data availability
No datasets were generated or analysed during the current study.
Abbreviations
- \(P\) :
-
Induced polarization
- \(E\) :
-
Applied electric field
- \(\chi^{(n)}\) :
-
nth-order susceptibility
- \(\alpha_{0}\) :
-
Linear absorption coefficient
- \(\alpha_{2}\) :
-
Two-photon absorption (2PA) coefficient
- \(\alpha_{3}\) :
-
Three-photon absorption (3PA) coefficient
- \(\tilde{n}\) :
-
Complex refractive index
- \(n_{0}\) :
-
Linear refractive index
- \(n_{2}\) :
-
3rd-order nonlinear refractive index
- \(n_{4}\) :
-
5th-order nonlinear refractive index
- \(\varepsilon_{0}\) :
-
Free space permittivity
- \(\lambda\) :
-
Wavelength
- \(k\) :
-
Wavenumber in free space
- \(\omega\) :
-
Radiation frequency
- \(I\) :
-
Intensity (Irradiance)
- \(I_{s}\) :
-
Saturation intensity
- \(\Delta \Phi\) :
-
Phase distortion arising from 3rd-order nonlinearity
- \(\Delta \Psi\) :
-
Phase distortion arising from 5th-order nonlinearity
- \(r\) :
-
Radial coordinate
- \(z\) :
-
Axial coordinate (sample position measured with respect to the beam waist)
- \(z^{\prime}\) :
-
Axial coordinate within the sample
- \(z_{R}\) :
-
Rayleigh length
- \(x = {z \mathord{\left/ {\vphantom {z {z_{R} }}} \right. \kern-0pt} {z_{R} }}\) :
-
Axial coordinate normalized with respect to the Rayleigh length
- \(w_{0}\) :
-
Beam waist radius
- \(w(z)\) :
-
Beam radius at distance z from waist
- \(R(z)\) :
-
Curvature radius of wavefront
- \(L\) :
-
Sample thickness
- \(L_{eff}\) :
-
Effective thickness of sample
- \(E_{p}\) :
-
Pulse energy
- \(\tau\) :
-
Pulse duration
- \(T\) :
-
Normalized transmittance
- \(f\) :
-
Lens focal length
- \(z_{0x}\) :
-
Position of minimum beam size in x-direction for an astigmatic beam
- \(z_{0y}\) :
-
Position of minimum beam size in y-direction for an astigmatic beam
- \(w_{0x}\) :
-
Beam waist radius in x-direction for an astigmatic beam
- \(w_{0y}\) :
-
Beam waist radius in y-direction for an astigmatic beam
- \(z_{Rx}\) :
-
Rayleigh length in x-direction for an astigmatic beam
- \(z_{Ry}\) :
-
Rayleigh length in y-direction for an astigmatic beam
- \(X\) :
-
Dimensionless geometric parameters defined as \(X = {{(z - z_{0x} )} \mathord{\left/ {\vphantom {{(z - z_{0x} )} {z_{Rx} }}} \right. \kern-0pt} {z_{Rx} }}\)
- \(Y\) :
-
Dimensionless geometric parameters defined as \(Y = {{(z - z_{0y} )} \mathord{\left/ {\vphantom {{(z - z_{0y} )} {z_{Ry} }}} \right. \kern-0pt} {z_{Ry} }}\)
- \(G\) :
-
Grean function
- \(r_{a}\) :
-
Aperture radius
- \(S\,(S_{a} )\) :
-
Aperture transmittance
- \(r_{d}\) :
-
Disk radius
- \(S_{d}\) :
-
Disk obscureness
References
D.N. Christodoulides, I.C. Khoo, G.J. Salamo, G.I. Stegeman, E.W. Van Stryland, Adv. Opt. Photonics 2, 60–200 (2010)
M. Moran, C.-Y. She, R. Carman, IEEE J. Quantum Electron. 11, 259–263 (1975)
E.J. Canto-Said, D.J. Hagan, J. Young, E.W. Van Stryland, IEEE J. Quantum Electron. 27, 2274–2280 (1991)
R. Philip, M. Ravikanth, G. Ravindra Kumar, Opt. Commun. 165, 91–97 (1999)
R. Gvishi, P.N. Prasad, B.A. Reinhardt, J.C. Bhatt, J. Sol-Gel Sci. Technol. 9, 157–167 (1997)
S.V. Rao, N.K.M.N. Srinivas, D.N. Rao, L. Giribabu, B.G. Maiya, R. Philip, G.R. Kumar, Opt. Commun. 182, 255–264 (2000)
R.W. Hellwarth, A. Owyoung, N. George, Phys. Rev. A 4, 2342 (1971)
M. Sheik-bahae, A.A. Said, E.W. Van Stryland, Opt. Lett. 14, 955–957 (1989)
M. Sheik-Bahae, A.A. Said, Y.Y. Wu, T.H. Wei, D.J. Hagan, E.W. Van Stryland, in Conference on Lasers and Electro-Optics, pp. 278–279 (1989)
C.B. De Araújo, A.S.L. Gomes, G. Boudebs, Rep. Prog. Phys. 79, 036401 (2016)
N. Liaros, J.T. Fourkas, Laser Photonics Rev. 11, 1700106 (2017)
J.D. Bhawalkar, G.S. He, P.N. Prasad, Opt. Commun. 119, 587–590 (1995)
X. Zhang, L. Wang, Y. Song, J. Mod. Opt. 55, 3639–3649 (2008)
P. Tian, W.S. Warren, Opt. Lett. 27, 1634–1636 (2002)
I. Kang, T. Krauss, F. Wise, Opt. Lett. 22, 1077–1079 (1997)
W.T. White, M.A. Henesian, M.J. Weber, JOSA B 2, 1402–1408 (1985)
G. Walters, B.R. Sutherland, S. Hoogland, D. Shi, R. Comin, D.P. Sellan, O.M. Bakr, E.H. Sargent, ACS Nano 9, 9340–9346 (2015)
G. Tsigaridas, I. Polyzos, P. Persephonis, V. Giannetas, Opt. Commun. 266, 284–289 (2006)
M. Sheik-Bahae, A.A. Said, T.-H. Wei, D.J. Hagan, E.W. Van Stryland, IEEE J. Quantum Electron. 26, 760–769 (1990)
J. Wang, M. Sheik-Bahae, A.A. Said, D.J. Hagan, E.W. Van Stryland, in Proceedings of SPIE—The International Society for Optical Engineering, vol. 1692, pp. 63–66 (1992)
V.P. Kozich, J.A. Castillo, F.E. Hernandez, A. Olaizola, in Proceedings of SPIE—The International Society for Optical Engineering, vol. 2208, pp. 215–216 (1995)
H. Ma, C.B. De Araujo, Appl. Phys. Lett. 66, 1581–1583 (1995)
M. Yang, Z. Yin, F. Li, Y. Song, C. Li, Chin. J. Lasers B (Engl. Edn.) B4, 463–468 (1995)
A. Marcano O, F.E. Hernández, A.D. Sena, J. Opt. Soc. Am. B Opt. Phys. 14, 3363–3367 (1997)
J. Wang, M. Sheik-Bahae, A.A. Said, D.J. Hagan, E.W. Van Stryland, J. Opt. Soc. Am. B Opt. Phys. 11, 1009–1017 (1994)
T. Shimada, N.A. Kurnit, M. Sheik-Bahae, in Proceedings of SPIE—The International Society for Optical Engineering, vol. 2714, pp. 52–60 (1996)
M. Balu, J. Hales, D.J. Hagan, E.W. Van Stryland, Opt. Express 12, 3820–3826 (2004)
M. Balu, J. Hales, D. Hagan, E. Van Stryland, Opt. Express 13, 3594–3599 (2005)
L. De Boni, L. Gaffo, L. Misoguti, C.R. Mendonça, Chem. Phys. Lett. 419, 417–420 (2006)
S.L. Oliveira, D.S. Correa, L. De Boni, L. Misoguti, S.C. Zilio, C.R. Mendonça, Appl. Phys. Lett. 88, 021911 (2006)
S.L. Oliveira, D.S. Corrêa, L. De Boni, L. Misoguti, S.C. Zilio, C.R. Mendonça, Appl. Phys. Lett. 88, 1–3 (2006)
D.S. Corrêa, S.L. Oliveira, L. Misoguti, S.C. Zilio, R.F. Aroca, C.J.L. Constantino, C.R. Mendonça, J. Phys. Chem. A 110, 6433–6438 (2006)
B. Anand, N. Roy, S. Siva Sankara Sai, R. Philip, Appl. Phys. Lett. 102, 93–96 (2013)
S. Perumbilavil, P. Sankar, T. Priya Rose, R. Philip, Appl. Phys. Lett. 107, 051104 (2015)
A. Ajami, W. Husinsky, M. Tromayer, P. Gruber, R. Liska, A. Ovsianikov, Appl. Phys. Lett. 111, 071901 (2017)
A. Ajami, W. Husinsky, A. Ovsianikov, R. Liska, Appl. Phys. B Lasers Opt. 124, 142 (2018)
M. Tromayer, A. Dobos, P. Gruber, A. Ajami, R. Dedic, A. Ovsianikov, R. Liska, Polym. Chem. 9, 3108–3117 (2018)
M. Tromayer, P. Gruber, A. Rosspeintner, A. Ajami, W. Husinsky, F. Plasser, L. González, E. Vauthey, A. Ovsianikov, R. Liska, Sci. Rep. 8, 17273 (2018)
A.S.L. Gomes, E.L. Falcão Filho, C.B. De Araujo, D. Rativa, R.E. De Araujo, Opt. Express 15, 1712–1717 (2007)
A.S.L. Gomes, E.L. Falcão Filho, C.B. De Araújo Diego Rativa, R.E. De Araujo, in Proceedings of SPIE—The International Society for Optical Engineering, vol. 6455 (2007)
V.C. Ferreira, R.R.B. Correia, Optica Publishing Group. Th4A-29 (2018)
M.V. Rao, V.V.R.K. Kumar, N. Shihab, D.N. Rao, Opt. Mater. 84, 178–183 (2018)
D. Babu, Optik 186, 350–362 (2019)
K.D. Babu, K. Murali, N. Karthikeyan, S. Karuppusamy, Laser Phys. 29, 095401 (2019)
A.S.L. Gomes, E.L.F. Filho, C.B. De Araújo, D. Rativa, R.E. De Araujo, Managing thermal effects in eclipse Z-scan technique. In: 2007 European Conference on Lasers and Electro-Optics and the International Quantum Electronics Conference (IEEE), p. 1–1 (2007)
V.C. Ferreira, R.R.B. Correia, in Ultrafast Phenomena and Nanophotonics XXV, vol. 11684 (SPIE, 2021), pp. 13–20
R.A. Ganeev, J. Opt. A Pure Appl. Opt. 7, 717 (2005)
R.A. Ganeev, A.I. Ryasnyansky, Physica Status Solidi A Appl. Mater. 202, 120–125 (2005)
R.A. Ganeev, A.I. Ryasnyansky, A.L. Stepanov, C. Marques, R.C. Da Silva, E. Alves, Opt. Commun. 253, 205–213 (2005)
K. Wang, Q.R. Xing, H.Y. Li, J.P. Li, Z.G. Zhang, N. Zhang, L. Chai, Q.Y. Wang, Opt. Commun. 265, 369–372 (2006)
R. Liu, Y. Shu, G. Zhang, J. Sun, X. Xing, B. Pi, J. Yao, Z. Wang, J. Xu, Opt. Quantum Electron. 39, 1207–1214 (2007)
M. Xiang, Z.H. Jia, X.Y. Lv, Optoelectron. Lett. 6, 226–228 (2010)
J. Jia, Y. Yang, Y. Yang, Z. Xiao, Y. Fang, Y. Song, in Proceedings of SPIE—The International Society for Optical Engineering, vol. 9297 (2014)
D. Petrov, A.S.L. Gomes, C.B. de Araujo, in European Quantum Electronics Conference (Optica Publishing Group, 1994), pp. 77–78
D.V. Petrov, A.S.L. Gomes, C.B. De Araujo, Appl. Phys. Lett. 65, 1067–1069 (1994)
D.V. Petrov, JOSA B 13, 1491–1498 (1996)
D.V. Petrov, A.S.L. Gomes, C.B. de Araújo, Opt. Commun. 123, 637–641 (1996)
F.Z. Henari, A.A. Dakhel, J. Appl. Phys. 108, 123109 (2010)
P. Roussignol, D. Ricard, C. Flytzanis, Appl. Phys. A 44, 285–292 (1987)
M. Martinelli, S. Bian, J.R. Leite, R.J. Horowicz, Appl. Phys. Lett. 72, 1427–1429 (1998)
R.A. Ganeev, Appl. Phys. B 91, 273–277 (2008)
K.D. Babu, P. Philominathan, K. Murali, J. Mater. Sci. Mater. Electron. 31, 17351–17364 (2020)
H. Garcia, J. Serna, E. Rueda, OSA Continuum 3, 498–504 (2020)
E. Rueda, J.H. Serna, A. Hamad, H. Garcia, Opt. Laser Technol. 119, 105584 (2019)
Q. Yang, J. Seo, S.J. Creekmore, D.A. Temple, K.P. Yoo, S.Y. Kim, S.S. Jung, A.G. Mott, SPIE. 4797, 101–109 (2003)
L. Rodriguez, L. Echevarria, A. Fernandez, Opt. Commun. 277, 181–185 (2007)
R.F. Souza, M.A.R.C. Alencar, J.M. Hickmann, R. Kobayashi, L.R.P. Kassab, Appl. Phys. Lett. 89, 171917 (2006)
I. Dancus, V.I. Vlad, A. Petris, T.B. Rujoiu, I. Rau, F. Kajzar, A. Meghea, A. Tane, Rom. Rep. Phys. 65, 966 (2013)
W.-W. Liu, X. Zeng, L. Lin, P.-F. Qi, N. Zhang, Opt. Lasers Eng. 146, 106693 (2021)
Y.L. Huang, C.K. Sun, J. Opt. Soc. Am. B Opt. Phys. 17, 43–47 (2000)
Y.-L. Huang, C.-K. Sun, JOSA B 17, 43–47 (2000)
W.-P. Zang, J.-G. Tian, Z.-B. Liu, W.-Y. Zhou, C.-P. Zhang, G.-Y. Zhang, Appl. Opt. 42, 2219–2225 (2003)
W.P. Zang, J.G. Tian, Z.B. Liu, W.Y. Zhou, F. Song, C.P. Zhang, J.J. Xu, J. Opt. Soc. Am. B Opt. Phys. 21, 349–356 (2004)
W.-P. Zang, J.-G. Tian, Z.-B. Liu, W.-Y. Zhou, F. Song, J.-J. Xu, Opt. Commun. 237, 221–227 (2004)
S.M. Mian, B. Taheri, J.P. Wicksted, J. Opt. Soc. Am. B Opt. Phys. 13, 856–863 (1996)
S.M. Mian, J.P. Wicksted, J. Appl. Phys. 77, 5434–5436 (1995)
A. Srinivasa Rao, J. Nonlinear Opt. Phys. Mater. 28, 1950038 (2019)
P. Chen, D.A. Oulianov, I.V. Tomov, P.M. Rentzepis, J. Appl. Phys. 85, 7043–7050 (1999)
J.A. Dávila-Pintle, E. Reynoso-Lara, Y.E. Bravo-García, Opt. Express 24, 21105–21112 (2016)
B. Gu, X.-C. Peng, T. Jia, J.-P. Ding, J.-L. He, H.-T. Wang, JOSA B 22, 446–452 (2005)
B. Gu, J. Wang, J. Chen, Y.-X. Fan, J. Ding, H.-T. Wang, Opt. Express 13, 9230–9234 (2005)
F. Kessi, H. Naima, J. Opt. 49, 305–310 (2020)
E. Koushki, M.H.M. Ara, Opt. Commun. 284, 5488–5494 (2011)
Y. Li, JOSA B 17, 555–560 (2000)
M. Martinelli, L. Gomes, R.J. Horowicz, Appl. Opt. 39, 6193–6196 (2000)
Y. Liu, J. Pu, H. Qi, JOSA A 26, 1989–1994 (2009)
S.-Z. Lu, K.-M. You, D.-Y. Zhang, F. Gao, Optik 123, 744–747 (2012)
L. Pálfalvi, B.C. Tóth, G. Almási, J.A. Fülöp, J. Hebling, Appl. Phys. B 97, 679–685 (2009)
G. Shi-Fang, T. Qiang, Chin. Phys. B 19, 067802 (2010)
G. Tsigaridas, M. Fakis, I. Polyzos, P. Persephonis, V. Giannetas, Appl. Phys. B 77, 71–75 (2003)
G. Tsigaridas, M. Fakis, I. Polyzos, P. Persephonis, V. Giannetas, Appl. Phys. B Lasers Opt. 76, 83–86 (2003)
G. Tsigaridas, M. Fakis, I. Polyzos, M. Tsibouri, P. Persephonis, V. Giannetas, JOSA B 20, 670–676 (2003)
R.E. Bridges, G.L. Fischer, R.W. Boyd, Opt. Lett. 20, 1821–1823 (1995)
P.B. Chapple, P.J. Wilson, J. Nonlinear Opt. Phys. Mater. 5, 419–436 (1996)
T. Shimada, N.A. Kurnit, M. Sheik-Bahae, Measurement of nonlinear index by a relay-imaged top-hat Zscan technique. In: 27th Annual Boulder Damage Symposium: Laser-Induced Damage in Optical Materials: 1995, vol. 2714, (SPIE), pp. 52–60 (1996)
A. Gnoli, L. Razzari, M. Righini, Opt. Express 13, 7976–7981 (2005)
G. Boudebs, K. Fedus, Appl. Opt. 48, 4124–4129 (2009)
J. Švanda, Y. Kalachyova, A. Ajami, W. Husinsky, P. Macháč, J. Siegel, Z. Kolská, P. Slepička, V. Švorčík, O. Lyutakov, Opt. Mater. 112, 110695 (2021)
A. Ajami, P. Gruber, M. Tromayer, W. Husinsky, J. Stampfl, R. Liska, A. Ovsianikov, Opt. Mater. 47, 524–529 (2015)
A. Ajami, W. Husinsky, B. Svecova, S. Vytykacova, P. Nekvindova, J. Non-Cryst. Solids 426, 159–163 (2015)
Z. Li, A. Ajami, E. Stankevičius, W. Husinsky, G. Račiukaitis, J. Stampfl, R. Liska, A. Ovsianikov, Opt. Mater. 35, 1846–1851 (2013)
Z. Li, N. Pucher, K. Cicha, J. Torgersen, S.C. Ligon, A. Ajami, W. Husinsky, A. Rosspeintner, E. Vauthey, S. Naumov, T. Scherzer, J. Stampfl, R. Liska, Macromolecules 46, 352–361 (2013)
Z. Li, E. Stankevicius, A. Ajami, G. Raciukaitis, W. Husinsky, A. Ovsianikov, J. Stampfl, R. Liska, Chem. Commun. 49, 7635–7637 (2013)
Z. Li, J. Torgersen, A. Ajami, S. Muhleder, X. Qin, W. Husinsky, W. Holnthoner, A. Ovsianikov, J. Stampfl, R. Liska, RSC Adv. 3, 15939–15946 (2013)
A. Ovsianikov, Z. Li, A. Ajami, J. Torgersen, W. Husinsky, J. Stampfl, R. Liska, Appl. Phys. A Mater. Sci. Process. 108, 29–34 (2012)
W. Husinsky, A. Ajami, P. Nekvindova, B. Svecova, J. Pesicka, M. Janecek, Opt. Commun. 285, 2729–2733 (2012)
Z. Li, M. Siklos, N. Pucher, K. Cicha, A. Ajami, W. Husinsky, A. Rosspeintner, E. Vauthey, G. Gescheidt, J. Stampfl, R. Liska, J. Polym. Sci. Part A Polym. Chem. 49, 3688–3699 (2011)
A. Ajami, W. Husinsky, R. Liska, N. Pucher, J. Opt. Soc. Am. B Opt. Phys. 27, 2290–2297 (2010)
A. Ajami, M.S. Rafique, N. Pucher, S. Bashir, W. Husinsky, R. Liska, R. Inführ, H. Lichtenegger, J. Stampfl, S. Lüftenegger, SPIE 7027, 70271H-H70281 (2008)
A. Ajami, Two-Photon Modification of Materials with Ultrashort Laser Radiation: Z-Scan Measurements and 3D-Modification of Selected Materials, vol. 195 (Institute of Applied Physics, Vienna University of Technology, Vienna, 2012)
F. Kessi, N. Hamadouche, J. Nonlinear Opt. Phys. Mater. 28, 1950022 (2019)
D.S. Corrêa, L. De Boni, L. Misoguti, I. Cohanoschi, F.E. Hernandez, C.R. Mendonça, Opt. Commun. 277, 440–445 (2007)
B. Gu, X.Q. Huang, S.Q. Tan, M. Wang, W. Ji, Appl. Phys. B Lasers Opt. 95, 375–381 (2009)
N.K.M.N. Srinivas, S.V. Rao, D.N. Rao, J. Opt. Soc. Am. B Opt. Phys. 20, 2470–2479 (2003)
A.E. Siegman, Lasers (University Science Books, Melville, 1986)
V.M. Akulin, N.V.E. Karlov, Intense Resonant Interactions in Quantum Electronics (Springer Science & Business Media, Berlin, 2012)
M. Samoc, A. Samoc, B. Luther-Davies, H. Reisch, U. Scherf, Opt. Lett. 23, 1295–1297 (1998)
B. Gu, Y.X. Fan, J. Wang, J. Chen, J. Ding, H.T. Wang, B. Guo, Phys. Rev. A At. Mol. Opt. Phys. 73, 065803 (2006)
J. Wang, B. Gu, H.-T. Wang, X.-W. Ni, Opt. Commun. 283, 3525–3528 (2010)
B. Gu, Y.-X. Fan, J. Chen, H.-T. Wang, J. He, W. Ji, J. Appl. Phys. 102, 083101 (2007)
J. Wang, B. Gu, X.-W. Ni, H.-T. Wang, Opt. Laser Technol. 44, 390–393 (2012)
M.A.X. Born, E. Wolf, Principles of Optics, 6th edn. (Pergamon, Oxford, 1980)
D. Weaire, B.S. Wherrett, D.A.B. Miller, S.D. Smith, Opt. Lett. 4, 331–333 (1979)
P.B. Chapple, J. Staromlynska, J.A. Hermann, T.J. McKay, R.G. McDuff, J. Nonlinear Opt. Phys. Mater. 6, 251–293 (1997)
G. Tsigaridas, M. Fakis, I. Polyzos, P. Persephonis, V. Giannetas: in Third GR-I International Conference on New Laser Technologies and Applications, vol. 5131 (SPIE, 2003), pp. 24–28
G. Tsigaridas, P. Persephonis, V. Giannetas, Mater. Sci. Eng. B Solid-State Mater. Adv. Technol. 165, 182–185 (2009)
G. Tsigaridas, Theory and applications of the Z-scan technique through beam dimension measurements, in Nonlinear Performance and Characterization Methods in Optics, pp. 41–62 (2013)
M.H. Majles Ara, S. Salmani, M. Esmaeilzadeh, S.H. Mousavi, E. Koushki, K. Shakouri, Curr. Appl. Phys. 9, 885–889 (2009)
M.G. Vivase, D.L. Silva, L. Misoguti, R. Zaleśny, W. Bartkowiak, C.R. Mendonca, J. Phys. Chem. A 114, 3466–3470 (2010)
U.M. Neves, L. De Boni, Z. Ye, X.R. Bu, C.R. Mendonça, Chem. Phys. Lett. 441, 221–225 (2007)
C.R. Mendonca, D.S. Correa, T. Baldacchini, P. Tayalia, E. Mazur, Appl. Phys. A Mater. Sci. Process. 90, 633–636 (2008)
L. De Boni, A.A. Andrade, L. Misoguti, S.C. Zílio, C.R. Mendonça, Opt. Mater. 32, 526–529 (2010)
R.R. Alfano, S.L. Shapiro, Phys. Rev. Lett. 24, 592–594 (1970)
R.R. Alfano, Q.X. Li, T. Jimbo, J.T. Manassah, P.P. Ho, Opt. Lett. 11, 626–628 (1986)
I. Ilev, H. Kumagai, K. Toyoda, I. Koprinkov, Appl. Opt. 35, 2548–2553 (1996)
S. Coen, A.H.L. Chau, R. Leonhardt, J.D. Harvey, J.C. Knight, W.J. Wadsworth, P.S.J. Russell, Opt. Lett. 26, 1356–1358 (2001)
P.B. Corkum, P.P. Ho, R.R. Alfano, J.T. Manassah, Opt. Lett. 10, 624–626 (1985)
A.K. Dharmadhikari, F.A. Rajgara, N.C.S. Reddy, A.S. Sandhu, D. Mathur, Opt. Express 12, 695–700 (2004)
P.B. Corkum, C. Rolland, T. Srinivasan-Rao, Phys. Rev. Lett. 57, 2268–2271 (1986)
M. Nisoli, S. Stagira, S. De Silvestri, O. Svelto, S. Sartania, Z. Cheng, M. Lenzner, C. Spielmann, F. Krausz, Appl. Phys. B 65, 189–196 (1997)
M. Balu, L.A. Padilha, D.J. Hagan, E.W. Van Stryland, S. Yao, K. Belfield, S. Zheng, S. Barlow, S. Marder, J. Opt. Soc. Am. B Opt. Phys. 25, 159–165 (2008)
M. Balu, J. Hales, D.J. Hagan, E.W. Van Stryland, in Optics InfoBase Conference Papers (JTuC2, 2006)
L. De Boni, A.A. Andrade, L. Misoguti, C.R. Mendonça, S.C. Zilio, Opt. Express 12, 3921–3927 (2004)
G.S. He, T.C. Lin, P.N. Prasad, R. Kannan, R.A. Vaia, L.S. Tan, J. Phys. Chem. B 106, 11081–11084 (2002)
G.S. He, T.C. Lin, P.N. Prasad, R. Kannan, R.A. Vaia, L.S. Tan, Opt. Express 10, 566–574 (2002)
G.S. He, T.C. Lin, J. Dai, P.N. Prasad, R. Kannan, A.G. Dombroskie, R.A. Vaia, L.S. Tan, J. Chem. Phys. 120, 5275–5284 (2004)
T. Xia, D.I. Hagan, M. Sheik-Bahae, E.W. Van Stryland, Opt. Lett. 19, 317–319 (1994)
A.O. Marcano, A.D. Sena, in European Quantum Electronic Conference (IEEE, 1996), pp. 115–115
M. Mohebi, N. Jamasbi, O. Morales, J. Garduno, A.A. Said, E.W. Van Stryland, Proc. SPIE Int. Soc. Opt. Eng. 3572, 236–239 (1999)
E. Fazio, A. Passaseo, M. Alonzo, A. Belardini, C. Sibilia, M.C. Larciprete, M. Bertolotti, J. Opt. A Pure Appl. Opt. 9, L3–L4 (2007)
F.E.P. Dos Santos, F.C. Fávero, A.S.L. Gomes, J. Xing, Q. Chen, M. Fokine, I.C.S. Carvalho, J. Appl. Phys. 105, 024512 (2009)
M.K. Pereira, R.R.B. Correia, J. Opt. Soc. Am. B 37, 478–487 (2020)
A.I. Petris, V.I. Vlad, Theoretical Analysis of Open Aperture Reflection Z-Scan on Materials with High-Order Optical Nonlinearities, vol. 12 (International Atomic Energy Agency IAEA, Vienna, 2010)
A.I. Ryasnyanskii, J. Appl. Spectrosc. 72, 712–715 (2005)
B. Taheri, H. Liu, B. Jassemnejad, D. Appling, R.C. Powell, J.J. Song, Appl. Phys. Lett. 68, 1317–1319 (1996)
I. Dancus, V.I. Vlad, A. Petris, V. Lesnyak, N. Gaponik, A. Eychmüller, SPIE 7469, 77–83 (2010)
D. Rativa, R.E. De Araujo, A.S.L. Gomes, B. Vohnsen, Opt. Express 17, 22047–22053 (2009)
T. Godin, M. Fromager, E. Cagniot, R. Moncorgé, K. Aït-Ameur, Opt. Lett. 36, 1401–1403 (2011)
Author information
Authors and Affiliations
Contributions
Aliasghar Ajami wrote the main manuscripd. Aleksandr Ovsianikov suggested the main idea of preparing such a comprehensive review. Robert Liska and Stefan Baudis prepared the the first draft. Aleksandr Ovsianikov and Robert Liska contributed to preparing figures 51-53. All authors reviewed the manuscript
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ajami, A., Ovsianikov, A., Liska, R. et al. Z-scan technique: a review from conventional Z-scan to white light Z-scan. Appl. Phys. B 130, 138 (2024). https://doi.org/10.1007/s00340-024-08262-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-024-08262-5