1 Introduction

Simultaneous dual-wavelength lasers have broad applications, such as terahertz sources, medical instruments, holographic microscopy, and multispectral lidar [1,2,3,4,5]. Notably, the generation of double pulse lasers emitting simultaneously at two orthogonally polarized wavelengths has garnered significant interest in dynamic holography detection, laser active imaging, and machining due to their unique properties in the time-frequency-spatial dynamic domain [6, 7]. To date, several research institutions have demonstrated remarkable achievements in the field of dual-wavelength double-pulse lasers. Various methods have been proposed to realize such lasers. One approach involves utilizing different combinations of single-wavelength master/slave pulse lasers. For instance, in 2018, Liu et al. achieved an alternating dual-wavelength pulse laser at 1506 nm and 1535 nm using a coaxial diode-end-pumped scheme with two crystals [8]. Another method involves generating master-slave pulses with two beams of dual wavelengths. In 2001, Chen et al. demonstrated a dual-wavelength double-pulse laser with a tunable range of 860 nm to 920 nm by combining two laser systems [9]. In 2009, Chen et al. achieved the visible dual-wavelength double pulses through external frequency doubling in a Cr: LiSAF laser [10]. Conventionally, dual-wavelength double pulse lasers are generated using two Q-switch elements. During this process, non-linear frequency conversion schemes are applied to convert infrared laser pulses into visible light pulses through second harmonic generation. However, the existing methods suffer from structural deficiencies and performance issues, notably the lack of synchronous control over the intensity ratio of dual-wavelength lasers, the delay between master-slave pulse pairs, and the energy ratio. Addressing these methodological drawbacks is crucial for advancing future laser technology. Efficiently integrated light sources are pivotal in overcoming these challenges. The ability to synchronously control dual-wavelength laser parameters, such as intensity ratio, master-slave pulse delay, and energy ratio, is essential for technological advancements. In experimental research, devising novel methods to enhance laser output efficiency and narrow pulse width without additional energy loss is a pressing concern. From a theoretical perspective, constructing a model that elucidates the oscillation mechanism is paramount. Such a theoretical model not only aids in understanding the underlying principles but also provides essential support for developing a parameter control system. Addressing these issues is pivotal for advancing both the experimental and theoretical aspects of dual-wavelength double-pulse laser technology.

In recent years, the rapid advancement of blue semiconductor lasers has drawn considerable attention to blue diode-pumped Pr: YLF lasers, primarily owing to their exceptional emission characteristics in the visible region. Notably, ultraviolet lasers can be efficiently generated through intracavity frequency doubling [11,12,13,14,15]. Leveraging the properties of praseodymium-doped laser gain media, coupled with an efficient dual-wavelength double pulse output method, presents opportunities for streamlining the laser system structure and enhancing the conversion efficiency of visible laser output. To date, there have been no reports on obtaining direct oscillation of orthogonally polarized dual-wavelength double pulse visible lasers without additional tuning elements. In this study, we employ only one acousto-optic element and a corresponding dual-step signal generator to actively control parameters such as the intensity ratio of orthogonally polarized dual-wavelengths, the energy of the master-slave pulses, and the time delay between the master and slave pulses. We successfully achieved π-polarized 604 nm and σ-polarized 607 nm orthogonally polarized dual-wavelength double pulse Pr: YLF laser generation. Compared with previous studies, this method does not need a longer cavity length or an additional F-P etalon to balance the orthogonally polarized dual-wavelength oscillation conditions of the master-slave pulses. This approach not only simplifies the laser structure and enhances energy conversion efficiency but also significantly narrows the pulse width [16].

2 Experimental setup

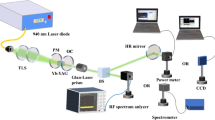
The experimental configuration of the diode-pumped orthogonally polarized dual-wavelength double-pulse Pr: YLF laser is shown in Fig. 1. The resonant cavity is a stable plane-concave structure. A 4 W InGaN blue diode laser at 444 nm is used as the pump source. A focusing lens with a focal length of 50 mm is placed at the output end of the pump source to focus the pump beam on the Pr: YLF crystal. The input mirror (IM) is a flat mirror with a high-transmission coating for 400–450 nm and high reflection for 600–650 nm. The output mirror (OC) is a plano-concave mirror with a radius of curvature of 100 mm and a transmission of 2% in the 590–630 nm band. The laser active medium is an uncoated, a-cut 0.5at.% Pr: YLF crystal with dimension of 3 × 3 × 5 mm3. The crystal is set in a water-cooled copper heat sink maintained at 5 °C. Pulsed operation is achieved using an Acousto-Optic Modulator (AOM), and the double-step loss is modulated by a dual-step signal generator. In the orthogonally polarized dual-wavelength double-pulse laser experiment, the total effective cavity length is optimized to approximately 78 mm.

Fig. 1
figure 1

Schematic of orthogonally polarized dual-wavelength double pulse Pr: YLF laser

Full size image

The Pr: YLF crystal has the emission cross sections in π and σ polarizations that are respectively near 604 nm(~ 1.4 × 10− 23 m−2) and 607 nm(~ 1.0 × 10− 23 m−2) [17]. During the model-building process, we introduce the boundary conditions for Q-switch double-step loss and the micro-loss term between adjacent modes caused by slight tilting of the A-O elements. Combining these factors with the theories of multi-mode oscillation, multi-mode competition, and the spectral properties of the Pr: YLF laser crystal, we establish a physical model for the orthogonally polarized dual-wavelength double pulse Q-switched laser. The resulting expression is as follows:

$$\frac{dN}{dt}={R}_{p}-c{\sigma }_{i}{\varphi }_{i}N-\frac{N}{{\tau }_{f}},\left(i=\text{1,2}\right)$$
(1)
$$\frac{d{\varphi }_{i}}{dt}=\frac{c{l}^{{\prime }}}{l}{\sigma }_{i}{\varphi }_{i}N-\frac{{\varphi }_{i}}{{\tau }_{ci}}+\frac{{\gamma }_{i}{\beta }_{i}N}{{\tau }_{f}},\left(i=\text{1,2}\right)$$
(2)
$${\tau }_{\text{c1}}=\frac{{t}_{r}}{\text{-ln}\left({R}_{i}\right)\text{-ln}\left({L}_{i}\right)+{L}_{Q}\left(t\right)}$$
(3)

Where \(N\) is the population inversion number in the upper level, \({R}_{p}\) is the pump rate, \(c\) is the speed of light, \(l\) is the effective length of resonator, \({l^\prime }\) is the effective length of gain medium, and \({t}_{r}\) is the round-trip time. The parameters \(\sigma_{i}\), \(\varphi _{i}\), \(\gamma_{i}\), \({\beta }_{i}\), \(\tau_{ci} \), \({R}_{i}\), and \({L}_{i}\) represent the stimulated-emission cross-section, the number of laser photons, the inversion factor, the energy level branch ratios, the photon decay lifetime, the reflectivity of the output mirror, and the transmission loss of the Acousto-Optic crystal, respectively. For a specific Q-switching loss term, we set the boundary conditions as follows:\({L}_{Q1}\left(0 < t <{ t}_{1}\right)= {\delta }_{max}\), \({L}_{Q2}({t}_{1}< t <{ t}_{2}) = -ln(1 - \eta )\), and \({L}_{Q}({t}_{2} < t < T) = 0\). The Q-switching process is typically extremely fast, causing no significant change in the inversion population during this period. Therefore, a step function is used to approximate \({L}_{Q}\left(t\right)\). To investigate the oscillation mechanism of the orthogonally polarized dual-wavelength double-pulse laser, it is essential to further deduce the internal relationships between the parameters (Table 1).

Table 1 Shows the theoretical calculated parameter data
Full size table

The effects of spontaneous emission and pumping rate can be ignored during the transient process of pulse output. Therefore, the following calculations are based on three assumptions: (1) There is no spontaneous emission before the Q-switch is turned on; (2) The optical pump stops immediately after the Q-switch is turned on; (3) The intra-cavity loss is a step change. Based on these assumptions, the equations describing the inversion population and photon number as functions of time can be formulated.

$$\frac{dN}{dt}=-c{\sigma }_{1}{\varphi }_{1}N-c{\sigma }_{2}{\varphi }_{2}N$$
(4)
$$\frac{d{\varphi }_{i}}{dt}=\frac{c{l}^{{\prime }}}{l}{\sigma }_{i}{\varphi }_{i}N-\frac{{\varphi }_{i}}{{\tau }_{ci}},i=\text{1,2}$$
(5)

By setting Eq. (5) equal to zero (\(d\varphi /dt = 0\)), we can derive the threshold population inversion \({\varDelta N}_{t1}\)and \({\varDelta N}_{t2}\).

$$\varDelta {N}_{ti}=\frac{{ln}\left(\frac{1}{{R}_{i}}\right)+{ln}\left(\frac{1}{{L}_{i}}\right)}{2{\sigma }_{i}l},\,i=\text{1,2}$$
(6)

By dividing Eqs. (4) and  (5), we can derive the following formula:

$$\frac{d{\varphi }_{1}}{dN}=-\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left(1-\frac{\varDelta {N}_{{t}_{1}}}{N}\right)$$
(7)
$$\frac{d{\varphi }_{2}}{dN}=-\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left(1-\frac{\varDelta {N}_{{t}_{2}}}{N}\right)$$
(8)

Integrate the above formula from the initial state to time \( t \):

$${\int }_{0}^{\varphi \left(t\right)}d{\varphi }_{1}={\int }_{{N}_{i}}^{N\left(t\right)}-\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left(1-\frac{\varDelta {N}_{t1}}{N}\right)dN$$
(9)
$${\int }_{0}^{\varphi \left(t\right)}d{\varphi }_{2}={\int }_{{N}_{i}}^{N\left(t\right)}-\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left(1-\frac{\varDelta {N}_{t2}}{N}\right)dN$$
(10)

\({N}_{i}\) is the initial inversion population number. When \(N\left(t\right) ={\varDelta N}_{t}\), the maximum photon number of 604 nm and 607 nm are:

$${\varphi }_{\text{1,max}}=\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left({N}_{i}-\varDelta {N}_{t1}+\varDelta {N}_{t1}{ln}\frac{\varDelta {N}_{t1}}{{N}_{i}}\right)$$
(11)
$${\varphi }_{\text{2,max}}=\frac{l}{{l}^{{\prime }}}\left(\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left({N}_{i}-\varDelta {N}_{t2}+\varDelta {N}_{t2}{ln}\frac{\varDelta {N}_{t2}}{{N}_{i}}\right)$$
(12)

We approximate that the photon escapes in the cavity with a lifetime of \(\tau_{c}\). Let the modular product of the number of photons in the cavity be \(V\), and the energy of each photon is \(h\nu\), then the instantaneous power is \(P=V\phi hv/{\tau }_{c}\), the instantaneous power expression of 604 nm and 607 nm can be written as:

$${P}_{\text{1,max}}=\frac{hvV{ln}\left({{R}_{1}}^{-1}\right)}{{t}_{r}}\left(\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left({N}_{i}-\varDelta {N}_{t1}+\varDelta {N}_{t1}{ln}\frac{\varDelta {N}_{t1}}{{N}_{i}}\right)$$
(13)
$${P}_{\text{2,max}}=\frac{hvV{ln}\left({{R}_{2}}^{-1}\right)}{{t}_{r}}\left(\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\right)\left({N}_{i}-\varDelta {N}_{t2}+\varDelta {N}_{t2}{ln}\frac{\varDelta {N}_{t2}}{{N}_{i}}\right)$$
(14)
$${P}_{\text{t}\text{o}\text{t},\text{m}\text{a}\text{x}}={P}_{1,\text{m}\text{a}\text{x}}+{P}_{2,\text{m}\text{a}\text{x}}$$
(15)

Regarding the master pulse laser initial and final states, we assume that the initial and final inversion population numbers can be defined as \({N}_{i}\) and \({N}_{f}\), respectively. The laser output energy can be determined by integrating the expression for instantaneous output power, which is as follows:

$${E}_{1}=\frac{hvV{ln}({{R}_{1}}^{-1})}{{ln}({{R}_{1}}^{-1})+{ln}({{L}_{1}}^{-1})}\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\left({N}_{i}-{N}_{f}\right)$$
(16)
$${E}_{2}=\frac{hvV{ln}({{R}_{2}}^{-1})}{{ln}({{R}_{2}}^{-1})+{ln}({{L}_{2}}^{-1})}\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\left({N}_{i}-{N}_{f}\right)$$
(17)
$${E}_{\text{t}\text{o}\text{t}}={E}_{1}+{E}_{2}$$
(18)
Fig. 2
figure 2

The ratio of dual-wavelength laser energy versus with the ratio of cavity round-trip loss and photon number

Full size image

Through the aforementioned expression, we can deduce the relationship between the energy ratio, round-trip loss ratio, and photon number ratio. The simulation results reveal the optimal round-trip loss ratio, as depicted in Fig. 2. Specifically, when the photon number ratio reaches 1:1, the dual-wavelength laser energy intensity ratio also attains 1:1. This provides a theoretical foundation for adjusting the cavity round-trip loss ratio by slightly tilting the Acousto-Optic (A-O) element in subsequent experiments. In Eqs. (16) to (18), we define the master pulse energy expression of the orthogonally polarized dual-wavelength laser. When establishing the state of the slave pulse laser, we assume that the inversion population number can be defined as \({N}_{i}^{{\prime }}\) and\({ N}_{f}^{{\prime }}\). Consequently, the energy ratio of the master-slave pulse satisfies the following formula:

$${{E}_{1}}^{{\prime }}=\frac{hvV{ln}({{R}_{1}}^{-1})}{{ln}({{R}_{1}}^{-1})+{ln}({{L}_{1}}^{-1})}\frac{{\sigma }_{1}{\varphi }_{1}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\left({{N}_{i}}^{{\prime }}-{{N}_{f}}^{{\prime }}\right)$$
(19)
$${{E}_{2}}^{{\prime }}=\frac{hvV{ln}({{R}_{2}}^{-1})}{{ln}({{R}_{2}}^{-1})+{ln}({{L}_{2}}^{-1})}\frac{{\sigma }_{2}{\varphi }_{2}}{{\sigma }_{1}{\varphi }_{1}+{\sigma }_{2}{\varphi }_{2}}\left({{N}_{i}}^{{\prime }}-{{N}_{f}}^{{\prime }}\right) \left(20\right)$$
(20)
$$\frac{{E}_{\text{m}\text{a}\text{s}\text{t}\text{e}\text{r}}}{{E}_{\text{s}\text{l}\text{a}\text{v}\text{e}}}=\frac{{E}_{1}+{E}_{2}}{{{E}_{1}}^{{\prime }}+{{E}_{2}}^{{\prime }}}$$
(21)

As shown in Eqs. (19)-(21), the energy ratio control of the master-slave pulse primarily relies on the difference between the initial and final inversion population numbers. It is important to note that the initial inversion population number of the master pulse\(\left({N}_{i}\right)\) and slave pulse (\({N}_{i}^{{\prime }}\)) are different. These values are mainly determined by the pumping rate and duration, parameters that directly impact the output energy and time delay of the slave pulse. For the master pulse, the final inversion population is affected by the degree of Q-switch partial opening, specifically represented by the value of \({L}_{Q2}\). Conversely, the inversion population for the slave pulse doesn’t start from zero but from the final inversion population number (\({N}_{f}\)) of the master pulse. Depending on the time of partially opening the Q-switch, the inversion population number is further accumulated. Consequently, effective control over the energy ratio and delay of the master-slave pulses can be achieved by manipulating the difference in Q-switch loss and the action time.

In the preceding analysis, we analyzed the output characteristics of the orthogonally polarized dual-wavelength double pulse lasers. It is found that the energy ratio of the dual-wavelength laser can be effectively controlled by manipulating the round-trip loss ratio. Additionally, the energy ratio and delay time of the master-slave pulse can be regulated by adjusting the difference between the initial and final inversion population numbers, which are influenced by the step loss and its duration. In this section, we delve deeper into the specific evolution process of the inversion population number and photon number, guided by specific parameters. Fig. 3 illustrates the relationship between the upper-level inversion population number (\(N\)) and the photon number \(\left({\varphi }_{i}\right)\) in each polarization mode over time during the operation of the orthogonally polarized dual-wavelength double pulse lasers. Clear double pulse pairs are observed, where both the master and slave pulses contain wavelengths of two different polarization modes with the same amplitude. Furthermore, it is observed that the master pulse initiates during the partial opening of the Q-switch, and not all inversion population number are consumed at this stage. When establishing the slave pulse, the inversion population number does not start from zero but begins from the final inversion population number of the master pulse. It consumes the entire inversion population number when the Q-switch is fully opened. Based on the theoretical derivation of the output characteristics and the simulation results, we affirm that the established model can elucidate the oscillation mechanism of the orthogonally polarized dual-wavelength double pulse laser. It can effectively regulate the orthogonally polarized dual-wavelength intensity ratio, master-slave pulse delay, and energy ratio through parameter adjustments.

Fig. 3
figure 3

The ratio of dual-wavelength laser energy versus with the cavity round-trip loss and photon number

Full size image

3 Results and discussion

As illustrated in Fig. 4, we achieved free-running operation of the single-wavelength continuous-wave laser at 607 nm. With an absorbed pump power of 2.55 W, the maximum output power reached 651 mW, corresponding to a slope efficiency of 28.4%. Because it is difficult to achieve the gain equalization of the orthogonally polarized dual-wavelength laser by adjusting only the cavity length and the OC without adding external turning elements, so we do not give the corresponding output power. According to theoretical simulation analysis, a double step signal generator is employed to introduce periodic step losses to the acousto-optic crystal, while the A-O element is slightly tilted to control the net gain equalization conditions of the orthogonally polarized dual-wavelength lasers. The experiment is conducted with a high-voltage Q-switched turn-off time of 35 µs and a low-voltage Q-switched turn-off time of 30 µs. It is important to note that the number of upper-level inversion populations accumulated varies under different pump power conditions. To ensure that the master-slave laser pulse pairs contain orthogonally polarized dual-wavelengths, different high-voltage and low-voltage amplitudes are set for various pump powers. This results in the generation of master-slave pulse lasers with dual-wavelengths at 35 µs and 65 µs, respectively. In essence, the accumulation of inversion population number by the master-slave pulse laser within a fixed time increases with the pumping rate, thereby altering the original gain equalization conditions for the orthogonally polarized dual-wavelengths and the energy ratio of the master-slave pulse.

Fig. 4
figure 4

Output power versus absorbed pump power of single wavelength 607 nm laser and spectrum

Full size image

Fig. 5 illustrates the output of the single-wavelength double pulse laser. With an absorbed pump power of 2.55 W, the maximum average output power reached 208 mW at a pulse repetition rate of 10 kHz. The master-slave pulse widths are 28.0 ns and 55.5 ns, respectively, with a corresponding slope efficiency of 11.5%. The pulse sequence of the orthogonally polarized dual-wavelength pulse laser, along with the corresponding double-step Q-switched loss, is depicted in Fig. 5. The double step signal generator can realize the periodic double step signal which changes with running time, and the signal with different amplitude corresponds to different diffraction rate to realize the control of the Q-switched loss in the cavity. The difference in signal amplitude and duration determines the energy ratio of the master-slave pulse and the time delay. The successful generation of orthogonally polarized dual-wavelength double pulse laser output is achieved through parameter optimization. At a pulse repetition rate of 10 kHz, the maximum average output power is 145 mW, with master-slave pulse widths of 29.6 ns and 65.4 ns, respectively, and a corresponding slope efficiency of 10.1%. Fig. 6 illustrates the temporal pulse profile of the master pulse and slave pulse. It is evident that the slave pulse width is broadened compared to the master pulse, which is attributed to lower diffraction loss when the Q-switch is not completely turned off.

Fig. 5
figure 5

Output power versus absorbed pump power of double pulse laser and the corresponding pulse sequence

Full size image
Fig. 6
figure 6

Temporal pulse profile of the master pulse and slave pulse

Full size image

Simulation analysis confirms that the proposed method effectively regulates the orthogonally polarized dual-wavelength laser intensity ratio, master-slave pulse energy ratio, and time delay. This is achieved by slight adjustments to the Acousto-Optic (A-O) element and the application of double step loss from the double-step signal generator, as shown in Fig. 7. The diffraction efficiency corresponding to the high voltage amplitude of the signal generator reaches 85%. The low voltage amplitude of the signal generator is set at 230 mV-260 mV according to the requirements of different energy ratios of the master and slave pulses. The turn-off time of the low-voltage Q-switch is set at 30 µs and 15 µs, resulting in corresponding time delays of 30 µs and 15 µs, respectively. The angle adjustment range of the acousto-optic element is between 1° and 2° to fulfill the requirement of the dual wavelength intensity ratio. It is worth noting that under different injection pump power conditions, the optimal values of the above parameters are different, and the corresponding fine-tuning needs to be made.

Several noteworthy conclusions can be drawn:

  1. A.

    The choice of crystal cooling temperature directly impacts the output characteristics of the orthogonally polarized dual-wavelength Pr: YLF laser at 604 nm and 607 nm. Lower crystal cooling temperatures facilitate higher gain for the corresponding oscillation mode, laying the foundation for improving laser conversion efficiency and narrowing pulse width.

  2. B.

    In the experiment involving the orthogonally polarized dual-wavelength Pr: YLF Q-switched laser output, the A-O element itself functions as the optical tuning element. The gain equalization conditions of the two oscillation modes can be directly controlled by slightly tilting the A-O element. Since no external optical tuning elements are required, this approach avoids additional losses caused by optical components and extended resonator length, supporting higher gain and pulse width narrowing in the quadrature polarization dual-wavelength mode.

  3. C.

    On the basis of controlling the gain balance condition of an orthogonally polarized dual-wavelength laser by slightly tilting the A-O element, the proposed method can realize the control of the master-slave pulse delays and energy ratios by only setting the double step loss, which simplifies the structure of the laser.

Fig. 7
figure 7

Controllable orthogonally polarized dual-wavelength master-slave pulse pair delay and energy ratio

Full size image

4 Conclusion

In this paper, we present a theoretical model of rate equations for orthogonally polarized dual-wavelength double pulse lasers and derive the intrinsic relationships between regulated orthogonally polarized dual-wavelength intensity ratios, master-slave pulse energy ratios, and time-delay parameters. The oscillation mechanism of the orthogonally polarized dual-wavelength double-pulse laser operation is revealed. We found that it is important to select the optimal parameters for the double step loss and the insertion angle of the A-O element to control the dual-wavelength double-pulse energy ratio, delay and dual-wavelength intensity ratio. The orthogonally polarized dual-wavelength double-pulse Pr: YLF laser at π-polarized 604 nm and σ-polarized 607 nm is obtained, and the experimental results is agree with the simulation very well. Compared to existing techniques, our proposed method does not require a longer cavity length or additional tuning elements to balance the dual-wavelength oscillation conditions of the master-slave pulse. This approach simplifies the laser structure, increases the average power, and significantly narrows the pulse width. It can be widely applied to most solid-state lasers, providing effective technical support for the development of integrated light sources.