1 Introduction

Acceleration gradient in the laser wake field acceleration (LWFA) is few order of magnitude greater than conventional accelerators, but acceleration length is limited by some substantial aspects [1,2,3,4,5]. In a normal focusing strategies, the wake field amplitude declines with diffraction of driver pulse, therefore without any converging procedure the electron is accelerated only within the Rayleigh length. Furthermore, wake field moves with group velocity of the laser pulse and dephasing between accelerated electrons and wake field occurs, so dephasing length is another limitation that prevents the continuation of the electron acceleration process [6,7,8].

In recent years, researchers have eliminated these two mentioned limitations with the concept of Spatiotemporal engineering of the laser pulse which known as "Flying Focus"[9]. In flying focus the intensity peak in the focusing region moves at arbitrary velocity (subluminal or superluminal) and almost maintains its profile several times the Rayleigh length. For this purpose, different optical techniques are used to control the spatiotemporal structure of laser pulses [10,11,12]. One of these techniques is passing a chirped pulse through a hyper-chromatic lens, in fact, each frequency reaches the lens at a certain time, depending on whether the chirp parameter sign is positive or negative, and after passing through the chromatic lens, each frequency focuses in a certain region. As a result of this path difference, the velocity of the focus point can be controlled and the focal length can be expanded (many times more than Rayleigh length)[13,14,15]. These novel properties, candidates flying focus as an efficient procedure in the laser acceleration schemes, such as, flying focus laser wake field acceleration (FF-LWFA).spatiotemporal controlling of the laser pulse was reached by combining spherical aberration with a novel cylindrically symmetric echelon optics to generate a plasma wave with phase velocity equal to the speed of light in the vacuum, preventing trapped electrons from outrunning the wake [10]. Using the relativistic intensities and ultra-short pulses by mixing spatiotemporal couplings, focusing point velocity of a quasi-Bessel beams was controlled independently [16]. In this method the quasi-Bessel beam is generated by focusing a pulse with an axiparabola that produces a long focal line by reflecting rays towards different focal positions. In all these works in the laboratory frame a moving focus were produced at an arbitrary velocity by spatiotemporal controlling of the focusing procedure.

One of the advantage of the FF-LWFA is small laser intensity in the focusing region but long acceleration length. Moreover, this advantage prevents nonlinear and turbulent behavior of the wake-field. In the relativistic regime of the LWFA, when the pulse scale is larger than plasma wavelength, incoherent wakefield is detected [17,18,19]. Laser pulse amplitude in the common flying focus schemes reduced to the nonrelativistic case due to the stretching of the focusing region.

In 2022, Martin et al. [20] derived exact solutions for the electromagnetic fields of a constant-velocity flying focus. This method is based on this concept that in the laboratory frame, during a normal focusing, all frequencies are focused to the same location and the pulse moves with a group velocity at the focal point and diffracts over the Rayleigh range but in any other Lorentz frame, the focus moves. For this purpose, they find multipole spherical (for subluminal foci) or hyperbolic (for superluminal foci) solutions to the wave equation that satisfy appropriate boundary conditions. Then multipole spherical or hyperbolic solution is converted into a beam-like solution with a stationary focus in space or time, respectively, by a displacement of one of the coordinates into its complex plane which is known as the complex source point method (CSPM) [21,22,23,24,25]. Finally, the exact six components of electromagnetic fields of a flying focus are obtained by Lorentz transformation of beam-like solution from a reference frame in which the stationary focus to the laboratory frame in which the focus moves with constant-velocity. The vector solutions presented in this method can be generalized for any arbitrary polarization and any higher order radial and orbital angular motion modes.

In this article, we use the exact solution of the electromagnetic fields to simulate the dynamic of the pulse which in focal point moves forward in with a velocity very close to the speed of light for first and second order radial and orbital angular motion modes. In section II The two-dimensional wakefield was calculated for plasma with a certain density. In section III compare the acceleration of electrons in the laser wakefield of first and second order radial and orbital angular motion modes was investigated and the optimal initial momentum was obtained to achieve the appropriate acceleration gradient.

2 Results

To simulate a pulse with a dynamic focal point, we used the exact solution of the electromagnetic field for the flying focus pulse presented by Martin et al. [20]. For subluminal velocity (\({\beta }_{fp}=\frac{{v}_{fp}}{c}<1\)), multipole spherical solutions \(S\left({x}_{\perp },z\right)\) are used in solving the wave equation. It is then shifted to its complex plane (\(S\left({x}_{\perp },z\right)\to S\left({x}_{\perp },z-i{Z}_{R}\right)\)) using the complex source point method (CSPM), which transforms a multipole spherical wave into a beam-like wave, in which \({Z}_{R}=\frac{1}{2}k{w}_{0}^{2}\) Rayleigh length and \(q\left(z\right)=z-\frac{1}{2}ik{w}_{0}^{2}\). Then by applying Lorentz transformations from stationary frame to the laboratory frame, spherical solutions of the focal point moving at subluminal velocities is obtained.

In this study, we considered two states n = l = 0 and n = l = 1 (n = Principal mode number and l = Azimuthal mode number), for which Gaussian and donut-like profiles is obtained, respectively. For n = l = 0, four-potential in the laboratory frame are as follows:

$${\Phi }^{\mathrm{^{\prime}}}=\frac{{\alpha }_{00}\left(1-{\beta }_{fp}\right)\gamma }{2}\frac{kx}{R}{j}_{1}\left(kR\right){e}^{-ikt}+c.c., {A}_{x}^{\mathrm{^{\prime}}}=-\frac{i{\alpha }_{00}}{2}k\left[{j}_{0}\left(kR\right)+i\frac{q\left(z\right)}{R}{j}_{1}\left(kR\right)\right]{e}^{-ikt}+c.c., {A}_{y}^{\mathrm{^{\prime}}}=0,{A}_{z}^{\mathrm{^{\prime}}}={\Phi }^{\mathrm{^{\prime}}}$$
(1)

\({\alpha }_{00}\) is a weighting factor, \(k\) is wave number, \(R={({x}^{2}+{y}^{2}+{q(z)}^{2})}^\frac{1}{2}\), \(\gamma ={(1-{{\beta }_{fp}}^{2})}^{-\frac{1}{2}}\), \({j}_{0}\) and \({j}_{1}\) are first and second order Bessel function respectively. For n = l = 1, four-potential in the laboratory frame are:

$${\Phi }^{\mathrm{^{\prime}}}=\frac{{\alpha }_{11}\left(1-{\beta }_{I}\right){\gamma }_{<}}{2R}\left[{j}_{1}\left(kR\right)-\frac{k{\rho }^{2}}{R}{\text{cos}}(\theta ){e}^{i\theta }{j}_{2}\left(kR\right)\right]{e}^{-ikt}+c.c., {A}_{x}^{\mathrm{^{\prime}}}=-\frac{i{\alpha }_{11}}{2}\frac{k\rho }{R}\left[{j}_{1}\left(kR\right)+i\frac{q\left(z\right)}{R}{j}_{2}\left(kR\right)\right]{e}^{i\theta -ikt}+c.c.,{A}_{y}^{\mathrm{^{\prime}}}=0,{A}_{z}^{\mathrm{^{\prime}}}={\Phi }^{\mathrm{^{\prime}}}$$
(2)

\({\alpha }_{11}\) is a weighting factor,\(\rho ={({x}^{2}+{y}^{2})}^\frac{1}{2}\), \({j}_{1}\) and \({j}_{2}\) second and third order Bessel function respectively. Then, components of the electromagnetic field can be found from the equations; \({E}^{\mathrm{^{\prime}}}=-{\nabla }^{\mathrm{^{\prime}}}{\Phi }^{\mathrm{^{\prime}}}-{\partial }_{{t}^{\mathrm{^{\prime}}}}{A}^{\mathrm{^{\prime}}}\) and \({B}^{\mathrm{^{\prime}}}={\nabla }^{\mathrm{^{\prime}}}\times {A}^{\mathrm{^{\prime}}}\).

In this study, \({\beta }_{fp}=0.9994 ,\) duration of the pulse is\(10fs\), Spot radius in focal region is\({w}_{0}=40\mu m\), focal region length is \({\text{L}}={{\text{f}}}_{0}\frac{\mathrm{\Delta \lambda }}{{\uplambda }_{0}}\cong 10{\text{cm}}\) for \({\uplambda }_{0}=0.8\mu m\) (\({{\text{n}}}_{{\text{c}}}=1.56\times {10}^{21}{cm}^{-3}\)) and the Rayleigh length is 6.28mm. The simulation was investigated in plasma with,\(\frac{{\omega }_{{\text{p}}}}{\omega }=0.3\), for which,\({{\text{n}}}_{{\text{e}}}=0.09{{\text{n}}}_{{\text{c}}}=1.4\times {10}^{20}{cm}^{-3}\).

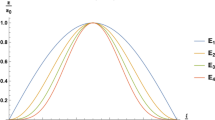
In Fig. 1, the pulse dynamics are shown for two different modes n = l = 0 and n = l = 1, that the intensity peak moving at velocity very close to the speed of light (\({\beta }_{fp}=0.99994\)). Pulse in both modes has been maintained its intensity up to 16 Rayleigh length. Since the intensity peak moving at velocity a little smaller than c, in \({-8Z}_{R}\) and \({8Z}_{R}\) pulse profile is asymmetrical and intensity peak is inclined towards the front and back, Respectively, but at the origin, \({z}{\prime}=0\), the pulse profile is completely symmetrical. The cross section for n = l = 0 (Fig. 1d) shows that the pulse profile is Gaussian and has the highest intensity on the axis \((r=0)\) and for n = l = 1 (Fig. 1h), the pulse profile is donut-like and the intensity is zero on the axis. In each cases, pulse normalized amplitudes are nonrelativistic (\({a}_{0}=0.27\)) and occurrence of the coherent wakefield acceleration is predicted.

Fig. 1
figure 1

Flying focus pulse dynamic from \({-8Z}_{R}\) to \({8Z}_{R}\) and its cross section. Up row is for Gaussian profile for n = l = 0, and down row is for n = l = 1, donut-like profile

Full size image

For modeling wakefield excitation in the FF-LWFA scheme, we use the general relation for the wake driven at an arbitrary velocity, \({\upbeta }_{{\text{fp}}}\) [5, 26]:

$$\frac{{\text{d}}^{2}\phi }{{\text{d}}{\zeta }^{2}}={\gamma }_{\text{fp}}^{2}{\text{k}}_{\text{p}}^{2}\left\{{\upbeta }_{{\text{fp}}}{\text{sign}}(1+\phi ){\left[1-\frac{{\gamma }_{1}^{2}}{{\gamma }_{\text{fp}}^{2}{(1+\phi )}^{2}}\right]}^{-1/2}-1\right\}$$
(3)

where, \(\zeta =z-{{\text{v}}}_{\text{fp}}{\text{t}},{\upgamma }_{{\text{fp}}}={\left(1-{\upbeta }_{{\text{fp}}}^{2}\right)}^{-1/2},{\upgamma }_{\perp }^{2}=1+\frac{1}{2}{\left|{\text{a}}\right|}^{2}\) and \({\text{a}}(\upzeta )\) is normalized laser pulse vector potential profile. Figure 2 shows the wake field of the pulse at z = 8ZR, for two modes n = l = 0 (Fig. 2a,c) and n = l = 1 (Fig. 2b,d). The longitudinal component wakefield profiles for n = l = 0 and n = l = 1, proportionally to the driver pulse is Gaussian and donut-like, respectively. The radial wakefield for both modes (Fig. 2b,d) on the axis are zero and their amplitude is two orders of magnitude less than longitudinal field.

Fig. 2
figure 2

Longitudinal and radial wakefeild for n = l = 0 (a,b) and for n = l = 1 (c,d). The dashed lines show suitable locations for electron injection

Full size image

The longitudinal field has the role of acceleration and the radial component causes the electrons to converge. Therefore, if we want to accelerate the electrons forward, they must be placed in the negative longitudinal field and in order to prevent the divergence of the electron, they must be placed in the positive radial field. The dashed line in figure shows the proper z place for electron injection in our subluminal flying focus scheme. For the Gaussian profile the phase difference between suitable acceleration and convergence field components is such that even though this place is at the beginning of the acceleration region, but it is at the end of the convergence zone. As a result, the electrons aren’t expected to a good convergence for n = l = 0, even for the proper injection place. For the Donut-like profile, beginning of the convergence zone locates at the middle point of the acceleration region. As a result, it is expected to cause a good convergence through the acceleration stage for n = l = 1.

In order to simulate the wakefield acceleration of electron, we consider 10,000 electrons randomly placed on a disc with a radius of 0.1 spot radius in the z indicated by the dashed line in Fig. 2. Although in both modes the pulse has maintained its intensity during 16 Rayleigh lengths, but in the n = l = 0 case, due to modest phase difference between longitudinal and radial wakefield components, injected electrons diverge after 1mm (< < ZR). But for the n = l = 1 case, injected electrons accelerate for the whole focal region length and acceleration stage extended to 10cm (> > ZR).

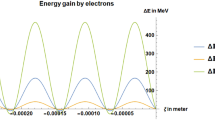
In our simulation electrons are injected to the suitable longitudinal position with initial velocity. Four different initial energy, \({\upgamma }_{0}=38.4, 48.7, 53.8, 102.5\), are selected for injected electrons. For each mode, energy distribution of electrons at the of acceleration stage are shown in Fig. 3. For both modes, the peak of each graph is around its initial energy. For n = l = 0, there are several peaks before the largest peak and this indicates that the some electrons are decelerated and a significant number of electron have final energies lower than the initial energy. Also the highest energy obtained in this mode for \({\upgamma }_{0}=102.5\) is approximately 180 MeV. For n = l = 1 There are several peaks after the largest peak and this indicates that considerable number of electrons are accelerated and have a significantly higher final energy than their initial energy. The highest energy obtained in this mode is approximately 350 MeV.

Fig. 3
figure 3

the energy distribution for different \({\gamma }_{0}\) (a) n = l = 0 and (b) n = l = 1

Full size image

Figure 4 shows the electron acceleration gradient and the percentage of accelerated electrons \((\gamma >{\gamma }_{0})\) for different values of the initial injection energy. For n = l = 0 (Fig. 4a), The maximum acceleration gradient (solid line) is \(10.5\frac{GeV}{m}\), which occurs at the optimum initial energy of \(53.8Mev\). The percentage of electrons that have more energy than the initial energy in this case (dashed line) is less than 50%, which is in agreement with the results of Fig. 3.

Fig. 4
figure 4

electron acceleration gradient (solid plot), the percentage of electrons that \(\gamma >{\gamma }_{0}\) (dash-dot plot) (a) for n = l = 0 (b) for n = l = 1. (c) maximum energy for different\({\gamma }_{0}\)

Full size image

in Fig. 4c the solid plot displays the maximum energy \(182Mev\) is obtained by the electron in the\({\gamma }_{0}=102.5Mev\). However, there is also a peak at the optimum value of\({\gamma }_{0}=53.8Mev\), which has gained more energy than its lower and higher values of \({\gamma }_{0}\).

For n = l = 1 according to the Fig. 4b, The acceleration gradient is around \(3\frac{GeV}{m}\) and higher acceleration gradient is obtained for lower injection energy \({\gamma }_{0}\). The percentage of electrons that have more energy than the initial energy in this case is even more than 90% for \({\gamma }_{0}=12.5MeV\). Figure 4c shows the maximum reached energy for two modes in terms of initial injection energy. Significently, maximum energy gain for Donut like profile is very biger than Gaussian curve and the maximum energy for all \({\gamma }_{0}\) is around \(350Mev\) for Donut case (dash line).

To better understand the acceleration features of these two modes, the trajectory and energy of 1000 electrons are shown in Fig. 5, during the acceleration length for \({\gamma }_{0}=102.5Mev\). The acceleration length for the n = l = 0 consideres to 10 mm (from—5 to 5 mm). In the first 3 mm, the electrons diverged, and at the end of the path, a large number of electrons scattered with energy much lower than the initial energy (small and darker spheres with energy less than \(50Mev\)), and a small number of electrons remained near the axis and gained energy (larger red spheres). The reason for this undesirable behaviour is the inappropriate phase difference between the longitudinal and transverse components of the wakefield, that cause divergence and decleration of huge number of electrons. Fourtunately, the acceleration length for the n = l = 1 consideres equal to 10 cm (from—5 to 5 cm). According to the Fig. 5b, the appropriate transverse field, has been prevented the divergence of the electrons, so the acceleration length of the electrons is one order of magnitude greater than the previous mode. A limited number of electrons began to diverge after about 6cm, and electrons closer to the axis gained more energy (about \(250Mev\)).

Fig. 5
figure 5

the trajectory and energy of 1000 electrons during the acceleration length for \({\gamma }_{0}\)=102.5MeV (a) n = l = 0, (b)n = l = 1

Full size image

3 Conclusion

In this article, we investigate the flying focus laser wakefield acceleration (FF-LWFA) by the subluminal pulse that moves near the velocity of light, \({\beta }_{fp}=0.99994\). Exact solution of the electromagnetic field is calculated by using complex source point method (CSPM). For this purpose, we considere two modes of n = l = 0 and n = l = 1 (Gaussian and donut-like profiles) and obtain the dynamics of the pulse profile of its cross-section, which revealed that the pulse was able to maintain its intensity about 16 times the Rayleigh length. Further, we calculate the wakefield for both modes and finding the appropriate place for electrons to start the acceleration together with focusing. For the n = l = 1 there was a suitable phase difference between the longitudinal and transverse fields, and the electrons could accelerate in the acceleration length without considerable divergence. While for n = l = 0, suitable injection location for efficent acceleration and convergence of electrons not defined and injected electrons diverge very quickly. For the mode n = l = 0, despite the higher acceleration gradient, but according to the energy distribution function, less than 50% of the electrons gained more energy than their initial energy. While for the n = l = 1 up to 90% of the injected electrons trapped and cosiderable energy gained at the end of the acceleration stage. The trajectory and energy of the all electrons also showed that in the n = l = 0, in the first part of the acceleration length, the electrons diverged and did not gain more energy. While for the n = l = 1, a large number of electrons remaine convergent to the end of the focusing region (16ZR) and gained energy. As a result, the donut-shaped profile has created a longitudinal and transverse wakefield with a suitable phase difference, which prevents the divergence of electrons and the electrons gain energy until the end of the acceleration length.