1 Introduction

Since the development of the first laser by Theodore Maiman in 1960 [1], research has been devoted to the study of ultrashort and ultra-intense laser pulses. With the successive introduction of Q-switching technology [2, 3], mode-locking [4, 5] and chirped pulse amplification (CPA) [6,7,8,9], it is now possible to generate attosecond laser pulses with laser field intensities up to \({10}^{23}W/{cm}^{2}\), which has driven the development of ultrafast laser physics [10, 11]. As an important field of intense laser-matter interaction [12], relativistic nonlinear Thomson forward scattering (RNTFS) is an important way to modulate \(X\)-rays [13] and \(\gamma\)-rays [14]. It attracts many scholars to study, and achieves a very wide range of applications in biomedicine [15,16,17], atomic physics [18] and modern astrophysics [19].

The effect of various parameters of the laser pulse on the electron radiation has been investigated in past works. Chen, et al. [20] investigated the effect of the laser intensity on the spatial radiation of high-energy electrons. While Zhang, et al. [21] and Yu, et al. [22] investigated the effect of the pulse width and beam waist radius, In addition, respectively, K. P. Singh [23] and Gupta, et al. [24] investigated the introduction of a static magnetic field or an ultra-intense pulsed magnetic field on top of a laser field, respectively. As the electron resonates with the electromagnetic field of the laser pulse, the electron absorbs a large amount of energy, significantly increasing the energy gain of the electron in the vacuum compound field. Furthermore, in contrast to Traveling-wave Thomson scattering (TWTS) studied by A. D. Debus, et al. [25] and K. Steiniger, et al. [26] and inverse Compton scattering studied by A. P. Potylitsyn, et al. [27] the two radiation modes, the usual Thomson scattering is studied in this paper. Ultra-high power radiation is obtained by laser-driven nonlinear Thomson scattering of electrons rather than by inverse scattering of electrons colliding with the laser. With the help of an applied magnetic field, higher radiation power and better collimation can be obtained in normal Thomson scattering than in inverse Thomson scattering.

However, in previous works, on one hand, the effect of beam waist radius on nonlinear Thomson scattering is only investigated from a certain angle of electron radiation properties. The intrinsic connection between individual radiation properties is not found. On the other hand, it is undeniable that the electron radiation is poorly collimated, low-peak-power, narrow-frequency-domain and poor-continuity. Therefore, it is particularly important to comprehensively study the methods of improving the radiation properties by various properties of nonlinear Thomson scattering.

In this paper, the effects of beam waist radius (laser transverse energy distribution) on the electrodynamic properties of electron, the full-angular distribution of radiated power and the spectral structure are investigated for the first time in all aspects, during the interaction of stationary electrons with Gaussian circularly polarized laser pulses. For the first time, it is found that the properties of the radiation are consistent when the beam waist radius is varied. Accordingly, we have selected the optimum beam waist radius so that all the properties of RNTFS are optimized at the same time. Meanwhile, an applied magnetic field is introduced in this paper to comparatively study its effect on the electron radiation properties. We found that RNTFS under an applied magnetic field has the advantages of high collimation, high power, supercontinuum and so on. In particular, the properties of the radiation are, in the order in which they are written in the paper, the peak radiated power, the directionality, the collimation, the harmonic peak power, the frequency domain bandwidth, and the number of higher harmonics of the RNTFS. The corresponding optimal radiation properties refer to the highest peak radiated power, the smallest polar angle \(\theta\), the smallest full angle at half maximum (FAHM) \(\Delta \theta\), the highest harmonic peak power, the widest frequency domain bandwidth, and the highest number of higher harmonics. In summary, this paper presents a multifaceted, all-encompassing, cross-cutting, and pioneering study of the combined effects of the beam waist radius and the applied magnetic field on the stimulated radiation of electrons. And accordingly, we select the best combination of parameters for the composite field of the magnetic field superimposed on the laser field. It is instructive for modulating \(X\)-rays with good radiation properties in practical experiments.

The rest of the paper is as follows: in Sect. 2, we propose a relativistic nonlinear Thomson forward scattering model. Based on classical electrodynamics, special relativity, Lienard-Wiechert theorem and Parseval's theorem, we derive the laser field vector potential under an applied magnetic field, the electron’s equations of motion, the full-angular distribution of the stimulated radiation, and analytical expressions for the spectrum. In Sect. 3, we analyze the coupling effect of the crossover parameters on the various properties of RNTFS in terms of the electrodynamic properties of the electrons, the full-angular distribution and spectral structure of the radiation. We summarize the intrinsic connection of the radiation properties and determine the optimal parameters of the composite field.

2 Theory and formulation

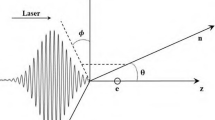
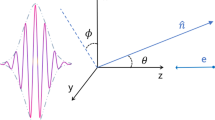
In this paper, based on the RNTFS model, we introduce a circularly polarized Gaussian laser pulse propagating along the reference frame \(+z\)-axis at an incident angle \({\sigma }_{in}\) = 0. At the same time, an applied magnetic field whose magnitude proportional to \(x\) and orientated along the \(+y\)-axis is introduced on top of the laser field. Assuming that the electron is initially stationary at the origin of the coordinates, we investigate the RNTFS of the electron under the action of a composite field of a circularly polarized laser field and a magnetic field, as shown in Fig. 1.

Fig. 1
figure 1

Geometric schematic of relativistic nonlinear Thomson forward scattering of stationary electrons driven by a Gaussian circularly polarized intense laser pulse in an applied magnetic field

Full size image

Firstly, it is stated that the laser wavelength \({\lambda }_{0}\) = 1 \(\mu m\) in this paper. For the definition of all the following formulas, the time and space coordinates are normalized by \({\omega }_{0}^{-1}\) and \({k}_{0}^{-1}\), respectively. \({\omega }_{0}=2\pi c/{\lambda }_{0}\) is the circular frequency of the incident laser, \({k}_{0}=2\pi /{\lambda }_{0}\) is the wave number of the laser in the vacuum, and \(c\) is the speed of light.

In this paper, by solving a paraxial approximate solution of the Helmholtz equation, the total vector potential of the composite field of a circularly polarized laser field and a static magnetic field can be expressed as [28]

$$\mathop{a}\limits^{\rightharpoonup} = a_{0} \,\exp \left( { - \frac{{\eta^{2} }}{{L^{2} }} - \frac{{\rho^{2} }}{{b^{2} }}} \right)\left( {\frac{{b_{0} }}{b}} \right)\left[ {\cos \left( \varphi \right)\mathop{x}\limits^{\rightharpoonup} + \sin \left( \varphi \right)\mathop{y}\limits^{\rightharpoonup} } \right] + B_{0} \,x\mathop{y}\limits^{\rightharpoonup}$$
(1)

where the first and second terms represent the laser pulse and the applied magnetic field, respectively. \({a}_{s}={{\text{a}}}_{0}{\text{exp}}(-\frac{{\upeta }^{2}}{{{\text{L}}}^{2}})\frac{{{\text{b}}}_{0}}{b}\) corresponds to the longitudinal envelope of the Gaussian laser pulse in the \(z\)-axis direction. While \({\text{exp}}(-\frac{{\uprho }^{2}}{{{\text{b}}}^{2}})\) corresponds to the radial envelope of the circularly polarized Gaussian laser pulse. In the formula, \({{\text{a}}}_{0}=0.85\times {10}^{-9}\lambda \sqrt{I}\) is the peak laser amplitude, and \(I\) is the laser intensity (normalized by \({m}^{2}{\omega }^{2}{c}^{3}/{e}^{2}\)). \(\upeta =z-t\), is an auxiliary quantity symbolising that time and space have coherence. \(L\) and \(b\) are the pulse width of the laser and the spot radius at which the laser travels to \(z\), respectively. \(b={{\text{b}}}_{0}{(1+{z}^{2}/{z}_{f}^{2})}^{1/2}\), where \({{\text{b}}}_{0}\) is the beam waist radius of the pulse, i.e., the radial distance of the beam at its narrowest point (in this paper, the position of the beam waist is \(z=0\)). \({z}_{f}\)=\({b}_{0}^{2}\)/2 corresponds to the Rayleigh distance of the laser, which is the turning point between the linear and spherical representations of the phase front, i.e., the boundary where a beam transitions from a collimated state to an evanescent state. \(\uprho ={({x}^{2}+{y}^{2})}^{1/2}\), which corresponds to the distance from a point in the coordinate system to the \(z\)-axis. \(\delta\) is the laser polarization parameter. \(\varphi =\upeta +{\varphi }_{R}-{\varphi }_{G}+{\varphi }_{0}\), \({\varphi }_{R}={\uprho }^{2}/2R(z)\) is related to the radius of curvature of the wavefront of the beam \(R\left(z\right)\), and \(R\left(z\right)=z(1+{z}_{f}^{2}/{z}^{2})\). \({\varphi }_{G}={tan}^{-1}(z/{z}_{f})\) is the Guoy phase shift of an axisymmetric light wave, when the beam passes through the focal point, there is an extra Guoy phase shift \(\pi\) in addition to the normal plane wave phase shift \({e}^{-ikz}\). \({\varphi }_{0}\) is the initial phase of the laser pulse, which corresponds to the phase of the laser pulse at the time of its encounter with the electrons, and in this paper \({\varphi }_{0}=0\). \({{\text{B}}}_{0}\) is the magnetic field strength of the applied magnetic field, in this paper, the dimensionless \({{\text{B}}}_{0}=0\) and \({{\text{B}}}_{0}=0.5\), whose corresponding magnitude strengths are \(0kT\) and \(5kT\).

Let \({a}_{l}={{\text{a}}}_{0}{\text{exp}}(-\frac{{\upeta }^{2}}{{{\text{L}}}^{2}}-\frac{{\uprho }^{2}}{{{\text{b}}}^{2}})\frac{{{\text{b}}}_{0}}{b}\), \(\theta =\pi -{tan}^{-1}(z/{z}_{f})\), and the normalized vector potential of the complex field can be further decomposed orthogonally in the rectangular coordinate system as

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {a_{x} = a_{l} cos\varphi } \\ {a_{y} = a_{l} sin\varphi + {\text{B}}_{0} x} \\ {a_{z} = 2a_{l} \left[ { - xsin\left( {\varphi + \theta } \right) + ycos\left( {\varphi + \theta } \right)} \right]/{\text{b}}_{0} b} \\ \end{array} } \right.} \\ \end{array}$$
(2)

In a laser field with a Gaussian envelope, the relativistic electron’s equations of motion can be introduced by the Lorentz equation and the Lagrange function as [29]

$$\begin{array}{*{20}c} {\partial _{t} \left( {\vec{p} - \vec{a}} \right) = - \nabla _{a} \left( {\vec{u} \cdot \vec{a}} \right)} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {d_{t} \gamma = \vec{u} \cdot \partial _{t} \vec{a},} \\ \end{array}$$
(4)

where \(\overrightarrow{p}=\gamma \overrightarrow{u}\) is the electron momentum normalized by \(mc\), \(\overrightarrow{u}\) is the electron velocity normalized by the speed of light \(c\). \(\gamma ={(1-{\overrightarrow{u}}^{2})}^{-1/2}={(1+{\overrightarrow{p}}^{2})}^{1/2}\) is the relativistic factor of the electron, and the velocity of the electron normalized by \(m{c}^{2}\).

Combining the above equations, a system of partial differential equations for the phase, light intensity amplitude envelope, and orthogonal vector potential of the composite field can be derived as

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\partial _{t} \varphi = - 1} \\ {\partial _{x} \varphi = x/R\left( z \right)} \\ {\partial _{y} \varphi = y/R\left( z \right)} \\ {\partial _{z} \varphi = 1 - \frac{{z_{f} }}{{z_{f} ^{2} + z^{2} }} - \frac{{(x^{2} + y^{2} )(z^{2} - z_{f} ^{2} )}}{{2(z^{2} + z_{f} ^{2} )^{2} }}} \\ \end{array} } \right.} \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\partial _{t} a_{l} = \frac{{2\eta }}{{L^{2} }}a_{l} } \\ {\partial _{x} a_{l} = \frac{{ - 2x}}{{b^{2} }}a_{l} } \\ {\partial _{y} a_{l} = \frac{{ - 2y}}{{b^{2} }}a_{l} } \\ {\partial _{z} a_{l} = a_{l} \left( { - \frac{{\partial _{z} b}}{b} + \frac{{2\left( {x^{2} + b^{2} } \right)\partial _{z} b}}{{b^{3} }} - \frac{{2\eta }}{{L^{2} }}} \right)} \\ \end{array} } \right.} \\ \end{array}$$
(6)
$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\partial _{t} a_{x} = \partial _{t} a_{l} cos\varphi - \partial _{t} \varphi a_{l} sin\varphi } \\ {\partial _{y} a_{x} = \partial _{y} a_{l} cos\varphi - \partial _{y} \varphi a_{l} sin\varphi } \\ {\partial _{z} a_{x} = \partial _{z} a_{l} cos\varphi - \partial _{z} \varphi a_{l} sin\varphi } \\ {\partial _{t} a_{y} = - [\partial _{t} a_{l} sin\varphi + \partial _{t} \varphi a_{l} cos\varphi ]} \\ {\partial _{x} a_{y} = - (\partial _{x} a_{l} sin\varphi + \partial _{x} \varphi a_{l} cos\varphi ) + B_{0} } \\ {\partial _{z} a_{y} = - [\partial _{z} a_{l} sin\varphi + \partial _{z} \varphi a_{l} cos\varphi ]} \\ {\partial _{t} a_{z} = - \left\{ {\frac{{2x}}{{bb_{0} }}\partial _{t} a_{l} sin\left( {\varphi + \theta } \right) + \frac{{2x}}{{bb_{0} }}a_{l} cos\left( {\varphi + \theta } \right)\partial _{t} \varphi + \left[ {\frac{{2y}}{{bb_{0} }}\partial _{t} a_{l} cos\left( {\varphi + \theta } \right) - \frac{{2y}}{{bb_{0} }}a_{l} sin\left( {\varphi + \theta } \right)\partial _{t} \varphi } \right]} \right\}} \\ {\partial _{x} a_{z} = - \left\{ {\frac{2}{{bb_{0} }}a_{l} sin\left( {\varphi + \theta } \right) + \frac{{2x}}{{bb_{0} }}\partial _{z} a_{l} sin\left( {\varphi + \theta } \right) + \frac{{2x}}{{bb_{0} }}a_{l} cos\left( {\varphi + \theta } \right)\partial _{x} \varphi + \left[ {\frac{{2y}}{{bb_{0} }}\partial _{x} a_{l} cos\left( {\varphi + \theta } \right) - \frac{{2y}}{{bb_{0} }}a_{l} sin\left( {\varphi + \theta } \right)\partial _{{\text{x}}} \varphi } \right]} \right\}} \\ {\partial _{y} a_{z} = - \left\{ {\frac{{2x}}{{bb_{0} }}\partial _{{\text{y}}} a_{l} sin\left( {\varphi + \theta } \right) + \frac{{2x}}{{bb_{0} }}a_{l} cos\left( {\varphi + \theta } \right)\partial _{{\text{y}}} \varphi + \left[ {\frac{2}{{bb_{0} }}a_{l} cos\left( {\varphi + \theta } \right) + \frac{{2y}}{{bb_{0} }}\partial _{{\text{y}}} a_{l} cos\left( {\varphi + \theta } \right) - \frac{{2y}}{{bb_{0} }}a_{l} sin\left( {\varphi + \theta } \right)\partial _{{\text{y}}} \varphi } \right]} \right\}} \\ \end{array} } \right.} \\ \end{array}$$
(7)

The term containing \({B}_{0}\) in Eq. (7) represents the effect of the applied magnetic field. From Eq. (7), it can be seen that the applied magnetic field affects the directional derivative \({\partial }_{t}{a}_{y}\) of the composite field vector potential, which further affects the electron trajectory and further the radiation properties of high-energy electron. From Eqs. (5–7), the full-time partial differential equation for the acceleration, velocity and energy of the electron moving in the complex field can be derived. Based on this, the full-time, full-space trajectory of the electron can be determined as

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma d_{t} u_{x} = \left( {1 - u_{x} ^{2} } \right)\partial _{t} a_{x} + u_{y} \left( {\partial _{y} a_{x} - \partial _{x} a_{y} } \right) + u_{z} \left( {\partial _{z} a_{x} - \partial _{x} a_{z} } \right) - u_{x} u_{y} \partial _{t} a_{y} - u_{x} u_{z} \partial _{t} a_{z} } \\ {\gamma d_{t} u_{y} = \left( {1 - u_{y} ^{2} } \right)\partial _{t} a_{y} + u_{x} \left( {\partial _{x} a_{y} - \partial _{y} a_{x} } \right) + u_{z} \left( {\partial _{z} a_{y} - \partial _{y} a_{z} } \right) - u_{x} u_{y} \partial _{t} a_{x} - u_{y} u_{z} \partial _{t} a_{z} } \\ {\gamma d_{t} u_{z} = \left( {1 - u_{z} ^{2} } \right)\partial _{t} a_{z} + u_{x} \left( {\partial _{x} a_{z} - \partial _{z} a_{x} } \right) + u_{y} \left( {\partial _{y} a_{z} - \partial _{z} a_{y} } \right) - u_{x} u_{z} \partial _{t} a_{x} - u_{y} u_{z} \partial _{t} a_{y} } \\ {d_{t} \gamma = u_{x} \partial _{t} a_{x} + u_{y} \partial _{t} a_{y} + u_{z} \partial _{t} a_{z} } \\ \end{array} ,} \\ \end{array} } \right.$$
(8)

where \({u}_{x}{,u}_{y},{u}_{z}\) are the velocity components of the electron in the \(x,y,z\) directions, respectively. Electrons in relativistic accelerated motion will emit electromagnetic radiation. According to the electrodynamics, the radiated power per unit solid angle of an accelerating electron is deduced from the Poynting vector as follows'

$$P\left( t \right)_{{\Omega }} = \frac{dP\left( t \right)}{{d{\Omega }}} = \left[ {\frac{{\left| {\vec{n} \times \left[ {\left( {\vec{n} - \vec{u}} \right) \times d_{t} \vec{u}} \right]} \right|^{2} }}{{\left( {1 - \vec{n} \cdot \vec{u}} \right)^{6} }}} \right]_{{t^{\prime}}}$$
(9)

Accordingly, the electromagnetic radiation can be derived from Eq. (8) as long as we determine the electron’s state of motion according to Eq. (7) where \(P\) is the radiated power, \(\Omega\) is the unit solid angle, and the direction of radiation is \(\vec{n} = {\text{sin}}\left( \theta \right){\text{cos}}\left( \varphi \right) \cdot \vec{x} + {\text{sin}}\left( \theta \right){\text{sin}}\left( \varphi \right) \cdot \vec{y} + {\text{cos}}(\theta ) \cdot \vec{z}\), \(\overrightarrow{u}\) and \({d}_{t}\overrightarrow{u}\) are the velocity and acceleration of the electron, respectively. \(t^{\prime}\) is the time for the electron to interact with the laser pulse, and there exists the following relation between \(t^{\prime}\) and \(t\)

$$t = t^{\prime} + R,R\sim R_{0} - \vec{n} \cdot \mathop{r}\limits^{\rightharpoonup}$$
(10)

where \({R}_{0}\) is the distance from the origin to the observer and \(\mathop{r}\limits^{\rightharpoonup}\) is the position vector of the electron. Assuming that the observation point is sufficiently distant from the electron. The radiation energy per unit solid angle and per unit frequency interval of the electron-laser interaction can be deduced by Parseval's theorem as

$$\frac{{d^{2} I}}{{d\omega d\Omega }} = \left| {\int\limits_{{ - \infty }}^{{ + \infty }} {\frac{{\vec{n} \times \left[ {\left( {\vec{n} - \vec{u}} \right) \times d_{t} \vec{u}} \right]}}{{\left( {1 - \vec{n} \cdot \vec{u}} \right)^{2} }}e^{{is\left( {t - \vec{n} \cdot \mathop r\limits^{ \rightharpoonup } } \right)}} } dt} \right|^{2}$$
(11)

where \(\omega\) is the radiation frequency, \(s={\omega }_{sb}/{\omega }_{0}\), \({\omega }_{sb}\) is the frequency of the high harmonics produced by the scattering. By solving Eqs. (8) and (9), the full-space, full-time, and full-spectrum radiation properties of Thomson nonlinear scattering can be obtained.

3 Numerical results

In this section, we investigate the radiation properties of relativistic nonlinear Thomson forward scattering of a Gaussian circularly polarized intense laser pulse under an applied magnetic field. A single electron is placed stationary at the origin of the coordinates. The incident circularly polarized laser pulse is an electromagnetic wave beam whose transverse electric field as well as irradiance distribution approximately satisfies the Gaussian envelope, propagating along the \(+z\)-axis at an incident angle \({\sigma }_{in}\) = 0. Its wavelength \({\lambda }_{0}=1\mu m\), light intensity parameter \({a}_{0}=5(I=3.45\times {10}^{19}W/{cm}^{2})\), pulse width \(L=5{\lambda }_{0}\), corresponding to a pulse duration of 16.67 \(fs\). Beam waist radius varies from \({{\text{b}}}_{0}=2\) to \({{\text{b}}}_{0}=9\) at unit value intervals. The properties of RNTFS have basically been stabilized when \({{\text{b}}}_{0}\ge 9\). But in order to prevent the influence of the jumping point phenomenon on the conclusion, for the sake of comprehensiveness, we additionally studied the cases of \({{\text{b}}}_{0}=20\) and \({{\text{b}}}_{0}=100\). The corresponding magnitude values of the beam waist radius are \(2\mu m \sim 9\mu m\), \(20\mu m\) and \(100\mu m\). We have investigated the electron motion properties, the full-angular and spectral properties of the electron radiation in the process of the change from tightly-focused laser to non-tightly-focused laser and even to plane wave. In addition, we applied a static magnetic field along the positive direction of \(y\)-axis with the magnitude proportional to \(x\). The intensity coefficients are \({{\text{B}}}_{0}=0\) and \({{\text{B}}}_{0}=0.5\), corresponding to \(0\,\, kT\) and \(5\,\,kT\), respectively.

3.1 Electron trajectory

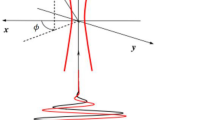
On the basis of classical electrodynamics, we solve the system of partial differential equations of Eq. (8) by the fourth-order Runge–Kutta algorithm, and then obtain the electron trajectory diagram as shown in Fig. 2. From Fig. 2I, we can find that in the absence of magnetic field, the stationary electron, driven by the Gaussian circularly polarized laser pulse, firstly makes a helical motion similar to equiangular spiral, and the change process of its pitch basically coincides with that of the Gaussian function. Then, when the electron lags behind the end of the falling edge of the circularly polarized laser pulse, the electron starts to do uniform linear motion.

Fig. 2
figure 2

Trajectories of electrons in the complex field at different beam waist radii. The magnetic field strength is 0 in group (I), 0.5 in group (II). The peak laser amplitude a0 = 5, and the pulse width L = 5λ0, the unit of beam waist radius throughout this paper is μm

Full size image

The radial displacement of the electron at \({b}_{0}=2\) is the largest, which is about \(1.5{\lambda }_{0}\). And with the increase of the beam waist radius, the radial displacement of the electron gradually decreases until the radial displacement reaches the minimum at \({b}_{0}=7\), about \(0.8{\lambda }_{0}\). In the whole process of the electron movement, the change law of radial displacement is completely consistent with that of \(\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}\). When the electron happens to act with the instantaneous peak of the Gaussian laser pulse, i.e., the electron in the \(z\)-direction is not stressed, the radial displacement is maximum.

The lateral drift distance of electrons along the \(+z\)-axis decreases with increasing beam waist radius, from \(100{z}_{f}\)(\(1300{\lambda }_{0}\)) at \({b}_{0}=2\) to \(0.065{z}_{f}\)(\(80{\lambda }_{0}\)) at \({b}_{0}=20\). The above phenomenon is due to the fact that the total angular distribution \({\uptheta }_{div}\cong 2\frac{{b}_{0}}{{z}_{f}}=\frac{2{\lambda }_{0}}{\pi }\cdot \frac{1}{{b}_{0}}\) keeps decreasing with the increasing beam waist radius, i.e., the laser intensity decay is getting smaller and smaller. Although the electrons all experience the ponderomotive force along the rising edge of the laser (electron acceleration region) and the falling edge (electron deceleration region), and the ponderomotive force at any position along the rising edge is greater than that at the symmetric position along the falling edge. But as the beam waist radius increases, the difference in the ponderomotive force at the symmetric position decreases continuously. Therefore, although the electrons in the laser acceleration region to obtain more and more energy, the peak energy becomes higher, but at the same time, the laser deceleration of the electrons is also more and more intense. And as the difference between the work done by the laser acceleration and the work done by the deceleration becomes smaller and smaller, the net gain of electron energy becomes smaller and smaller. From tight focusing (\({b}_{0}=2\)) \({\gamma }_{end}=9.5\), when the electron is still in relativistic motion, corresponding to the electron trajectory is realized as a comet tail trailing. By the time of non-tight focusing (\({b}_{0}=20\)) \({\gamma }_{end}=1\), at which point the electron can be considered stationary. It is the large gap in velocity that leads to the large difference between the lateral drift distances.

At the same time, we can find that the electron trajectory in Fig. 2a has a spiral front. While electron trajectories in Fig. 2b–f all present fourfold symmetry with the \(z\)-axis as the axis of symmetry and front-back symmetry. It can be deduced from Eqs. (3, 4) that for an initially stationary electron, we can learn that the longitudinal drift distance of the electron \(s=0.63{a}_{0}{L}^{2}=0.63\times 5\times {5}^{2}=78.75\,\,{\lambda }_{0}\) [29]. In Fig. 2a, \({z}_{f}={b}_{0}^{2}/2=2{\lambda }_{0}\ll s\), at which point the effect of the beam waist radius on the variation of the field strength magnitude of the laser field should not be neglected. Since the beam waist radius is particularly small at this time, the energy decay of the laser is very rapid, compared with Fig. 2f, the electron needs to experience more time to accelerate to close to the speed of light, which is manifested in the trajectory, i.e., the longitudinal distance of the frontier part of the motion is very limited. This results in a relatively small laser energy decay compared to the rest of the trajectory, and the longitudinal pondermotive power is still large. Since \(\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}\), which determines the longitudinal winding radius of the electron, depends on the longitudinal pondermotive power of the laser, so winding radius of the electron is larger at this point compared to the rest of the trajectory. When the electrons interact with the falling edge of the laser pulse, according to \({a}_{l}={{\text{a}}}_{0}{\text{exp}}\left(-\frac{{\upeta }^{2}}{{{\text{L}}}^{2}}-\frac{{\uprho }^{2}}{{{\text{b}}}^{2}}\right)\frac{{{\text{b}}}_{0}}{b}\) can be obtained from the intensity of the laser is less than \(0.001\mathrm{\%}\) of the origin. The radial field is similar to the planar electromagnetic field, radial pondermotive force is very weak, the electron's trajectory is limited to the \(z\)-axis near. Summarize the above two points, there is a spiral front to the electron trajectory when the beam waist radius is small. Since the laser decelerating effect on the electrons can be basically negligible, the energy gained by electrons at the rising edge of the laser is basically equal to the net gain in electron energy. Additionally, the asymmetry of the laser leads to the asymmetry of the electron trajectories, and the direction of motion of the electrons is not the \(+z\)-axis, but points to the III Octant. In Fig. b, \({z}_{f}={b}_{0}^{2}/2=200{\lambda }_{0}\gg s\), at this time, the influence of the beam waist radius on the distribution of the laser field intensity is basically negligible. And the radial displacement of the electron is much smaller than the size of the beam waist, the interaction of the electron's electromagnetic wave is approximated to a planar wave, the formula can be rewritten as \({a}_{l}={{\text{a}}}_{0}{\text{exp}}\left(-\frac{{\upeta }^{2}}{{{\text{L}}}^{2}}\right)\), the force on the rising and falling edges of the electron is perfectly symmetrical, the electron trajectory is perfectly symmetrical, and the net electron energy gain is \(0\). The velocity properties of the electrons are small on both sides and high in the middle, making the two ends of the trajectory dense and the middle sparse.

Through the pairwise comparison between Fig. 2II and I, we find that with all other parameters being equal, the applied magnetic field causes the electron to drastically increase both the radial displacement and the lateral drift distance. We decompose the velocity in two directions, parallel to the \(z\)-axis and perpendicular to the \(z\)-axis. The Lorentz force \({f}_{z}\) generated by \({v}_{z}\) pulls the electron to a larger winding radius. And the Lorentz force \({f}_{\perp }\) generated by \({v}_{\perp }\), since both the electron velocity and radial displacement are increasing during the interaction of the electron with the rising edge of the laser, so in the process of the electron around an optical circle on the whole Lorentz force to the + z axis drive electricity. So, \({v}_{z}\) increases, thus the electron radial displacement is further increased, and drives the total velocity \(v\) increases. On one hand, \(f=qvB\) increases. On the other hand, the interaction time of the electrons with the laser pulse is lengthened. The applied magnetic field contributes to a positive feedback between the radial displacement and \({v}_{z}\).

Due to the presence of an applied magnetic field, when the electron ends its interaction with the laser, the electron does not move along the + z axis in a uniform linear motion, but rather does a constant rate of equal-pitch solenoidal motion, with the size of the pitch being proportional to the final energy of the electron. From Fig. 2h, we find that when \({b}_{0}=5\), the pitch of the electron is the largest when it finally does a stable cyclotron oscillation motion. The pitch of the whole process is firstly increasing, and finally remains stable without any obvious reduction process, which is manifested in the energy of the electron that there is no attenuation of the electron energy in the whole process. This indicates that when there is an applied magnetic field, there is an optimal beam waist radius that allows the electrons to obtain the most energy after interacting with the laser. When \({b}_{0}<5\), the laser intensity decays too quickly to give enough energy to the electron. And when \({b}_{0}>5\), the electron only moves a few or even less than a Rayleigh distance when it interacts with the falling edge. The energy decay of the laser is extremely limited, which causes the electron to lose a lot of energy when decelerating. At the same time, we can find that when \({b}_{0}\,\,=\,\,5\), the radial displacement of the electron also reaches 5 \({\lambda }_{0}\), which means that the intensity of the laser here is approximately equal to zero, and the electron directly skips the deceleration stage. When the electron leaves the range of action of the laser field, the \({v}_{z}\) on the one hand drives the electron to move at a uniform speed in the \(+z\) direction. And on the other hand, the Lorentz force \({f}_{z}\) generated by \({v}_{z}\) provides the electron with centripetal acceleration, which drives the electron to do a circular motion with a constant radius. The electron's \({v}_{\perp }\) is symmetric with the center of the origin as the electron travels around in one circle and the radial displacement is unchanged, so the effect of \({f}_{\perp }\) generated by \({v}_{\perp }\) on the electron motion during one revolution is canceled out. In summary, the electron flies out of the laser pulse and then makes a steady solenoidal motion.

3.2 Full-angular distribution properties of electron radiation

First, for per unit solid angle, we calculated the radiated power at each point in time throughout the electron–laser interaction. We define the maximum of these as the maximum radiated power for that unit solid angle, and the maximum of the maximum radiated powers for all unit solid angles is the peak radiated power, denoted as \({P}_{max}\), and the angle at which it is located is denoted as (\({\theta }_{pmax},{\phi }_{pmax}\)) in the spherical coordinate system. We normalize the maximum radiated power by the peak radiated power. We find that the normalized full-angular radiation is distributed in a narrow scattering set on a conic surface with an angle \(\theta\) (\(\theta \approx {\theta }_{pmax}\)) to the \(+z\) axis, and the lengths of the busbars on this conic surface are essentially equal. This indicates that the maximum radiated power can be approximated as the peak radiated power at different azimuthal angles \(\phi\) for the same polar angle \(\theta\). This is because the laser drives the electrons to oscillate, emitting radiation in the tangential direction of the trajectory. When peak radiated power is radiated outward, the energy change when the electrons travel around the circle is minimal, so the radiated power of the electrons is essentially unchanged.

We can observe that when there is no applied magnetic field, the polar angle \(\theta\) decreases with increasing beam waist radius. Until \({{\text{b}}}_{0}=20\), there exists a minimum value of the polar angle \({\theta }_{min}=22^\circ\). When there is an applied magnetic field, on one hand, \(\theta\) all decreases significantly compared to the absence of magnetic field, which means that the directionality is generally enhanced. On the other hand, as the beam waist radius increases \(\theta\) becomes smaller and then larger, reaching a minimum value of \({\theta }_{min}=3.375^\circ\) at \({{\text{b}}}_{0}=5\). This indicates that there is always an optimal beam waist radius that makes the best directionality of electron radiation regardless of the presence or absence of an applied magnetic field, which will be explained below. At the same time, it is worth mentioning that in Fig. 3a we observe the vortex phenomenon of electron radiation, where the full-angular distribution of the maximum radiated power takes on a rosette shape and is no longer conical.

Fig. 3
figure 3

Full-time and full-space distribution of maximum radiated power for different beam waist radii. The radiated power has been normalized by the peak radiated power. The magnetic field strength is 0 in group (I), 0.5 in group (II). The peak laser amplitude a0 = 5, and the pulse width L = 5λ0

Full size image

Figure 4 gives the explanation of the full angle at half maximum \(\Delta \theta\), which is an extremely important property of the RNTFS and an important criterion for determining the radiative collimation. Figure 4II demonstrates the vortex angular distribution of the radiative full-angular distribution [30], which will be given an explanation in the following. Whereas Fig. 4III shows the universal full-angular distribution of the maximum radiated power in the cylindrical coordinate system. Its angular radiation is mainly concentrated on a complete circle with perfect origin symmetry, while the rest of the plane remaining receives almost no radiation. This indicates that the distribution of radiation is only related to the polar angle \(\theta\), while the azimuthal angle \(\phi\) has a very small effect on it.

Fig. 4
figure 4

The full angle at half maximum ∆θ of the full-angular distribution of electron radiation is described in two coordinate systems. (I) is observed from the azimuthal angle ϕ = ϕpmax where the peak radiated power is located in the rectangular coordinate system. The two polar angles are taken when the radiated power is half of the peak radiated power, and the difference between the two polar angles is ∆θ. (II) (III) is the projection of the angular distribution of the maximum radiated power in the xOy plane in the cylindrical coordinate system. Taking the azimuth angle ϕ = ϕpmax where the peak radiated power is located, for the vortex radiation distribution, ∆θ is defined as the angular width between the peak radiated half-power points on the main peak of radiation. And for the toroidal radiation distribution, ∆θ is defined as the minimum angular width between the peak radiated half-power points

Full size image

In Fig. 5, we observe the full-angular properties of electron radiation in a cylindrical coordinate system. The peak power of the radiation can be judged intuitively by the height of the power cylinder in the figure, while the radius and width of the circle in the projection correspond to the polar angle \(\theta\) and the full angle at half maximum \(\Delta \theta\) of the radiation, respectively. When there is no applied magnetic field, as the beam waist radius grows, the peak radiated power \({P}_{max}\) becomes larger and larger, while the corresponding polar angle \(\theta\) and full angle at half maximum \(\Delta \theta\) are decreasing. When the beam waist radius \({b}_{0}=20\), \({P}_{max}\) reaches the maximum, and both \(\theta\) and \(\Delta \theta\) reach the minimum. And when there is an applied magnetic field, \({P}_{max}\) becomes larger and then decreases with the increase of beam waist radius. And there is obvious radiation only when \({{\text{b}}}_{0}=3\sim 6\). When \({{\text{b}}}_{0}=5\) , \({P}_{max}\) reaches the maximum, and correspondingly, both \(\theta\) and \(\Delta \theta\) reach the minimum at this time. This indicates that there is always an optimal beam waist radius that makes the electron radiation have the highest peak power, the best directionality (smallest \(\theta\)), and the best collimation (smallest \(\Delta \theta\)), regardless of the presence of an applied magnetic field.

Fig. 5
figure 5

Full-angular distribution of the maximum radiated power of electrons in the cylindrical coordinate system for different beam waist radii, the circular angular plane above the column is the projection of the corresponding radiated power onto the xOy plane. Uniform longitudinal coordinates are applied to the two groups (I) (II), respectively. The magnetic field strength is 0 in group (I), 0.5 in group (II). The peak laser amplitude a0 = 5, and the pulse width L = 5λ0

Full size image

With the increase of the beam waist radius, the vortex angular radiation in Fig. 5I gradually transitions to the circular angular radiation, and \({{\text{b}}}_{0}=4\) is the boundary beam waist radius of the two distributions. As shown in Fig. 6a and d, the full-angular distribution of the radiation at this time shows a long-tailed vortex radiation, encircling from the center of the circle outwards in a circle in the form of a yearly cycle, with the most obvious vortex properties. Starting from the longitudinal vector potential term \({\text{exp}}(-{\upeta }^{2}/{{\text{L}}}^{2})\) in Eq. (1), initially \({\eta }_{0}=6L=30\mu m\), at which time the magnitude of the exponential term is \({\text{exp}}(-36)\approx 0\). And when the electron interacts with the middle section of the pulse, \({\text{exp}}(-{\upeta }^{2}/{{\text{L}}}^{2})\approx {\text{exp}}\left(-{0}^{2}/{{\text{L}}}^{2}\right)=1\). It is thus found that the longitudinal vector potential terms of the electrons differ greatly when interacting with different parts of the laser. The electrons are highly excited only in the middle part of the laser pulse [30], i.e., the middle region where the trajectories in Fig. 2b–f do significant radial oscillations. And the symmetry of the electron trajectory is seriously broken when the beam waist radius is exceedingly small, because the energy decay in the transverse direction is too fast. Therefore, when the electron in Fig. 2a is doing radial oscillation with increasing radius of curvature the electron has been highly excited. The full-angular distribution of RNTFS coincides with the changing optical circumference of the electron trajectory currently.

Fig. 6
figure 6

a–c The full-angular distributions of the maximum radiated power of the election in the cylindrical coordinate system for different beam waist radii, normalized by the peak radiated power, respectively. d–f The projections of the corresponding radiated power on the xOy plane. The peak laser amplitude a0 = 5 and the pulse width L = 5λ0

Full size image

Next, we will explain the reason of the above phenomenon in detail by the data of simulation calculations in Figs. 7 and 8. When there is no applied magnetic field, through Figs. 7I and 8I we can find that when \({{\text{b}}}_{0}=1\), the pole angle \(\theta =39^\circ\) and the full angle at half maximum \(\Delta \theta =35^\circ\), both are the maximum of all beam waist radius, while the peak radiated power \({P}_{max}\) is the minimum. As the beam waist radius keeps getting larger, both \(\theta\) and \(\Delta \theta\) decrease rapidly, and the \({P}_{max}\) increases even more close to four orders of magnitude. However, when\({{\text{b}}}_{0}=5\), the above properties turn to continue the above changes with a very small magnitude. All three radiation properties reach the optimum point when \({{\text{b}}}_{0}=8\) ,\({\theta }_{min}=22.5^\circ\) ,\(\Delta {\theta }_{min}=5^\circ\) ,\({P}_{max}=8.5\times {10}^{6}\).The course of all three is approximated as a logarithmic function. In particular, although all curve fitting in this paper takes the form of quartic or quintic function fitting, the corresponding descriptions are in terms of the shape of the fitted curves due to the consideration of being able to visually characterize the changing patterns of the radiation properties. When we add an applied magnetic field of \({{\text{B}}}_{0}\,\,=\,\,0.5\) in the space, the data on Figs. 7II and 8 show that the above rule of change of the three radiation properties is no longer applicable. The processes of\(\theta\), \(\Delta \theta\) and \({P}_{max}\) can all be approximated as a quadratic function, where the process of \({P}_{max}\) change is arch-bridge-like, the complete opposite of \(\theta\) and \(\Delta \theta\). As the beam waist radius keeps getting larger, \(\theta\) and \(\Delta \theta\) decrease and reach a minimum at \({{\text{b}}}_{0}=4.6\), with \({\theta }_{min}=3.375^\circ\) and \(\Delta {\theta }_{min}=0.34^\circ\). The peak radiated power reaches the maximum value exactly currently with \({P}_{max}=5.64\times {10}^{12}\). Currently, the electronic radiation properties of high collimation, good directionality, and high peak power are the best radiation properties, which indicates that this is the best beam waist radius. As the beam waist radius continues to increase, the above three radiation properties are all shifted to the poor direction.

Fig. 7
figure 7

The polar angle θ (dark cyan line segment) and the coverage area of full angle at half maximum ∆θ (light cyan band) of electron radiation full-angular distribution as a function of the beam waist radius. The magnetic field strength is 0 for group (I) and 0.5 for group (II)

Full size image
Fig. 8
figure 8

In (I), the polar angle θ (black line with cyan mark) and the peak radiated power Pmax (orange line with pink mark) under different beam waist radii and applied magnetic field intensity B0 = 0.5 (circle) and B0 = 0 (triangle) are plotted. The peak radiated power is treated by lg function. In group (II), we subdivide the beam waist radius and study in detail the influence of beam waist radius on the full angle at half maximum ∆θ (black line) and the peak radiated power Pmax (orange line) when the applied magnetic field intensity B0 = 0.5, where the meaning of the error bar is the error between the actual data and the fitting curve

Full size image

Next, let us dissect Figs. 7 and 8 from a completely new perspective, rather than from the perspective of the influence of the beam waist radius on the radiative properties. In Fig. 7, we describe the variation of \(\theta\) and \(\Delta \theta\) in a new and comprehensive way, visualizing the practical significance of the full angle at half maximum in the form of the angular range covered by the strips. From the figure, we can not only know the trend of these two angles, but also visualize the position of the peak radiated power \({\theta }_{pmax}\), and the radiated range of the effective radiated power (half of the peak power). This is another way of visualizing the collimation of a laser beam, i.e., whether the radiant energy is focused in a very small area.

Figure 8 shows the consistency of the electronic radiation properties. We find that the polar angle is strictly positively correlated with the magnitude of the full angle at half maximum, and both in turn are strictly negatively correlated with the magnitude of the peak radiated power. The advantages and disadvantages of the three properties are completely bound during the variation. For the polar angle \(\theta\), this is because in Eq. (9), the effect due to the special spatial relation between \(\overrightarrow{u}\) and \({d}_{t}\overrightarrow{u}\) determines the meticulous angular distribution. Whereas for extremely relativistic electrons, \(\left(1-\overrightarrow{n}\cdot \overrightarrow{u}\right)\) dominates in the angular momentum distribution. When the electron undergoes relativistic accelerated motion, the relation between \(\theta\) and the Lorentz factor \(\gamma\) satisfies \(\theta \propto 1/2\gamma\). As the maximum velocity of the electron motion increases, on one hand, the minimum value of the denominator term \({\left(1-\overrightarrow{n}\cdot \overrightarrow{u}\right)}^{6}\) of Eq. (9) is getting smaller and smaller, gradually approaching towards 0, so that the peak power radiated by the electron is increasing. On the other hand, the energy \(\gamma =\sqrt{1-{v}^{2}/{c}^{2}}\) (Lorentz factor) of the electron increases, and θ, which has an inverse relationship with it, decreases correspondingly, resulting in the angular distribution that tends more and more forwards in the direction of motion. Meanwhile, for the full angle at half maximum \(\Delta \theta\), on one hand, we have explained above that electrons radiate outwards at high power only in the middle region of the laser pulse. In this region the laser has very little ponderomotive force on the electrons, and for the parameter combination with a greater maximum speed, the less ponderomotive force there is. On the other hand, the speed of the electron in relativistic motion is already very close to the speed of light, when the difficulty of increasing the speed is proportional to the speed itself. Due to the above two reasons, the larger the maximum motion velocity is, the smaller the change in the velocity of the electron during the period when it is highly excited, which corresponds to the smaller change in \(\theta\), i.e., the smaller \(\Delta \theta\) is. In addition, since \(\theta \propto 1/2\gamma\) and \(\gamma\) is constantly greater than 1, which leads to an inverse ratio between the maximum motion velocity and \(\Delta \theta\).

The data in Figs. 7 and 8I and the example in Fig. 9, on the other hand, jointly show the effect of the applied magnetic field on the peak radiated power, the pole angle and the full angle at half maximum from multiple angles. For \({{\text{b}}}_{0}=20\), in the presence of an applied magnetic field, the electrons have the worst radiation properties, \({\theta }_{max}=11.5^\circ\), \(\Delta {\theta }_{max}=4.025^\circ\), and \({P}_{min}=6.85\times {10}^{9}\). In the absence of an applied magnetic field, the best radiation properties are achieved, \({\theta }_{min}=22^\circ\), \(\Delta {\theta }_{min}=1.429^\circ\), and \({P}_{max}=1.24\times {10}^{7}\). Figure 9II compared with (I), \({P}_{max}\) is nearly three orders of magnitude higher. And in the projection map of radiation full-angular distribution, the bright yellow radiated power bands of (II) are distributed in half of the polar angles in (I) with a much smaller dispersion than that of (I). Even the worst radiation properties with an applied magnetic field are much better than the best radiation properties without a magnetic field, indicating that an applied magnetic field significantly improves the radiation properties of electrons.

Fig. 9
figure 9

Distribution of maximum radiated power per unit solid angle of electrons in rectangular coordinate system for beam waist radius b0 = 20.The magnetic field strength is 0 in group (I), 0.5 in group (II). The peak laser amplitude a0 = 5, and the pulse width L = 5λ0

Full size image

3.3 Spectral properties of electron radiation

Through Fig. 10, it is easy to see that the spectrum of electron space radiation is mirror symmetric about the \(+z\) axis (\(\theta =0^\circ\)). The polar angle \(\theta\) where the maximum spectral harmonic peak power is located is \({\theta }_{pmax}\), where the peak radiated power is located. While the degree of divergence of the bright yellow beam on the spectrum corresponds to the full angle at half maximum \(\Delta \theta\), and the colour scale at the brightest part of the beam corresponds to \({P}_{max}\). Accordingly, it is very well explained why with the increase of beam waist radius, the beams of group (I) gradually converge to the laser center axis, and the aggregation of the spectrum keeps getting better and the maximum harmonic peak power keeps getting higher. As for the beam in group (II), when \({{\text{b}}}_{0}=5\), the beam has the best directionality, the most aggregated energy, the highest harmonic peak power, and the highest number of harmonics. It shows a bright yellow thin line with the smallest angle to the \(+z\) axis, which is exactly what we need for optimal electron radiation.

Fig. 10
figure 10

The θ-angle distribution of full-angular spectrum of electron radiation at the observation angle (θ, ϕpmax) at different beam waist radii. The magnetic field strength is 0 for group (I) and 0.5 for group (II). The two groups are normalized by the maximum harmonic peak power of all the radiated spectrum. The red numbers in the figure then correspond to the harmonic angular frequency here being n times the fundamental angular frequency ω0. The peak laser amplitude a0 = 5 and the pulse width L = 5λ0

Full size image

In addition, combining (I) and (II), we are surprised to find that except for the direction where the radiation is directly irradiated, all the other directions must first go through an ultra-low power region, and we define the terminal frequency of this region as \({\omega }_{min}\). The sharp increase in the intensity of the harmonic component after \({\omega }_{min}\) is due to the upshift in the spectrum caused by the presence of the nonlinear Doppler effect in nonlinear Thomson scattering. From the Doppler effect formula of light wave \(\omega /{\omega }_{0} =\sqrt{(1+{u}_{z})/(1-{u}_{z})}\), it can be seen that it is \({u}_{zmax}\) that determines \({\omega }_{min}\). In the process of turning from \(\theta =180^\circ\) to \(\theta =0^\circ\) along the clockwise or anticlockwise direction, the component of \({u}_{zmax}\) along the \(+z\)-axis gradually increases, which leads to the gradual increase of \({\omega }_{min}\).

In the \(\theta\)-angle distribution of full-angular radiation spectrum in Fig. 10, select the polar angle \({\theta }_{pmax}\) where the peak radiated power is located, i.e., select the radius with the highest color scale in the figure, so as to draw the spectrum in Fig. 11 when the observation direction is (\({\theta }_{pmax},{\phi }_{pmax}\)). Figure 11 depicts the variation of energy \(\frac{{d}^{2}I}{d\omega d\Omega }\) with frequency for electron radiation per unit solid angle, per unit frequency. In group (I), the overall power of the spectrum as well as the harmonic peak power increases as the beam waist radius increases, but the harmonic peak is always located at \(\omega =50{\omega }_{0}\). The harmonic peak power is maximum at \({{\text{b}}}_{0}=20\), which is two orders of magnitude larger than at \({{\text{b}}}_{0}=2\). In Fig. 11II, the power change of the spectrum increases and decreases by multiples when the beam waist radius changes, and the harmonic peak power is as high as \(9.8\times {10}^{6}W\) at \({{\text{b}}}_{0}=5\). Therefore, there are obvious power harmonics in the normalized spectrum only at \({{\text{b}}}_{0}\le 7\).

Fig. 11
figure 11

The electron radiation spectra at different beam waist radii with the observation direction of (θpmax, ϕpmax). The magnetic field strength is 0 for group (I) and 0.5 for group (II), and the two groups are normalized by the maximum harmonic peak power of the respective spectrum. The peak laser amplitude a0 = 5 and the pulse width L = 5λ0

Full size image

In order to clarify the improvement effect of the applied magnetic field on the spectral properties, we compare the spectrum with the best properties without magnetic field (\({{\text{b}}}_{0}=20\)) with the spectrum with the worst properties with the applied magnetic field (\({{\text{b}}}_{0}=20\)) in Fig. 12. We can clearly notice that the harmonic peak power in (II) is still an order of magnitude higher than that in (I) and the width of the spectrum is ten times wider than that in (I). Meanwhile, we can notice that the spectrum in Fig. 12 has an excellent envelope with a very low number of harmonics compared to Fig. 11. This is reflected in the time domain reflecting the symmetry and monochromaticity of the time spectrum.

Fig. 12
figure 12

Distribution of maximum radiated power per unit solid angle and per unit frequency interval for electrons at different beam waist radii. The magnetic field strength is 0 in group (I), 0.5 in group (II). The peak laser amplitude a0 = 5, and the pulse width L = 5λ0

Full size image

In the case of an applied magnetic field, in order to study the influence of the beam waist radius on the electron radiation spectrum in a clearer and more intuitive comparative way, we have plotted it in a single figure, Fig. 13. These three arch-bridge shaped fitted curves with the same trend of change show the properties of the spectrum in three dimensions. As the beam waist radius increases, the harmonic peak power, harmonic peak frequency, and frequency domain bandwidth of the spectrum all increase and then decrease, which coincides with the changing law of collimation. This is because the smaller \(\Delta \theta\) is, the more radiation pulses can be observed simultaneously in the direction of \({\theta }_{pmax}\), and the spectrum of different main frequencies are coupled and superimposed on each other. The spectral properties are optimized at \({{\text{b}}}_{0}=4\), when the spectrum of electron radiation is ultra-high-energy, ultra-continuous, and broadband. The highest frequency of the spectrum can even reach \(2\times {10}^{18}\), and with the help of RNTFS we modulated X-rays. Mapped into the time domain, we obtained arrays of ultrashort, ultra-intense attosecond pulses through the interaction of lasers with electrons.

Fig. 13
figure 13

Electronic radiation spectrum at different beam waist radii with observation direction of (θpmax, ϕpmax) when the applied magnetic field strength is 0.5. All three blue lines are fitted lines, (I) is the fitted curve of the harmonic peak power projection, (II) is the fitted curve of the harmonic peak power, and (III) is the fitted curve of the highest frequency of each spectrum. The peak laser amplitude a0 = 5 and the pulse width L = 5λ0

Full size image

3.4 Consistency of electronic radiation properties

Through Fig. 14, the various properties of electron radiation are summarized, we find that the electronic radiation properties are consistent and there always exists an optimal beam waist radius which makes the high-energy electrons have the best radiation properties. Through the arrangement of the bubbles in the figure, we can find that, regardless of the presence or absence of an applied magnetic field, the radiation properties at the same beam waist radius are strongly correlated. Specifically, the bubbles in the same column have exactly the same change process about the beam waist radius, which is a logarithmic function in the absence of a magnetic field and a quadratic function in the presence of a magnetic field. Accordingly, we can easily infer the pros and cons of other radiation properties of a certain beam waist radius, by comparing the pros and cons of any radiation characteristic of this beam waist radius with other beam waist radii. This means that in the future, when determining the beam waist radius as a parameter, it is possible to measure only any one of the easily measurable radiation properties of the electron radiation, which will save a great deal of time and material.

Fig. 14
figure 14

Various properties of electron radiation at different beam waist radii. Magnetic field strength is 0.5 for Pro1 ~ 5 (five rows below) and 0 for Pro6 ~ 10 (five rows above). Pmax: peak radiated power, θ: polar angle θ, ∆θ: full angle at half maximum ∆θ, HPP:harmonic peak power, BW: frequency domain bandwidth. The radiation properties of each row are, respectively, normalized by the best value of the properties of that row, and the area of the bubble and the color scale are used together to indicate the superiority of the radiation properties

Full size image

At the same time, we can find that there is one and only one optimal beam waist radius that makes all the radiation properties optimal simultaneously, regardless of the presence or absence of an applied magnetic field. When an applied magnetic field is present, the electronic radiation properties become first better and then worse with increasing beam waist radius. Among them, HPP and BW have the best radiation properties at \({{\text{b}}}_{0}=4\), while the remaining properties have the best radiation properties at \({{\text{b}}}_{0}=5\). This side may seem to violate the consistency of the radiation properties, but it is not. In Fig. 8II, by simulating the beam waist radius with high accuracy, we find that the optimal beam waist radius is \({{\text{b}}}_{0}=4.6\) at \({{\text{B}}}_{0}=0.5\). Since the change law of electronic radiation properties currently is similar to a quadratic function with \({{\text{b}}}_{0}=4.6\) as the axis of symmetry, the radiation properties at \({{\text{b}}}_{0}=4\) and \({{\text{b}}}_{0}=5\) are approximately the same due to symmetry. The two are tied for the best beam waist radius at general accuracy and share the best radiation properties. And when there is no applied magnetic field, we can find that all the radiation properties become gradually better with the increase of beam waist radius, and the best radiation properties are obtained at the optimum beam waist radius \({{\text{b}}}_{0}=20\).

4 Conclusions

In summary, we have investigated the effects of beam waist radius and applied magnetic field on the relativistic nonlinear Thomson forward scattering of stationary electrons, during interaction with a Gaussian circularly polarized laser pulse.

Through numerical computational simulations, the electron dynamical properties, the full-angular distribution of the maximum radiated power and the spectral properties are investigated. We have investigated the energy gain during the electron motion from the perspective of transverse drift and radial displacement. We comprehensively studied the peak radiated power, collimation, directionality, harmonic peak power, frequency domain properties, and super-continuity of RNTFS from the perspectives of full-angular distribution of radiated power, polar angle \(\theta\), full angle at half maximum \(\Delta \theta\), and spectrum. At the same time, we find that each above characteristic of electron radiation always maintains strict consistency when the parameters are varied.

We find that there always exists an optimal beam waist radius that optimizes all the properties of electron radiation simultaneously. When the \({a}_{0}=5\), \(L=5{\lambda }_{0}\) and no applied magnetic field is present, the radiation properties of the non-tightly focused laser are better than those of the tightly focused laser and plane wave, and the optimal beam waist radius is \({{\text{b}}}_{0}=20{\lambda }_{0}\). However, in the presence of an applied magnetic field, the radiation properties of a tightly focused laser are much better than those of a non-tightly focused laser, and the optimal beam waist radius is \({{\text{b}}}_{0}=4.6{\lambda }_{0}\).

In addition, a comprehensive comparison shows that an applied magnetic field significantly improves all properties of electron radiation, and that the worst radiation properties with an applied magnetic field are much better than the best radiation properties without an applied magnetic field.

By studying the effect of beam waist radius and applied magnetic field, we find out the optimal parameter combination and summarize the change rule of electronic radiation properties with the parameter combination. We aim to modulate the \(X\)-rays with optimal properties by traversing the parameter combinations, which provides a good modulation method for the use of relativistic nonlinear Thomson forward scattering as a source of radiation for scientific experimental research and biomedical therapy.