1 Introduction

Topological photonics provide attractive approaches to reduce photon losses in waveguides or cavities thus gain great developments in past few years. Photonic topological insulators (PTIs), as the extension of topological insulators from electronics to optics, have been realized using different mechanism such as photonic quantum anomalous Hall (QAH) [1,2,3,4,5,6,7,8], quantum spin Hall (QSH) [9,10,11,12,13,14,15,16] or quantum valley Hall (QVH) effects [17,18,19,20,21,22]. Due to small magnetic response of magneto-optical materials in optical band, great efforts have been made in exploring PTIs which do not need external magnetic field to break the time reversal symmetry. A powerful solution is discovered by applying the concept of valley degree of freedom from valleytronics [23,24,25] to photonic crystal (PhC). By introducing structural asymmetry in the photonic lattice, the Berry curvature: the “magnetic field” in momentum space, can be nonvanishing and opposite signed at the time-reversal valleys (K and K′), resulting in nonzero valley Chern number exhibiting nontrivial topological phase [17,18,19]. Because of zero coupling between forward-moving K-valley and backward-moving K′-valley fields, robust topological waveguiding with reflection suppressed through sharp turns is possible, which is newly experimentally demonstrated at telecommunication band [22].

In recent years, PTIs in the absence of Berry curvatures are proposed in simple square lattices [26, 27]. Their topological invariants are characterized by two-dimensional (2D) electric polarization related to 2D Zak’s phase [28, 29]. Although this kind of PTIs cannot avoid backscattering at the turnings, they reveal that a nonvanishing Berry curvature may not be necessary for topologically nontrivial systems. Supplementary understandings of the classical QSH PTIs in hexagonal-lattice PhCs with C6 point-group symmetry (PGS) [13] are explained using this theory in the earlier reports [30]. Those square-lattice PTIs with zero Berry curvature, which can be considered as 2D photonic generalization of the Su–Schrieffer–Heeger (SSH) model, are also used to construct high-order topological insulators (HOTIs) [31]. In the second-order PTIs, besides one-dimensional topological edge states (TES) there are important zero-dimensional topological corner states (TCS). Then the observation of high-order topological acoustic states in Kagome-lattice acoustic metamaterial was demonstrated [32, 33]. The research on high-order topological states in photonic Kagome crystals is soon published [38]. Whereafter, related investigations of novel topological polaritonic phases, topological metasurfaces and topological lasers continue to be reported [39,40,41,42,43,44,45].

Although many aspects of Kagome HOTI structures have been researched in recent publications, the particulars of the TES and TCS in all available edge and corner structures have not been carefully examined. In this work, we detailly analyze the TES and TCS in almost all possible domain walls of valley-Hall-like photonic Kagome insulators made of periodic circular air-hole array in pure dielectrics. We theoretically demonstrated that the topological nontrivial phase of its photonic band gap when expanding the C3v PGS Kagome PhC unit cell is better to be characterized by a quantized fractional electric polarization \((\frac{1}{3},\frac{1}{3})\) connected to 2D Zak’s phase, but not the conventional valley Chern number. Numerical simulations illustrate the TES can emerge at all these zigzag-type and armchair-type interfaces between two PhCs with different topological phases. Unlike those square-lattice HOTIs with non-negligible wave reflection at edge turnings, the Kagome PTI preserves the key features of valley transport with little reflection when turning along the same valley in some specific structures. Furthermore, TCS can exist in oblique corners formed by zigzag-type or armchair-type edges, showing high-order PTI properties. Since not all the edges or corners can support robust TES or TCS, different edge and corner structures are compared to obtain the best performance. This principle can also be used to construct Kagome-lattice rod-type PTIs with similar features through proper structural designs.

2 Valley-Hall-like photonic Kagome insulators

2.1 Topological invariant

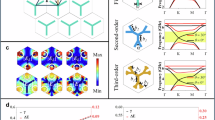
We consider a Kagome-lattice PhC, the unit cell of which is composed of three identical air holes with C3v PGS embedded in pure dielectrics, as shown in Fig. 1a. The reason we focus on the hole-based Kagome lattice in this paper is explained in S1 of Supplementary Material. The permittivity of the dielectric is ε = 13. We set the diameter of the holes d = 0.36a where a is the lattice constant. We explore the topological phase transition by a method of shrinking or expanding the air-hole array within the unit cell, similar to the method in the publications [13].

Fig. 1
figure 1

a The structure of a hole-type PhC with three identical air holes in the unit cell forming Kagome lattice; b–d Band structures of the PhC with the distance between the center of each air hole and the center of the unit cell \(W = a/4, \, a/(2\sqrt 3 ), \, a/3\) respectively; e The schematics of a shrunken unit cell with W = a/4 and a expanded unit cell with W = a/3; f Normalized field distributions of the lowest three bands at K point under W = a/4 and W = a/3 cases, showing the band inversion. The white arrows present the direction of power flux; g Berry curvature of the first band under W = a/3 case

Full size image

According to the 2D Su-Schrieffer-Heeger (SSH) model, the two parameters of the intracellular coupling γ and the intercellular coupling γ′ determine the topology of the system. Thus the dominant thing is the distance W between the center of each air hole and the center of the unit cell. One can easily find \(W = a/(2\sqrt 3 )\) as a critical value when the intracellular coupling equals to the intercellular coupling (|γ′|/|γ|= 1). With this specific structural size of the PhC, the photonic band structure of the lowest three bands is shown in Fig. 1c. Here, we only focus on the TE modes propagating in the x–y plane. Obviously there are Dirac cones formed by the lowest two bands as marked with a red circle at K(K′) point in the first BZ. We then vary the distance W with respect to a to get the three holes shrunken (\(W < a/(2\sqrt 3 )\)) or expanded (\(W > a/(2\sqrt 3 )\)) as shown in Fig. 1e. The corresponding band structures for W = a/4 and W = a/3 are shown in Fig. 1b, d, respectively. It is found the transformation of the bands has many things in common with that of a typical valley-Hall PTI, such as band inversions take place between the 1st and 2nd bands at K(K′) degeneracy when \(W = a/(2\sqrt 3 )\). The variations of the field at K in Band 1, 2 and 3 are illustrated in Fig. 1f, showing the inversion of the bands. During this process, the original existing lowest band gap starts from open to closed and then reopened.

The nth-band Berry curvature is defined as \(F_{{\mathbf{k}}}^{(n)} = \nabla_{{\mathbf{k}}} \times A_{{\mathbf{k}}}^{(n)}\) with \(A_{{\mathbf{k}}}^{(n)}\) denoting the Berry connection of the nth band energy unk [34]. By using an efficient algorithm [35], we did a fast calculation on the Berry curvature of the first band over a roughly discretized portion of the Brillouin zone (BZ). Results in Fig. 1g show that the 1st-band Berry curvature near K(K′) point in the BZ is non-zero but very small, which is different from the case of ordinary valley-Hall PTI having valley Chern number CK/K′ =  ± 0.5. Since the band inversions will not cause large exchange of the curvature at K(K′) points, the traditional valley Chern number is not ± 0.5 in this case. We further show in Supplementary Material that the valley Chern number here is not a topological invariant, thus is not suitable to describe the topology of a Kagome-lattice PTI system. Here 2D electric polarization can be used as a complimentary quantum number to characterized the topology instead. The 2D polarization P = (p1, p2) is given by the integral of the Berry connection over the 2D BZ and expressed as [29]

$$p_{i} \user2{ = - }\frac{1}{{(2\pi )^{2} }}\iint_{BZ} {dk_{1} dk_{2} {\text{Tr}} \left[ {A_{i} ({\mathbf{k}})} \right]},$$
(1)

with i indicating the component of P along the reciprocal lattice vector bi (i = 1,2). Here \(\left[ {A_{i} ({\mathbf{k}})} \right]^{mn} = - i\left\langle {u^{m} ({\mathbf{k}})|\partial k_{i} |u^{n} ({\mathbf{k}})} \right\rangle\) is the Berry connection matrix where m and n run over occupied energy bands. \(|u^{n} ({\mathbf{k}})\rangle\) is the periodic Bloch function for the nth band. \({\mathbf{k}} = k_{1} {\mathbf{b}}_{1} + k_{2} {\mathbf{b}}_{2}\) is the wave vector. Via a direct integration with Eq. (1), it is found the 2D polarization P of the proposed PhC along b1,2 (as illustrated in Fig. 1a) equals \((\frac{1}{3},\frac{1}{3})\) for \(W > a/(2\sqrt 3 )\) showing topological nontrivial phase, while it equals (0,0) for \(W < a/(2\sqrt 3 )\) showing topological trivial phase. The calculation is conducted using the Wilson-loop approach following Refs.[36, 37]. Its mathematical details are presented in Supplementary Material. This polarization can also be obtained by making use of C3 PGS principle. Under the specific PGS, the 2D polarization can be written as [29]

$$\exp (i2\pi p_{1,2} ) = \prod\limits_{n \in occ} {\frac{{\beta_{n} (K)}}{{\beta_{n} (K^{\prime})}}} ,$$
(2)

where \(\beta_{n} ({\mathbf{k}})\) is the eigenvalue of the operator R3 at C3-invariant k point on the nth band. Its derivation is also given in Supplementary Material. The 2D electric polarization is applicable as the topological invariant instead of Chern number mainly in the cases of second-order topological phase, such as Kagome-lattice PTI in this paper or square-lattice C4 PGS PTI with a fractional electric polarization \((\frac{1}{2},\frac{1}{2})\) [26].

2.2 Edge states

We then thoroughly investigate the TES through analyzing the supercell composed of shrunken and expanded PhCs with different 2D polarization. In order to obtain wider band gap, here the diameter of the holes is set as d = 0.4a. Different types of edges named zigzag-type and armchair-type in six different structures are considered. By applying periodic boundary condition on the x direction, we calculated the projected band diagrams of the supercell as shown in Fig. 2. All these edges support TES in red color, which are guaranteed by the different topology of the upper and lower regions rather than the edge type. The time-reversal partners respectively at plus and minus kx region are in y-axial symmetry but always with opposite group velocity. These TES do not connect the lower bulk bands to upper ones. The two zigzag-type edges in Fig. 2a, b are formed by an expanded PhC (W = a/3) with \({\mathbf{P}} = (\frac{1}{3},\frac{1}{3})\) or \({\mathbf{P}} = ( - \frac{1}{3}, - \frac{1}{3})\) and a shrunken PhC (W = a/4) with \({\mathbf{P}} = (0,0)\). They each support only one TES proved to be confined at the edge through the simulation of the field distributions, and the field of the second edge seems less confined at the interface compared to the first edge. It is found that such phenomena may attribute to the pseudospin mechanism, although the pseudospin in the Kagome system is not as common as in those C6-lattice systems with typical spin hall phase. The zigzag-type interface in Fig. 2a or b supports unique TES corresponding to pseudospin up (down) mode along the Γ-K(K′) direction. This pseudospin separation can be verified by the LCP (RCP) power flux in Fig. 1f and also suppresses backscattering. More evidence about the pseudospin TES is appended in S4 of Supplementary Material.

Fig. 2
figure 2

Projected band diagrams and topologically protected states of the edges between two PhCs with different 2D polarization. The blue regions correspond to the bulk modes and the red curves correspond to TES inside the band gap. a, b, c are zigzag-type edges; d, e, f are armchair-type edges

Full size image

In the third zigzag-type edge consisting of lower expanded PhC possessing \({\mathbf{P}} = (\frac{1}{3},\frac{1}{3})\) and upper expanded PhC possessing \({\mathbf{P}} = ( - \frac{1}{3}, - \frac{1}{3})\) in Fig. 2c, the number of the TES changes from one to two. This can be considered as the superposition of the pseudospin up and pseudospin down modes. On the other hand, when the wave vector is along Γ-M direction in all three armchair-type edges shown in Fig. 2d–f, double TES are always found due to both pseudospin up and down states exist. Similar to the TES of C6 PGS PhC [13, 46], the pseudospin up and down states do not separate in these three cases thus the TES will suffer from backscattering. For this reason, it can be expected that the edge propagation will be affected by the inclination and termination of the interface.

To demonstrate the influence brought by the edge structure, the topological protected edge wave propagation in different domain walls is comprehensively studied. We at first calculate the transmission spectra of four straight-line edges shown in Fig. 3 for comparison. It is numerically proved that the robust topological transport is supported by all these four edges, since they all have a nearly unitary transmittance in the topological transmission band, which is defined as the frequency band having transmittance larger than 95%. The presented field distributions are obtained at a specific frequency of 0.24 c/a locating inside the transmission band. The difference between two zigzag-type straight-line edges A and B illustrated in Fig. 3a and b is that their expanded PhC cells in lower region have an orientation difference of 60°, leading to the change of 2D polarization from \({\mathbf{P}} = (\frac{1}{3},\frac{1}{3})\) to \({\mathbf{P}} = ( - \frac{1}{3}, - \frac{1}{3})\). It can be clearly seen that edge A has wider transmission band as well as more confined field distributions than edge B. This attributes to the red-colored TES of edge A in Fig. 2a covers a larger frequency range than that of edge B in Fig. 2b. This rule also applies to two armchair-type straight-line edges C and D with opposite 2D polarization in lower PhC region illustrated in Fig. 3c, d. For armchair-type cases, due to there is a frequency gap between the two red-colored TES in Fig. 2d and e, an additional transmission gap is found within the band gap frequency range.

Fig. 3
figure 3

The transmission spectra of four straight-line edges and their field distributions at a specific frequency. a, b are zigzag-type edges; c, d are armchair-type edges. The transmission band with transmittance larger than 95% is marked out by two black dash lines in each case

Full size image

Furthermore, the topological transport with turns is investigated. Based on the analysis of straight-line edges, we can have a clearer understanding about the edge guiding through sharp oblique turnings with different angles. During a 120° turn along zigzag-type edges in Fig. 4a, the waves always propagate in edge A of Fig. 3 before and after the turning. Therefore, the topological transport is robust with wide transmission band and high transmittance larger than 95% through the turning, as shown in Fig. 4e. The mechanism lies on that the lowest band of the expanded nontrivial PhC owns helical field properties, as shown the white arrowed power flux at K point for W = a/3 case in Fig. 1f. Ideally there is no field coupling between the forward propagating state along Γ-K direction and backward propagating state along Γ-K′ direction with opposite helicity, thus the back-reflection is suppressed, exhibiting the photonic valley-Hall effect [17]. For a 60° turn along zigzag-type edges in Fig. 4b, the transmittance through the turning is still high within the band. It is easy to understand that the bandwidth of topological turning depends on the one with narrower bandwidth of the two edges. Referring to the turn in Fig. 4b, the waves firstly propagate in edge A before the turning and then enter edge B after the turning. As a result, edge B with a smaller band determines the total transmission bandwidth, leading to that the bandwidth shown in Fig. 4f is obviously narrower than that of a 120° turn and the field distributions are less confined. For 60° and 120° turns in Fig. 4c and d formed by the armchair-type edge C (or reversed edge C), the transmission gaps still exist inside the band gap frequency range as shown in Fig. 4g, h, which is dominated by the transport feature of edge C in Fig. 3c. When waves propagate though an orthogonal turning in Fig. 4i with first zigzag-type edge then armchair-type edge, backscattering takes place with the transmittance reducing to 76%. This is because at orthogonal corner the forward states can flip to backward states with opposite group velocity and helicity. To show the influence brought by structural disorders, a missing lattice is introduced on the edge between a nontrivial expanded PhC and a trivial shrunken PhC. As shown in Fig. 4j, the edge waves can go around the defect to some degree while the existing back scattering causes a transmittance reduction of about 10% through the disorder. In summary, above results have demonstrated the valley-Hall-like edge transport of Kagome-lattice PTI. In practical applications, we should pay attention to the bandwidth problem when constructing bending topological waveguides. To get widest working band, it is better to make the wave propagate along the same Γ-K direction in zigzag-type interfaces.

Fig. 4
figure 4

Topological edge transport at different interfaces with turns. a Transmission on zigzag-type edges with 120° turning; b Transmission on zigzag-type edges with 60° turning; c Transmission on armchair-type edges with 120° turning; d Transmission on armchair-type edges with 60° turning; e Transmission spectrum of (a); f Transmission spectrum of (b); g Transmission spectrum of (c); (h) Transmission spectrum of (d); i Transmission first on zigzag-type edge then on armchair-type edge with 90° turning; j Transmission through a disorder formed by removing a unit cell close to the edge

Full size image

2.3 Corner states

The last important thing is, the Kagome-lattice PhC can support TCS in various oblique corners, which are constructed by two edges between topologically nontrivial PhC and trivial PhC. Through establishing the tight-binding Hamiltonian, to obtain the zero energy states, the eigenvalue equation satisfies \(H\left| \psi \right\rangle = 0\), where \(\left| \psi \right\rangle\) is the eigenstate of the zero energy [32]. It is derived that the decay length of the zero energy corner state is

$$l = \log \frac{\gamma ^{\prime}}{\gamma },$$
(3)

with γ and γ’ respectively denoting the intracellular and intercellular coupling as mentioned in Fig. 1. If γ’ > γ, the decay length l is positive thus the corner decay mode is predicted to exist. If γ’ < γ the decay length l is negative, revealing non-decay modes thus corner modes do not exist. In another word, corner modes can only exist in those corners with decay modes away from the corner along both the edge vector directions. To prove the prediction, we numerically find out the TCS in a 60° corner formed by two zigzag-type edge B in Fig. 3. The field is clearly localized in the corner having the nontrivial expanded PhC inside the corner and the trivial shrunken PhC outside the corner, as shown in Fig. 5a. As illustrated in the projected band gap, the frequency of the existing TCS drawn with orange dash line differs from that of the TES drawn with red solid line. This TCS is protected by the nontrivial topology, which is a smoking-gun evidence of the second-order photonic topological insulators.

Fig. 5
figure 5

Corner states in different corner constructions. The two edges forming the corner are indicated by black bold lines in each case. The frequency of the existing corner state is drawn with orange dash line in the projected band gap. a A 60° zigzag-type corner having the expanded PhC with \({\mathbf{P}} = (\frac{1}{3},\frac{1}{3})\) inside the corner and shrunken PhC with \({\mathbf{P}} = (0,0)\) outside the corner. b Another 60° zigzag-type corner having the expanded PhC with \({\mathbf{P}} = ( - \frac{1}{3}, - \frac{1}{3})\) inside the corner. c A 60° armchair-type corner having the nontrivial PhC inside the corner and trivial PhC outside the corner. d A 120° corner having the nontrivial PhC inside the corner and trivial PhC outside the corner

Full size image

More detailly, the TCS under different corner constructions are discussed. Obviously a 60° zigzag-type corner formed by two zigzag-type edge A in Fig. 3 should support TCS, as shown in Fig. 5b. In fact, the TCS can exist as long as the 60° zigzag-type corners have nontrivial PhC with non-zero 2D polarization (such as \({\mathbf{P}} = (\frac{1}{3},\frac{1}{3})\)) inside and any other PhC with different 2D polarization (such as \({\mathbf{P}} = ( - \frac{1}{3}, - \frac{1}{3})\)) outside. However, the TCS cannot appear in a 60° corner having trivial PhC inside the corner and nontrivial PhC outside the corner because the states grow away from the corner rather than decay. Moreover, a 120° corner formed by two zigzag-type edges does not support corner modes either even if it has nontrivial PhC inside, since the mode along one of the lattice vectors is not a decay mode away from the corner. On the other hand, those corners consisting of two armchair-type edges illustrated in Fig. 5c, d also support the TCS if they satisfy the inside PhC is nontrivial, no matter the angle of the corners is 60° or 120°. It is worth to mention that even in the same corner structure, there are two different types of corer states like Type-I localized and Type-II delocalized state [40], which is verified in S5 of Supplementary Material.

For practical use, such corner structures can be utilized for optical cavities. The value of quality factor Q of the corner modes in different corners with limited layers of the unit cells are numerically evaluated as labeled in Fig. 5. The highest Q can reach 103 in approximation in the corner formed by two edge B, which should be the best choice to construct cavities. Actually, the performance Q has intense connection with the confinement degree of the localized TCS thus will be influenced by the number of the surrounding layers of the corner in numerical results. More discussion about the Q factor is also given in S5 of Supplementary Material. Above discussions show the possibility of the implementation of high-Q cavities or even lasers with highly localized corner modes in oblique corners, which needs further demonstration by experimental studies.

3 Conclusion

We have detailly studied the Kagome-lattice PhCs with three air holes in the unit cell obeying C3v point-group symmetry. They show valley-Hall-like topological phases but their topology is protected by 2D electric polarization rather than valley Chern numbers. We numerically compared the transmittance and working band of the TES in all possible zigzag-type and armchair-type edge structures with straight or turning channels and found the TES performance is in considerable connection with the edge construction. These structures of air holes in pure dielectrics are easy to fabricate and can also extend to rod-type photonic crystals with the same point-group symmetry. In the end, through numerical comparison we show TCS is only supported in some of the zigzag-type and armchair-type corners with specific angles, which may be used to realize high-Q optical cavities.