1 Introduction

The theory of quantum mechanics has transformed our perception of the natural world. Its fundamental principles are now inspiring the creation of innovative technologies. Quantum communication is one such area where there is a growing interest in developing new technologies. Quantum communication aims to surpass classical communication and introduce new functions that were previously unavailable in the classical regime.

Many technologies in quantum communication are being developed and also, some are in test. For example, quantum key distribution [1] allows two parties to share a common key with provable unconditional security. This level of secrecy is completely unachievable in classical communication. Also, quantum communication will be the backbone of the quantum network and quantum internet [2]. A network of devices that will revolutionize how we perform our communications and computational tasks [3].

Recently, several experiments have been done demonstrating the feasibility and implementation of quantum communication technologies even with satellite-to-ground links [4]. For example, the Chinese Academy of Science satellite Micius has applied fundamental tests in space, quantum communication protocols, and also satellite-to-ground quantum key distribution. The development of such quantum satellite technologies prepares a situation in which quantum communication can be developed for broader use in our life [5, 6].

One of the main issues in developing quantum communication technologies is the clock synchronization between bases. In classical mechanics [7], when special relativity is taken into account, two basic methods are available to synchronize clocks. Einstein’s synchronization [8] and Eddington’s slow clock transport [9]. However, despite the superb stabilities of the next generation of atomic clocks [10], the question of how best to synchronize clocks with high precision is frequently addressed, such as time transfer laser links for the Einstein protocol [11], and quantum adaptations of Eddington’s protocol [12]. Accordingly, a third method of clock synchronization proposed by Josza and co-workers [13], based on quantum entanglement. In this method an entangled quantum state shares between the spatial locations and uses the non-local features of quantum mechanics for clock synchronization. In all classical methods, light or matter is exchanged between locations. Also, using entanglement the two-party protocol can be extended to multi-parties and several experiment verification have been reported [14, 15]. Despite the reasonable results of clock synchronization with quantum entanglement, in real cases, the effect of the environmental noise and the dissipation of the quantum states is causing problems. Decoherence theory is broadly used in quantum information and communication as a source of noises and error [16,17,18], and also for modeling quantum open systems in physical and biological processes [19,20,21]. The environment effect on quantum states is due to the decoherence theory. With more distance between the locations, decoherence acts more effectively quantum properties decay faster and clock synchronization shows more error. In long distances and high environmental noise, quantum clock synchronization cannot be reliable at all.

In this paper, we review the modern quantum clock synchronization model and describe the decoherence process in the spin-1/2 model. Furthermore, we calculate the dissipation effect of the decoherence on our clock synchronization model through the master equation. At last, we numerically solve the master equation and study the effect of the environmental noise on the system in different environmental conditions.

This paper is organized as follows: in Sect. 2, we define the model of clock synchronization with quantum entanglement. In Sect. 3, we describe the decoherence theory and calculate the master equation. In Sect. 4, we numerically solve the master equation and discuss the results in a practical case. In Sect. 5, We apply a new error correction method and we show that the final error is far negligible compared to other quantum clock synchronization methods. Finally, in the last section, we conclude the paper.

2 Clock synchronization model

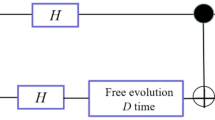
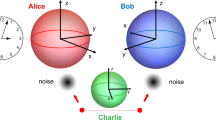
In this section, we simply describe the quantum entanglement clock synchronization protocol between two locations [22], where Alice and Bob want to synchronize their clocks. Alice and Bob share the well-known entangled Bell-state with each other:

$$\begin{aligned} |\psi ^-\rangle =\frac{1}{\sqrt{2}}\left(|0\rangle _A|1\rangle _B-|1\rangle _A|0\rangle _B\right) .\end{aligned}$$
(1)

We assume that the state prepared at Alice location and one of the particles is sent to Bob. However, the definitions of the states are respect to Alice’s basis:

$$\begin{aligned} |\psi ^-\rangle =\frac{1}{\sqrt{2}}\left(|0\rangle _A^{(A)}|1\rangle _B^{(A)}-|1\rangle _A^{(A)}|0\rangle _B^{(A)}\right), \end{aligned}$$
(2)

where indexes under the states shows which particle is sent to Bob and which one remain in Alice’s location. The appropriate basis to view the state in Alice and Bob’s respective local bases are

$$\begin{aligned} \psi ^-\rangle ^{(loc)}=\frac{1}{\sqrt{2}}\left(|0\rangle _A^{(A)}|1\rangle _B^{(B)}-e^{\theta _1^{(B)}-\theta _0^{(B)}}|1\rangle _A^{(A)}|0\rangle _B^{(B)}\right), \end{aligned}$$
(3)

where for simplicity we chose the irrelevant global phase \(\theta _0^{(B)}+\theta _1^{(B)}=0\). Here, by performing an entanglement purification circuit [22], on both sides, we can reach the desired entangled state shared between Alice and Bob:

$$\begin{aligned} |\psi ^-\rangle =\frac{1}{\sqrt{2}}\left(|0\rangle _A^{(A)}|1\rangle _B^{(B)}-|1\rangle _A^{(A)}|0\rangle _B^{(B)}\right), \end{aligned}$$
(4)

As our time evolution operator (U) is diagonal in \(|0\rangle ,|1\rangle\) basis, our state is stationary. By applying a Hadamard gate on (4), we have

$$\begin{aligned} |\psi ^-\rangle =\frac{1}{\sqrt{2}}\left(|pos\rangle _A^{(A)}neg\rangle _B^{(B)}-|neg\rangle _A^{(A)}pos\rangle _B^{(B)}\right), \end{aligned}$$
(5)

in which we have

$$|{\text{pos}}(t)\rangle = \frac{1}{{\sqrt 2 }}\left( {e^{{ - i\Omega T/2}} |0\rangle + e^{{i\omega t/2}} |1\rangle } \right)$$
(6)
$$|{\text{neg}}(t)\rangle = \,\frac{1}{{\sqrt 2 }}\left( {e^{{ - i\Omega T/2}} |0\rangle - e^{{i\omega t/2}} |1\rangle } \right).$$
(7)

For a system in \(|{\text{pos}}\rangle\) state, by measuring the system in \(\sigma _1\) basis we will have probabilities below to find the system in \(|0\rangle\) and \(|1\rangle\) states, respectively,

$$\begin{aligned} P_0(t)&=\frac{1}{2}(1+\cos \Omega t) \end{aligned}$$
(8)
$$\begin{aligned} P_1(t)&=\frac{1}{2}(1-\cos \Omega t), \end{aligned}$$
(9)

where

$$\begin{aligned} \sigma _1=\begin{pmatrix} 0 &{} 1\\ 1 &{} 0 \end{pmatrix} \end{aligned}$$
(10)

After sharing the state (5), at \(t=0\), Alice simultaneously measures all particles in \(\sigma _1\) basis (\(|pos\rangle\) and \(|neg\rangle\)). In this situation, both A and B particles collapse to one of the states as follows:

$$\begin{aligned} |\psi ^I\rangle&=|{\text{pos}}\rangle _A|{\text{nrg}}\rangle _B \end{aligned}$$
(11)
$$\begin{aligned} |\psi ^{II}\rangle&=|{\text{nrg}}\rangle _A|{\text{pos}}\rangle _B. \end{aligned}$$
(12)

The probability of collapsing to each one of these states is 1/2. Alice and Bob’s clocks start to evolve according to equations (8). Both set of particles started evolving at \(t=0\).

Here, we have to subsets of states I, II that Alice has full information on them regarding her measurements, but Bob has no knowledge about the subsets. In such situation, Bob cannot gain any knowledge about time by random measurements. Therefore, Alice needs to send Bob a classical message. For example, Alice chooses I subset of qubits. Now Alice can inform Bob with the subsets label. Now, Bob can choose his particles among the I and II subsets. With choosing II subset, Bob will have particles in a same phase as Alice’s. Then, Bob will measure his particles in \(\sigma _1\) basis and observes \(P_0(t)\) oscillations. In this case, Alice and Bob are synchronized.

However, the presence of the environmental noise change the state’s phase and prevents Bob from synchronizing his clock with Alice’s. In the next section, we describe the decoherence model for calculating the environmental noise via the quantum Brownian motion master equation.

3 Lindblad master equation of quantum Brownian motion

In this section, we are employing the model of the quantum Brownian Motion provided by Maniscalco et al. [23], who applied Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) master equation [24]. In this system-noise (environment) model, the total Hamiltonian is

$$\hat{H} = \hat{H}_{s} + \hat{H}_{\varepsilon } + \hat{H}_{{{\text{int}}}} ,$$
(13)

where in this equation \(\hat{H}_s\), \(\hat{H}_\varepsilon\) and \(\hat{H}_{{{\text{int}}}}\) are system, environment and system–environment interaction, respectively. We consider the central system as a two level harmonic oscillator (equivalent to spin-1/2 system), and a thermal bath of electromagnetic harmonic oscillators as the environment. Considering the system and environment as explained above, we can write the total Hamiltonian as

$$\begin{aligned} \hat{H}=\frac{1}{2}\left(\hat{P}^2+\Omega ^2 \hat{X}^2\right)+\sum _i \frac{1}{2}\left(\hat{p}_i^2+\omega _i^2 \hat{q}_i^2\right)+\hat{H}_{int}, \end{aligned}$$
(14)

where \(\Omega\) (\(\omega\)) is the system (the environment) frequency, and \(\hat{P}\) and \(\hat{X}\) (\(\hat{p}\) and \(\hat{q}\)) are momentum and position operators of the system (the environment), respectively. For simplicity, we removed mass from the equations and considered \(\hbar =1\). The interaction Hamiltonian defines as

$$\begin{aligned} \hat{H}_{{{\text{int}}}} =\hat{X}\otimes \hat{E}=\hat{X}\otimes \sum _i c_i \hat{q}_i, \end{aligned}$$
(15)

where the position coordinate of the central system \(\hat{X}\) linearly couples to the position \(\hat{q}_i\) of the i-th thermal bath oscillator with the coupling strength \(c_i\). Here, \(\hat{E}\) is the environment operator.

By defining \(\hat{\rho }\) as the total density matrix, the following assumptions are in order:

1. The system and the environment are supposed to be uncorrelated at t=0, i.e., \(\hat{\rho }(0)=\hat{\rho }_s(0)\otimes \hat{\rho }_\varepsilon (0)\) where \(\hat{\rho }_s\) and \(\hat{\rho }_\varepsilon\) are the system and the environment density matrices, respectively.

2. The environment is stationary, i.e., \([\hat{H}_\varepsilon ,\hat{\rho }_\varepsilon (0)]=0\), and also the expectation value of \(\hat{E}\) is zero; i.e., \(\text {Tr}_E [\hat{\rho }_E(0)] = 0\).

3. The system–environment coupling is weak and we neglect the effect of the oscillator frequency renormalization since it is negligible under the weak coupling.

Therefore, by averaging over rapidly oscillating terms, one gets the following secular approximated master equation [23]:

$$\begin{aligned} \frac{d\hat{\rho }_s}{dt}=-\frac{\Delta (t)+\gamma (t)}{2}\left[\hat{a}^\dagger \hat{a}\hat{\rho }_s-2\hat{a}\hat{\rho }_s \hat{a}^\dagger +\hat{\rho }_s \hat{a}^\dagger \hat{a}\right] \nonumber \\-\frac{\Delta (t)-\gamma (t)}{2}\left[\hat{a}\hat{a}^\dagger \hat{\rho }_s-2\hat{a}^\dagger \hat{\rho }_s \hat{a}+\hat{\rho }_s \hat{a} \hat{a}^\dagger\right ], \end{aligned}$$
(16)

where \(\hat{a}=(\hat{X}+i\hat{P})/\sqrt{2}\) and \(\hat{a}^\dagger =(\hat{X}-i\hat{P})/\sqrt{2}\) are the annihilation and creation operators, respectively. The time-dependent coefficients \(\gamma (t)\) and \(\Delta (t)\) represent the classical damping and diffusive terms, defined as

$$\begin{aligned} \Delta (t)&=\int _0^t\kappa (\tau )\cos (\Omega \tau )\text {d}\tau , \end{aligned}$$
(17)
$$\begin{aligned} \gamma (t)&=\int _0^t\mu (\tau )\sin (\Omega \tau )\text {d}\tau , \end{aligned}$$
(18)

where

$$\begin{aligned} \kappa (\tau )=\sum _ic_i^2\langle \{q_i(\tau ),q_i\}\rangle , \end{aligned}$$
(19)

and

$$\begin{aligned} \mu (\tau )=i\sum _ic_i^2\langle [q_i(\tau ),q_i]\rangle , \end{aligned}$$
(20)

are noise and dissipation kernels, respectively. If the quantity \(\Delta \pm \gamma\) remains positive in all times, the master equation (16) will be in the Lindblad form [25]. For environment frequency distribution, we consider the case of an Ohmic spectral density for the bath with Lorentz–Drude cutoff [26]:

$$\begin{aligned} J(\omega )=\frac{2\gamma _0\omega }{\pi }\frac{\Lambda ^2}{\Lambda ^2+\omega ^2}, \end{aligned}$$
(21)

where \(\Lambda\) is the cutoff frequency and the dimensionless factor \(\gamma _0\) describes the system–environment effective coupling strength. Thus, for the expressions of noise and dissipation kernels, we have

$$\begin{aligned} \kappa (\tau )&=\sum _i\frac{c_i^2}{2\omega _i}\text {coth} \left( \frac{\omega _i}{2kT}\right) \text {cos}(\omega _i\tau ) \nonumber \\&\equiv \int _0^\infty \text {d}\omega J(\omega )\text {coth} \left( \frac{\omega }{2kT}\right) \text {cos}(\omega \tau ) \end{aligned}$$
(22)
$$\begin{aligned} \mu (\tau )&=\sum _i\frac{c_i^2}{2\omega _i}\text {sin}(\omega _i\tau ) \nonumber \\&\equiv \int _0^\infty \text {d}\omega J(\omega )\text {sin}(\omega \tau ), \end{aligned}$$
(23)

where k is the Boltzmann constant and T denotes the temperature. In long-time limit assumption, the coefficients \(\Delta (t)\) and \(\gamma (t)\) approach their stationary values. Therefore, their expressions up to the second order of coupling constant are

$$\begin{aligned} \Delta&=\gamma _0^2\Omega \frac{r^2}{1+r^2}\coth \left( \frac{\Omega }{2kT}\right) \end{aligned}$$
(24)
$$\begin{aligned} \gamma&=\gamma _0^2\Omega \frac{r^2}{1+r^2}, \end{aligned}$$
(25)

with \(r=\Lambda /\Omega\), where the master equation (16) becomes similar to the well-known Markovian master equation of damped harmonic oscillator:

$$\begin{aligned} \frac{d\hat{\rho }_s}{dt}=&-\Gamma (\bar{n}+1)\left[\hat{a}^\dagger \hat{a}\hat{\rho }_s-2\hat{a}\hat{\rho }_s \hat{a}^\dagger +\hat{\rho }_s \hat{a}^\dagger \hat{a}\right] \nonumber \\&-\Gamma \bar{n}\left[\hat{a}\hat{a}^\dagger \hat{\rho }_s-2\hat{a}^\dagger \hat{\rho }_s \hat{a}+\hat{\rho }_s \hat{a} \hat{a}^\dagger \right], \end{aligned}$$
(26)

in which \(\Gamma =\gamma _0^2\Omega r^2/(1+r^2)\) and \(\bar{n}=\left(e^{\Omega /kT}-1\right)^{-1}\). The positiveness of the coefficients \(\Delta \pm \gamma\) assures us that the master equation (16) is in the Lindblad form.

Regarding GKSL master equation (26), for a dissipative spin-1/2 master equation, we can write

$$\begin{aligned} \frac{d\rho _s(t)}{dt}=-i[H(t),\rho _s(t)]+L[\rho _s(t)] \end{aligned}$$
(27)

where independent of time Hamiltonian reads as

$$\begin{aligned} H&=H_0+H_1 \end{aligned}$$
(28)
$$\begin{aligned} H_0&=\Omega S_z \end{aligned}$$
(29)
$$\begin{aligned} H_1&=c(|1\rangle \langle 0|+|0\rangle \langle 1|), \end{aligned}$$
(30)

in which c is the oscillation (tunneling) rate. Also, L is Lindblad superoperator and reads as

$$\begin{aligned} L[\rho _s(t)]=\gamma \left( S_-\rho _s S_+-\frac{1}{2}S_+S_-\rho _s-\frac{1}{2}\rho _sS_+S_-\right) \end{aligned}$$
(31)

where \(S_+,S_-\) are ladder operators and are similar and act similarly to creation and annihilation operators:

$$\begin{aligned} S_\pm =\frac{1}{\sqrt{2}}(S_x\pm iS_y). \end{aligned}$$
(32)

Here, we write the equations in interaction picture. For density matrix and tunneling Hamiltonian \((H_1)\) in the interaction picture, we have

$$\begin{aligned} \rho ^D(t)&=e^{itH_0}\rho _s(t)e^{-itH_0} \end{aligned}$$
(33)
$$\begin{aligned} H_1^D(t)&=e^{itH_0}H_1e^{-itH_0}. \end{aligned}$$
(34)

For master eq. (31) in the interaction picture, we have

$$\begin{aligned}&\frac{d\rho _s^D(t)}{dt}=-i\left[H_1^D(t),\rho _s^D(t)]+L^D[\rho _s^D(t)\right] \end{aligned}$$
(35)
$$\begin{aligned}&L^D[\rho _s^D(t)]=\gamma \left( S_-^D\rho _s^D S_+^D-\frac{1}{2}S_+^DS_-^D\rho _s^D-\frac{1}{2}\rho _s^DS_+^DS_-^D\right) \end{aligned}$$
(36)

Applying a desired density matrix and writing equations in matrix form, we reach the set of equations as follows:

$$\begin{aligned} \frac{d\rho _{00}^D}{dt}&=\frac{1}{2}ic\left(\rho _{10}^D-\rho _{01}^D\right)+2\gamma \rho _{01}^D \nonumber \\ \frac{d\rho _{01}^D}{dt}&=\frac{1}{2}i(2F+c)\left(\rho _{11}^D-\rho _{00}^D\right)-2\gamma \rho _{11}^D+(4D-i\Omega )\rho _{01}^D \nonumber \\ \frac{d\rho _{10}^D}{dt}&=\frac{1}{2}i(2F+c)\left(\rho _{00}^D-\rho _{11}^D\right)-2\gamma \rho _{00}^D+(4D-i\Omega )\rho _{10}^D \nonumber \\ \frac{d\rho _{11}^D}{dt}&=\frac{1}{2}ic\left(\rho _{01}^D-\rho _{10}^D\right)+2\gamma \rho _{10}^D \end{aligned}$$
(37)

where in the equations above, we have

$$\begin{aligned} J&=\frac{2\gamma _0c\Lambda ^2}{\pi (\Lambda ^2+c^2)} \end{aligned}$$
(38)
$$\begin{aligned} \gamma&=\frac{1}{2}\pi J \end{aligned}$$
(39)
$$\begin{aligned} F&=\frac{2\gamma _0kT\Lambda c}{c^2+\Lambda ^2} \end{aligned}$$
(40)
$$\begin{aligned} D&=\frac{1}{2}\pi J \coth {\frac{c}{2kT}}. \end{aligned}$$
(41)

In the following section, we solve the equation numerically and discuss the effect of the noise on the clock synchronization error and will compare it to a practical classical clock synchronization method.

4 Results and discussion

Fig. 1
figure 1

a The changes in \(P_1(t)\) and b in \(P_2(t)\) with \(T=300\, K\) and \(\Omega =1\times 10^{12} \,s^{-1}\), in variety of oscillation rates in \(s^{-1}\). The probabilities deviation from value 0.5 represents the error resulted from environmental noise. In lower oscillation rates, the effect of decoherence and environmental noise becomes negligible

Full size image

Once the entangled states are transmitted to Bob’s location, they evolve over time. However, environmental noise affects the states through a process known as decoherence theory, which causes the states to change in two ways. First, the noise causes the system to dephase over time, resulting in the loss of quantum properties after a specific time called the decoherence time. This time depends on the environment’s properties and the strength of the interaction between the system and the environment. Second, the dissipation effect of decoherence causes the system to lose energy over time. Both of these effects lead to a change in the state phase and an error in clock synchronization.

Let us have a look at the order of the magnitude of the decoherence time. Using the thermal de Broglie wavelength \(\lambda _{dB}=1/\sqrt{2mk_BT}\), we can define a corresponding decoherence time as

$$\begin{aligned} \tau _D=\frac{\Delta X^2}{\gamma \lambda _{dB}^2} \end{aligned}$$
(42)

where \(\Delta X\) is the dispersion in position space and we have

$$\begin{aligned} \gamma =\gamma _0\omega \bar{n}\frac{r^2}{1+r^2}. \end{aligned}$$
(43)

In our case, the decoherence time can be small, but in suitable conditions, like a desired temperature and isolating system to have a weak interaction with the environment can rise and be acceptable in our case. As it is relevant in Eq. (42), increasing the frequency of the photons of the chosen electromagnetic wave, can significantly increase the decoherence time. Therefore, waves with high frequencies have higher decoherence times, respectively.

To show how the decoherence affects the clock synchronization, after solving the Eq. (37), we sketch the changes in the probability of Bob, finding the system in states \(|0\rangle\) and \(|1\rangle\) versus the time that the system interacts with the environment in variety of oscillation (tunneling) rate. Oscillation rates in the system heavily depend on temperature and central system frequency.

After Bob receives the particles and chooses his subset to measure, after measuring an acceptable number of particles, he can define the probabilities \(P_0(t)\) and \(P_1(t)\) and synchronize his clocks. However, as we showed in Fig. 1, the system interacts with the environment, decohere the states, and results in probabilities to decay and applies error to Bob’s clock. In this model, the oscillating rates in the system Hamiltonian have the main role in the environmental noise. As we can see in Fig. 1, with decreasing the oscillating rates, the error resulting from environmental noise can be negligible.

Considering a practical case, in which, Alice and Bob with a distance equal to 100km between them want to synchronize their clocks. Classically, according to Sathyamoorty and co-workers [27] showed that in a perfect scenario, the classical clock synchronization would have about \(0.3\%\) error in clock synchronization. However, in the next section, we show that in our case, the error in clock synchronization will be very negligible and higher efficiency in comparison with the current used methods.

5 Error correction and its comparison with experiments

Fig. 2
figure 2

The changes of \(P_1(t)\) in \(1\times 10^8\,s\), with a \(c=1\times 10^8\,s^{-1}\) b \(c=1\times 10^10\,s^{-1}\) c \(c=5\times 10^10\,s^{-1}\). With greater values of c, the probability oscillates with higher frequency

Full size image

As we discussed before, in this model, the parameter c indicates the tunneling effect. With greater values of c, the greater probability is for the system to change due to the environmental noise. However, surprisingly, in great values of c after passing time by taking a mean from probability \(P_1\) through the time, we can achieve the initial state with high precision. Let us have a better look at the changes in the probability in longer times.

As we sketched in Fig. 2 in higher tunneling (oscillating) rates, the system oscillates with higher frequency and the environmental noise is more effective. Now, let us take a look at the error in clock synchronization using the mean of the probability of finding the state in its initial form through time (Table 1). Interestingly, as Table 1 shows, in greater oscillations, we can correct the error accurately and synchronize our clocks with higher precision (as Fig. 2 shows).

Table 1 The error of the clock synchronizations versus the oscillation rates, in the case that we use the mean of the outcome probability through time
Full size table

We can simulate clock synchronization in real-life scenarios by adjusting and calibrating various environmental factors such as the system-environment coupling factor, temperature, tunneling rate, cutoff frequency, and others. Once calibrated, we can use the model to calculate the mean probability outcome over time. This manner of calibration provides us with a method of clock synchronization with the least possible error.

Quan and co-workers [28] demonstrated a proof of principle experiment for synchronizing two clocks separated in a 4 km fiber link, based on quantum interference between frequency entangled photons. In this case, they showed that their setup for clock synchronization can reduce the error up to 73.2 ps. In the case of ours, regarding Table 1 in about of \(c=5\times 10^{12}\,s^{-1}\), the clock error is in the order of \(1\times 10^{-12}\,s\) and is in accordance with Quan’s work. Furthermore, by reaching higher oscillating rates, the clock’s error is even more negligible.

6 Conclusion

In this paper, we addressed the problem of environmental noise on quantum clock synchronization. First, we discussed a quantum model for clock synchronization using quantum entangled states. Then, we describe a model for the decoherence effect on the system.

In this regard, we used a Lindblad quantum Brownian motion master equation and discussed both the dephasing and dissipation effect of the decoherence on the system. Also, we considered the tunneling effect in this model and studied that the error due to the environmental noise can depend on many parameters such as temperature, the system electromagnetic wave frequency, the strength of the system and environment coupling, and the oscillation rates. Furthermore, we showed that by preparing a desired condition, the error in the quantum model of clock synchronization can be far negligible in comparison to classical methods. Finally, by applying an error correction method that implies the mean of the outcome through time, we show that the final error in great values of tunneling rate would be completely negligible even compared to other quantum clock synchronization methods.