Unique soliton solutions to the nonlinear Schrödinger equation with weak non-locality and cubic–quintic–septic nonlinearity in nonlinear optical fibers

Abstract

In this article, we will introduce new types of private soliton solutions to the higher order nonlinear Schrödinger equation (HOSE), containing cubic–quintic–septic nonlinearity, weak nonlocal nonlinearity, self-frequency shift, and self-steepening effect. The suggested model describes the propagation of an optical pulse in the weakly nonlocal nonlinear parabolic law media. We will derive these new types of soliton solutions in the framework of impressive, effective technique, namely, the Riccati–Bernoulli Sub-ODE method (RBSODM) which is one of the well-known ansatz methods that does not surrender to the homogeneous balance theory, reduce the volume of calculations and continuously achieves distinct results. In addition, to confirm and clarify our achieved results we will explore the identical numerical solutions for all realized soliton solutions using the Haar–Wavelet Method (HWM). The Haar–Wavelet Method that usually achieves good results is considered one of the recent numerical schemas. The 2D, 3D figures simulations between the soliton solutions and the numerical solutions have been demonstrated. The obtained soliton solutions are new when it compared with Zhou et al. (Chin Phys Lett 39: 044202, 2022) who solved this model by other technique.

1 Introduction

Newly, the nonlinear complex physical problems can be demonstrated via various forms of the nonlinear partial differential equations (NLPDEs). The optical solitons are the famous one of these nonlinear complex physical problems that govern the optical soliton communication theory in which data are transmitted using optical fiber is particularly interesting, has implications for many areas of research and development. In the past few decades, the propagation of optical solitons in optical fibers had attracted much attention. The nonlinear Schrödinger equation is considered one of the famous nonlinear complex physical problems that possess widely applications in optical fiber. Many forms of these nonlinear complex physical problems were scrutinized, simplified in different published articles through strive effort of scientists [1,2,3,4,5,6,7,8,9,10,11]. The final goal of most base researches arising in different of physics fields explains the particle-like behavior of solitons in interaction, which is either dark soliton or bright soliton. When accurate balance between the group velocity dispersion (GVD) and the self-phase modulation these optical localized waves will be detected. The bright and dark solitons that are existing, respectively, in the normal and anomalous dispersion from the envelope soliton. Moreover, Optical solitons are a form of solitary wave that has the ability of wave propagation and will not spread over a long distance. Optical fiber transmission through long distances needs single-mode fiber, while transmission through short distance needs multimode fiber, to ensure the safety, security of the send signs. These properties will frequently be done over metal cables. In the same connection, there are recent studies that explain the concept of weak non-locality as well as the cubic–quintic–septic nonlinearity and the Sub-ODE method and its influence on the soliton dynamic behaviors see, for example, Triki, et al. [12] who studied the characteristics of pure-quartic optical solitons in a nonlinear medium having a weakly nonlocal response by proposing a nonlinear Schrödinger equation incorporating pure fourth-order diffraction, Kerr nonlinearity and weak nonlocality to describe the transmission of solitons in the system and obtained analytic pure-quartic soliton solutions in forms bright and dark type waveforms in the transmission system to this model in a variety of shapes without taking into account the weak nonlocal contribution, Zhou et al. [13] who constructed the explicit solutions the three-dimensional nonlocal nonlinear Schrödinger equation with time-dependent parabolic law nonlinearity and an external potential that describes the propagation of an optical pulse in the weakly nonlocal nonlinear parabolic law media using the Jacobian elliptic equations expansion method, Zhou et al. [14] who derived explicit solutions which include optical bright solitons, singular solutions and singular triangular periodic solution to the (1 + 1)-dimensional spatial optical solitons in weakly nonlocal nonlinear media with cubic–quintic nonlinearity (fifth order nonlinear media) and cubic–quintic–septic nonlinearity (seventh order nonlinear media), Zhou et al. [15] who studied the dynamics of solitons in an optical system possessing third-order dispersion and nonlinearity, derived the exact three-soliton solutions of a third-order nonlinear Schrödinger equation using the Hirota’s bilinear method, and discussed the interaction properties of those solitons, Sun et al. [16] who investigated the nonlinear dynamic characteristics of three-soliton interactions in optical fibers, obtained exact three-soliton solution of the nonlinear Schrödinger equation, conducted theoretical simulations of the formation process of those obtained three solitons, discussed the effects of initial phase, initial spacing and initial amplitude on the interaction of three solitons and analyzed the evolution of three solitons in optical fibers, Zhong et al. [17] who investigated the generalized variable–coefficient nonlinear Schrödinger equation that models the dynamical evolution of solitons by the analytical method of similarity transformation and the numerical mixed method of split-step Fourier method and Runge–Kutta method and derived the analytical self-similar bright and kink solitons, as well as their associated frequency chirps, Zhou et al. [18] who investigated the transmission of localized waves through a dual-power law medium exhibiting the perturbations including the inter-modal dispersion, self-steepening, and self-frequency shift effects and reported a novel class of nonlinear waves that are periodic wave, kink soliton, algebraic soliton and bright soliton, along with the corresponding chirping, Zhou et al. [19] who used the Hirota method to construct the exact dark solitons, anti-dark solitons and dark double-hump solitons that are widely applied in optical fiber communication system due to the characteristics of strong anti-interference and slow attenuation to the coupled nonlinear Schrödinger equations with the higher order effects of third-order dispersion, self-steepening and self-frequency shift, which modeled the propagation of ultra-short optical pulse through a multimode fiber or birefringence fiber, Zhou et al. [20] who constructed three analytical soliton solutions to nonlinear Schrödinger equation with variable coefficients to study the effective amplification of optical solitons in high power transmission systems, Zhou et al. [21] who investigated theoretically all-optical logic devices using three-soliton solutions through solving the coupled nonlinear Schrödinger equations, discussed the condition for forming all-optical logic devices, Zhou et al. [22] who investigated the propagation properties of soliton pulses in a multimode fiber with higher order effects such third-order dispersion and self-steepening nonlinearity, studied the control of propagation characteristic factors of single soliton in the fiber medium within the framework of a coupled pair of higher order nonlinear Schrödinger equations and derived analytical one-soliton solution of such coupled wave system using the Hirota method, Zhou et al. [23] who derived and used the optical soliton interactions for the nonlinear Schrodinger equation to analyze the interaction of two solitons that will contribute to improve the communication quality and system integration, Ding et al. [24] who used the binary Darboux transformation method to investigate the propagation and interaction dynamics of the optical dark bound solitons for the defocusing Lakshmanan–Porsezian–Daniel equation "which is a physically relevant generalization of the nonlinear Schrödinger equation involving the higher order effects" and constructed the explicit N-dark soliton solutions in the compact determinant form to it, Younas, et al. [25] who adopted successfully the Hirota bilinear method with different test approaches to obtain different kinds of solutions, such as lump-periodic, breather-type, and two-wave solutions for the (2 + 1)-dimensional KdV equation arising in the diversity of fields with the properties, Younas, et al. [26] who used modified direct algebraic method to investigate new exact wave structures to Kadomtsev–Petviashvili–Benjamin–Bona–Mahony and the Benney–Luke equations which explain the behavior of waves in shallow water, obtained the exact structures in the shapes of hyperbolic, singular periodic, rational as well as solitary, singular, shock, shock-singular solutions, Nasreen et al. [27] who extracted various wave structures in solitons in different forms, such as bright, dark, combo, and singular soliton solutions using the new extended direct algebraic method to the system of ion sound under the influence of ponderomotive force that is caused by non-linear force and is experienced by a charged particle in an oscillating electromagnetic field of inhomogeneity, Nasreen et al. [28] who discussed the higher order generalized extended classical nonlinear Schrodinger equation by the assistance of truncated-fractional derivative and composed of self-steepening, and stimulated Raman scattering effects in nonlinear optical fibers, extracted variety of optical solitons, such as bright, dark, combo, singular soliton solutions, periodic, exponential, and hyperbolic type solutions using the modified Sardar sub-equation method, Ismael et al. [29] who used the Hirota method to extract the exact solutions in the shapes of lump-periodic, breather-type and two wave solutions through studying the dynamics of waves to the conformable fractional (2 + 1)-dimensional Nizhnik–Novikov–Veselov equation which is the isotropic Lax integrable extension of the (1 + 1)-dimensional Korteweg–de Vries equations, Nasreen, et al. [30] who extracted diverse pulses as bright, dark, combo, and singular soliton solutions for the coupled time fractional nonlinear Schrödinger equation using the new extended direct algebraic method, Islam et al. [31] who investigated stable and efficient solitary solutions to the (3 + 1)-dimensional Kadomtsev–Petviashvili equation through the improved Bernoulli sub-equation function method and the auxiliary equation method that provide generic solutions, such as exponential functions, trigonometric functions, hyperbolic functions, etc., Yao et al. [32] who applied the improved Bernoulli sub-equation function method and the new auxiliary equation technique to establish soliton solutions as a combination of hyperbolic, exponential, rational, and trigonometric functions to the variant Boussinesq wave equation, Fatema, et al. [33] who investigated the symmetric regularized long-wave equation that describes the attribute of the nonlinear ion acoustic waves, space charge waves, undular bore in meteorology to rummage transcendental shape of surface wave solution using the auxiliary equation approach and the improved Bernoulli sub-equation function technique and obtained soliton solutions in the form of trigonometric, hyperbolic, rational and exponential functions containing several ascendant parameters as well as parabolic, kink, bell-shaped, lump soliton solutions, Islam, et al. [34] who introduced the advanced Bernoulli sub-equation function method to search for stable and effective solitary solutions of the Cahn–Allen equation, reported stable solitary solutions as an integration of exponential functions, hyperbolic functions, Arafat, et al. [35] who investigated scores of broad-spectral soliton solutions to the two-dimensional nonlinear complex coupled Maccari system via the auxiliary equation technique, established solutions as an integration of the rational function, hyperbolic function, trigonometric function and exponential function, Fatema, et al. [36] who located the closed-form travelling and solitary wave solutions to the (3 + 1)-dimensional modified KdV–Zakharov–Kuznetsov equation through the new auxiliary equation method.

The nonlinear Schrödinger equation with weak non-locality and cubic–quintic–septic nonlinearity [11] is one of important models that describes the propagation of waves in nonlinear optical fibers, specially describes the chirped solitons in nonlinear optical fibers with weak non-locality and cubic–quantic–septic nonlinearity which is important phenomenon in optical fiber, according to [11] the suggested model can be written as

$$ iu_{x} - \frac{{\beta_{2} }}{2}u_{\tau \tau } + \gamma_{1} \left| {u^{2} } \right|u + \gamma_{2} \left| {u^{4} } \right|u + + \gamma_{3} \left| {u^{6} } \right|u + i\varepsilon u(\left| {u^{2} } \right|)_{\tau } + + i\delta (\left| {u^{2} } \right|u)_{\tau } + \chi u(\left| {u^{2} } \right|)_{\tau \tau } = 0. $$

(1)

where $\gamma_{1} ,\gamma_{2} ,\gamma_{3}$ denote, respectively, to the respective cubic, quantic, and septic nonlinearities, while $\varepsilon ,\delta ,\chi$ are the coefficients of the terms that represent the self-frequency shift, self-steepening effect, and weak nonlocal nonlinearity, respectively, $\beta_{2}$ is group velocity dispersion and $u(x,\tau )$ denotes to the complex envelope of the electromagnetic field.

Let us admit the complex transformation

$$ u(x,\tau ) = R(\eta )e^{i\Psi (\eta )} ,\eta = \lambda x + \tau . $$

(2)

where $R(\eta )$ is the wave amplitude, while $\Psi (\eta ) = w\tau + \mu x + \psi (\eta )$ denotes to the phase amplitude and $\lambda ,w,\mu$ are the inverse grope velocity, frequency and wave number, respectively, and by taking the nonlinear phase shift assumption $\psi (\eta )$ to be

$$ \psi^{\prime}(\eta ) = \frac{2\varepsilon + 3\delta }{{2\beta_{2} }}R^{2} (\eta ) + \frac{{\lambda - \beta_{2} w}}{{\beta_{2} }}. $$

(3)

Then, Eq. (1) will be converted to

$$ (\beta_{2} - 4\chi R^{2} )R^{{\prime}{2}} + S_{2} R^{2} + S_{4} R^{4} + S_{6} R^{6} + S_{8} R^{8} = 0. $$

(4)

where

$$ \begin{gathered} S_{2} = \frac{{\lambda^{2} - 2\lambda \beta_{2} w + 2\mu \beta_{2} }}{{\beta_{2} }},S_{4} = \frac{{\delta \chi - \beta_{2} \gamma_{1} }}{{\beta_{2} }}. \hfill \\ S_{6} = \frac{{(2\varepsilon + 3\delta )(2\varepsilon - \delta ) + 8\beta_{2} \gamma_{2} }}{{12\beta_{2} }},S_{8} = \frac{{ - \gamma_{3} }}{2}. \hfill \\ \end{gathered} $$

(5)

The rest of this article is organized as follows, in the 2^nd section we introduce the RBSODM [33,34,35,36,37,38,39] and its applications to explore the soliton solutions for the suggested model, in the third section we established the HWM [40,41,42,43] and its applications to obtain the numerical solutions corresponding to the achieved soliton solutions, and in the last section the conclusion of our work is presented.

2 The RBSODM concept

To discuss the mathematical concept of the RBSODM, let us first introduce the nonlinear partial differential equation (NLPDE) perception by adimting the function $\Upsilon$ in terms of $R(x,t),$ its partial derivatives and nonlinear terms as,

$$ \Upsilon (R,R_{x} ,R_{\tau } ,R_{xx} ,R_{\tau \tau } ,...) = 0. $$

(6)

When Eq. (6) executes to the relation $R(x,t) = R(\eta ),\,\eta = \lambda x + \tau$ it will be

$$ \Xi (R^{\prime},R^{\prime\prime},R^{\prime\prime\prime},...) = 0. $$

(7)

where $\Xi$ in Eq. (7) includes $R(\eta )$ and its total drivatives.

The RBSODM scheme admits this assumption to construct its solution forms

$$ R^{\prime} = aR^{2 - m} + bR + cR^{m} . $$

(8)

That has two profile names if $ac \ne 0$ and $m = 0$, Eq. (8) will be Riccati equation and if $a \ne 0,c = 0$ and $m \ne 1$, Eq. (8) will be Bernoulli equation, Eq. (8) has the following types of solutions:

$$ 1 - \,\,\,R(\eta ) = w\,e^{(a + b + c)\eta } ,m = 1. $$

(9)

$$ 2 - \,\,\,R(\eta ) = \left( {a(n - 1)(\eta + w)} \right)^{{\frac{1}{(1 - n)}}} ,b = 0,c = 0,m \ne 1. $$

(10)

$$ 3 - \,\,R(\eta ) = \left( { - \frac{a}{b} + we^{b(m - 1)\eta } } \right)^{{\frac{1}{(m - 1)}}} ,c = 0,b \ne 0,m \ne 1. $$

(11)

$$ \begin{gathered} 4 - \,\,R(\eta ) = \left( {\frac{ - b}{{2a}} + \frac{{\sqrt {4ac - b^{2} } \,\tan [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{^{{\frac{1}{(1 - m)}}} }} . \hfill \\ \,\,\,\,\,\,\,\,\,R(\eta ) = \left( {\frac{ - b}{{2a}} - \frac{{\sqrt {4ac - b^{2} } \,\cot [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{\frac{1}{(1 - m)}}} . \hfill \\ \end{gathered} $$

(12)

where $m \ne 1,a \ne 0$ and $b^{2} - 4ac$ < 0

$$ \begin{gathered} 5 - \,\,R(\eta ) = \left( {\frac{ - b}{{2a}} - \frac{{\sqrt {4ac - b^{2} } \,\tanh [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{^{{\frac{1}{(1 - m)}}} }} . \hfill \\ \,\,\,\,\,\,\,\,R(\eta ) = \left( {\frac{ - b}{{2a}} - \frac{{\sqrt {4ac - b^{2} } \,\coth [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{\frac{1}{(1 - m)}}} . \hfill \\ \end{gathered} $$

(13)

where $m \ne 1,a \ne 0$ and $b^{2} - 4ac$ > 0.

$$ 6 - \,\,R(\eta ) = \left( {\frac{1}{a(m - 1)(\eta + w)} - \frac{b}{2a}} \right)^{1/(1 - m)} . $$

(14)

where $m \ne 1,a \ne 0,$ $b^{2} - 4ac = 0$

And $w$ is an arbitrary constant.

Let us now focus on applying the RBSODM, to get the solitary wave solutions for the suggested model after suitable choice of m and inserting $R^{\prime}$ into Eq. (4), setting the coefficients of various powers of ${\text{u}}$ $R^{i}$ to zero yields a system of equations in $a,b,c$ and $w$ which is

$$ R^{8} \,\,\,\,\, \Rightarrow S_{8} = 0. $$

(15)

$$ R^{6} \,\,\,\,\, \Rightarrow - 4\chi a^{2} + S_{6} = 0. $$

(16)

$$ R^{5} \,\,\,\,\, \Rightarrow - 8\chi ab = 0. $$

(17)

$$ R^{4} \,\,\,\,\, \Rightarrow \beta_{2} a^{2} - 4\chi b^{2} - 8\chi ac + S_{4} = 0. $$

(18)

$$ R^{3} \,\,\,\,\, \Rightarrow 2\beta_{2} ab + 2bc = 0. $$

(19)

$$ R^{2} \,\,\,\,\, \Rightarrow \beta_{2} (b^{2} + 2ac) - 4\chi c^{2} + S_{2} = 0. $$

(20)

$$ R\,\,\,\,\,\,\,\, \Rightarrow 2\beta_{2} bc = 0. $$

(21)

When the above system is solved by any computer program we obtain unique solution which is:

$$ a = \pm \left( {\frac{{S_{6} }}{\chi }} \right)^{\frac{1}{2}} ,b = 0,c = \left( {\frac{{aS_{4} + a^{3} \beta_{2} }}{{S_{6} }}} \right),S_{2} = \left( {\frac{{S_{6} c^{2} - 2ca^{3} \beta_{2} }}{{a^{2} }}} \right). $$

(22)

From which more than one solution have been explored according to the sign $\pm a$ in the parameter a and all related terms that are introduced from the other parameters, we will construct only one of them in which the sign is positive that can be simplified to be

$$ \begin{gathered} w = \mu = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,c = 3,b = 0,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda = 6\,or\,\lambda = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered} $$

(23)

That implies the solution form, Eq. (12), that has the following two branches.

That we will implement individually as follow.

(1) For the first part which is

$$ R(\eta ) = \left( {\frac{ - b}{{2a}} + \frac{{\sqrt {4ac - b^{2} } \,\tan [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{^{{\frac{1}{(1 - m)}}} }} . $$

That can be simplified in the framework of the parameters values, Eq. (23), to be

$$ R(\eta ) = 2\sqrt 2 \tan [2\sqrt 2 (\eta + 1)]. $$

(24)

$$ u(x,\tau ) = \left( {2\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)]} \right)e^{i(\tau + x + \psi (\eta ))} . $$

(25)

where $\psi (\eta )$ is computed from Eq. (3)

$$ \psi^{\prime}(\eta ) = \frac{2\varepsilon + 3\delta }{{2\beta_{2} }}R^{2} (\eta ) + \frac{{\lambda - \beta_{2} w}}{{\beta_{2} }} = \frac{5}{2}R^{2} (\eta ) + 2. $$

(26)

Integrating Eq. (26) with the help of Eq. (24), we get

$$ \psi (\eta ) = - 18\eta + 5\sqrt 2 \tan [2\sqrt 2 (\eta + 1)]. $$

(27)

Then

$$ {\text{Re}} \,\,u(x,\tau ) = \left( {2\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)]} \right)\cos (\tau + x + 5\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)] - 18(6x + \tau )). $$

(28)

$$ {\text{Im}} \,\,u(x,\tau ) = \left( {2\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)]} \right)\sin (\tau + x + 5\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)] - 18(6x + \tau ). $$

(29)

(2) For the second part which is:

$$ R(\eta ) = \left( {\frac{ - b}{{2a}} - \frac{{\sqrt {4ac - b^{2} } \,\cot [\frac{{\sqrt {4ac - b^{2} } (\eta + w)}}{2(1 - m)}]}}{2a}} \right)^{{\frac{1}{(1 - m)}}} . $$

$$ R(\eta ) = - 2\sqrt 2 \cot [2\sqrt 2 (\eta + 1)]. $$

(30)

$$ u(x,\tau ) = \left( { - 2\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]} \right)e^{i(\tau + x + \psi (\eta ))} . $$

(31)

where $\psi (\eta )$ in this case equals

$$ \psi (\eta ) = - 18\eta - 5\sqrt 2 \cot [2\sqrt 2 (\eta + 1)]. $$

$$ {\text{Re}} \,\,u(x,\tau ) = \left( { - 2\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]} \right)\cos (\tau + x - 18(6x + \tau ) - 5\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]). $$

(32)

$$ {\text{Im}} \,\,u(x,\tau ) = \left( { - 2\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]} \right)\sin (\tau + x - 18(6x + \tau ) - 5\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]). $$

(33)

3 The Haar wavelet method (HWM)

The wavelet analysis is used to represent a function in terms of a set of basic functions, called wavelets, that is reduced from dilation and transformation of mother wavelet. The wavelet function takes the form

$$ \Phi_{j,k} (t) = 2^{\frac{j}{2}} \Phi (2^{j} t - k),\,\,0 \le k \prec 2^{j} ,\,\,0 \le t \prec 1.\,\, $$

(34)

According to the wavelet basis the following properties will be explored.

• (i) The orthogonally property

  $$ \int\limits_{0}^{1} {\Phi_{i} (\tau )\Phi_{j} (\tau )} d\tau = \left\{ {\begin{array}{*{20}c} {1;\,\,\,i = j,} \\ {0;\,\,\,\,i \ne j.} \\ \end{array} } \right. $$

  (35)

  Most of the functions in Eq. (32) have a small interval support [41].

There exist a lot of types of wavelet functions; one of them is the Haar functions, which is mathematically considered the simplest wavelets. The Haar functions are defined as a group of square waves with magnitude of $\pm 1$ in some intervals and zero elsewhere. They are step functions (piecewise constant functions). The Haar wavelet transform has been used as an earliest example for orthonormal wavelet transform with compact support [39].

The Haar wavelet functions [40] are given as

$$ h_{i} (t) = \left\{ {\begin{array}{*{20}c} {1;\,\,\,for\,t \in [\omega_{1} ,\,\omega_{2} ],} \\ \begin{gathered} - 1;\,\,\,for\,t \in [\,\omega_{2} ,\,\omega_{3} ] \hfill \\ 0;\,\,\,\,\,\,elsewhere. \hfill \\ \end{gathered} \\ \end{array} } \right., $$

(36)

where $\omega_{1} = \frac{k}{m},\,\omega_{2} = \frac{k + 0.5}{m},\,\,\omega_{3} = \frac{k + 1}{m}$, the integer number $m = 2^{j} ;\,j = 0,1,2,...,J$ indicates the level of wavelet (dilation parameter); $k = 0,1,2,...,m - 1$ is the translation parameter. The integer $J$ is the maximal level of resolution, the index $i$ is computed from $i = m + k + 1$ which has minimum value $i = 2\,(m = 1,k = 0)$, for which Haar function called mother function, and maximum value $i = 2M,\,M = 2^{J}$.the index $i = 1$ corresponds to the scaling (father) function

$$ h_{1} (t) = \left\{ {\begin{array}{*{20}c} {1;\,\,\,for\,0 \le t \prec 1,} \\ {0;\,\,\,\,\,\,elsewhere.} \\ \end{array} } \right. $$

(37)

The following relations according to [43] are important to be introduced

$$ p_{i} (t) = \int\limits_{0}^{t} {h_{i} (x)} dx;\,\,\,\,\,\,\,\,Q_{i} (t) = \int\limits_{0}^{t} {p_{i} (x)} dx. $$

(38)

From which one can deduce the following important relations

$$ p_{1} (t) = \left\{ {\begin{array}{*{20}c} {t;\,\,\,for\,0 \le t \prec 1,} \\ {0;\,\,\,\,\,\,elsewhere.} \\ \end{array} } \right.\,\,\,;\,\,\,\,\,Q_{1} (t) = \left\{ {\begin{array}{*{20}c} {\frac{{t^{2} }}{2};\,\,\,for\,0 \le t \prec 1,} \\ {0;\,\,\,\,\,\,elsewhere.} \\ \end{array} } \right. $$

(39)

In general

$$ p_{i} (t) = \left\{ {\begin{array}{*{20}c} {t - \omega_{1} ;\,\,\,for\,t \in [\omega_{1} ,\,\omega_{2} ],} \\ \begin{gathered} \omega_{3} - t;\,\,\,for\,t \in [\,\omega_{2} ,\,\omega_{3} ], \hfill \\ 0;\,\,\,\,\,\,elsewhere. \hfill \\ \end{gathered} \\ \end{array} } \right.\, $$

(40)

$$ Q_{i} (t) = \left\{ {\begin{array}{*{20}c} {\frac{{(t - \omega_{1} )^{2} }}{2};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,for\,t \in [\omega_{1} ,\,\omega_{2} ],} \\ \begin{gathered} \frac{{(\omega_{1} - \omega_{2} )^{2} + (\omega_{2} - \omega_{3} )^{2} - (\omega_{3} - t)^{2} }}{2};\,\,\,for\,t \in [\,\omega_{2} ,\,\omega_{3} ], \hfill \\ \frac{{(\omega_{1} - \omega_{2} )^{2} + (\omega_{2} - \omega_{3} )^{2} }}{2};\,\,\,for\,t \in [\,\,\omega_{3} ,1], \hfill \\ 0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,elsewhere. \hfill \\ \end{gathered} \\ \end{array} } \right. $$

(41)

3.1 Approximation using Haar wavelet functions [39,40,41,42]

To obtain the solution of any differential equation we discretize the equation in Haar functions $h_{i} (t)$ as the following:

First, we will divide the interval $t \in [0,1][0,1]$ into $2M$ parts of equal length $\Delta (t) = \frac{1}{2M}$, then.

we compute the collocation points from

$$ t_{l} = \frac{l - 0.5}{{2M}}.\, $$

(42)

Any function ${\rm E}(t),\,\,t \in [0,1]$ can be written as

$$ {\rm E}(t) = \sum\limits_{i = 1}^{2M} {a_{i} } h_{i} (t) = a_{1} h_{1} (t) + a_{2} h_{2} (t) + ... + a_{2M} h_{2M} (t). $$

(43)

where a_i are the Haar coefficients, which can be determined as, [34]

$$ \int_{0}^{1} {{\rm E}(t)h_{m} } (t)dt = a_{i} \sum\limits_{i = 1}^{2M} {\int_{0}^{1} {h_{i} (t)h_{m} } (t)dt} . $$

From the orthogonally property one can get

$$ \int_{0}^{1} {h_{i} (t)h_{m} } (t)dt = \left\{ \begin{gathered} 2^{ - j} ;\,\,if\,i = m, \hfill \\ 0;\,\,\,\,\,if\,i \ne m. \hfill \\ \end{gathered} \right. \Rightarrow \,\,\,\,\,\,\,\,\left[ {a_{i} = 2^{j} \int_{0}^{1} {\varphi (t)h_{m} (t)dt} } \right]\,. $$

(44)

The discrete form of Eq. (41) at collocation points is

$$ \varphi (t_{l} ) = \sum\limits_{i = 1}^{2M} {a_{i} } h_{i} (t_{l} ) = \sum\limits_{i = 1}^{2M} {a_{i} } H_{il} . $$

(45)

Which can be written in matrix form as $\Lambda = aH$, where $\Lambda$ and $a$ are $2M$ vectors and $H = H_{il} = h_{i} (t_{l} )$ are the coefficients matrix with dimension ($2M\times 2M)$

3.2 HWM corresponding to RBSODM

Computationally it is very useful to introduce the numerical solution corresponding to RBSODM method, so consider Eq. (4) with the same values used in analytical treatment

$$ \begin{gathered} w = \mu = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda = 6\,or\,\lambda = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered} $$

(46)

Equation (4) becomes

$$ 2R^{{\prime}{2}} - 4R^{2} R^{{\prime}{2}} - 2R^{2} + R^{4} + R^{6} = 0. $$

(47)

According to the first solution, Eq. (24), the initial condition is

$$ R(\eta ) = 2\sqrt 2 \tan [2\sqrt 2 (\eta + 1)] \to R(0) = - 0.9159 $$

(48)

From HWM point of view we consider

$$ R^{\prime}(\eta ) = \sum\limits_{i = 1}^{2M} {a_{i} } h_{i} (\eta ) \Rightarrow R(\eta ) = - 0.9159 + \sum\limits_{i = 1}^{2M} {a_{i} } p_{i} (\eta ). $$

(49)

Taking the level of resolution $J = 1 \Rightarrow M = 2^{J} = 2 \Rightarrow 2M = 4 \Rightarrow i = 1 \to 4.$ and satisfying Eq. (47) at the collocation points given in Eq. (42) we obtain

$$ \begin{gathered} 2\left( {\sum\limits_{i = 1}^{4} {a_{i} } h_{i} (\eta_{l} )} \right)^{2} - 4\left( {\left( { - 0.9159 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{2} *\left( {\sum\limits_{i = 1}^{4} {a_{i} } h_{i} (\eta_{l} )} \right)^{2} } \right) \hfill \\ - 3\left( { - 0.9159 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{2} + \left( { - 0.9159 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{4} \hfill \\ + \left( { - 0.9159 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{6} = 0,\,l = 1 \to 4. \hfill \\ \end{gathered} $$

(50)

Substituting by $l = 1 \to 4$ in Eq. (50) we get on a nonlinear system in the unknowns $a_{1} ,a_{2} ,a_{3} ,a_{4} .,$ solving the reduced system we receive the following results:

$$ (1)\,\,\,\,\,a_{1} = - 3.1375,a_{2} = 0.071,a_{3} = 0.0264,a_{4} = 0.079. $$

(51)

$$ (2)\,\,\,\,\,a_{1} = 0,a_{2} = 3.9,a_{3} = a_{4} = 0.058. $$

(52)

$$ (3)\,\,\,\,\,\,\,\,\,\,a_{1} = a_{2} = 0,a_{3} = a_{4} = - 6.7678. $$

(53)

$$ (4)\,\,\,\,\,a_{1} = 0.3615,a_{2} = 40.46,a_{3} = - 2.4,a_{4} = - 3.7. $$

(54)

$$ (5)\,\,\,\,\,a_{1} = 0.528,a_{2} = - 1.368,a_{3} = 0.2956,a_{4} = 14.55\,. $$

(55)

$$ (6)\,\,\,\,\,a_{1} = 4.37,a_{2} = - 0.45,a_{3} = 0.134,a_{4} = 1.7887. $$

(56)

Using the first result, Eq. (51), then the HWM solution corresponding to (24) is

$$ \begin{gathered} R(\eta )_{HWM} = - 0.9159 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta ) = - 0.9159 - 3.1375p_{1} (\eta ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + 0.071p_{2} (\eta ) + 0.0264p_{3} (\eta ) + 0.079p_{4} (\eta ). \hfill \\ \end{gathered} $$

(57)

Which is identical with the analytical solution, Eq. (24); then

$$ u(x,\tau )_{HWM} = \left( \begin{gathered} - 0.9159 - 3.1375p_{1} (x,\tau ) + 0.071p_{2} (x,\tau ) \hfill \\ + 0.0264p_{3} (x,\tau ) + 0.079p_{4} (x,\tau ) \hfill \\ \end{gathered} \right)e^{i(\tau + x + \psi (x,\tau ))} . $$

(58)

$$ \begin{gathered} {\text{Re}} \,\,u(x,\tau )_{HWM} = \left( \begin{gathered} - 0.9159 - 3.1375p_{1} (x,\tau ) + 0.071p_{2} (x,\tau ) \hfill \\ + 0.0264p_{3} (x,\tau ) + 0.079p_{4} (x,\tau ) \hfill \\ \end{gathered} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,*\cos \left( {\tau + x + 5\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)] - 18(6x + \tau )} \right). \hfill \\ \end{gathered} $$

(59)

$$ \begin{gathered} {\text{Im}} \,\,u(x,\tau )_{HWM} = \left( \begin{gathered} - 0.9159 - 3.1375p_{1} (x,\tau ) + 0.071p_{2} (x,\tau ) \hfill \\ + 0.0264p_{3} (x,\tau ) + 0.079p_{4} (x,\tau ) \hfill \\ \end{gathered} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,*\sin \left( {\tau + x + 5\sqrt 2 \tan [2\sqrt 2 (6x + \tau + 1)] - 18(6x + \tau )} \right). \hfill \\ \end{gathered} $$

(60)

By the same procedure for the second RBSODM solution given in Eq. (30):

$$ R(\eta ) = - 2\sqrt 2 \cot [2\sqrt 2 (\eta + 1)] \Rightarrow R(0) = 8.7345. $$

(61)

Using the HWM algorithm with the same level of resolution $J = 1$ then for Eq. (47), we get

$$ \begin{gathered} 2\left( {\sum\limits_{i = 1}^{4} {a_{i} } h_{i} (\eta_{l} )} \right)^{2} - 4\left( {\left( {8.7345 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{2} *\left( {\sum\limits_{i = 1}^{4} {a_{i} } h_{i} (\eta_{l} )} \right)^{2} } \right) \hfill \\ - 3\left( {8.7345 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{2} + \left( {8.7345 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{4} \hfill \\ + \left( {8.7345 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta_{l} )} \right)^{6} = 0,\,l = 1 \to 4. \hfill \\ \end{gathered} $$

(62)

Satisfying Eq. (62) at the values $l = 1 \to 4.$ we access a nonlinear system, by solving this system, we have the coming results

$$ (1)\,\,\,\,\,a_{1} = - 21.8686,a_{2} = - 6.389,a_{3} = - 168.365,a_{4} = - 14.27\,\,. $$

(63)

$$ (2)\,\,\,\,\,a_{1} = - 9.12,a_{2} = - 201.875,a_{3} = - 21,a_{4} = - 20. $$

(64)

$$ (3)\,\,\,\,\,\,\,\,\,\,a_{1} = a_{2} = 0,a_{3} = a_{4} = 11.69. $$

(65)

$$ (4)\,\,\,\,\,a_{1} = 41.77,a_{2} = 22.22,a_{3} = - 14.69,a_{4} = - 16.24. $$

(66)

$$ (5)\,\,\,\,\,a_{1} = 54.8,a_{2} = - 1.16,a_{3} = - 10,a_{4} = - 12.3\,. $$

(67)

$$ (6)\,\,\,\,\,a_{1} = 0,a_{2} = 64,a_{3} = a_{4} = - 11.48. $$

(68)

The HWM solution for the first result, Eq. (63), corresponding to RBSODM, Eq. (30):

$$ \begin{gathered} R(\eta )_{HWM} = 8.7345 + \sum\limits_{i = 1}^{4} {a_{i} } p_{i} (\eta ) = 8.73.45 - 21.8686p_{1} (\eta ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 6.389p_{2} (\eta ) - 168.365p_{3} (\eta ) - 14.27p_{4} (\eta ). \hfill \\ \end{gathered} $$

(69)

So

$$u(x,\tau )_{HWM} = \left( \begin{gathered} 8.73.45 - 21.8686p_{1} (x,\tau )\, - 6.389p_{2} (x,\tau ) \hfill \\ - 168.365p_{3} (x,\tau ) - 14.27p_{4} (x,\tau ) \hfill \\ \end{gathered} \right)e^{i(\tau + x + \psi (x,\tau ))} .$$

(70)

$$ \begin{gathered} {\text{Re}} \,\,u(x,\tau )_{HW} = \left( \begin{gathered} 8.73.45 - 21.8686p_{1} (x,\tau )\, - 6.389p_{2} (x,\tau ) \hfill \\ - 168.365p_{3} (x,\tau ) - 14.27p_{4} (x,\tau ) \hfill \\ \end{gathered} \right)* \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\cos \left( {\tau + x - 18(6x + \tau ) - 5\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]} \right). \hfill \\ \end{gathered} $$

(71)

$$ \begin{gathered} {\text{Im}} \,\,u(x,\tau )_{HW} = \left( \begin{gathered} 8.73.45 - 21.8686p_{1} (x,\tau )\, - 6.389p_{2} (x,\tau ) \hfill \\ - 168.365p_{3} (x,\tau ) - 14.27p_{4} (x,\tau ) \hfill \\ \end{gathered} \right)* \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin \left( {\tau + x - 18(6x + \tau ) - 5\sqrt 2 \cot [2\sqrt 2 (6x + \tau + 1)]} \right). \hfill \\ \end{gathered} $$

(72)

4 Conclusion

In this paper, we successfully applied the RBSODM for the first time as a new basic technique to obtain the soliton solutions as new solitary solutions to the higher order nonlinear Schrödinger equation, containing cubic–quintic–septic nonlinearity, weak nonlocal nonlinearity, self-frequency shift, and self-steepening effect. In same connection, parallel direction we apply the HWM to construct the identical numerical solutions of the obtained soliton solutions to ensure its validity. The 2D, 3D figures simulations for the soliton and numerical solutions have been demonstrated to show the agreements between the soliton and numerical solutions. It is clear that our obtained analytical soliton solutions in shapes as combination bright soliton solution and dark soliton solution, periodic soliton solution, W-like shape soliton solution and other rational solution, Figs. 1, 2, 3, 4, 5, 6, 7, 8, which were not obtained before are new when the comparison is implemented with these obtained by other authors [11]. The performance of attained solutions shows that the applied computational methodology used is brief, concise, and effective, resulting in fewer computations and broad applicability. The inspected wave’s outcomes are trustworthy to the researchers and also have imperious applications in mathematical physics and optical physics.

Fig. 1

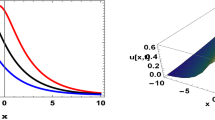
The 2D, 3D soliton behavior of the real part, Eq. (28): $\begin{gathered} w = \mu = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,c = 3,b = 0,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda = 6\,or\,\lambda = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered}$

Fig. 2

The 2D, 3D soliton behavior of the imaginary part, Eq. (29) $\begin{gathered} w = \mu = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,c = 3,b = 0,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda = 6\,or\,\lambda = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered}$

Fig. 3

The 2D, 3D soliton behavior of the real part, Eq. (32) $\begin{gathered} w = \mu_{1} = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,c = 3,b = 0,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{1} = 6or\lambda_{1} = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered}$

Fig. 4

The 2D, 3D soliton behavior of the imaginary part, Eq. (33) $\begin{gathered} w = \mu_{1} = S_{6} = S_{4} = \chi = a = 1,\beta_{2} = 2,S_{2} = - 3,c = 3,b = 0,\varepsilon = 2,\delta = 3, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{1} = 6or\lambda_{1} = - 2,\gamma_{1} = 0.5,\gamma_{2} = 0.7,\gamma_{3} = 0. \hfill \\ \end{gathered}$

Fig. 5

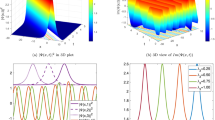
The 2D, 3D soliton behavior using HWM, Eq. (59)

Fig. 6

The 2D, 3D soliton behavior using HWM, Eq. (60)

Fig. 7

The 2D, 3D soliton behavior using HWM, Eq. (71) corresponding to RBSODM (32)

Fig. 8

The 2D, 3D soliton behavior of HWM, Eq. (72) corresponding to RBSODM (33)