Estimation of spectral absorption function range via LII measurements of flame-synthesized TiO₂ nanoparticles

Abstract

The Laser-Induced Incandescence (LII) technique is widely used for the study of soot production in flames. More recently, it has also drawn attention also for the characterization of metal-oxide flame synthesis. To retrieve the particle volume fraction from the LII signal, information on the effective particle temperature and the absorption function $E(m_{\lambda })$ depending on the wavelength are needed. In this study, a new approach is proposed to determine these parameters from LII measurements at a given laser fluence by accounting for the spectral shape of $E(m_{\lambda })$ obtained from the estimated effective particle temperature. The feasibility of the method is first demonstrated on a carbon black nanoparticle aerosol in a non-reactive cold environment. A good agreement with the literature data for $E(m_{\lambda })$ is found. The developed approach is then applied to TiO$_2$ nanoparticles produced by flame synthesis. The obtained spectral response of $E(m_{\lambda })$ is in line with the literature results for TiO$_2$. The proposed approach represents an essential step toward in-situ estimation of particle volume fraction from the LII signal, which can be a valuable tool for further characterization of metal-oxide flame synthesis.

1 Introduction

Flame synthesis is increasingly raising attention as a promising technology for the production of metal oxides with tunable characteristics [1]. To optimize this aerosol technology, it is essential to have access to the spatial evolution of the characteristics of the particle population along the flame, such as the volume fraction $f_v$ or the primary particle size $d_{\text {pp}}$. In this context, the Laser-Induced Incandescence (LII) technique is an in-situ laser diagnostic that is widely used for the study of soot formation in flames [2]. This technique is more and more often applied to the study of metal-oxide flame synthesis [3, 4].

When using LII measurements to characterize nanoparticle production in flames, the volume fraction $f_v$ can be obtained from the LII signal $S_{\text {LII}}{(\lambda _{\text {em}})}$ emitted from particles at emission wavelength $\lambda _{\text {em}}$ as [5]

$$\begin{aligned} f_v = \dfrac{\eta _C {\lambda ^{6}_{\text {em}} } }{ 12 \pi h c^2} \frac{S_{LII}(\lambda _{\text {em}}) }{E( m_{\lambda _{\text {em}}} )} \left[ \exp \left( \dfrac{hc}{\lambda _{\text {em}} k_B T_{\text {eff}} } \right) -1 \right] , \end{aligned}$$

(1)

where $\eta _C$ is a calibration factor related to the optical detection system, h is the Planck constant, c is the speed of light in a vacuum, and $k_B$ is the Boltzmann constant. $E(m_{\lambda })$ is the absorption function of the refractive index $m_{\lambda }$. It describes the ability of a particle to absorb/emit light at the wavelength $\lambda$. $T_{\text {eff}}$ is the effective particle temperature [6], i.e., a mean temperature attained by the particle population in the probe volume during the LII process. From Eq. (1), it is clear that to correctly interpret the LII signal in terms of particle volume fraction, accurate estimations of $E( m_{\lambda _{\text {em}}} )$ and of $T_{\text {eff}}$ are needed.

In this work, we propose a new approach to estimate these two key quantities by accounting for the spectral dependence of the absorption function $E(m_{\lambda })$, i.e., its evolution with the wavelength $\lambda$, when no prior information on $E(m_\lambda )$ is available from the literature or from additional experimental diagnostics. The difficulty stands by the fact that the incandescence signal emitted at wavelength $\lambda _{\text {em}}$ by the particles depends on both $E( m_{\lambda _{\text {em}}} )$ and $T_{\text {eff}}$ [7, 8]. Therefore, it is not possible to obtain information from the LII signal on one of these two key quantities without knowing the other one.

On the one side, the effective temperature obtained via two-color pyrometry as a function of two wavelengths $\lambda$ and $\lambda _{\text {ref}}$ [9]

$$\begin{aligned} T_{\text {eff}}=\frac{hc}{k_B} \left( \frac{1}{\lambda _{\text {ref}}}-\frac{1}{\lambda }\right) \left[ \ln \left( \frac{1}{{\mathcal {E}}(\lambda )}\left( \frac{\lambda }{\lambda _{\text {ref}}}\right) ^6 \frac{I_{\text {SLII}}(\lambda )}{I_{\text {SLII}}(\lambda _\text {ref})}\right) \right] ^{-1} \text { for }\lambda \ne \lambda _{\text {ref}}, \end{aligned}$$

(2)

where $I_{\text {SLII}}(\lambda )$ is the LII emission signal at wavelength $\lambda$ already corrected by the detection efficiency at $\lambda$, and $\lambda _{\text {ref}}$ is a reference wavelength different from $\lambda$. ${\mathcal {E}}(\lambda )$ is the ratio of the absorption function at $\lambda$ and $\lambda _{\text {ref}}$

$$\begin{aligned} {\mathcal {E}}(\lambda )=E(m_{\lambda })/E(m_{\lambda _{\text {ref}}}), \end{aligned}$$

(3)

which signifies the spectral shape of the absorption function.

On the other side, using Eq. (3), the emission value $E(\lambda _{\text {em}})$ can be obtained as

$$\begin{aligned} E( m_{\lambda _{\text {em}}})= \frac{{\mathcal {E}}(\lambda _{\text {em}})}{ {\mathcal {E}}(\lambda _{\text {laser}})} E(m_{\lambda _{\text {laser}}}), \end{aligned}$$

(4)

where $E(m_{\lambda _{\text {laser}}})$ corresponds to the absorption function at the laser excitation wavelength $\lambda _{\text {laser}}$. Once $T_{\text {eff}}$ is known, the value of $E(m_{\lambda _{\text {laser}}})$ can be measured with various approaches based on LII measurements [10, 11].

To close such an underdetermined system, the absorption function $E(m_\lambda )$ is often assumed to be nearly constant in visible spectral range (${\mathcal {E}}(\lambda )\approx 1$) [7]. Thus, the effective temperature can be estimated directly from Eq. (2) once the LII signal is available for 2 wavelengths ($\lambda$, $\lambda _{\text {ref}}$), allowing to determine $E(m_\lambda )$ in a second step [10, 11]. Such an assumption can be reasonable in the visible and near-infrared range when considering mature soot particles [12]. However, evidences in the literature report variable function ${\mathcal {E}}(\lambda ) \ne$ 1 for carbonaceous particles [13,14,15]. When it comes to metal-oxide nanoparticles, different spectral shapes of ${\mathcal {E}}(\lambda )$ and values of $E(m_\lambda )$ can be found in the literature for the same material. In specific, data for TiO$_2$ present a large variability for ${\mathcal {E}}(\lambda )$ and $E(m_\lambda )$, since they depend on the optical properties, which can be determined by the production process [16,17,18,19]. Therefore, disposing of a method allowing for the estimation of $T_{\text {eff}}$ and of $E(m_\lambda )$ by accounting for the spectral shape ${\mathcal {E}}(\lambda )$ is essential to obtain quantitative information on metal-oxide production in flames within the context of LII measurements.

Various approaches can be found in the literature to determine $T_{\text {eff}}$ and $E(m_\lambda )$ from LII signals [13, 20,21,22]. Snelling et al. [13] determined the particle effective temperature via optical pyrometry by assuming that $E(m_\lambda )$ varies linearly with wavelength. Subsequently, simulation results based on the LII model were used to determine the value of $E(m_{\lambda _{\text {laser}}})$ at the laser excitation wavelength. Alternatively, Therssen et al. [21] proposed to employ two laser excitation wavelengths to determine the absorption function ratio between them, i.e., the spectral shape by achieving the same temperature of the particles. Another method, the dual-pulse absorption spectra technique [22], has been recently developed to investigate in-situ optical properties in transient conditions by considering two laser excitation wavelengths.

In line with these previous works, this work proposes a new method to estimate the particle effective temperature $T_{\text {eff}}$ and the absorption function $E(m_\lambda )$ by accounting for its spectral shape ${\mathcal {E}}(\lambda )$. This method only requires the spectral emission information from the LII signal at a given fluence. First, the used experimental setup is described in Sect. 2. Then, the theoretical developments are proposed in Sect. 3. Then, the feasibility of the approach is demonstrated in Sect. 4.1 by considering carbon black nanoparticles in a non-reactive N$_2$ environment, for which an extensive experimental database is available in the literature [12,13,14,15, 23,24,25]. Finally, the approach is used for TiO$_2$ flame synthesis in Sect. 4.2. To the best of the author’s knowledge, the proposed results represent the first time the optical properties of flame-synthesized metal-oxide nanoparticles have been estimated using the LII technique.

2 Experimental setup

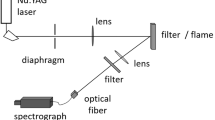
The experimental setup considered in this work is composed of three parts, schematically presented in Fig. 1a: the particle generation, the laser excitation, and the signal collection. The same setup was used in our previous work [26], where the feasibility of LII measurements for high-purity TiO$_2$ nanoparticles was demonstrated. Thus, only a general description of the setup is provided here. More details can be found in [26].

For the laser excitation of the particles, a pulsed Nd:YAG laser (Quantel, Q smart 850) operates at a third harmonic wavelength of 355 nm with a repetition rate of 10 Hz. The choice of the laser wavelength has been optimized to induce an LII signal from TiO$_2$ nanoparticles [26]. The laser fluence is controlled by a laser attenuator (Eksma, 990-0070-355). A rectangular aperture (x = 0.88 mm and z = 0.91 mm) is used to have a nearly top-hat shape laser beam, which is then 1:1 relay-imaged onto the target detection point using a 300 mm focal length lens.

The LII signal of TiO$_2$ particles is collected at a 90$^{\circ }$ angle using a telescope consisting of two lenses with focal lengths of 200 mm and 100 mm, respectively. Two notch filters at wavelengths of 355 nm and 532 nm are employed to suppress the laser harmonic signal. The collected signal is then focused on 365 $\mu m$ multimode optical fiber (Thorlabs, FG365UEC), which is connected to the entrance slit of a spectrometer (Princeton Instrument, Spectra Pro HRS-500, f = 500 mm, 150 grooves/mm) and coupled with an ICCD camera (Princeton Instruments, PI-MAX 4 1024EMB) for spectral measurement at detection wavelength $\lambda _{\text {em}} \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}] = [430, 730]$ nm. The emission signal is collected with a gate width of 20 ns. The signal is then calibrated using a tungsten lamp for intensity and a mercury lamp for wavelength.

Fig. 1

a Schematic presentation of the experimental setup developed to investigate laser-induced emission at the target detection volume, where particles are dispersed or generated, using a pulse YAG laser at 355 nm. Illustration of the two considered particle generators: b dispersion of carbon black nanoparticles in a non-reactive environment at ambient temperature, and c synthesis of TiO$_2$ nanoparticles in a hydrogen–argon laminar diffusion flame

In this study, two different systems are employed for particle dispersion or production. First, carbon black nanoparticles are studied in a non-reactive environment at ambient temperature to verify the feasibility of the approach under well-controlled conditions for particles whose properties are widely characterized in the literature [12,13,14,15, 23]. The aerosol is obtained by dispersing 200 mg of carbon black nanoparticles (nanografi, NG04EO0709, $d_{\text {pp}}$ = 20 nm, spherical) at each measurement using ultrasonication with the aid of nitrogen (16.67 slm, 9.8 m/s) inside a 1 L flask. After passing through an additional 1 L flask for homogenous mixing, the solid–gas aerosol is sent into an optical cell with two 1-inch windows (UVFS, Thorlabs WG41010) allowing the laser beam to pass through and heat the nanoparticles, as shown in Fig. 1b. Detection of the emitted radiation is performed through a 2-inch window (UVFS, Thorlabs WG42012).

Once validated, the approach will be used in the application of interest in this work, i.e., the characterization of TiO$_2$ nanoparticles during flame synthesis. For the study of flame-generated TiO$_2$, a Yale diffusion burner [27] has been modified to allow the injection of pre-vaporized metal precursors. The burner is fed with a mixture of H$_2$ (${\dot{m}}_{\hbox { H}\ _2}$ = 5.1 g/h), Ar (${\dot{m}}_{\text {Ar}}$ = 2.3 g/h), and pre-vaporized titanium tetraisopropoxide (TTIP, Sigma-Aldrich, 97% purity, ${\dot{m}}_{\text {TTIP}}$ = 0.5 g/h). The precursor is injected using a Coriolis flowmeter (Bronkhorst, MINI CORI-FLOW, ML120V21-BAD-11-0-S) and is vaporized with a custom-made heating system before mixing with H$_2$ and Ar. All the lines are heated over 350 K to prevent condensation of the precursor. At the exit of the burner, the temperature measured with a thermocouple is 380K for the fuel injection, and 412 K for the coflow of air (${\dot{m}}_{\text {air}}$=7759 g/h). A diffusion flame visualized in Fig. 1c is obtained. The reaction zone due to H$_2$ combustion is located at a height above the burner HAB < 30 mm, as visualized by the surrounding semi-transparent blue emission. In the central zone, a very strong emission indicates the presence of TiO$_2$ nanoparticles starting from HAB > 10 mm. The visible nanoparticle trail is observed until HAB $\sim$ 80 mm. In this work, all measurements are conducted at HAB = 60 mm on the centerline, far from the the white glowing part, where the highest temperature is expected to be observed. At HAB = 60 mm, the temperature is expected to be lower than the TiO$_2$ melting temperature ($T_{\text {melting}} \approx$ 2150 K [28]), so that particles are assumed to be in the solid state prior to LII measurements.

3 Methodology

The LII signal obtained using the experimental setup described in the previous section will be postprocessed to obtain information on $T_{\text {eff}}$ and $E(m_\lambda )$ while accounting for the spectral shape ${\mathcal {E}}(\lambda )$. For this, a theoretical methodology composed of four steps is proposed in this work:

• 1. A range of possible values of the particle effective temperature $T_{\text {eff}}$ is estimated by considering the spectral LII signal.

• 2. The spectral shape ${\mathcal {E}}(\lambda )$ is derived from $T_\text {eff}$ estimation.

• 3. The value of the ${E}(m_{\lambda _\text {laser}})$ at laser wavelength has to be known. If not available from the literature, ${E}(m_{\lambda _\text {laser}})$ can be estimated from $T_{\text {eff}}$ choosing among established methods at low fluences [10, 11, 29].

• 4. The value of $E(m_{\lambda })$ is estimated over the whole wavelength $\lambda$ range using information on ${\mathcal {E}}(\lambda )$ and ${E}(\lambda _{\text {laser}})$.

Each of these steps is detailed in the following.

Estimation of the particle effective temperature To estimate the effective temperature of particles using the two-color pyrometry technique via Eq. (2), it is necessary to know the ratio of ${E}(m_\lambda )$ at the two wavelengths of interest. If this ratio is unknown, the spectral shape ${\mathcal {E}}(\lambda )$ has to be presumed. Typically for soot particles, the absorption function $E(m_\lambda )$ can be assumed spectrally constant, i.e., ${\mathcal {E}}(\lambda )=1$, allowing the estimation of effective particle temperature from Eq. (5) for two different wavelengths $\lambda _{\text {em}_1}$, $\lambda _{\text {em}_2}$

$$\begin{aligned} T_{\text {eff}} \approx T_{\text {eff}}^{\text {const}} =\frac{hc}{k_B} \left( \frac{1}{\lambda _{\text {em}_2}}-\frac{1}{\lambda _{\text {em}_1}}\right) \left[ \ln \left( \left( \frac{\lambda _{\text {em}_1}}{\lambda _{\text {em}_2}}\right) ^6 \frac{I_{\text {SLII}}(\lambda _{\text {em}_1}) }{I_{\text {SLII}}(\lambda _{\text {em}_2})} \right) \right] ^{-1}. \end{aligned}$$

(5)

As described in the study of Liu et al. [30], the $T_{\text {eff}}^{\text {const}}$, inferred effective temperature depends on the selection of the two emission wavelengths $\lambda _{\text {em}_1}$ and $\lambda _{\text {em}_2}$ due to errors such as uncertainty of the ratio of the absorption functions at the two detection (emission) wavelengths or signal shot noises. Therefore, properly choosing the emission wavelengths $\lambda _{\text {em}_1}$ and $\lambda _{\text {em}_2}$ is important when estimating the particle temperature from Eq. (5). In specific, Liu et al. [30] suggest avoiding close wavelengths, since the ratio of the corresponding LII signals may be strongly affected by shot noises.

Alternately, Snelling et al. [13] proposed to consider that the $E(m_\lambda )$ of soot particles is linearly proportional to the wavelength $\lambda$, based on the experimental evidence of [25, 31]. This assumption is not general and is not expected to be verified for other kinds of particles. As an example, Table 1 presents the ratio of the absorption function at two distinct wavelengths, $E(m_{\text {550nm}})/ E(m_{\text {710nm}})$, for both carbonaceous and TiO$_2$ nanoparticles. For carbonaceous particles, $E(m_{\lambda })$ maintains a constant value across the specified wavelength range [550, 710 nm]. In contrast, TiO$_2$ exhibits a more pronounced spectral variation of $E(m_\lambda )$ of $\lambda$, which largely varies in the literature database.

Table 1 $E(m_{\text {550nm}})/ E(m_{\text {710nm}})$ value for carbonaceous and TiO$_2$ particles in the literature

Therefore, a more general procedure to estimate the evolution of ${\mathcal {E}}(\lambda )$ as a function of $\lambda$ has to be found, such as the one proposed by [22]. For this, the function $E(m_{\lambda _{\text {0}}+\Delta \lambda })$ at a given wavelength $\lambda _0+\Delta \lambda$ can be expanded using the Taylor series

$$\begin{aligned} E(m_{\lambda _{\text {0}}+\Delta \lambda }) = E(m_{\lambda _{\text {0}}}) + \dfrac{ \partial E(m_\lambda )}{\partial \lambda } {\vert _{\lambda _{0}} } \Delta \lambda + {\mathcal {O}}(\Delta \lambda ^2). \end{aligned}$$

(6)

At zeroth order, we propose to assume that $E(m_{\lambda })$ is constant over a sufficiently small range of wavelength $\Delta \lambda$, so that $E(m_{\lambda _{\text {0}}+\Delta \lambda })$ reads as

$$\begin{aligned} E(m_{\lambda _{\text {0}}+\Delta \lambda })\approx E(m_{\lambda _{\text {0}}}). \end{aligned}$$

(7)

This condition is less restrictive than assuming a constant $E(m_\lambda )$ for the overall spectral range and is verified for $\Delta \lambda \rightarrow 0$. By combining Eqs. (2) and (7), the effective temperature $T_{\text {eff}}^{\lambda _0}$ for a given $\lambda _0$ can then be estimated from

$$\begin{aligned} T_{\text {eff}}^{\lambda _0} = \frac{hc}{k_B} \left( \frac{1}{\lambda _0+\Delta \lambda }- \frac{1}{\lambda _0}\right) \left[ 6\text {ln}\left( \frac{\lambda _0}{\lambda _0+\Delta \lambda }\right) + \text {ln} \left( \frac{I_{\text {SLII}}(\lambda _0)}{I_{\text {SLII}}(\lambda _0+\Delta \lambda )}\right) \right] ^{-1}. \end{aligned}$$

(8)

The accuracy of the estimated temperature $T_{\text {eff}}^{\lambda _0}$ through Eq. (8) will depend on the validity of Eq. (7), i.e., how realistic is the assumption $E(m_{\lambda _{\text {0}}+\Delta \lambda })\approx E(m_{\lambda _{\text {0}}})$. As deduced for Eq. (6), this will depend on $\dfrac{ \partial E(m_\lambda )}{\partial \lambda } {\vert _{\lambda _{0}} }$ and $\Delta \lambda$ values. The smaller these quantities are, the more valid this assumption will be. Thus, the estimated $T_{\text {eff}}^{\lambda _0}$ may depend on $\lambda _0$ and $\Delta \lambda$ values. Concerning $\lambda _0$, it is not possible to know a priori which $\lambda _0$ value leads to a minimum $\dfrac{ \partial E(m_\lambda )}{\partial \lambda } {\vert _{\lambda _{0}} }$ when no information on $E(m_{\lambda })$ shape is available. Thus, $T_{\text {eff}}^{\lambda _0}$ will be calculated over a range of $\lambda _0 \in [\lambda _0^{\text {min}},\lambda _0^{\text {max}}]$. The minimum and maximum values of $T_{\text {eff}}^{\lambda _0}$, namely $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$, will then provide the range of possible effective temperatures

$$\begin{aligned} T_{\text {eff}} \in [T_{\text {eff}}^{\text {min}},T_{\text {eff}}^{\text {max}}]. \end{aligned}$$

(9)

Concerning $\Delta \lambda$, small values should be considered to reduce the effect of assumption $E(m_{\lambda _{\text {0}}+\Delta \lambda })\approx E(m_{\lambda _{\text {0}}})$ as seen in Eq. (6). Still, as already mentioned, Liu et al. [30] have extensively discussed the need for widely separated wavelengths, i.e., large $\Delta \lambda$, to reduce the effect of signal noise on temperature estimation. Thus, a trade-off $\Delta \lambda$ value should be considered to minimize errors due to the assumption of Eq. (7) and signal noise. Here, $\Delta \lambda =$ 5 nm is retained.

A spectral range smaller than the measured emission spectrum is considered for $\lambda _0 \in [\lambda _{0}^{\text {min}},\lambda _{0}^{\text {max}}]= [550, 710]$ nm $\subset [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]=[430, 730]$ nm. This choice is motivated by the fact that the LII nature of the signal is the most evident in this range of detection wavelengths for TiO$_2$ nanoparticles, since LIF emission from TiO$_2$ may be observed in the range of 450–550 nm [26, 33, 34].

To conclude, the proposed approach does not provide a single value of $E(m_{\lambda })$ but a range of possible values. Still, this approach allows accounting for the uncertainties in the estimation of $T_{\text {eff}}$, which are hidden when using the classical pyrometric estimation $T_{\text {eff}}^{\text {const}}$, i.e., by assuming a constant $E(m_{\lambda })$. The extreme values $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ will depend on the values retained for $\lambda _0^{\text {min}}$, $\lambda _0^{\text {max}}$, and $\Delta \lambda$ as well as the postprocessing procedure used to obtain $I_{\text {SLII}}(\lambda _0)$ and $I_{\text {SLII}}(\lambda _0+\Delta \lambda )$ from the spectral emission, which can be affected by experimental uncertainties. This is discussed in detail in Appendix A.

Estimation of spectral shape ${\mathcal {E}}(\lambda )$ Once the range of possible $T_{\text {eff}}$ is known, the possible shapes of ${\mathcal {E}}(\lambda )$ are obtained from Eq. (2) over the spectral range considered at emission by considering the minimum and maximum effective temperatures, i.e., $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ via

$$\begin{aligned} {\mathcal {E}}(\lambda )=\text {exp}\left( \text {ln}\left( \frac{I_{\text {SLII}}(\lambda )}{I_{\text {SLII}}(\lambda _{\text {ref}})}\right) + 6\text {ln}\left( \frac{\lambda }{\lambda _{\text {ref}}}\right) +\frac{ \frac{hc}{k_B} \left( \frac{1}{\lambda }-\frac{1}{\lambda _{\text {ref}}}\right) }{T_{\text {eff}}}\right) \text {for } \lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}] \end{aligned}$$

(10)

with $\lambda _{\text {ref}} =$ 650 nm in this study.

Estimation of $E(m_{\lambda _\text {laser}})$ Once the spectral shape ${\mathcal {E}}(\lambda )$ is known, the value of $E(m_{\lambda _\text {laser}})$ at the laser excitation wavelength should be estimated to obtain $E(m_\lambda )$. Various results for $E(m_\lambda )$ at $\lambda =355$ nm, i.e., the laser wavelength used in this work, can be found in the literature for both carbonaceous and TiO$_2$, as summarized in Tables 2 and 3, respectively. A factor of 2 is observed for the carbonaceous particles regarding the value reported in Table 2. On the contrary, a higher variability is observed for the TiO$_2$ nanoparticles of almost one order of magnitude. This is most probably due to the fact that the optical properties of TiO$_2$ nanoparticles are strongly governed by the intrinsic characteristics of the particles, such as the crystallinity phase and surface defects, which may depend on the process used for their production [16]. Due to the large dispersion of the $E(m_{\lambda _\text {laser}})$ data for TiO$_2$, in this work, we would rather measure it with a very simple, yet widely used and well-established method for estimating $E(m_{\lambda _\text {laser}})$ at low laser fluences [10, 11].

Table 2 $E(m_{\text {355nm}})$ and $E(m_{\text {450nm}})/ E(m_{\text {355nm}})$ value for carbonaceous particles in the literature

Table 3 Absorption function value at 355 nm for TiO$_2$ particles in the literature

It consists in working at a fluence (F) low enough to avoid phase change (vaporization and/or sublimation), where a linear relationship between laser fluence and temperature can be found [36]. If thermal losses due to radiation and conduction are negligible at prompt and under Rayleigh approximation, the $E(m_{\lambda _\text {laser}})$ can be estimated as

$$\begin{aligned} E(m_{\lambda _{\text {laser}}})=\rho c_p \frac{\lambda _{\text {laser}}}{6\pi }\frac{T_{\text {eff}}-T_{\text {gas}}}{F}, \end{aligned}$$

(11)

where $\rho$ is the density of particles, $c_p$ is the heat capacity of particles, $T_{\text {gas}}$ is ambient gas temperature, and F is laser fluence. In this work, $E(m_{\lambda _{\text {laser}}})$ is evaluated considering three values for the effective particle temperatures, i.e., $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$, and $T_{\text {eff}}^{\text {const}}$, which have been estimated at step 1. The other parameters are summarized in Table 4. The validation of this method for $E(m_{\lambda _{\text {laser}}})$ estimation is out of the scope of this paper. The validity of the assumptions used for this method can be found in [36].

Table 4 Parameters used to calculate $E(m_{\lambda _{\text {laser}}})$ from Eq. (11)

Estimation of $E(m_{\lambda })$ Once the possible values of $T_{\text {eff}}$ are known together with the corresponding ${\mathcal {E}}(\lambda )$ and $E(m_{\lambda _{\text {laser}}})$, the absorption function $E(m_{\lambda })$ over the measured spectral range can be obtained using Eq.(4) for $\lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$. If the laser excitation wavelength $\lambda _{\text {laser}}$ is included in the acquired spectral emission range, i.e., $\lambda _{\text {laser}} \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {min}}]$, ${\mathcal {E}}({\lambda _{\text {laser}}})$ is known, so that the estimation of $E(m_{\lambda _{\text {em}}})$ via Eq. (4) is quite straightforward. However, in this work, a more challenging scenario is considered where the laser excitation wavelength $\lambda _{\text {laser}}$ does not belong to the acquired spectral range, $\lambda _{\text {laser}} \notin [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$. Consequently, the ${\mathcal {E}}({\lambda _{\text {laser}}})$ is not known. In this case, to calculate $E(m_{\lambda _{\text {}}})$ in the range $\lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$, Eq. (4) could be rewritten with a specific wavelength $\lambda ^* \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$ as

$$\begin{aligned} \begin{aligned} E(m_{\lambda _{\text {}}})&= \frac{ E( m_{\lambda _{\text {}}})}{ E(m_{\lambda _{\text {ref}} }) } \frac{ E( m_{\lambda _{\text {ref}} } ) }{ E(m_{\lambda ^{*}) }} \frac{ E(m_{\lambda ^*}) }{ E(m_{ \lambda _{\text {laser}} }) } E(m_{\lambda _{\text {laser}}}) \\&= \frac{{\mathcal {E}}({\lambda _{\text {}})}}{{\mathcal {E}}({\lambda ^*})} \frac{ E(m_{\lambda ^*}) }{ E( m_{\lambda _{\text {laser}}} ) } E(m_{\lambda _{\text {laser}}}), \end{aligned} \end{aligned}$$

(12)

where $\lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$. The ratio $E(m_{\lambda ^*})/ E(m_{ \lambda _{\text {laser}}}) = {\mathcal {E}}({\lambda ^*})/ {\mathcal {E}}({ \lambda _{\text {laser}}})$ could be inferred, for example, by extrapolating ${\mathcal {E}}({\lambda _{\text {}}^{\text {}}})$ at wavelength $\lambda _{\text {}}^{\text {*}}$

$$\begin{aligned} {\mathcal {E}}({\lambda _{\text {laser}}}) = {\mathcal {E}}({\lambda _{\text {}}^{\text {*}}}) + {\mathcal {K}}_{\lambda _{\text {laser}}}(\lambda _{\text {laser}} -\lambda _{\text {}}^{\text {*}}), \end{aligned}$$

(13)

where ${\mathcal {K}}_{\lambda _{\text {laser}}}$ can be obtained using a linear regression. Then, $E( m_{\lambda _{\text {}}})$ can be calculated from Eq. (12). To minimize the effect of the presumed shape, $\lambda ^*$ should be chosen as close as possible to $\lambda _{\text {laser}}$. In this work, $\lambda ^*$ = 450 nm is chosen for $\lambda _{\text {laser}}=355$ nm. The experimental data of the ratio $E(m_{\lambda ^*})/ E(m_{\lambda _{\text {laser}}})$ for carbonaceous and TiO$_2$ nanoparticles are reported in Tables 2 and 3, respectively. Concerning carbonaceous particles, a small variation between $E(m_{\text {355nm}})$ and $E(m_{\text {450nm}})$ is observed for reported measurements. On the contrary, the ratio $E(m_{\text {450nm}})/ E(m_{\lambda _{\text {355nm}}})$ for TiO$_2$ nanoparticles largely varies with the database going from 0.0004 up to 0.74. Such variability justifies the development of in-situ measurements for the characterization of $E(m_\lambda )$ directly into the flame by accounting for its spectral evolution, since its evolution seems to strongly vary according to the particle production process. To avoid arbitrarily choosing the values between the ones available in the literature, the ratio via Eq. (13) is inferred in this work, where ${\mathcal {K}}_{\lambda _{\text {laser}}}$ is obtained by performing a linear regression using information from ${\mathcal {E}}(\lambda )$ over the range 430–470 nm. Since ${\mathcal {E}}(\lambda )$ will depend on the effective temperature, three values of ${\mathcal {E}}({\lambda _{\text {}}^{\text {*}}})$ will be obtained by considering $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$, and $T_{\text {eff}}^{\text {const}}$. Once the ratio is obtained, $E(m_\lambda )$ is finally provided using Eq.(12).

In the following, the described 4-step methodology will be applied to two different kinds of particles: carbon black and flame-synthesized nanoparticles.

4 Results

In this section, the procedure will be first applied on carbon black particles, whose absorption function is well characterized in the literature and presents a low variability depending on the experimental database (Table 2). Once validated, the approach will be applied to flame-synthesized TiO$_2$ particles whose absorption function is expected to strongly depend on the used production process.

To perform the proposed methodology, only one laser fluence is needed. However, various laser fluences have been tested to verify the LII-like nature of the emitted signal. The corresponding results are presented in Supplementary Materials. The retained fluence represents the best compromise to obtain an LII signal with a good S/N ratio while avoiding particle sublimation, i.e., F=0.06 J/cm$^2$ for carbon black and F=0.15 J/cm$^2$ for TiO$_2$.

4.1 Carbon black

The developed approach requires the collection of the emitted signal only at prompt, i.e., at the peak of the signal. However, the signal has been collected by considering various detection gate delays to investigate the effect of a delayed acquisition on results. Spectral dependence results at F=0.06 J/cm$^2$ and three acquisition delay times (0, 60, 100 ns) from the signal peak are considered. The corresponding signals are available in the Supplementary materials.

4.1.1 Particle effective temperature

Figure 2 presents the evolution of the three effective temperatures ($T_{\text {eff}}^{\text {max}}$,$T_{\text {eff}}^{\text {min}}$, and $T_{\text {eff}}^{\text {const}}$) as a function of time. It can be noticed that the $T_{\text {eff}}^{\text {const}}$, corresponding to assumption ${\mathcal {E}}(\lambda )$ = 1, is always included in the range of possible effective temperatures identified by the gray zone. A variability of approximately ±15% on the effective temperature is obtained compared to the $T_{\text {eff}}^{\text {const}}$ value. The temperatures obtained at the prompt ($\approx$ 3300–3800 K) are in line with the literature results for the effective temperature of carbonaceous particles during the LII process [37, 38]. Additionally, the consistency of the first step of the developed methodology is demonstrated by the observed particle cooling over time in Fig. 2. This indicates that the method can be used to estimate the effective temperature of particles when there is no information available about the spectral dependence of $E(m_\lambda )$, without assuming a constant value of $E(m_\lambda )$ across the entire range of wavelengths of interest.

Fig. 2

Evolution of the range of possible effective temperatures $T_{\text {eff}}$ over time for carbon black nanoparticles. The gray zone represents the range between $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$. The evolution of $T_{\text {eff}}^{\text {const}}$ is also shown. The results were obtained using LII spectral emission data between 550 and 710 nm for three acquisition delay times (0, 60, 100 ns) for F=0.06 J/cm$^2$. Note that the melting point of carbon black is around 3823 K [39] and the boiling point is around 4473 K [39]

4.1.2 Spectral shape ${\mathcal {E}}(\lambda )$

The evolution of ${\mathcal {E}}(\lambda )$ is derived for carbon black from Eq. (10) once $T_{\text {eff}}$ is known. The spectral dependence ${\mathcal {E}}(\lambda )$ is illustrated in Fig. 3 as a function of $\lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$. The colored zone represents the possible shape of ${\mathcal {E}}(\lambda )$. It corresponds to the temperatures between $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ calculated at the previous step (the values are indicated inside the legend). It can be observed that the obtained areas look alike for the three acquisition delay times (0, 60, 100 ns), proving the robustness of the proposed technique. Results for $T_{\text {eff}}^{\text {const}}$ are not reported in Fig. 3, since their derivation classically relies on the assumption ${\mathcal {E}}(\lambda )=1$. Note that even though we have assumed that the $E(m_\lambda )$ is constant for a small $\Delta \lambda$, the spectral form of $E(m_\lambda )$ is not constant for the entire range of the wavelength spectrum. As expected, this assumption is less restrictive than imposing a constant $E(m_\lambda )$ for all visible ranges once the emission level with enough S/N ratio is assured.

The evolution of $E(m_\lambda )$ as a function of $\lambda$ from results at prompt is compared with literature data in Fig. 4, where ${\mathcal {E}}(\lambda ) \ne$ 1 is assumed. The estimated spectral shape ${\mathcal {E}}(\lambda )$ obtained based on the estimated $T_{\text {eff}}$ at prompt cover the variabilities found in the literature, exhibiting both increasing and decreasing tendencies across the whole spectral range. Thus, the estimated range of the evolution of $E(m_\lambda )$ as a function of $\lambda$ is quite reasonable, confirming the feasibility of this technique.

Fig. 3

Spectral shape ${\mathcal {E}}(\lambda )$ for carbon black nanoparticles. The results are obtained using LII spectral emission at $F=$0.06 J/cm$^2$ at three different acquisition delay times (0, 60, and 100 ns) with $\lambda _{\text {ref}}$=650 nm. The legend shows the retained values of $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ used to estimate ${\mathcal {E}}(\lambda )$

Fig. 4

Spectral evolution of $E(m_\lambda )$ normalized at 650 nm. Results at prompt with F= 0.06 J/cm$^2$ are compared with literature data of carbonaceous nanoparticles [13,14,15, 24, 25, 32]

4.1.3 Estimation of ${E}(m_{\lambda _{\text {laser}}})$

Once the range of possible $T_{\text {eff}}$ is known, the absorption function $E(m_{\lambda _{\text {laser}}})$ at the excitation wavelength can be estimated by considering the experimental data at prompt. $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {const}}$ are considered to calculate three values of $E(m_{{\text {355nm}}})$ using Eq. (11). Results are reported in Table 5. The obtained values belong to the range of the experimental data in the literature reported in Table 2 (comprised between approximately 0.2 and 0.4) and are in quite good agreement with the experimental data of Yon et al. [15] (${E}(m_{\lambda _{\text {laser}})}$= 0.4094 ). A variation of approximately 15% in $E(m_{\lambda _{\text {laser}}})$ is observed over the range of possible effective temperatures. Such uncertainty, due to the use of a range of possible effective temperatures, will directly affect the estimation of the volume fraction $f_v$ via Eq. (1), but it is of the same order of magnitude as the uncertainties classically associated with $f_v$ measurements [40].

Table 5 Effective temperatures, $E(m_{\text {355nm}})$, and $E(m_{\text {450nm}})/E(m_{\text {355nm}})$ for carbon black nanoparticles

4.1.4 Estimation of $E(m_\lambda )$

To obtain an estimation of $E(m_\lambda )$ from ${\mathcal {E}}(\lambda )$ and $E(m_{\lambda _{\text {laser}}})$, it is necessary to estimate the ratio $E(m_{\text {450nm}})/E(m_{\text {355nm}})$, since the laser excitation wavelength does not belong to the spectral range measured by our experimental setup. Thus, a linear regression of ${\mathcal {E}}(\lambda )$ is performed to extrapolate ${\mathcal {E}}(\text {450nm})/{\mathcal {E}}(\text {355nm})=E(m_{\text {450nm}})/E(m_{\text {355nm}})$ using $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {const}}$ (cfr Eq. (13)). The obtained ratios are reported in Table 5. A maximum variability of 22% is observed among the three values. The obtained ratios recover the experimental data by Yon et al. [15], i.e., 0.8703, and are in line with the literature values reported in Table 2 (comprised between 0.87 and 1.04).

By combining this information with the spectral dependence ${\mathcal {E}}(\lambda )$, the range of possible $E(m_\lambda )$ values can be calculated. The estimated $E(m_\lambda )$ is compared with the values found in the literature for soot particles [13,14,15, 23, 25, 32] in Fig. 5. However, it should be mentioned that the carbon black has been bought from a nanoparticles provider (nanografi, https://nanografi.com/). Therefore, the particles employed in our experiments are not necessarily identical to those corresponding to the literature results at Table 1 as these could encompass a variety of compositions and may even undergo modifications due to various external factors, such as oxidation [2]. The range of $E(m_\lambda )$ covers the variability of the data in the literature quite well, including both constant and wavelength-dependent cases under various experimental conditions for soot particle generation. It can be concluded that the developed methodology allows obtaining a quite reasonable estimation of the spectral evolution of $E(m_\lambda )$ and of the effective particle temperature, accompanied by information on uncertainties of a maximum of a factor of 2.5 for carbonaceous nanoparticles.

In the following, the methodology is applied for the characterization of flame-synthesized TiO$_2$.

Fig. 5

$E(m_{\lambda })$ for carbon black nanoparticles obtained by LII signals at $F=$0.06 J/cm$^2$ at prompt. The results are compared to literature data of carbonaceous nanoparticles [13,14,15, 23, 25, 32]

4.2 Flame-synthesized TiO$_2$

Spectral dependence results at F = 0.15 J/cm$^2$ and three acquisition delay times from the peak signal (0, 50, 100 ns) are considered to investigate TiO$_2$ nanoparticles in flames.

4.2.1 Particle effective temperature

Figure 6 displays the temporal evolution of the three effective temperatures ($T_{\text {eff}}^{\text {max}}$, $T_{\text {eff}}^{\text {min}}$, and $T_{\text {eff}}^{\text {const}}$) for TiO$_2$ nanoparticles. The effective temperature shows a variation of approximately ± 13% relative to the $T_{\text {eff}}^{\text {const}}$ value. The obtained effective temperature values range from around 3000 K to 3400 K, which are relatively lower compared to those of carbon black nanoparticles (Fig. 2) even if a higher laser fluence is used. This can be attributed to the smaller absorption coefficient of TiO$_2$ nanoparticles, resulting in a lower absorption of laser fluence and subsequently lower peak temperature. As in the case of carbon black, the particle cooling is observed over time in Fig. 6. One can notice that $T_{\text {eff}}^{\text {min}}$ is higher than TiO$_2$ melting point $T_{\text {melting}}$ = 2150 K [28]. Thus, it is unknown if the TiO$_2$ particles are in a solid state during the laser heating and the subsequent particle cooling process. A deeper characterization of the TiO$_2$ particle state during the LII process is out of the scope of this work, and solid particles will be considered in LII signal interpretation in the following.

Fig. 6

Evolution of the range of possible effective temperatures ($T_{\text {eff}}$) over time for flame-synthesized TiO$_2$. The gray zone represents the range between $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$. The evolution of $T_{\text {eff}}^{\text {const}}$ is also shown. The results were obtained using LII spectral emission between 550 and 710 nm for F = 0.15 J/cm$^2$, and three acquisition delay times (0, 50, 100 ns). Note that the melting point of TiO$_2$ is around 2150 K [28] and the boiling point is around 2773–3273 K [41]

4.2.2 Spectral shape ${\mathcal {E}}(\lambda )$

The evolution of ${\mathcal {E}}(\lambda )$ is investigated for TiO$_2$ generated by flames, utilizing Eq. (10) once $T_{\text {eff}}$ is obtained. By acquiring spectral emission data at three different times (0, 50, and 100 ns), the evolution of ${\mathcal {E}}(\lambda )$ for $\lambda \in [\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {max}}]$ is depicted in Fig. 7, where the colored zone represents the range of ${\mathcal {E}}(\lambda )$ for temperatures between $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ (indicated in the legend). The results show similar estimated areas for the three acquisition delay times, even if results obtained with a 100 ns delay display a larger estimated region. This is most probably due to a low S/N ratio of the LII signal. Nonetheless, the same zone is overlaid over time, demonstrating the robustness of the methodology. A more significant variation in the dynamics of ${\mathcal {E}}(\lambda )$ in the visible spectral range is observed in Fig. 7 for flame-generated TiO$_2$ compared to the carbon black case in Fig. 3. This finding highlights the effectiveness of this methodology in capturing variable ${\mathcal {E}}(\lambda )$ functions, such as for TiO$_2$ nanoparticles in the visible range.

The estimation of ${E}(m_{\lambda _{\text {}}})$ as a function of $\lambda$ is compared in Fig. 8 to the literature results. Here, data have been normalized at $\lambda _{\text {ref}}$= 450 nm, since results from De Iuliis et al. [35] are not available for $\lambda$ =650 nm. The estimated range of possible spectral shape of $E(m_\lambda )$ is included between the literature data, illustrating the capability of the technique to obtain information on the spectral evolution of $E(m_\lambda )$ for metal oxides.

Fig. 7

Spectral shape ${\mathcal {E}}(\lambda )$ for flame-generated TiO$_2$ nanoparticles. The results were obtained using LII spectral emission at laser fluence $F=$0.15 J/cm$^2$ and three different acquisition delay times at 0, 50, and 100 ns. The legend shows the values of $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ used to estimate ${\mathcal {E}}(\lambda )$

Fig. 8

Spectral evolution of $E(m_\lambda )$ normalized at 450 nm. Results at prompt with F= 0.15 J/cm$^2$ are compared with literature data of TiO$_2$ nanoparticles [19, 35]

Fig. 9

$E(m_\lambda )$ for flame-synthesized TiO$_2$ nanoparticles obtained by LII signals at $F=$0.15 J/cm$^2$ at prompt. The results are compared to literature data of solid TiO$_2$ nanoparticles/films [16, 19, 35]

4.2.3 Estimation of ${E}(\lambda _{\text {laser}})$

Based on the determined possible range of effective temperatures $T_{\text {eff}}$, the absorption function ${E}(m_{\lambda _{\text {laser}}})$ at the excitation wavelength can be estimated using experimental data obtained at prompt. Three values of ${E}(m_{\lambda _{\text {laser}}})$ are then computed for $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$, and $T_{\text {eff}}^{\text {const}}$ utilizing Eq.(11). They are presented in Table 6. It is worth noting that these values are in line with results from De Iuliis et al. [35] (${E}(m_{\lambda _{\text {laser=355nm}}})$=0.066). These ${E}(m_{\lambda _{\text {laser}}})$ data are generally higher than the other results from the literature resumed in Table 3 and comprised between 0.002 and 0.015. Still, results from De Iuliis et al. [35] are only available for TiO$_2$ particles produced by flame synthesis as in our case. The estimation of ${E}(m_{\lambda _{\text {laser}}})$ varies by roughly 15% over the range of possible effective temperatures $T_{\text {eff}}$. This level of uncertainty is acceptable when compared to the much higher variability observed in the literature-reported values. The values obtained for TiO$_2$ nanoparticles, ranging from 0.06$-$0.08, are considerably lower than those obtained for carbon black nanoparticles. Supplementary materials provide additional validation of the calculated ${E}(m_{\lambda _{\text {laser}}})$ values. Overall, the obtained values can be considered as acceptable.

Table 6 Effective temperatures, $E(m_{\text {355nm}})$, and $E(m_{\text {450nm}})/E(m_{\text {355nm}})$ for flame-generated TiO$_2$ nanoparticles

4.2.4 Estimation of $E(m_\lambda )$

To estimate $E(m_\lambda )$ from ${\mathcal {E}}(\lambda )$ and $E(m_{\lambda _{\text {laser}}})$, the ratio $E(m_{\text {450nm}})/E(m_{\text {355nm}})$ is calculated using a linear regression of ${\mathcal {E}}(\lambda )$ to extrapolate $E(m_{\text {450nm}})/E(m_{\text {355nm}})$ for $T_{\text {eff}}^{\text {min}}$, $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {const}}$ (Eq. (13)). The obtained ratios are reported on the right column of Table 6. A maximum variability of 15% is observed among the three values. The obtained ratios stand between the experimental data by Liu et al. (0.52, [19]) and De Iuliis et al. (0.74, [35]) in Table 3.

Using information from spectral shape ${\mathcal {E}}(\lambda )$, the possible range of $E(m_\lambda )$ values can finally be determined. The calculated values of $E(m_\lambda )$ are compared in Fig. 9 to previously reported values for TiO$_2$ particles in the literature [16, 19, 35]. The data used in this figure were obtained during prompt detection timing, since the estimation of $E(m_{\lambda _\text {laser}})$ at the previous step requires the use of the effective temperature at prompt. The estimated range of $E(m_\lambda )$ values falls between those reported by Liu et al. [19] and the one from De Iuliis et al. [35].

5 Discussion

The optical properties of nanoparticles constitute a crucial parameter for various in-situ measurements employing laser diagnostics. To obtain optical properties, many ex-situ techniques, such as reflectometry technique [44] or extinction method [32], exist. Unfortunately, they may be not convenient, since they require performing additional measurements and specific equipments. In addition, the particle characterization obtained with ex-situ techniques may not be representative of the particle optical property in a reactive environment, which is needed to interpret signals from in-situ measurements.

A method was presented in this work to identify a plausible range for the spectral absorption function $E(m_{\lambda })$ of nanoparticles based on LII measurements without requiring ex-situ measurements. The presented technique is subject to two major sources of errors/uncertainties:

• 1. The assumption $E(m_{\lambda _{\text {0}}+\Delta \lambda })\approx E(m_{\lambda _{\text {0}}})$. Since $E(m_{\lambda _{\text {0}}+\Delta \lambda })\approx E(m_{\lambda _{\text {0}}})$ for $\Delta \lambda \rightarrow 0$, it can be deduced that the smaller $\Delta \lambda$, the smaller will be the effect of this assumption.

• 2. The effect of noise when calculating the ratio $\left( \frac{I_{\text {SLII}}(\lambda _0)}{I_{\text {SLII}}(\lambda _0+\Delta \lambda )}\right)$ at Eq. (8). As extensively discussed by Liu et al. [30], the bigger $\Delta \lambda$ is, the smaller is expected to be the error on $T_{\text {eff}}^{\lambda _0}$.

These two sources of errors cannot be simultaneously minimized, since they have an opposite behavior as a function of $\Delta \lambda$. Thus, this technique is not expected to be optimized for all kinds of particles. On the one side, when $E(m_{\lambda })$ is known to be almost constant, as for soot particles, it is more convenient to impose constant $E(m_{\lambda })$ and working with large $\Delta \lambda$ values, i.e., classically pyrometry as in [30], since the errors coming from (1) are expected to be smaller than errors from (2). On the other side, when no information on the $E(m_{\lambda })$ shape is available or large variability is found in the literature, such for TiO$_2$ nanoparticles, the proposed technique should be envisaged, since the errors due to signal noise can be quantified and are expected to be less significant than assuming constant $E(m_{\lambda })$.

This analysis is confirmed by the experimental results for soot and TiO$_2$ presented in Figs. 5 and 9, respectively. Indeed, the range of possible values of $E(m_{\lambda })$ for soot covers the whole literature variability, so that no useful gain is actually obtained with the new approach. On the contrary, the results for TiO$_2$ nanoparticles allow to identify a range of possible $E(m_{\lambda })$ values that are included and narrower than the literature data. This proves the interest of the newly developed techniques for materials whose $E(m_{\lambda })$ is unknown and expected to largely vary with $\lambda$.

6 Conclusion

This study introduces a methodology for determining the spectral evolution of the absorption function $E(m_\lambda )$ through spectral emission analysis of laser-induced incandescence (LII) of nanoparticles. The method involves the assumption that $E(m_{\lambda }) \approx E(m_{\lambda +\Delta \lambda })$ for small $\Delta \lambda$ interval to derive an initial estimation of the effective temperature values. This information is then utilized to derive the spectral profile of $E(m_\lambda )$. The method has been verified for carbon black nanoparticles and then applied to flame-generated TiO$_2$ nanoparticles. The interest of this approach relies on the fact that the spectral LII emission information is needed only for one laser excitation wavelength and fluence.

Thus, the method is useful to obtain a reasonable estimation of the spectral evolution of $E(m_{\lambda })$ accompanied by a rough uncertainties quantification when no additional measurements are available. In future works, some aspects could be improved. First, the determination of the ${E}(m_{\lambda _\text {laser}})$ value at step 3. The approach retained in this work has been utilized by various research groups [10, 11] to investigate the properties of different types of nanoparticles. However, it is important to note that the method is subject to several assumptions that may introduce errors in the results. Specifically, changes in the density $\rho$ and specific heat $c_p$ [45] of the material during laser heating and changes in the optical properties of the material (for example, the band-gap energy of TiO$_2$ thin films changes with annealing [46]) could significantly affect the inferred value of $E(m_{\lambda })$. In addition, if the particles are not in the Rayleigh regime, the particles will heat to different peak temperatures, as demonstrated in [47]. Therefore, it is crucial to exercise caution and carefully consider these factors when employing this approach. Second, the ultimate goal of this research would be to narrow down the range of possible values, eventually obtaining a precise value for $E(m_{\lambda })$. For instance, one of the uncertainties is attributed to the extrapolation utilized in Eq. (13), since $\lambda _{\text {laser}}$ does not belong to the interval of the measured emission wavelength $[\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {min}}]$. This could be avoided by implementing an improved system where the excitation wavelength $\lambda _{\text {laser}}$ is effectively encompassed within the range of detection wavelength $[\lambda _{\text {em}}^{\text {min}},\lambda _{\text {em}}^{\text {min}}]$. Alternately, methods allowing to measure $E(m_{\lambda })$ at one specific wavelength [38] combined with the proposed approach can determine the absolute absorption function $E(m_{\lambda })$ for nanoparticles in all spectra. Finally, the uncertainties due to the postprocessing procedure at step 1 should also be accounted for.

Postprocessing procedure to estimate \(T_{\text {eff}}\) from the LII spectral emission

The proposed methodology relies on the estimation of a possible range for the effective temperature. However, the range of the possible effective particle temperatures, i.e., $T_{\text {eff}}^{\text {min}}$ and $T_{\text {eff}}^{\text {max}}$ may depend on the postprocessing procedure used to estimate them from the LII spectral emission.

First of all, the LII signal $I_{SLII}$ at $\lambda _0$ and $\lambda _0+\Delta \lambda$ have to be known to calculate $T_{\text {eff}}^{\lambda _0}$. As an example, the prompt spectral emission for carbon black particles at laser fluence F = 0.06 J/cm$^2$ is visualized in Fig. 10. The presented signal exhibits a certain degree of noise. A postprocessing procedure is then needed to obtain an estimation of $I_{SLII}$ for very close wavelengths. A piecewise linear reconstruction is first considered here. For this, the spectral emission is averaged over a 20 nm interval as visualized by the bars in Fig. 10a. The signal emission is then reconstructed by supposing a linear behavior of $I_{SLII}$ between the sampling points (represented by the symbols). The reconstructed signal is visualized by the blue line in Fig. 10a. Alternatively, a polynomial fitting of the fifth order is also considered. The obtained fitted signal is visualized by the red line in Fig. 10b.

The two reconstructed signals are then used to calculate $T_{\text {eff}}^{\lambda _0}$ using Eq. (2) for $\lambda _0 \in [560,700]$ nm. Results are visualized in Fig. 11a. As expected, the estimation of $T_{\text {eff}}^{\lambda _0}$ varies with the retained $\lambda _0$ value where condition $E(m_{\lambda _0})=E(m_{\lambda _0+\Delta \lambda })$ is imposed. Since it is not possible to know which is the exact value, the maximum and minimum values are chosen, namely $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {min}}$, respectively. The $T_{\text {eff}}^{\text {const}}$ value is also reported. It can be noted that $T_{\text {eff}}^{\text {const}}$ belongs to the region of possible $T_{\text {eff}}$ values, illustrating the possible error associated with the assumption $E(m_{560 nm})=E(m_{700nm})$. It can be noticed that the obtained $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {min}}$ depend on the reconstruction method retained (piecewise linear reconstruction or polynomial fitting). In addition, their values are expected to depend also on the size of the interval $\Delta \lambda$. The values $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {min}}$ obtained with both reconstruction methods are illustrated as a function of $\Delta \lambda$ in Fig. 11b. While increasing the interval size $\Delta \lambda$, the impact of the assumption $E(m_{\lambda _0})=E(m_{\lambda _0+\Delta \lambda })$ is expected to increase. The results slowly converge toward the $T_{\text {eff}}^{\text {const}}$ value as expected. Even if the extreme values of possible effective temperature depend on the postprocessing procedure, the proposed methodology allows having an estimation of the effective temperature value and of the spectral evolution of $E(m_\lambda )$ with a quantification of the uncertainties due to theoretical assumptions and the signal postprocessing. In this work, results were obtained using the piecewise linear reconstruction for $\Delta \lambda =$5 nm. Uncertainties due to the postprocessing are not considered in this work and should be included in future works.

Fig. 10

Postprocessing procedure to estimate $T_{\text {eff}}$ from the LII spectral emission: a piecewise linear reconstruction with an interval window of 20 nm; b reconstruction using a fifth-order polynomial fitting

Fig. 11

a Spectral dependence of the effective particle temperature $T_{\text {eff}}^{\lambda _0}$ obtained using Eq. (2) for $\lambda _0 \in [560,700]$ nm. The obtained $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {min}}$ depend on the reconstruction method retained. b The effect of $\Delta \lambda$ on the estimation of $T_{\text {eff}}^{\text {max}}$ and $T_{\text {eff}}^{\text {min}}$ effective temperatures for different reconstruction methods