1 Introduction

Heseinberg’s uncertainty principle stands out in the Quantum Theory (QT) scenario, in such a way as to delimit the confidence interval in the relationship between physical quantities and naturally shows itself as a pillar of QT, with notoriety as highlighted by Richard Faynman [1].

In the scenario of quantum computing and information, as well as those in which QT has wide employment, the uncertainty principle is always present adjusting the contour of the variables involved. In Physical Optics with emphasis on new technologies and concepts for computing and information, variables such as orbital angular momentum (OAM) and spin angular momentum (SAM) are treated with modulations [2,3,4,5,6], which in turn satisfy their quantizations and are bounded by the uncertainty principle while the minimum standard deviation is expected.

Although Relativity and Quantum theories are in different scenarios, they naturally interrelate through the quantization of light and relativistic energy if one considers the quasi-relativistic Shrörendiger wave function, for cases where the momentum is well defined [7]. In turn, relativistic effects do not arise naturally in the context of quantum theory [8]. Most of the time, the triggers for transposition between theories arise through the relativistic constant, considering quantized particles with speeds close to that of light in a vacuum.

The uncertainty principle can be considered in three treatments: Heisenberg uncertainty, Bohr indeterminacy, and dispersion uncertainty. In agreement with Chibeni [9], the Heisenberg uncertainty relation assumes that the observed object is a particle, where experimental measurements cannot have arbitrarily large precision, characterizing the term uncertainty properly. In Bohr's derivation of the Heisenberg uncertainty relation, quantum objects are assumed to be wave entities, and can be represented in wave packets, where the location of the wave packet is associated with the uncertainty of the wave number, establishing a relation of indeterminacy of quantities conjugated to the pairs [9, 10]. The third relation is the statistical version, which presents a minimum of dispersion between conjoined quantities in pairs [9, 10].

In recent studies, we have discussed the relativistic properties of photon dynamics at transmission with angular orientation, in the transition between two media [8, 11,12,13], demonstrating that the Abraham moment appears as a relativistic ignition device of the Minkowski moment. In this scenario, the photon is subjected to two torques in different scenarios, one classical and one relativistic, where the relativistic one is able to introduce its trajectory with the increase of the predominance of the relativistic inertia from the classical–relativistic synchronization points, region of incidence in which the photon has the facility to change its directional properties [12].

In this analysis, the uncertainty associated with relativistic properties is verified [8, 11, 12] of light for certain materials in transmission with angular orientation non-zero, in the face of Heisenberg, Bohr, and statistical dispersion uncertainties, considering deformations associated with linear momentum and angular orientation in transmission processes.

2 Methodology

From the perspective of Heisenberg gamma-ray microscopy, for small wavelengths of the order of λ ~ Δx, in accord with Boughn [14], in scattering measurement, the impulse imparted to the electron is proportional to the photon’s momentum, where the impulse can be treated as an unknown momentum disturbance:

$$\delta p\sim \frac{h}{\lambda },$$
(1)

from which one can describe the laws of Quantum Mechanics as thought by Heisenberg [14]:

$$\delta p\delta x\approx h.$$
(2)

In turn, the Bohr indeterminacy admits a wider range of values:

$$\delta p\delta x\ge \hslash .$$
(3)

The uncertainty associated with statistical dispersion presents a larger range of uncertainty in the same way as Bohr, although it introduces a smaller minimum uncertainty when compared to Heisenberg's and Bohr's, where:

$$\delta p\delta x\ge \hslash /2.$$
(4)

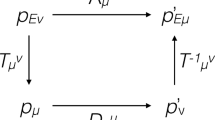
In the Abraham and Minkowski moment analysis, the deformations of linear momentum and angular orientation were described [11], where:

$$\frac{\Delta p}{p}=\frac{\Delta \theta }{\theta }=\gamma \left(\theta ,{n}_{12}\right)\left(1-{n}_{12}\right),$$
(5)

where n12 is the relative refractive index between media 1 and 2, and the relativistic angular constant [8, 11, 12]:

$$\gamma \left(\theta ,{n}_{12}\right)=\frac{\mathrm{sin}{\theta }_{1}}{\sqrt{1-{n}_{12}^{2}}}$$
(6)

In the treatment of quantized particles at the microscopic level, the uncertainty of trajectories and dispersion, the interpretations are slightly associated with the results and expectations discussed for the position and momentum of the electron, considering the basis of Heisenberg's arguments [10]. The present analysis considers that the uncertainty principle can be extended to all quantized particles, such as the photon, even subject to relativistic effects. Considering that the Heisenberg uncertainty principle does not consider the effects associated with the intervention of the observer in the simple act of extracting measurements, and therefore does not consider measurements in the relativistic scenario, we will check whether relativistic effects are able to disturb the Heisenberg scenario, in the perception of an observer.

In this work, we assume the photon to be a quantized particle, under relativistic effect, of which the trajectories can be easily verified in transmission processes instantaneously before and after the photon–matter interaction that takes place on the separating surface between media pairs. Thus, in an analog to determine the standard deviation of energy when we know the finite interval of an event, considering that we can completely know one of the variables while the other is uncertain [15, 16], we will obtain the standard deviation (uncertainty) of the photon's linear momentum assuming the determination of the photon's angular orientation variation in transmission.

We will consider that at the interface between two material media, there is a tolerance to the angular orientation of the photon, where \(\theta ={\theta }_{0}\pm \Delta \theta\). The tolerance \(\Delta \theta\) is positive or negative depending on the direction of growth of the refringence field, or depending on the pairs of media involved, weighting the negative refractive index in metamaterials [13, 17,18,19,20].

The uncertainty associated with angular deviation is already addressed in other studies, although it always goes back to the original Heinsenberg relation transposing it to the relation between angular momentum and angular orientation [21,22,23]. It is demonstrated in this work that the relativistic effects associated with the properties of the photon in the transmission between two media with angular orientation report the uncertainty relationship between linear momentum and angular orientation, in accordance with Eq. (5).

3 Development and discussion

From Eq. (5), we can establish the specific uncertainty relation for certain materials, considering the relativistic effects that do not arise naturally in the quantum theory setting:

$$\Delta p\Delta \theta ={\gamma }^{2}\left(\theta ,{n}_{12}\right)\left[p\left(1-{n}_{12}\right)\right]\left[\theta \left(1-{n}_{12}\right)\right],$$
(7)

where \(p\left(1-{n}_{12}\right)\) and \(\theta \left(1-{n}_{12}\right)\) are the variations of the classical linear momentumFootnote 1 and angular orientation for small angles, respectively. Thus, we can constitute the relation of relativistic uncertainty from the perspective of the referential of the source with respect to the referential of the observer in the laboratory:

$${\left[\Delta p\Delta \theta \right]}_{\mathrm{source}}={\gamma }^{2}\left(\theta ,{n}_{12}\right){\left[\Delta p\Delta \theta \right]}_{\mathrm{observer}}.$$
(8)

Let us consider that the observer in the laboratory considers the uncertainty principle, for a single photon (Heisenberg uncertainty), \({\left[\Delta p\Delta \theta \right]}_{\mathrm{observer}}\approx \hslash\), so that the specific relativistic uncertainty for a single photon is given by:

$${\left[\Delta p\Delta \theta \right]}_{\mathrm{relativistic}}\ge {\gamma }^{2}\left(\theta ,{n}_{12}\right)\hslash$$
(9 )

In Fig. 1, we see that the uncertainty relation given by Eq. (9) for large angles is in agreement with the expected uncertainty in statistical dispersion and Bohr indeterminacy, although the uncertainty of scattering and Bohr indeterminacy agree for values larger than ħ. It seems clear that we can separate these regions by the classical–relativistic synchronization angle (θsync) [8, 11, 12], exactly at the intersection of the curves with the straight line in green.

Fig. 1
figure 1

(Source: author)

Minimum specific relativistic uncertainty in angular incidence

Full size image

In these terms, for large angles before source–observer synchronizations, we find that the relativistic uncertainty agrees with the scattering uncertainty, while for incidence angles larger than θsync, it agrees with Bohr. The synchronization points are found just when the relativistic uncertainty agrees with the Heisenberg uncertainty. For small angles, Footnote 2 the relativistic uncertainty is smaller compared to the minimum expected dispersion uncertainty.

In the analysis of the momentum uncertainty of the relativistic energy wave (REW) [11], the accuracy of the angular orientation variation between the incident and refracted angles was considered. The refraction data known in the literature constituted the angular orientations of the photon before and after the photon–matter interaction, in the scenario of constant frequency transmission, with conservation of the linear and angular moments for both particles involved, photon and electron interaction [8, 11, 12].

Note that the estimates treated in Figs. 1 and 2 report the relativistic effects considering the minimum Heisenberg uncertainty and naturally could be reduced by half if we choose the dispersion uncertainty in Eq. (9). It is noteworthy that the model given by Eq. (9) reports the relativistic effects for the QT scenario, without requiring changes in the Heisenberg algebra, because according to Faizal et al. [24], it is subject to deformation whenever the uncertainty principle is deformed.

Fig. 2
figure 2

(Source: author)

Specific relativistic minimum uncertainty of the photon's linear momentum at angular incidence

Full size image

It can be seen in Fig. 2 that the maxima of the minimum uncertainty are found in the vicinity of Brewster’s angle. The classical–relavistic synchronization angles between source and observer [11, 12], which in the quantum-relativistic scenario characterize incidences in which the chances are equal of finding one or another quantized state of light [8], are pseudo Brewster angles [8, 25]. In this sense, the maxima of the minimum uncertainties of the photon linear momentum at transmission with angular orientation lie in the range of the reflectance minima.

The region of dashed curves characterizes the range of incidence of anomalies of the uncertainty principle in the unique scenario of Quantum Mechanics, because the uncertainty of the linear momentum decreases in proportion to the sharp drop in the uncertainty of the angular orientation. After the maxima of the linear momentum, the relativistic uncertainty agrees with what is expected by Quantum Mechanics (QM) where the certainty of one decreases with increasing uncertainty of the other physical quantity.

The causes of the anomalies are not in the QM scenario, as they are due to the characteristic relativistic effects of the relativistic angular constant in determining the photon's trajectory. The switch from classical predominance of the photon mass to relativistic occurs at classical–relativistic synchronization angles, with increasing relativistic effects for large angles until γ(θ, n12) =  γ(n12) [8, 11, 12].

In QM, De Broglie's wavelength is consistent with the wave function considering Schrödinger's own interpretation that his mechanics was an analog to optics [26], and naturally in the description of microscopic particles with speeds close to that of light in vacuum, relativistic mass is assumed, although one expects the best relativistic representation of kinetic energy and momentum for a wave function that reports relativistic effects [7]. Therefore, it is precisely in this assumption that the anomaly arises, because MQ does not predict the classical predominance of the photon mass preceding the synchronizations, nor the alternation of predominances in transmission with angular orientation.

The minima of the momentum uncertainty for small angles do not indicate a region (incidence range) in the classical domain where the effects are deterministic, although the predominance of the classical photon inertia, because these limits are not predicted in the classical theory. The relativistic effects occur from transmission with normal incidence [8, 11, 12], although the relativistic trajectory appears with relativistic delay until inertial predominance switches to relativistic. In the present case, the uncertainty minima reside in the quantum scenario under the relativistic effects of the recent relativistic properties of photon dynamics at transmission with angular orientation [8, 11, 12].

The inversion of photon linear momentum uncertainty near the pseudo Brewster angles where OAM inversions occur [11, 27], not surprising even considering the observer effect, it seems natural but not necessarily correct that we have less uncertainty in the vicinity of the normal incidence.

The uncertainty principle showed inconsistencies in the uncertainty relation of noise and disturbances where the universal uncertainty principle was derived [28, 29]. It is important to note that in experimental analysis of the universal uncertainty relation itself [30], considering the error associated with perturbations in neutron spin measurements and the detuning angular range, that for small angles the universal uncertainty equation fails, where the accuracy of one is not associated with the imprecision of the other.

The behavior of the linear momentum uncertainty presented in Fig. 2 is proportional to the behavior of the wavenumber, where in metamaterials, the same profile of the wavenumber in relation to the index of refraction can be found, although there is an angular dalay [31].

Figures 1 and 2 show that the minimum uncertainty in the perception of the source reference is different from that recorded by the observer in the laboratory, increasing as the angle of incidence increases. In turn, it is also verified that the refringencies of the pairs of media involved in the transmission are determinant for the different records of the minimum uncertainty, found between the source and observer references.

These effects are associated with the behavior of the angular relativistic constant (Eq. 6), which is a function of the angle of incidence and the relative refractive index, which we now discuss in terms of the relativistic properties of the photon in angular transmission and the Theory of Relativity.

In recent studies [8, 11, 12], we report the alternation between the predominance of photon inertia, as classical or relativistic, showing that the variation of the linear momentum of the photon in angular transmission is associated with the variability of the photon mass, between its classical and relativistic predominance. This effect is not unexpected, as it is one of the main differences between Classical and Relativistic Theory whereas mass is constant in the Newtonian perspective.

In turn, quantum theory also does not predict the alternation of photon mass regimes in angular transmission, and cannot estimate the variability of the minimum uncertainty of the photon in angular transmission presented in this analysis. In this sense, we can understand that the inertial properties of the photon as a function of the angle of incidence and the refraction of the medium are related to the causes of the uncertainty variability \(\Delta p\Delta \theta\) presented in this paper.

In the Theory of Relativity, Einstein indicates that the relativistic effects occur with sense between the observers, where in the paradox of the twins, it is clear that only in the referential of one of the brothers, time will pass more slowly, precisely the one who really had perception of the changes in its dynamic properties along the way. If he wants to meet his brother again, he will have to reverse his direction of movement.

In Fig. 1, it can be seen that there is a direction of increase of the minimum uncertainty recorded in the source reference, compared to the record of the observer in the laboratory, which agrees with the direction of the increase of the angle of incidence. In turn, this increase is smaller and angularly delayed with increasing refringence field, an effect that is due to the decrease in linear momentum uncertainty with increasing refringence as seen in Fig. 2. The decrease of the linear momentum uncertainty considering the velocity decrease in more refringent media indicates that the variability of the mass, as a consequence of the employed energyFootnote 3 to the translational movement, partially compensates for the effects of the decrease in velocity and its consequences for the uncertainty of the linear momentum.

The results presented from the transposition of perceptions between the references of the source and the observer, represented by eqs. (8) and (9), are similar to the results discussed by Putra [32, 33], when dealing with the relativistic uncertainty from the mass-action equivalence relation. In turn in this paper we do not consider this equivalence relation, also we do not consider mass losses or gains, while the effects are in the domain of classical-relativistic variability of the photon inertia  [8, 11, 12], and the transposition between observers' perceptions are consistent with our recent work where we present relativistic effects on the probabilities of quantized states of light at angular incidence [8].

4 Considerations

In this analysis, the consistency of the specific relativistic uncertainty of some materials was verified, with the uncertainty principle from the perspective of Heisenberg, Bohr, and statistical dispersion. The transposition of the relativistic effects associated with the photon in transmission with angular orientation to the uncertainty principle was treated through the uncertainties of the linear momentum and angular orientation of the photon, before and after the photon–matter interaction.

The specific relativistic uncertainty before clock synchronizations in matter is consistent with the statistical scattering uncertainty, showing smaller specific uncertainty for small angles of incidence. At synchronizations, it agrees with the Heisenberg uncertainty for a particle, while for larger angles get confused between the scattering uncertainty and the Bohr indeterminacy for an energy wave.

It was found that the relativistic specific uncertainty reports anomalies to the uncertainty principle that do not arise in the quantum theory setting, showing agreement in the uncertainty drops of the pair of variables considered, in the incidence range that precedes the maxima of the minimum specific uncertainty of the linear momentum. The anomalies in the uncertainty principle of Quantum Mechanics are due to the fact that the alternation between the classical and relativistic predominances of photon inertia arise in the relativistic setting and are not predicted in the Quantum Theory.

While the uncertainty principle of Quantum Mechanics is generalized, the specific relativistic uncertainty is a property that reports the particularities of photon–matter interaction, presenting smaller minimum uncertainties compared to those expected by quantum theory, which are distinguished among different materials and angles of incidence.

Stands out that the specific relativistic uncertainty is distinguished from Heisenberg, Bohr, and statistical dispersion uncertainty in that it considers the records of an observer who performs relativistic measurements, relative to those that perturb the system in an inertial referential.

Considering that the anomalies indicated in the Quantum Mechanics scenario arise with the new relativistic properties of light and the effects associated with the observer are relativistic, further studies in the quantum scenario are indicated to verify the results presented.