1 Introduction

The experimental study of diffraction-free beams was pioneered by Durnin et al. [1], when they solved Whittaker’s solutions of the Helmholtz equation. The diffraction-free beams have been extensively developed due to their interesting properties and potential applications in optical alignment, surveying, optical interconnections, etc [2]. In addition, the non-diffraction property of the Bessel Beams (BBs), invariance during propagation, and the high length/diameter ratio are some significant features of BBs [3] that make Bessel beams, especially in numerous research fields. For instance, optical imaging [4], optical tweezers [5], laser welding [6], multifocal optical coherence tomography [7], protected sharing of cryptographic keys [8], high harmonics generation [9], and laser particle acceleration [10] can be mentioned. Passive methods employed optical elements outside the resonator to reshape the output beam. The refractive or diffractive axicons [11], Fabry–Perot interferometers [12], diffractive phase elements [13], holographic methods [14, 15], spatial light modulators [16], transmissive or reflective axicons [17], and anisotropic crystals [18] are examples showing elements of the passive methods. In addition to the passive methods, some active methods of Bessel beam laser generation are of great interest [19,20,21]. As reported in the literature, the direct generation of a non-diffracting in the resonator saves the application of external optical elements, resulting in a high-power output non-diffracting beam [22]. Various intra-cavity laser resonator arrangements have been suggested to generate non-diffracting beams, especially Bessel and Bessel–Gaussian beams. For instance, Uehara et al. [23] presented a laser resonator based on converting a ring field to a Bessel beam by applying a Fourier lens. This technique may not be helpful since the beam propagation distance is slightly more than a comparable Gaussian beam [24]. Another setup, proposed by Jabzynski et al., is based on a confocal resonator with an annular-aperture cylindrical gain medium. However, as adopted by authors, it is incapable of doing what Bessel or Bessel–Gauss beam’s demonstration method does [25]. Also, Turunen and Pääkkönen [26] have reported a configuration consisting of an aspheric phase conjugation mirror to produce a Bessel beam. Achieving a high order of Bessel beams and getting high discrimination of transverse modes to ensure the resonator’s single-mode operation is regarded as the advantages of resonators with spherical mirrors [27]. Hakola et al. [28] have also proposed a plano-concave laser resonator scheme for Bessel–Gauss beam generation scheme; it includes a concave end mirror replaced with a diffractive phase element. Rogel et al. [27] and Khilo et al. [29] have also independently suggested an axicon-based resonator configuration. They used an intra-cavity axicon instead of a slit resulting in a smoother intensity variation because it could remove the on-axis intensity oscillations as a hard aperture was utilized [24]. Their studies have been followed and developed by Gutiérrez-Vega et al. [30], et al. [31], Hernández-Aranda et al. [32], and Rao et al. [33]. The axicon-based laser resonator has several benefits: Bessel–Gaussian beams generation, selection of high-order modes, the increased depth of focus in material processing and generation of the radially polarized beams can be mentioned [34]. Also, the simplicity of employing the transmissive axicon and its low energy loss are the advantages of this optical element [34].

On the other hand, the thin-disk laser (TDL) is a diode-pumped solid-state laser Giesen presented in 1994 for the first time [35]. TDLs have received much attention due to their unique properties (high output power with high efficiency and good beam quality), and studies have shown that they could be a real candidate for high-power laser beam generation [36,37,38,39,40], for instance Outputs 10 kW [41], 27 kW [42], 100-kW-systems [43] in continuous wave operation, and up to 2 kW in ultrafast [44] operation. The TDL with the axicon-based resonator has been applied for the first time to generate a free-diffraction beam by authors [45].

In this article, an axicon-based TDL resonator is described analytically for the first time. Transmission of the axicon and propagation of the Bessel–Gauss beam is analytically described by solving the Huygens–Fresnel diffraction integral. The proposed resonator is introduced briefly, and the nondiffracting mode propagation is investigated in one round-trip. In addition, the results of the numerical and analytical approaches are compared and analyzed. Next, self-consistency equations were derived through an analytical solution process.

2 Optical resonator arrangement

The proposed laser resonator is demonstrated in Fig. 1. It contains Yb: YAG thin-disk as an active medium which acts as the back mirror, axicon, and the output coupler mirror (OCM). The backside of the thin disk is mounted on a heat sink to compensate for the high thermal load. The disk’s backside and opposite sides have been configured with highly reflective and anti-reflective coatings for the pump and laser emission wavelengths.

At this arrangement, \(\theta _0\) is the conicity angle of the refracted wave (or the characteristic angle of axicon), which is equal to \(\theta _0=\sin ^{-1}\left( n\sin \gamma ^\prime \right)\), L is the resonant cavity length, which can be described by \(\frac{a_1}{2\tan \left( \theta _0\right) }\) (\(a_1\) is the transverse radius of the axicon), k is the wave number, and \(\gamma\) is the wedge angle of the axicon.

Fig. 1
figure 1

Design of an axicon-based thin-disk laser resonator with Bessel–Gauss modes. (1) Heat-sink for reducing thermal loading; (2) high-reflecting coating; (3) the thin active medium which acts as a back mirror; (4) anti-reflective coating; (5) axicon with the parameter \(\gamma ^\prime\); (6) spherical mirror with a radius of curvature \(R_{\textrm{OC}}\) placed at the distance of \(L_0\) from the back mirror. Also, the \(\mathrm a_1\) and \(\mathrm a_2\) parameters describe the transverse radius of OCM and the axicon, respectively

Full size image

One can construct a resonator with Bessel modes by utilizing just two plane mirrors and an axicon, as reported by Khilo et al. [29]. One mirror is set just behind the axicon, and the other is located at a distance of L with respect to it. It is worth noting that the theoretical formation of the near-ideal Bessel beam occurs when the curvature of the spherical mirror approaches infinity. It should be noted that the diffraction loss is high (about a hundredth) [30]. Thus, an axicon bounded in front of a disk (the active medium) with an anti-reflection coating can provide the axicon-based thin-disk laser resonator, supporting the Bessel modes.

3 Bessel beam transmission through linear axicon

Transmission of a Bessel beam through a linear axicon, and its propagation through a distance \(z_{\max }\), can be described with the Huygens–Fresnel diffraction integral. Its schematic has been demonstrated in Fig. 2

Fig. 2
figure 2

Shows transmission of Bessel–Gauss beam from the axicon and its propagation through a non-diffracting length \(z_{\max }\)

Full size image

Huygens–Fresnel diffraction integral, a relationship between the input and the output field distributions, has always been employed by many researchers. Besides numerical methods, one can use an analytical approach to solve the Collins’ diffraction integral formula. For instance, the stationary phase method [46, 47], Fast-Fourier-transform (FFT) method [48, 49], and single two-dimensional fast Fourier transform (S-FFT) [50, 51] are commonly preferred approaches. However, direct analytical solving of Huygens–Fresnel diffraction integral is a simple simulation process without requiring a professional system. In addition, the direct analytical approach leads to the self-consistency equations derivation for the first time, along with the investigation of any medium with a linear phase.

The Huygens–Fresnel diffraction integral, in cylindrical coordinates is given by:

$$\begin{aligned} \begin{aligned} u_{\textrm{final}}\left( \rho _{\xi }\right) =&\int \limits _{0}^{a_{\eta }} \frac{-ik}{B}\exp \left[ \frac{ik}{2B} \left( A\rho _{\eta }^2+D\rho _{\xi }^2\right) \right] \\&J_0\left( \frac{k}{B}\rho _{\eta }\rho _{\xi }\right) T\left( \rho _{\eta }\right) u_{\textrm{initial}}\left( \rho _{\eta }\right) \rho _{\eta }d\rho _{\eta }, \end{aligned} \end{aligned}$$
(1)

where the functions \(u_{\textrm{initial}}\left( \rho _{\eta }\right)\) and \(u_{\textrm{final}}\left( \rho _{\xi }\right)\) describe the initial and final beam transverse distributions in the \(\left( \rho _{\eta },\varphi \right)\) and \(\left( \rho _{\xi },\varphi \right)\) plans, respectively. The initial can be considered as a Bessel function multiplied to a constant amplitude \(A_0\) where it is modulated by a Gaussian beam, i.e., \(A_0J_0(\rho )\exp (-\rho ^2/w_0^2)\). The parameter \(J_0\) represents the well-known zero-order Bessel function, k is the wave number, and \(T\left( \rho _{\eta }\right)\) is the transmittance function of the axicon or other optical elements. The transmission function of a linear axicon is defined as:

$$\begin{aligned} T_{ax}(\rho _{\eta })=\exp (-ib\rho _{\eta })~, \end{aligned}$$
(2)

where b is a constant parameter which will be introduced in the next section. The constants A, B, and D parameters are the ABCD ray transform matrix elements.

By considering a mentioned field in front of the axicon, and insert in the Eq. (1) along with \(T_{ax}(\rho _{\eta })\), the transmission of the considered Bessel beam through the linear axicon has been described by (with assumption \(\eta =1\) and \(\xi =2\)):

$$\begin{aligned}{} & {} \int \limits _{0}^{\infty }J_0\left( \alpha '\rho _2\right) J_0\left( \beta ''\rho _2\right) \exp \left( {-q^2\rho _2^2-ib\rho _2}\right) \rho _2d\rho _2. \end{aligned}$$
(3)

The Eq. (3) has answer as (Note: \(\mathrm {Re~~q>0}\) and \(\mathrm {\beta ''=\rho _{1}\beta '}\)):

$$\begin{aligned}{} & {} =\frac{1}{2q^2}J_0\left( \frac{i}{2q^2}\alpha '\beta ' \left( 1+\frac{b}{\alpha '}\right) \rho _{1}\right) \nonumber \\{} & {} \quad \exp \left[ {-\frac{\left( 1+\frac{b}{\alpha '}\right) }{4q^2} \left( \left( 1+\frac{b}{\alpha '}\right) \alpha '^2+\beta '^2\rho _{1}^2\right) }\right] . \end{aligned}$$
(4)

It should be mentioned that to find the proving process of Eq. (3) see Appendix A.

4 Self-consistency equations

In this section, we describe one round-trip propagation of the Bessel–Gauss beam around the cavity to fulfil some goals. One of them is to show that the Bessel functions can consider the eigenmode of the axicon-based thin-disk laser resonator. The next target is to extract and analyze the analytical solution results. In the next section, we compare the results with the profiles obtained in the numerical simulation. First, we assume that the Bessel–Gauss beam is propagated toward the axicon-thin-disk combination from the OC aperture plane. The Bessel–Gauss beam can be assumed at the plane just before reflection at the OC mirror, as follows:

$$\begin{aligned} u_{\textrm{initial}}\left( \rho _{1}\right) =J_n\left( k_t\rho _1\right) \exp \left[ -\left( \frac{1}{W_1^2}+\frac{ik}{R_{\textrm{OC}}}\right) \rho _1^2\right] , \end{aligned}$$
(5)

where \(k_t\) is the angular wavenumber, described by \(k\sin \left( \theta _0 \right)\), \(W_1\) is the beam size on the OC mirror, \(R_{\textrm{OC}}\) is the radius of the curvature of the OC mirror, and n is the order of the Bessel function. Note that, the fundamental mode, i.e., zero-order Bessel–Gauss beam, is considered in this case; thus, the order of n is zero. Also, the radius of the beam at which the Gaussian term falls to \(1/\mathrm e^2\) of its maximum value on-axis must be much smaller than the axicon’s aperture [28].

Now, by following the beam propagation from the OC mirror to the front of the axicon, one can obtain:

$$\begin{aligned} \begin{aligned} u_{\mathrm{TD{\_}}Ax{\_}Comb}\left( \rho _{2}\right)&=\frac{-ik}{B}\exp \left( \frac{iAk\rho _{2}^2}{2B} \right) \\&\quad \int \limits _{0}^{a_{1}} J_0\left( \frac{k\rho _{1}\rho _{2}}{B}\right) J_0\left( k_t\rho _{1}\right) \\&\quad \exp \left[ \left( \frac{iDk}{2B} -\left( \frac{1}{W_1^2}+\frac{ik}{R_{\textrm{OC}}}\right) \right) \rho _1^2\right] \rho _1d\rho _1. \end{aligned} \end{aligned}$$
(6)

where the ABCD parameters are the ray’s matrix elements of the free space located between the OC mirror plane and the axicon-thin-disk combination plane:

$$\begin{aligned} \begin{bmatrix} A &{} B \\ C &{} D \end{bmatrix}= \begin{bmatrix} 1 &{} L \\ 0 &{} 1 \end{bmatrix}. \end{aligned}$$
(7)

At the reflection from the axicon-thin-disk combination plane, we assume \(T\left( \rho _1 \right) \approx 1\), because of the journeying of Bessel–Gauss in the free space. By applying the mentioned assumption, we have

$$\begin{aligned} u_{\mathrm{TD{\_}}Ax{\_}Comb}\left( \rho _{2}\right)&=\frac{-ik}{L}\exp \left( \frac{ik}{2L}\rho _{2}^2 \right) \nonumber \\ {}&\quad \int \limits _{0}^{a_{1}} J_0\left( \frac{k}{L}\rho _{1}\rho _{2}\right) J_0\left( k_t\rho _{1}\right) \nonumber \\&\quad \times \exp \left[ -\left( \frac{1}{W_1^2}+\frac{ik}{R_\textrm{OC}}-\frac{ik}{2L}\right) \rho _1^2\right] \rho _1d\rho _1. \end{aligned}$$
(8)

By making use of the well-known relation (Note: \(\text {Re}~~\gamma>0;~~\nu >-1\)):

$$\begin{aligned}{} & {} \int \limits _{0}^{\infty }J_\nu \left( \beta \rho _1\right) J_\nu \left( k_t\rho _1\right) \exp \left( -\gamma ^2\rho _1^2 \right) \nonumber \\{} & {} \rho _1d\rho _1=\frac{1}{2\gamma ^2}I_\nu \left( \frac{\beta k_t}{2\gamma ^2}\right) \exp \left( -\frac{\beta ^2+k_t^2}{4\gamma ^2} \right) ~~, \end{aligned}$$
(9)

where the \(I_0\) is the modified Bessel function of the first kind; so it is easy to show that the transverse field distribution in front of the axicon-thin-disk combination is given by

$$\begin{aligned} \begin{aligned} u_{\mathrm{TD{\_}}Ax{\_}Comb}\left( \rho _{2}\right)&=\frac{k}{2iL\gamma ^2}\exp \left( -\frac{k_t^2}{4\gamma ^2} \right) J_0\left( \frac{k_tk}{2iL\gamma ^2}\rho _2\right) \\&\quad \exp \left[ -\left( \frac{k^2}{4L^2\gamma ^2}-\frac{ik}{2L}\right) \rho _2^2\right] , \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned} \gamma ^2=\frac{1}{W_1^2}+\frac{ik}{R_{\textrm{OC}}}-\frac{ik}{2L}. \end{aligned}$$
(11)

Now, to get access to the transverse distribution at the output coupler, we must replace Eq. (10) by Eq. (1) along with employing the \(\textit{ABCD}\) travelling matrix in free space, Eq. (7), thus,

$$\begin{aligned} u_{\textrm{final}}\left( \rho _{1}\right)&=\frac{-k^2}{2L^2\gamma ^2}\exp \left( \frac{ik}{2L}\rho _{1}^2-\frac{k_t^2}{4\gamma ^2}\right) \nonumber \\&\quad \int \limits _{0}^{a_2} J_0\left( \frac{k_tk}{2iL\gamma ^2}\rho _2\right) J_0\left( \frac{k}{L}\rho _{1}\rho _{2}\right) \nonumber \\&\quad \times T_{\mathrm{TD{\_}}Ax{\_}Comb}\left( \rho _2\right) \exp \left[ -\left( \frac{k^2}{4L^2\gamma ^2}-\frac{ik}{L}\right) \rho _2^2 \right] \nonumber \\&\quad \rho _2d\rho _2. \end{aligned}$$
(12)

One can easily apply the axicon-thin-disk combination effect to the laser resonator’s resonant mode phase by passing through the axicon-thin-disk. From the mathematical point of view, multiplication of the transmittance function to Eq. (12) is sufficient. Their reflectance functions are defined as

$$\begin{aligned}{} & {} T_{\mathrm{TD{\_}}Ax{\_}Comb}\left( \rho _2\right) =\exp \left( -2ik\theta _0\rho _2-\frac{ik\rho _2^2}{R_\textrm{TD}}\right) . \end{aligned}$$
(13)

The first and second terms in the arc of the Eq. (13), respectively describe the linear and spherical phases a given beam suffers when passing through the axicon and being reflected from the back of the disk. Also, \(R_{\textrm{TD}}\) describes the curvature of the thin-disk which is caused by the thermal loading. By inserting Eq. (13) in Eq. (12) and using the ray propagation matrices, we will have

$$\begin{aligned} \begin{aligned}&u_{\textrm{final}}\left( \rho _{1}\right) =\frac{-k^2}{2L^2\gamma ^2}\exp \left( \frac{ik}{2L}\rho _{1}^2-\frac{k_t^2}{4\gamma ^2}\right) \\&\int \limits _{0}^{a_2} \exp \left[ -\left( \frac{k^2}{4L^2\gamma ^2}-\frac{ik}{L}+\frac{ik}{R_\textrm{TD}}\right) \rho _2^2-2ik\theta _0\rho _2\right] \\&J_0\left( \frac{k_tk}{2iL\gamma ^2}\rho _1\right) J_0\left( \frac{k}{L}\rho _{2}\rho _{2}\right) \rho _2d\rho _2. \end{aligned} \end{aligned}$$
(14)

By making use of the Eq.(4) with supposing \(S^2=1+\frac{b}{\alpha '}\), the transverse distribution at the output plane is

$$\begin{aligned} \begin{aligned}u_{\textrm{final}}\left( \rho _1\right) &= -\frac{k^2}{4L^2\gamma ^2q^2} \exp \left( -\frac{k_t^2}{4\gamma ^2}-\frac{\alpha '^2S^4}{4q^2}\right) \\&\quad\times J_0\left( \frac{i\alpha '\beta 'S^2}{2q^2}\rho _1\right) \exp \left[ \left( \frac{ik}{2L}-\frac{\beta '^2S^2}{4q^2}\right) \rho _1^2\right] , \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} q^2= & {} \frac{k^2}{4L^2\gamma ^2}-\frac{ik}{L}+\frac{ik}{R_{\textrm{TD}}},\\ \alpha '= & {} \frac{k_tk}{2iL\gamma ^2},\\ \beta '= & {} \frac{k}{L}. \end{aligned}$$

Indeed, Eq. (15) indicates that the Bessel–Gauss mode is still considerable as an eigenmode of the resonator, even if the deformation of the active medium happens. As well, it is helpful to peruse Eq. (15). The argument of the Bessel function is complex. Therefore, their discrimination into two parts, imaginary and real, is necessary. And one can do it. To that end, after some simple algebra, we have

$$\begin{aligned} u_{\textrm{final}}\left( \rho _1\right)&= \overbrace{ \frac{-\frac{k^2}{4L^2} \left( \delta ^{'}-i\delta ^{'}_i\right) }{{\delta ^{'}}^2+{\delta ^{'}_i}^2}}^{U_0} \nonumber \\&\times \overbrace{\exp \left( \frac{-\frac{k_t^2}{4W_0^2}}{\frac{1}{W_1^4}+\left( \frac{k}{2L}\right) ^2\left( \frac{2L}{R_{\textrm{OC}}}-1\right) ^2}+ \frac{\left( \frac{kk_t}{4L}\right) ^2\left( \left( S_r^2-S_i^2\right) \delta +2\delta _iS_rS_i\right) }{{\delta }^2+{\delta }_i^2}\right) }^{U_1} \nonumber \\&\underbrace{ J_0\left( \frac{k_tk^2\left( S_r-iS_i\right) \left( \delta ^{'}-i\delta ^{'}_i\right) }{2L^2\left( {\delta ^{'}}^2+{\delta ^{'}_i}^2\right) }\rho _1 \right) }_{U_2} \nonumber \\&\underbrace{ \exp \left( -\frac{\rho _1^2}{W^2}\right) }_{U_3} \underbrace{ \exp \left( i\varphi \right) }_{U_4} \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{aligned}&\frac{1}{W^2}=\frac{\left( \frac{k}{2L}\right) ^2 \left( S_r\delta ^{''}-S_i\delta ^{''}_i\right) }{{\delta ^{''}}^2+{\delta ^{''}_i}^2}~~,\\&\varphi =\left( \frac{k}{2L}+\frac{\left( \frac{k}{2L}\right) ^2 \left( \delta _i^{''}S_r+\delta ^{''}S_i\right) }{{\delta ^{''}}^2+{\delta ^{''}_i}^2} \right) \\&\rho _1^2-\frac{\left( \frac{kk_t}{4L}\right) ^2 \left( \delta \left( S^2_r-S^2_i\right) -2\delta _iS_rS_i\right) }{{\delta }^2+{\delta _i}^2}\\&+\frac{\frac{k_t^2k}{8L}\left( \frac{2L}{R_\textrm{OC}}-1\right) }{\frac{1}{W_1^4}+\left( \frac{k}{2L}\right) ^2\left( \frac{2L}{R_\textrm{OC}}-1\right) ^2} \\&\delta =\left( \frac{k}{2W_1L}\right) ^2\left[ 1-\left( \frac{2L}{R_\textrm{OC}}-1\right) \left( \frac{L}{R_{\textrm{TD}}}-1\right) \right] \\&\delta _i=\frac{k}{L}\left( \frac{L}{R_{\textrm{TD}}}-1\right) \left( {\frac{1}{W_1^4}+\left( \frac{k}{2L}\right) ^2\left( \frac{2L}{R_\textrm{OC}}-1\right) ^2} \right) \\&+\left( \frac{k}{2L}\right) ^3 \left( \frac{2L}{R_{\textrm{OC}}}-1\right) \\&\delta ^{'} = \left( \frac{k}{2L}\right) ^2 \left[ 1-2\left( \frac{L}{R_{\textrm{TD}}}-1\right) \left( \frac{2L}{R_\textrm{OC}}-1\right) \right] \\&\delta ^{'}_i=\frac{k}{LW_1^2}\left( \frac{L}{R_{\textrm{TD}}}-1\right) \\&\delta ^{''}=\frac{1}{W_1^2}\left[ \left( \frac{2L}{kW_1^2}\right) ^2 + \left( \frac{2L}{R_{\textrm{OC}}}-1\right) ^2 \right] ^{-1} \\&\delta ^{''}_i=\frac{k}{L}\left( \frac{L}{R_\textrm{TD}}-1\right) -\frac{k}{2L}\left( \frac{2L}{R_{\textrm{OC}}}-1\right) \\&\left[ \left( \frac{2L}{kW_1^2}\right) ^2 + \left( \frac{2L}{R_\textrm{OC}}-1\right) ^2 \right] ^{-1}\\&S_r=\left[ 1-2\left( \frac{2L}{R_{OC}}-1\right) \right] ~~,\\&S_i=\frac{4L}{kW_1^2}~~. \end{aligned} \end{aligned}$$

In Eq. (16), \(U_0\times U_1\) terms are constant coefficients and representing a measure of losses in a complete round trip, and \(U_2\) describes the quasi Bessel nature of the output beam, and \(U_3\) represents the Gaussian property of the Bessel–Gaussian beam. \(U_4\) describes the phase shifting of the transmitted and reflected beam from the cavity’s components in one round trip. The phase term contains both the radial and the axial phase components. The radial phase depends on both the inverse cavity resonant length and the wavelength when one selects \(R_\textrm{TD}=1\,L\) and \(R_{\textrm{OC}}=2\,L\).

The eigenmode condition requires that the beam size remains invariant at the reference plane after one round trip through the optical resonator arrangement. It means that the beam size \(W^2\) must be equal to \(W_1^2\). By comparing Eqs. (5) and (16), the eigenmode condition can be obtained as follows:

$$\begin{aligned} W_1=\left[ \frac{\frac{4L^2}{k^2}\left[ \left( \frac{2L}{R_\textrm{TD}}-3\right) ^2-1\right] }{1-\left[ 1-2\left( \frac{L}{R_\textrm{TD}}-1\right) \left( \frac{2L}{R_\textrm{OC}}-1\right) \right] ^2-4\left( \frac{L}{R_\textrm{TD}}-1\right) \left( \frac{2L}{R_{\textrm{OC}}}-1\right) ^2}\right] ^{1/4}. \end{aligned}$$
(17)

The Eq. (17) provides the acceptable answer of \(W_1^2\) and \(W^2\) equality. In addition, Eq. (17) gives interesting results, which shown for \(R_\textrm{TD} \gg L\) and \({R _{\text{ O }C}=L}\) condition. By inserting it in Eq. (17) and making simple algebraic, the beam size \(W_1^4\) can be obtained as \(\frac{-12\textrm{L}^{2}}{\textrm{k}^{2}}\). By substituting it in Eq. (5), we have:

$$\begin{aligned} U\left( \rho _{1}\right){} & {} =J_n\left( k_t\rho _1\right) \exp \left[ -\left( \frac{-ik^2}{12L^2}+\frac{ik}{R_{\textrm{OC}}}\right) \rho _1^2\right] . \end{aligned}$$
(18)

Eq. (18) shows that the Bessel function describes the domain of the beam since the Gaussian term describes the spherical phase characteristics; as a result, a near-ideal Bessel beam is constructed in the output plane. It is in an excellent agreement with [52]. The resonance condition depends on both the laser’s wavelength and cavity length. Based on this condition, the laser waves constructively interfere when reflected from end mirrors and strongly amplified; otherwise, they are canceled for destructive interference. The resonance condition requires that the total phase shift along the axes of the cavity be multiple of \(2n\pi\) [32]; namely,

$$\begin{aligned} \phi -\varphi _0=2n\pi , \end{aligned}$$
(19)

where \(\phi\) refers to the eigenmode’s phase per round trip and \(\varphi _0\) describes the initial Bessel–Gauss beam phase. By considering the ratio of Eqs. (16) and (5), one can calculate \(\phi\) as follows:

$$\begin{aligned} \phi =\frac{\frac{U_{\textrm{final}}}{|U_{\textrm{final}} |}}{\frac{U_{\textrm{initial}}}{|U_{\textrm{initial}} |}}=\tan ^{-1}\left( -\frac{\delta _i}{\delta ^{'}} \right) +\varphi '+ \varphi , \end{aligned}$$
(20)

where,

$$\begin{aligned}&\varphi '= \arg \left[ {J_0\left( \frac{k_tk^2\left( S_r-iS_i\right) \left( \delta ^{'}-i\delta _i^{'}\right) \rho _1 }{2L^2 \left( {\delta ^{'}}^2+{\delta ^{'}_i}^2\right) } \right) }\right] \nonumber \\&=\arctan \left[ \tan \left( \frac{{\mathcal {R}}\left( S_r\delta ^{'} -S_i\delta ^{'}_i\right) \rho _1}{{\delta ^{'}}^2+{\delta ^{'}_i}^2} -\frac{\pi }{4}\right) \right. \nonumber \\&\left. \tanh \left( \frac{{\mathcal {R}} \left( S_i\delta ^{'}+S_r\delta ^{'}_i\right) \rho _1}{{\delta ^{'}}^2+{\delta ^{'}_i}^2}\right) \right] \nonumber \\&\varphi ' \xrightarrow [~~~~~~~~\textrm{if}~~x\ge 3~~~~~~~~]{\tanh \left( x\right) \approx 1}\nonumber \\&\frac{{\mathcal {R}}\left( S_r\delta ^{'}-S_i\delta ^{'}_i\right) \rho _1}{{\delta ^{'}}^2+{\delta ^{'}_i}^2} -\frac{\pi }{4} ~~. \end{aligned}$$
(21)

The parameter \({\mathcal {R}}\) equals the constant coefficients of Bessel’s function arc. In Eq. (20), the first term describes the phase of constant parameters. The second one refers to Bessel’s phase, which demonstrates the aspheric nature of the formula. In addition, besides \(W^2=W_1^2\) and \(\phi -\phi _0=2n\pi\) conditions, the eigenmode condition requires that the argument of the Bessel function be the same after one round trip, i.e., it is equal to \(k_t\); so, we have:

$$\begin{aligned} \frac{k_tk^2\left( S_r-iS_i\right) \left( \delta ^{'}-i\delta _i^{'}\right) }{2L^2 \left( {\delta ^{'}}^2+{\delta ^{'}_i}^2\right) }= & {} kt\nonumber \\ ~~~\Longrightarrow \frac{k^2\left( S_r-iS_i\right) \left( \delta ^{'}-i\delta _i^{'}\right) }{2L^2 \left( {\delta ^{'}}^2+{\delta ^{'}_i}^2\right) }= & {} 1. \end{aligned}$$
(22)

Proper working for the axicon-based thin disk resonator requires the three mentioned conditions, i.e., Eqs. (17), (19) and (22)are simultaneously satisfied very well. In addition, simultaneously solving Eqs. (17), (19) and (22) is essential to get more information about cavity parameters. They are called self-consistency equations.

5 Results and discussion

The previous section obtained a relation for analytically describing the field distribution of resonant cavity mode on the OC plane, as can be seen in Eq. (16). One of the significant properties of this equation is the transverse distribution of the beam after one round-trip still is Bessel–Gauss with some multiplied terms. It directly shows the nondiffracting characteristics of the output beam.

By considering the Bessel beam as an initial beam with \(W_0 \longrightarrow \infty\), the beam pattern also is a Bessel with \(W_0 \longrightarrow \infty\) after one round trip through a plane-plane axicon based the resonator; this is described as follows:

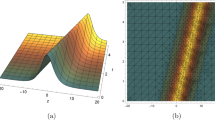
$$\begin{aligned} u'_{\textrm{Output}}\left( \rho _1\right) =J_0\left( -6k_t\rho _1\right) \exp \left[ -i\frac{Lk_t^2}{2k}\right] . \end{aligned}$$
(23)

Equation (23) shows that the beam profile still is near-ideal-Bessel after one round trip. This result shows the ability of our presented approach. The transverse beam distribution in front of the OC mirror is plotted in Fig. 3 when a Bessel beam is considered as an initial incidence beam. In fact, the power spectrum of the Bessel beam is a ring in k-space (Fourier transformation); it directly shows the non-diffracting characteristics of the Bessel beam. In practice, one can use a lens for the Fourier transform of a Bessel beam [53].

Fig. 3
figure 3

Shows the Bessel beam distribution in the front of the OC

Full size image

For start the numerical simulation process, i.e., the well-known classic round-trip Fox–Li method, it is worthwhile to mention that one needs to have some considerations. Along with Using the trapezoidal method to perform the numerical process, the signal reaches its stability after about 400 round trips. In addition, the transverse radius, wavelength, radial step, refractive index, and the wedge angle of the axicon are \({a_1 = 5}\) mm, \({\theta _0 = 0.0071}\) rad, \({\lambda = 1030}\) nm, \({\delta r = 3.3~\mu }\)m, and \({\alpha = 0.5^{\circ }}\), respectively.

In the following, as shown in Fig. 4, the results of the analytical approach, according to Eq. (16), are depicted (blue-circle-line). The amplitude \(\left| U\right|\) at the OC surface in Fig. 4a, b has been plotted for \(0.1 \le R_{\textrm{OC}}/100\,L \le 0.5\) and \(1\le R_{\textrm{OC}}/100\,L \le \infty\), respectively.

Fig. 4
figure 4

The results of the numerical and analytical approaches are plotted with respect to \(R_{\textrm{OC}}\). The red line and blue line indicate the numerical results, and the analytical results, respectivly. Thin-disk is assumed to be flat

Full size image

The simulations show that for \(R_{\textrm{OC}}\) equal to L, the blue-circle and red-solid lines did not find a perfect match. On the other hand, the match expectation is satisfied for \(R_{\textrm{OC}}\) equal to 2L and one other large radius of curvatures; at least the beam size and lateral rings proximate matching could be observed. For more accuracy, the analytical approach can display its success when only a relatively large radius of curvatures is considered (i.e., \(R_{\textrm{OC}}\ge 30L\)) and the transverse radius of OC is restricted in the interval \(\left[ -0.5~0.5 \right]\) mm, as can be seen in Fig. 3a. What’s more, after \(R_{\textrm{OC}}>L\), the optical cavity is no longer a hemispherical optical cavity; perhaps, it is the reason for matching the beam sizes after \(R_{\textrm{OC}}=L\). It seems, therefore, reasonable to consider that perfect matching is visible for \(R_{\textrm{OC}}\) higher than 30L.

The transverse distributions of the output Bessel–Gauss beam are plotted for the different values of the radius curvature of the thin disk, as can be seen in Fig. 4. At this stage, OC is assumed to be flat. One can directly understand from Fig.  4 that the analytical results can not satisfy the numerical ones. However, the analytical approach illustrates a sensible behavior when higher radius curvatures are considered, namely, the beam sizes are stable. Also, the analytical method can not work effectively for radius curvatures smaller than 10L, especially for \(R_{\textrm{TD}}\) equal to 2L; so the full width half maximum (FWHM) of the blue-circle-line can not be match with the red line one. The results show that small \(R_\textrm{TD}\)’s effects on the beam size are significant. On the other hand, the importance of the back mirror (thin disk) on the cavity modes is visible when one considers the slight radius curvatures for the back mirror such that the beam size does not possess predictable variations. Also, an interesting case is that a Gaussian-like beam appears for \(R_{\textrm{TD}}\) equal to 2L. It shows that the effect of the axicon on the circulating wave has vanished.

The curved plotted for \(R_{\textrm{TD}}=2L\) has a Gaussian-like shape. A reason for describing such a shape may be that, as shown in Eq. (16), the Bessel function arc’s numerical value is the multiple of order \(10^{-12}\), and this could cause \(J_0\left( \rho _1\right) \approx 1\). Of course, the Bessel function has no answer for such values. Properly, one can correct this fault by expanding the Bessel function. Control capability of the beam size in a way simultaneous with the laser’s intracavity generation can be helpful in various fields, such as medicine and technology (Fig. 5).

Fig. 5
figure 5

The comparative mode between the analytical and numerical approaches for \(R_{\textrm{TD}}\) a smaller than 50L and b larger than 50L. The flat \(\mathrm OC\) mirror is considered

Full size image

As presented data, the analytical approach can predict the W of the traveled Bessel–Gauss beam through the ABCD optical system. It is in a good agreement with numerical results for a large radius of curvatures.

\(\gamma ^2\) and \(q^2\) parameters contain a real part and an imaginary part; see Eqs. (11) and (15). One can discuss their real and imaginary parts more accurately for some particular cases. To have a general view of particular cases, see Table 1. It is worth mentioning that the approximation \(\left( \frac{k}{2L}\right) ^2 \ll \left( \frac{1}{W_1}\right) ^4\) is used. The results show that the \(q^2\) parameter differs from others only for \(R_{\textrm{OC}}=2L\) and \(R_{\textrm{TD}}= L\) conditions, where they are real. It means that only the Gaussian beam waist is modulated, and the phase term vanishes during propagation from OCM to TD. In addition, the reflection phase of curved TD vanished. It seems,therefore, that the \(R_{\textrm{OC}}=2L\) and \(R_{\textrm{TD}}= L\) condition is the critical curvature for resonator.

However, for \(R_{\textrm{OC}}=L\) and \(R_{\textrm{TD}} \gg L\) and for \(R_{\textrm{OC}} \gg L\) and \(R_{\textrm{TD}} \gg L\) conditions, \(q^2\) is the same and \(\gamma ^2\) differs as the \(-\frac{ik}{L}\) value. It shows that the resonator behavior is similar for both conditions and predicts that the output profile must be the same. These results are viewed in the numerical simulations, and these show that our analytical approach can adequately describe the axicon-based thin-disk resonator.

Table 1 The values of \(q^2\) and \(\gamma ^2\) parameters in specific cases; \(W_1\) is the order of micrometer, and L and \(\lambda\) are equal to 0.3514 m and 1030 nm
Full size table

6 Conclusion

This paper employed an analytical approach to study self-consistency equations of an axicon-based thin-disk laser resonator. A Bessel–Gaussian profile was assumed to be the distribution function in the reference plane. The Bessel–Gauss beam propagation, through an ABCD optical system, was described within the Huygens–Fresnel diffraction integral formula framework. The ROCs of TD and OC mirrors effects on the cavities eigenmode were surveyed and then compared to more precise numerical simulations based on the Fox-Li method. The intensity transverse distributions obtained in front of the OC mirror from the analytical method were in an excellent agreement with those from the numerical simulation under conditions of the large radius of curvatures. The presented job could adequately describe the numerical results in the case of \({R_\mathrm{OC\left( TD\right) }}\ge {100\,L}\) and give more information about the self-consistency equations; i.e, phase shift and spot-size of the output beam after passing through the resonator’s optical elements. In addition, the self-consistency equation can predict the output near ideal Bessel beam based on the \({R_\mathrm{{OC}}}=L\) and \(\mathrm {R_{\textrm{TD}}=\infty }\) consideration, as reported before [52]. Furthermore, the presented technique has the potential to investigate the effects of the axicon’s backside curvature or active medium’s curvature on the resonant modes of the cavity and the diffraction loss. Also, its other advantage is the ability to describe any transmission medium with linear phase, apart from axicon.

7 Appendix

This section presents the mathematical approach based on the Fourier transform to obtain Eq.(4). Now, we start from the Parseval theorem, which is defined as follows [54]:

$$\begin{aligned} \int \limits _{0}^{\infty } f_1\left( r\right) f_2\left( r\right) d^2{\varvec{r}}=\frac{1}{\left( 2\pi \right) ^2 }\int \limits _{0}^{\infty } F_1\left( k\right) F_2\left( k\right) d^2{\varvec{k}}. \end{aligned}$$
(24)

where \({F_1\left( k\right) }\) and \({F_2\left( k\right) }\) are,respectively, the Fourier Transforms of \({f_1\left( r\right) }\) and \({f_2\left( r\right) }\).

As the next step, firstly, we get the answer of the following integral (note that \(q>0\)):

$$\begin{aligned} \xi _1=\int \limits _{0}^{\infty }rdrJ_0\left( \alpha r\right) \exp \left( -q^2r^2-ibr\right) . \end{aligned}$$
(25)

One can solve the integral of Eq. (25) by demonstrating it in 2D position space and going to the Fourier space. By comparing the left side of Eqs.(24) and (25), we have:

$$\begin{aligned} f_1\left( r\right)&=\exp \left( -q^2r^2-ibr\right) \nonumber \\ f_2\left( r\right)&=\frac{1}{2\pi }J_0\left( \alpha r\right) . \end{aligned}$$
(26)

By some simple algebraic calculations, it is easy to show that the Fourier transformation of Eq. (26) is as follows,

$$\begin{aligned} \begin{aligned} {\tilde{F}}_1\left( k\right)&=\int \limits _{0}^{\infty } 2\pi rdrf_1\left( r\right) e^{-i{\varvec{k}}\cdot {\varvec{r}}}\\&=2\pi \int \limits _{0}^{\infty } rdre^{-q^2r^2-\left( 1+\frac{b}{k} \right) ikr} \\&=\frac{\pi }{q^2}\exp \left( -\frac{k^2S^{\prime 2}}{4q^2}\right) \end{aligned} \end{aligned}$$
(27)

where \(S^{\prime }=1+\frac{b}{k}\). Also, the Hankel transform of the Bessel function is [55]:

$$\begin{aligned} {\tilde{F}}_2\left( k\right) =\frac{\delta \left( k-\alpha \right) }{\alpha } \end{aligned}$$
(28)

By inserting Eq. (26) and Eq. (27), respectively, on the left and right sides of Eq. (24), one can obtain

$$\begin{aligned}{} & {} \int \limits _{0}^{\infty } J_0\left( \alpha r\right) \exp \left( -q^2r^2-ibr\right) rdr \nonumber \\{} & {} = \frac{1}{\left( 2\pi \right) ^2 } \int \limits _{0}^{\infty } \frac{\pi }{q^2}\exp \left( -\frac{k^2S^{\prime 2}}{4q^2}\right) \frac{\delta \left( k-\alpha \right) }{\alpha }d^2{\varvec{k}} \end{aligned}$$
(29)

For \(k=\alpha\), have:

$$\begin{aligned} \xi _1= & {} \int \limits _{0}^{\infty } J_0\left( \alpha r\right) \exp \left( -q^2r^2-ibr\right) rdr \nonumber \\= & {} \frac{1}{q^2 } \exp \left( -\frac{\left( \alpha +b\right) ^2}{4q^2}\right) \end{aligned}$$
(30)

As the next step, we solve the following integral,

$$\begin{aligned} \xi _2=\int \limits _{0}^{\infty } J_0\left( \alpha r\right) J_0\left( \beta r^{\prime } r\right) \exp \left( -q^2r^2-ibr\right) rdr \end{aligned}$$
(31)

Based on Graf’s addition theory, it is easy to show that,

$$\begin{aligned}{} & {} J_0\left( \alpha r\right) J_0\left( \beta r^\prime r\right) =\int \limits _{0}^{2\pi } \frac{d\theta }{2\pi }J_0\left( r\sqrt{\alpha ^2+\beta ^2 r^{\prime 2}-2\alpha \beta r^{\prime }\cos \theta } \right) e^{-in\theta } \end{aligned}$$
(32)

Now, by inserting Eq. (32) in Eq. (31), we have:

$$\begin{aligned}{} & {} \xi _2=\int \limits _{0}^{2\pi }\frac{d\theta }{2\pi }e^{-in\theta }\int \limits _{0}^{\infty } J_0\left( r\sqrt{\alpha ^2+\beta ^2r^{\prime 2}-2\alpha \beta r^{\prime }\cos \theta } \right) \nonumber \\{} & {} \quad \exp \left( -q^2r^2-ibr\right) rdr \end{aligned}$$
(33)

The second integral is similar to the integral in Eq. (30); so for Eq. (33), we have:

$$\begin{aligned} \xi _2= & {} \int \limits _{0}^{2\pi }\frac{d\theta }{2\pi q^2}e^{-in\theta }\nonumber \\{} & {} \exp \left( -\frac{\left( \sqrt{\alpha ^2+\beta ^2r^{\prime 2}-2\alpha \beta r^{\prime }\cos \theta }+b\right) ^2}{4q^2} \right) \end{aligned}$$
(34)

After squaring the power term of exponential function and using the Taylore series for the expansion of the radical term, we have:

$$\begin{aligned} \begin{aligned} \xi _2&=\exp \left( -\frac{\left( 1+\frac{b}{\alpha }\right) ^2 \alpha ^2}{4q^2}-\frac{\left( 1+\frac{b}{\alpha }\right) \beta ^2r^{\prime 2}}{4q^2}\right) \int \limits _{0}^{2\pi } \frac{d\varphi }{2\pi q^2}e^{-in\theta }\\&\exp \left( \frac{1}{2q^2}\left( \left( 1+\frac{b}{\alpha }\right) \alpha \beta r^{\prime }-\frac{b}{2\alpha ^2}\beta ^3 r^{\prime 3}\right) \cos \theta \right) . \end{aligned} \end{aligned}$$
(35)

Now, by the taking account the integration by substitution \(\theta =\varphi -\frac{\pi }{2}\) and by applying the simple algebraic, we have:

$$\begin{aligned} \begin{aligned} \xi _2&=\frac{1}{2q^2}exp\left( -\frac{S^4\alpha ^2}{4q^2} -\frac{S^2\beta ^2r^{\prime 2}}{4q^2}\right) \int \limits _{0}^{2\pi } \frac{d\varphi }{2\pi } e^{-in\varphi }e^{-in\frac{\pi }{2}} \\&\quad \exp \left[ i\left( \frac{-i}{2q^2}\left( S^2\alpha \beta r^{\prime }-\frac{b}{2\alpha ^2}\beta ^3 r^{\prime 3}\right) \right) \sin \varphi \right] \end{aligned} \end{aligned}$$
(36)

where \({S^2=1+\frac{b}{\alpha }}\). Moreover, it is well known that [56],

$$\begin{aligned} \begin{aligned} J_n\left( \frac{-i}{2q^2}\left( S^2\alpha \beta r^{\prime } -\frac{b}{2\alpha ^2}\beta ^3r^{\prime 3}\right) \right)&=\int \limits _{0}^{2\pi }\frac{d\varphi }{2\pi }e^{-in\varphi }e^{-in\frac{\pi }{2}}\\&\exp \left( i\left( \frac{-i}{2q^2}\left( S^2\alpha \beta r^{\prime }-\frac{b}{2\alpha ^2}\beta ^3r^{\prime 3}\right) \right) \sin \varphi \right) \end{aligned} \end{aligned}$$
(37)

Finally, by substituting Eq. (37) in Eq. (35), we have (note: \({Re~~q>0;~~n>-1}\)):

$$\begin{aligned} \begin{aligned} \xi _2&=\int \limits _{0}^{\infty } J_n\left( \alpha r\right) J_n\left( \beta r^{\prime } r\right) \exp \left( -q^2r^2-ibr\right) rdr\\&=\frac{1}{2q^2}i^nJ_n\left( \frac{-i}{2q^2}\left( S^2\alpha \beta r^{\prime }-\frac{b}{2\alpha ^2}\beta ^3r^{\prime 3}\right) \right) \\&\exp \left( -\frac{S^4\alpha ^2}{4q^2}-\frac{S^2\beta ^2r^{\prime 2}}{4q^2}\right) \end{aligned} \end{aligned}$$
(38)

It is worth to mentioning that the second term in the Bessel function arc is ignorable for small \(\textrm{r}\); so by using the \(\mathrm {i^nJ_n(-ix)=i^{-n}J_n(ix)}\) equality, we have:

$$\begin{aligned} \begin{aligned} \xi _2&=\int \limits _{0}^{\infty } J_n\left( \alpha r\right) J_n\left( \beta r' r\right) \exp \left( -q^2r^2-ibr\right) rdr\\&=\frac{1}{2q^2}i^{-n}J_n\left( \frac{i}{2q^2}S^2\alpha \beta r^{\prime }\right) \exp \left( -\frac{S^4\alpha ^2}{4q^2}-\frac{S^2\beta ^2}{4q^2}r^{\prime 2}\right) \end{aligned} \end{aligned}$$
(39)

More precisely, we have numerically solved the left side of Eq.(39) by the trapezoidal method and compared it with the analytical answer of Eq.(39) (i.e., the right side), as can be seen in Fig. 6. Note that the red-line and black-line curves belong to the analytical and numerical solutions, respectively. The conformity between both curves is visible.

Fig. 6
figure 6

Comparison of the numerical method and the analytical approach

Full size image