Unfolding frequency and spatial multimode through parametric amplified cascade four-mode process

Abstract

We present a theoretical and experimental investigation of four quantum correlated beams’ properties generated through the parametrically amplified cascaded four-wave-mixing (PA-CFWM) process in rubidium vapor. The research explores the signal excitation efficiency of different energy levels by scanning the probe detuning and identifies three different ways to light up the cascade four-mode process. Specially, two pairs of Einstein Podolsky Rosen (EPR) entangled light fields can be generated, leading to a quantum correlation between two previously uncorrelated signals. In addition, the multimode characteristics of output signals are observed in the frequency and spatial domain, and the number of frequency multimode and spatial multimode can be controlled through dressing effect. In our system, the number of spatial modes in four entangled beams can reach up to 1200. Further, the line shift of the PA-CFWM signal resonant frequency can be controlled by experimental parameters, such as the detuning and power of the dressing field. These results are important not only for fundamental tests of quantum effects but also for their numerous applications in quantum technologies, such as quantum imaging and quantum metrology.

1 Introduction

The study of multimode properties has greatly contributed to the development of quantum information technology [1, 2]. Multimode systems expand the capacity of quantum communication systems in the frequency domain and provide more modes with better resolution for quantum entanglement imaging in the spatial domain [3,4,5]. There are two main types of multimode systems: spatial multimode, which transverses to the direction of propagation (cross-section and divergence), and temporal multimode, which is defined along the direction of propagation (time and frequency). The optical nonlinear effect of the medium is the main mechanism for generating nonclassical multimode light.

Three mainstream methods are used to generate nonclassical multimode light. The first method is the spontaneous parameter down conversion (SPDC) of crystals or quasi-phase-matching crystals based on second-order nonlinear effects [6]. Multimode photons generated by this approach usually has big emission bandwidth. However, its disadvantages of very short coherence time and coherence length limit its application in long-distance quantum communication. The second method is generation of optical parameters including optical parametric amplification (OPA) with no resonant cavity and optical parametric oscillation (OPO) requiring an optical resonant cavity, which is also based on the crystal's second-order nonlinear optical effect [7]. The third method is the non-degenerate four-wave mixing (FWM) process based on third-order optical nonlinear effect without any need for an optical cavity because of the embedded nonlinearity and spatial separation of the twin output fields [8]. Compared to the first two methods, the FWM system still possesses narrower bandwidth, longer coherence time and coherence length, higher conversion efficiency and spectral brightness [9, 10]. Hence it is expected to be applied in further multimode configurations such as cascaded four-wave mixing (CFWM) process, quantum entangled imaging and long-distance quantum communication.

In the future, quantum technology will be required to generate and control multiple photons and construct a large quantum network. A combination of multiple SPDC processes has been used to obtain entangled multiphoton [4, 11]. Tripartite telecom photons can be generated via a cascaded process [12, 13]. In addition, investigations of the dressing mechanisms and interactions are highly useful for generating high-order nonlinear optical outcomes [14]. And in the hot Rb atomic vapor, the weak probe light of the same frequency is injected into the Stokes signal channel of the spontaneous four-wave mixing process [15], the weak signal will be amplified, and the energy and momentum conservation conditions are satisfied at the same time. A FWM process in hot rubidium vapor is an efficient method to generate and manipulate nonclassical optical nonlinearities, which can successfully generate a pair of multimode intensity-dependent beams and quantum entangled images [16,17,18,19,20]. And the generation of three beams with strong quantum correlation by cascading two four-wave mixing processes in hot atomic vapor has been demonstrated [21]. Even the use of two/multiple pump beams to generate four-mode [22] or ten-mode correlated beams [23, 24] has been demonstrated experimentally or theoretically.

Many investigations have been done on the multimode characteristics. The study of spatio-temporal properties theoretically and experimentally was reported, where a type I LBO crystal is used to generate the spontaneous parametric emission [25]. And a phase sensitive amplification (PSA) achieved via a FWM process in Rb vapor has been researched, which can support at least hundreds of spatial modes [26]. Our group reported the multimode research in a system coexisting of four- and six-wave mixing (SWM) with good responses to the dressing modulation [27] and analysis of multimode spatial and frequency degrees of freedom in a parametric amplified multi-wave mixing (MWM) process where dressing lasers are used to modulate the phase-matching conditions and nonlinear susceptibilities [28]. Nevertheless, the relationship between frequency and spatial multimode as well as spectrum and entanglement imaging based on parametric amplified CFWM entangled four beams is valuable for research.

This paper proposes to generate multimode quantum states by parametric amplified cascaded four-wave mixing process through injection, and study the relationship between frequency multimode and spatial multimode from the analysis of theory and experiment. The frequency domain and the spatial domain correspond to each other through dressing coherent channels, the evolution of a single peak into multiple gain peaks is observed through modulating the detuning, power or angle of the two pump fields. In the spatial domain, the area of the spot becomes larger, and the spatial spot evolves into multiple unevenly distributed light spots.

2 Experimental setup and basic theory

2.1 Experimental setup

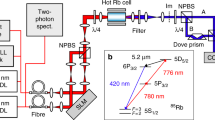
Our experiments were performed in a paraffin-coated ⁸⁵Rb vapor chamber at 125 °C as shown in Fig. 1a, the first strong pump laser beam E₁ (frequency ω₁, wave vector k₁, and Rabi frequency G₁, vertical polarization) is generated by a tunable semiconductor Topica laser through a tapered laser amplifier, and another pump laser E₃ (ω₃, k₃ and G₃, vertically polarized) is obtained from the same Toptica laser by beam splitting in a half-wave plate (λ/2) and polarization beam splitter (PBS) and then frequency shifted by an acousto-optic modulators (AOMs) by 0.8 GHz. The angle between the laser beams E₁ and E₃ generated by the same Toptica laser is 0.48°; the weak probe laser beam E₂ (ω₂, k₂ and G₂, horizontal polarization) is generated by another Toptica laser, where G_i = µ_iE_i/h_i (i = 1,2,3) is the Rabi frequency with transition dipole moment µ_i. When the phase-matching condition in Fig. 1b is satisfied, four FWM processes are generated simultaneously: FWM1 (2k₁ = k_S1 + k_S2), FWM2 (k₁ + k₃ = k_S1 + k_S4), FWM3 (k₁ + k₃ = k_S2 + k_S3), and FWM4 (2k₃ = k_S3 + k_S4). And four signal beams E_s1, E_s2, E_s3, and E_s4 will be formed. To detect the spatial image and spectral intensity of the signal, one branch of the beam splitter is coupled to a charge-coupled device (CCD) for spatial image, and the other to a balanced photodetector (PD) for spectral image.

Fig. 1

a Simple experimental setup for the PA-CFWM process. b Spatial distribution and momentum relations of the light spots

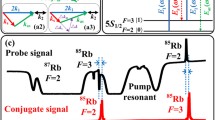
In Fig. 2a, when the independent laser is used to scan the detuning Δ_s1 in a large range of the probe field, six different output signals (a–f) appear in the probe (E_s1) channel. With ω₁—ω_s1 > 0, curves (a–d) in Fig. 2a output signals are obtained, and (e–f) in Fig. 2a output signals are obtained with ω₁—ω_s1 < 0. At the same time, the conjugate (E_s2) channel, cascade I (E_s3) channel, and cascade II (E_s4) channel will appear with b and f output signals. Figure 2b1–b6 shows the energy-level diagrams that correspond to output (a–f) signals. Figure 2b2 shows that the Λ-type atomic energy-level system of the curve (b), which contains two hyperfine ground states 5S_1/2[F = 2(|1 >), 5S_1/2[F = 3(|2 >)] and a excited state 5P_1/2[F = 2(|3 >)]. The laser beam E₁ acts on the energy levels |1 > →|3 > and |2 > →|3 >, and the detuning Δ₁ and Δ₂, respectively. The laser beam E₂ transitions at the energy level |2 > →|3 >, and the detuning is Δ_s1. The laser beam E₃ connects the energy levels |1 > →|3 > and |2 > →|3 > with a detuning Δ₃ and Δ₄, respectively. Frequency detuning Δ_i denotes the difference between the resonant transition frequency Ω_i and the frequency ω_i of field E_i (i = 1, 2, 3, 4). In the large-scale scanning in Fig. 2a, the intensity of the (b) signal is stronger ten times than the (a) signal. The reason is that the detuning of E_s2 in the (a) signal (Fig. 2b1) is larger by 0.8 GHz than that of the (b) signal (Fig. 2b2), and E_s1 and E_s2 signals are generated synchronously, so the (a) signal in probe channel is weak. Similarly, the detuning of the E_s2 in the (e) signal (Fig. 2b5) is 0.8 GHz larger than that of the (f) signal (Fig. 2b6), so the (e) signal is weak. The low generation efficiency of the (c) and (d) signals in energy level of Fig. 2b3 and (b4) is because of the degenerate energy levels. Meanwhile, the signal gain is also related to the dressing effect. Because the dressing effect is inversely proportional to the detuning of the dressing field, the (e) signal is stronger than (a) signal due to the smaller dressing effect by comparing the detuning Δ₁ of the dressing field E₁ in Fig. 2b1 and b5.

Fig. 2

a Measurement of the probe transmission (probe) signal, the corresponding conjugate signal, the cascaded I channel signal, and the cascaded II channel signal varying with the detuning of the probe field. b1–b6 Energy level diagrams of the a-f peaks

As shown in Fig. 2b1, when the weak probe E₂ is injected into the E_s1 channel, both FWM1 and FWM2 processes have the injection of probe E₂, which is equivalent to two pairs of EPR entangled beams (E_s1 and E_s2, E_s1 and E_s4) as input signals, corresponding Hamilton quantity are:

$$H_{{1}} = i\hbar (\kappa_{1} \hat{a}_{1}^{\dag } \hat{a}_{2}^{\dag } {\text{) + H}}{\text{.c}}{.}$$

(1)

$$H_{{1}} = i\hbar (\kappa_{1} \hat{a}_{1}^{\dag } \hat{a}_{4}^{\dag } {\text{) + H}}{\text{.c}}{.}$$

(2)

The output signals of two FWM processes are used as input to the PA-CFWM process to generate four brightly entangled beams [30]. Notably, EPR injection affects the quantum properties and produces a PA-CFWM process with high production efficiency [31]. In addition to lighting the PA-CFWM process by two FWM processes as injection, there are also cascaded three-mode processes as injection [32], the first case (CFWM1), E_s1, E_s2, E_s3 signals are injected into the system, equivalent to a pair of strong EPR injections (E_s1 and E_s2), and the second case (CFWM2), E_s1, E_s2, E_s4 signals are injected into the system, equivalent to two pairs of strong EPR injections (E_s1, E_s2 and E_s1, E_s4). The corresponding Hamiltonian for these injections are:

$$H_{{1}} = i\hbar (\kappa_{1} \hat{a}_{1}^{\dag } \hat{a}_{2}^{\dag } + \kappa_{2} \hat{a}_{2}^{\dag } \hat{a}_{3}^{\dag } { + }\kappa_{3} \hat{a}_{1}^{\dag } \hat{a}_{3}^{\dag } {\text{) + H}}{\text{.c}}{.}$$

(3)

$$H_{{1}} = i\hbar (\kappa_{1} \hat{a}_{1}^{\dag } \hat{a}_{2}^{\dag } + \kappa_{2} \hat{a}_{1}^{\dag } \hat{a}_{4}^{\dag } + \kappa_{3} \hat{a}_{2}^{\dag } \hat{a}_{4}^{\dag } {\text{) + H}}{\text{.c}}{.}$$

(4)

and eight-wave mixing processes (E_s1, E_s2, E_s3, and E_s4) as injection, the corresponding Hamiltonian is:

$$H_{{1}} = i\hbar \kappa_{{1}} \hat{a}_{{1}}^{\dag } \hat{a}_{{2}}^{\dag } \hat{a}_{{3}}^{\dag } \hat{a}_{{4}}^{\dag } + {\text{H}}{\text{.c}}{.}$$

(5)

Theoretically, two generated beams of idle signals E_s1 and E_s3 are not in a four-wave mixing process and there is no quantum correlation between them. However, from Fig. 2(a), the cascaded I (E_s3) channel signal can be observed, indicating that EPR injection causes a quantum correlation between the E_s3 signal and the E_s1 signal.

2.2 Frequency multimode

The interaction Hamiltonians of entangled four beams generated by cascaded FWM amplifier can be expressed as

$$H = i\hbar \kappa_{1} \hat{a}_{1}^{\dag } \hat{a}_{2}^{\dag } { + }i\hbar \kappa_{2} \hat{a}_{2}^{\dag } \hat{a}_{3}^{\dag } { + }i\hbar \kappa_{3} \hat{a}_{4}^{\dag } \hat{a}_{1}^{\dag } { + }i\hbar \kappa_{4} \hat{a}_{3}^{\dag } \hat{a}_{4}^{\dag } {\text{ + H}}{\text{.c}}{.}$$

(6)

where $\hat{a}_{i}^{\dag }$ (i = 1,2,3,4) is the boson creation operator that act on the electromagnetic excitation of the anti-Stokes and Stokes channel, $k_{1} = - i\varpi_{1} \chi_{1}^{\left( 3 \right)} E_{1}^{2} /2c$, $k_{2} = - i\varpi_{2} \chi_{2}^{\left( 3 \right)} E_{1} E_{3} /2c$, $k_{3} = - i\varpi_{3} \chi_{3}^{\left( 3 \right)} E_{3}^{2} /2c$, $k_{4} = - i\varpi_{4} \chi_{4}^{\left( 3 \right)} E_{1} E_{3} /2c$, are the pumping parameters of the SP-FWM. The boson creation (-annihilation) operator satisfies the Heisenberg operator equation of motion in the dipole approximation, as follows $\partial E_{s1} /c\partial z = k_{1} E_{s2} E_{1}^{2} + k_{2} E_{s4} E_{1} E_{3}$, $\partial E_{s2} /c\partial z = k_{1} E_{s1}$$E_{1}^{2} + k_{2} E_{s3} E_{1} E_{3}$, $\partial E_{s3} /c\partial z = k_{3} E_{s2} E_{1} E_{3} + k_{4} E_{s4} E_{3}^{2}$, and $\partial E_{s4}$ $/c\partial z = k_{4} E_{s3} E_{3}^{2} + k_{3} E_{s1} E_{1} E_{3}$.$\chi_{si}^{(3)} = N\mu_{1}^{2} \mu_{2}^{2} *\rho^{(3)} /G^{3} \hbar^{3} \varepsilon_{0}$ can be described by the perturbation chains, where N is atom density, ε₀ is permittivity, and µ_i is the transition dipole moment between the energy levels.

Guided by the Liouville pathway [33], the third-order density matrix elements of E_s1, E_s2, E_s3, and E_s4 signals can be given by

$$\rho_{S1}^{{({3})}} = \frac{{ - iG_{1}^{2} G_{S2} }}{{\left( {\Gamma_{32} + i\Delta_{2} } \right)(\Gamma_{12} + i\delta_{2} + D_{1} )(\Gamma_{32} + i\delta_{2} + i\Delta_{1} + D_{2} )}}$$

(7)

$$\rho_{S2}^{{({3})}} = \frac{{ - iG_{1}^{2} G_{S1} }}{{(\Gamma_{31} + i\Delta_{1} )(\Gamma_{21} + i\delta_{1} )(\Gamma_{31} + i\delta_{1} + i\Delta_{2} )}}$$

(8)

$$\rho_{S3}^{{({3})}} = \frac{{ - iG_{3}^{2} G_{S4} }}{{(\Gamma_{32} + i\Delta_{4} )(\Gamma_{12} + i\delta_{4} )(\Gamma_{32} + i\delta_{4} + i\Delta_{3} )}}$$

(9)

$$\rho_{S4}^{{({3})}} = \frac{{ - iG_{3}^{2} G_{S3} }}{{(\Gamma_{31} + i\Delta_{3} )(\Gamma_{21} + i\delta_{3} )(\Gamma_{31} + i\delta_{3} + i\Delta_{4} )}}$$

(10)

where Δ_S1, Δ_S2, Δ_S3, and Δ_S4 represent the frequency detuning of the E_S1, E_S2, E_S3, and E_S4 signals. Frequency detuning Δ_i denotes the difference between the resonant transition frequency Ω_i and the frequency ω_i of E_i. The Δ₁, Δ₂, Δ₃, and Δ₄ are the frequency detuning of the E_i (i = 1, 2, 3, 4) field, respectively. Γ_ij = (Γ_i + Γ_j)/2 is the de-coherence rate between |i and |j, G_i = μ_ijE_i/ħ is the Rabi frequency of E_i, δ_i(i = 1,2,3,4) represents the quantum shift of the E_Si(i = 1,2,3,4) signal, respectively, which can be expressed as Δ_Si = Ω_i − ω_Si = Ω_i − (ϖ_Si + δ_i) = Δ_i − δ_i, then δ_i = Δ_i − Δ_Si.

Considering the parallel double-dressing effect of E₁ and E₃, it can be rewritten as: D₁ = G₁²/ (Γ₃₂ + iδ₂ + iΔ₁) and D₂ = G₃²/ (Γ₁₂ + iδ₂ + iΔ₁ − iΔ₃). When changing the angle α between the pump fields E₁ and E₃, which is equivalent to adding an additional phase factor e^iΦ to the dressing term, the dressing terms D₁ = G₁²/ (Γ₃₂ + iδ₂ + iΔ₁) and D₂ = G₃²/ (Γ₁₂ + iδ₂ + iΔ₁ − iΔ₃) can be modified to D'₁ = G₁²e^iΦ/ (Γ₃₂ + iδ₂ + iΔ₁) and D'₂ = G₃²e^iΦ/ (Γ₁₂ + iδ₂ + iΔ₁ − iΔ₃).

Also, with E₂ and E₁ viewed as probe and coupling fields, respectively, the first-order density matrix of the probe transmission signal with dressing effect is EIA (electromagnetic induction absorption), as follows:

$$\rho_{s2}^{(1)} = iG_{2} /\left[ {\left( {\Gamma_{32} + i\Delta_{s2} } \right) + \left| {G_{1} } \right|^{2} /\left[ {\Gamma_{22} + i\left( {\Delta_{s2} - \Delta_{1} } \right)} \right]} \right]$$

(11)

With a strong pumping field E₁ switched on, the second-order FL signal is generated through the perturbation chain $\rho_{11}^{(0)} \mathop{\longrightarrow}\limits^{{E_{1} }}\rho_{31}^{(1)} \mathop{\longrightarrow}\limits^{{ - E_{1} }}\rho_{11}^{(2)}$, the diagonal density matrix element is given by:

$$\rho_{FL}^{\left( 2 \right)} = \frac{{ - \left| {G_{1} } \right|^{2} }}{{(\Gamma _{31} + i\Delta _{1} + \left| {G_{2} } \right|^{2} /\left( {\Gamma _{21} + i\Delta _{1} - i\Delta _{2} } \right))(\Gamma _{33} )}}$$

(12)

2.3 Spatial multimode

To describe the spatial splitting of the signal E_s1, E_s2, E_s3, and E_s4 by lasers E₁ and E₃ beams via kerr nonlinearity, the propagation equations are introduced as following:

$$\frac{{\partial E_{{s{1}}} }}{\partial z} - \frac{{i\nabla_{ \bot }^{2} E_{s1} }}{{{2}k_{s1} }} = \frac{{ik_{s1} }}{{n_{1} }}[n_{2}^{S1} \left| {E_{s1} } \right|^{2} + 2n_{2}^{X1} \left| {E_{1} } \right|^{2} + 2n_{2}^{X2} E_{1} E_{{3}} ]E_{s1}$$

(13)

$$\frac{{\partial E_{{s{2}}} }}{\partial z} - \frac{{i\nabla_{ \bot }^{2} E_{{s{2}}} }}{{{2}k_{{s{2}}} }} = \frac{{ik_{{s{2}}} }}{{n_{1} }}[n_{2}^{S2} \left| {E_{{s{2}}} } \right|^{2} + 2n_{2}^{X3} \left| {E_{1} } \right|^{2} + 2n_{2}^{X4} E_{1} E_{{3}} ]E_{{s{2}}}$$

(14)

$$\frac{{\partial E_{{s{3}}} }}{\partial z} - \frac{{i\nabla_{ \bot }^{2} E_{{s{3}}} }}{{{2}k_{{s{3}}} }} = \frac{{ik_{{s{3}}} }}{{n_{1} }}[n_{2}^{S3} \left| {E_{{s{3}}} } \right|^{2} + 2n_{2}^{X5} \left| {E_{3} } \right|^{2} + 2n_{2}^{X6} E_{1} E_{{3}} ]E_{{s{3}}}$$

(15)

$$\frac{{\partial E_{s4} }}{\partial z} - \frac{{i\nabla_{ \bot }^{2} E_{s4} }}{{{2}k_{{s{3}}} }} = \frac{{ik_{s4} }}{{n_{1} }}[n_{2}^{S4} \left| {E_{s4} } \right|^{2} + 2n_{2}^{{X{7}}} \left| {E_{3} } \right|^{2} + 2n_{2}^{{X{8}}} E_{1} E_{{3}} ]E_{s4}$$

(16)

where z is the longitudinal coordinate, $k_{si} { = }\omega_{si} n_{1} /c$. n₁ is the linear refractive index,$n_{2}^{S1 - 4}$ are the self-Kerr nonlinear coefficients of E_s1-4, $n_{2}^{X1 - 8}$ are the cross-Kerr nonlinear coefficients of E_s1-4 induced by E_1,3. On the left of the equations above are two terms that describe the beam’s longitude propagation and diffraction factor during the propagation of different fields, respectively. On the right side, the first term gives the nonlinear self-Kerr effect, and the rest of the terms describe the nonlinear cross-Kerr effects. Then, the Kerr nonlinear coefficient n₂ values should be evaluated in Rb vapor and can be expressed as:

$$n_{{2}} = \frac{{{\text{Re}} \rho_{si}^{\left( 3 \right)} }}{{\varepsilon_{0} cn_{1} }} = n_{2}^{S} + n_{2}^{X} = \sum\limits_{i = 1}^{4} {n_{2}^{Si} } + \sum\limits_{j = 1}^{8} {n_{2}^{Xj} }$$

(17)

The third-order nonlinear self-Kerr density matrix element and cross-Kerr density matrix element are expressed as follows:

$$\rho_{s1}^{s\left( 3 \right)} { = }\frac{{ - iG_{s1} \left| {G_{s1} } \right|^{2} }}{{\Gamma_{22} \left( {\Gamma_{32} - i\Delta_{s1} } \right)^{2} }}$$

(18)

$$\rho_{s1}^{x\left( 3 \right)} { = }\frac{{ - iG_{S1} \left| {G_{3} } \right|^{2} }}{{\left( {\Gamma_{32} - i\Delta_{S1} } \right)\left( {\Gamma_{12} - i\Delta_{S1} - i\Delta_{3} } \right)\left( {\Gamma_{32} - i\Delta_{S1} } \right)}}$$

(19)

$$\rho_{s1}^{x\left( 3 \right)} { = }\frac{{ - iG_{S1} \left| {G_{1} } \right|^{2} }}{{\left( {\Gamma_{32} - i\Delta_{S1} } \right)\left( {\Gamma_{12} - i\Delta_{S1} - i\Delta_{1} } \right)\left( {\Gamma_{32} - i\Delta_{S1} } \right)}}$$

(20)

If the diffraction and self-phase modulation (SPM) terms are ignored, the solutions of Eqs. (13–16) are: $E_{si} (y,z) = E_{si} (y,0)\sum\nolimits_{i} {\exp (i\varphi_{si} (y))} (i = 1,2,3,4)$. The nonlinear phase shift $\varphi_{si} (y)$ can be expressed as $\varphi_{si} (y) =$ $2k_{s1,s2,s3,s4} n_{2} I_{i} e^{{ - (y - y_{i} )^{2} /2}} /(n_{0} I_{s1,s2,s3,s4} )$, where I_i is the intensity of the dressing field (coupled field), I_s1,s2,s3,s4 are the intensity of generated fields, y is the center of E₁ in the lateral dimension with E_s1, E_s2, E_s3, and E_s4 as the origin coordinates. Self-Kerr and cross-Kerr nonlinear effects are critical for achieving large refractive index modulation [29] and are also used to study laser beam self-focusing [27] and image formation [28].

2.4 The spatial multimode due to frequency multimode

The frequency linewidth δ is introduced in calculation of $\chi_{si}^{\left( 3 \right)}$, which causes the wave vector k to change in scale in a spatial degree of freedom as $\Delta k + {\updelta }k = \Delta k + \delta \omega_{i} n_{j} /c$, where Δk is the phase mismatch and δk is the quantum momentum parameter. Therefore, phase mismatching can be quantitatively analyzed by the exact values of frequency resonant linewidth δ_i. It can be seen from this that the frequency mode determines the spatial mode. And n_j represents the reflective index; ω_si is defined as the actual frequency of E_S1 (_S2, _S3, _S4), which is assumed as ω_S1 = ϖ_S1—δ₂—δ₃—δ₄ (ω_S2 = ϖ_S2 + δ₂, ω_S3 = ϖ_S3 + δ₃, ω_S4 = ϖ_S4 + δ₄), and ϖ_S1 (ϖ_S2, ϖ_S3 and ϖ_S4) is the central frequency of ω_S1(ω_S2, ω_S3 and ω_S4).

Through the third-order nonlinear density matrix element (Eqs. 7–19), we can solve the value of δ_i under different dressing conditions, and the real part of δ_i is the resonance position and the imaginary part is the linewidth. Corresponding results of δ_i are presented in Tables 1, 2, 3. The expressions of the parameters in Tables 1, 2, 3 are a_1±  = (− Δ₁ ± (Δ₁² + 4Γ₁₂Γ₃₂ + 4G₁²)^1/2)/2; Γ_e1,e2 =  − (Γ₁₂ + Γ₃₂)/2 − Γ₁₂Δ₁/2a_1±; a_2±  = (− (2Δ₁ − Δ₃) ± ((2Δ₁ − Δ₃)² + 4Γ₁₂Γ₃₂ − 4Δ₁² + 4Δ₁Δ₃ + 4G₃²)^1/2)/2; Γ_e3,e4 =  − (Γ₁₂ + Γ₃₂)/2 − (Γ₁₂Δ₁ + Γ₃₂Δ₁ − Γ₃₂Δ₃)/2a_2±; a_3±  = (− Δ₃ ± (Δ₃² + 4Γ₁₂Γ₃₂ + 4G₃²)^1/2)/2; Γ_e5,e6 =  − (Γ₁₂ + Γ₃₂)/2 − Γ₁₂Δ₃/2a_3±; c_1±  = ((2a₁₊  + Δ₃) ± ((2a₁₊  + Δ₃)² − 4(Δ₃a₁₊  + Γ_e1Γ₃₂ + a₁₊²)/2. According to the energy conservation condition of δ_i, (δ₁ + δ₂ + δ₃ + δ₄ = 0), we can define the coherent channels [34]. For instance, from Table 1, coherent channels C₁ and C₂ both satisfy the energy conservation condition: δ₁ + δ₂ + δ₃ + δ₄ = 0. Therefore, 2 coherent channels can be obtained without dressing effect. Similarly, 3 and 4 coherent channels can be obtained from Table 2 for the single-dressing effect and Table 3 for the parallel double-dressing effect, respectively.

Table 1 Coherent channels for PA-CFWM processes without dressing field

Table 2 Coherent channels for PA-CFWM processes with single-dressing field

Table 3 Coherent channels for PA-CFWM processes with parallel double-dressing fields

Further, the simulation of nonlinear susceptibility of E_s1 signal versus δ₂ without dressing laser is shown in Fig. 3a. The results show that E_s1 signal has two maxima. These two maxima correspond to two CFWM processes existing in the system, and each process satisfies the energy conservation condition. When the dressing field E₁ is turned on, we can get three maxima for E_s1 signal. Furthermore, both the dressing fields E₁ and E₃ are turned on, and Fig. 3b and c displays four resonant peaks of E_s1 signal, respectively. The exact roots of δ₂ under different dressing effect are consistent with the resonance positions of δ₂ in Tables 1, 2, 3, respectively. These simulation results suggest more frequency modes in PA-CFWM caused by the dressing effect. Figure 3d–f shows the simulation results of the E_s1 signal, at a certain cross-section of the pump axis. The number of momentum rings increases with the dressing effect. It indicates that dressing effect will result in more possibility of spatial multimode. The linewidth of δ_i describes the full width at half maximum of the formant in the frequency domain and determines the width of the spatial momentum ring in the spatial domain. And these results show that the dressing field can control the number of modes in the frequency and spatial domains. Therefore, the δ_i can describe the number of dressing coherent channels and determines how many frequency modes the E_Si can generate.

Fig. 3

Third-order nonlinear susceptibility of E_s1 signals versus frequency linewidth δ₂. a Without dressing effect. b With E₁ field single-dressing effect. c With E₁ and E₃ double-dressing effect. d–f Cross-section of output E_s1 signal cone without dressing, with single and double-dressing effect, respectively

3 Results and discussion

3.1 Frequency multimode analysis

Figure 4a–f, respectively, represents the a, b, c, d, e, and f signal spectrum in the probe channel (E_s1) at different detuning Δ₁. The detuning Δ₁ corresponding to the a, b, c, and d peaks is − 1.95 GHz, − 1.7 GHz, − 1.55 GHz, − 1.35 GHz, − 1.3 GHz, and − 1.1 GHz in order from top to bottom. The detuning Δ₁ corresponding to the e and f signals is − 1.2 GHz, − 1 GHz, − 0.9 GHz, − 0.8 GHz, − 0.7 GHz, and − 0.55 GHz in order from top to bottom.

Fig. 4

Measured signal intensities versus laser E₂ frequency detuning Δ_s1 when pumping frequency detuning Δ₁ is set at different discrete detuning. The experimental parameters are: P₁ = 123 mW, P₂ = 127 μW, P₃ = 53.5 mW and T_Rb = 125 °C. Signal intensities of the a, b, c, and d signals in the probe channel. a a signal. b b signal. c c signal. d d signal. e e signal. f f signal

Figure 4a and b shows that both the a and b signals contain EIA and third-order gain peak signals (I₀ − Imρ_S2⁽¹⁾ +|ρ_S1⁽³⁾|²), which change from the absorption dip near the 85Rb (F = 2) resonance energy level to near the ⁸⁵Rb(F = 3) resonance level absorption dip. The EIA signals in the a and b signals first become larger and then become smaller, while the gain peak satisfy the electromagnetically induced transparency (EIT) window (Δ₂ − Δ_s2 + Δ₁ = 0), which increases as it gradually approaches the ⁸⁵Rb (F = 3) resonance level absorption dip, with a maximum at Δ₁ = − 1.1 GHz. When the frequency shift Δ₁ = − 1.35 GHz, the dressing effect of E₁ strongly influences the a and b signals. This is because the dressing effect becomes stronger as the generated signal weakens, resulting in the appearance of double and multiple peaks. The ordinate range of Fig. 4a is 0 ~ 0.75, and the ordinate range of Fig. 4b is 0 ~ 2.1. Comparing the optimal gain peak size, we can see that the intensity of b signal is more than three times larger than the a signal.

Figure 4c and d shows that both the c signal and the d signal containing EIA and third-order gain peak signals (I₀ − Imρ_S1⁽¹⁾ +|ρ_S1⁽³⁾|²), and the maximum value of the gain peak signal is at Δ₁ = − 1.35 GHz and Δ₁ = − 1.7 GHz. Different from the change trend of the a and b signals, the third-order gain peak signal (|ρ_S1⁽³⁾|²) in the c and d signals gradually decreases. It can be explained the c and d signals are absorbed by the ⁸⁵Rb (F = 2) resonance absorption dip as the signal gradually approaches the resonance level, and when the value of Δ₁ becomes small, the dressing effect will also enhance and reduce the intensity of the peak. Meanwhile, the first-order signals (linear optical responses) in the a and b signals dominate, while the third-order signals (nonlinear optical responses) in the c and d signals dominateThe ordinate interval of Fig. 4c is 0.18, and the ordinate range of Fig. 4d is 0 ~ 1. Comparing the optimal gain peak size, it is found that the intensity of the d signal is more than twice that of the c signal.

Both the e and f signals contain the third-order gain peak signal (|ρ_S1⁽³⁾|²) with optimal positions at Δ₁ =  − 0.9 GHz and Δ₁ =  − 0.55 GHz, respectively. The ordinate range of Fig. 4e is 0.5 ~ 4.25, and the ordinate range of Fig. 4f is 1.8 ~ 6. Comparing the optimal gain peak, we can see that the intensity f signal is 1.5 times stronger than the e signal. The change from the a signal to the f signal indicates that the signal has changed from a linear optical response dominated to a nonlinear optical response. This is because the signal on the left is close to the ⁸⁵Rb (F = 3) and ⁸⁷Rb (F = 2) resonance absorption dips, the atomic density and the dipole moment are large, and the dressing effect is strong, so the third-order gain signal is absorbed, and the first-order signal dominates. At the same time, the best gain peak positions from the a signal to the f signal are connected by a curve, and the contour is the shape of a peak. From the results of the analysis of the signals in different energy levels (Fig. 2), it can be seen that the b and f signals have the highest gain, which is consistent with the experimental results in Fig. 4, the energy level with high gain can be selected to produce multimode quantum states.

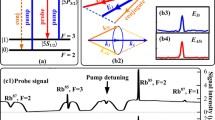
Figure 5 shows that when the detuning Δ₁ = − 1.3 GHz, the b signal of E_S1, E_S2, E_S3, and E_S4 channels is obtained by scanning the detuning Δ_s1. As shown in Fig. 5a2 and a4, the gain peak shows Autler–Townes (A–T) splitting. This is due to the dressing effect of E₁ splitting the energy level |3 > into |G1 +  > and |G1 −  > , which can be written as $H|G_{1 \pm } \rangle = \lambda_{ \pm } |G_{1 \pm } \rangle$. The energy-level position is $\lambda_{ \pm } = [ - \Delta_{1} \pm (\Delta_{3}^{2} + 4|G_{1} |^{2} )^{1/2} ]/2$, and then double peaks from left to right correspond to |G1 +  > and |G1 −  > . The corresponding dressing energy level of E_s2 and E_s4 is shown in Fig. 5b2 and b4. However, Fig. 5a1 and a3 shows three peaks, and the dressing effect of E₃ should be considered. The energy level |G1- > is divided into two secondary dressing states (|G3− +  > and |G3– >) due to the dressing effect of E₃. Therefore, from left to right, three gain peaks appear. The corresponding dressing energy level of E_s2 and E_s4 is shown in Fig. 5b1 and b3. The above situation shows that multiple peaks caused by dressing effect are direct evidence of frequency multimode [28]. From single-dressing effect to double-dressing effect, the increase of dressing effect will increase the frequency mode.

Fig. 5

Measured signal intensity versus laser E₂ frequency detuning Δ_s1 when pumping frequency detuning Δ₁ is set at − 1.3 GHz

Next, we study the multicomponent signal and background obtained by scanning the detuning Δ_s1 of the probe field E₂ when the detuning Δ₁ of E₁ is discretely changed in Fig. 6. In Fig. 6a–c, the detuning Δ₁ varies from − 1.95 to − 0.95 GHz with step of of 0.1 GHz. The signal in Fig. 6a is the superposition result of the fluorescence signal and gain peaks (|ρ_FL⁽²⁾|² +|ρ_S3⁽³⁾|²). The curve of fluorescence signal is presented as a dip, which is formed by the dressing effect of E₂ ($G_{2}^{2} /\left[ {\Gamma_{22} + i\left( {\Delta_{s2} - \Delta_{2} } \right)} \right]$). As the absolute value of detuning Δ₁ becomes smaller, the dip deepens and has a maximum value at − 1.75 GHz, then shallows. And the profile of fluorescence signal in Fig. 6a shows a peak (Eq. 11) with a range of 500 MHz, and a center frequency of − 1.75 GHz. The intensity of the gain peak (|ρ_S3⁽³⁾|²) increases with decrease in the absolute value of Δ₁ (Eq. (4)). Figure 6a1 and a2 shows the cases where the fluorescence and gain peak signals coexist (|ρ_FL⁽²⁾|² +|ρ_S3⁽³⁾|²). To make the description clearer, we simulated the fluorescence signal (|ρ_FL⁽²⁾|²), the gain peak signal (|ρ_S3⁽³⁾|²), and the total superimposed signal (|ρ_FL⁽²⁾|² +|ρ_S3⁽³⁾|²), as shown in Fig. 6e1 and e2. The experimental results are consistent with the theory.

Fig. 6

Measured signal intensity curves of the detuning Δ_s1 of the probe field E₂ at different pump fields E₁ detuning Δ₁. a The “a” signal in the cascade I channel. b The “a” signal in the cascade II channel. c The “b” signal in the cascade II channel. From left to right, these three figures are changing Δ₁ from − 1.95 to − 0.95 GHz. d The “a” signal in the probe channel. From left to right, changing the detuning Δ₁, from -0.95 GHz to -0.35 GHz. e1 and e2 represent theoretical simulations of Figures a1 and a2. e3 and e4 represent theoretical simulations of the graphs c1 and c2. f Single-dressing fluorescence energy level

Figure 6b and c shows the a and b signals in the E_s4 channel under the same experimental conditions. The E_s4 signals include the superposition of fluorescence signal and gain peaks (|ρ_FL⁽²⁾|² +|ρ_S4⁽³⁾|²). Specifically, the theoretical superposition simulation diagram of Fig. 6c1 and c2 is shown in Fig. 6e3 and e4, which shows that the experimental results are consistent with the theoretical simulation. Comparing Fig. 6b and c shows that the fluorescence dip in Fig. 6b is deeper at the same Δ₁, which indicates that the “a” signal in Fig. 6b is subjected to a stronger dressing effect than the b signal.

In Fig. 6d, the E_S1 signal by scanning Δ_s1 at different values of Δ₁ in a large range varies from − 0.95 to 0.35 GHz from left to right in 0.1 GHz intervals. The background of signals in Fig. 6d shows a Doppler fluorescence peak with a background range of 700 MHz and a center frequency of 0.175 GHz. When the detuning Δ₁ gradually approaches the resonance, the intensity of gain peak first increases and then decreases. This due to the Eq. (7), as the detuning Δ₁ decreases, the intensity of the gain peak increases. But when the Δ₁ is too close to the resonance, the gain peak is absorbed resulting to a decrease in intensity.

Finally, we investigate the line shift of the PA-CFWM signal resonant frequency through different parameters (∆₁, power E₁ (P₁) and angle α between E₁ and E₃). In Fig. 7a, from bottom to top, the value of ∆₁ is − 1.45 GHz, − 1.35 GHz, − 1.3 GHz, − 1.2 GHz, and − 1.05 GHz, respectively. The dip of each sub-curve represents the EIA (bright state), which satisfies the enhancement condition $\Delta_{2} - (\Delta_{1} + (\Delta_{1}^{2} + 4\left| {G_{1} } \right|^{2} )^{1/2} )$$/2 = 0$.The peak is third-order gain peak, which is related to Eq. (7). As the detuning ∆₁ decreases, the intensity of EIA signal in Fig. 7a can be described with the term $iG_{2} /\left[ {\left( {\Gamma_{32} + i\Delta_{s1} } \right) + \left| {G_{1} } \right|^{2} /\left[ {\Gamma_{12} + i\left( {\Delta_{s1} - \Delta_{1} } \right)} \right]} \right]$, the EIA dip gradually shallows, the intensity of the gain peak increases. When the ∆₁ = -1.3 GHz, the signal is composed of EIA dip and third-order gain peaks (I₀ −|ρ_s1⁽¹⁾|² +|ρ_S1⁽³⁾|²). However, when the ∆₁ = -1.05 GHz, only the third-order gain peak can be observed. The position of the resonant peak shifts in the direction of dΔ_s1/dΔ₁ = 3/4 + (ε + G₁)/4((ε + G₁)2 + 4G₁²)^1/2, where ε = ΔE/ћ, G₁ represents the intensities of the dressing fields E₁, which affects not only the signal intensity but also the resonance position; and the line shift of the signal can be directly described by the equation. By analyzing the equation, we can conclude that the line shift satisfies 3/4 <|d∆_s1/d∆1|< 2. These results manifest a negative correlation between ∆₂ and ∆₁ with a large shift in the linear speed.

Fig. 7

Similar to Fig. 6. a The b signal in the probe channel. From bottom to top, change the detuning Δ₁ from − 1.45 to − 1.05 GHz. b, c The b signal in the probe channel and cascade I channel. From bottom to top, change the power of E₁ from 50 to 147 mW. d, e The b signal in the probe channel and cascade I channel. From bottom to top, changing the angle between E₁ and E₃, moving vertically

Figure 7b–c shows the measured E_s1 signals and E_s4 signals by scanning ∆₂ at different discrete values of P₁. From bottom to top, the value of P₁ is 50 mW, 70 mW, 110 mW, 130 mW, and 147 mW, respectively. Similar to EIA in Fig. 7a, the EIA dip of Fig. 7b becomes shallow due to increasing G₁ in the denominator term. And the intensity of gain peak in Fig. 7b increases and gradually oscillates to form multiple peaks. According to Eq. (10), the gain peak in Fig. 7c can increase with G₁. Specially, the increase of P₁ increases the nonlinear effect of the system to show a periodic oscillation peak with dynamic instability [33]. In addition, the position of the resonant peak shifts in the direction of dG₁/dΔ_s1 = 1/(3/2 + (ε + G₁)/((ε + G₁)² + 4G₁²)^1/2, the shift rate of power E₁ to Δ₂ satisfying 0 <|dG₁/dΔ_s1|< 1.

As with Fig. 7d–e, E_s1 signal and E_s4 signal can be measured by scanning ∆₂ at different discrete values of angle α between E₁ and E₃. Altering the angle α is equivalent to introducing a phase factor e^iΦ into the dressing term, the corresponding dressing item can be expressed as G₁²e^iΦ/ (Γ₃₂ + iδ₂ + iΔ₁). The EIA signal and the third-order gain peak are present in Fig. 7 (d), and the third-order gain signal is shown in Fig. 7e. From bottom to top, due to the change of angle α, the dressing effect first decreases, then increases and then decreases, and the intensity of the gain peak first increases, then decreases and then increases (Fig. 7d). In Fig. 7e, the double peaks are caused by G₁ dressing effect, and the conversion of left and right peaks indicates the conversion of light and dark states. The line shift rate of α can be expressed as dα/dΔ₂ = 1/((3/2G₁ + 1/(G₁²))^1/2) cosΔΦ, which satisfying 0 <|dα/dΔ_s1|< 1. By comparing the line shift of ∆₂ with ∆₁, power E₁ and angle α between E₁ and E₃, it can be known that the line shift of changing ∆₁ is much larger than that of changing the power E₃ and angle α. This is because the position of the ∆₁ will directly affect the position of the ∆_s1, while the power E₁ and angle α only affect the dressing field, the effect on the line shift will be smaller. But the adjustment of all three parameters can cause light–dark state conversion. The above research results can be applied to optical communication. Moreover, multipeaks appear when adjusting the parameters (∆₁, power E₁ (P₁) and angle α between E₁ and E₃), indicating that regulation of these three parameters in dressing items can appear frequency multimode.

3.2 Spatial multimode analysis

In this section, we will explore the properties of spatial multimode. With probe field E₂ injected to this system, E_s1, E_s2, E_s3, E_s4 signals are amplified. The spatial images by changing power E₃ and detuning Δ₁ are shown in Fig. 8a, b, respectively. And Fig. 8c, d shows the spectrum of E_s1, E_s2, E_s3, E_s4 signals corresponding to Fig. 8a, b, respectively. As shown in Fig. 8a1, a2, the spot areas at E_s1, E_s2, E_s3, E_s4 signal channels were all approximately doubled with increasing power E₃. This is because the detuning Δ₁ = -1.7 GHz of the spatial spots (Fig. 8a1, a2) is in the defocusing region (Δn < 0)[29]. As the power E₃ increases, the Kerr effect of the spatial spot increases (Eq. 19), so the area of the spot increases due to defocusing effect. Since the number of spatial modes can be obtained from the phase-matching area and the area ratio of a single mode [27], the number of spatial modes in all single channels is also doubled, and can be estimated to be more than 800.

Fig. 8

a1, a2 Injected spatial images by changing P₃ = 35mw to P₃ = 50mw, respectively. b1, b2 Injected spatial images by changing Δ₁ = − 1.7 GHz to Δ₁ = − 1.2 GHz, respectively. c1–c4 Measured signal intensity of E_s1, E_s2, E_s3 and E_s4 versus Δ₂, from top to bottom, by changing P₃ = 35mw to P₃ = 50mw, respectively. d1–d4 Measured signal intensity of E_s1, E_s2, E_s3, and E_s4 versus Δ₂, from top to bottom, by changing Δ₁ = − 1.7 GHz to Δ₁ = − 1.2 GHz, respectively. e1–e3 Spontaneous spatial images of single pump field by changing different Δ₁. f1–f3 Spontaneous spatial images of double pump field by changing different Δ₁. Experimental parameters: P₁ = 133 mW, P₂ = 197 μW, P₃ = 45 mW, and T_Rb = 125 °C. g Double dressing energy level

When the detuning Δ₁ approaches resonance, the spatial spots at E_s1, E_s2, E_s3, E_s4 signal channels not only increased the area but also split unevenly to more spots (Fig. 8b1, b2). This is because, as the detuning Δ₁ changes from Δ₁ = − 1.7 GHz to Δ₁ = − 1.2 GHz (Δn < 0), the Kerr effect increases as shown in Eq. (20), thus increasing the defocusing effect of spatial spot. Therefore, the spatial spot area increases or even split. Similarly, all single channels can, on total, reach more than 1200 spatial modes.

As shown in Fig. 8c, the signals of E_s1, E_s2, E_s3, and E_s4 all split into two peaks from the red signal curve (P₃ = 35mw) to the signal blue curve (P₃ = 50mw). This can be explained by the enhanced dressing effect of E₃, which splits the energy level |1 > into |G₃₊ > and |G_3- > ; thus, the E_s1, E_s2, E_s3, E_s4 signals are split into double peaks. The double peaks in red signal curve of Fig. 8d should be caused by the E₃ single-dressing effect. When the detuning Δ₁ is close to the resonance, the E_s1, E_s2, E_s3, E_s4 signals are split into three peaks. This is due to the detuning Δ₁ approaching resonance, the dressing effect of E₁ increases, splitting the energy level |G_3- > into |G_1-+ > and |G_1– > , the corresponding dressing energy-level diagram of ⁸⁵Rb as shown in Fig. 8g, so the three peaks can be observed. The existence of multiple peaks represents the existence of frequency multimode, and the increase in the number of peaks indicates the increase in the number of frequencies modes. Whether changing P₃ or detuning Δ₁, the dressing effect is increased; thus, the dressing effect increases the frequency modes.

Figure 8e–f shows the evolution of spontaneous spatial spot with different detuning Δ₁ in the single and double pump field, respectively. As the detuning Δ₁ approaches the resonance, the spatial spot gradually defocuses due to the Kerr effect, and the spatial spot splits into multiple parts. In Fig. 8e3, the spot shows a spontaneous four-wave mixing process, and the spot shows a two-cascade spontaneous four-wave mixing process in Fig. 8f3. Compared with Fig. 8e3, the number of spatial spot splitting in Fig. 8f3 is much higher, which indicates that the dressing field can get more spatial modes.

The relationship between frequency domain and spatial domain can be reflected by the expression δk_i = δ_in/c. It shows that the frequency coherent channel and the spatial coherent channel correspond to each other. As shown in Fig. 3, the number of peaks and the rings increase and correspond one to one as the dressing effect increases. The relationship of δ_i and δk_i demonstrates the concord of multimode in both frequency and spatial domains. Because the probe field is a single longitudinal mode, every amplified signal channel in Figs. 8(a)–(b) is equivalent to a peak in Fig. 8c, d, respectively. Therefore, the splitting of the spatial spot in Fig. 8a, b can only be due to the Kerr effect. Moreover, the number of coherent channels obtained from the sum of each set of signal peaks in Fig. 8c, d should be on the same order of magnitude as the number of spots generated by the spontaneous cascade four-wave signals in Fig. 8f. But when considering the Kerr effect, the number of spontaneous spatial spot divisions will be more. Therefore, the frequency domain and the spatial domain have a good correspondence on the dressing coherent channel, and when the dressing effect is larger, the frequency multimode and the spatial multimode both will increase.

4 Conclusion

In summary, this study investigates the properties of four quantum correlated beams generated through the PA-CFWM process in rubidium vapor. The research explores the signal excitation efficiency of different energy levels by scanning the probe detuning and identifies three different ways to light up the cascade four-mode process. The energy-level with high gain can be selected to produce multimode quantum states, and two pairs of EPR entangled light fields are generated, resulting in quantum correlation between two previously uncorrelated signals. The multimode characteristics of output signals are observed in the frequency and spatial domain. The multimode characteristic is reflected as the multipeak of the spectral signal, and in the spatial domain, the multimode properties appear as an increase of the spatial spot area and a splitting of the spatial spot. The number of frequency multimode and spatial multimode can be controlled through the dressing effect, with the number of spatial modes in four entangled beams reaching up to 1200. Furthermore, the line shift of the PA-CFWM signal resonant frequency can be controlled through experimental parameters such as the detuning and power of the dressing field. These results are important not only for fundamental tests of quantum effects but also for their numerous possible applications in quantum technologies, such as quantum imaging and quantum metrology, opening up possibilities for future research in quantum communication and quantum information processing.