1 Introduction

Integrating cavities are important optical devices for studying light-matter interactions in confined spaces. These cavities are typically coated with high diffuse reflectance material, which allows any point on the inner wall to be an ideal Lambertian reflector [1]. The scattering characteristic of light propagation inside these cavities makes them ideal for a wide range of applications, including spectrum analysis [2,3,4], metrology [5], and quantum physics [6].

The propagation of light inside an integrating cavity is governed by several cavity parameters, such as port fraction, effective optical path length (EOPL) and diffuse reflectance. Among them, port fraction plays an essential role when considering the loss of radiant flux in the cavity. However, it is difficult to continuously adjust the port fraction of the integrating sphere, making it challenging to study the effect of port fraction on other cavity parameters using the integrating sphere [7]. In contrast, a cubic integrating cavity (CIC) can flexibly change its port fraction by moving the lid of the cavity. Therefore, Yu and Zhou et al. proposed to use a CIC to study the effect of port fraction on other cavity parameters [8,9,10]. Recently, the formula of EOPL for the CIC as a function of diffuse reflectance, port fraction, and the side length was proposed and validated through TDLAS technology by Yu [11]. With the help of TDLAS technique, Yu et al. found that the EOPL for the tandem CIC can be expressed as the sum of EOPL of two single CICs when the port fraction in the middle of two cavities is less than 0.01 [12]. After that, Yu proposed a method for measuring the diffuse reflectance of a CIC based on TDLAS technique [13]. This method can measure the diffuse reflectance by adjusting the port fraction in the presence of gas absorption inside the cavity.

However, obtaining these research results all rely on the premise of the presence of gas absorption inside the cavity, the relationship between the parameters of the cavity in the absence of gas absorption is rarely reported or verified. or an integrating, integrating cavity, the radiant flux is still influenced by the diffuse reflectance and port fraction even when no gas absorption is present. If the relationship between the parameters of a cavity in the absence of gas absorption can be revealed, it would be of significant importance for establishing new measurement methods for cavity parameters and for understanding the process of light propagation within the cavity.

In this paper, we investigated the effect of the port fraction on the radiant flux of the integrating cavity. A theoretical model of the light propagation in an arbitrary-shaped integrating cavity was established. The relationship between port fraction, radiant flux and diffuse reflectance was derived in the absence of gas absorption. Using five different wavelengths of laser as light source, the variation of the radiant flux with the additional port fraction was verified. A method for measuring the diffuse reflectance of the cavity was proposed based on the relationship.

2 Theory

Here, the reflection process for a light beam passing through an arbitrary-shaped cavity was investigated theoretically when no gas absorption exists. In brief, an ideal arbitrary-shaped integrating cavity is defined as a cavity in which any two points on the inner wall can be connected to a segment inside the cavity. The inner wall of the cavity is coated with high reflectance material, which can be considered as an ideal Lambertian reflector. Hence, an incident light beam could be diffused continuously. A simplified model of the light beam propagation in a arbitrary-shaped integrating cavity is shown in Fig. 1. Neglect the coupling losses when light enters the cavity through the input port, and the reflection losses at the detector window when light exits through the output port. The radiant flux received by the detector \(\Phi\) is equal to the sum of all the output radiation escaping from the output light aperture [14]:

$$\Phi = \frac{{f_{out} }}{f}[\Phi_{0} \rho f + \Phi_{0} \rho^{2} (1 - f)f + \Phi_{0} \rho^{3} (1 - f)^{2} f \cdots + \Phi_{0} \rho^{n} (1 - f)^{n - 1} f \cdots ].$$
(1)
Fig. 1
figure 1

Simplified model of the light propagation process in an arbitrary-shaped integrating cavity

Full size image

Here, \(f_{out}\) is the port fraction of the output light aperture. \(f\) is the total port fraction of the cavity. \(\Phi_{0}\) is the incident radiant flux. \(\rho\) is the diffuse reflectance of the cavity. According to the sum of the first n series formula of geometric progression, Eq. (1) can be written as:

$$\Phi = \frac{{f_{out} }}{f}\Phi_{0} \mathop {\lim }\limits_{{{\text{n}} \to \infty }} \frac{{\rho f[1 - \rho^{n} (1 - f)^{n} ]}}{1 - \rho (1 - f)}.$$
(2)

Because \(\rho (1 - f) < 1\), as n approaches infinity, Eq. (2) can be expressed as:

$$\Phi = \frac{{f_{out} }}{1/\rho - (1 - f)}\Phi_{0} .$$
(3)

Since \(f\) is the total port fraction, so we have \(f > f_{out}\). In addition, \(\rho < 1\), which indicates \(\frac{{f_{out} }}{1/\rho - (1 - f)} < 1\). This means the radiant flux received by the detector \(\Phi\) will always be weaker than the incident radiant flux of the cavity \(\Phi_{0}\) due to the loss of the cavity wall and the escape of light at the port [15, 16]. To further verify Eq. (3), we write \(f\) as the sum of \(f_{0}\) and \(f_{x}\):

$$\Phi = \frac{{f_{out} }}{{1/\rho - (1 - f_{0} - f_{x} )}}\Phi_{0} .$$
(4)

where, \(f_{0}\) is the initial port fraction, which equals to the sum of all the initial port areas divided by the total internal surface area of the cavity. \(f_{x}\) is additional port fraction, it can be generated, for example, by moving the lid of the cavity, which equals to the area of additional port divided by the total inner surface area of the cavity.

From Eq. (4), there are three port fractions \(f_{out}\), \(f_{0}\) and \(f_{x}\) that affect \(\Phi\) when no gas absorption exists. However, both \(f_{out}\) and \(f_{0}\) are constant because they only depend on the geometry feature of the cavity. In addition, Eq. (3) and Eq. (4) is derived under the condition of an arbitrary-shaped integrating cavity. For CICs, it satisfies the definition of arbitrary-shaped integrating cavity mentioned above. Hence, Eq. (3) and Eq. (4) are applicable to CICs. Therefore, it is possible to test whether Eq. (3) is valid by changing \(f_{x}\) to observe whether \(\Phi\) varies according to Eq. (4) using CIC.

3 Experiments

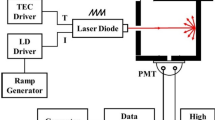
To to verify the above idea, we constructed an experimental setup for measuring the variation of radiant flux with the port fraction of a CIC using a laser. A schematic of the experimental setup is presented in Fig. 2. Light emerging from the laser diode directly entered the air-filled CIC through the input light aperture. After that, a stable light field within the cavity formed rapidly due to the multiple diffuse reflections of the laser. The light escaped from the output light aperture of the cavity was collected by the photomultiplier tube (Zolix Instruments, CR131) and converted into digital signal by data acquisition card (Zolix Instruments, DCS103). Finally, the digital signal was sent to the computer for further processing.

Fig. 2
figure 2

Schematic of experimental setup for measuring the radiant flux of CIC at different port fraction

Full size image

The 8 cm-sized CIC with input and output light aperture was made of black polymethylmethacrylate sheets with the thickness of 8 mm. The inner surface of the cavity was coated with high diffuse reflectance paint [17] (Avian Technologies, Avian-D), which its diffuse reflectance matches that of barium sulfate-based coating in the visible region of the spectrum. In addition, a movable lid on the top of the CIC can be adjusted to generate an additional port fraction \(f_{x}\) for the cavity as shown in Fig. 2. The length x caused by moving the lid was measured by a digital vernier caliper with an accuracy of 0.03 mm. In addition, the walls of the movable port, as well as the walls of the input and output light ports of the cavity, are not coated with Avian-D painting, ensuring that the output light passing through these ports will not be reflected back into the cavity due to the real port effects [18, 19], thus not affecting the determination of the diffuse reflectance. The laser diodes with wavelengths of 405, 450, 520, 650 and 785 nm were selected as light source due to the high diffuse reflectance of the inner coating and the high sensitivity of photomultiplier tube (PMT) in the visible region. In order to stabilize the output of the laser diodes, the laser diodes were mounted on a TE-Cooled base (Thorlabs, TCLDM9). The temperature and current of the laser diodes were controlled by temperature controller (Thorlabs, TED 200C, − 45 °C to + 145 °C, ± 0.01 °C) and current controller (Thorlabs, LDC 205C, − 0-500 mA, ± 0.1 mA) respectively.

4 Results and discussion

Figure 3a shows the radiant flux versus time under different \(f_{x}\). It is apparent from Fig. 3a that \(\Phi\) decreases when \(f_{x}\) increases from 0 to 0.0609. When the \(f_{x}\) is unchanged, the \(\Phi\) hardly changes with time. The data in Fig. 3b indicates that there are still small random fluctuations in \(\Phi\). Under the experimental conditions where the optical path is fixed and \(f_{x}\) remains unchanged, we believe that the small random fluctuations of \(\Phi\) may be primarily caused by fluctuations in the light source. Moreover, we calculated the relative error of the \(\Phi\) based on the fluctuation of \(\Phi\) with time in 20 s as shown in Fig. 3b. The \(\Phi\) fluctuates between 12.709 and 12.766 and therefore \(\Delta \Phi\) = 0.057. The average value of \(\Phi\) in 20 s is 12.741. Hence, the relative error of radiant flux \(\Delta \Phi /\Phi\) = 0.0045. The corresponding residual of Fig. 3b is shown in Fig. 3c, the data indicates that residual are all within 0.3%, which indicates reliability of the measurement results.

Fig. 3
figure 3

a The radiant flux versus time at the wavelength of 405 nm under different \(f_{x}\). The insets are the enlarged view b and the corresponding residual c of the radiant flux from 70 to 90 s when \(f_{x}\) = 0.0609

Full size image

Figure 4a shows the experimental and fitted \(\Phi\) based on Eq. (4) for each wavelength. The result indicates that when the \(f_{x}\) of CIC increases, a greater amount of light in the cavity escapes from the port, resulting in a weakened light field formed in the cavity. Therefore the \(\Phi\) received by the detector decreases. In addition, it is apparent from Fig. 4a that the falling trend of \(\Phi\) with the increase of \(f_{x}\) varies depending on the wavelength of light source. We can see this difference from the perspective of Eq. (4). Since both port fractions \(f_{out}\) and \(f_{0}\) are determined by the geometry of the cavity (independent of the wavelength), \(\Phi_{0}\) is constant during measurement. Hence, the difference of falling trend in Fig. 4a is caused by the wavelength-dependent diffuse reflectance \(\rho (\lambda )\).

Fig. 4
figure 4

a Experimental and fitting radiant flux when different \(f_{x}\) values were added to the CIC at the incident wavelengths of 405, 450, 520, 650, and 785 nm. b-f Residuals of radiant flux for each wavelength

Full size image

In the same port fraction, a higher diffuse reflectance will cause a greater amount of light to be reflected by the cavity wall and escape from the cavity port. This explains why the radiant flux at wavelengths with higher diffuse reflectance decreases faster with the increase of the port fraction. More importantly, the data points in Fig. 4a coincide with the fitting curves, which indicates that the light propagation law in CIC satisfies Eq. (3). Based on the fitting results, we obtain the diffuse reflectance at five wavelengths of 0.9625 (405 nm), 0.9746 (450 nm), 0.9886 (520 nm), 0.9960 (650 nm), 0.9921 (785 nm) respectively. Therefore, by measuring the radiant flux of cavity with different port fraction, we obtain a method to measure the diffuse reflectance of cavity. Figures 4b–f show the corresponding residuals of each wavelength in Figs. 4a. The residuals fluctuate up and down around zero with the increase of \(f_{x}\), and the absolute values of all residuals are within 0.02.

Since the effect of fluctuation of light source on measurement is usually unavoidable, it is necessary to study the effect of fluctuation of light source on the proposed method of measuring diffuse reflectance. The relationship between the relative error of diffuse reflectance caused by the fluctuation of light source and the relative error of \(\Phi\) is obtained by calculating the derivatives of \(\Phi\) and \(\rho\) from Eq. (4):

$$\frac{\Delta \rho }{\rho } = [1 - \rho (1 - f_{0} - f_{x} )]\frac{\Delta \Phi }{\Phi } = k\frac{\Delta \Phi }{\Phi }.$$
(5)

where, \(\Delta \rho /\rho\) and \(\Delta \Phi /\Phi\) are the relative error of \(\rho\) and \(\Phi\) respectively. We define \([1 - \rho (1 - f_{0} - f_{x} )]\) as the factor k. As a rule of thumb \(f_{0} \le 0.03\), \(f_{x} \le 0.05\), \(\rho \le 0.99\). Hence, we can obtain that \(k \le 0.09\) approximately. The estimation of the factor k indicates that the effect of light source fluctuations on the relative error of \(\rho\) can be reduced approximately by an order of magnitude, which indicates that the method can effectively reduce the influence of light source fluctuations on diffuse reflectance measurement. In the previous it has been obtained that \(\Delta \Phi /\Phi\) = 0.0045 and \(k \le 0.09\). Therefore, we obtained that the relative error of diffuse reflectance caused by the fluctuation of light source \(\Delta \rho /\rho = 0.0004\) according to Eq. (5), which indicates that the measured diffuse reflectance has four significant digits.

In order to make the relative error of \(\rho\) caused by the fluctuation of light source smaller, according to Eq. (5), k ideally should be as close to 0 as possible, which means \(f_{0}\) and \(f_{x}\) should be close to 0, and \(\rho\) should be close to 1. \(f_{0}\) close to 0 suggests that all the initial ports that can cause light to escape from the cavity should be as small as possible. \(f_{x}\) close to 0 indicates that \(f_{x}\) should be selected as small as possible when measuring diffuse reflectance by moving the lid of the cavity. \(\rho\) close to 1 indicates that the method is more suitable for measuring materials with high diffuse reflectance, such as PTFE (polytetrafluoroethylene) and barium sulfate-based materials, which are often used as standard whiteboard coatings. If a material with low diffuse reflectance is measured, according to Eq. (5) the decrease in \(\rho\) will lead to an increase in the coefficient k, so the effect of light source fluctuations on the relative error of diffuse reflectance will increase.

Another source of error stems from the detection system itself, specifically, the dark current of PMT. Typically, a PMT's dark current sits at 10nA, while its output signal current exceeds 10 μA. Thus, the error caused by the dark current is about 0.1%. It is worth noting that when studying the influence of port fraction on the radiant flux of an integrating cavity in the presence of air, one should consider whether there is gas absorption at the investigated wavelengths and assess whether the absorption intensity, combined with the effective optical path length of the cavity, would have a non-negligible impact on the measured light intensity.

5 Conclusion

In summary, we investigated the effect of the port fraction on the radiant flux of the integrating cavity. A theoretical model of the light propagation in an arbitrary-shaped integrating cavity was established. The relationship between port fraction, radiant flux and diffuse reflectance was derived and verified in the absence of gas absorption. Based on the verified relationship, we propose a method to measure the diffuse reflectance of the integrating cavity and found that the method can reduce the influence of light source fluctuations on the measurement. Next, we will investigate the effect of the port fraction on the light field distribution in integrating cavity and its potential application for light field manipulation.