1 Introduction

Multi-pass cell (MPC) is an optical setup consisting of highly reflective mirrors, enabling the laser beam to bounce multiple times between mirrors within a constrained space. Certain patterns arising from the reflection spots of the light beam can be observed on the mirrors. One can obtain complex beam patterns once the light beam enters the cell with proper positions and angles. The beam pattern is an important measure of the number of bounces and thus the optical path length. For a given cell size, the more bounces, the longer the optical path length (OPL). Therefore, the MPC features an extended OPL; this merit makes it widely used in the field of gas sensing by laser absorption spectroscopy [1,2,3].

There are various types of MPC configurations, including Pfund [4], White [5], Herriott [6, 7], and the more recent circular type [8, 9]. Among the aforementioned MPC types, the Herriott-type cell is of great interest for its stability and simplicity (only two highly reflective mirrors are needed in most cases), which is also our focus in this work. We call the Herriot-type cell HMPC thereafter for simplicity in this work. In principle, the mirrors employed for HMPC can be either spherical or astigmatic. A recent study [10] has demonstrated that spherical mirrors are capable of generating similar spot patterns to aspherical mirrors. Therefore, spherical mirrors are favored in HMPC design, considering the relative complexity of aspherical mirrors.

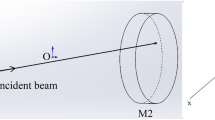
Over the past years, the design rules of HMPC have matured [11,12,13]. A generic prerequisite for HMPC is the non-intersection of the beam spot. Otherwise, beam interference occurs and makes the MPC application problematic. A stronger focus on HMPC design is the OPL; this quantity is mostly used to characterize the performance of HMPC. It is appealing to achieve longer OPL to improve the sensitivity of trace gas detection, provided that the laser power loss is acceptable. The OPL is determined by the geometry parameters, including the focal length of the mirrors (Rf), the distance between the two mirrors (D) and the incident position (x0, y0) and angles (x0’, y0’) of the beam. These parameters are indicated in Fig. 1. Often, a longer OPL features a larger size of MPC, i.e., larger Rf and \(D\). However, real applications are often limited by space usage and thus set very stringent requirements on the compactness of the HMPC.

Fig. 1
figure 1

Geometrical parameters of Herriot-type multipass cell. (\(x_{0}\), \(y_{0}\), \(z_{0}\)) and (\(x_{0}^{^{\prime}}\),\(y_{0}^{^{\prime}}\)) denote the incident location and angles of the ray beam. R is the radius of curvature of the mirrors, D is the spacing distance between the mirrors

Full size image

It is of growing interest to design compact HMPCs with sufficiently long OPL. Several recent efforts [3, 14] have proposed miniature HMPCs to build up palm-sized gas sensors. A literature study shows that a variety of HMPCs have been proposed and designed with sizes ranging from several tens of millimeters to hundreds of millimeters [2, 3, 14, 15]. The HMPC design is mostly carried out by modeling the ray transfer and scrutinizing the resultant beam patterns in the cell. Despite the well-establishment of HMPCs, practical HMPC fabrication often involves with the somewhat tedious trial-and-error process. Very recently, an informative work by Cui et al. [12] implied the possible scalability in HMPC configuration. However, more details about the principle and application of such scalability have not been elaborated. So far, it remains unclear on the fundamental rules of miniaturizing or expanding the HMPC size for a designated application.

A widely used approach to this problem is the application of scaling methods and similarity laws. The application of these principles potentially leads to an improvement in development speed and optimization of costs throughout the development phase of the system and components [16]. Thus, an open question arises under which conditions the geometrical parameters of HMPCs are scalable and which constraints are to be considered. A decisive obstacle in overcoming the challenges described above can be found in currently used HMPC designs, which have so far mostly developed to the specific test setups and for individual environments. These approaches are limited in their generality and do not offer the possibility to design and manufacture HMPCs in a cost and material efficient way.

In this communication, we report the linear scalability existing in the design of HMPCs. Unlike other efforts in developing new beam patterns in HMPCs, the focus of the present study is to provide a more mathematically and physically sound proof for the HMPC design. Note that the scalability is mostly suggested in an intuitive way. In the present study, this scalability is derived from the modified ABCD matrix model by Cui et al. [11]. Several exotic patterns were first designed to reproduce the previous results. Then, as a validation, HMPCs with varied cell sizes are simulated to obtain the beam pattern and OPL.

2 Theory

Figure 1 shows the geometry parameters in HMPC design. In line with the previous work [11], we define \(x_{n}\), \(y_{n}\),\(x_{n}^{^{\prime}}\), \(y_{n}^{^{\prime}}\) as the ray position parameters at the nth reflection, where \(x_{n}\), \(y_{n}\) are the incident displacement of the beam, and the \(x_{n}^{^{\prime}}\), \(y_{n}^{^{\prime}}\) are the incident angles. For a given HMPC, the aforementioned variables are calculated as:

$$x_{n} = x_{n - 1} + d_{n} \cdot \sin x_{n}^{^{\prime}} ,$$
(1)
$$y_{n} = y_{n - 1} + d_{n} \cdot \sin y_{n}^{^{\prime}} ,$$
(2)
$$x_{n}^{^{\prime}} = - 2 \cdot \arcsin \left( {{{x_{n} } \mathord{\left/ {\vphantom {{x_{n} } {R_{f} }}} \right. \kern-0pt} {R_{f} }}} \right) + x_{n - 1}^{^{\prime}} ,$$
(3)
$$y_{n}^{^{\prime}} = - 2 \cdot \arcsin \left( {{{y_{n} } \mathord{\left/ {\vphantom {{y_{n} } {R_{f} }}} \right. \kern-0pt} {R_{f} }}} \right) + y_{n - 1}^{^{\prime}} ,$$
(4)

where \(d_{n}\) is the optical path length from the \(n^{th}\) reflection, \(R_{f}\) is the focal length of the mirror. Herein, we hypothesize that the geometry of a given HMPC is scalable without beam pattern changes; the scaling factor is set as \(k\). Similarly, \(x_{n}^{S}\), \(y_{n}^{S}\), \(x_{n}^{S^{\prime}}\), \(y_{n}^{S^{\prime}}\) denotes the corresponding ray parameters of the scaled HMPC, where \(S\) stands for scaling.

In the \(x\) direction, the scalability is as follows:

$$k = \frac{{x_{n}^{S} }}{{x_{n} }} = \frac{{x_{n - 1}^{S} + d_{n}^{S} \cdot \sin x_{n - 1}^{S^{\prime}} }}{{x_{n - 1} + d_{n} \cdot \sin x_{n - 1}^{^{\prime}} }},$$
(5)

We further have:

$$d_{n}^{S} \cdot \sin x_{n - 1}^{S^{\prime}} = k \cdot d_{n} \cdot \sin x_{n - 1}^{^{\prime}} ,$$
(6)

which holds only when

$$d_{n}^{S} = k^{M} \cdot d_{n} ,$$
(7a)
$$\sin x_{n - 1}^{S^{\prime}} = k^{{\left( {1 - M} \right)}} \cdot \sin x_{n - 1}^{^{\prime}} ,$$
(7b)

where M is the index (natural number). Clearly, one can justify the scalability of x-component ray displacement when Eqs. (7a) and (7b) hold. Mathematically, Eq. (7a) always holds as it only relates to size scaling; while Eq. (7b) is not always guaranteed since \(\sin x_{n}^{S^{\prime}}\) may become unbounded for a large scaling factor \(k^{{\left( {1 - M} \right)}}\). Note that the incident angles \(x_{n}^{S^{\prime}}\) and \(x_{n}^{^{\prime}}\) can be varied from 0 to 90◦ and thus \(\sin x_{n}^{S^{\prime}}\) or \(\sin x_{n}^{^{\prime}}\) ranges from 0 to 1. Nevertheless, it is necessary to check the physical soundness of Eq. (7b).

We hypothesize that Eqs. (7a) and (7b) always hold for any k and M valves. For Eq. (7a), one can thus have:

$$k^{M} = {{d_{n}^{S} } \mathord{\left/ {\vphantom {{d_{n}^{S} } {d_{n} }}} \right. \kern-0pt} {d_{n} }},$$
(8)

Equation (7b) can be further expressed as:

$$x_{n - 1}^{S^{\prime}} = \arcsin \left( {k^{{\left( {1 - M} \right)}} \cdot \sin x_{n - 1}^{^{\prime}} } \right),$$
(9)

Equation (9) is tenable only for \(0 \le k^{{\left( {1 - M} \right)}} \cdot \sin x_{n - 1}^{^{\prime}} \le 1\). Note that the function of \(\sin x_{n - 1}^{^{\prime}}\) is bounded within 0–1, one can thus have

$$0 \le k^{{\left( {1 - M} \right)}} \le 1 \le \frac{1}{{\sin x_{n}^{^{\prime}} }},$$
(10)

Equation (10) should hold for any k (positive) and M value pairs. It is apparent to see that Eq. (10) only holds for \(M = 1\). Therefore, Eqs. (7a) and (7b) evolve into:

$$d_{n}^{S} = k \cdot d_{n} ,$$
(11a)
$$x_{n - 1}^{S^{\prime}} = x_{n - 1}^{^{\prime}} ,$$
(11b)

Further, one can have:

$$R_{f}^{S} = kR_{f} ,$$
(12)

Similarly, the same scaling also exists in y- and z-components. A self-consistent criterion is obtained to retain the linear scalability in HMPC design, which dictates

$$\frac{{x_{n}^{S} }}{{x_{n} }} = \frac{{y_{n}^{S} }}{{y_{n} }} = \frac{{z_{n}^{S} }}{{z_{n} }} = \frac{{R_{f}^{S} }}{{R_{f} }} = \frac{{D^{S} }}{D} = k,$$
(13a)
$$\frac{{x_{n}^{S^{\prime}} }}{{x_{n}^{^{\prime}} }} = \frac{{y_{n}^{S^{\prime}} }}{{y_{n}^{^{\prime}} }} = \frac{{z_{n}^{S^{\prime}} }}{{z_{n}^{^{\prime}} }} = 1,$$
(13b)

So the final OPL in the scaled HMPC is determined as:

$$\sum\limits_{n = 0}^{{n^{S} }} {d_{n}^{S} = k \cdot } \sum\limits_{n = 0}^{n} {d_{n} } .$$
(14)

Therefore, the so-called linear scalability in OPL is physically sound once the criteria are satisfied in Eq. (11a, b). This law holds for both the paraxial and non-paraxial approximations. In other words, the OPL of arbitrary HMPC can be tailored by adjusting the geometrical parameters of MPC simultaneously by the same factor, regardless of the possible manufacturing difficulties.

3 Results and discussion

To verify the linear scalability relationship, we modeled the beam patterns in the HMPCs of different sizes. Further, two HMPC prototypes were also fabricated by 3D printing with the resulted beam pattern compared to the modeling.

We validated the linear scalability of HMPC design by modeling the beam patterns of various HMPCs by Zemax Optic Studio. Several exotic beam patterns in ref. [11] were first reproduced to validate the Zemax model [11] (see Fig. 2). In this communication, we consider the seven-circle beam pattern as the example to illustrate the linear scalability. As a proof of principle, 12 sets of HMPCs were designed and simulated with their size proportionally scaled from 10 to 120.0 mm in R, from 0.683 mm to 7.608 mm in \(x_{0}\), from – 1.108 to – 13.296 mm in \(y_{0}\) and 12.308 mm to 147.696 mm in D (see Table 1). Figure 2c demonstrates the typical seven-circle beam patterns at the end (or exit) mirrors of two MPCs with proportionally varied \(x_{0}\), \(y_{0}\), R, D.

Fig. 2
figure 2

Reproduction of some typical exotic beam patterns 10 for the multipass cell by Zemax modeling. Reproduction of some typical exotic beam patterns [11] for the multipass cell by Zemax modeling. The initial beam spot size is 2 mm

Full size image
Table 1 Geometrical parameter of HMPC and the maximum allowed beam spot size (δ) at different scaling factors
Full size table

One key implication of the linear scalability is that the linear scaling of \(x_{0}\), \(y_{0}\), R, D values leads to the OPL variation by the same scaling factor. To verify this point, we take the smallest HMPC among the 12 HMPC sizes considered in Table 1 as the reference to investigate their OPLs. Figure 3 shows that the geometrical parameters as well as the OPL increase linearly with a larger k. In specific, larger scaling factor k leads to larger R, D and thus larger OPL. Such observation from simulation results is identical to the prediction by Eqs. (11a, b) and (12), justifying the rationale of linear scalability.

Fig. 3
figure 3

Linear scaling relationship in geometrical parameters of HMPC and the resultant optical path length. The geometrical parameters include incident position x0 and y0, mirror curvature radius R, mirror distance D and the minimum mirror size radius rm

Full size image

For demonstration purposes, we fabricated two sets of HMPCs. For the manufacturing of the optomechanical components, the stereolithography 3D-printing process is chosen due to its rapid prototyping ability [17]. The designed geometrical parameters include \(x_{0}\) = 3.170 ± 0.1 mm, \(y_{0}\) =  – 5.540 ± 0.1 mm, \(R\) = 50 ± 0.1 mm, \(D\) = 61.540 ± 0.1 mm and \(x_{0}\) = 6.3640 ± 0.1 mm, \(y_{0}\) =  – 11.080 ± 0.1 mm, \(R\) = 100 ± 0.1 mm, \(D\) = 123.08 ± 0.1 mm. The laser entry and exit holes were set as 1 mm in diameter by grinding.

A He–Ne laser diode with the optical output power of 539.4 µW at 632 nm was utilized to reproduce the seven-circle beam patterns, as seen in Fig. 4b and d. Note that we only verified the seven-circle beam pattern for two sets of HMPCs. It is also possible to reproduce other beam patterns by adjusting the incident position of the laser diode, which is somewhat less accessible in the present 3D-printed HMPC with a fixed house for the laser diode. Conceptually, other different beam patterns are technically available with the incident laser beam position carefully adjusted. A systematic comparison of the geometry parameters (outline circle, inner circle and unit circle) indicates good agreements have been achieved with a maximum deviation of < 15% between the modeling and experiment. The linear scalability is justified in HMPC design for consistency in theory, modeling and experiment.

Fig. 4
figure 4

Seven-circle beam patterns on the end mirror in the multipass cell of two different sizes: x0 = 3.170 mm, y0 = 5.540 mm, R = 50 mm, D = 61.540 mm for the small-sized HMPC; and x0 = 6.340 mm, y0 = 11.080 mm, R = 100 mm, D = 123.080 mm for the large-sized HMPC. The beam pattern for the small-sized HMPC (1-inch) is obtained by (a) zemax modeling and (b) experimental observation; the beam pattern for the large-sized HMPC (2-inch) is also obtained by (c) zemax modeling and (d) experimental observation

Full size image

The linear scalability provides straightforward guidance for tailored HMPC design. One promising application is to miniaturize the HMPC for compact and portable sensor design. In principle, the HMPC can be arbitrarily small, but this is constrained by the difficulty of minimizing the beam spot size. Note that the beam spot size is intrinsically determined by the optical setups and further reducing the spot size involves extra lens and other devices, making the optical system complicated. Given the beam spot size, the lower limit of the HMPC size is determined by the non-intersection requirement for beam patterns. Table 1 lists the maximum beam spot size available for a given HMPC, which indicates that a smaller spot size allows for better miniaturization of HMPC. For example, the minimal HMPC size is calculated as 23.48 × 23.48 × 61.54 mm3 for a spot size of 0.94 mm. Very likely, the beam spots in the miniature HMPCs may look somewhat blurry, leading to concerns on the non-intersection prerequisite. Indeed, the blurry appearance is mostly caused by the light scattering, rather than spot overlapping once the initial beam spot size satisfies the requirements listed in Table 1. Besides, the beam patterns as observed in the experiments can hardly be the same with the modeling due to the constrains in beam diameter and laser power. In particular, some spots are less visible due to the weak laser power; further improvement of the experimental beam patterns is possible but not pursued in this work. Nevertheless, the two experimental observations agree modestly well with the modeling and collaborate with the linear scalability.

Another application of this law is to escalate the HMPC for longer OPL. However, a special concern should also be taken for escalating the HMPC to obtain longer OPL and intuitively better signal-to-noise ratio (SNR). This is because the signal-to-noise ratio (SNR) presents as a non-monotonic function of OPL and reflectivity [14]. On the contrary, the SNR follows a "parabolic" trend and its peak value locates at longer OPL for higher reflectivity.

Figure 5 plots the variation of maximum SNR and the associated number of bounces with the scaling factor k and reflectivity. It is observed that the maximum SNR also increases linearly with scaling factors and their slopes are dominated by the reflectivity. In practice, reflectivity and HMPC size should be considered to achieve the optimal SNR. To achieve this theoretic optimum according to Cui’s calculation method [14], a mirror reflectivity of 99.525% is required for the demonstrator in this work. Alternatively, as shown in Fig. 5, the laser beam can be outcoupled after a smaller number of reflections to optimize the SNR.

Fig. 5
figure 5

Variation of the maximum achievable optical signal-to-noise ratio and the associated optimum number of beam reflections nopt with the linear scaling factor k and reflectivity R. The HMPC with the seven-circle beam pattern and the geometrical parameters according to Table 1 is set as reference case

Full size image

4 Conclusion

In summary, we derived the self-consistent criteria in the HMPC geometry to achieve the linear scaling in its OPL. This so-called linear scalability was justified by the good agreements in theory, modeling and experiment. Consideration in miniaturizing and escalating the HMPC for given OPL was also discussed. Mainly, it is required to consider the beam spot size and the SNR in customizing the HMPC. One primary requirement for HMPC design is to avoid the intersection of the beam spots and simultaneously optimize the SNR by defining the number of bounces inside the HMPC.