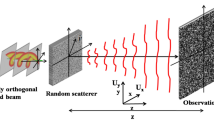
Abstract
Many researchers have been interested in finding elements that help in calculating the orbital angular momentum (OAM) of perturbed vortex beams i.e., after propagating through turbulence in recent years. In this work, we realized a method that utilizes the area of spatial auto-correlation function of scattered optical vortices for finding the topological charge. We have also established an analogy between the area of the intensity auto-correlation profile of the partially coherent vortices and the radii of the related coherent ring-shaped vortex beam transverse profiles which helps us finding the topological charge in a simpler way. This method is independent of the beam waist of Gaussian laser beam for generating the vortex beams. Our experimental results are in good agreement with the theoretically obtained results. These results may find applications in free space optical communication and ghost imaging with vortex beams.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The optical vortices have gained special focus and attention of many researchers in the past years due to their helical wave fronts, phase singularity and dark core at the center [1]. These beams possess a new degree of freedom, orbital angular momentum which is given by mħ per photon where m being the topological charge (TC) or order of the vortex beam. The order has been defined as number helices completed by the light in one wavelength [2]. These beams are known for their applications in optical micromanipulation [3,4,5], optical communication [6, 7], and data transmission [8].
The singularities have been realized in both coherent and partially coherent optical beams. When we propagate coherent vortices through the atmospheric turbulence, they become partially coherent, and the mode also gets disturbed. In these beams, the phase is ill-defined and becomes a promising research field due to the applications in communication. A new class of singularities have also realized in correlation functions and named as coherence vortices [9]. The value of the effective TC obtained in a correlation between two partially coherent beams possessing OAM is bounded by the TC of each beam [10].
Due to these high potential applications, developing the techniques to measure TC has been a constant task for many optical scholars. The interferometric techniques were the first to reveal the helical phase of the vortices [11, 12]. In recent years, the inference of the TC through the pattern formed by the diffraction of the field through specific elements has gained more attention by practical application. Many other techniques have been implemented for finding the TC for both coherent and partially coherent vortices by transmitting them through double slits [13], annular apertures [14], triangular apertures [15, 16], square apertures [17], among others, are diffraction techniques used. All these techniques work very effectively when light beams have high coherence. In our earlier studies, we have explored the geometry of the intensity profiles of both coherent and partially coherent ring-shaped beams [18–20]. In addition to the geometry of intensity profiles, work has also been done on measuring the topological charge and its sign of partially coherent beams using statistical properties such as cross spectral power density [21,21,22,23,25]. However, the observation of number of dark rings in correlation function becomes difficult with the increase in order and one may not be able to use the above techniques for higher order optical vortex beams.
In this work, we design a method for diagnosing the TC using the relation between the properties of coherent and partially coherent singular beams. We explore the dependence of area of intensity auto-correlation profile of partially coherent vortices obtained by scattering vortices through a rough surface and compare them with the respective properties of coherent vortices. We further verify our proposed method experimentally which are in good agreement with our numerical results. It is also noted that our results are independent of the beam waist used for producing the vortex beams.
2 Theoretical analysis
2.1 (a) Simulating the scattered light field
For numerically simulating the speckle patterns obtained by scattering the optical vortex beams, we start with the field distribution of OV beams which can be expresses mathematically as
where w0 is beam waist of the Gaussian beam used to generate the vortex beams. One can get the random phase introduced by the ground glass plate by taking the convolution between the Gaussian correlation function with finite width and the 2-D random pattern. This can be written as [26]
where σ is width of the correlation function defined by the size of the grains present in the ground glass plate and * indicates the convolution operation. Now, the scattered field i.e., the speckle pattern can be represented with the following:
We perform numerical simulations based on Van-Cittert-Zernike theorem that states that the far-field intensity distribution i.e., the Fourier transform of near field light is given by auto-correlation function. Now, mathematically the auto-correlation function can be written as
where F indicates the Fourier transform operator. All simulation results presented here have an average of 50 calculations and were obtained in the Matlab® software.
2.2 (b) Formalism used for coherent vortices:
We analyze the intensity distribution of coherent optical vortex beams using the methodology provided in Ref. [19]. Figure 1 shows the transverse intensity profile of a coherent vortex beam with m = 10. The inner and outer radii (r1, r2) are the radial distances at which the intensity falls to 1/e2 of the maximum intensity [19] and r0 is understood as the radius of the optical vortex beam defined by the distance from the beam center to the points where the maximum intensity is obtained.
One can find the ratio of two radii theoretically using our recent formalism provided in ref. [19], showing that there is a dependence of the radii of the vortices on their topological charge m. The radii r1, r0andr2 of the vortex beams assuming w0 = 1was obtained and given by
where \({q}_{m}={\left(m+1.3\right)}^{2}-{m}^{2}{e}^{-\frac{1.4}{m}}\)
Using the above two formalisms, we find the area of auto-correlation intensity profile and match its variation with the ratio of two radii (r2/r0) as a function of topological charge.
3 Experimental details
For generating the intensity profiles of auto-correlation functions, we produce optical vortices using computer-generated holography. We illuminate the laser beam on the spatial light modulator (SLM) on which we display the computer-generated holograms corresponding to the vortices of different orders and shown in Fig. 2. The vortices have been produced in first diffraction order and selected through an aperture and scatter them through a ground glass plate (Thorlabs DG10-600). We have used an intensity and frequency stabilized He–Ne laser (from spectra) of wavelength 632.8 nm and power ˂ 5 mW in our experiment. The coherent vortices at 40 cm from SLM and the corresponding speckle patterns have been recorded using a CCD camera with a pixel size 3.45 μm at a distance of 20 cm from the ground glass plate (GGP).
4 Results and discussion
Figure 3 shows the results obtained from the numerical simulations of the transversal intensity profiles of optical vortices for different TC values. In (A) we have the intensity profiles of the coherent vortex beams with m equal to 2, 8, 14, and 20. In row (B) the related partially coherent LG beams are shown. In (C) are present the intensity auto-correlation profiles performed from row (B). The numerical simulations used matrices of 200 × 200 pixels in (A) and (B), but in (C) the matrices were cut out and presented with 100 × 100 pixels for better viewing. We can clearly observe in Fig. 2 that with the increase in the TC values there is an increase in the annular area of the coherent vortex (A) and a decrease in the respective correlation profile area (C). At the same time, it is possible to observe the decrease of the average size of speckle grains. (B).
We further generated the experimental auto-correlation functions using the speckle patterns obtained after scattering the vortex beams. The coherent optical vortices with order m = 0, 3, 6, 8 (top), the corresponding speckle patterns (middle) along with their auto-correlation functions (bottom) have been shown in Fig. 4. The number of rings or dark points present in the auto-correlation function is equal to the topological charge [25]. However, it is difficult to observe the dark rings at high separation of two field points of the speckle pattern. Due to the same, we utilize the area of auto-correlation function for finding the topological charge.
To measure the area of the intensity auto-correlation profile of the optical vortices, we count the number of pixels with intensity values from 1/e2of the maximum intensity. The results for these areas obtained with w0 equal to 0.9, 1.0 and 1.1 when m varies from 1 to 20 are shown in Table 1. We observe that regardless of the beam waistw0, the pixel number decreases with increasing of the TC values.
Figure 5 shows the variation of area of the intensity auto-correlation profiles Am as a function of the TC for w0 = 1 mm. One can clearly observe that the experimental results are in good agreement with the numerically obtained results. We also observe that the behavior describes a negative exponential, represented by the solid green line, whose best fit for w0 = 1is given by
where m is the TC of the vortex. For the other values of w0 we observe only a vertical displacement of the points around the curve.
5 Correlation with the geometry of coherent vortices
After studying the behavior of the area of the intensity auto-correlation profile of partially coherent vortices when submitted to change of TC, we analyzed the geometry of the intensity profile of the respective coherent vortices. Using the analytical Eqs: [5,6,7], we have found the theoretical values for the values of (r1, r0, r2) and Table 2 shows the results for radius ratio r2/r0 with m varying from 1 to 20 for different values of w0. It is easily observable that, with the increase of the ratio r2/r0 values, the m values are reduced. However, for a fixed m, the ratio does not change significantly with the variation of w0.
For a better understanding of the result presented in Table 2, the ratio r2/r0 as a function of the topological charge m is plotted in Fig. 6. We observed that the behavior describes a negative exponential as well as what was observed with the behavior of the area of the intensity auto-correlation profiles shown in Fig. 5. The solid green line in Fig. 6 is the best fit for the points obtained with w0 = 1.
Figure 6 shows the relation between radius ratio r2/r0, obtained from the Eqs. (5) and (6), and topological charge \(m\). In the same figure are also shown the numerical results obtained. We observed a great agreement between the theoretical results with the experimental findings.
From here, we will note the ratio r2/r0byRm.Thus, the equation that best describes the fit above is given by
where \(m\) is the TC of the optical vortex. Surprisingly, the term exp (− m/3.2) in the above equation is identical to that in Eq. (8). Then, making a combination between Eqs. (8) and (9), after some adjustments, we obtain the relation between Rm and Am with good approximation as
Equation (10) presents the most important result of this work. We discover that there is a linear dependence between the radius ratio \({R}_{m}\) and the area of the intensity auto-correlation profile Am of the vortices. Thus, in a specific configuration, it is possible to determine the radius ratio Rm of an optical coherent vortex from the area of the intensity auto-correlation profile of the same vortex in the partially coherent system. Since the ratio r2/r0does not depend on the beam waist w0 for each value of m (see Table 2), we can estimate the TC value of the optical vortex.
Further we have evaluated the accuracy in finding the topological charge using the formula \(\alpha =1-\frac{{{R}_{m}}_{th}-{{R}_{m}}_{exp}}{{{R}_{m}}_{th}}\). It is observed that we can find the TC with the accuracy greater than 94% as shown in Fig. (7). These results provide a significant way for measuring the topological charge as the radii ratio is independent of the beam waist used to generate the vortex beams.
6 Conclusion
In conclusion, we have shown numerically, theoretically, and experimentally that it is possible to estimate the topological charge of an optical vortex beam through of the area of the intensity auto-correlation profile. This area has a linear dependence to the radii ratio r2/r0 of coherent optical vortices with negative exponential dependence on their topological charge m. We also observe that this ratio is independent of beam waist although the area of auto-correlation function depends on w0 which makes the finding of topological charge simpler. These results may find applications in ghost imaging with vortices and free space optical communication [27,27,28,29].
Data Availability
All data generated or analysed during this study are included in this published article.
References
J.E. Curtis, D.G. Grier, Structure of optical vortices. Phys. Rev. Lett. 90, 133901 (2003)
L. Allen, M.W. Beijersbergen, R.J. Spreeuw, J.P. Woerdman, “Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes,” Physical review. A Atom. Mole. Opt. Phys. 45, 8185–8189 (1992)
M.J. Padgett, Orbital angular momentum 25 years on [Invited]. Opt. Exp. 25, 11265–11274 (2017)
D.G. Grier, A revolution in optical manipulation. Nature 424, 810–816 (2003)
A. van der Horst, N.R. Forde, Calibration of dynamic holographic optical tweezers for force measurements on biomaterials. Opt. Exp. 16, 20987–21003 (2008)
C.I. Osorio, G. Molina-Terriza, B.G. Font, J.P. Torres, Azimuthal distinguishability of entangled photons generated in spontaneous parametric down-conversion. Opt. Exp. 15, 14636–14643 (2007)
J.M. Hickmann, E.J.S. Fonseca, A.J. Jesus-Silva, Born’s rule and the interference of photons with orbital angular momentum by a triangular slit. Europhys. Lett. 96, 64006 (2011)
J. Wang, J.-Y. Yang, I.M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. Ren, Y. Yue, S. Dolinar, M. Tur, A.E. Willner, Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 6, 488 (2012)
G. Gbur, T.D. Visser, Coherence vortices in partially coherent beams. Opt. Commun. 222, 117–125 (2003)
A.J. Jesus-Silva, J.M. Hickmann, E.J.S. Fonseca, Strong correlations between incoherent vortices. Opt. Exp. 20, 19708–19713 (2012)
M. Harris, C.A. Hill, P.R. Tapster, J.M. Vaughan, Laser modes with helical wave fronts. Phys. Rev. A 49, 3119–3122 (1994)
M. Harris, C.A. Hill, J.M. Vaughan, Optical helices and spiral interference fringes. Opt. Commun. 106, 161–166 (1994)
H.I. Sztul, R.R. Alfano, Double-slit interference with Laguerre-Gaussian beams. Opt. Lett. 31, 999–1001 (2006)
C.-S. Guo, L.-L. Lu, H.-T. Wang, Characterizing topological charge of optical vortices by using an annular aperture. Opt. Lett. 34, 3686–3688 (2009)
J.M. Hickmann, E.J.S. Fonseca, W.C. Soares, S. Chávez-Cerda, Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 105, 053904 (2010)
L.E.E. de Araujo, M.E. Anderson, Measuring vortex charge with a triangular aperture. Opt. Lett. 36, 787–789 (2011)
J.G. Silva, A.J. Jesus-Silva, M.A.R.C. Alencar, J.M. Hickmann, E.J.S. Fonseca, Unveiling square and triangular optical lattices: a comparative study. Opt. Lett. 39, 949–952 (2014)
S.G. Reddy, A. Kumar, S. Prabhakar, R.P. Singh, Experimental generation of ring-shaped beams with random sources. Opt. Lett. 38, 4441–4444 (2013)
S.G. Reddy, S. Prabhakar, A. Kumar, J. Banerji, R.P. Singh, Higher order optical vortices and formation of speckles. Opt. Lett. 39, 4364–4367 (2014)
C.R. Alves, A.J. Jesus-Silva, E.J.S. Fonseca, Characterizing coherence vortices through geometry. Opt. Lett. 40, 2747–2750 (2015)
Y. Yang, M. Mazilu, K. Dholakia, Measuring the orbital angular momentum of partially coherent optical vortices through singularities in their cross-spectral density functions. Opt. Lett. 37, 4949–4951 (2012)
J. Chen, X. Liu, J. Yu, Y. Cai, Simultaneous determination of the sign and the magnitude of the topological charge of a partially coherent vortex beam. Appl. Phys. B 122, 1–12 (2016)
M. Dong, C. Zhou, Y. Cai et al., Partially coherent vortex beams: fundamentals and applications. Sci. China Phys. Mech. Astron. 64, 224201 (2021)
M. Dong, X. Lu, C. Zhao, Y. Cai, Y. Yang, "Measuring topological charge of partially coherent elegant Laguerre-Gaussian beam. Opt. Exp. 26, 33035–33043 (2018)
J. Zhang, S.-J. Huang, F.-Q. Zhu, W. Shao, M.-S. Chen, Dimensional properties of Laguerre-Gaussian vortex beams. Appl. Opt. 56, 3556–3561 (2017)
P. Vanitha, S.G. Reddy, R.P. Singh, “Correlations in scattered singular beams,” Holography - Recent Advances and Applications, Intechopen (2023).
S. Crosby, S. Castelletto, C. Aruldoss, R.E. Scholten, A. Roberts, Modelling of classical ghost images obtained using scattered light. New J. Phys. 9, 285 (2007)
K.W.C. Chan, M.N. O’Sullivan, R.W. Boyd, High-order thermal ghost imaging. Opt. Lett. 34, 3343–3345 (2009)
K.W.C. Chan, M.N. O’Sullivan, R.W. Boyd, Optimization of thermal ghost imaging: high-order correlations vs. background subtraction. Opt. Exp. 18, 5562–5573 (2010)
Funding
This work was supported by SRM University AP, SRMAP/URG/E&PP/2022-23/003, SRMAP/URG/E & amp; PP/2022-23/003, Science and Engineering Research Board, SRG/2019/000857
Author information
Authors and Affiliations
Contributions
Vinny cris and Vanitha patnala have conducted the experiment and analysed the results. Vinny Cris has prepared initial manuscript which has been subsequently corrected by Vanitha, Gangi and Cleberson. The theoretical calculations have been done by Cleberson and Gangi. They also supervised the entire work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Cris, M.V., Patnala, V., Reddy, S.G. et al. Correlation between coherent and scattered optical vortices: diagnosis of the topological charge. Appl. Phys. B 129, 85 (2023). https://doi.org/10.1007/s00340-023-08027-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-023-08027-6