1 Introduction

Electromagnetic waves having a wavelength of 30 μm–3 mm (0.1–10 THz) are typically referred to as terahertz (THz) waves [1]. The THz waves have a wide range of applications in communications, imaging, medical, and security screening. To advance the development of THz technology, there is an urgent need for efficient THz functional devices. Metasurfaces have extraordinary physical characteristics, such as negative refraction, perfect lenses, and The abnormal Brewster effect [2]. These properties offer new suggestions for the creation of various THz functional devices. In recent years, they have been widely used in the development of ultra-thin and miniaturized polarization converters to control the polarization of electromagnetic waves [3]. However, the polarization convertor made of traditional metallic and dielectric materials lacks dynamic tunability, which restricts their suitability for use in real-world applications [4].

The use of materials having tunable dielectric characteristics, which may be actively regulated by external parameters, such as light intensity, voltage, or temperature, is one technique to obtain a controllable function. Graphene is a 2D monolayer of carbon atoms where the Fermi level can be changed by applying a bias voltage, and tunable polarization converters based on graphene [5] have been much investigated. However, the thinness, instability, and low coupling to incident light of graphene are its drawbacks. Recently, Dirac semimetals called “three-dimensional (3D) graphene” have the potential to dynamically control conductivity by changing the Fermi energy through surface doping [6] or bias voltage [7]. Dirac semimetals have higher carrier mobility (9 × 106cm2V−1 s−1, 5 K) than graphene (2 × 105cm2V−1 s−1, 5 K) [8] under the same conditions [9]. The Dirac semimetals have already achieved tunable linear-to-linear [10] and linear-to-circular [11] polarization conversion. In addition, another tunable material, the phase change material vanadium oxide can also be used to accomplish the switching effect of the polarization converter [12]. Recently, there has been a lot of attention in physics and materials science for Weyl semimetals (WSMs) with distinctive properties of ultra-high electrical conductivity [13, 14], and TaAs [15], TaP [16], NbAs [17], NbP [18], etc. are experimentally confirmed as WSMs. The chemical potential of WSMs can be modulated by doping, temperature, or pressure changes [19,20,21].

In this work, a split-ring Weyl semimetals (WSMs) nanostructure is proposed to realize a dual-band THz tunable cross-polarization converter and beam modulation. The proposed split-ring polarization converters enable tunable dual-band polarization conversion for linearly polarized and circularly polarized THz waves. The cross-polarization conversion frequency can be tunable in 1.21–1.29 THz, and 1.97–2.04 THz by altering the chemical potential of the WSMs.

After that, we constructed coding metasurfaces based on the unit cell of the polarization converter to achieve beam splitting and anomalous refraction. It is exciting that these tunable coding metasurfaces can complete the amplitude and reflection angle modulation of linear to linear, circular to circular, and linear to circular polarized convertors in the broadband range 1.21–1.29 THz, 1.97–2.04 THz. Furthermore, the angular range of beam deflection can be widened through the 3-bit Fourier convolution operation.

2 Design and material

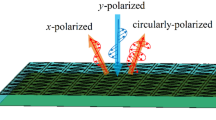
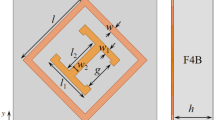
Figure 1 depicts the unit cell of the split-ring polarization converter and three function coding metasurfaces. The unit cell of the polarization converter consists of a three-layer structure. A 45° opening angle split-ring with the azimuth angle 45° away from the x-axis makes up the top layer. Zirconium dioxide (ZrO2) has a dielectric constant of 2.1 and is used as the spacer layer [22]. The conductivity of the gold was 4.56 × 107 S/m. The structural parameters are specified in Fig. 1: p = 80 μm, r = 32 μm, w = 5 μm, α = 45°, θ = 45°, t = 0.2 μm, h1 = 10 μm, h2 = 0.2 μm. The full-wave simulation is used with the finite element method of the electromagnetic software COMSOL Multiphysics. Figure 1 also displays the polarization conversion function of our designed split-ring polarization converter, which can accomplish the cross-polarization conversion of linear polarization (x- and y- polarization), and circular polarization waves (left-handed circular polarization (LCP) and right-handed circular polarization (RCP) waves. Based on the unit cell of the polarization converter, we further designed beam-modulated coding metasurfaces with three functions of beam modulation: linear–linear, circular–circular, and linear–circle. Interestingly, beam modulation can be controlled by the chemical potential of the WSMs. Unlike graphene, which changes the Fermi energy level using gate voltage [23], Weyl semimetals modulate the chemical potential by voltage heating the ion-gel to raise the temperature. In Fig. 1, we coated the ion-gel layer above the metasurface [24]. After that, gold electrodes are deposited on the ionic gel layer to be used as gold electrodes for the top gate. The end of the electrode is grounded and a voltage is applied to pass current through the ion-gel to raise the temperature of the ion-gel. With the temperature change, the chemical potential of WSMs is tunable. By constructing coding metasurfaces, the beam modulation of linear–linear, circular–circular, and linear–circular can be realized. By changing the chemical potential of WSMs, we can change the reflected beam amplitude and elevation angle.

Fig. 1
figure 1

Schematic diagram of dual-band tunable cross-polarization converter and three functional coding metasurface

Full size image

The dielectric constant of WSMs is anisotropic, following [25] expressed as

$$\mathop \varepsilon \limits^{ = } = \left( {\begin{array}{*{20}c} {\varepsilon_{{{\text{xx}}}} \left( \omega \right)} & {\varepsilon_{{{\text{xy}}}} \left( \omega \right)} & 0 \\ {\varepsilon_{{{\text{yx}}}} \left( \omega \right)} & {\varepsilon_{{{\text{yy}}}} \left( \omega \right)} & 0 \\ 0 & 0 & {\varepsilon_{{{\text{zz}}}} \left( \omega \right)} \\ \end{array} } \right)$$
(1)

The diagonal components εxx and εyy are equal and can be written analytically as

$${\varepsilon }_{\mathrm{xx},\mathrm{yy}}\left(\omega \right)=1+\frac{\alpha }{3\pi }\left[\mathit{ln}\left|\frac{4{\Gamma }^{2}}{4{\mu }^{2}-{\omega }^{2}}\right|-\frac{4{\mu }^{2}}{{\omega }^{2}}+i\pi \Theta \left(\omega -2\mu \right)\right],$$
(2)

where \(\alpha ={e}^{2}/(4\pi {\varepsilon }_{0}\hslash {v}_{F})\), \({v}_{F}=4\times 1{0}^{7}\mathrm{cm}/\mathrm{s}\) is the Fermi velocity obtained from the analysis of experimental data, \(\Gamma \sim {v}_{F}|Q|\), Q = 1 nm−1 is the node separation parameter, μ is the chemical potential, ω is the angular frequency, and Θ(X) denotes the usual step function. The off-diagonal components are denoted as \({\varepsilon }_{\mathrm{xy}}(\omega )=-{\varepsilon }_{\mathrm{yx}}(\omega )=i\gamma (\omega )\), while γ(ω) is the frequency-independent off-diagonal component, expressed as

$$\gamma \left(\omega \right)=\frac{\alpha }{\pi \omega }\left[2{v}_{F}Q-{\sum }_{s=\pm 1}\frac{s\mu }{2{\beta }_{s}}\left(\frac{1}{{\beta }_{s}}\mathit{ln}\left|\frac{1+{\beta }_{s}}{1-{\beta }_{s}}\right|-2\right)\right]\gamma , \left|{\beta }_{s}\right|\ll 1$$
(3)

βs is the tilting parameter, and the type I WSMs corresponds to |βs|< 1, and the type II WSMs correspond to |βs|> 1. When |βs|< 1, the εzz component of the dielectric tensor decomposes into the real and imaginary parts \(\varepsilon_{zz} = \varepsilon_{zz}^{^{\prime}} + i\varepsilon_{zz}^{^{\prime\prime}}\), which are expressed as follows

$$\varepsilon_{zz}^{^{\prime}} = 1 + \frac{{\alpha \mu^{2} }}{{\pi \omega^{2} }}\sum\nolimits_{s = \pm 1} {\frac{1}{{\beta_{s}^{3} }}} \left\{ \begin{gathered} \frac{8}{3}\beta_{s} - 4\arctan h\beta_{s} + {\text{In}}\left| {\frac{{4\mu^{2} - \omega^{2} \left( {1 + \beta_{s} } \right)^{2} }}{{4\mu^{2} - \omega^{2} \left( {1 - \beta_{s} } \right)^{2} }}} \right| \hfill \\ + \frac{{\omega^{2} }}{{12\mu^{2} }}\sum\nolimits_{t = \pm 1} {\left[ \begin{gathered} t\left( {1 + 2t\beta_{s} } \right)\left( {1 - t\beta_{s} } \right)^{2} {\text{In}}\left| {\frac{{4\Gamma^{2} - \left( {1 + t\beta_{s} } \right)^{2} }}{{4\mu^{2} - \omega^{2} \left( {1 - t\beta_{s} } \right)^{2} }}} \right| \hfill \\ - \frac{2\mu }{\omega }\left( {\frac{{4\mu^{2} }}{{\omega^{2} }} + 3 - 3\beta_{s}^{2} } \right){\text{In}}\left| {\frac{{2\mu - t\omega \left( {1 + t\beta_{s} } \right)}}{{2\mu - t\omega \left( {1 - t\beta_{s} } \right)}}} \right| \hfill \\ \end{gathered} \right]} \hfill \\ \end{gathered} \right\}$$
(4)
$$\varepsilon_{zz}^{^{\prime\prime}} = \frac{\alpha }{6}\mathop \sum \limits_{s = \pm } \Theta \left( {\omega - \frac{2\mu }{{1 + \left| {\beta_{s} } \right|}}} \right)\left\{ {1 - \frac{1}{2}\left[ {1 + \frac{3}{{2\left| {\beta_{s} } \right|}}\left( {\frac{2\mu }{\omega } - 1} \right)(1 - \frac{1}{{3\beta_{s}^{2} }}\left( {\frac{2\mu }{\omega } - 1)^{2} } \right)} \right]\Theta \left( {\frac{2\mu }{{1 - \left| {\beta_{s} } \right|}} - \omega } \right)} \right\}$$
(5)

Figure 2 shows the real and imaginary parts of the dielectric constants for WSMs with different normalized chemical potentials μ/(vF |Q|). The real part of the dielectric constant is expressed in terms of the normalized magnetization χ, defined as χxx = (\(\varepsilon_{xx}^{^{\prime}}\)–1)3π/α and χzz = (\(\varepsilon_{zz}^{^{\prime}}\)–1)3π/α. In this simulation, the normalized chemical potential and tilting parameters of the WSMs are assumed to be μ/(vF |Q|) = 0.3 and βs = 0.5, respectively.

Fig. 2
figure 2

WSMs dielectric constants for βs = 0.5 as a function of frequency. a and c correspond to the normalized susceptibility χxx and χzz. b and d correspond to the imaginary components \(\varepsilon_{{{\text{xy}}}}^{^{\prime\prime}} /\alpha\) and \({\upvarepsilon }_{{{\text{zz}}}}^{{^{\prime\prime}}} /{\upalpha }\)

Full size image

3 Cross-polarization conversion

3.1 Linear–linear cross-polarization conversion

Figure 3(a) and (b) show the reflection amplitude, and phase difference ∆Φ of this dual-band polarization converter. As can be seen in Fig. 3(a), co-polarization components Rxx and Ryy are nearly zero, and cross-polarization components Rxy and Ryx are 0.976 and 0.974 at 1.21 THz and 1.97 THz. The phase difference for 1.21 THz and 1.97 THz in Fig. 3(b) is ∆Φ = arg(Rxy)–arg(Ryy) = −π. The results display that our proposed device can convert co-polarized waves to cross-polarized waves. The incident angle dependence as well as the physical mechanism of the polarization converter are given in Fig. S1 of Supplement 1, and the polarization converter is well robust within an incident angle of 60°. In Fig. S2 of Supplement 1, we construct the u–v coordinate system to further explain the physical mechanism of the cross-polarization conversion. As can be seen from Fig. 3(a), the split ring polarization converter can achieve 1.21 THz and 1.97 THz with two reflection peaks, and the designed device can realize the polarization conversion of double band. In Fig. S3 of Supplementary 1, we explain the physical mechanism of the two-band polarization conversion by the surface current density distribution of the metasurface. Figure 3(c) shows that PCR is more strongly influenced by the normalized chemical potential μ/(vF |Q|). The first polarization conversion frequency increased from 1.21 to 1.29 THz, while the second polarization conversion frequency shifted from 1.97 to 2.03 THz when the normalized chemical potential increased from 0.3 to 0.8. To account for the shift of the resonant frequency, Liu et al. [26] used perturbation theory to explain the tunable of the resonant frequency, the change of resonance peak of absorption spectra is caused by material perturbation of the Dirac semimetal. Wang et al. [27] give the wave vector of surface plasmon polaritons along the graphene satisfies \({k}_{spp}\propto \hslash {f}_{r}^{2}/(2{\alpha }_{0}{E}_{f}c)\). Therefore, the resonance frequency satisfies \({f}_{r}\propto {E}_{f}^{1/2}\). When the graphene Fermi level Ef increases, the corresponding resonant frequency will blueshift. In Fig. 2, the dielectric constant decreases gradually as the chemical potential increases, which is the reason for the frequency shift.

Fig. 3
figure 3

a Reflection amplitude Rxx, Ryx and Rxy, Ryy b Phase difference ΔΦ c PCR of polarization converters under y-polarized wave illumination at different normalized chemical potentials

Full size image

3.2 Circular–circular cross-polarization conversion

The proposed split-ring polarization converter can also convert circular polarization into cross-polarization. Figure 4(a) depicts the reflection amplitude of the co-polarization and cross-polarization of the unit cell under the normal incidence of LCP and RCP waves at resonance frequencies of 1.21 THz and 1.97 THz. The co-polarization reflection amplitude is less than 0.01, while the cross-polarization reflection amplitude is greater than 0.9. The cross-polarization conversion of circularly polarized (CP) is because the metal ground plate inverts the polarization state of the incident CP wave. To explain the cross-polarization conversion of CP, we used the u-v coordinate system in Supplement 2 The co-polarized reflection amplitude and cross-polarized reflection amplitude of the incident circularly polarized light can be expressed as \({R}_{RR}=\frac{1}{4}{\left|{R}_{l}+{R}_{s}{e}^{i\Delta \phi }\right|}^{2}\), \({R}_{LR}=\frac{1}{4}{\left|{R}_{l}-{R}_{s}{e}^{i\Delta \phi }\right|}^{2}\), where Rl and Rs denote the reflection coefficients for incident linear polarization along u- and v- axes in the u–v coordinate system. Achieving complete conversion of the two orthogonal circular polarization states requires the satisfaction of Rl = Rs, Δ \(\phi\) = π. As shown in Fig. 4(b), it can be seen that a reflection phase difference π and over 0.9 reflection amplitude values at the polarization conversion frequencies of 1.21 THz and 1.97 THz. Hence, there is a high conversion between two orthogonal circular polarization states. This polarization converter has dual polarization features and can be used as a half-wave piece, which requires a phase delay of π between the fast and slow axes. In Fig. S2(b) of supplementary 1, the split-ring polarization converter has a phase difference of –π between the Ruu and Rvv when the linear polarization wave is incident, so it can be considered as a half-wave piece with its fast axis oriented at 45° to the x-axis. The Jones matrix of linearly polarized light is expressed as \(\left[\begin{array}{c}\mathrm{cos\theta }\\ \mathrm{sin\theta }\end{array}\right]\), θ is the angle between the direction of the incident wave electric field and the x-axis. The Jones matrix of the split-ring polarization converter is expressed as \(\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\) with its fast axis oriented at 45° to the x-axis. The Jones matrix of the outgoing light passing through the polarization converter is expressed as \(\left[\begin{array}{c}\mathrm{sin\theta }\\ \mathrm{cos\theta }\end{array}\right]\). In Fig. 4(b), the phase difference between the Rl and Rs is π. Thus, when circularly polarized light is incident, our devices can also be viewed as the half-wave piece. The Jones matrix for right circularly polarized waves is expressed as \(\left[\begin{array}{c}\mathrm{cos\theta }\\ -i\mathrm{sin\theta }\end{array}\right]\). The outgoing light passing through the polarization converter is \(-i\left[\begin{array}{c}\mathrm{sin\theta }\\ i\mathrm{cos\theta }\end{array}\right]\), and the emitted light is left circularly polarized waves. The left circularly polarized wave \(\left[\begin{array}{c}\mathrm{cos\theta }\\ i\mathrm{sin\theta }\end{array}\right]\) changes to right circularly polarized light \(i\left[\begin{array}{c}\mathrm{cos\theta }\\ -is\mathrm{in\theta }\end{array}\right]\). Therefore, the polarization converter has a dual-polarization feature.

Fig. 4
figure 4

a Schematic diagram of reflection at normal LCP and RCP incidence. b Reflection amplitude and phase difference for linear polarization along u- and v- axes

Full size image

Frequency tunability of the polarization converter of circularly polarized waves can also be achieved by tuning the chemical potential of the WSMs. Figure 5(a) shows the PCR for different WSMs normalized chemical potentials, with the RCP incident wave. It can be found that the first polarization conversion frequency increases from 1.21 to 1.29 THz, and the second polarization conversion frequency increases from 1.97 to 2.04 THz. The polarization conversion frequencies corresponding to the normalized chemical potential are (I) 1.21 THz, 1.97 THz for μ/(vF |Q|) = 0.3, (II) 1.25 THz, 1.99 THz for μ/(vF |Q|) = 0.4, (III) 1.26 THz, 2.01 THz for μ/(vF |Q|) = 0.5, (IV) 1.27 THz, 2.02 THz for μ/(vF |Q|) = 0.6, not shown in Fig. 5(a) (V) 1.28 THz, 2.03 THz for μ/(vF |Q|) = 0.7, not shown in Fig. 5(a) (VI) 1.29 THz, 2.04 THz for μ/(vF |Q|) = 0.8. As seen in Fig. 5(b), a linear phase profile of a 2π range is obtained by rotating the azimuth angle from 0° to 157.5° of the split-ring, and the incident wave is RCP wave at 1.21 THz, the normalized chemical potential of WSMs is selected as 0.3. After that, we design a Pancharatnam-Berry (PB) coding metasurface to control the THz wave by fusing PB metasurfaces with various predesigned coding sequences. In Fig. 5(c), the coding particles corresponds to phase −π, −3π/4, −π/2, −π/4, 0, π/4, π/2, and 3π/4 construct the 1-, 2-, and 3-bit coding PB phase metasurfaces. In the following, the coding ‘000, 001, 010, 011, 100, 101, 110, 111’ are referred to as numbers ‘0, 1, 2, 3, 4, 5, 6, 7’ for ease of description.

Fig. 5
figure 5

a PCR of polarization converters under RCP wave illumination at different normalized chemical potentials. b Reflection amplitude and phase gradient of the coding particle at different azimuth angles under RCP waves incident. c Eight coding particles for the coding metasurfaces

Full size image

The performance of various dual-band THz polarization converters is compared in Table 1. It is clear that certain dual polarization converter devices only have one function while others are capable of performing numerous tasks. Additionally, the majority of the devices are unable to perform dual polarization conversion that is tunable. Reference [28] is capable of three polarization conversions of linear-to-linear, linear-to-circular, and circular-to-circular, but it only operates at two fixed points of frequency and has a PCR of only 90%. Reference [29] enables a tunable multifunctional polarization converter, but the polarization conversion efficiency can be as low as 69%. Although in [30] and [31] the higher PCR of 99% and 93% were obtained, their devices can only perform a linear cross-polarization conversion. Reference [32] can implement a dual-function polarization converter with a polarization conversion efficiency of 90% while the frequency band of reference [33] is inconsistent. In contrast, in the proposed work, the polarization converter can achieve a PCR of 99% in all operating bandwidths and can enable polarization conversion types of both linear-to-linear and circular-to-circular functions for the same frequency bands.

Table 1 Comparison of polarization conversion with the previously published works
Full size table

4 Coding metasurfaces

In this section, we obtain the particles covering the 2π phase gradient by rotating the azimuth angle of the split ring and designing a 3-bit coding metasurface. Three functions of linear–linear, circular–circular, and linear–circular can be realized at two bands through the sequence of the coding particles. The regulation of the beam amplitude and reflection angle can be completed by changing the chemical potential of WSMs.

4.1 Linear–linear coding metasurfaces

By changing the azimuth angle θ of the split ring, the amplitude of the transmitted linear polarized wave can be changed, thus achieving amplitude modulation (see Supplement 2). Figure 6 shows the 2D polar coordinate far field and 3D far field with amplitude coding (Not the phase encoding in Fig. 5) ‘100,100…’. The 1-bit amplitude coding ‘100,100…’ shows the ± 1st order diffraction waves. As the normalized chemical potential of the WSMs increases from 0.3 to 0.7, the amplitude intensity of the reflected beam gradually decreases, and tunability of the amplitude is achieved. According to the generalized Snell’s law \({n}_{r}\mathrm{sin}{\theta }_{r}={n}_{i}\mathrm{sin}{\theta }_{i}+\frac{c}{2\pi f}\frac{d\phi }{d\mathrm{x}}\) of reflection, the elevation angle of reflection under normal incidence is \({\theta }_{r}=\mathrm{arcsin}(nc/(f\bullet\Gamma ))\). In which Г is the physical length of a period of the coding sequence, c is the speed of light in a vacuum, n is the number of diffraction levels, and f is the anomalous reflection frequency. The elevation angle of reflection under normal incidence is 39.4°, 38.5°, and 38.0° for normalized chemical potential μ/(vF |Q|) = 0.3, 0.5, and 0.7. The elevation angles obtained from the simulation are 40.0°, 38.9°, and 38.2°, which are consistent with the results calculated by the generalized Snell’s law. After that, we set the amplitude coding to ‘10,001,000…’, and the obtained 2D polar coordinate far-field and 3D far-field are shown in Fig. 6(b), and it is clear from the results that the reflected beam with ± 1st and ± 2nd order diffraction.

Fig. 6
figure 6

2D scattering patterns and 3D far-field scattering patterns under amplitude coding sequences ‘100,100…’ and ‘10,001,000…’ at different normalized chemical potential μ/(vF |Q|) of the WSMs

Full size image

4.2 Circular–circular coding metasurfaces

Intriguingly, the frequency tunability property of the proposed polarization converter enables the frequency tunability of anomalous reflection. The device can accomplish anomalous reflection over a wide range of frequencies, and only the normalized chemical potential of WSMs needs to be changed. By changing the azimuth angle of the split ring, it is possible to cover the phase from 0 to 2π (see Supplement 3). Then, eight-phase coding particles for coding metasurfaces are completed, after which the 1-bit phase coding metasurface was constructed with two bits, ‘0’ and ‘4’, to verify the beam splitting of LCP reflection waves. Figure 7 shows the far-field for three coding metasurfaces ‘0044…’, ‘000,444…’, and ‘00,004,444…’. Of course, the elevation angle is not consistent because the coding way is not the same. The azimuth angle can be given by \(\varphi =\pm \mathrm{arctan}({\Gamma }_{x}/{\Gamma }_{y})=180^\circ\), where Γx and Γy represent the length and width of the coding lattice, respectively. It can be noted in Fig. 7(a–f) that the normal incidence terahertz wave is mainly divided into two symmetric reflection waves with the directions of (θ, \(\varphi\)) = (48.7°, 180°), (θ, \(\varphi\)) = (27.4°, 180°), (θ, \(\varphi\)) = (30.3°, 180°), (θ, \(\varphi\)) = (18.7°, 180°), (θ, \(\varphi\)) = (21.9°, 180°), and (θ, \(\varphi\)) = (13.1°, 180°).

Fig. 7
figure 7

3D far-field scattering patterns at the frequencies of 1.21 THz and 1.97 THz for the 1-bit phase coding a and b ‘0044…’ c and d ‘000,444…’ e and f ‘00,004,444…’

Full size image

Next, the fundamental sequences of coding metasurfaces as S1 = ‘0, 2, 4, 6…’, S2 = ‘0, 0, 2, 2, 4, 4, 6, 6…’, S3 = ‘0, 1, 2, 3, 4, 5, 6, 7…’ S4 = ‘0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7…’ are designed. A visible wave can be reflected in a different direction for different coding sequences based on the PB phase theory. Under the normal incidence of RCP waves, the far-field mode of the coding metasurfaces S1, S2, S3, and S4 are shown in Fig. 8. We chose the normalized chemical potentials of WSMs with μ/(vF |Q|) = 0.3, 0.5, 0.7. Also, anomalous reflection can be achieved with other normalized chemical potentials, and the proposed designed coding metasurfaces can achieve anomalous reflection in the broadband range of 1.21–1.29 THz, and 1.97–2.04 THz. The reflection angle of the beam is verified theoretically by generalized Snell's law (see Supplement 3), and the results of the theoretical calculations and simulations are in good agreement. The polar coordinate far-field in Fig. 8 demonstrates that the amplitude and elevation angle of the antenna radiation beam change with the normalized chemical potential of the WSMs, which proves the amplitude and reflection angle modulation of the electromagnetic wave. To flexibly obtain an arbitrary scattering angle, the principle of Fourier convolution is used for encoding. The 8-particle convolution calculation is demonstrated in Supplement 3.

Fig. 8
figure 8

Far-field scattering patterns and 2D scattering patterns for coding metasurfaces a S1, b S2, c S3, and d S4, at different normalized chemical potential μ/(vF |Q|) of the WSMs

Full size image

4.3 Linear–circular coding metasurfaces

To achieve beam splitting of linear polarized waves to LCP and RCP waves, the phase gradients must remain opposite, and Supplement 4 shows that the phase gradients of LCP and RCP are opposite. We use x-polarized waves incident on the coding metasurface S3, and the normalized intensity spectrum and 3D far-field scattering patterns of the reflected electric field modes are shown in Fig. 9. As the normalized chemical potential increases, both the intensity and the angle of the reflected beam can be modulated. The normalized intensity of the reflected wave electric field modes is tuned in the range of 0.81–1 (LCP), 0.78–0.96 (RCP), and the angle is tuned in the range of − 23.8° to − 20.6° (LCP), 22.8° to 20.2° (RCP) for band 1. For band 2, the reflected wave has the normalized intensity of electric field in the range of 0.84–0.95 (LCP), 0.89–1 (RCP), and an angle tuned in the range of − 12.5° to − 11.8° (LCP), 11.4° to 13.5° (RCP). This implies the amplitude and angle modulation of the reflected wave. The beam deflection can achieve tunable amplitude and angle because the change of chemical potential of Weyl semimetal can make the resonant frequency shift and different normalized chemical potentials in Fig. 9 have different resonant frequencies, but the amplitude and angle of the reflected wave at the same frequency are not the amplitude and angle corresponding to the resonant frequency, so it can achieve tunable amplitude and angle at the same frequency. In Supplement 4, we give the convolution principle of linear–circular coding metasurface, the result shows the tunable reflection of a four-circular polarized beam.

Fig. 9
figure 9

Normalized intensities and far-field scattering patterns of the electric field modes for coding metasurfaces S3 for the different normalized chemical potential of WSMs a band one and b band two

Full size image

In Table 2, the proposed and the most recently reported coding metasurface are compared. Most of the polarization conversions for coding metasurfaces are linear–linear. In contrast, the proposed coding metasurfaces can realize not only the coding of linear–linear but also the coding of linear–circular and circular–circular. Furthermore, the proposed work can achieve a 3-bit tunable coding. Reference [34] designed a 1-bit coding metasurface of vanadium oxide, and the coding sequence was varied by the voltage to achieve different angular beam steering. But the beam steering is achieved only at 2 different frequencies, however, the proposed work can achieve beam steering in two different bands. Reference [35] achieves a 2-bit coding in the frequency band of 2.5–4.5 kHz and is non-tunable. Compared to references [36, 37], and [38] the proposed design operates at a wider frequency and can be able to achieve beam steering for both linearly and circularly polarized waves.

Table 2 Comparison of coding metasurface with the previously published works
Full size table

5 Conclusion

In this article, we present a tunable dual-band THz cross-polarization converter based on WSMs. The polarization converter can convert the linearly polarized and circularly polarized THz waves to their cross-polarization at the same frequency. Additionally, the normalized chemical potential of the WSMs can be altered to produce the tunable effect of the polarization conversion frequency. By rotating the azimuth angle of the split ring, eight Pancharatnam-Berry phase particles were obtained, the particles were then used to build coding metasurfaces, which allow beam modulation of linear and circularly polarized waves. The amplitude and angle of beam splitting and anomalous reflection can be modulated by varying the normalized chemical potential of WSMs at 1.21–1.29 THz and 1.97–2.04 THz. The proposed tunable polarization converter has potential uses in the development of sensors, radiometers, spectrometers, and other photonic devices.