1 Introduction

Orbital angular momentum (OAM) photons [1] attract intensive attention in recent years [2]. In free space optical communication and imaging, OAM beams have tremendous information capacity through mode multiplexing [3, 4, 5, 6, 7] where multiple OAM modes are combined into one beam propagating over a shared medium. However, after long-distance free space propagation, the usability of multiplexed OAM photons decreases dramatically because of the power fading and environmental disturbances [8, 9]. Although increasing the input power of the transmitter can be one solution to the power fading problem of the beam in long-distance transmission, nonlinear and thermal effects of optical materials limit the efficiency of a high-power single beamlet output [10, 11]. The generation of high-power OAM beams still faces some challenges [12, 13].

Recently, the coherent beam combination method provides a new direction to generate high-power OAM beams in free space, according to which the combined vortex beams can be produced and output from a coherent beam array [14, 15, 16, 17, 18, 19, 20, 21]. The coherent beam combination technology has advantages in increasing the output power of the OAM beam which reaches as high as kilowatt level [18, 21], but the generated beam suffers from environmental turbulence when the totally coherent combined vortex beams propagate in long distance. Beam wander and turbulence ruin the wave front of the vortex light and cause serious mode crosstalk, beam scintillation and relative power fluctuation [22, 23].

Reducing the coherence of a beam reduces the influence from turbulence [24]. Partially coherent light beams have smaller scintillation index and lower power fluctuations than completely coherent light beams in atmospheric turbulence [25]. Correlation vortices which are a type of partially coherent OAM beams put forward a new direction in the study of atmospheric OAM optics [26]. Correlation vortex beams have the phase singularities embedded in the two-point spatial correlation function \(\left\langle {E({\mathbf{r}}_{1} )E^{*} ({\mathbf{r}}_{2} )} \right\rangle\) of the form \(\exp [ - iL(\varphi_{1} - \varphi_{2} )]\), where \(E({\mathbf{r}})\) is the field of the light, \(\varphi_{1}\) and \(\varphi_{2}\) are the azimuthal angles of the two spatial points \({\mathbf{r}}_{1}\) and \({\mathbf{r}}_{2}\). L is the topological charge. Different from a traditional optical vortex which is of complete coherence, correlation vortex beams do not carry the OAM mode with the phase singularities in its wave function [27] and hence is less affected by environmental disturbance [28, 29, 30].

Correlation vortex multiplexing combines multiple partially coherent vortices into one signal over a shared medium. In a turbulence environment, for the purpose of communication and imaging, one can increase the capacity of a correlation vortex beam through mode multiplexing [31]. The generation of multiplexed correlation vortex provides a solution to the power fading and environmental disturbance problems in the long-distance and free space applications of OAM beams.

In this work, we theoretically design and experimentally demonstrate a correlation vortex multiplexing scheme that is less affected by the environmental disturbance and compatible for the high-power output schemes such as the coherent beam combination. This scheme is called as partially coherent beam combining technology which can generate multiplexed correlation vortex beams by modulating spatial correlation functions of a partially coherent beam array. In a wander environment, the OAM beams produced by the partially coherent beam combining technology is evidenced to have smaller scintillation index and lower power fluctuation than completely coherent OAM beams such as those produced by the coherent beam combination method.

2 Theory

Partially coherent beam combining technology is a method for modulating the spatial correlation of a light field according to partially coherent beam array design. We consider the light field of a partially coherent beam array with N beamlets at the light source plane (z = 0) [32] to be:

$$E(x,y;z = 0) = \sum\nolimits_{j = 1}^{N} {E_{j} } (x,y)\exp (i\beta_{j} ),$$
(1)

where \(E_{j}\) denotes the field of a beamlet numbered as j:

$$E_{j} (x,y) = \exp \left[ { - \frac{{(x - a_{j} )^{2} + (y - b_{j} )^{2} }}{{\omega^{2} }}} \right]\exp (i\varphi_{0j} ).$$
(2)

\(\beta_{j}\) is a random phase. The center of \(E_{j}\) is located at \((a_{j} ,b_{j} )\), and the beamlet waist radius is \(\omega\). The initial phase of the \(j{\text{ - th}}\) beamlet is \(\varphi_{0j} = L_{{0}} \alpha_{{\text{j}}}\), and \(\alpha_{{\text{j}}} = \pi (2j - 1)/N\) at its azimuth. \(L_{0}\) is a positive integer limited to the range \(0 < L_{0} \le N\) due to the azimuthal periodicity.

It is known that the first-order spatial correlations of a light field at a single frequency can be characterized by a two-point correlation function called cross-spectral density (CSD) [33], i.e., \(W({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ) \equiv \left\langle {E^{*} ({\mathbf{r}}_{1} )E({\mathbf{r}}_{2} )} \right\rangle\) with \(*\) representing the complex conjugate, 〈 〉 represents ensemble average. The CSD of the light field of a partially coherent beam array with N beamlets is \(W({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ) = \sum\nolimits_{m = 1}^{N} {\sum\nolimits_{n = 1}^{N} {W_{mn} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right)} }\). Here, \(W_{mn}\) is the CSD function between the field of beamlets \(E_{m}\) and \(E_{n}\) can be written as:

$$\begin{gathered} W_{mn} \left( {x_{1} ,y_{1} ,x_{2} ,y_{2} } \right) = E_{m}^{*} (x_{1} ,y_{1} )E_{n} (x_{2} ,y_{2} )g_{mn} (x_{1} ,x_{2} ;y_{1} ,y_{2} ), \hfill \\ \end{gathered}$$
(3)

where \((x_{1} ,y_{1} )\) and \((x_{2} ,y_{2} )\) are two arbitrary spatial positions at a cross-sectional plane perpendicular to the propagation direction. The function \(g_{mn} (x_{1} ,x_{2} ;y_{1} ,y_{2} )\) is the degree of coherence (DOC) between the \(m{\text{ - th}}\) and \(n{\text{ - th}}\) beamlets. For the case of partial coherence, \(0 < |g_{mn} | < 1\)[33]. The \(W({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} )\) of the partially coherent beam array consists of two-point correlations inside a single beamlet (\(m = n\)) and between different beamlets (\(m \ne n\)).

According to the Gaussian Schell model [33], the DOC function of the combined field at the source is:

$$\begin{gathered} {\text{g}}_{mn} (x_{1} ,y_{1} ;x_{2} ,y_{2} ) = \exp \left[ { - \frac{{(x_{1} - a_{m} - x_{2} + a_{n} )^{2} + (y_{1} - b_{m} - y_{2} + b_{n} )^{2} }}{{2\sigma_{g}^{2} }}} \right], \hfill \\ \end{gathered}$$
(4)

where \(\sigma_{g}\) is the transverse coherence width of the beamlet. \((a_{m} ,b_{m} )\) and \((a_{n} ,b_{n} )\) denote the coordinates of the centers of beamlets m and n, respectively. Substituting Eq. (4) into Eq. (3) and utilizing the generalized Fresnel integral formula [34], one obtains the CSD function of the combined field after free space propagation:

$$W(u_{1} ,v_{1} ,u_{2} ,v_{2} ;z) = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {W_{mn} \left( {u_{1} ,v_{1} ,u_{2} ,v_{2} ;z} \right)} } ,$$
(5)

where \((u_{1} ,v_{1} )\) and \((u_{2} ,v_{2} )\) are two spatial positions at the output plane located at \(z > 0\), and

$$\begin{aligned} W_{{mn}} \left( {u_{1} ,v_{1} ,u_{2} ,v_{2} ;z} \right) =& C\frac{{\pi ^{2} }}{{M_{1} M_{2} }}\left( {\frac{1}{{\lambda z}}} \right)^{2} \exp \left( {i\varphi _{{mn}} } \right) \times \exp \left( {\frac{{N_{2}^{2} + N_{1}^{2} }}{{4M_{2} }}} \right) \\ & \times \exp \left[ { - (\frac{{i\pi }}{{\lambda z}} + \frac{{\pi ^{2} }}{{\lambda ^{2} M_{1} z^{2} }})(u_{1}^{2} + v_{1}^{2} ) + \frac{{i\pi }}{{\lambda z}}(u_{2}^{2} + v_{2}^{2} )} \right] \\ & \times \exp \left\{ {\frac{{i2\pi }}{{M_{1} \lambda z}}\left[ {(\frac{{a_{m} - a_{n} }}{{2\sigma _{g}^{2} }} + \frac{{a_{m} }}{{\omega ^{2} }})u_{1} + (\frac{{b_{m} - b_{n} }}{{2\sigma _{g}^{2} }} + \frac{{b_{m} }}{{\omega ^{2} }})v_{1} } \right]} \right\}, \\ \end{aligned}$$
(6)

with

$$M_{1} = \frac{1}{{\omega^{2} }} + \frac{1}{{2\sigma_{g}^{2} }} + \frac{i\pi }{{\lambda z}}{, }\,M_{2} = \left( {M_{1} } \right)^{*} - \frac{1}{{4\sigma_{g}^{4} M_{1} }},$$
$$\begin{gathered} N_{1} = \frac{{2a_{n} }}{{\omega^{2} }} + \frac{{a_{m} }}{{\sigma_{g}^{2} M_{1} \omega^{2} }} + i\frac{2\pi }{{\lambda z}}\left( {\frac{1}{{2\sigma_{g}^{2} M_{1} }}u_{1} - u_{2} } \right) \\ + \left(\frac{1}{{2\sigma_{g}^{4} M_{1} }} - \frac{1}{{\sigma_{g}^{2} }}\right)(a_{m} - a_{n} ), \\ N_{2} = \frac{{2b_{n} }}{{\omega^{2} }} + \frac{{b_{m} }}{{\sigma_{g}^{2} M_{1} \omega^{2} }} + i\frac{2\pi }{{\lambda z}}\left( {\frac{1}{{2\sigma_{g}^{2} M_{1} }}v_{1} - v_{2} } \right) \\ + \left(\frac{1}{{2\sigma_{g}^{4} M_{1} }} - \frac{1}{{\sigma_{g}^{2} }}\right)(b_{m} - b_{n} ), \\ \end{gathered}$$
$$\begin{gathered} C = \exp \left[ {(a_{m}^{2} + b_{m}^{2} )\left(\frac{1}{{4M_{1} \sigma_{g}^{4} }} - \frac{1}{{\omega^{2} }} - \frac{1}{{2\sigma_{g}^{2} }} + \frac{1}{{M_{1} \sigma_{g}^{2} \omega^{2} }} + \frac{1}{{M_{1} \omega^{4} }}\right)} \right] \, \\ \, \times \exp \left[ {(a_{m} a_{n} + b_{m} b_{n} )\left( - \frac{1}{{2M_{1} \sigma_{g}^{4} }} - \frac{1}{{M_{1} \sigma_{g}^{2} \omega^{2} }} + \frac{1}{{\sigma_{g}^{2} }}\right)} \right] \\ \, \times \exp \left[ {(a_{n}^{2} + b_{n}^{2} )\left(\frac{1}{{4M_{1} \sigma_{g}^{4} }} - \frac{1}{{\omega^{2} }} - \frac{1}{{2\sigma_{g}^{2} }}\right)} \right]. \\ \end{gathered}$$

The above analytical expression of \(W(u_{1} ,v_{1} ,u_{2} ,v_{2} ;z)\) provides a theoretical tool for designing the spatial coherence of the combined field of the partially coherent beam array. The average intensity can be recovered from the CSD function by \(I(u,v) \equiv W(u,v,u,v;z)\).

To examine the OAM spectrum of the generated beam at a propagation distance z, one can project \(W\left( {u_{1} ,v_{1} ,u_{2} ,v_{2} ;z} \right)\) onto the OAM basis [35, 36]:

$$\begin{aligned} P(L) \propto & \left( {\frac{1}{{2\pi }}} \right)^{2} \int_{0}^{R} {\int_{0}^{R} {\int_{0}^{{2\pi }} {\int_{0}^{{2\pi }} {W\left( {u_{1} ,v_{1} ,u_{2} ,v_{2} ;z} \right)} } } } \\ & \times \exp \left( {iL \cdot \Delta \theta } \right)\rho _{1} \rho _{2} {\text{d}}\rho _{1} {\text{d}}\rho _{2} {\text{d}}\theta _{1} {\text{d}}\theta _{2} \\ \end{aligned}$$
(7)

\(P(L)\) is the weight coefficient of the OAM mode with topological charge L. The two spatial points, \((u_{1} ,v_{1} )\) and \((u_{2} ,v_{2} )\), are expressed in polar coordinates \((\rho_{1} ,\theta_{1} )\) and \((\rho_{2} ,\theta_{2} )\), respectively, and \(\Delta \theta = \theta_{1} - \theta_{2}\). The differences between the two spatial points are limited to the angular coordinates, which means \(\rho_{1} = \rho_{2} = \rho\). Since apertures are commonly encountered in optical applications, the region of interest of the output light field is defined by a finite integration of the radial coordinate, \(\rho\), with the upper limit at a finite value of \(R\).

Equations (5)–(7) present the theoretical tools to predict the correlation function, the average intensity, and the normalized OAM spectrum, of the partially coherent beam array field after propagation.

3 Experiment

To realize the partially coherent beam array field designed in the theoretical section, we adopt a beam wander model [37] to synthesize the correlated vortex beams in the laboratory. In addition, the topological charges of correlation vortices are different when the initial phase of the sub-beams is different [38]. A video of computer-generated holograms (CGHs) is used to reconstruct the optical field in Eq. (1). At the \(k{\text{ - th}}\) frame of the CGH video, the generated light field is:

$$\begin{gathered} E^{(k)} (x,y) \\ = \sum\limits_{p = 1}^{M} {\left( {\sum\limits_{j = 1}^{N} {\exp \left\{ { - \frac{{[x - a_{j} - x_{j}^{(p)} ]^{2} + [y - b_{j} - y_{j}^{(p)} ]^{2} }}{{\omega^{2} }}} \right\}\exp (i\varphi_{0j} )} } \right)} \, e^{{i\beta_{p} }} , \\ \end{gathered}$$
(8)

where \(a_{j}\), \(b_{j}\),\(\omega\), N and \(\varphi_{0j}\) are the same as those defined in Eq. (1). \(E^{(k)} (x,y)\) can be regarded as a temporal light field with the same duration as the \(k{\text{ - th}}\) frame. There is no time correlation between the fields at different frames, i.e., \(\left\langle {E^{{(k_{1} ) * }} (x,y)E^{{(k_{2} )}} (x,y)} \right\rangle_{{k_{1} \ne k_{2} }} = 0\), and the averaged intensity is \(I(x,y) \propto \sum\nolimits_{k = 1}^{num} {E^{{({\text{k)}} * }} (x,y)E^{(k)} (x,y)}\). Here, num is the number of CGH frames played in this video. As seen in Eq. (8), the field of the partially coherent beam array, i.e., \(E^{(k)} (x,y)\), is a superposition of M completely coherent beam arrays. In this experimental design, num = 3000 and M = 500. \(\beta_{p}\) is a random phase that makes the superposition of coherent beam arrays incoherent. The instantaneous center of the coherent beam arrays, \((x_{j}^{(p)} ,y_{j}^{(p)} )\), has a position chosen from a random distribution at the cross section of the output beam. The root mean square (RMS) of the distribution of the randomized center locations is \(c_{0}\). Given that the centers of the composite fields are distributed normally at the cross-section plane, the probability distribution function is Gaussian. Hence, \(c_{0}\) and \(\sigma_{{\text{g}}}\) satisfy the relationship [39] \({2}\sigma_{{\text{g}}}^{2} { = 2}\omega^{2} + \omega^{4} /{\text{c}}_{0}^{2}\), meaning the spatial coherence of the output field of the partially coherent beam array can be controlled by \(c_{0}\).

Figure 1a shows the experimental setup for the generation of the partially coherent beam array. A He–Ne laser (\(\lambda = 632.8\) nm, linearly polarized, 2 mW) is incident upon the spatial light modulator SLM1 (phase modulation type, \(1280 \times 720\), 6.3 \(\mu m\), 60 Hz; UPO Labs, HDSLMM63R). Phase-modulated SLM can encode both phase and amplitude according to computer-generated holograms (CGHs). The CGH method has been proposed in Ref. [40]. Light from the first-order diffraction pattern of SLM1 is selected by CA1 and then detected by the CMOS at a propagation distance z. The video of the CGHs is played at a certain frame rate in SLM1 to construct the designed partially coherent beam array. Given that the number of video frames is 3000, and each frame lasts for 20 ms. The whole number of frames take 60 s.

Fig. 1
figure 1

a Experimental setup for generating a partially coherent beam array and detecting the intensity. The CGH played by SLM1 constructs the partially coherent beam array with b \(N = 5,L_{0} = 2,c_{0} = 0.2\omega\) and c \(N = 5,L_{0} = 2,c_{0} = 1\omega\). d Schematic of generating an OAM beam according to the partially coherent beam array with the parameters from (b). The left image in d shows the instantaneous positions of the beamlets (the red circles) and the distribution of the randomized center locations (the pink circular areas) in the partially coherent beam array at the cross section. The right image in d is the correlation phase of the combined field. BS beam splitter, SLM1 phase spatial light modulator, CA1 circular aperture, CMOS complementary metal oxide semiconductor camera

Full size image

Figure 1b and c are two examples of CGHs that generate two kinds of partially coherent beam arrays. For the construction of each partially coherent beam array, a specific number of frames of CGHs are prepared in advance and played dynamically on SLM1 at a selected frame rate.

Figure 1d shows the strategy of the partially coherent beam combining method for the synthesis of the correlation vortex field via partially coherent beam array. The left image in Fig. 1d is the design for the experimental generation of the partially coherent beam combining according to Eq. (8). The smaller red circles are the instantaneous positions of the beamlets. The distribution RMS of the randomized center locations, \(c_{0}\), is indicated by pink circular areas. The five pink circles in Fig. 1d represent the five beamlets defined in Eq. (8). The positions of the beamlets are set by \((a_{j} ,b_{j} )\). The total field which is a combination of five beamlets is generated by the SLM1 according to the CGH. The purpose of CA1 is to select the first-ordered diffraction light from the SLM. Because the field designed in Eq. (8) has been encoded in the first diffraction order of the SLM by the CGHs. The size of circular aperture allows the first diffraction pass through. The right image in Fig. 1d is the correlation phase of the partially coherent beam array. The correlation phase is the phase of the CSD function \(W(x,y,x_{0} ,y_{0} ) \equiv \left\langle {E^{(k) * } (x,y)E^{(k)} (x_{0} ,y_{0} )} \right\rangle\). Several phase singularities appear at the cross section of the beam, which indicates generation of the correlation vortex field.

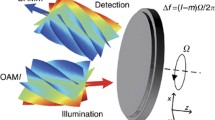
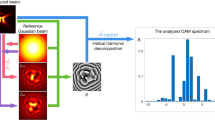
Figure 2a shows the setup for the measurement of the normalized OAM spectrum of the generated partially coherent beam array. OAM modal decomposition is used for this detection scheme. After the generation of the designed partially coherent beam array by SLM1, the OAM beam to be measured propagates a distance z and is sent to SLM2 (phase modulation type, \(1920 \times 1200\), 8 \(\mu m\)). The first-order diffraction light generated by SLM2 is selected by CA2. To prevent the Gouy phase-shift effect, a 4f system is placed between SLM2 and the output plane of the beam from SLM1. The distance between SLM1 and the output plane is the propagation distance z. In Fig. 2, the input plane of the 4f system is actually at the output plane of SLM1. SLM2 and CMOS are used to select the signal mode and record its intensity. The CGH of the signal mode is encoded onto SLM2. The CMOS camera obtains the averaged intensity of the signal mode at the Fourier plane of lens L3. The weight of the signal mode in the generated beam is obtained according to the method proposed in Ref. [41], which describes summing the gray values of the pixels in the central bright spot of the image of the averaged intensity. Figure 2c1 shows the CGH of a stationary signal mode at SLM2. An LG mode with topological charge S is encoded into SLM2 [40]. The OAM spectrum of the generated beam from SLM1 can be obtained by scanning the topological charge of the signal mode at SLM2.

Fig. 2
figure 2

a Experimental setup for measuring the OAM spectrum of the generated beam. The CGH is played by SLM2 for the purpose of OAM modal decomposition. The projection OAM mode in SLM2 is c1 a stationary LG mode with topological charge S = 2. L1, L2, L3: convex lens; CA1, CA2: pinhole (aperture radius R = 3 mm); BS: beam splitter, which is used to select linearly polarized light that makes SLM responsive; b Schematic of the complex perturbation mimicked by SLM2 with beam wander and turbulent phase. The turb refers to the turbulent phase. The wander is wandering perturbation, where the small colorful circles at the cross-section plane present the instantaneous positions of the wandering signal at different time points. The outer brown circular area indicates the distribution range of the wandering signal mode, with a radius of \(c_{s}\). c2 shows one of the CGH frames played by SLM2 to produce a dynamically wandering LG mode with topological charge S = 2. The signal wander radius is \(c_{{\text{s}}} { = }2\omega\). c3 is one CGH in SLM2 corresponding to a dynamically LG mode with both wandering and turbulent phase perturbations, with S = 2, \(c_{{\text{s}}} { = }2\omega\) and \(C_{n}^{2} = 10^{ - 13}\)

Full size image

Figure 2b shows the strategy for mimicking a perturbed environment with a dynamic signal mode. Two kinds of perturbations are simulated by SLM2. One is the beam wander; the other is the atmospheric turbulent phase. The wandering perturbation is mimicked by the randomly varied modes at the cross-section plane of the optical beam, and the strength of the perturbation is controlled by the RMS radius of the wandering center \(c_{s}\). A bigger \(c_{s}\) corresponds to a larger wandering perturbation. A time-varying sequence of CGHs is designed to produce a dynamically changed LG mode at SLM2. The center and initial phase of the LG mode change randomly from frame to frame. The atmospheric turbulent phase is mimicked with the method developed by von Karman [42]. Under the Markov approximation, the phase spectrum of a wave propagating in turbulent medium can be expressed as [23]

$$\phi_{\varphi }^{{}} (\kappa ) = 2\pi k^{2} z\phi_{n} (\kappa ),$$
(9)

where \(\kappa\) is the spatial wavenumber, and

$$\phi_{n}^{{}} (\kappa ) = 0.033C_{n}^{2} \cdot (\kappa^{2} + k_{0}^{2} )^{ - 11/6} \exp ( - \kappa^{2} /k_{m}^{2} ).$$
(10)

\(k_{0}^{{}} = 2\pi /L_{t}\) and \(k_{m}^{{}} = 5.92/l_{t}\). Parameters \(L_{t}\) and \(l_{t}\) are the outer and inner scale of turbulence, respectively. \(C_{n}^{2}\) is the structure constant of the refractive index, which represents the turbulence strength. In a medium turbulence, \(C_{n}^{2} = 10^{ - 14} {\text{m}}^{{ - 2/3}}\); in a strong turbulence, \(C_{n}^{2} = 10^{ - 13}\). In our simulation, \(L_{t}\) = 1 m, \(l_{t}\) = 0.01 m and \(C_{n}^{2} = 10^{ - 13}\).

Figures 1, 2 and Eq. (8) present an experimental scheme to generate the partially coherent beam array field designed in the theoretical section and measure the averaged intensity and normalized OAM spectrum of the generated beam at a distance.

4 Results and analysis

Based on Eqs. (5)–(7) and the experimental scheme proposed in Figs. 1, 2, one can theoretically design the OAM behavior of the partially coherent beam array and verify its properties using experimental results.

Figure 3a shows the theoretical results of the averaged intensity and the normalized OAM spectrum of the partially coherent beam array with N = 6 and \(\sigma_{g} = 3.67\omega\). The distance between SLM1 and the input plane of the 4f system is z = 160 cm. The wavelength is \(\lambda = 632.8\) nm, and the upper radial limit of the integration in \(P(L)\) is set at R = 3 mm. The parameters for the beamlets at the source are \(\omega = 0.157\) mm and \(r_{0} = 1.5\omega\).

Fig. 3
figure 3

Numerical simulations of the averaged intensity and normalized OAM spectrum of the partially coherent beam array. a N = 6, \(\sigma_{g} = 3.67\omega\); b N = 5, \(\sigma_{g} = 3.67\omega\); c N = 5, \(\sigma_{g} = 1.22\omega\)

Full size image

One can observe that the averaged intensity \(I(u,v)\) and normalized OAM spectrum P(L) vary with the initial phase parameter \(L_{0}\). When \(L_{0} = 1\) (or 5), the field of the partially coherent beam array is in a single OAM state whose topological charge is \(L = 1\) (or \(- 1\)). When \(L_{0} = 2\) (or 4), there are two modes observed in the OAM spectrum, with the highest mode located at \(L = 2\) (or \(- 2\)) and the second highest mode located at \(L = - 4\) (or 4). When \(L_{0} = 3\), the two modes are equally weighted in the OAM spectrum and are located at \(L = 3\) and \(- 3\), respectively. When \(L_{0} = 6\), the only mode is at \(L = 0\), which means that the light field does not have any OAM.

Figure 3b shows the simulation for a partially coherent beam array with N = 5 and \(\sigma_{g} = 3.67\omega\). In the graphs of \(L_{0} = 1,2,3,4\), there are two OAM modes in the generated beam that have nonzero weights. One of the OAM modes is at \(L_{1} = L_{0}\), and the other is at \(L_{2} = \left( {L_{0} - N} \right)\). The weights of the two modes, \(P(L_{1} )\) and \(P(L_{2} )\), depend on the absolute values of \(L_{1}\) and \(L_{2}\). A smaller absolute value of \(L_{1,2}\) leads to a higher probability amplitude for the OAM mode \(P(L_{1,2} )\). The graphs for \(\left( {L_{0} { = 1, }N = 5} \right)\) and \(\left( {L_{0} { = 6, }N = 5} \right)\) show that the influence of \(L_{0}\) has a periodicity of N. For \(L_{0} < N\), one OAM mode is at \(L_{1} = L_{0}\), and the other is at \(L_{2} = \left( {L_{0} - N} \right)\); for \(L_{0} = cN\)(c is a positive integer), the OAM mode is at \(L_{1} = 0\); for \(L_{0} > N\), one OAM mode is at \(L_{1} = (L_{0} - N)\), and the other is at \(L_{2} = (L_{0} - 2N)\).

According to the modulations of \(L_{0}\) and N shown in Fig. 3a and b, one can observe that the output beam of the partially coherent beam array can be shifted from a state with a single OAM mode to a multiplexed state with two modes, and vice versa.

Figure 3c shows the theoretical results of the normalized OAM spectrum, P(L), of the partially coherent beam array with N = 5 and a decreased coherence width \(\sigma_{g} = 1.22\omega\). In the low coherence case shown in Fig. 3c, when \(L_{0} = 1,2,3,4\), there are two OAM bands in the generated beam, with central peaks at \(L_{1} = L_{0}\) and \(L_{2} = \left( {L_{0} - N} \right)\). The positions of the peaks are the same as those in Fig. 3b, indicating that the multiplexing of the modes of \(L_{1}\) and \(L_{2}\) survives in the field of the correlation vortex. Given that the OAM modes of \(L_{1}\) and \(L_{2}\) are the signal, the comparison of the graphs of \(P(L)\) in Fig. 3c to the P(L) in Fig. 3b shows that the decrease of \(\sigma_{g}\) increases the bandwidth in OAM space. In a multiplexed correlation vortex, instead of several single OAM modes being multiplexed, multiple OAM bands are observed in the beam. The ability to produce multiplexed OAM bands distinguishes the partially coherent beam combining method from coherent beam combination.

Figure 4 shows the experimental results of the averaged intensity and normalized OAM spectrum of the designed partially coherent beam array. The settings in the experiment are the same as those in Fig. 3. Comparing Fig. 4 with Fig. 3, one can see that the experimental results are consistent with the theoretical predictions. A slight deviation is seen in the zero mode and its nearby low-order modes, in which the experimental zero modes are higher than those in theoretical predictions. This is due to the contribution of environmental noise in the experiment to the zero mode and its nearby low-order modes. Moreover, the radius of the circular apertures in the experiment also affects the measured OAM spectrum.

Fig. 4
figure 4

Experimental results of the averaged light intensity and normalized OAM spectrum \(P(L)\) of the partially coherent beam array. a N = 6, \(c_{0} = 0.2\omega\); b N = 5, \(c_{0} = 0.2\omega\); c N = 5, \(c_{0} = \omega\)

Full size image

The OAM spectrums recovered in theory and in experiment utilized different methods. The theoretical prediction of the OAM spectrum is obtained from the CSD function in Eq. (5) according to the partial coherence theory. While in experiment the OAM spectrum is obtained according to the modal decomposition of the optical field in Eq. (8). It is worth mentioning that although we utilized different methods to recover the OAM spectrum, the OAM spectrum itself is unchanged.

Figure 5 shows the experimental results of the relative power fluctuation and scintillation index of a perturbed signal OAM mode in a coherent beam array and a partially coherent beam array. Beams are initiated with N = 5 and \(L_{0} = 2\). In Fig. 5a, b, the wander perturbation is mimicked with a dynamically wandering LG mode at SLM2 which has S = 2 and \(c_{{\text{s}}} = 2\omega\). In Fig. 5c, d, a perturbation consisting of beam wander and turbulent phase is mimicked in the same way with S = 2, \(c_{{\text{s}}} = 2\omega\), and \(C_{n}^{2} = 10^{ - 13}\). It is worth noting that since the main purpose of this work is to reveal the resilience of the partially coherent beam array when it encounters a wandering perturbation, the experiment is designed to mimic a situation with randomly varied modes at the cross-section plane of the beam. Although the wandering perturbation alone did not present all the non-ideal situations that a beam propagating in complex environment encounters, knowing and understanding how the beam wander influences the light field is still important for the applications given that beam wander is one of the main factors that destroys the amplitude and phase of the light field.

Fig. 5
figure 5

Experimental results of the relative power fluctuation and scintillation index of a perturbed OAM signal mode embedded in a beam of a, c a coherent beam array with N = 5, \(L_{0} = 2\), \(c_{0} = 0\); b, d a partially coherent beam array with N = 5, \(L_{0} = 2\),\(c_{0} = \omega\). In the case of a, b, the signal mode is transmitted through a wandering perturbation with S = 2 and \(c_{{\text{s}}} = 2\omega\). In the case of c, d, the signal mode is transmitted through a complex perturbation consisting of beam wander and turbulent phase with S = 2, \(c_{{\text{s}}} = 2\omega\) and \(C_{n}^{2} = 10^{ - 13}\)

Full size image

To detect the relative power fluctuation of the signal mode, the CMOS camera in the setup of Fig. 2a is replaced by an optical power meter (OPM). We utilized the OPM to detect the instantaneous power of the beam. The detected signal is digitized and recorded by a data acquisition system. The scintillation index of the signal mode can be obtained from the following [43]:

$$\sigma_{P}^{2} { = }\frac{{\left\langle {P^{2} } \right\rangle }}{{\left\langle P \right\rangle^{2} }} - 1,$$
(11)

where \(\left\langle \cdot \right\rangle\) denotes ensemble average, and P represents instantaneous power of the beam. The power fluctuation of the beam can be calculated by (Pmax – Pmin)/ < P > .

In the wander environment, the relative power fluctuation and scintillation index of the signal mode of the coherent beam array are 1.838 and 0.071, respectively, while those of the partially coherent beam array are 0.955 and 0.029. The signal mode in a partially coherent beam array has a lower relative power fluctuation and a lower scintillation index, which are 52% and 41% of those in a coherent beam array, respectively. In the wander and turbulent phase environment, similar results can be observed. This means that in the perturbation, the OAM mode embedded in the partially coherent beam array is more stable than that embedded in the coherent beam array.

It is worth mentioning that in the work of Ref. [37] where the OAM of the output beam is from the input optical vortices, the role of the incoherent superposition was to decrease the coherence of the combined beam. To realize an OAM output beam, the superposed beamlets must be optical vortices in the work of Ref. [37]. However, in the work here, the superposed beamlets are not optical vortices. The incoherent superposition makes the output beam being twist in correlation phases and leads to an OAM beam. In other words, the roles of the incoherent superposition are completely different in the two works. One is to decrease the coherence, while the other is to control the topological charge of the output beam. Therefore, this work reports different results.

5 Conclusion

This work proposes an optical beam combining method to generate multiplexed correlation vortex beams that are partially coherent vortex beams and have multiplexed bands in the OAM space. The differences between the existing coherent beam combination method and the partially coherent beam combining method proposed here are described. The former uses wave functions of the optical field to control the OAM state of the beam, while the latter uses the spatial correlation function. The partially coherent beam combining method benefits from this difference and enables tailoring of the OAM spectrum of vortex beams when the optical field is in low coherence; it also has advantages when used in propagation of signal OAM modes in turbulent environments. According to the theoretical formula of the cross-spectral density of the partially coherent beam array, this work presents a strategy for realizing partially coherent beam combining and controlling the averaged light intensity and the OAM spectrum of the output OAM beam in the laboratory. The feasibility of the beam combining method in multiplexed correlation vortex generation is verified experimentally. Experimental results of the relative power fluctuation and scintillation index show that in a wander environment, the OAM mode embedded in the partially coherent beam array is more stable than the one embedded in the coherent beam array. The results of this paper have potential applications in OAM transmission as well as applications in complex environments.