1 Introduction

Quantum systems with non-local behaviour is a counter-intuitive concept of quantum mechanics which plays a crucial role in modern physics field [1]. Since the inception of the Einstein–Podolsky–Rosen (EPR) paradox [1, 2], entanglement has been considered the fundamental and most useful resource for the quantum advantage, without classical counterpart, in information processing. However, there are available measures that can capture the quantum correlation even in unentangled states. This purely quantum mechanical phenomenon is regarded as a complete measure of non-local behaviour for a pure state. Correspondingly, a perfect definition of non-locality for the mixed state is not available yet. The closer connection between the entanglement and Bell version of non-locality can be identified through the EPR steering. In the context of quantum correlation between a composite quantum system’s parts, the quantum steering was discussed by Schrödinger, where another party can influence the wave function of one party in the event of a measurement [3]. The measurement-induced non-locality (MIN) was derived to quantify locally invariant eigenprojective measurements from a geometric perspective which is dual to quantum discord based on Hilbert–Schmidt norm [4,5,6].

When coupled with its surrounding environment, a quantum system undergoes decoherence, and its unique quantum feature gets destroyed, namely in an open quantum system. The deterioration of coherence, described mainly by Lindblad master equation in a dynamic quantum system, leads to loss of information [7,8,9]. Information is irreversibly lost when interacting with the environment and properties of the system merge with the macroscopic scale. Milburn proposed another simple way of studying this decaying dynamic process without an external reservoir [10]. Recently, much investigation was performed to study decaying quantum correlations in physically relevant systems, called as intrinsic decoherence. Jaynes–Cummings model with Heisenberg exchange interaction was studied under the influence of intrinsic decoherence exhibited decay in entanglement [11]. Three-qubit XY chain was studied to observe the dynamical behaviour of trace distance discord (TDD), MIN and Bures entanglement [12]. Two-qubit Heisenberg spin chain described by anisotropic and Dzyaloshinskii–Moriya (DM) interactions showed dynamic decaying behaviour of MIN [13] and local quantum uncertainty (LQU) [14]. Similarly, the dynamics of LQU were studied on the Heisenberg XXZ spin chain model [15]. Also, the dynamics of quantifiers based on skew information such as LQU and uncertainty-induced nonlocality (UIN) were studied by considering two-qubit spin models as resource [16]. The influence of intrinsic decoherence on the quantum correlations was quantified by logarithmic negativity and TDD in a two-qubit Heisenberg XYZ spin chain in the presence of the z–DM interaction [17]. The dynamics of Bell nonlocality, entanglement and entropic uncertainty were studied under intrinsic decoherence in a two nearest spin-1/2 Heisenberg XYZ model subjected to a transverse uniform magnetic field and under the interplay of DM along with Kaplan–Shekhtman–Entin–Wohlman–Aharony (KSEA) interactions [18].

From a practical standpoint, entanglement plays a crucial role in implementing numerous tasks related to quantum communication and information processing [1, 19, 20]. One key use of quantum entanglement is quantum dense coding (QDC) [21,22,23]. This significant protocol can guarantee the transmission of more classical information through a quantum channel via passing on fewer quantum resources. Operationally, the QDC enables the transmission of two classical bits of information by sharing a two-qubit maximally entangled state [24, 25] between a sender (Alice) and receiver (Bob). The perfect transmission can be ensured by the availability of a noiseless quantum channel between Alice and Bob. Nevertheless, this is impossible in the real world, where noise is present everywhere. A quantum channel’s quality and the amount of information that can transmit are tightly connected. It is interesting to notice that dense coding in a two-qubit system dynamics by considering the combined effects of the bosonic reservoir, and dipole-dipole interaction is recently examined [26].

Here, we considered studying the dynamics of quantum correlation quantified by EPR steering, MIN and entanglement by taking dipolar-coupled spin systems under intrinsic decoherence and in the influence of a DM interaction. The dipolar spin system is useful in realizing and understanding various quantum phenomenon in solid-state systems such as nitrogen-vacancy centers in diamond [27, 28], quantum spin systems [29, 30] and rotational states of molecules [31]. Recently, it was predicted that other correlations beyond entanglement could endure decoherence [32,33,34,35,36]. Quantum dynamics of such two-qubit have also been quantitatively studied under different analytical approaches [37, 38]. The layout of this paper is as follows. In Sect. 2, we give a brief overview of the quantum correlation measures used in our work. The intrinsic decoherence dynamics of the suggested quantifiers, in the ambit of the dipolar spin system under the interplay of z–DM interaction, are studied in Sect. 3. Section 4 is devoted to a detailed description and discussion of the obtained results. The effects of the intrinsic decoherence on the dynamics of the Holevo dense coding quantity are examined in the Sect. 5. Finally, Sect. 6 is devoted to concluding remarks.

2 Quantum correlation measures

In this section, we review the quantum correlation measures to be studied in this paper. To quantify the quantum correlation contained in a bipartite system, we consider a state \(\rho\) shared between the subsystems a and b associated with the separable Hilbert space \({\mathcal {H}}^{ab}={\mathcal {H}}^{a} \otimes {\mathcal {H}}^{b}\). Here, \({\mathcal {H}}^{a}\) and \({\mathcal {H}}^{b}\) are the respective Hilbert spaces of marginal states \(\rho ^a\) and \(\rho ^b\).

2.1 Wootters’ concurrence

The most widely used non-local property of the bipartite state \(\rho\) is quantum entanglement as well as its quantified by the concurrence. Wootters’ formula of concurrence is [39]

$$\begin{aligned} C(\rho ) = \max \{0, \lambda _1 - \lambda _2 - \lambda _3 - \lambda _4\}, \end{aligned}$$
(1)

where \(\lambda _i~(i\equiv 1,2,3,4)\) denote the eigenvalues, arranged in descending numerical values, of the matrix \(R=\sqrt{\sqrt{\rho }{\tilde{\rho }}\sqrt{\rho } }\). In which, the spin flipped matrix is defined by \({\tilde{\rho }}=(\sigma _y \otimes \sigma _y) \rho ^{*} (\sigma _y \otimes \sigma _y)\) wherein the asterisk (\(*\)) refers to the complex conjugate in computational basis \({{{\mathcal {B}}}}\equiv \{ \vert 00 \rangle , \vert 01\rangle , \vert 10\rangle , \vert 11\rangle \}\). It is worth mentioning that the quantum entanglement \(C(\rho )\) ranges between 0 and 1, where the minimal and maximal values corresponding to unentangled (product) and maximally entangled states, respectively.

2.2 Measurement-induced non-locality

MIN, captures the maximal non-local effects of bipartite state due to locally invariant eigenprojective measurements, is defined as the maximal distance between the quantum state taken into consideration and the corresponding state after performing a local measurement on one of the subsystems, say a i.e., [40]

$$\begin{aligned} {\mathcal {N}}_{2} {(\rho )}= {}^{{max}}_{\Pi ^{a}}\Vert \rho - \Pi ^{a}(\rho )\Vert ^{2}, \end{aligned}$$
(2)

where \(\Vert {\mathcal {O}}\Vert ^{2}=\text {Tr}({\mathcal {O}}{\mathcal {O}}^{\dagger })\) expresses the Hilbert–Schmidt norm of operator \({\mathcal {O}}\). In Eq. (2), the maximum is taken over the locally invariant projective measurements on subsystem a which does not change the state. The post-measurement is defined as \(\Pi ^{a}(\rho ) = \sum _{k} (\Pi ^{a}_{k} \otimes \mathbbm {1} ^{b}) \rho (\Pi ^{a}_{k} \otimes \mathbbm {1}^{b} )\), with \(\Pi ^{a}= \{\Pi ^{a}_{k}\}= \{|k\rangle \langle k|\}\) being the projective measurements on the subsystem a. The general expression of a two-qubit density operator acting in the separable composite Hilbert space \({\mathcal {H}}^a\otimes {\mathcal {H}}^b\) is

$$\begin{aligned} \rho =\frac{1}{4}\left( \mathbbm {1}^{a} \otimes \mathbbm {1}^{b}+ {\textbf{s}} \cdot \varvec{\sigma }\otimes \mathbbm {1}^{b} + \mathbbm {1}^{a} \otimes {\textbf{r}}\cdot \varvec{\sigma }+\sum _{m,n=1}^{3} t_{mn} \sigma _{m} \otimes \sigma _n\right) , \end{aligned}$$
(3)

where \(\sigma _j~(j=1,2,3)\) are the standard 2D Pauli operators. The vectors \({\textbf{s}}\) and \({\textbf{r}}\) are real, their components being \(s_j=\textrm{Tr}(\rho (\sigma _j\otimes \mathbbm {1}^b))\), \(\mathbbm {1}^{a(b)}\) is the \(2\times 2\) identity operator acting on the subsystem a(b), \(r_{j}=\textrm{Tr}(\rho (\mathbbm {1}^a\otimes \sigma _{j} ))\) and \(t_{mn}=\textrm{Tr}(\rho (\sigma _{m} \otimes \sigma _{n}))\) being real matrix elements. Without loss of generality, the canonical form of the Fano parametrization of the density operator (3) is written as

$$\begin{aligned} \rho =\frac{1}{4}\left( \mathbbm {1}^{a} \otimes \mathbbm {1}^{b}+ {\textbf{s}} \cdot \varvec{\sigma }\otimes \mathbbm {1}^{b} + \mathbbm {1}^{a} \otimes {\textbf{r}}\cdot \varvec{\sigma }+\sum _{j= 1}^{3} c_{j} \sigma _{j} \otimes \sigma _{j} \right) \end{aligned}$$
(4)

with \(c_j=\text {Tr}(\rho (\sigma _{j} \otimes \sigma _{j}))\).

For a given state with decomposition (3), the MIN has a closed formula

$${\mathcal{N}}_{2} \left( \rho \right) = \left\{ {\begin{array}{*{20}l} {{{\rm Tr}}\left( {TT^{t} } \right) - \frac{1}{{\left\| \textbf{s} \right\|^{2} }}\textbf{s}^{t} TT^{t} \textbf{s}{\text{ }}} \hfill & {\mbox{if}\,~~\textbf{s} \ne 0,} \hfill \\ {{{\rm Tr}}\left( {TT^{t} } \right) - T_{{\min }} } \hfill & {\mbox{if}\,~~\textbf{s} = 0,{\text{ }}} \hfill \\ \end{array} } \right.$$
(5)

where \(T_{\min }\) is the least eigenvalue of matrix \(TT^t\).

2.3 Quantum steering


Quantum (EPR) steering, introduced by Einstein, Podolsky and Rosen in 1935, describes the non-local phenomenon of a bipartite state in which one party can non-locally affect the other’s state through a local measurements. It captures the quantum correlation between the entanglement and non-locality in the Bell realm. For a pair of continuous observables \(x^a (x^b)\) and \(p^a(p^b)\) corresponding, respectively, to the subsystem a(b), it is shown that the states admitting a local hidden state (LHS) model in position and momentum satisfying the following inequality [41]

$$\begin{aligned} h(p^b\vert p^a)+h(x^b\vert x^a)\ge \log (\pi e). \end{aligned}$$
(6)

Due to the positivity of the entropic measure, the above constrain is derived for discrete observables \(R^a(S^b)\) as [41]

$$\begin{aligned} H(R^b\vert R^a)+H(S^b\vert S^a)\ge \log (\Omega ^b) \end{aligned}$$
(7)

where \(H(R)=-\sum _iP(R_i)\log P(R_i)\) is the Shannon entropy of the discrete observable \(R_i\) and \(\text {log}(\Omega ^b)={\min }_{ij}(1/\vert \langle R_i\vert S_j \rangle \vert )\) with \(\vert R_i \rangle\) and \(\vert S_j \rangle\) are the eigenbasis of respective marginal states. Employing the Pauli measurements on each side of the two dimensional systems and hence the entropy uncertainty relation (EUR), the steering inequality reads

$$\begin{aligned} H(\sigma _x^b\vert \sigma _x^a)+ H(\sigma _y^b\vert \sigma _y^a)+ H(\sigma _z^b\vert \sigma _z^a)\ge 2 \end{aligned}$$
(8)

where quantum steering demonstrate the presence of non-local character of the system when the above inequality is violated. For any bipartite state \(\rho\) in the form Eq. (4), the expression of steering inequality reads as [42].

$$\begin{aligned}&\sum _{j=1,2}\left[ (1+c_j)\text {log}_2(1+c_j)+(1-c_j)\text {log}_2(1-c_j)\right] \\&\quad - (1+r)\text {log}_2(1+r)+(1-r)\text {log}_2(1-r) \\&\quad +\frac{1}{2}(1+c_3+r+s)\text {log}_2(1+c_3+r+s)\\&\quad +\frac{1}{2}(1+c_3-r-s)\text {log}_2(1+c_3-r-s) \\&\quad +\frac{1}{2}(1-c_3-r+s)\text {log}_2(1-c_3-r+s)\\&\quad +\frac{1}{2}(1-c_3+r-s)\text {log}_2(1-c_3+r-s)\le 2 \end{aligned}$$

where \(c_1=2(\rho _{23}+\rho _{14}),~ c_2=2(\rho _{23}-\rho _{14}), ~c_3=\rho _{11}+\rho _{44}-\rho _{22}-\rho _{33}, ~~ r=\rho _{11}+\rho _{22}-\rho _{44}-\rho _{33}~ \mbox {and}~ s=\rho _{11}-\rho _{44}-\rho _{22}+\rho _{33}\).

3 Dynamical behaviours of correlations

3.1 Intrinsic decoherence master equation

The intrinsic decoherence effect, introduced by Milburn [10], is mainly taken into account when the temporal evolution of a quantum system is dealt with assuming sufficiently short time steps. In this context, the considered quantum system does not evolve continuously under unitary evolution but rather in a stochastic sequence of identical unitary transformations. The time evolution of a quantum system’s state \(\rho (t)\) insured by an Hamiltonian H is governed by the following master equation [10]

$$\begin{aligned} \frac{d\rho (t)}{dt} = -i[H,\rho (t)]-\frac{\gamma }{2}\left[ H,[H,\rho (t)]\right] , \end{aligned}$$
(9)

where \(\gamma\) is the intrinsic decoherence parameter. It is worth of mentioning that there is no intrinsic decoherence in the limit \(\gamma ^{-1}\rightarrow \infty\).

The convenient solution of the Eq. (9) can be written in operator-sum picture using Kraus operators \(M_k\) such as [10]

$$\begin{aligned} \rho (t)= \sum ^{\infty }_{k=0} M_k(t) \rho (0)M_k{}^{\dagger }(t) \end{aligned}$$
(10)

where \(\rho (0)\) is the initial density operator of the considered quantum system and the operator \(M_k(t)\) is defined as

$$\begin{aligned} M_k(t) = \sqrt{\frac{(\gamma t)^{k}}{k!}} {{{ {H}}}}^k \exp \left( -i{{{ {H}}}}t\right) \exp \left( -\frac{\gamma t}{2}{{{ {H}}}}^{2}\right) . \end{aligned}$$

By considering the Hamiltonian H, the evolved state of \(\rho (0)\) can be obtained as

$$\begin{aligned}{} & {} \rho (t) = \sum _{m,n} \exp {- \frac{\gamma t}{2}(E_m-E_n)^2-i(E_m-E_n)t}{\langle {\phi _m}|}\rho (0)\nonumber \\{} & {} \quad |\phi _n\rangle |\phi _m\rangle {\langle {\phi _n}|}, \end{aligned}$$
(11)

where \(E_{m(n)}\) denote the eigenvalues of H and \(|\phi _{m(n)}\rangle\) their corresponding eigenvectors. Recently this way of analysis was performed on physically relevant systems [12,13,14,15,16,17,18].

3.2 Dipolar spin system and initial state

In order to examine the behaviour of quantum correlations dynamics in a physical system under the intrinsic decoherence effects, we consider the two-spin-1/2 particles coupled with dipolar and DM interactions described by the following Hamiltonian[43,44,45,46].

$$H\, = \, - \frac{1}{3}\overrightarrow {S} _{1} \cdot \overleftrightarrow {\mathcal{D}}\cdot \overrightarrow {S} _{2} + \overrightarrow {D} .\left( {\overrightarrow {S} _{1} \times \overrightarrow {S} _{2} } \right).$$
(12)

Here \(D\) is the DM anisotropic interaction coupling vector [47,48,49] and \(\overleftrightarrow {{\mathcal {D}}}=\text {diag}(\Delta -3\epsilon , \Delta +3\epsilon ,-2\Delta )\) is the traceless diagonal tensor between the spins, with \(\Delta\) and \(\epsilon\) acting as dipolar coupling constants. The quantity \(\Delta\) specifies the space spins orientation. \(\Delta > 0\) reflects that the spins are oriented following the z-axis where the DM interaction acts, i.e. \(D = (0,0,D)\), whereas the spins are in the \(x-y\) plane when \(\Delta < 0\). Upon solving the Schrödinger equation \(H|\phi _i\rangle =E_i|\phi _i\rangle\) with respect to the Hamiltonian (12), one gets in the basis \({{{\mathcal {B}}}}\)

$$E_{{1,4}} \, = \,\frac{1}{6}\left( {\Delta \pm 3 \epsilon } \right),\,\,\left| {\phi _{{1,4}} } \right\rangle \, = \,\frac{1}{{\sqrt 2 }}\left( {\left| {11} \right\rangle \pm \left| {00} \right\rangle } \right),$$
(13a)
$$E_{{2,3}} \, = \,\frac{1}{6}\left( {\Delta \pm \eta } \right),\,\,\left| {\phi _{{2,3}} } \right\rangle \, = \,\frac{1}{{\sqrt 2 }}\left( {\left| {10} \right\rangle \pm \left| {01} \right\rangle } \right)$$
(13b)

with the amount \(\eta =\sqrt{9D^2+\Delta ^2}\). Accordingly, we can say that the presence of z–DM interaction serves to reinforce the effect of the dipolar constant \(\Delta\). It is worth mentioning that the considered physical model is useful in realization of quantum gates [50]. To study the influence of intrinsic decoherence on dynamical behaviours of quantum correlation, we consider the well-known two-qubit generic X-state [51]

$$\begin{aligned} \rho (0) =\left( \begin{array}{cccc} a &{} 0 &{} 0 &{} w \\ 0 &{} b &{} z &{} 0 \\ 0 &{} z &{} c &{} 0 \\ w &{} 0 &{} 0 &{} d \\ \end{array} \right) \end{aligned}$$
(14)

as the initial state in the same two-qubit computational basis \({{{\mathcal {B}}}}\). Reporting Eqs. (13) and (14) in Eq. (11), it follows that the time evolved state, corresponding to the initial state (14), can be straightforwardly derived to be

$$\begin{aligned} \rho (t) = \left( \begin{array}{cccc} \rho _{11}(t) &{} 0 &{} 0 &{} \rho _{14}(t) \\ 0 &{} \rho _{22}(t) &{} \rho _{23}(t) &{} 0\\ 0 &{} \rho _{32}(t) &{} \rho _{33}(t) &{} 0\\ \rho _{41}(t) &{} 0 &{} 0 &{} \rho _{44}(t) \end{array}\right) \end{aligned}$$
(15)

with the diagonal entries

$$\begin{gathered} \rho _{{11}} \left( t \right) = \frac{1}{2}\left( {\left( {a - d} \right)e^{{ - \frac{1}{2}\gamma t \epsilon^{2} }} \cos \left( {t\epsilon } \right)\, + \,a + d} \right), \hfill \\ \rho _{{22}} \left( t \right) = \,\frac{1}{2}\left( {\left( {b - c} \right)e^{{ - \frac{1}{{18}}\gamma \eta ^{2} t}} \cos \left( {\frac{{\eta t}}{3}} \right) + b + c} \right),\\\rho _{{33}} (t) = \frac{1}{2}\left( {(c - b)e^{{ - \frac{1}{{18}}\gamma \eta ^{2} t}} \cos \left( {\frac{{\eta t}}{3}} \right) + b + c} \right),~~\\\rho _{{44}} (t) = \frac{1}{2}\left( {\left( {d - a} \right)e^{{ - \frac{1}{2}\gamma t\epsilon^{2} }} \cos (t\epsilon ) + a + d} \right)~~~~ \hfill \\ \end{gathered}$$
(16)
$$\%\rho _{{33}} (t) = \frac{1}{2}\left( {(c - b)e^{{ - \frac{1}{{18}}\gamma \eta ^{2} t}} \cos \left( {\frac{{\eta t}}{3}} \right) + b + c} \right){\text{and}}\,\rho _{{44}} (t) = \frac{1}{2}\left( {\left( {d - a} \right)e^{{ - \frac{1}{2}\gamma t\smallint ^{2} }} \cos (t\smallint ) + a + d} \right)$$
(17)

and off-diagonal ones

$$\begin{aligned} & \rho _{{14}} (t) = \rho _{{41}}^{*} (t) = w + \frac{1}{4}(a - d)\left( { - 1 + e^{{2it\epsilon }} } \right)e^{{ - \frac{1}{2}t\epsilon (\gamma \epsilon + 2i)}} ,\\ & \rho _{{23}} (t) = \rho _{{32}}^{*} (t) = z + \frac{1}{4}(b - c)\left( { - 1 + e^{{\frac{{2i\eta t}}{3}}} } \right)e^{{ - \frac{1}{{18}}\eta t(\gamma \eta + 6i)}} \end{aligned}$$
(18)

It is interesting to notice that in the asymptotic limit (\(t \rightarrow \infty\)), the evolved state \(\rho (t)\) (10) reduces simply to

$$\begin{aligned} \rho (t\rightarrow \infty ) =\left( \begin{array}{cccc} \frac{a+d}{2} &{} 0 &{} 0 &{} w \\ 0 &{} \frac{b+c}{2} &{} z &{} 0 \\ 0 &{} z &{} \frac{b+c}{2} &{} 0 \\ w &{} 0 &{} 0 &{} \frac{a+d}{2} \\ \end{array} \right) . \end{aligned}$$
(19)

This result shows that the correlations are enhanced primarily by initial state and only the dynamics are affected by the system parameters, which is discussed extensively in next section. This is quite in contrast with existing studies where system parameters determine the robustness of quantum correlations [12,13,14,15,16]. For our investigations of intrinsic decoherence effects on different suggested quantum correlations, we deal with a special kind of initial X-state with form

$$\begin{aligned} \rho (0) = \frac{(1-p)}{4}\mathbbm {1}_{4}+p |\varphi > <\varphi | \end{aligned}$$
(20)

where \(p\in [0,1]\) refers to the initial state purity, \(\mathbbm {1}_{4}\) is the \({4\times 4}\) identity matrix and \(|\varphi \rangle =|00\rangle\) which is a pure separable state. In other words, we consider the generic state (14) by fixing their elements as

$$\begin{aligned} a=(1+3p)/4,~b=c=d=(1-p)/4,~w=0~~~~~~~\text {and}~~~~~~~~z=0. \end{aligned}$$

It is of a paramount importance to notice that the initial matrix density (20) is a fully separable state for any value of the purity p. In the next, we show that the dipolar spin-spin interaction can induce the correlation in such initial state (20) as time increases and demonstrate the super dense coding in dipolar system.

4 Results and discussions

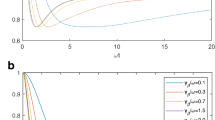
In what follows, we study the influence of phase decoherence on quantum correlations of two-spin system coupled with the dipolar and z–DM interactions. First, we analyze the generation of quantum correlation when the two-qubit system is initially in a separable pure state. Otherwise, we consider the state \(\rho (0)=|00\rangle {\langle {00}|}\) by setting \(p=1\) in Eq. (20). The dynamical behaviour of MIN, QS and concurrence of time evolved state are depicted in Fig. 1. The values of the suggested quantum measures in plots are scaled for easy comparison. The Fig. 1 results confirm that there are no quantum correlation at \(t=0\). Furthermore, we show that the MIN and entanglement behave in the same trend by respecting the following relationship \({\mathcal {N}}(\rho (t))=C^2(\rho (t))/2\). As time evolves, quantum correlations have a dynamic oscillating nature with exponentially decaying behavior. It is worth of mentioning that our model seems to be very useful for the development of quantum technologies due to quantum resources generation. After a finite time, the entanglement undergoes the sudden death process. Based on the nature of quantum steering (QS), the evolved state is steerable only for QS \(\ge\) 2 [42]. Notice that the companion quantity of QS relevant to the initial state (\(|\varphi \rangle =|00\rangle\)) is 2. Thing which confirms the absence of quantum correlation between the spins.

Fig. 1
figure 1

Dynamical behaviour of QS, MIN and concurrence for \(\epsilon =0.1\), \(\gamma =5\) when the two-qubit system are initially prepared in the pure separable state \(\rho (0)=|00\rangle {\langle {00}|}\) (i.e., \(p=1\) is taken into Eq. (20))

Full size image

Next, we investigate the energy parameter \(\epsilon\) influence on quantum correlation measures under the intrinsic decoherence effects. In Fig. 2, we have plotted the time variations of suggested measures by considering the initial product state \(\rho (0)=|00\rangle {\langle {00}|}\) (\(p=1\)) for various values of \(\epsilon\). Here again, we observe the generation of quantum correlation due to the dipolar coupling and exponential decaying behaviour due to the factor proportional to the \(\exp (-\gamma t)\). In addition, we observe that the increasing of the energy parameter \(\epsilon\) leads to a rapidly decay of the quantum correlation due to the factor \(\exp \left( {-\frac{1}{2} \gamma t \epsilon ^2}\right)\) and decreases therefore the oscillations numbers. Nevertheless, it was shown that the parameter \(\epsilon\) strengthen quantum resources if we immerse the system in the thermal bath [44]. Further, we also notice that the another energy parameter \(\Delta\) and DM interaction do not affect the any quantum correlation measures. These interaction parameters are strongly influence the quantum correlations when the system is embedded in a thermal bath.

Fig. 2
figure 2

Comparing dynamic behaviour of QS, MIN and concurrence for \(p=1\), \(\gamma =0.1\) and varying \(\epsilon\)

Full size image

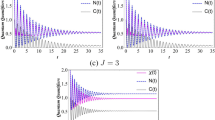
The dependence of intrinsic decoherence parameter \(\gamma\) on different quantum correlation quantifiers are displayed in Fig. 3. Here also, the evolution under intrinsic decoherence generates the correlation in two separable qubits as long as the energy parameter \(\epsilon\) different to zero. To manifest the correlation, we have consider the different \(\gamma\) values such as \(\gamma =0.2,~1,~1.5\) and 2. At \(t=0\), there are no quantum correlations between the spin because of the initial state separability. As time evolves, the generated correlation undergoes pseudo-periodic oscillations which collapses at a finite time. The correlations are decayed due to the exponential factor. The maximal correlation decreases with increasing values of decoherence parameter \(\gamma\). In addition, the increase of \(\gamma\) accelerates the dissociation of the spins in the diploar system.

Fig. 3
figure 3

Comparing dynamic behaviour of QS, MIN and concurrence for \(p=1\), \(\epsilon =1\) and varying \(\gamma\)

Full size image

To understand the dynamics behaviours of correlation measures under phase decoherence, we consider the different initial conditions in Fig. 4. The quantum correlations for varying p (Fig. 4) show that the maximum correlation measured in the system is determined by initial X-state. However, the time t where maximum correlations are induced is quantified by the state parameter \(\epsilon\) and intrinsic decoherence parameter \(\gamma\) as can be observed in Figs. 2 and 3.

Fig. 4
figure 4

Dynamical behaviour of QS, MIN and concurrence for \(\epsilon =0.1\), \(\gamma =5\) and varying p

Full size image

5 Dense coding Holevo quantity

In dense coding operation, a local unitary transformation \(U_i\) is performed on the initial probe entangled state \(\rho\) such as \(\rho _i=(U_i \otimes \mathbbm {1}) \rho (U_i^{\dagger } \otimes \mathbbm {1})\) with probability \(p_i (i=0,1,...i_{max})\) [52, 53]. The Holevo quantity which determines the quality of measurement on the state \(\rho _i\) is determined from \(\chi =S({\overline{\rho }})-S(\rho )\) where the von Neumann entropy is \(S(\rho )=- \textrm{Tr}(\rho \log _2 \rho )\) and average density matrix is defined as \(S({\overline{\rho }})=\sum _{i=0}^{i_{max}} p_i \rho _i\). We study the influence of the intrinsic decoherence dynamic on the Holevo quantity for the evolved state \(\rho (t)\) (Eq. (15)) [54]. It should be indicated that the dense coding is most optimal when \(\chi =2\) and dense coding is not valid when \(\chi <1\). For the general evolved two-qubit X-state (15), the dense coding capacity \(\chi\) can be calculated as follows

$$\begin{aligned}{} & {} \chi = \sum _{i=1}^{4} \rho _{ii}(t)\log _{2}\left(2 \rho _{ii}(t)\right)-\left(\rho _{11}(t)+\rho _{33}(t)\right)\log _{2}(\rho _{11}(t)\nonumber \\{} & {} \quad +\rho _{33}(t))+\left(\rho _{22}(t) +\rho _{44}(t)\right)\log _{2}\left(\rho _{22}(t)+\rho _{44}(t)\right). \end{aligned}$$
(21)

To reduce the parameters, we consider the initial state like to that we addressed in previous section, i.e., the initial separable state (20). For a purely two-qubit initial state, with \(p=1\), the dynamical behaviour of \(\chi\) is shown in Fig. 5a. The oscillating nature of \(\chi\) is similar to the correlations. Also, we plot the time evolution of \(\chi\) by fixing system parameters and varying the purity p. The main results are displayed in Fig. 5b. This again shows results similar to previous section where the initial state and the value of purity p determines the optimal behaviour of dense coding where it becomes invalid for \(p<0.8\).

Fig. 5
figure 5

Illustrating the dynamic behaviour of \(\chi\)

Full size image

6 Concluding remarks

To summarize, we have investigated the intrinsic decoherence effects on the quantum correlations and the dense coding capacity in dipolar spin system under the interplay of the z–DM interaction. The evolved state entries were evaluated by considering a mixture of a separable state and using the Milburn’s master equation. We highlight the dynamic behaviours of the suggested criteria in terms of the dipolar spin system parameters and the initial state purity. We found that even for a pure separable initial state, its intrinsic dynamics display an oscillating behaviour. This dynamic behaviour means that the intrinsic decoherence governed by the dipolar spin system induces the correlation between two separable qubits. For the same initial states, an oscillating nature of suggested criteria, including dense coding capacity, is always present. We also found that the increase of the \(\epsilon\) parameter causes the loss of correlations rapidly. A likewise behaviour was seen in the intrinsic decoherence rate \(\gamma\) consistent with existing studies.