1 Introduction

The photothermal lens (PTL) spectrometry technique is the most sensitive among the photothermal techniques. It can be used to determine absorption coefficients [1,2,3,4,5,6], thermal diffusivities of different materials [7, 8] and chemical traces in aqueous solutions [9,10,11,12]. PTL can also be used for microscopy and imaging studies of complex turbid bio-samples [13], which have potentially important biomedical applications. There are two types of dual-beam photothermal lens (PTL) standard techniques. Mode-matched dual-beam photothermal lens configuration is the first type. The sample cell lies closest to the focal point of the excitation and probe beams, which have almost the same radius. The second type is a mode-mismatched dual-beam experiment. The sample cell is arranged at the focal point of the excitation beam with waists lower than the probe beam. The excitation laser is used to heat a small region of the sample by the absorption of optical radiation (excitation beam). This leads to a production of thermal waves in the medium and eventually to the formation of a temperature gradient. A second laser (probe beam) is then used to detect the PTL effect on its wavefronts by measuring the relative change in its transmitted power through a slight aperture situated at the far field and on the optical beam axis. The PTL also manifests itself by the analysis of the probe beam reflection. Several examples of this latter mechanism are found in the photothermal displacement technique, where it is demonstrated that it is possible to measure thermal diffusivity in thin films [14] and solid materials [15, 16]. It uses the deflection of the probe beam reflected from the sample surface to detect the thermoelastic deformation of the sample. The measurement of this deflection contains information on the thermo-optical properties of the sample. More recently, Daniel et al.[17] have developed a new method based on the reflective PTL effect to measure the thermal diffusivity of a variety of liquids and liquid mixtures placed in contact with metal films to an accuracy better than 2%. Doiron et al.[18] applied this method for the measurement of thermal diffusivity of a wide variety of solid and opaque materials. In this method, the thermal displacement caused by a focused excitation beam on a substrate can be determined from the divergence it induces in the probe beam, and not from its deflection as is commonly assumed. In addition, the reflective PTL effect occurs when both probe and excitation beams are focused at the same position which corresponds to the mode-matched configuration.

Several comparisons were performed between theory [19,20,21] and experiments. All of them were focused on the optimization of the experimental arrangement to enhance the amplitude of the PTL signal with a little interest to the reduction of the aberration effects caused by the photothermal lens. Berthoud et al. [22] studied the influence of beam positions and showed that when the excitation beam was focused on the sample cell, the maximum PTL signal was obtained. It is also demonstrated that the PTL signal varies with distance between the focus of the probe and excitation beams, and yields a maximum signal approximately at a square root of three times the confocal distance of the probe beam [19, 22, 23]. In addition, theoretical and experimental studies have shown that a collimated probe beam in the presence of a focused excitation beam can be used to optimize PTL experiments [24]. The collimation of the probe beam provides greater simplicity to obtain the maximum value of the stationary PTL signal in this scheme, but as a result the time evolution of the transient PTL signal and photothermal aberrations increase. All previous results are valid for the transmission PTL method and the experimental schemes based on the mismatched configuration are the most used to study the thermo-optical properties of solids and liquids. Although these experimental arrangements improve the PTL signal amplitude, they place further degrees of freedom (focus positions and mismatching degree) and introduce more aberration effects on the photothermal lens element. This is because the probe beam rays cross an area larger than the waist of the excitation beam and then a more complexity in the photothermal lens profile should be taken into account in the theoretical description. In contrast, the assumption of the parabolic photothermal lens medium greatly simplifies the calculations since it consider the medium as a simple lens defined by only a focal length. The validity of the latter approximation occurs when the beam waists are matched, which corresponds to the mode-matched configuration. Thus, as the excitation laser is of a Gaussian profile, the influence of the induced photothermal lens on the propagation characteristics of the probe beam can be assumed to be due to propagation through a parabolic medium.

In this work, we investigate the experimental arrangements used in the transmission PTL technique by temporal analysis of the PTL signal of a liquid sample. Particular interest is given to the mode-matched configuration and the improvement of the PTL signal amplitude. In this paper, we explain two optical collinear dual-beam (probe-excitation) schemes, both theoretical and experimental. As a result of the placement of the probe beam waist, the two schemes are mismatched and mode-matched configuration. In the first, the waist is located far with respect to the excitation beam waist position, while in the second scheme the waist of the probe beam is focused at the cell sample and adjusted within the excitation beam radius where the photothermal lens could be treated as an ideal lens.

1.1 Experimental setup

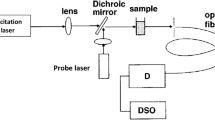
The experimental setup used in this work is shown in Fig. 1 and similar to that reported in a previous work [25]. The excitation laser was a solid-state laser (Excelsior) with a power of 11.4 mW at 375 nm. A UV-fused silica lens L1 having a focal length of f1 = 20 cm is used for focusing. An XYZ linear translation stage (Newport M-DS65, with a sensitivity of 1 µm) is used to adjust the distance between the probe and excitation beam. A 2 mW He–Ne laser emitting a laser beam at 632.8 nm is used as the probe laser. The probe laser is aligned with respect to the excitation laser in a counter propagation direction and focused with the use of a lens L2 at focal length f2 = 10 cm (AR coated: 430–700 nm, Newport). The sample used in this work is paraffin oil, which is put in a 1 cm optical path length quartz cell. Paraffin oil is chosen for the present study not only because it is readily available and due to previous experiments showing its thermal properties, but also due to its high temperature coefficient of refractive index compared to other fluids, since paraffin oil is recognized as an excellent material for thermal energy storage [26]. The PTL signal is recorded using an Si photodetector (Newport), which was in front of a longpass optical filter (λ > 600 nm) and a pinhole with a diameter of 500 μm. A low noise current-to-voltage amplifier (Newport) is then used to preamplify the signal before it is directed to a digital oscilloscope (Tektronix TDS2012) and a lock-in amplifier (SR810). The reference signal used to modulate the excitation beam is fixed by a chopper (SR540). All the operation of data acquisition and instruments control were made with the TraQ-Basic 6.5 spectroscopy software.

Fig. 1
figure 1

PTLS experimental setup. DM dichroic mirror, M mirror, S sample, F1, F2 and F3 filters, CH optical chopper, PH pinhole, PD2 Si photodetector, PD1 quadrant cell photodiode, L1 (f1 = 20 cm) and L2 (f2 = 10 cm) lenses, Amp current amplifier, OSC oscilloscope

Full size image

1.2 Theoretical basis

The PTL signal is normally monitored by measuring the power change of a probe laser. A typical optical arrangement propagates the probe beam along the z-axis, and the power change is measured at a distance much beyond the sample cell. The relative power change is determined by the phase shift caused by the temperature change in the sample and acting as an optical element (with a thickness of about thermal diffusion length). Sheldon et al. and Shen et al.[19, 20] have proposed an aberrant thermal lens model allowing the description of the photothermal lens behavior. For the mode-match dual-beam configuration, corresponding to a mismatching degree of around one, when the waists of the probe and pump beams do not change significantly across the sample and when the sample absorbance is sufficiently small, the probe beam can be considered as a collimated beam all along the sample path and treated as a plane wave. In this situation, all the rays pass through a thin section where the temperature distribution and the refractive index change are in good agreement with quadratic approximation. The photothermal lens, therefore, could be treated as an ideal thin lens, of a particular focal length \(f\left(r,t\right)\). In this case, the radial phase shift, given by Eq. 1, corresponds to an addition of a term \(-1/f\left(r,t\right)\) to the inverse curvature \(1/R\left(z\right)=1/\left(1+\frac{{z}_{0,p}^{2}}{{z}^{2}}\right)\).

$$\phi \left( {r,t} \right) = \frac{k}{{2f\left( {r,t} \right)}}r^{2} ,$$
(1)

where \({z}_{0,p}=\pi {\omega }_{0,p}^{2}/{\lambda }_{p}\) is the confocal distance of the probe beam with a wavelength \({\lambda }_{p}\) and k is the probe beam wave number. According to the basic equation for beam propagation, the inverse focal length of the thermal lens depends on the curvature of refractive index [27] and is given by:

$$\frac{1}{{f\left( {r,t} \right)}} = - \frac{dn}{{dt}}l\frac{{\partial^{2} T\left( {r,t} \right)}}{{\partial r^{2} }},$$
(2)

where \(dn/dT\) denotes the variation of the refractive index with temperature (typically 10−4 °C−1 for liquids and 10−5 °C−1 for solids) and \(\mathcal{l}\) is the thickness of the absorbing medium. The temperature change \(T\left(r,t\right)\) is found from the solution of the thermal diffusion equation for a sample heated with a Gaussian laser beam in collinear configuration (z-axis) [28, 29]. Two hypotheses are considered to solve this equation. The first assumption considers a low absorbent sample to suppose that the attenuation of the excitation beam along the laser path does not cause a significant difference in the temperature profile. The second assumes an infinite radius for the sample and thus a boundary condition \(T\left(\infty ,t\right)=0\). As a result, the obtained temperature change in the solution is:

$$T\left( {r,t} \right) = \frac{{2P_{e} \alpha }}{{\pi \rho c_{p} \omega _{e}^{2} }}\int\limits_{0}^{t} {\frac{{e^{{ - 2r^{2} /\omega _{e}^{2} \left( {1 + 2t^{\prime } /t_{c} + 2\delta t/t_{c} } \right)}} }}{{\left( {1 + 2t^{\prime } /t_{c} + 2\delta t/t_{c} } \right)}}} dt^{\prime } ,$$
(3)

Where \(\delta t=\left\{\begin{array}{cc}0& t<{t}_{1}\\ t-{t}_{1}& t\ge {t}_{1}\end{array}\right.\), the time at which the excitation source is active is t1, \({t}_{c}=\frac{{\omega }_{e}^{2}}{4D}\) is a characteristic thermal time constant, D is the diffusivity, \({\omega }_{e}\) is the excitation beam radius, Pe is the optically exciting beam power, α is the absorption coefficient and cp and ρ are the specific heat and the density of the sample, respectively. On the basis of Eq. 2 and Eq. 3, the expression of the inverse focal length can be expressed more explicitly as follows:

$$\frac{1}{{f\left( {r,t} \right)}} = \frac{dn}{{dT}}\frac{{8P_{e} \alpha \ell }}{{\pi \rho c_{p} \omega_{e}^{2} }}\int\limits_{0}^{t} {\left( {1 - \frac{{4r^{2} }}{{\omega_{e}^{2} \left( {1 + 2\left( {t^{\prime} + 2\delta t} \right)/t_{c} } \right)}}} \right)} \times \frac{{e^{{ - 2r^{2} /\omega_{e}^{2} \left( {1 + 2t^{\prime}/t_{c} + 2\delta t/t_{c} } \right)}} }}{{\omega_{e}^{2} \left( {1 + 2\left( {t^{\prime} + 2\delta t} \right)} \right)^{2} }}dt^{\prime}.$$
(4)

The temperature changes in the heating part of the cycle \((\delta t=0\), \(t={t}_{1})\) and near the z-axis are parabolic. We can derive the inverse focal length as follows:

$$\frac{1}{{f_{0} \left( t \right)}} = \frac{1}{f\left( \infty \right)}\frac{1}{{\left( {1 + t_{c} /2t} \right)}},$$
(5)

where \(1/f\left(\infty \right)=\frac{dn}{dT}\frac{2{P}_{e}\alpha \mathcal{l}}{\pi \rho {c}_{p}D{\omega }_{e}^{2}}\) is the inverse of the maximum focal length value.

The complex amplitude of the electric field at the detector and at a radial distance \({r}_{d}\) from the beam center can be calculated based on Fresnel diffraction theory:

$$E\left( {r_{d} ,z_{1} + z_{2} ,t} \right) = \frac{ik}{{z_{2} }}e^{{ - ikz_{2} }} \mathop \smallint \limits_{0}^{ + \infty } E_{0} \left( {r,z_{1} ,t} \right)e^{{ - j\frac{k}{{2z_{2} }}\left( {r^{2} - r_{d}^{2} } \right)}} rdr,$$
(6)

where z1 is the distance between the positions of the probe beam waist and the sample, and z2 is the distance between the sample and the detector. \({E}_{0}\) is the electric field just behind the sample (\({z}_{2}=0)\) and can be calculated as follows:

$$E_{0} \left( {r,z_{1} ,t} \right) = \sqrt {\frac{2P}{\pi }} \frac{1}{{\omega_{p} \left( t \right)}}e^{{ - ikz_{1} }} e^{{r^{2} /\omega_{p}^{2} \left( t \right) - i\left( {\frac{k}{2R}r^{2} - \phi \left( {r,t} \right)} \right)}} ,$$
(7)

where \({\omega }_{p}\left(t\right)\) is the time-dependent radius of the probe beam perturbed by the photothermal lens. The PTL signal \(S\left(t\right)\), as shown in Eq. 8, is then calculated by taking the complex square of the electric field summed over the aperture radius. The first integral corresponds to the power change of the probe beam in the presence of the PTL effect when the excitation beam is on and the second integral is the initial value when the excitation beam is off.

$$S\left( t \right) = \frac{{\mathop \smallint \nolimits_{0}^{a} \left| {E\left( {r_{d} ,z_{1} + z_{2} ,t} \right)} \right|^{2} r_{d} dr_{d} - \mathop \smallint \nolimits_{0}^{a} \left| {E\left( {r_{d} ,z_{1} + z_{2} ,0} \right)} \right|^{2} r_{d} dr_{d} }}{{\mathop \smallint \nolimits_{0}^{a} \left| {E\left( {r_{d} ,z_{1} + z_{2} ,0} \right)} \right|^{2} r_{d} dr_{d} }}.$$
(8)

2 Results and discussions

The position of the probe beam waist with respect to that of excitation beam affects significantly the PTL signal. Several authors have shown that the mismatched dual-beam configuration leads to a higher PTL signal amplitude than the other configurations [19, 22, 23]. For the considered experimental arrangement, we have shown that when z1 is around six times greater than the confocal distance of the probe beam, a maximum PTL signal is reached and the error does not exceed 5% [25]. However, when the probe beam waist position approaches z1 \(\cong\) z0,p, we have observed a significant variation of PTL signal from a very low to a high signal amplitude, reaching the same order of magnitude as that given with the far z1 position. This is obtained after a tight adjustment between the probe and excitation beams waists. Indeed, we have experimentally investigated this scheme corresponding to a mode-matched configuration for which the probe beam waist is placed at the waist position of the excitation beam. The probe and excitation beam waists were measured using the knife-edge technique [30] and the obtained results are ω0p = 54.9 μm and ωe = 70.81 μm, respectively. The corresponding confocal distances were 1.5 cm and 4.2 cm, respectively. The parameters used for plotting the curves obtained for paraffin oil using Eq. 8 were as follows: λp = 632.8 nm, Pe = 11.4 mW, dn/dT =  − 1 × 10−4 K−1, ρcp = 1.81 × 106 Jm−3 K−1 and \(\ell\)=1 cm. Figure 2 shows the evolution of the PTL signal with the variation of the probe beam waist position z1 into a region of the order of magnitude of confocal distance, for which the radius of the probe beam is lower than that of excitation. Within this region, all the rays are similar in phase since the longitudinal phase shift is negligible and the radial curvature is close to infinite. The obtained results show a significant variation of the PTL signal amplitude with an error varying from 4 to 9% and a coefficient of variation from 5 to 75%. These values were deduced from 100 measurements of the PTL amplitude. The lower error and coefficient of variation were obtained when the photothermal lens was placed before the waist of the probe beam and became higher when placed beyond. We also note that the PTL signal is positive, when the probe beam is focused at the confocal distance or after the sample, and it is expected to be negative, when the probe beam is focused in front of the sample. However, in our condition the sign of the PTL signal does not change immediately, but remains close to zero until a distance from the sample of around two times the confocal distance of the probe beam. Given that the temperature refractive index coefficient of paraffin oil is negative, the thermal lens behaves as a diverging lens in the center. Thus, for the scheme where the PTL signal is negative, the probe beam waist is placed before a diverging thermal lens and then its effect simply increases the divergence of the beam. While for the scheme where the PTL signal is postive, the same lens is placed before the waist inducing a decrease in the probe beam convergence which, in turn, decreases the divergence after its propagation beyond the waist. Moreover, the radial scan of the waist excitation beam position was achieved by using XYZ linear stages to control the distance between the axis of the excitation and probe beams. Figure 3 shows the theoretical predictions based on the temporal integration of Eq. 8 over 1/2F, corresponding to the time when the excitation beam is on, and for different distances between the probe and the excitation beams. This distance was measured in units of \({\omega }_{e}\). For distances between probe and excitation beams lower than \({0.5\omega }_{e}\), the contribution of the photothermal lens effect is dominant allowing then the use of Eq. 8 without taking into account the probe beam deflection effect. Outside of this region, the PTL signal decreases significantly as shown in Fig. 3, indicating that the thermal lens effect becomes negligible.

Fig. 2
figure 2

A plot of PTL signal of paraffin oil from different probe beam waist positions against the sample cell position at z1 = 0 in relation to the position of the probe beam waist

Full size image
Fig. 3
figure 3

Normalized PTL signal of paraffin oil at different probe and excitation beam distances

Full size image

A study of the dependency of the PTL signal on the detector position z2 from the sample cell was also conducted, and the results are shown in Fig. 4. A probe beam waist position fixed at z1 \(\cong\) z0,p was used to perform measurements for values ranging from 15 cm up to around 200 cm. A significant increase in PTL signal has been noted for z2 > 60 cm, practically reaching a maximum value. Similar results were obtained for mismatched configuration [25] where it was shown that PTL amplitude keeps a constant starting from z2 close to 80 cm. The signal accuracy ranges from 10 to 40% for PTL signals; it is mainly due to the difficulty of centering the waist probe beam at the pinhole aperture at high z2 distances.

Fig. 4
figure 4

Dependence of the PTL signal of paraffin oil on the detector positions

Full size image

The temporal evolution of the PTL signal was recorded and is shown in Fig. 5. The theoretical PTL signal \(S\left(t\right)\), computed from Eq. 8, was used to fit the experimental results. The experimental PTL signal corresponds to the change in the detector output (first term of Eq. 8). An amplifier was used to amplify all measurements, and the experimental signal was used to normalize the results when the laser was turned off (second term of Eq. 8). The repeatability was granted by performing several times the same amplitude measurement where the uncertainty was lower than 2%. This was mainly due to the uncertainty of the irradiation times \({t}_{1}=1/2F\) (times that the excitation source is on) estimated to around 15% and induced by the mechanical chopper. For all measurements, the average modulation frequency of the excitation beam was 1.5 Hz and all the fitting parameters of the PTL signal were obtained from the average of five recordings. As shown in Figs. 3 and 5, the obtained results show that for a zero radial displacement between the pump and probe beams axes, an increase was noted in the PTL signal, followed by a rapid decline to its weak value at about 40 μm from this position. For the first position, the increase of the intensity at the detector (positive value of PTL signal) suggests that the photothermal lens formed reduces the divergence of the probe beam at the detector. When the pump beam was displaced in the radial direction with respect to the probe beam, we noticed a strong reduction of the PTL amplitude and a deformation in its temporal behavior. This huge reduction of PTL signal is mainly caused by the photothermal deflection, which becomes dominant when the waist of the probe beam is smaller than that of the excitation and crosses the greatest refractive index gradient. According to the previous results, as well as the radial scan of PTL, the maximum of the PTL signal occurs whenever the distance between the probe and excitation beams waists is smaller than \(0.5{\omega }_{e}\). Within this region, the curvature of the refractive index is negative giving rise to a divergent lens element. Aside from these cases, the PTL signal remains lower whatever the radial position. So, it appears that the mode-match configuration can improve the PTL amplitude if the probe beams used to monitor the photothermal lens element do not deviate more than \({\mp 0.5\omega }_{e}\) from the center of the temperature perturbation. This experiment configuration requires more accuracy in terms of control of the focusing of the probe and excitation beams and allows to get an appropriate collimated beam within the confocal distance. In passing through the lens, the on-axis rays have their wave fronts retarded, and the exiting waves have a spherical wavefront with curvature radius equal to the focal length of the lens. Therefore, the use of this experimental arrangement allows, on the one hand, circumventing the problem of the photothermal lens aberrations and then to treat the PTL as an ideal thin lens, and on the other hand, to extract much accurate and reliable thermo-optical parameters of samples from experimental data.

Fig. 5
figure 5

Solid lines are the PTL signals as a function of the time obtained with mode-matched configuration at two radial positions distance of around 40 µm for paraffin oil. The red-colored dashed line corresponds to the fitting of the experimental data using Eq. 8

Full size image

As shown in Fig. 6, the time evolution of the PTL signal was obtained by using the mismatched configuration at \({z}_{1}\cong 10{z}_{0,p}\). This arrangement leads to an increase in the probe beam radius at the interaction region and gives a negative PTL signal, indicating that the formed photothermal lens is divergent. In this case, the probe beam propagates in inhomogeneous medium where the refractive index increases with position away from the propagation axis. Indeed, a larger waist probe beam means that it will probe more of the sample and, consequently, more rays will cross an area that is outside the diameter of the excitation beam. The photothermal lens aberrations are therefore increased, which affects the accuracy of the thermo-optical parameters extracted from the fitting of the experimental data [31, 32]. While with the reduction of the probe beam radius to be in the order or less than that of excitation, the refractive index change can be described by a parabolic equation. As theoretically predicted [1, 2, 31], the parabolic approximation holds fairly well when\({r\le \omega }_{e}\). Within this radius, 87% of the light energy is concentrated, resulting in a lens with little spherical aberration. Therefore, Eq. 5 should give a good approximation to its focal length allowing thus a greater accuracy in the modeling of the PTL signal and more reliability in the measurement of the physical parameters.

Fig. 6
figure 6

PTL signal with mismatched configuration as a function of time

Full size image

The time-resolved photothermal lens method is often used to measure the thermal diffusivity, especially when the signal-to-noise ratio is important. Figure 4 shows that the use of Eq. 8 provides a good fit of the experimental data and then allows the measurement of the thermal diffusivity from the obtained fitting parameter. The value obtained for the paraffin oil was 0.42 × 10−3 which is similar to that obtained by the method of photothermal deflection [33], giving a value of 0.4 × 10−3 cm2s−1. In addition, we measured the PTL signal for different values of the excitation power. The results are shown in Fig. 7. For the mode-matched configuration \(\left({z}_{1}\cong {z}_{0,p}\right)\), we note a linear dependence of the PTL results corresponding to a one-photon absorption process. From the slope of this dependence and by using the linear form of the PTL signal\(S\left(t=\infty ,{P}_{e}\right)\cong -2{z}_{0,p}/f\left(t=\infty ,{P}_{e}\right)\), we obtained the absorption coefficient of paraffin oil which is 0.069 cm−1. This result is close to that given by Raj et al. [34], around 0.05 cm−1 at 375 nm obtained from the absorbance spectra of paraffin oil, while for the mismatched configuration \(\left({z}_{1}\cong 10{z}_{0,p}\right)\), we note a non-linearity in the PTL signal with the increase in the power excitation. As a result, the PTL signal is saturated due to the divergence of a large proportion of the probe beam rays from the pinhole aperture. However, for the mode-matched configuration, as the major probe beam power is outside of the pinhole aperture and the PTL is positive, the linearity in the PTL signal is preserved for higher excitation power. It is clear that this effect becomes negligible for low PTL signal, especially for the samples with low absorption coefficient, and then the mismatched configuration continues to be performed for all thermo-optical measurements. Indeed, the mode-matched configuration is more appropriate for samples with high values of temperature coefficient of refractive index.

Fig. 7
figure 7

The PTL signal of paraffin oil as a function of the excitation power

Full size image

At the final step, to confirm the applicability of our experimental arrangement, experiments were performed on ethanol to measure its thermal diffusivity and absorption coefficient and compared with literature data. The first performed measurements concern the time evolution of the PTL signal for mode-matched configuration (z1 \(\cong\) z0,p). The positive PTL signal results, as shown in Fig. 8, confirm the converging character of the thermal lens effect when the probe beam is focused beyond the sample and the enhancement of the PTL signal to be of the order than that given by the mismatched configuration. The second performed measurements deal with the power excitation effect on PTL signal. As shown in Fig. 9, a non-linearity in the PTL signal, less pronounced than that obtained for paraffin oil, appears from a given power excitation value with the use of the mismatched configuration, contrary to the mode-matched configuration where the PTL signal presents a good linearity over the whole power excitation range. Indeed, the use of the time-resolved method based on Eq. 8 to fit the time evolution of the PTL signal of ethanol gives a thermal diffusivity value of 0.835 × 10−3 cm2s−1. This experimental data agree well with the measured results obtained by Mohebbifar et al.[35], using both experimental fall time measurement and numerical simulation (based on finite element method) of the PTL behavior. The given values were 0.808 × 10−3 cm2s−1 and 0.809 × 10−3 cm2s−1, respectively. However, the results obtained by rodriguez et al. [36] and Cabrera et al. [37], based on the frequency-resolved photothermal lens method, are relatively higher since the diffusivities values were 0.86 × 10−3 cm2s−1 and 0.90 × 10−3 cm2s−1, respectively. Recently, the dynamic light scattering method with photon correlation spectroscopy technique [38] was used as an alternative method and a successful approach to measure the thermal diffusivity of ethanol. The obtained results depend on sample temperature where the thermal diffusivity increases from 0.836 × 10−3 cm2s−1 to 0.879 × 10−3 cm2s−1 when the temperature decreases from 20 to 30 °C. Thus, besides the effect of the experimental configuration on the experimental results, the sample temperature can also explain the relative deviation between the measured thermal diffusivities of ethanol. Otherwise, the absorption coefficient of ethanol at 375 nm, obtained from the slope of Fig. 9, was 1.33 × 10−3 cm−1. This result can give an extension of the measured absorption spectra of ethanol given by Cabrera et al. [39] using a photothermal lens spectrophotometer. Their results show an increase of the absorption coefficient from around 0.12 × 10−3 cm−1 at 460 nm to reach 1.08 × 10−3 cm−1 at 430 nm.

Fig. 8
figure 8

Solid lines are the PTL signals as a function of the time obtained with mode-matched configuration for ethanol. The red-colored dashed line corresponds to the fitting of the experimental data using Eq. 8 and the following parameters: λp = 632.8 nm, Pe = 11.4 mW, dn/dT =  − 4.0 × 10−4 K−1, ρcp = 1.85 × 106 Jm−3 K−1 and \(\ell\)=1 cm

Full size image
Fig. 9
figure 9

The PTL signal of ethanol as a function of the excitation power

Full size image

3 Conclusion

The effects of the position and waist values of the probe beam have been studied for different dual-beam photothermal lens experiments. It is clearly raised from experimental results that the maximum of the PTL signal depends on the experimental configuration. Our studies have demonstrated that photothermal lens aberrations can be avoided using the mode-matched configuration, where the probe beam should be minutely focused on the sample cell. Using this experimental arrangement, the PTL signal increases by the same magnitude as when the configurations are mismatched and the linearity is preserved for high power excitations. Finally, we note that this experimental configuration brings substantial improvement that enables raising the precision of the thermal–optical measurements and getting an appropriate collimated beam that may be useful for the amplification of the PTL signal based on the multi-pass probe beam configuration and on the self-mixing effect [40, 41].