1 Introduction

Widely used asymmetric and symmetric cryptography techniques are both intractable problems based on complexity conjecture P\(\ne\)NP [3]. Albeit based on conjecture, this cryptography is more about how long it will take to solve the problem using the brute force method with unlimited resources. Due to Shor’s algorithm, tools such as quantum computers can render public-key cryptography insecure [17]. Moreover, this insecurity cannot be physically detected should the public key be compromised.

Quantum cryptography provides hardware-based information-theoretic security, providing eavesdropper detection without underlying conjectures. One of the implementations of quantum cryptography is Quantum Key Distribution (QKD), which allows the exchange of random keys on the quantum channel. An ideal QKD provides a provable secure implementation. However, an imperfection in these implementations often opens doors to side channels [9, 10, 12]. Ideally, the source for QKD should emit one photon at a time and on-demand. Unfortunately, single-photon sources are expensive and have low collection efficiency, making them no better than alternative sources. Moreover, a high rate single-photon source is yet to be demonstrated [4]. Implementation of QKD using alternative sources has been widely discussed in [2, 11, 14].

We propose generating indistinguishable signal/-decoy in the temporal domain using a gain-switched single laser diode for each polarization encoded qubit. The behavior of a free-running laser diode at room temperature for a low-cost QKD framework has been studied. As discussed in [1], this work addresses the challenge of implementing decoy-state-based QKD using direct laser modulation by fine-tuning the shape of the injection. We have estimated theoretical parameters to control distinguishability for small-signal excitation, and have extended our analysis to include large-signal excitation by numerically solving the laser rate equation for the quantum well-based laser diodes. Furthermore, we have theoretically characterized the emission and explained its origin from a vacuum state. Trends predicted by theoretical estimation for small-signal excitation and numerical simulation for large-signal excitation agree with the experimental results, and indistinguishability of the signal and decoy state are quantified. Apart from discussing indistinguishability using these canonical coherent states, we have also explored the potential to implement such indistinguishable states using non-classical states.

2 Decoy state-based quantum key distribution

A weak coherent source (WCS) from an attenuated laser diode is a widely used photon source in QKD. In a single electromagnetic mode of the photon, coherent state \(|\alpha \rangle\) can be represented as (in the ideal case; practically, it will be a mixed state):

$$\begin{aligned} |\alpha \rangle =e^{-{\dfrac{|\alpha |^{2}}{2}}}\sum ^{\infty }_{n=0}\dfrac{\alpha ^{n}}{\sqrt{n!}}|n\rangle \end{aligned}$$
(1)

where \(\alpha\) is a complex number and n represents the single mode photon number

The density matrix for the coherent field state in the \(|n\rangle\) basis state can be written as

$$\begin{aligned} \rho =\sum \rho _{nm}|n\rangle \langle m| \end{aligned}$$
(2)

where

$$\begin{aligned} \rho _{nm}=\langle n|\alpha \rangle \langle \alpha |m\rangle =\dfrac{\alpha ^{n}\alpha ^{*m}}{\sqrt{n!m!}}e^{-|\alpha |^{2}} \end{aligned}$$
(3)

Then, the probability distribution \(P_{n}\) of an ideal coherent source in the number state can be expressed as

$$\begin{aligned} P_{n}=\rho _{nn}=\dfrac{|\alpha |^{2n}e^{-|\alpha |^{2}}}{n!} \end{aligned}$$
(4)

The theoretical bound for the probability of obtaining more than one photon can then be approximated from Eq. (4) as a conditional probability:

$$\begin{aligned} P_{multi-photon}&=\dfrac{1-P_{0}-P_{1}}{1-P_{0}}\nonumber \\& =\dfrac{1-e^{-|\alpha |^{2}}-|\alpha |^2e^{-|\alpha |^{2}}}{1-e^{-|\alpha |^{2}}}\nonumber \\& =\dfrac{1-e^{-|\alpha |^{2}}(1+|\alpha |^{2})}{1-e^{-|\alpha |^{2}}}\nonumber \\& \cong \dfrac{|\alpha |^{4}/2}{|\alpha |^{2}(1-\dfrac{|\alpha |^{2}}{2})}\nonumber \\& P_{wcs}\cong \dfrac{|\alpha |^{2}}{2} \end{aligned}$$
(5)

where \(\alpha\) is the eigenvalue of the destruction operator representing the mean number of the photon in a laser pulse, and \(P_{WCS}\) represents the probability of obtaining more than one photon in a weak coherent source approximation. This is one of the major drawbacks and a security flaw because the practical implementation of the coherent source emits multiple photons. Consequently, if Alice sends a multi-photon state to Bob, the eavesdropper can split the multi-photon state, retain one copy of Alice’s state and send the remaining state to Bob while selectively suppressing the signal state without being detected(photon number splitting attack). Finally, when Alice and Bob exchange basis selections on a public channel, Eve will have access to the entire/partial key.

In order to overcome this drawback, decoy-state-based QKD was proposed [5, 6, 15]. In a decoy-state implementation, for any given transmission, the sender, Alice, can send either a signal pulse or a decoy pulse to the receiver, Bob. The decision between using a signal state or the decoy state–which differs from the signal state only in terms of the average number of photons–, is made randomly by Alice. Due to this random selection of the signal state and the decoy state for a given transmission, the eavesdropper cannot identify whether the detected photon belongs to the signal state or the decoy state since these pulses differ only in terms of the mean number of photons but have indistinguishable characteristics such as pulse width, frequency, etc. Alice can transmit either a signal or decoy state to Bob by simply varying the mean number of the photon (intensity) of the Weak Coherent State pulse, as defined in Eq. (4). If \(Y_{j}\) represents the yield by Bob’s detector to a pulse sent by Alice containing j photons, i.e. the conditional probability of detection of the photon at Bob’s receiver when Alice sends a signal with j photons, then:

$$\begin{aligned} Y_{j}=1-(1-Y_{0})(1-\eta )^{j} \end{aligned}$$
(6)

where \(Y_{0}\) is the yield with zero photons, i.e. representing the dark count rate, and \(\eta\) is the transmission probability of a signal containing j photons. Considering the probabilistic distribution of photons in a weak coherent pulse, we can define the gain \(Q_{j}\) of detecting a pulse for Bob with j photons sent by Alice as

$$\begin{aligned} Q_{j}=Y_{j}P_{j} \end{aligned}$$
(7)

Thus, the overall gain or probability of a pulse at Bob’s receiver is

$$\begin{aligned} Q=\sum _{j}^{\infty }Q_{j} \end{aligned}$$
(8)

If \(\eta\) represents the overall efficiency of the bit transmission from Alice to Bob, including channel efficiency, then the error rate \(e_{j}\) of detecting a pulse with j photons, considering the setup efficiency, dark count error yield of \(e_{darkcount}\) and Bob’s detection efficiency \(e_{detector}\), is defined as

$$\begin{aligned} e_{j}=\dfrac{e_{darkcount}+e_{detector}\eta }{Y_{j}} \end{aligned}$$
(9)

The QBER (Quantum Bit Error Rate) \(E_{j}\) for each yield is given as

$$\begin{aligned} E_{j}=e_{j}Q_{j} \end{aligned}$$
(10)

and the overall QBER (EQ) is expressed as

$$\begin{aligned} E Q=\sum _{j}^{\infty }E_{j} \end{aligned}$$
(11)

Alice and Bob can experimentally determine the gain Q and the overall QBER EQ. Based on Eqs. 8 and 11, \(e_{j}\) and \(Y_{j}\) can be estimated for a pulse containing j photons, and acceptable ranges can be determined. Any attempt by Eve will affect \(e_{j}\) and \(Y_{j}\) beyond the acceptable range, thereby revealing her presence.

Based on the equation for yield and error rate, the secure key rate for WCS-based QKD can be written as [22]

$$\begin{aligned} S\ge q(-Q_{\mu }f(E_{\mu })H_{2}(E_{\mu })+Q_{1}[1-H_{2}(e_{1})]) \end{aligned}$$
(12)

where S is the key rate, q = the ratio of the signal state for both Alice and Bob to the total number of pulses sent by Alice. The mean photon number \(\mu\) depends on the injection current, \(Q_{\mu }\)is the fractional yield rate, and \(E_{\mu }\) represents the error rate of the signal state detected by Bob. \(Q_{1}\) and \(e_{1}\) are fractional yield and error rates of the decoy detection by Bob for a single-photon state. \(H_{2}\) is the Shannon information entropy, which represents a statistical fluctuation in error rate due to a pulse with \(\mu\) photons, and \(f(E_{\mu })\) represents the error correction function. \(Q_{\mu }, E_{\mu }\) can be determined as discussed in Eqs. 8–12.

Indistinguishability between the signal state and decoy state is one of the fundamental requirements in order to detect the presence of Eve. Consequently, Eve can only know the number of photons in each pulse detected but must not be able to differentiate between whether the photon detected was from the signal state or the decoy state. If the yield and the error rates are tightly bounded, it will then be possible to detect the presence of Eve because any attempt by Eve to detect these states will impact the statistical distribution of the signal and decoy states.

For the signal state and decoy state to be completely indistinguishable, they must have the same spatial, spectral and temporal behavior. One of the interesting ways to implement this is to use photons from resonantly excited systems, such as quantum dots and 2D materials [16], which results in Fourier transform limited characteristics of the emitted photon.

3 Non-classical states based indistinguishable coherent state generation

Schrodinger [29] introduced the coherent states in the context of a quantum harmonic oscillator with a minimum uncertainty product. Later, Glauber proposed them for studying photon statistics of arbitrary radiation fields [30]. Sudarshan introduced the coherent state as an overcomplete set of eigenstates of the destruction operator [31]. Meanwhile, Klauder proposed Overcomplete Families of States (OFS) for the continuous representation of Hilbert space [32]. Broadly, a set of generalized coherent states is an overcomplete set in Weyl–Heisenberg group [33]. For a Lie group G, if \({\hat{T}}(g)\) is a unitary representation and an irreducible representation operator, with \(g\in G\), and \(|\psi _i\rangle\) is a vector \(\in H\) space, then:

$$\begin{aligned} |\alpha \rangle ={\hat{T}}(g)|\psi _i\rangle \end{aligned}$$
(13)

represents a set of general coherent states {\(|\alpha \rangle\)}. For a vacuum state as an initial state i.e. \(|\psi _i\rangle = |0\rangle\), then {\(|\alpha \rangle\)} represents canonical coherent states (more discussion in Sect. 4).

Aligned towards Quantum Key Distribution, we now discuss different types of coherent states and explore numerous parameters to generate their indistinguishable states. Such indistinguishability will potentially open doors towards implementing decoy-state-based QKD using these coherent states.

3.1 Nonlinear coherent state-based indistinguishable states

The indistinguishable states can also be implemented using a special class of non-classical states called nonlinear coherent states (NCS). Equation (1) represents an ordinary coherent state in the number basis. These coherent states are the eigenstates of the annihilation operator. If we introduce the “distorted” creation and annihilation operators for f-oscillators [28] as

$$\begin{aligned} {\hat{A}}={\hat{a}}f({\hat{n}}) \end{aligned}$$
(14)

and

$$\begin{aligned} {\hat{A}}^\dagger =f({\hat{n}}){\hat{a}}^\dagger \end{aligned}$$
(15)

where f(\({\hat{n}})\) can be real or complex. For a selected f(\({\hat{n}}\)), NCS, a coherent state \(|\xi \rangle\) based on the “distorted” operators, can be expressed in the Fock state as

$$\begin{aligned} {\hat{A}}|\xi \rangle =\xi N_{\xi }\sum _{n=0}^{\infty }\dfrac{\xi ^{n}}{\sqrt{n!}}|n\rangle \end{aligned}$$
(16)

with \(N_{\xi }\) as the normalization fraction. Such NCS has been proposed to be implemented using ion-trapped in a harmonic potential, tuned by two laser fields [26, 27]. The eigenvalue \(\xi\) in Eq. 16 can be expressed in terms of Rabi frequency \(\Omega _{0}\) and \(\Omega _{1}\) of the laser fields as [26, 27]

$$\begin{aligned} \xi =\dfrac{i\Omega _{0}}{\eta \Omega _{1}} \end{aligned}$$
(17)

As evident from Eqs. 16 and 17, coefficients of the eigenstates and the photon number distribution of the NCS can be tuned using the laser Rabi frequency to generate indistinguishable states.

3.2 Para-Bose oscillator based indistinguishable states

Para-Bose oscillator has been introduced and thoroughly discussed in [34,35,36]. If we represent Hamiltonian \({\hat{H}}\) in terms of creation and annihilation operators as

$$\begin{aligned} {\hat{H}}=\dfrac{1}{2}({\hat{a}}^{\dagger }{\hat{a}}+{{\hat{a}}{\hat{a}}^\dagger }) \end{aligned}$$
(18)

where \({\hat{a}},{\hat{a}}^\dagger\) destroys and creates a boson with momentum p and satisfies the commutation relation:

$$\begin{aligned}{}[\hat{a_{p_i}},\hat{a_{p_j}}^\dagger ]=\delta _{p_{i},p_{j}} \end{aligned}$$
(19)

then, from Eq. 18 and Eq. 19, we can derive

$$\begin{aligned}{}[{\hat{a}},{\hat{H}}]={\hat{a}} \end{aligned}$$
(20)

Para-Bose coherent states can then be represented as an eigenstates of such para-bose operators, i.e.

$$\begin{aligned} {\hat{a}}|\alpha \rangle =\alpha |\alpha \rangle \end{aligned}$$
(21)

In Fock space representation with arbitrary minimum eigenvalue factor for \({\hat{H}}\) as \(k_0\), they can be expressed as [34]

$$\begin{aligned} |\alpha \rangle _{k_0}=\dfrac{1}{\sqrt{{f(|\alpha |^2)}}}\sum _n \sqrt{\dfrac{\Gamma (k_0)}{2^n\Gamma (\dfrac{n}{2}+1)\Gamma (\dfrac{n+1}{2}+k_0)}}\alpha ^n|n\rangle _{k_0} \end{aligned}$$
(22)

where f(x) is defined as

$$\begin{aligned} f(x)=\sum _n \dfrac{x^n\Gamma (k_0)}{2^n\Gamma (\dfrac{n}{2}+1)\Gamma (\dfrac{n+1}{2}+k_0)} \end{aligned}$$
(23)

Associated with these para-Bose states, Gilmore–Perelomov-type nonlinear coherent state has been studied by [37, 38]. In Fock space representation for first-order para-Bose state, this is expressed as

$$\begin{aligned} \begin{aligned} |\alpha , f\rangle&= e^{-|\alpha |^2/2}\sum _n \dfrac{2^n \alpha ^{2n}}{(2n)!}\sqrt{n!(\dfrac{p}{2})_n}F_1(\dfrac{1-p}{2}, n+\dfrac{1}{2};\dfrac{|\alpha |^2}{2})|2n\rangle\\&\quad + e^{-|\alpha |^2/2}\sum _n \dfrac{2^{n+1/2} \alpha ^{2n+1}}{(2n+1)!}\sqrt{n!(\dfrac{p}{2})_{n+1}}F_1(\dfrac{1-p}{2}, n\\&\quad +\dfrac{3}{2};\dfrac{|\alpha |^2}{2})|2n+1\rangle \end{aligned} \end{aligned}$$
(24)

\((p)_n=\dfrac{\Gamma (p+n)}{\Gamma (n)}\), \(F_1\) is the confluent hypergeometric function.

In one of the implementations, the analog of Gilmore–Perelomov-type nonlinear coherent states for the effective para-Bose oscillators has been proposed using a single trapped ion excited by two pairs of orthogonal lasers [39]. As seen from Eq. 24, parameter \(\alpha\) controls the coefficient of the eigenstates. In this analogous experimental implementation, it is related to the effective coupling strength g as \(\alpha =gt\). For a given para-Bose order, g can be tuned by the drive field strength. In an alternate implementation [37], Gilmore–Perelomov-type coherent states for the para-Bose oscillators can be realized using a two-level system interacting with a cavity and classical field with phase \(\phi\). If \(\gamma\) represents the coupling strength of the two-level system with the cavity, and \(\chi\) represents the coupling strength of the atom with the classical field, then the coefficient of eigenstates of the para-Bose coherent states can be tuned by controlling \(\phi , \gamma , \chi\). Moreover, \(\alpha\) in Eq. 24 and the photon distribution can be tuned by varying \(\gamma\) and \(\phi\). The possibility of generating indistinguishable analogs of Gilmore–Perelomov-type coherent states for the para-Bose oscillators can be explored by fine-tuning these parameters. A similar approach can be explored towards the generation of indistinguishable states using the Wigner Cat States that resemble the canonical coherent states for proper selection of Wigner parameter and the absolute eigenvalues [40].

4 Generation of indistinguishable canonical coherent states

Economical implementations of the signal/-decoy state have been analyzed in terms of Weak Coherent State (a canonical coherent state) by [1, 2]. The decoy state can be implemented either using an external intensity modulator with a dedicated driver circuit or by varying injected pump current in the laser diode [1]. In the former case, a separate optical attenuator and a dedicated driving circuit are needed. This impacts the overall form factor of the implementation and adds to cost. In the latter case, indistinguishability was lost due to relaxation oscillation of the laser diode and delay in emission with regard to the injected current. In addition, due to the distinguishability of the pulse generated from the injection current pumping technique, the security rate was zero, i.e., the transmission was insecure. The implementation mentioned in [2] requires two diodes for each basis state. Thus, for four basis states, eight diodes are needed in a specially constructed holder. This arrangement not only adds to the cost but also restricts the selection of eight laser diodes and the positioning of the laser diodes in the setup. In this study, for a smaller form factor and lower cost of implementation, we propose generating the indistinguishable signal and decoy state using direct modulation of the laser diode.

Direct modulation of the injection pumps current results in distinguishability of the signal and decoy states [1]. This distinguishability is due to relaxation oscillation and characteristic delay between the signals. Characterization of this relaxation oscillation has been widely described in detail [8, 13]. An increase in injection current increases photon emission; as a result, the electron carrier density rate decreases. At a certain electron density, the rate of generation of photons starts to decrease and the contribution of stimulated emission decreases, increasing carrier concentration. This cycle results in relaxation oscillation until it achieves a steady-state level. These distinguishable attributes in the pump current will have a signature in the laser’s output pulse, i.e., if there are multiple peaks in the injection current, the laser output will follow this profile.

We generate indistinguishable signal states and decoy states by direct modulation and temporal tuning of the injection current into an AlGaInP-based laser diode with heterojunction quantum well, as shown in Fig. 1.

Fig. 1
figure 1

General representation of a quantum well-based laser diode: current injection, spontaneous emission, stimulated emission, and intra-band relaxation change the carrier concentration and govern the emission rate from the laser diode. Above the injection threshold, stimulated emission dominates, and below the threshold, the phenomenon of spontaneous emission is dominant. Photon density in the active region builds up when emission overcomes the cavity loss. We have considered carrier lifetime \(\tau _{n}\) and photon lifetime \(\tau _{p}\)

Full size image

Lasers and it properties have been extensively discussed in [8, 13]. Exciton wave function: electrons in the conduction band and holes in the valence band at lattice point i and j in a quantum well, with the wave vector \(k_{e}\) and \(k_{h}\), can be represented as

$$\begin{aligned} |\psi (t)\rangle =|\psi ^{i,j}_{n}\rangle =\sum _{k_{e},k_{h},i,j}\psi _{k_{e},k_{h},i,j}|k_{e},i,k_{h},j\rangle \end{aligned}$$
(25)

In addition, the individual wave function of the electron and hole in the periodic lattice potential at a lattice point i and j, respectively can be expressed as the Fourier transform:

$$\begin{aligned} |\psi _{e,i}\rangle =\dfrac{1}{\sqrt{NV_{c}}}\sum e^{ik.R} \phi _{i}(r) \end{aligned}$$
(26)
$$\begin{aligned} |\psi _{h,j}\rangle =\dfrac{1}{\sqrt{NV_{c}}}\sum e^{ik.R} \phi _{j}(r) \end{aligned}$$
(27)

This represents a Bloch function where \(\phi\) represents the variation in local potential around the lattice point, r is the relative position of e-h pair, N is the number of cells, and \(V_{c}\) is the volume of the cell. For the exciton wave function, the density matrix can then be represented as

$$\begin{aligned} \rho =\sum _n P_n|\psi ^{i,j}_{n}\rangle \langle \psi ^{i,j}_{n}| \end{aligned}$$
(28)

Considering that the probability distribution \(P_n\) of the electron and hole are time-independent, the rate of change of density matrix representing the change in electron distribution can be represented as

$$\begin{aligned} \dfrac{d\rho }{dt}=\sum P_e\dfrac{|\psi _{e,i}\rangle }{dt}\langle \psi _{e,i}|+P_e|\psi _{e,i}\rangle \dfrac{d\langle \psi _{e,i}|}{dt} \end{aligned}$$
(29)

Based on the time-dependent Schrodinger equation and expressing Hamiltonian \(H_{e}\) for optical wave interacting with the electron in the quantum well as

$$\begin{aligned} H_{e}=\dfrac{1}{2m}(p-qA)^{2}+qU(r) \end{aligned}$$
(30)

where A is the vector potential associated with the electromagnetic field, U(r) is the potential energy of the electron, m and p are the mass and momentum of the particle, and for the isolated system, the time evolution of the density matrix representing the interaction between the optical wave and electron wave function in a laser cavity can then be derived as

$$\begin{aligned} \dfrac{\mathrm{d}\rho }{\mathrm{d}t}=\dfrac{1}{i\hbar }[H_{e}-er.E,\rho ] \end{aligned}$$
(31)

where \(H_{e}\) is the Hamiltonian of the electron, and r is the position vector. For the derivation of the rate equation, E is a classical electric field. Eq. 31 represents the interaction between optical wave and electron wave function in the laser cavity, resulting in stimulated emission, which further changes the electron distribution.

Current pumping in the laser diode results in population inversion. In addition, based on the dynamic equation for diagonal and off-diagonal elements, the rate of change of electron density in the conduction band due to light-matter interaction, intra-band relaxation, spontaneous emission, and current pumping can be expressed as [13]

$$\begin{aligned}&\dfrac{\mathrm{d}N_{cb}}{\mathrm{d}t}=N_{0}\sum _{cb}\dfrac{i}{h}(R_{nm}\rho _{mn}-\rho _{mn}R_{nm})E\nonumber \\&\quad -N_{0} \sum \dfrac{\rho _{nn}-\rho _{b}}{\tau _{b}} -N_{0}\sum \dfrac{\rho _{nn}-\rho _{0}}{\tau _{spon}}+N_{0}\sum _{i} \Delta _{i} \end{aligned}$$
(32)

where \(N_{cb}\) is the electron distribution in the conduction band, \(\Delta _{i}\) is the charge injection, \(N_{0}\) is the total electron density conduction and valence band, \(R_{nm}\) is the dipole moment of charge particles, \(\rho _{0}\) and \(\rho _{b}\) represents electron distribution at thermal equilibrium and quasi electron distribution at higher electron energy, respectively,\(\tau _{b}\) and \(\tau _{spon}\) are intra-band relaxation and spontaneous rate, respectively.

Considering the entire spatial volume of the active region, we can express the rate of change of electron density and photon density in terms of the following variables, as seen in Eq. (33), where n is the carrier concentration(same as electron distribution \(N_{cb}\)), I is the injected current, q is the charge, V is the volume of the active region, d is the thickness of the active region, \(\tau _{n}\) is the carrier lifetime, \(\tau _{p}\) is the photon lifetime in the cavity, \(\tau _{mode}\) is the radiative lifetime, \(n_{g}\) is the carrier concentration when the active region becomes transparent, \(\epsilon\) is the gain compression factor, a is the tangential coefficient, \(N_{s}\) is the photon concentration, \(\Gamma\) is the mode confinement factor.

Our analysis evaluates: (I) small-signal excitation around the steady-state value such that the laser injection current follows the step response near the threshold. Here, excitation is maintained above the threshold for a specific duration before turning off. Once the excitation is turned off, the steady-state value reached is below the threshold. This use-case emulates the behavior of the laser diode near its threshold region. (II) Another scenario is the large-signal excitation of the laser diode where the laser is pre-biased near the threshold, and then excited by a short-duration, large-signal excitation. This also models the behavior of the laser diode in [1] if the pre-bias current is set to zero. From Eq. (32), as discussed in [8], we can define the rate of change of electron distribution and photon output density for a single resonating mode as

$$\begin{aligned} \dfrac{\mathrm{d}n}{\mathrm{d}t}=-\dfrac{\Gamma a(n-n_{g})}{1+\epsilon N_{0}}N_{s}-\dfrac{n}{\tau _{n}}+\dfrac{I}{qV} \end{aligned}$$
(33)
$$\begin{aligned} \dfrac{\mathrm{d}N_{s}}{\mathrm{d}t}=\dfrac{\Gamma a(n-n_{g})}{1+\epsilon N_{0}}N_{s}+\dfrac{\Gamma \beta n}{\tau _{mode}}-\dfrac{N_{s}}{\tau _{p}} \end{aligned}$$
(34)

where

$$\begin{aligned} \dfrac{1}{\tau _{n}}=\dfrac{1}{\tau _{nr}}+\dfrac{1}{\tau _{mode}} \end{aligned}$$
(35)

with  \(\tau _{nr}\) being the non-radiative rate; in Eq. 33, \(\Gamma a\) is the gain coefficient, n is the electron distribution above the threshold where stimulated emission dominates and remains constant around the steady-state value. Furthermore, in the laser diode, Eq. 33 governs emission of the optical modes with different frequency range. First two terms represents the contribution to stimulated and spontaneous emission term due to the radiative recombination process of the electron transitioning from the conduction to the valence band [13]. If \(\beta\) represents the fraction of these optical modes that couples to the lasing mode, with non-trivial photon loss in cavity, the rate of change of the photon output density is described by Eq. (34).

For small-signal excitation, linearizing the change in electron distribution and output emission around its steady-state value, we can write

$$\begin{aligned}&\dfrac{d^{2}\Delta n}{dt^{2}}+ \left[\dfrac{1}{\tau _{n}}+\dfrac{\Gamma aN_{s}}{1+\epsilon (N_{s}+\Delta N_{s})}\right]\dfrac{\mathrm{d}\Delta n}{\mathrm{d}t}\\&\quad +\dfrac{\Gamma a N_{s}}{1+\epsilon (N_{s}+\Delta N_{s})}\dfrac{1}{\tau _{p}}\Delta n =0 \end{aligned}$$

where \(\Delta n\) is the small change in electron density in the conduction band and \(\Delta N_{s}\) is the corresponding change in photon density. Since \(\Delta N_{s}\) is smaller than \(N_{s}\), it can be ignored. On solving the second-order differential equation above, \(\Delta n\) can then be written as

$$\begin{aligned} \Delta n=\Delta n_{0} e^{-{\left[\dfrac{1}{2}\left(\dfrac{1}{\tau _{n}}+\dfrac{\Gamma a N_{s}}{1+\epsilon N_{s}}\right)-i\omega \right]t}} \end{aligned}$$
(36)

In Eq. (36), for \(t>0\), the secondary peak will attenuate with the increase in its real part. It is this behavior that we tune in order to suppress secondary peaks. Here,

$$\begin{aligned} \omega =\sqrt{\dfrac{\Gamma a N_{s}}{1+\epsilon N_{s}}\dfrac{1}{\tau _{p}}-\dfrac{1}{\tau ^{2}_{n}}-\dfrac{1}{4}\left[\dfrac{\Gamma a N_{s}}{1+\epsilon N_{s}}\right]^{2}-\dfrac{\Gamma a N_{s}}{2 \tau _{n}(1+\epsilon N_{s})}} \end{aligned}$$
(37)

if we represent \(N_{p}=\dfrac{\Gamma a N_{s}}{1+\epsilon N_{s}}\), we can then simplify \(\omega\) as

$$\begin{aligned} \omega =\sqrt{\dfrac{N_{p}}{\tau _{p}}-\dfrac{1}{\tau ^{2}_{n}}-\dfrac{N_{p}^{2}}{4}-\dfrac{N_{p}}{2 \tau _{n}}} \end{aligned}$$
(38)

For sub-threshold region:

$$\begin{aligned} N_{s}=\dfrac{\tau _{n}\tau _{p}\Gamma \beta I}{\tau _{mode} qV} \end{aligned}$$
(39)

above the threshold:

$$\begin{aligned} N_{s}=\dfrac{\tau _{p}}{qd} \left[\dfrac{Id}{V}-\dfrac{n_{sp}qd}{\tau _{n}}\right] \end{aligned}$$
(40)

From Eq. (36) to (40), secondary fluctuation in electron density will reduce as the injection bias current increases at \(t>0\). A similar relationship holds true for photon density and can be expressed as

$$\begin{aligned}&\dfrac{d^{2}\Delta N_{s}}{\mathrm{d}t^{2}}+\left[\dfrac{1}{\tau _{n}}+\dfrac{\Gamma aN_{s}}{1+\epsilon (N_{s}+\Delta N_{s})}\right]\dfrac{\mathrm{d}\Delta N_{s}}{\mathrm{d}t}\\&\quad +\dfrac{\Gamma a N_{s}}{1+\epsilon (N_{s}+\Delta N_{s})}\dfrac{1}{\tau _{p}}\Delta N_{s} =0 \end{aligned}$$

on neglecting the \(\Delta N_{s}\)

$$\begin{aligned} \Delta N_{s}=\Delta N_{0}e^{-[{\dfrac{1}{2}(\dfrac{1}{\tau _{n}}+\dfrac{\Gamma a N_{s}}{1+\epsilon N_{s}})-i\omega }]t} \end{aligned}$$
(41)

When excitation current below the threshold is injected into the laser diode, carrier concentration increases from a specific initial value \(n_{i}\) to a final value \(n_{f}\). This change in carrier concentration has an associated rise time, \(t_{r}\). When the increase in this carrier concentration is such that the spontaneous emission rate is more than the cavity loss in the active medium, based on Eq. (34) the photon concentration gradually increases. Above the threshold region, the electron concentration can be approximated to a constant value \(n_{constant}\). This rise time for the electron concentration where photon emission begins can be expressed as

$$\begin{aligned} t_{r}=\tau _{n} ln\dfrac{I-\dfrac{qVn_{i}}{\tau _{n}}}{I-\dfrac{qVn_{constant}}{\tau _{n}}} \end{aligned}$$
(42)

where \(\tau _{n}\) represents carrier lifetime and Eq. (42) can be interpreted as follows: If the injected current is very high with regard to the threshold, this rise time or characteristic delay in output emission theoretically approaches zero. Moreover, any other residual delay can be adjusted by a tunable laser driver [21, 24].

To further characterize emission from the laser diode: How do we prove that the output of such laser diodes can be realized as a (weak) coherent source? What are its origin and dynamics?

If the dipole moment d vector due to the injection current is written as

$$\begin{aligned} d(t)=e(r_{0}e^{i\omega t}+r^{*}_{0}e^{-i\omega t}) \end{aligned}$$
(43)

where \(r_{0}\) is the position vector associated with the electron and is expressed as a real quantity, then the interaction Hamiltonian from Eq. (43) can be written in terms of the quantized electric field operator \(E_{t}\) as

$$\begin{aligned} H_{interaction}(t)=d(t).E_{t} \end{aligned}$$
(44)

If \(\kappa\) is a propagation vector, \(\epsilon\) represents the polarization modes, and V represents quantization of the volume, we can write the quantized transverse electric field as

$$\begin{aligned} E_{t}=i\sum _{\kappa , \epsilon _{k}}\sqrt{\dfrac{\hbar \omega _{\kappa}}{2\epsilon _{0} V}}(a_{\kappa ,\epsilon _{k}} \epsilon _{k} e^{i\kappa \cdot R}-a_{\kappa , \epsilon _{k}}^{\dagger }\epsilon _{k}e^{-i \kappa \cdot R}) \end{aligned}$$
(45)

with the Hamiltonian for the charge particle and free field expressed as

$$\begin{aligned}&H_{0} = -\dfrac{\hbar ^{2}}{2m_{e}}\nabla ^{2}_{Re} -\dfrac{\hbar ^{2}}{2m_{h}}\nabla ^{2}_{Rh}-\dfrac{e^{2}}{\epsilon |r_{e}-r_{h}|}\nonumber \\&\quad +\sum _{\kappa }\hbar \omega _{\kappa }(a^{\dagger }_{\kappa }a_{\kappa }+\dfrac{1}{2}) \end{aligned}$$
(46)

The eigenvalue equation is

$$\begin{aligned} H_{0}|n\rangle = E_{n} |n\rangle \end{aligned}$$
(47)

so the overall Hamiltonian can be written as

$$\begin{aligned} \begin{aligned}&H_{total} =H_{0}-\mathrm{d}(t)\cdot i\sum _{\kappa , \epsilon _{k}}\sqrt{\dfrac{\hbar \omega _{\kappa}}{2\epsilon _{0} V}}(a_{\kappa ,\epsilon _{k}} \epsilon _{k} e^{i\kappa \cdot R}\\&\quad -a_{\kappa , \epsilon _{k}}^{\dagger }\epsilon _{k}e^{-i \kappa \cdot R}) \end{aligned} \end{aligned}$$
(48)

In the Dirac interpretation, the Hamiltonian can then be written as

$$\begin{aligned}&H_i(t)=e^{iH_{0}t/\hbar } H_{interaction}(t) e^{-iH_{0}t/\hbar } \end{aligned}$$
(49)
$$\begin{aligned}&H_{i}(t)= -d(t)\cdot i\sum _{\kappa , \epsilon _{k}}\sqrt{\dfrac{\hbar \omega _{\kappa}}{2\epsilon _{0} V}}(e^{iH_{0}t/\hbar }a_{\kappa ,\epsilon _{k}}e^{-iH_{0}t/\hbar } \epsilon _{k} e^{i\kappa \cdot R}\nonumber \\&\quad -e^{iH_{0}t/\hbar }a_{\kappa , \epsilon _{k}}^{\dagger }e^{-iH_{0}t/\hbar }\epsilon _{k}e^{-i \kappa \cdot R}) \end{aligned}$$
(50)

In the interaction picture, the time evolution of the quantum state is obtained from the time-dependent Schrodinger equation:

$$\begin{aligned} i\hbar \dfrac{d}{dt}|\psi (t)\rangle =H(t)|\psi (0)\rangle \end{aligned}$$
(51)

Considering the vacuum state as the initial state, the solution to Eq. (51) can be represented as

$$\begin{aligned} |\psi (t)\rangle =U(t,t_{0})|0\rangle \end{aligned}$$
(52)

Due to the injection current profile, the Hamiltonian at time \(t_{1}\) and \(t_{2}\) is such that \([H(t_{1}),H(t_{2})]\ne 0\), therefore, U(t,\(t_{0}\)) can be expressed in terms of the Dyson series as

$$\begin{aligned} \begin{aligned}&U(t,t_{0})=I+\sum _{n=0}^{\infty }[-\dfrac{i}{\hbar }]^{n}\int _{t_{0}}^{t}dt_{1} \int _{t_{0}}^{t_{1}}\mathrm{d}t_{2}\cdot \cdot \cdot \cdot \\&\quad \int _{t_{0}}^{t_{n-1}}\mathrm{d}t_{n}H(t_{1})H(t_{2})\cdot \cdot \cdot \cdot ~H(t_{n}) \end{aligned} \end{aligned}$$
(53)

From Eq. (53), the limit of the integration determines the integration variable in a later instance for \(t_{n}\) and so on. In order to avoid this, we can re-write it in terms of the time-product of operators as

$$\begin{aligned} \begin{aligned}&U(t,t_{0})=I+\sum _{n=0}^{\infty }\dfrac{1}{n!}[-\dfrac{i}{\hbar }]^{n}\int _{t_{0}} ^{t}\mathrm{d}t_{1}\int _{t_{0}}^{t}\mathrm{d}t_{2}\cdot \cdot \cdot \cdot \\&\quad \int _{t_{0}}^{t}\mathrm{d}t_{n}T[H(t_{1})H(t_{2}) \cdot \cdot \cdot \cdot ~H(t_{n})] \end{aligned} \end{aligned}$$
(54)

or,

$$\begin{aligned} U(t,t_{0})=Te^{-\dfrac{i}{\hbar }\int _{t_{0}}^{t}H(t)\mathrm{d}t} \end{aligned}$$
(55)

where T is the time-ordered product operator.

$$\begin{aligned} |\psi _i(t)\rangle = Te^{-\dfrac{i}{\hbar }\int _{t_{0}}^{t}H(t)\mathrm{d}t}|0\rangle \end{aligned}$$
(56)

and the exponential term can be expressed following the approach discussed in [18]:

$$\begin{aligned} -\dfrac{i}{\hbar }\int _{0}^{t}H_{i}(t)dt=\sum _{\kappa ,\epsilon _{k}}[-\alpha ^{*}_{\kappa}(t)a_{\kappa,\epsilon_k} +\alpha _{\kappa}(t)a^{\dagger }_{\kappa,\epsilon_k }] \end{aligned}$$
(57)

where

$$\begin{aligned}&\alpha ^{*}_{\kappa}(t)=\dfrac{1}{\hbar }\sqrt{\dfrac{\hbar \omega _{\kappa}}{2\epsilon _{0} V}}\int _{0}^{t}\mathrm{d}t \mathrm{d}(t)\cdot\epsilon _{k} e^{i(\kappa\cdot R-\omega_\kappa t)} \end{aligned}$$
(58)

from Eq. (56) to (58):

$$\begin{aligned} |\psi _{i}(t)\rangle = Te^{\sum _{\kappa , \epsilon _{k}}[-\alpha _{\kappa}^{*}(t)a_{\kappa}+\alpha _{\kappa}(t)a_{\kappa }^{\dagger }]}|0\rangle \end{aligned}$$
(59)

or

$$\begin{aligned} |\psi _{i}(t)\rangle =T\prod _{\kappa,\epsilon_k }e^{[-\alpha _{k}^{*}(t)a_{k}+\alpha _{k}(t)a_{\kappa }^{\dagger }]}|0\rangle \end{aligned}$$
(60)

in terms of the displacement operator:

$$\begin{aligned} |\psi _{i}(t)\rangle =\prod _{\kappa,\epsilon_k }D_{\kappa,\epsilon_k }|0\rangle \end{aligned}$$
(61)

From Eq. (61), in a laser diode, a displacement operation on a vacuum state due to current injection results in multi-mode coherent state emission. To understand the dynamics of evolution of the vacuum state, if we define the scattering matrix as

$$\begin{aligned} S(t',t)=U(t,0)U^{\dagger }(t',0) \end{aligned}$$
(62)

we can write S(t',t) as

$$\begin{aligned} \begin{aligned}&S(t',t)=I+\sum _{n=0}^{\infty }\dfrac{1}{n!}[-\dfrac{i}{\hbar }]^{n}\int _{t'}^{t}\mathrm{d}t_{1}\int _{t} '^{t}dt_{2}\cdot \cdot \cdot \cdot \\&\quad \int _{t'}^{t}dt_{n}T[H(t_{1})H(t_{2})\cdot \cdot \cdot \cdot ~H(t_{n})] \end{aligned} \end{aligned}$$
(63)

We can then define two-particle zero-temperature Green’s function(or causal Green’s function):

$$\begin{aligned} \begin{aligned}&G(x_{1},t_{1};x_{2},t_{2};x_{1}^{'},t_{1}^{'};x_{2}^{'},t_{2}^{'})\\&\quad =-i\langle GS|T[a_{x_{2}^{'}}(t_{2}^{'}) a_{x_{1}^{'}}(t_{1}^{'})a_{x_{1}}^{\dagger }(t_{1})a_{x_{2}}^{\dagger }(t_{2})]|GS\rangle \end{aligned} \end{aligned}$$
(64)

Since the ground state of the non-interacting Hamiltonian is calculated based on the Schrodinger equation, it is an eigenstate of the non-interacting Hamiltonian. Thus, \(\langle GS|\), the eigenstate of the overall Hamiltonian, comprising of non-interacting and interacting Hamiltonian, is then estimated using the Gell-Mann and Low equation [20]:

$$\begin{aligned} |GS\rangle ={{\hat{S}}}(0,-\infty )|0\rangle \end{aligned}$$
(65)

For the electron–hole pair (EHP), Eq. (64) can be written in terms of creation and annihilation operators as

$$\begin{aligned} \begin{aligned}&G(x^{'},t^{'};x,t)\\&\quad =-i\langle GS|T[a_{x^{'}}(t^{'}) a_{x^{'}}(t^{'})a_{x}^{\dagger }(t)a_{x}^{\dagger }(t)]|GS\rangle \end{aligned} \end{aligned}$$
(66)

Physical interpretation of Green’s function [19] for EHP can be visualized from Eq. (66). EHP is created at time  \(t(t^{'}> t)\). EHP then propagates through the system, as the resulting state is not the overall Hamiltonian eigenstate. At \(t'\), EHP is removed from the system by annihilation operators. Writing operators in an interaction picture, we can then express Green’s function in terms of S-matrix, with electron and hole momentum as |k| as

$$\begin{aligned} \begin{aligned}G(x^{'},t^{'};x,t) &=-i\langle 0|T[{{\hat{S}}}(0,\infty ){{\hat{S}}}(\infty ,t)a_{-k}(t^{'})a_{k}(t^{'}){{\hat{S}}}(t,t')\\& a_{-k}^{\dagger }(t)a_{k}^{\dagger }(t)]{{\hat{S}}}(t',0) {{\hat{S}}}(0,-\infty )|0\rangle /(\langle 0|{{\hat{S}}}(\infty ,-\infty )|0\rangle ) \end{aligned} \end{aligned}$$
(67)

A Feynman diagram for spontaneous emission can then be represented from Eq. (67) as

Fig. 2
figure 2

Feynman diagram for spontaneous emission from EHP recombination. EHP with momentum |k| annihilates at time \(t'\) to emit photon of wavelength \(\lambda\)

Full size image

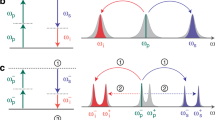
An EHP with momentum |k| annihilates at time \(t'\) to emit a photon of wavelength \(\lambda\). When the emission rate builds up, the photon density increases before a steady value of carrier density and photon density is reached. Then, an increase in photon density results in EHP reduction due to recombination. Further, the spatial coherence of the emission is ensured by selecting the cavity such that the emission wavelength is near the spectral peak, resulting in the narrow spectrum of the laser emission (Fig. 2).

5 Numerical simulation

We applied a large-step excitation to the laser diode under study (Fig. 3). This condition was simulated [25] by solving the rate equation using Euler’s iterative method for parameters defined as

Fig. 3
figure 3

Parameters defined for the laser diode simulation

Full size image
Fig. 4
figure 4

Simulation of large-signal step function: if the step function is turned off at  1.5ns, the responses will resemble a pulse excitation with two peaks

Full size image

Figure 4 represents the response of the carrier and photon concentration when the laser diode is excited by the large-signal step function. It can be observed that photon concentration follows the carrier concentration graph with some delay. Had this excitation been turned off at 1.5 ns, it would have resembled the excitation profile described in [1]. In order for the decoy state described in [1] to be indistinguishable from the signal state, the secondary peak of the signal state must cease to exist; otherwise, the decoy state will have one peak, while the signal will have two peaks. Following the trend predicted by Eqs. (36) and (41) for small-signal excitation and Fig. 4 for large-step excitation, Fig. 5 represents the solution to the rate equation under a large-signal excitation profile with a short-duration pulse and a non-zero bias current.

Fig. 5
figure 5

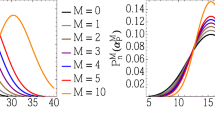
Simulation of relaxation oscillation for different values of injection current. a The change in carrier concentration and photon concentration when the laser diode is excited by a short-duration pulse, with the pre-bias current of 13 mA, i.e., below the threshold. b The change in carrier concentration and photon concentration when the laser diode is excited by a short-duration pulse, with the pre-bias current of 20 mA, i.e., above the threshold. As seen from a and b, the amplitude of the secondary oscillation peak decreases when the pre-bias current is increased. The difference between the primary peak and secondary peak also increases

Full size image

We have considered two simulation models: In the first model, the constant pre-bias current is defined as \(< I_{threshold}\), Fig. 5a. In the second model, the pre-bias is current defined as \(> I_{threshold}\), Fig. 5b. No other simulation parameters were varied. Perturbation of duration 2 ps was then superimposed on the pre-bias current, and the relaxation oscillation due to the perturbation was characterized. It was ensured that the perturbation is applied at \(t>>0\) so that the response due to perturbation was not affected by initial startup transients. In Fig. 5, the amplitude of secondary oscillation decreases as the injection current increases, and the difference between the primary amplitude and the amplitude of secondary oscillation increases as the injection current increases. This result correlates with the estimation made in Sect. 2 for the small-signal consideration (Initial transients seen in the waveform are due to switching of pre-bias current.) Consequently, to suppress the peak of the secondary oscillation, the pre-bias current must be increased. The driver circuit can filter any residual peak.

6 Experiment

Fig. 6
figure 6

Experimental setup for the characterization of laser diode: Emission from a tuned laser diode is detected using an avalanche photo-diode (APD) biased in the linear region. An oscilloscope measures the differential current into the laser diode and response from the APD. The threshold current of the laser diode is  18.4 mA

Full size image

The measurement setup, as shown in Fig. 6 comprises a transmitter. We developed a tunable laser driver [21, 24] capable of generating dc bias superposed on modulated sub-nanosecond injection current into a HL6748MG laser diode at room temperature. It was our aim to create a laser diode with as low a cost as possible and with a minimal form factor. Measurement was carried out without using a constant optical attenuator because weak photon pulses in a single-photon regime will follow the same characteristics as the un-attenuated pulse. The polarization basis of the photon is selected using a polarizer and half-wave plate. We developed a SAP500 APD-based detector capable of measuring photons in linear mode and Geiger mode for detection.

The injection current through the laser diode was measured using differential probe D420-A-PB with 4 GHz DX20 tip connected to a 4 GHz, Lecroy 640Zi Waverunner. This interface has a rise time of 122.5 ps. The output of the APD was interfaced to the same oscilloscope with active probe ZS2500, 2 GHz bandwidth; the rise time of the interface was  175 ps. In addition, considering the 500 ps rise/fall time of the APD, sharp peaks in the ideal waveform of the period  300 ps will still be observed, albeit not as sharp as reported in [1].

7 Results

Figure 7 represents a differential current profile measured across terminals of the laser diode when excited by a peak current pulse of near-threshold amplitude. A secondary peak due to relaxation oscillation at 800 ps can be observed.

Fig. 7
figure 7

Differential profile across the laser diode terminal. The graph has been averaged over 1500 samples

Full size image

Bandwidth limitation in the setup will affect the absolute accuracy of the rise time and periods of the peaks due to the comparatively slow rise time of the probe cable and the detector. In Fig. 7, we are expecting relaxation oscillation so why is the secondary peak higher than the primary peak? Our measuring probe rise time (122.5 ps) is more than the pulse’s actual rise/fall time, which positively offsets the measurement. In order to produce an indistinguishable signal state and decoy state, this profile must be indistinguishable, i.e., a secondary peak in this waveform must be suppressed.

Figure 8 represents the variation of the peak of secondary oscillation as a function of the injected current (no additional electronic filter was implemented). As observed, the magnitude of the injected bias current and the amplitude of the secondary peak is inversely related. For the injected bias current above the threshold, the amplitude of the secondary peak is non-zero. On implementing an electronic filter in the laser driver, the secondary peak was further reduced and approached zero for the injected current of 11 mA (Fig. 9).

Fig. 8
figure 8

Variation of the oscillation peak as a function of the injected dc bias current (without filters). As observed, the secondary oscillation peak is still non-zero. This secondary peak must be suppressed to zero and should approach zero or below

Full size image

The difference between the amplitude of the primary and secondary peaks increases with the biased current near the threshold value (Fig.10) due to a reduction in the amplitude of the secondary peak and an increase in the magnitude of the primary peak.

Fig. 9
figure 9

Variation of the oscillation peak as a function of the injected dc bias current (with filters). The non-zero peak is suppressed at approximately 11 mA

Full size image

Figure 11 represents a numerical simulation result for estimating the variation in difference between the primary and secondary peaks, which increases with the injection current.

Fig. 10
figure 10

Variation of the difference in the signal peak and secondary oscillation (without filters). As the current injection increases and approaches the threshold level, the difference the between the primary and secondary oscillation peaks increases

Full size image
Fig. 11
figure 11

Simulation of the variation of difference in the signal peak and secondary oscillation. As compared with Fig. 10, the trend observed in the measurement result is corroborated in simulation. The difference between the amplitude values for the measurement and the simulation can be attributed to deviations in the simulation model from the actual device values

Full size image
Fig. 12
figure 12

Variation of the peak of secondary oscillation (simulation result). The trend observed during measurement, as seen in Figs. 9 and 8 is corroborated by simulation

Full size image

Further, Fig. 12 represents the numerical simulation result of variation in the amplitude of the secondary peak, which decreases as the injection current into the laser diode increases.

8 Discussions

The voltage drop across the APD series resistor of 500 K was 10 V, corresponding to the maximum permitted APD current of 200 μA. With sub-nanosecond peak pulse emission from the laser diode, with power of  120 mW, the overall coupling efficiency of 2.5\(\%\), the APD load resistor in the range of around 50 ohm and responsivity of 14.8 A/W for 672 nm wavelength, the expected output voltage on the oscilloscope considering attenuation due to probes, is around 555 mV (Fig. 13). Thus, the graph plotted in Fig.14 looks reasonable (Fig. 15).

Fig. 13
figure 13

The current profile for the signal state is measured across the laser diode. Pre-bias current is maintained above the laser threshold level. The peak current injected into the laser diode is less than the absolute maximum rating of 45 mA

Full size image

Figure 16 represents the APD output response for the laser diode pre-biased near the current threshold level. Comparing it with Fig. 14, the light pulse profile looks similar, hence is indistinguishable in shape. Side bumps observed in Fig.14 and 16 are due to parasitic impedance on the transmitter and receiver PCB. The limited bandwidth of the APD and probes results in some positive offset instead of the expected zero line at 5 ns.

Fig. 14
figure 14

APD output for the laser diode biased near the threshold at 19.3 mA bias current. Multiple oscillations are due to the large inductance in the receiver. The voltage drop across the APD series resistor of 500 K was 10 V, which corresponds to 200 μA of APD current. With sub-nanosecond peak pulse emission from the laser diode, the power is  120 mW. Considering the overall coupling efficiency of 2.5\(\%\), with 50-ohm (+/- tolerance) APD load resistor and responsivity of 14.8 A/W for 672 nm wavelength, the expected output voltage on the oscilloscope is around 555 mV

Full size image
Fig. 15
figure 15

Current injection profile for the decoy state measured across the laser diode. The pre-bias level is maintained near the threshold level, with the peak current reaching 37 mA

Full size image
Fig. 16
figure 16

APD output for the laser diode is biased near the threshold (at 15 mA bias current). Multiple oscillations are due to the large inductance, and the appearance of a double peak above the threshold is due to the delay introduced by the oscilloscope probe. The profile with the pre-bias current of 19.3 mA (Fig. 14) and the profile for the pre-bias current of 15 mA are the same

Full size image

Another factor that can distinguish these pulses is the delay between the signal and the decoy state. As observed in Eq. (42), the delay between the laser excitation and the laser output depends on the current injection. Based on Figs. 14 and 16, the relative delay between two output pulses is around 400 ps. This can be attributed to the difference in injection current, which governs the delay between carrier density and photon emission. Moreover, from Figs. 13 and 14, the absolute delay between the laser excitation pulse and the output of the APD is in the range of ns. This can be attributed to the distance of the APD from the laser (3.3 ns), the APD response time, and the rise time of the probe. Furthermore, in the implementation, the decoy state can be achieved by varying the pre-bias current level or the magnitude of the perturbation pulse [24].

Fig. 17
figure 17

Comparison of the signal state and the decoy state. Amplitude has been normalized in the graphs. Relative delay between the response has been ignored so that peaks of both the responses are temporally aligned for better comparison. Any PCB-relevant parasitic oscillations have been eliminated at the zero reference level

Full size image

In addition, we statistically evaluated the distributions shown in Fig. 17 using the Kolmogorov–Smirnov test. The estimated p-value is 0.999664, i.e., greater than 0.05. Therefore, we can accept the hypothesis that both of these responses came from the same distribution, i.e., both are indistinguishable. In addition, Fig. 18 represents the cumulative distribution function for the signal state and the decoy state.

Fig. 18
figure 18

The cumulative distribution function for the signal state and the decoy state. Based on p value = 0.999664050220288 and statistic = 0.024875621890547265, it can be concluded that both the signal state and the decoy-state data belong to the same distribution

Full size image

In this paper, we have considered indistinguishability in the temporal domain only. Distinguishability in the spectral domain during a transient process can occur due to pump current excitation or when an external optical modulator is used for optical pulse generation [7]. It has been observed that the shift depends on the magnitude of current change, laser pre-bias condition, and oscillation damping rate. It will be of great interest to understand how the pre-bias current in our approach reduces drift in the signal’s wavelength and the decoy state.

9 Conclusion

We analyzed the cause of distinguishability between the signal state and the decoy state in a pump modulated laser diode. Further, theoretical derivation for the stimulated emission originating from the vacuum state explains coherent state emission in a laser diode. We have further demonstrated indistinguishability of the signal and the decoy state by suppressing relaxation side peaks. The proposed relaxation oscillation suppression technique will be of interest in implementing two-photon interference [23] and reducing transient chirps for indistinguishability in the frequency domain.