1 introduction

Quantum entanglement plays a very important role in quantum information processing. As the most important physical resource, it has been widely applied in quantum computation [1], quantum teleportation [2,3,4], quantum key distribution (QKD) [5], and biological organisms [6], etc. Although there has been a remarkable progress on the entangled state of bipartite entanglement, multipartite entanglement state has also attracted considerable attention with its more complex and diverse entangled structures. When the particles of multiparticle entangled state exceeds two, there are many different kinds of states: for instance W states [7], GHZ states [8], and cluster states [9], etc. These inequivalent classes of states can not be converted into each other with stochastic local operations and classical communication (SLOCC) [10]. In these entangled states, the W state has attracted increasing interest for its usefulness in the entanglement robust against particle loss [7]. For the maximally entangled W state, the loss of any particle does not affect the remaining particles to form the entanglement. Because of this property, W state has been widely concerned in the field of quantum information [11,12,13,14,15,16,17].

As the current most popular preparation scheme, the quantum state expansion and fusion technology are seen as an effective way to generate large-scale maximally entangled W states [18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Especially the fusion scheme, it has attracted considerable attention in its obviously increase the particles of final W state by fusing two or more initial W states, simultaneously. The expansion scheme receives less notice because it can only add one or two particles to the initial W state at a time. In recent studies, the premise of most current fusion schemes is that only one particle can be extracted from each seed entangled state to achieve the fusion process. This fusion idea of W states was first proposed by Ozdemir et al. in 2011, with which a \(W_{n+m-2}\) state can be generated by fusing two initial small-size W states (\(W_n\), \(W_m\), \(n,m \ge 3\)) [18]. Motivated by this idea, several new preparation schemes of W state fusion with the help of controlled quantum gates and ancilla particles have been proposed in optical system [25,26,27]. The other preparation schemes also have been proposed conditioned on the same idea which one particle from each initial W state is permitted to enter the different fusion system. For example, in 2015, Han et al. proposed a scheme to fuse one \(W_{m+n-1}\) from one \(W_n\) and one \(W_m\) via the weak cross-Kerr nonlinearities [32]. In 2016, Zang et al. presented scheme to prepare a \(W_{m+n-2}\) state from one \(W_n\) and one \(W_m\) in cavity QED [33]. In 2018, Li et al. designed a scheme to create a \(W_{m+n+t-1}\) state by fusing a \(W_n\), a \(W_m\) and a \(W_t\) states with an H-polarized ancilla photon in optical system. In 2020, Bugu et al. created an electric \(W_{m+n-2}\) state with a success probability of \((n+m-2)/nm\) based on Pauli spin blockade in DQD devices [34]. Wei et al. have proposed a scheme for fusing \(|W\rangle _n\) and \(|W\rangle _m\) states into a large-size \(|W\rangle _{n+m-1}\) state using a partial-swap gate [35]. Based on the polarization-dependent beam splitter (PDBS), Li et al. propose an optical scheme to fuse small-size polarization entangled W states into a large-scale W states, and two \(|W\rangle _{n+m+t-2}\), two \(|W\rangle _{n+m+t+q-3}\) can be generated [36]. But in most of these fusion schemes, one or more particles entering the fusion mechanism must be measured so as to complete the whole fusion process. This qubit loss will inevitably lead to the result that the number of the final entangled particles is smaller than the sum of numbers of the input entangled particles, which will inevitably decrease the fusion efficiency and increase the number of fusion steps.

Recently, the currently existing fusion schemes focus on how to realize the qubit-loss-free fusion scheme for fusing W states. For example, in 2016, Yang Ming research group first proposed a universal approach of QLF fusion scheme to prepare a large-scale W state which is based on a two-outcome positive-operator valued measurement(POVM) on two qubits extracting from two small-size W states [37]. Motivated by this idea, Wang et al. proposed a QLF fusion scheme for fusing three polarization entangled W states simultaneously [38]. Subsequently, Ding et al. proposed the QLF fusion schemes in cavity QED system based on the resonant interaction between the atoms and the cavity modes [39]. In the same mechanism, Li et al. proposed a qubit-loss-free fusion scheme to prepare larger-scale atom W state by fusing three or four small-scale entangled states on the condition that one or two qubit of each W state is permitted to enter the fusion mechanism [40]. In 2021, Zheng et al. proposed three schemes to generate polarization W-states of size \(n+m\), \(n+m+t\), and \(n+m+t+z\) without qubit loss via weak cross-Kerr nonlinearities [41].The most obvious advantages of this QLF fusion scheme is that it clearly increase the fusion efficiency and greatly reduces the number of fusion steps.

Motivated by the idea in Ref. [39], we design a QLF fusion scheme for preparing large-scale W states by fusing n different or same particles W states in cavity quantum electrodynamics (QED) system. Although the QLF fusion scheme of fusing three W states seems realized in Ref. [39], the essence of the scheme is still the fusion of two W states: the first target W state which is prepared from the first two initial W states in the previous cavity mode, will be fused with the third initial W state in the next cavity mode, then the final W state can be obtained. Hence, the fusion scheme of the three W states in Ref. [39] was not really achieved, simultaneously. In our scheme, we have made a few improvements that access two atoms from the initial W state. The \(W_{n+m+q}\) states can be prepared by fusing state \(W_m\), \(W_n\) and \(W_q\) and we also generalized this QLF fusion scheme to the case of fusing n W states, simultaneously when adding \((n-1)\) cavity fields.

2 Three small-size W states fusion

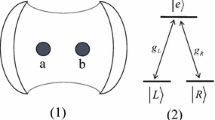
In this section, the QLF fusion scheme for fusing three small-size W states to a large-scale W state will be introduced. The key component of our fusion mechanism is based on the atom–cavity–field resonant interactions. As shown in Fig. 1, two identical \(\Lambda\)-type three-level atoms a and b are trapped in a resonant optical cavity, each with an excited state \(|e\rangle\) and two degenerate ground states \(|R\rangle\) and \(|L\rangle\). The \(|e\rangle \leftrightarrow |R\rangle\) transition is coupled by right-circularly polarized light, while the \(|e\rangle \leftrightarrow |L\rangle\) transition is coupled by left-circularly polarized light. We assume that the distance between the two atoms is large compared with the wavelength of the \(|e\rangle \leftrightarrow |R\rangle\) or \(|e\rangle \leftrightarrow |L\rangle\) transition so that the dipole–dipole interaction can be neglected. Under the rotating-wave approximation (RWA), the interaction Hamiltonian \(H_I\) of the total system is given by [42]

$$\begin{aligned} H_{I}=i\hbar \sum _{i=a,b}\sum _{\lambda =R,L}(g_\lambda c_\lambda |e\rangle _{ii}\langle \lambda |-g_\lambda c_\lambda ^\dagger |\lambda \rangle _{ii}\langle e|) \end{aligned}$$
(1)

where \(g_\lambda\) (\(\lambda =R,L\)) represents the coupling constants between the atom and the corresponding polarized photons, \(c_\lambda\) and \(c_\lambda ^\dagger\) (\(\lambda =R,L\)) represent the annihilation and creation operators for the right-circularly or left-circularly polarized, \(|e\rangle _i\) (\(i = a, b\)) represents the excited state of the atom a or b, \(|\lambda \rangle _i\) (\(i = a, b; \lambda = L, R\)) represents the “left” or “right” ground state. In order to simplify the process, we define the single mode cavity field state is in \(|R\rangle\) and \(|L\rangle\) rather than \(|0\rangle\) state, and assume that the cavity field is prepared in the \(|R\rangle\) state initially. Therefore, the four basic evolutions induced by the Hamiltonian in Eq. (1) can be expressed as follows [39]:

$$\begin{aligned} |R,R;R\rangle \rightarrow&k_4|R,R;R\rangle +k_5(|L,R;L\rangle +|R,L;L\rangle ) \nonumber \\ |R,L;R\rangle \rightarrow&k_1|L,L;L\rangle +k_2|R,L;R\rangle +k_3|L,R;R\rangle \nonumber \\ |L,R;R\rangle \rightarrow&k_1|L,L;L\rangle +k_3|R,L;R\rangle +k_2|L,R;R\rangle \nonumber \\ |L,L;R\rangle \rightarrow&|L,L;R\rangle \end{aligned}$$
(2)

where

$$\begin{aligned}&k_1=-\frac{2g_Lg_R}{\alpha ^2}sin^2\frac{\alpha t}{2} k_2=cos^2\frac{g_Rt}{2}-\frac{g_R^2}{\alpha ^2}sin^2\frac{\alpha t}{2}\nonumber \\&\quad k_4=\frac{2g_R^2cos\beta t+g_L^2}{\beta ^2} k_3=sin^2\frac{g_Rt}{2}-\frac{g_R^2}{\alpha ^2}sin^2\frac{\alpha t}{2}\nonumber \\&\quad k_5=-\frac{2g_Lg_R}{\beta ^2}sin^2\frac{\beta t}{2} \nonumber \\&\quad \alpha =\sqrt{2g_L^2+g_R^2} \beta =\sqrt{2g_R^2+g_L^2} \end{aligned}$$
(3)

It should be emphasized that the detection and selection of target W states are based on the cases where there is only one photon in the cavity mode during the process of temporal evolution, hence, the terms with the cavity mode in \(|0\rangle\) state has been neglected.

Fig. 1
figure 1

Resonant interaction between atom, cavity and field: \(|e\rangle\) is the excited state, \(|R\rangle\) and \(|L\rangle\) are the two degenerate ground states, \(g_R\) and \(g_L\) are the coupling constants between the atom and the right-circularly or left-circularly polarized field

Full size image

In Ref. [39], only one particle can be extracted from each W state to input the cavity mode, but with the progress of experimental technology, two particles can be extracted. Motivated by this idea, we propose a new QLF fusion scheme for fusing three or four W states simultaneously, by accessing one or two atoms from each W state. The scheme for fusing three W states in Ref. [39] is actually divided into two parts: One part is the first cavity mode A with fusing the two W states (\(|W\rangle _n\), \(|W\rangle _m\)). Another part is the fusion scheme of the third W state (\(|W\rangle _q\)) with the generated W state in one part (\(|W\rangle _{n+m}\)) in the cavity mode B. That is to say, the fusion scheme of the three W states was not really achieved simultaneously. Based on the fusion method presented in Ref. [39], we have propose the new fusion scheme of a few improvements that access two atoms from the \(|W\rangle _m\) state. One atom together with the atom from \(|W\rangle _n\) state is sent into the cavity A, another atom with the atom from \(|W\rangle _q\) state is input into the cavity B. They will complete the fusion process at the same time, which indicates that the three W states are also achieving the purpose of simultaneous fusion. The three initial W states can be written as [18]:

$$\begin{aligned}&|W_n\rangle = \frac{1}{\sqrt{n}}[|({n-1})_L\rangle |R\rangle _1 + \sqrt{n-1}|W_{n-1}\rangle |L\rangle _1], \end{aligned}$$
(4a)
$$\begin{aligned}&|W_m\rangle = \frac{1}{\sqrt{m}}[|({m-2})_L\rangle (|L\rangle _2|R\rangle _3+|R\rangle _2|L\rangle _3) \nonumber \\&\qquad \quad+ \sqrt{m-2}|W_{m-2}\rangle |L\rangle _2|L\rangle _3], \end{aligned}$$
(4b)
$$\begin{aligned}&|W_q\rangle = \frac{1}{\sqrt{q}}[|({q-1})_L\rangle |R\rangle _4 \nonumber \\&\qquad \quad + \sqrt{q-1}|W_{q-1}\rangle |L\rangle _4] \end{aligned}$$
(4c)

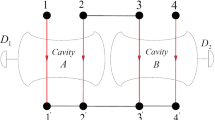
where \(n,m \ge 2\), to explicitly explain this kind of expression of W state, we give the explicit expressions for \(n=2,3\) cases, i.e. a tripartite W state is written as \(|W_3\rangle =\frac{1}{\sqrt{3}}(|LLR\rangle +|LRL\rangle +|RLL\rangle )=\frac{1}{\sqrt{3}}(|2_L\rangle |R\rangle _1+\sqrt{2}|W_2\rangle |L\rangle _1)\) with \(W_2\) being \(|W_2\rangle =\frac{1}{\sqrt{2}}(|LR\rangle +|RL\rangle )\). The detailed fusion process for generating a \(|W\rangle _{n+m+q}\) state by fusing states \(|W\rangle _n\), \(|W\rangle _m\) and \(|W\rangle _q\) is depicted in Fig. 2. The two atoms labeled as 1, 2, from states \(|W_n\rangle\), \(|W_m\rangle\) will be sent into the cavity A, and the two atoms 3, 4 from states \(|W_m\rangle\), \(|W_q\rangle\) will be send into the cavity B, simultaneously. The remaining atoms are kept intact at their sites. The state of the total system can be described as:

$$\begin{aligned}&|W_n\rangle \otimes |W_m\rangle \otimes |W_q\rangle \otimes |R\rangle _A\otimes |R\rangle _B\nonumber \\&\quad =\frac{\sqrt{n-1}\sqrt{m-2}\sqrt{q-1}}{\sqrt{nmq}}|W_{n-1} \rangle _g\nonumber \\&\quad |W_{m-2}\rangle |W_{q-1}\rangle |L_1,L_2;R_A\rangle |L_3,L_4;R_B\rangle \nonumber \\&\quad +\frac{1}{\sqrt{nmq}}|(n-1)\rangle _L|(m-2)\rangle _L|(q-1) \rangle _L(|R_1,L_2;R_A\rangle \nonumber \\&\quad |R_3,R_4;R_B\rangle +|R_1,R_2;R_A\rangle |L_3R_4R_B\rangle )\nonumber \\&\quad +\frac{\sqrt{q-1}}{\sqrt{nmq}}|(n-1)\rangle _L|(m-2)\rangle _L|W_{q-1} \rangle (|R_1,L_2;R_A\rangle \nonumber \\&\quad |R_3,L_4;R_B\rangle +|R_1,R_2;R_A\rangle |L_3L_4R_B\rangle )\nonumber \\&\quad +\frac{\sqrt{n-1}}{\sqrt{nmq}}|W_{n-1}\rangle |(m-2)\rangle _L|(q-1)\rangle _L(|L_1,L_2;R_A \rangle \nonumber \\&\quad |R_3,R_4;R_B\rangle +|L_1,R_2;R_A\rangle |L_3R_4R_B\rangle )\nonumber \\&\quad +\frac{\sqrt{n-1}\sqrt{q-1}}{\sqrt{nmq}}|W_{n-1}\rangle |(m-2)\rangle _L\nonumber \\&\quad |W_{q-1} \rangle (|L_1,L_2;R_A\rangle |R_3,L_4;R_B\rangle \nonumber \\&\quad +|L_1,R_2;R_A\rangle |L_3L_4R_B\rangle )\nonumber \\&\quad +\frac{\sqrt{m-2}}{\sqrt{nmq}}|(n-1)\rangle _L|W_{m-2}\rangle |(q-1) \rangle _L\nonumber \\&\quad |R_1,L_2;R_A\rangle |L_3,R_4;R_B\rangle \nonumber \\&\quad +\frac{\sqrt{m-2}\sqrt{q-1}}{\sqrt{nmq}}|(n-1)\rangle _L|W_{m-2} \rangle \nonumber \\&\quad |W_{q-1}\rangle |R_1,L_2;R_A\rangle |L_3,L_4;R_B\rangle \nonumber \\&\quad +\frac{\sqrt{n-1}\sqrt{m-2}}{\sqrt{nmq}}|W_{n-1} \rangle | W_{m-2}\rangle |(q-1)\rangle _L\nonumber \\&\quad |L_1,L_2;R_A\rangle |L_3,R_4;R_B\rangle \end{aligned}$$
(5)

After the resonant interaction between the atoms and the cavity modes in Eq. (2), a \((n+m+q)\)-qubit W-class state can be described as follows when the results \(L_A\), \(L_B\) are detected in \(D_1\) and \(D_2\):

$$\begin{aligned}&|\widetilde{W}_{n+m+q}\rangle = \frac{1}{\sqrt{nmq}}k_1k_5|(n-1)\rangle _L|(m-2)\rangle _L\nonumber \\&\quad |(q-1)\rangle _L|L_1,L_2,L_3,R_4\rangle \nonumber \\&\quad +\frac{1}{\sqrt{nmq}}k_1k_5|(n-1)\rangle _L|(m-2)\rangle _L|(q-1)\rangle _L|L_1,L_2,R_3,L_4\rangle \nonumber \\&\quad +\frac{1}{\sqrt{nmq}}k_5k_1|(n-1)\rangle _L|(m-2)\rangle _L|(q-1)\rangle _L|L_1,R_2,L_3,L_4\rangle \nonumber \\&\quad +\frac{1}{\sqrt{nmq}}k_5k_1|(n-1)\rangle _L|(m-2)\rangle _L|(q-1)\rangle _L|R_1,L_2,L_3,L_4\rangle \nonumber \\&\quad +\frac{\sqrt{m-2}}{\sqrt{nmq}}k_1^2|(n-1)\rangle _L|W_{m-2}\rangle _L|(q-1)\rangle _L|L_1,L_2,L_3,L_4\rangle \nonumber \\&\quad +\frac{\sqrt{q-1}}{\sqrt{nmq}}k_1^2|(n-1)\rangle _L|(m-2)\rangle _L|W_{q-1}\rangle _L|L_1,L_2,L_3,L_4\rangle \nonumber \\&\quad +\frac{\sqrt{n-1}}{\sqrt{nmq}}k_1^2|W_{n-1}\rangle _L|(m-2)\rangle _L|(q-1)\rangle _L|L_1,L_2,L_3,L_4\rangle \end{aligned}$$
(6)

when \(\alpha = \beta\) (namely \(g_L = g_R\)), the state in Eq. (6) will become a maximally entangled state \(|W_{n+m+q}\rangle\):

$$\begin{aligned} |\psi \rangle = \frac{4}{9}sin^4\frac{\alpha t}{2} \frac{\sqrt{n+m+q}}{\sqrt{nmq}}|W_{n+m+q}\rangle \end{aligned}$$
(7)

By controlling the interaction times of the atom-cavity modes are satisfied \(t =(2r + 1)\pi /\alpha , (r = 0, 1, 2, . . .)\), the maximum success probability for the fusion process is:

$$\begin{aligned} Ps(W_n,W_m,W_q) = \frac{16(n+m+q)}{81nmq} \end{aligned}$$
(8)
Fig. 2
figure 2

QLF fusion scheme for fusing three W states: atom 1 from \(|W_n\rangle\), atom 2 from \(|W_m\rangle\) cross the cavity A, atom 3 from \(|W_m\rangle\), atom 4 from \(|W_q\rangle\) cross the cavity B, simultaneously. \(D_1\), \(D_2\) are the detection mechanism for the cavity mode. The output atoms are labeled as \(1^{\prime }\), \(2^{\prime }\), \(3^{\prime }\), \(4^{\prime }\)

Full size image

3 Multiple small-size W states fusion

In this section, the scheme will be generalized to the case of the QLF fusion for fusing n different or same particles W states. In Ref. [39], although the fusion of multiple W states is not covered in the manuscript, multiple small-size W states can be fused with more cavity modes. However, the essence of the scheme is still the fusion of two W states, i.e.: the target W state, which is prepared from the two small-size W states in the previous cavity mode, will be fused with a new small-size W state in the next cavity mode. It is not completely achieve the fusion of multiple W states, simultaneously. In our scheme, we realize the QLF fusion of fusing n small-size W states at the same time by accessing two atoms from each W state from the second to the \((n-1)\) W state. The QLF fusion scheme for fusing n small-size W state is depicted in Fig. 3. The n initial W states can be written as follows:

$$\begin{aligned} |W_{k_1}\rangle= & {} \frac{1}{\sqrt{k_1}}[|({k_1-1})_L\rangle |R\rangle _1 + \sqrt{k_1-1}|W_{k_1-1}\rangle |L\rangle _1],\nonumber \\ |W_{k_2}\rangle= & {} \frac{1}{\sqrt{k_2}}[|({k_2-2})_L\rangle (|L\rangle _2|R\rangle _3+|R\rangle _2|L\rangle _3)\nonumber \\&\quad + \sqrt{k_2-2}|W_{k_2-2}\rangle |L\rangle _2|L\rangle _3],\nonumber \\ |W_{k_3}\rangle= & {} \frac{1}{\sqrt{k_3}}[|({k_3-2})_L\rangle (|L\rangle _4|R\rangle _5+|R\rangle _4|L\rangle _5)\nonumber \\&\quad + \sqrt{k_3-2}|W_{k_3-2}\rangle |L\rangle _4|L\rangle _5],\nonumber \\&.&\nonumber \\&.&\nonumber \\ |W_{k_n}\rangle= & {} \frac{1}{\sqrt{k_n}}[|({k_n-1})_L\rangle |R\rangle _{2n-2}\nonumber \\&\quad + \sqrt{k_n-1}|W_{k_n-1}\rangle |L\rangle _{2n-2}]] \end{aligned}$$
(9a)

The n W states fusion need \(n-1\) cavity modes, then a consecutive round of \(n-1\) fusion schemes in parallel can realize the QLF fusion of fusing this n W states to a maximally entangled state \(|W_{k_1+k_2+k_3+\cdots +k_n}\rangle\) if the \(|L\rangle\) has been detected in all detectors after those atoms flying out of the cavity-based fusion system. Here, the equation \(\alpha = \beta\) (namely \(g_L = g_R\)) also can be satisfied. When the atom-cavity mode interaction times are all equal to \(t =(2r + 1)\pi /\alpha , (r = 0, 1, 2, . . .)\), the maximum success probability for the fusion process is:

$$\begin{aligned}&Ps(W_{k_1},W_{k_2},W_{k_3},..W_{k_n}) \nonumber \\&\quad = (\frac{4}{9})^{n-1}\frac{k_1+k_2+k_3+..+k_n}{k_1k_2k_3..k_n} \end{aligned}$$
(10)
Fig. 3
figure 3

QLF fusion scheme for fusing multiple W states: one or two atoms from each \(|W_{k_n}\rangle\) state will be permitted to enter the (\(n-1\)) cavity modes. The entanglement of input atoms will be formed after the atom–cavity–field resonant interactions. The target W state can be generated if the results \(|L\rangle\) has been detected in each detection mechanism

Full size image

Compared to the most of current schemes, our scheme dose not only realize the QLF fusion of fusing n different or same particles initial W states simultaneously, but also prepare the target W states without any controlled quantum gates and ancillary atom. Therefore, our scheme have a great advantage in generating the target W state with any number of particles. Especially the larger the particle number of target W state is, the greater the advantage of our QLF scheme is. In addition, by detecting the photonic state rather than the atomic states in the cavity mode, the loss of particles in the initial W states have been effectively reduced. Because of no particle loss, the main advantage of this scheme is that it greatly reduces the number of fusion steps to achieve a W state of a target size.

In addition, a brief discussion should be given on the experimental feasibility of this scheme. The radiative time of the Rydberg atoms with principal quantum numbers 49, 50 and 51 is \(T_{r}=3\times 10^{-2}s\), and the atom–cavity coupling strength is \(g=2\pi \times 24\)KHz [43,44,45]. In this scheme, in order to obtain the target W state, the interaction time should satisfy the relation \(t =(2r + 1)\pi /\alpha =\pi /\sqrt{3}g\) (\(r=0\)), i. e. the required atom–cavity interaction time is about \(t=10^{-5} s\). However, In Ref. [45], the efficient decay time of the cavity is about \(10^{-2}s\). In this case, the time required for accomplishing the whole process of QLF fusion scheme is much shorter than the time of cavity decay and atomic radiative. Therefore, this schemes can be realized in the current cavity QED technology.

4 Analysis and discussion

In this section, we will study the resource costs of the proposed schemes and compare them with those of the previously proposed schemes. In view of the fact that our scheme starts with the fusion of three initial W states, we only compare the schemes that fuses three W states. The resource cost of preparing a \(|W_{n+m+q}\rangle\) state by fusing \(|W_n\rangle\), \(|W_m\rangle\) and \(|W_q\rangle\) is defined as follows [18]:

$$\begin{aligned} R[W_{n+m+q}]=\frac{R[W_n]+R[W_m]+R[W_q]}{P_s(W_n,W_m,W_q)} \end{aligned}$$
(11)

where \(P_s(W_n,W_m,W_q)\) is the success probability of fusing three small-size W states. Since the three target W states can be obtained by our QLF fusion scheme, the success probability of fusing three W states is

$$\begin{aligned} Ps(W_n,W_m,W_q) = \frac{16(n+m+q)}{81nmq} \end{aligned}$$
(12)

Although our QLF fusion scheme can work for \(|W_2\rangle\) states, most of the previously schemes can only start with \(|W_3\rangle\) states, therefore, for the purpose of comparison, we are going to define the basic resource for preparing \(|W_3\rangle\) state as unit cost, i.e. \(R[W_3]=1\). According to the discussion in Ref. [18], the closer the sizes of the two resource states are, the lower the cost is. Based on this principle, we numerically evaluate the optimal cost of our fusion schemes for W states and previous ones in Fig. 4. From Fig. 4, we can clearly see that the resource cost increases with the increase of the particle number N \((N=n+m+q)\) of the final target W state, and the success probability decreases accordingly. Although the resource cost of this scheme is higher than that of the two schemes in Ref. [25, 38], there is no requirement for any controlled quantum gates and ancillary atoms here, means our QLF schemes are more feasible. In addition, because only one qubit from each component W state will enter the fusion setup and the W state only occupies a special subspace of the full Hilbert space of the multi-qubit system rather than the full Hilbert space itself, the fusion process of W states has to be probabilistic and there is no deterministic fusion scheme of W states. Therefore, the success probability of all currently existing fusion schemes small as compared to unity.

Fig. 4
figure 4

The resource cost comparison: our fusion scheme for fusing three W states (red square), the fusion scheme in Ref. [38] (green triangle), and the fusion scheme in Ref. [25](black circle). The vertical axis is the resource cost and horizontal axis is the size of final target W state

Full size image

5 Conclusion

In conclusion, motivated by the fusion method for fusing three W states presented in Ref. [39], we have proposed this scheme of a few improvements that access two atoms from the initial W state. Based on the atom–cavity–field resonant interactions, a \(|W_n+m+q\rangle\) state can be prepared by fusing state \(W_m\), \(W_n\) and \(W_q\). This qubit-loss-free fusion scheme can be realized for fusing n different or same particles W states, simultaneously if adding \((n-1)\) cavity fields. The extension of this scheme to realize the fusion of multiple entangled W states without particle loss, which makes it possible to prepare maximally entangled W states with a larger number of particles. In the fusion scheme, it is a very important issue that the state fusion in a repeated fusion operation is the availability of quantum memories to store the throughput W states obtained at each fusion step. By detecting the cavity mode state rather than the atomic states in this scheme, there is no atom loss, which greatly reduces the number of fusion steps as well as the requirement of quantum memories required to achieve a W state of a target size. Another distinct advantage of our schemes is the combination of the easier storage of solid qubits and the easier detection of flying qubits, which makes our schemes easier to implement in practice than most of the currently existing fusion schemes in cavity QED. Moreover, there are no controlled quantum gates operations and no ancillary qubits required, which confirms that the present preparation scheme is simpler and easier to be implemented.